Abstract
What is the value of just a few bits to a guesser? We study this problem in a setup where Alice wishes to guess an independent and identically distributed (i.i.d.) random vector and can procure a fixed number of k information bits from Bob, who has observed this vector through a memoryless channel. We are interested in the guessing ratio, which we define as the ratio of Alice’s guessing-moments with and without observing Bob’s bits. For the case of a uniform binary vector observed through a binary symmetric channel, we provide two upper bounds on the guessing ratio by analyzing the performance of the dictator (for general ) and majority functions (for ). We further provide a lower bound via maximum entropy (for general ) and a lower bound based on Fourier-analytic/hypercontractivity arguments (for ). We then extend our maximum entropy argument to give a lower bound on the guessing ratio for a general channel with a binary uniform input that is expressed using the strong data-processing inequality constant of the reverse channel. We compute this bound for the binary erasure channel and conjecture that greedy dictator functions achieve the optimal guessing ratio.
1. Introduction
In the classical guessing problem, Alice wishes to learn the value of a discrete random variable (r.v.) X as quickly as possible by sequentially asking yes/no questions of the form “Is ?”, until she makes a correct guess. A guessing strategy corresponds to an ordering of the alphabet of X according to which the guesses are made and induces a random guessing time. It is well known and simple to verify that the guessing strategy which simultaneously minimizes all the positive moments of the guessing time is to order the alphabet according to a decreasing order of probability. Formally, for any , the minimal sth-order guessing-time moment of X is
where returns the index of the symbol x relative to the order induced by sorting the probabilities in a descending order, with ties broken arbitrarily. For brevity, we refer to as the guessing-moment of X.
Several motivating problems for studying guesswork are fairness in betting games, computational complexity of sequential decoding [1], computational complexity of lossy source coding and database search algorithms (see the introduction of Reference [2] for a discussion), secrecy systems [3,4,5], and crypt-analysis (password cracking) [6,7]. The guessing problem was first introduced and studied in an information-theoretic framework by Massey [8], who drew a relation between the average guessing time of an r.v. to its entropy. It was later explored more systematically by Arikan [1], who also introduced the problem of guessing with side information. In this problem, Alice is in possession of another r.v. Y that is jointly distributed with X, and then, the optimal conditional guessing strategy is to guess by decreasing order of conditional probabilities. Hence, the associated minimal conditional sth-order guessing-time moment of X given Y is
where returns the index of x relative to the order induced by sorting the conditional probabilities of X given that in a descending order. Arikan showed that, as intuition suggests, side information reduces the guessing-moments ([1], Corollary 1)
Furthermore, he showed that, if is an i.i.d. sequence, then ([1], Proposition 5)
where is the Arimoto-Rényi conditional entropy of order . As was noted by Arikan a few years later [9], the guessing moments are related to the large deviations behavior of the random variable . However, in Reference [9], he was only able to obtain right-tail large deviation bounds since asymptotically tight bounds on were only known for positive moments (). Large deviation principle for the normalized logarithm of the guessing time was later established in Reference [10] using substantial results from References [11,12]. Throughout the years, information-theoretic analysis of the guessing problem was extended in multiple directions, such as guessing until the distortion between the guess and the true value is below a certain threshold [2], guessing under source uncertainty [13], and improved bounds at finite blocklength [14,15,16], to name a few.
In the conditional setting described above, one may think of as side information observed by a “helper”, say Bob, who sends his observations to Alice. Nonetheless, as other problems employing a helper (e.g., source coding [17,18]), it is more realistic to impose communication constraints and to assume that Bob can only send a compressed description of to Alice. This setting was recently addressed by Graczyk and Lapidoth [19,20], who considered the case where Bob encodes at a positive rate using bits before sending this description to Alice. They then characterized the best possible guessing-moments attained by Alice for general distributions as a function of the rate R. In this paper, we take this setting to its extreme and attempt to quantify the value of k bits in terms of reducing the guessing-moments by allowing Bob to use only a k-bit description of . The major difference from previous work is that, here, k is finite and does not increase with n, and for some of our results, we further concentrate on the extreme case of —a single bit of help. To that end, we define (Section 2) the guessing ratio, which is the (asymptotically) best possible ratio of the guessing-moments of obtained with and without observing a function , i.e., the minimal possible ratio as a function of , in the limit of large n.
Sharply characterizing the guessing ratio appears to be a difficult problem in general. Here, we mostly focus on the special case where is uniformly distributed over the Boolean cube and is obtained by passing through a memoryless binary symmetric channel (BSC) with crossover probability (Section 3). We derive two upper bounds and two lower bounds on the guessing ratio in this case. The upper bounds are derived by analyzing the ratio attained by two specific functions, k-Dictator, to wit , and Majority, to wit , where is the indicator function, and for simplicity, we henceforth assume that n is odd when discussing majority functions. For , we demonstrate that neither of these functions is better than the other for all values of the moment order s. The first lower bound is based on relating the guessing-moment to entropy using maximum-entropy arguments (generalizing a result of Reference [8]), and the second one on Fourier-analytic techniques combined with a hypercontractivity argument [21]. Furthermore, for the restricted class of functions for which the constituent k-bit functions operate on disjoint sets of bits, a general method is proposed for transforming a lower bound valid for to a lower bound valid for any . Nonetheless, we remark that our bounds are valid for and obtaining similar bounds for in order to obtain large deviation principle for the normalized logarithm of the guessing time remains an open problem. In Section 4, we briefly discuss the more general case where is still uniform over the Boolean cube, but is obtained from via a general binary-input, arbitrary-output channel. We generalize our entropy lower bound to this case using the strong data-processing inequality (SDPI) applied to the reverse channel (from Y to X). We then discuss the case of the binary erasure channel (BEC), for which we also provide an upper bound by analyzing the greedy dictator function, namely where Bob sends the first bit that has not been erased. We conjecture that this function minimizes the guessing-moments simultaneously at all erasure parameters and all moments s.
Related Work. As mentioned above, Graczyk and Lapidoth [19,20] considered the same guessing question if Bob can communicate with Alice at some positive rate R, i.e., can use bits to describe . This setup facilitates the use of large-deviation-based information-theoretic techniques, which allowed the authors to characterize the optimal reduction in the guessing-moments as a function of R to the first order in the exponent. This type of argument cannot be applied in our setup of finite number of bits. Furthermore, as we shall see, in our setup, the exponential order of the guessing moment with help is equal to the one without it and the performance is therefore more finely characterized by bounding the ratio of the guessing-moments. For a single bit of help , characterizing the guessing ratio in the case of the BSC with a uniform input can also be thought of as a guessing variant of the most informative Boolean function problem introduced by Kumar and Courtade [22]. There, the maximal reduction in the entropy of obtainable by observing a Boolean function is sought after. It was conjectured in Reference [22] that a dictator function, e.g., , is optimal simultaneously at all noise levels; see References [23,24,25,26] for some recent progress. As in the guessing case, allowing Bob to describe using bits renders the problem amenable to an exact information-theoretic characterization [27]. In another related work [28], we have asked about the Boolean function that maximizes the reduction in the sequential mean-squared prediction error of and showed that the majority function is optimal in the noiseless case. There is, however, no single function that is simultaneously optimal at all noise levels. Finally, in a recent line of works [29,30], the average guessing time using the help of a noisy version of has been considered. The model in this paper is different since the noise is applied to the inputs of the function rather than to its output.
2. Problem Statement
Let be an i.i.d. vector from a distribution , which is transmitted over a memoryless channel of conditional distribution . A helper observes at the output of the channel and can send k bits to a guesser of . Our goal is to characterize the best possible multiplicative reduction in guessing-moments offered by a function f, in the limit of large n. Precisely, we wish to characterize the guessing ratio, defined as
for an arbitrary . In this paper, we are mostly interested in the case where , i.e., is uniformly distributed over , and where the channel is a BSC with crossover probability . With a slight abuse of notation, we denote the guessing ratio in this case by . Furthermore, some of the results will be restricted to the case of a single bit of help (), and in this case, we will further abbreviate the notation from to . We note the following basic facts.
Proposition 1.
The following properties hold:
- 1.
- The minimum in Equation (5) is achieved by a sequence of deterministic functions.
- 2.
- is a non-decreasing function of which satisfies and . In addition, is attained by any sequence of functions such that is a uniform Bernoulli vector, i.e., for all .
- 3.
- For a BSC , the limit-supremum in Equation (5) defining is a regular limit.
- 4.
- If and is a uniformly distributed vector, then the optimal guessing order given that is reversed to the optimal guessing order when .
Proof.
See Appendix A. □
3. Guessing Ratio for a Binary Symmetric Channel
3.1. Main Results
We begin by presenting the bound on the guessing ratio obtained by k-dictator functions and then proceed to the bound obtained by majority functions for a single bit of help, . The proofs are given in the next two subsections.
Theorem 1.
Let for . The guessing ratio is upper bounded as
and this upper bound is achieved by k-dictator functions, .
Specifically, for , Theorem 1 implies
Theorem 2.
Let and , and denote by the tail distribution function of the standard normal distribution. Then, the guessing ratio is upper bounded as
and this upper bound is achieved by majority functions, .
We remark that, if , the guessing ratio of functions similar to the dictator and majority functions, such as single-bit dictator on inputs ( if and only if ) or unbalanced majority ( for some t), may also be analyzed in a similar way. However, numerical computations indicate that they do not improve the bounds of Theorems 1 and 2, and thus, their analysis is omitted.
We next present two lower bounds on the guessing ratio . The first is based on maximum-entropy arguments, and the second is based on Fourier-analytic arguments.
Theorem 3.
The guessing ratio satisfies the following lower bound:
where is Euler’s Gamma function (defined for ).
Remark 1.
When restricted to , the proof of Theorem 3 utilizes the bound (see Equation (63)). For balanced functions, this bound was improved in Reference [23] for . Using this improved bound here leads to an immediate improvement in the bound of Theorem 3. Furthermore, it is known [24] that there exists such that the most informative Boolean function conjecture holds for all . For such crossover probabilities,
holds, and then, Theorem 3 may be improved to
Our Fourier-based bound for is as follows:
Theorem 4.
Let . The guessing ratio is lower bounded as
This bound can be weakened by the possibly suboptimal choice , which leads to a simpler yet explicit bound:
Corollary 1.
The bound in Theorem 4 is only valid for the case . An interesting problem is to find a general way of “transforming” a lower bound which assumes to a bound useful for . In principle, such a result could stem from the observation that a k bit function provides k different conditional optimal guessing orders for each of its output bits. For a general function, however, distilling a useful bound from this observation seems challenging since the relation between the optimal guessing order induced by each of the bits and the optimal guessing order induced by all k bits might be involved. Nonetheless, such a result is possible to obtain if each of the k single-bit functions operate on a different set of input bits. For this restricted set of functions, there is a simple bound which relates the optimal ordering given each of the bits and all the k bits together. It is reasonable to conjecture that this restricted sub-class is optimal or at least close to optimal, since it seems that more information is transferred to the guesser when the k functions operate on different sets of bits, which make the k functions statistically independent.
Specifically, let us specify a k-bit function by its k constituent one-bit functions , . Let be the set of sequences of functions , , such that each specific sequence of functions satisfies the following property: There exists a sequence of partitions of , such that, for all and , only depends on and for all . In particular, this implies that is mutually independent for all . For example, when , , and , we can choose to be the odd/even indices. For and , the sets are the first and second halves of . As in Equation (5), we may define the guessing ratio of this constrained set of functions as
where, in general, .
Proposition 2.
We demonstrate our results for in Figure 1 (resp. Figure 2) which display the bounds on for fixed values of s (resp. ). The numerical results show that, for the upper bounds, when , dictator dominates majority (for all values of ), whereas for , majority dominates dictator. For , there exists such that majority is better for and dictator is better for . Figure 2 demonstrates the switch from dictator to majority as s increases (depending on ). As for lower bounds, we first remark that the conjectured maximum-entropy bound (Equation (11)) is also plotted (see Remark 1). The numerical results show that the maximum-entropy bound is better for low values of whereas the Fourier-analysis bound is better for high values of . As a function of s, the maximum-entropy bound (resp. Fourier-analysis bound) is better for high (resp. low) values of s. We also mention that, in these figures, the maximizing parameter in the Fourier-based bound (Theorem 4) is and the resulting bound is as in Equation (13). However, for values of s as low as 10, the maximizing may be far from 1, and in fact, it continuously and monotonically increases from 0 to 1 as increases from 0 to . Finally, Figure 3 demonstrates the behavior of the k-dictator and maximum-entropy bounds on as a function of k.
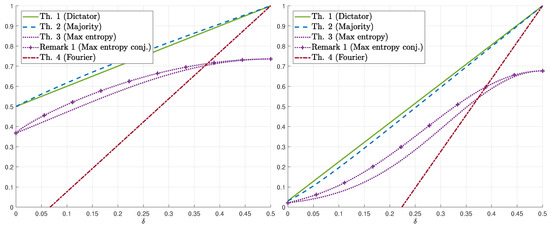
Figure 1.
Bounds on for (left) and (right) as a function of .
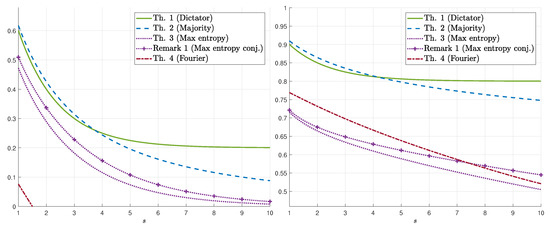
Figure 2.
Bounds on for (left) and (right) as a function of .
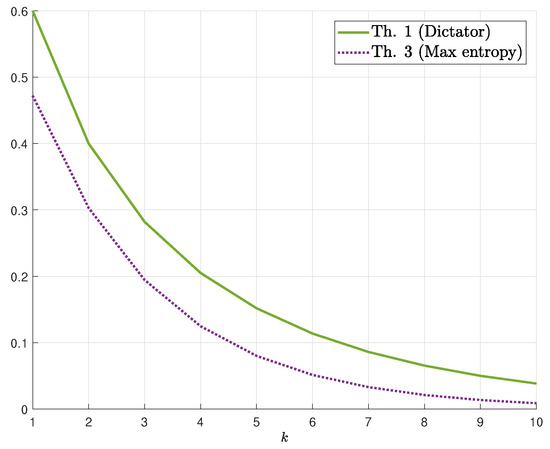
Figure 3.
Bounds on for and as a function of k.
3.2. Proofs of the Upper Bounds on
Let , be given. The following sum will be useful for the proofs in the rest of the paper:
where we will abbreviate . For a pair of sequences , {, we will let mean that .
Lemma 1.
Let and be non-decreasing integer sequences such that for all n and . Then,
Specifically, .
Proof.
See Appendix A. □
We next prove Theorem 1.
Proof of Theorem 1.
Consider a k-dictator function which directly outputs k of the bits of , say, without loss of generality (w.l.o.g.) . Let be the Hamming distance of and , and recall the assumption . It is easily verified that the optimal guessing order of given has parts, such that the wth part, , is comprised of an arbitrary ordering of the vectors for which . From symmetry, for any . Then, from Lemma 1
where in the first equality, , and the last equality is obtained by telescoping the sum. The result then follows from Equation (5) and Lemma 1. □
We next prove Theorem 2.
Proof of Theorem 2.
Recall that we assume for simplicity that n is odd. The analysis for an even n is not fundamentally different. To evaluate the guessing-moment, we first need to find the optimal guessing strategy. To this end, we let be the Hamming weight of and note that the posterior probability is given by
where Equation (25) follows from symmetry. Evidently, is an increasing function of . Indeed, let be a binomial r.v. of n trials and success probability . Then, for any , as ,
where, in each of the above probabilities, the summation is over an independent binomial r.v. Hence, we deduce that, whenever (resp. ), the optimal guessing strategy is by decreasing (resp. increasing) Hamming weight (with arbitrary order for inputs of equal Hamming weight).
We can now turn to evaluate the guessing-moment for the optimal strategy given the majority of . Let for . From symmetry,
where . Thus,
where and is independent. For evaluating the asymptotic behavior (for large n) of this expression, we note that the Berry–Esseen central-limit theorem ([31], Chapter XVI.5, Theorem 2) leads to (see, e.g., Reference [28], proof of Lemma 15)
for some universal constant . Using the Berry–Esseen central-limit theorem again, we have that , where and denote convergence in distribution. Thus for a given w,
where the last equality follows from the fact that for all . Using the Berry–Esseen theorem once again, we have that . Hence, Portmanteau’s lemma (e.g., Reference [31], Chapter VIII.1, Theorem 1) and the fact the is continuous and bounded result in the following:
Similarly to Equation (34), the upper bound
holds, and a similar analysis leads to an expression which asymptotically coincides with the right-hand side (r.h.s.) of Equation (41). The result then follows from Equation (5) and Lemma 1. □
3.3. Proofs of the Lower Bounds on
To prove Theorem 3, we first prove the following maximum entropy result. With a standard abuse of notation, we will write the guessing-moment and the entropy of a random variable as functions of its distribution.
Lemma 2.
The maximal entropy under guessing-moment constraint satisfies
where vanishes as .
Proof.
To solve the maximum entropy problem ([32], Chapter 12) in Equation (43) (note that the support of P is only restricted to be countable), we first relax the constraint to
i.e., we omit the requirement that is a decreasing sequence. Assuming momentarily that the entropy is measured in nats, it is easily verified (e.g., using the theory of exponential families ([33], Chapter 3) or by Lagrange duality ([34], Chapter 5)) that the entropy maximizing distribution is
for , where is the partition function and is chosen such that . Evidently, is in decreasing order (and so is ) and is therefore the solution to Equation (43). The resulting maximum entropy is then given in a parametric form as
Evidently, if , then . In this case, we may approximate the limit of the partition function as by a Riemann integral. Specifically, by the monotonicity of in ,
where the last equality follows from the definition of the Gamma function (see Theorem 3) or from the identification of the integral as an unnormalized generalized Gaussian distribution of zero mean, scale parameter , and shape parameter s [35]. Further, by the convexity of in , Jensen’s inequality implies that
for every (the r.h.s. can be considered as averaging over a uniform random variable ) and so, similarly to Equation (50),
Therefore,
where as . In the same spirit,
where in Equation (56), as ; in Equation (57), the identity for was used; and in Equation (58), as .
Returning to measure entropy in bits, we thus obtain that, for any distribution P,
or, equivalently,
where and is a vanishing term as . In the same spirit, Equation (60) holds whenever . □
Remark 2.
In Reference [8], the maximum-entropy problem was studied for . In this case, the maximum-entropy distribution is readily identified as the geometric distribution. The proof above generalizes that result to any .
Proof of Theorem 3.
Assume that f is taken from a sequence of functions which achieves the minimum in Equation (5). Using Lemma 2 when conditioning on for each of possible , we get (see a rigorous justification to Equation (61) in Appendix A)
where in Equation (61), and Equation (62) follows from Jensen’s inequality. For the bound in Equation (63) is directly related to the Boolean function conjecture [22] and may be proved in several ways, e.g., using Mrs. Gerber’s Lemma ([36], Theorem 1); see ([23], Section IV), References [27,37]. For general , the bound was established in Reference ([27], Corollary 1). □
Before presenting the proof of the Fourier-based bound, we briefly remind the reader of the basic definitions and results of Fourier analysis of Boolean functions [21], and to that end, it is convenient to replace the binary alphabet by . An inner product between two real-valued functions on the Boolean cube is defined as
where is a uniform Bernoulli vector. A character associated with a set of coordinates is the Boolean function , where by convention, . It can be shown ([21], Chapter 1) that the set of all characters forms an orthonormal basis with respect to the inner product (Equation (64)). Furthermore,
where are the Fourier coefficients of f, given by . Plancherel’s identity then states that . The p norm of a function f is defined as .
The noise operator operating on a Boolean function f is defined as
where is the correlation parameter. The noise operator has a smoothing effect on the function which is captured by the so-called hypercontractivity theorems. Specifically, we shall use the following version.
Theorem 5
([21], p. 248). Let and . Then, .
With the above, we can prove Theorem 4.
Proof of Theorem 4.
From Bayes law (recall that )
and from the law of total expectation
Let us denote and and abbreviate . Then, the first addend on the r.h.s. of Equation (68) is given by
where, in the last equality, (Lemma 1). Let , and denote and . Then, the inner-product term in Equation (72) is upper bounded as
where Equation (73) holds since is a self-adjoint operator and Equation (74) follows from the Cauchy–Schwarz inequality. To justify Equation (75), we note that
where Equation (80) follows from Plancherel’s identity, Equation (81) is since for all and , and Equation (82) follows from . Equation (76) follows from Theorem 5, and in Equation (78), . The second addend on the r.h.s. of Equation (68) can be bounded in the same manner. Hence,
as . □
We close this section with the following proof of Proposition 2:
Proof of Proposition 2.
Let be a vector of indices in such that , and let be the components of in those indices. Further, let . Then, it holds that
as well as
Hence,
and the stated bound is deduced after taking limits and normalizing by . □
4. Guessing Ratio for a General Binary Input Channel
In this section, we consider the guessing ratio for general channels with a uniform binary input. The lower bound of Theorem 3 can be easily generalized to this case. To that end, consider the SDPI constant [38,39] of the reverse channel , given by
where is the X-marginal of . As was shown in Reference ([40], Theorem 2), the SDPI constant of is also given by
Theorem 6.
We have
Proof.
See Appendix A. □
Remark 3.
The bound for the BSC case (Theorem 3) is indeed a special case of Theorem 6 as the reverse BSC channel is also a BSC with uniform input and the same crossover probability. For BSCs, it is well known that the SDPI constant is ([38], Theorem 9).
Next, we consider in more detail the case where the observation channel is a BEC. We restrict the discussion to the case of a single bit of help, .
4.1. Binary Erasure Channel
Suppose that is obtained from by erasing each bit independently with probability . As before, Bob observes the channel output and can send one bit to Alice, who wishes to guess . With a slight abuse of notation, the guessing ratio in Equation (5) will be denoted by .
To compute the lower bound of Theorem 6, we need to find the SDPI constant associated with the reverse channel, which is easily verified to be
with an input distribution . Letting for yields for . The computation of is now a simple three-dimensional constrained optimization problem. We plotted the resulting lower bound for in Figure 4.
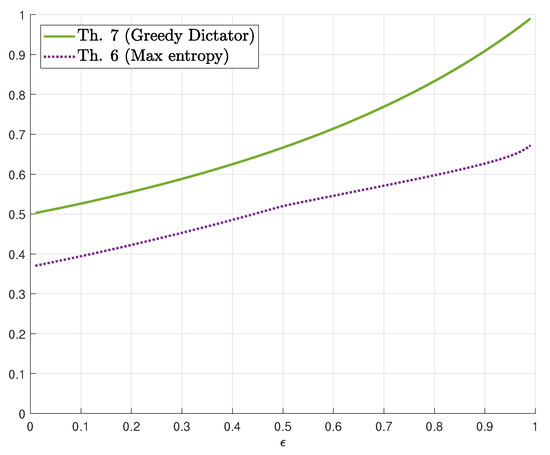
Figure 4.
Bounds on for as a function of .
Let us now turn to upper bounds and focus for simplicity on the average guessing time, i.e., the guessing-moment for . To begin, let S represent the set of indices of the symbols that were not erased, i.e., if and only if . Any function is then uniquely associated with a set of Boolean functions , where designates the operation of the function when S is the set of non-erased symbols. We also let be the probability that the non-erased symbols have index set S. Then, the joint probability distribution is given by
and, similarly,
In accordance with Proposition 1, the optimal guessing order given that is reversed to the optimal guessing order when . It is also apparent that the posterior probability is determined by a mixture of different Boolean functions . This may be contrasted with the BSC case, in which the posterior is determined by a single Boolean function (though with noisy input).
A seemingly natural choice is a greedy dictator function, for which sends the first non-erased bit. Concretely, letting
the greedy dictator function is defined by
where is a Bernoulli r.v. of success probability . From an analysis of the posterior probability, it is evident that, conditioned on , an optimal guessing order must satisfy that is guessed before whenever
(see Appendix A for a proof of Equation (100)). This rule can be loosely thought of as comparing the “base expansion” of and . Furthermore, when is close to 1, then the optimal guessing order tends toward a minimum Hamming weight rule (or maximum Hamming weight in case ).
The greedy dictator function is “locally optimal” when , in the following sense:
Proposition 3.
If , then an optimal guessing order conditioning on (resp. ) is lexicographic (reverse lexicographic). Also, given lexicographic (resp. reverse lexicographic) order when the received bit is 0 (resp. 1), the optimal function f is a greedy dictator.
Proof.
See Appendix A. □
The guessing ratio of the greedy dictator function can be evaluated for , and the analysis leads to the following upper bound:
Theorem 7.
For , the guessing ratio is upper bounded as
and the r.h.s. is achieved with equality by the greedy dictator function in Equation (99) for .
Proof.
See Appendix A. □
The upper bound of Theorem 7 is plotted in Figure 4. Based on Proposition 3 and numerical computations for moderate values of n, we conjecture:
Conjecture. 1.
Greedy dictator functions attain for the BEC.
Supporting evidence for this conjecture include the local optimality property stated in Proposition 3 (although there are other locally optimal choices) as well as the following heuristic argument: Intuitively, Bob should reveal as much as possible regarding the bits he has seen and as little as possible regarding the erasure pattern. So, it seems reasonable to find a smallest possible set of balanced functions from which to choose all the functions , so that they coincide as much as possible. Greedy dictator is a greedy solution to this problem: it uses the function for half of the erasure patterns, which is the maximum possible. Then, it uses the function for half of the remaining patterns, and so on. Indeed, we were not able to find a better function than G-Dict for small values of n.
However, applying standard techniques in attempt to prove Conjecture 1 has not been fruitful. One possible technique is induction. For example, assume that the optimal functions for dimension are . Then, it might be perceived that there exists a bit, say , such that the optimal functions for dimension n satisfy if is erased; in that case, it remains only to determine when is not erased. However, observing Equation (95), it is apparent that the optimal choice of should satisfy two contradicting goals—on the one hand, to match the order induced by
and, on the other hand, to minimize the average guessing time of
It is easy to see that taking a greedy approach toward satisfying the second goal would result in if and performing the recursion steps would indeed lead to a greedy dictator function. Interestingly, taking a greedy approach toward satisfying the first goal would also lead to a greedy dictator function, but one which operates on a cyclic permutation of the inputs (specifically, Equation (99) applied to ). Nonetheless, it is not clear that choosing with some loss in the average guessing time induced by Equation (103) could not lead to a gain in the second goal (matching the order of Equation (102)), which outweighs that loss.
Another possible technique is majorization. It is known that, if one probability distribution majorizes another, then all the nonnegative guessing-moments of the first are no greater than the corresponding moments of the second ([29], Proposition 1). (The proof in Reference [29] is only for , but it is easily extended to the general case.) Hence, one approach toward identifying the optimal function could be to try and find a function in which induced posterior distributions majorize the corresponding posteriors that induces by any other functions with the same bias (it is of course not clear that such a function even exists). This approach unfortunately fails for the greedy dictator. For example, the posterior distributions induced by setting to be majority functions are not always majorized by those induces by the greedy dictator (although they seem to be “almost” majorized) even though the average guessing time of greedy dictator is lower (this happens, e.g., for and ). In fact, the guessing moments for greedy dictator seem to be better than these of majority irrespective of the value of s.
Author Contributions
Conceptualization, N.W. and O.S.; Investigation, N.W. and O.S.; Methodology, N.W. and O.S.; Writing—original draft, N.W. and O.S.; Writing—review and editing, N.W. and O.S. Both authors contributed equally to the research work and to the writing process of the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by an ERC grant no. 639573. The research of N. Weinberger was partially supported by the MIT-Technion fellowship and the Viterbi scholarship, Technion.
Acknowledgments
We are very grateful to Amos Lapidoth and Robert Graczyk for discussing their recent work on guessing with a helper [19,20] during the second author’s visit to ETH, which provided the impetus for this work. We also thank the anonymous reviewer for helping us clarify the connection between the guessing moments and large deviation principle of the normalized logarithm of the guessing time.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BEC | binary erasure channel |
| BSC | binary symmetric channel |
| i.i.d. | independent and identically distributed |
| r.h.s. | right-hand side |
| r.v. | random variable |
| SDPI | strong data-processing inequality |
| w.l.o.g. | without loss of generality |
Appendix A. Miscellaneous Proofs
Proof of Proposition 1.
The claim that random functions do not improve beyond deterministic ones follows directly from that property that conditioning reduces guessing-moment ([1], Corollary 1). Monotonicity follows from the fact that Bob can always simulate a noisier channel. Now, if , then and are independent and for any f (Lemma 1). For , let
and let be a sequence of functions such that achieves . We show that must satisfy for all . If we denote , then this is equivalent to showing that for all and . Assume towards contradiction that the optimal function does not satisfy this property for, say, . Let us denote and assume w.l.o.g. that for all (for notational simplicity). Further, let . Then,
As equality can be achieved if we modify to satisfy for all , this contradicts the assumed optimality of . The minimal is thus obtained by any function for which is a uniform Bernoulli vector and equals to (Lemma 1).
To prove that the limit in Equation (5) exists, we note that
where
As before, let be a sequence of functions such that achieves . Denote the order induced by the posterior as , and the order induced by as . As before (when breaking ties arbitrarily)
and
Thus,
Hence,
To continue, we further analyze . The summation in the numerator of Equation (A7) may be started from from , and so Equations (A31) and (A33) (proof of Lemma 1 below) imply that
Thus, there exists such that
and consequently,
as . Hence, Equation (A14) implies that
is a non-increasing sequence which is bounded below by 0 and, thus, has a limit. Since as , also has a limit.
We finally show the reverse ordering property for . The guessing order given that is determined by ordering
or equivalently, by ordering . It then follows that the order, given that , is reversed compared to the order given that since
□
Proof of Lemma 1.
The monotonicity of and standard bounds on sums using integrals lead to the bounds
and
The ratio between the upper and lower bound is
which satisfies given the premise of the lemma. □
Proof of Equation (61).
Denote by a function which achieves the minimal guessing ratio in Equation (5). Then, it holds that is a monotonic non-increasing function of n. To see this, suppose that is an optimal function for . This function can be used for guessing on the basis of k bit of help computed from as follows: Given , the helper randomly generates , computes , and send these bits to the guesser. The guesser of then uses the bits to guess , and the resulting conditional guessing moment is , which is less than since conditioning reduces guessing moments. Thus, the optimal function can only achieve lower guessing moments, which implies the desired monotonicity property. For brevity, we henceforth simply write the optimal function as f (with dimension and optimality being implicit).
Define the set
to wit, the set of k-tuples such that the conditional guessing moment grows without bound when conditioned on that k-tuple. By the law of total expectation
So, since grows without bound as a function of n, it must hold that is not empty and that there exists such that , where as . Let be given. The monotonicity property previously established and Equation (60) imply that there exists such that for all both
and
hold for any . Thus, also
and
hold, and the last equation implies that the term on its left-hand side is unbounded. Moreover, Equation (60) and the sentence that follows it both imply that, if is bounded, then is bounded too. Thus, there exists which satisfies as such that
Combining Equation (A40) with the last equation and noting that is arbitrary completes the proof. □
Proof of Theorem 6.
The proof follows the same lines as the proof of Theorem 3 up to Equation (62), yielding
Now, let be such that forms a Markov chain. Then,
where Equation (A46) follows since the SDPI constant tensorizes (see Reference [40] for an argument obtained by relating the SDPI constant to the hypercontractivity parameter or its extended version, Reference ([40], p. 5), for a direct proof). Thus, for all f,
Inserting Equation (A49) into Equation (A43) yields
and substituting this in the definition of the guessing ratio of Equation (5) completes the proof. □
Proof of Equation (100).
Let us evaluate the posterior probability conditioned on . Since G-Dict is balanced, Bayes law implies that
This immediately leads to the guessing rule in Equation (100). From Proposition 1, the guessing rule for is on reverse order. □
Proof of Proposition 3.
We denote the lexicographic order by . Assume that and that . Then, there exists such that (where is the empty string) and . Then,
This proves the first statement of the proposition. Now, let () be the guessing order given that the received bit is 0 (resp. 1), and let be the Boolean functions (which are not necessarily optimal). Then, from Equations (97) and (95)
where for , the projected orders are defined as
It is easy to verify that, if () is the lexicographic (resp. revered lexicographic) order, then the greedy dictator achieves Equation (A61) with equality due to the following simple property: If , then
for all . This can be proved by induction over n. For , the claim is easily asserted. Suppose it holds for , let us verify it for n. If , then whenever
where the inequality follows from the induction assumption and since . If then, similarly,
□
Proof of Theorem 7.
We denote the lexicographic order by . Then,
where and for
So,
Hence,
Noting that , we get
□
References
- Arikan, E. An inequality on guessing and its application to sequential decoding. IEEE Trans. Inf. Theory 1996, 42, 99–105. [Google Scholar] [CrossRef]
- Arikan, E.; Merhav, N. Guessing subject to distortion. IEEE Trans. Inf. Theory 1998, 44, 1041–1056. [Google Scholar] [CrossRef]
- Merhav, N.; Arikan, E. The Shannon cipher system with a guessing wiretapper. IEEE Trans. Inf. Theory 1999, 45, 1860–1866. [Google Scholar] [CrossRef]
- Hayashi, Y.; Yamamoto, H. Coding theorems for the Shannon cipher system with a guessing wiretapper and correlated source outputs. IEEE Trans. Inf. Theory 2008, 54, 2808–2817. [Google Scholar] [CrossRef][Green Version]
- Hanawal, M.K.; Sundaresan, R. The Shannon cipher system with a guessing wiretapper: General sources. IEEE Trans. Inf. Theory 2011, 57, 2503–2516. [Google Scholar] [CrossRef]
- Christiansen, M.M.; Duffy, K.R.; du Pin Calmon, F.; Médard, M. Multi-user guesswork and brute force security. IEEE Trans. Inf. Theory 2015, 61, 6876–6886. [Google Scholar] [CrossRef]
- Yona, Y.; Diggavi, S. The effect of bias on the guesswork of hash functions. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 2248–2252. [Google Scholar]
- Massey, J.L. Guessing and entropy. In Proceedings of the 1994 IEEE International Symposium on Information Theory, Trondheim, Norway, 27 June–1 July 1994; p. 204. [Google Scholar]
- Arikan, E. Large deviations of probability rank. In Proceedings of the 2000 IEEE International Symposium on Information Theory, Washington, DC, USA, 25–30 June 2000; p. 27. [Google Scholar]
- Christiansen, M.M.; Duffy, K.R. Guesswork, large deviations, and Shannon entropy. IEEE Trans. Inf. Theory 2012, 59, 796–802. [Google Scholar] [CrossRef]
- Pfister, C.E.; Sullivan, W.G. Rényi entropy, guesswork moments, and large deviations. IEEE Trans. Inf. Theory 2004, 50, 2794–2800. [Google Scholar] [CrossRef]
- Hanawal, M.K.; Sundaresan, R. Guessing revisited: A large deviations approach. IEEE Trans. Inf. Theory 2011, 57, 70–78. [Google Scholar] [CrossRef]
- Sundaresan, R. Guessing under source uncertainty. IEEE Trans. Inf. Theory 2007, 53, 269–287. [Google Scholar] [CrossRef]
- Serdar, B. Comments on “An inequality on guessing and its application to sequential decoding”. IEEE Trans. Inf. Theory 1997, 43, 2062–2063. [Google Scholar]
- Sason, I.; Verdú, S. Improved bounds on lossless source coding and guessing moments via Rényi measures. IEEE Trans. Inf. Theory 2018, 64, 4323–4346. [Google Scholar] [CrossRef]
- Sason, I. Tight bounds on the Rényi entropy via majorization with applications to guessing and compression. Entropy 2018, 20, 896. [Google Scholar] [CrossRef]
- Wyner, A. A theorem on the entropy of certain binary sequences and applications—II. IEEE Trans. Inf. Theory 1973, 19, 772–777. [Google Scholar] [CrossRef]
- Ahlswede, R.; Körner, J. Source coding with side information and a converse for degraded broadcast channels. IEEE Trans. Inf. Theory 1975, 21, 629–637. [Google Scholar] [CrossRef]
- Graczyk, R.; Lapidoth, A. Variations on the guessing problem. In Proceedings of the 2018 IEEE International Symposium on Information Theory, Vail, CO, USA, 17–22 June 2018; pp. 231–235. [Google Scholar]
- Graczyk, R. Guessing with a Helper. Master’s Thesis, ETH Zurich, Zürich, Switzerland, 2017. [Google Scholar]
- O’Donnell, R. Analysis of Boolean Functions; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Courtade, T.A.; Kumar, G.R. Which Boolean functions maximize mutual information on noisy inputs? IEEE Trans. Inf. Theory 2014, 60, 4515–4525. [Google Scholar] [CrossRef]
- Ordentlich, O.; Shayevitz, O.; Weinstein, O. An improved upper bound for the most informative Boolean function conjecture. In Proceedings of the 2016 IEEE International Symposium on Information Theory, Barcelona, Spain, 10–15 July 2016; pp. 500–504. [Google Scholar]
- Samorodnitsky, A. On the entropy of a noisy function. IEEE Trans. Inf. Theory 2016, 62, 5446–5464. [Google Scholar] [CrossRef]
- Kindler, G.; O’Donnell, R.; Witmer, D. Continuous Analogues of the most Informative Function Problem. Available online: http://arxiv.org/pdf/1506.03167.pdf (accessed on 26 December 2015).
- Li, J.; Médard, M. Boolean functions: Noise stability, non-interactive correlation, and mutual information. In Proceedings of the 2018 IEEE International Symposium on Information Theory, Vail, CO, USA, 17–22 June 2018; pp. 266–270. [Google Scholar]
- Chandar, V.; Tchamkerten, A. Most informative quantization functions. Presented at the 2014 Information Theory and Applications Workshop, San Diego, CA, USA, 9–14 February 2014. [Google Scholar]
- Weinberger, N.; Shayevitz, O. On the optimal Boolean function for prediction under quadratic Loss. IEEE Trans. Inf. Theory 2017, 63, 4202–4217. [Google Scholar] [CrossRef]
- Burin, A.; Shayevitz, O. Reducing guesswork via an unreliable oracle. IEEE Trans. Inf. Theory 2018, 64, 6941–6953. [Google Scholar] [CrossRef]
- Ardimanov, N.; Shayevitz, O.; Tamo, I. Minimum Guesswork with an Unreliable Oracle. In Proceedings of the 2018 IEEE International Symposium Information Theory, Vail, CO, USA, 17–22 June 2018; pp. 986–990, Extended Version. Available online: http://arxiv.org/pdf/1811.08528.pdf (accessed on 26 December 2018).
- Feller, W. An Introduction to Probability Theory and Its Applications; John Wiley & Sons: New York, NY, USA, 1971; Volume 2. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Wainwright, M.J.; Jordan, M.I. Graphical models, exponential families, and variational inference. Found. Trends® Mach. Learn. 2008, 1, 1–305. [Google Scholar] [CrossRef]
- Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Nadarajah, S. A generalized normal distribution. J. Appl. Stat. 2005, 32, 685–694. [Google Scholar] [CrossRef]
- Wyner, A.; Ziv, J. A theorem on the entropy of certain binary sequences and applications—I. IEEE Trans. Inf. Theory 1973, 19, 769–772. [Google Scholar] [CrossRef]
- Erkip, E.; Cover, T.M. The efficiency of investment information. IEEE Trans. Inf. Theory 1998, 44, 1026–1040. [Google Scholar] [CrossRef]
- Ahlswede, R.; Gács, P. Spreading of sets in product spaces and hypercontraction of the Markov operator. Ann. Probab. 1976, 925–939. [Google Scholar] [CrossRef]
- Raginsky, M. Strong data processing inequalities and Φ–Sobolev inequalities for discrete channels. IEEE Trans. Inf. Theory 2016, 62, 3355–3389. [Google Scholar] [CrossRef]
- Anantharam, V.; Gohari, A.; Kamath, S.; Nair, C. On hypercontractivity and a data processing inequality. In Proceedings of the 2014 IEEE International Symposium on Information Theory, Honolulu, HI, USA, 29 June–4 July 2014; pp. 3022–3026. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).