An Investigation of Fractional Bagley–Torvik Equation
Abstract
1. Introduction
2. Preliminaries
3. General Form of the Bagley–Torvik Equation and Its Solution
4. Results and Discussion
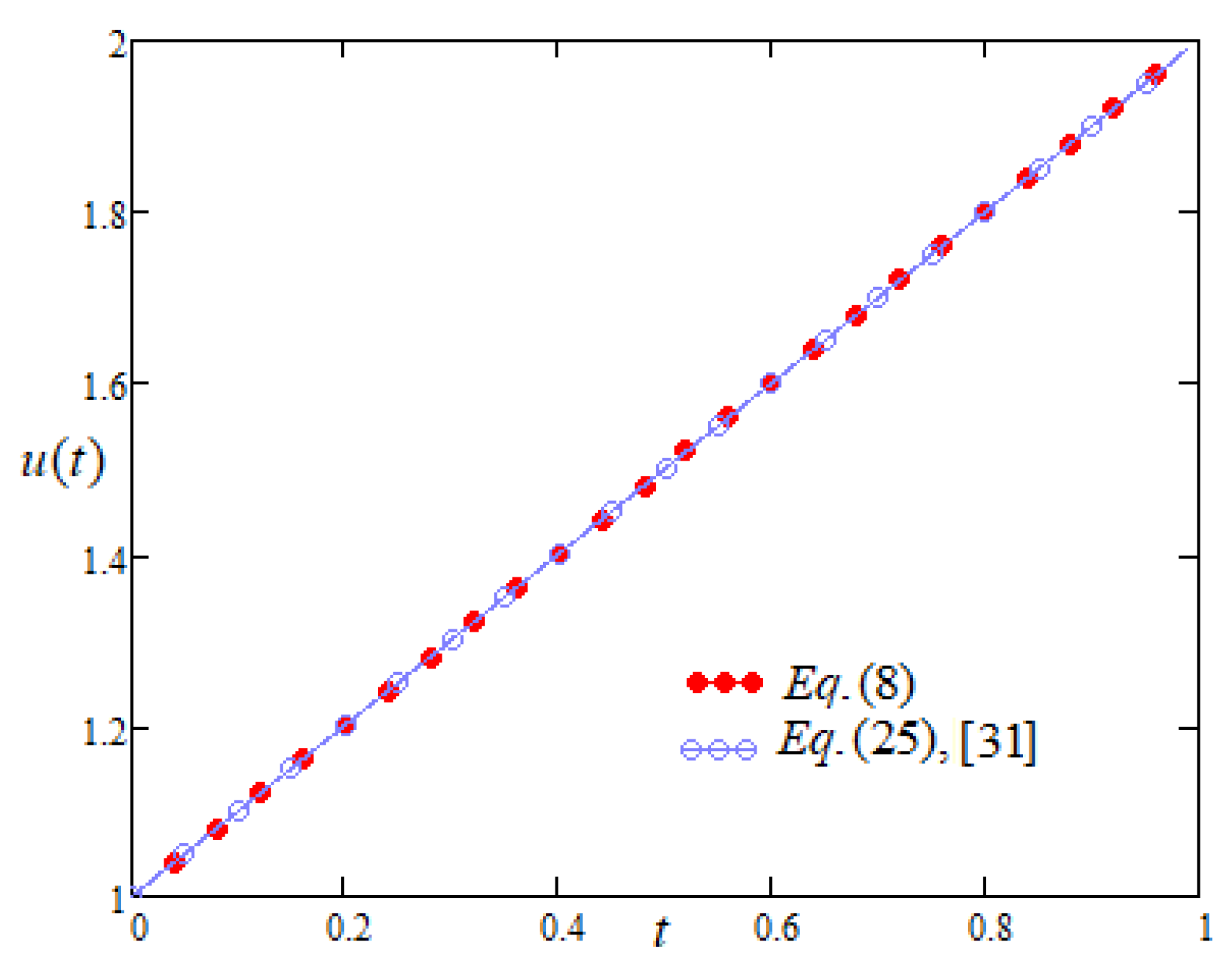
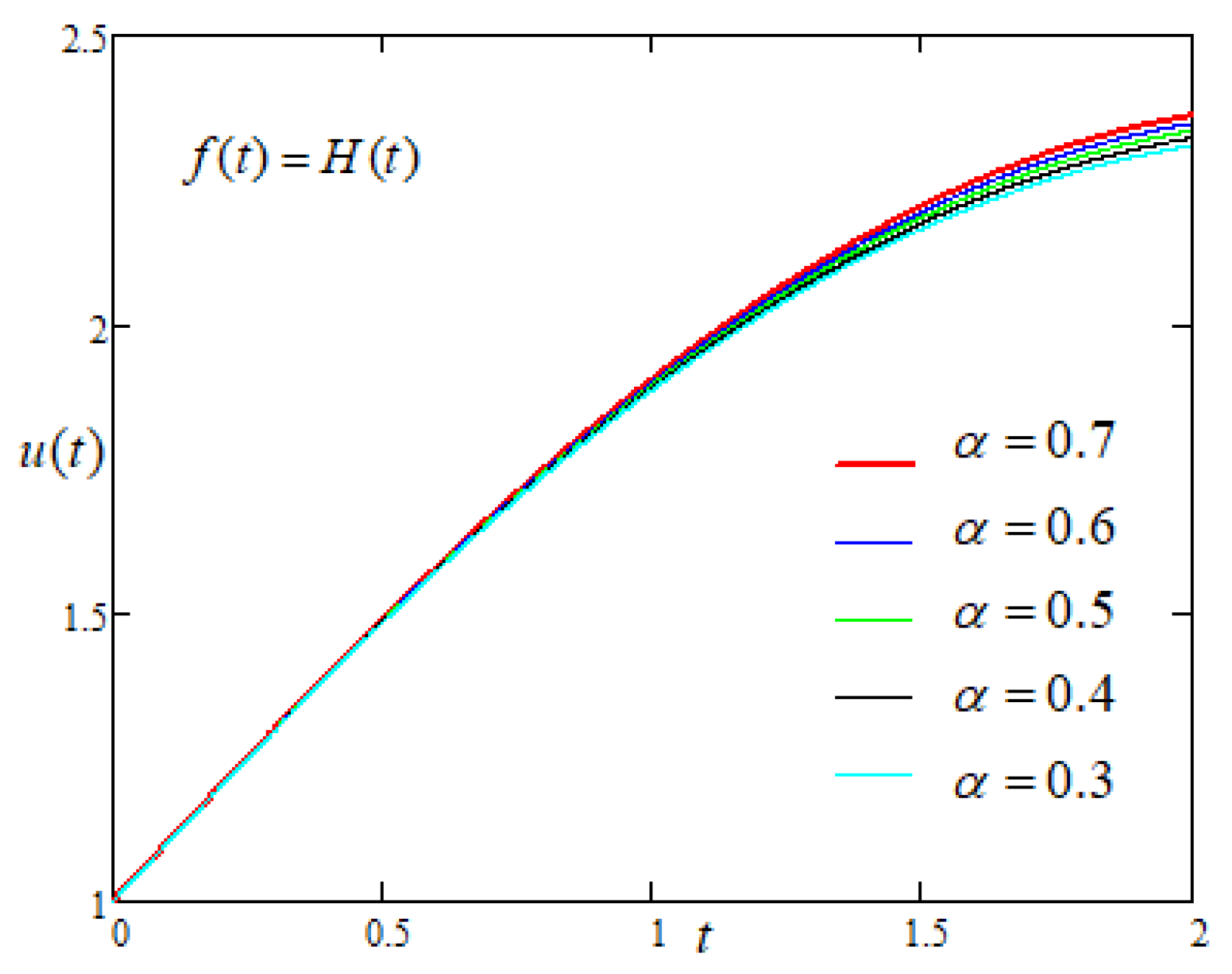
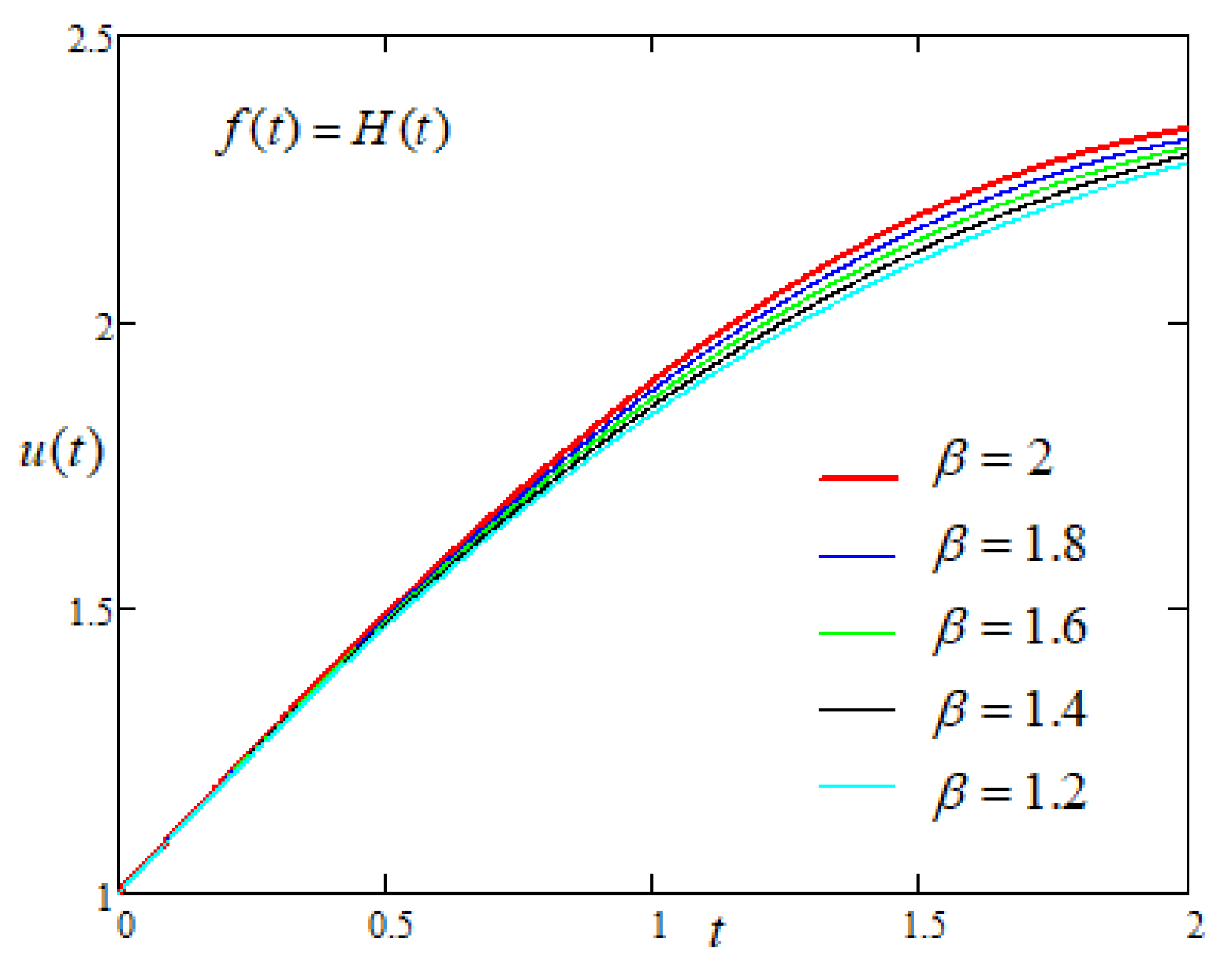
4.1. Case-I: When Driving Force on the Plate Is Constant
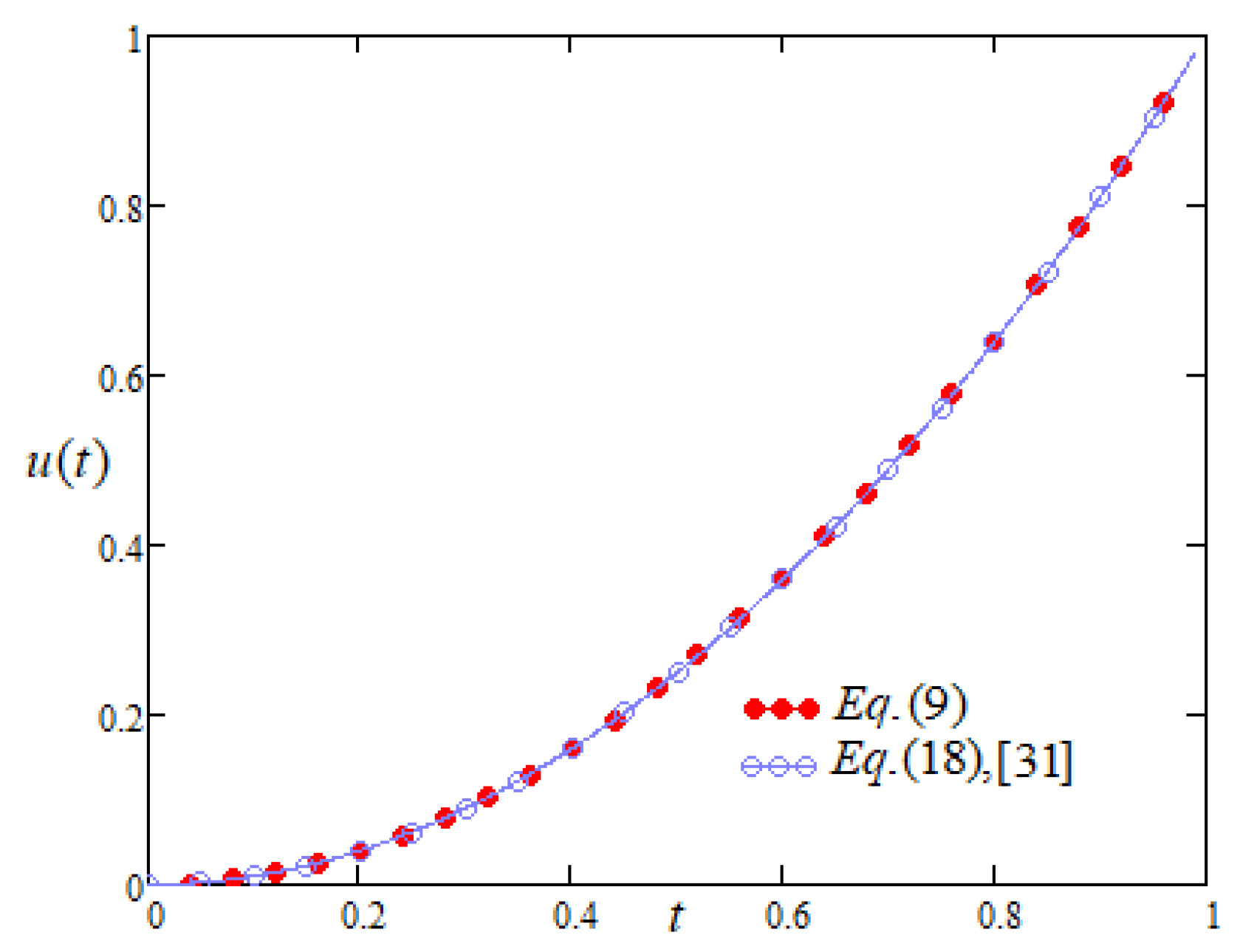
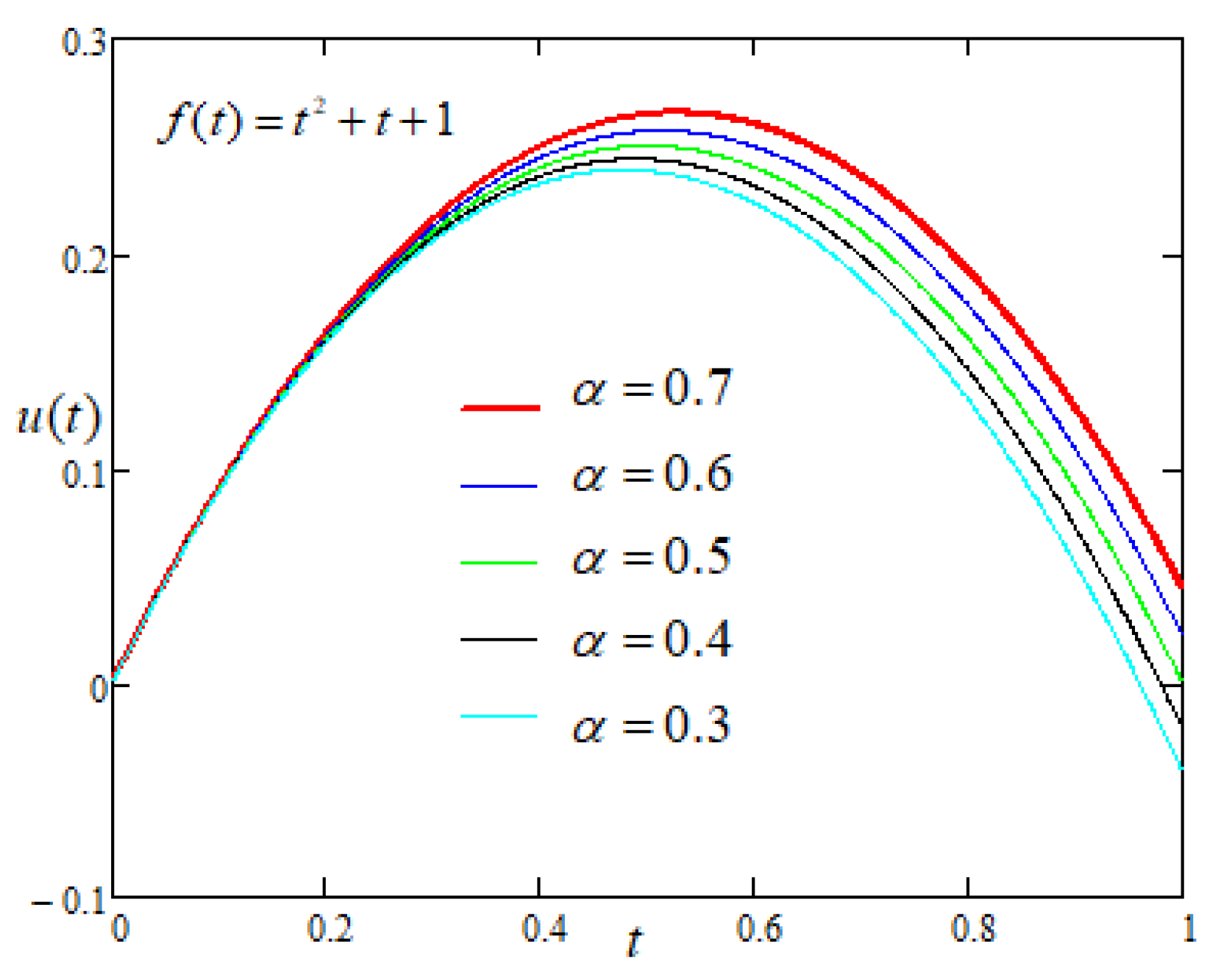
4.2. Case-II: When Driving Force on the Plate Is a Quadratic Function of Time
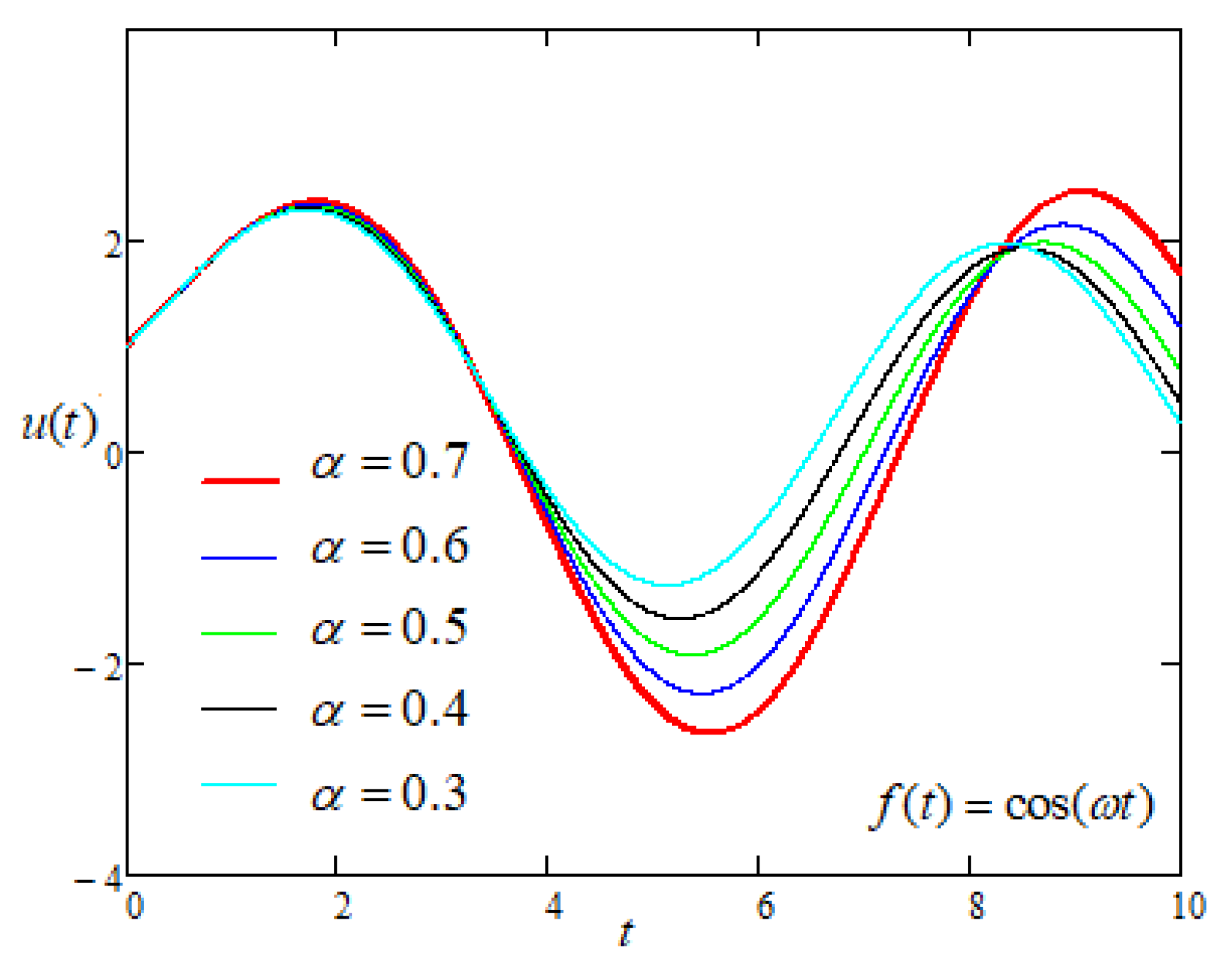
4.3. Case-III: When Driving Force on the Plate Is a Periodic Function of Time
5. Modelling of Experimental One-Degree-of-Freedom Mechanical Oscillator
6. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| FC | Fractional calculus |
| FDE | Fractional differential equation |
| BTE | Bagley–Torvik equation |
References
- Machado, J.A.T. Entropy analysis of integer and fractional dynamical systems. Nonlinear Dynam. 2010, 62, 371–378. [Google Scholar]
- Lopes, A.M.; Machado, J.A.T. Entropy analysis of soccer dynamics. Entropy 2019, 21, 187. [Google Scholar] [CrossRef]
- Ubriaco, M.R. Entropy based on fractional calculus. Phys. Lett. A 2009, 373, 2516–2519. [Google Scholar] [CrossRef]
- Prehi, J.; Boldt, F.; Hoffmann, K.; Essex, C. Symmetric fractional diffusion and entropy production. Entropy 2016, 18, 275. [Google Scholar] [CrossRef]
- Luchko, Y. Entropy production rate of a one dimensional alpha-fractional diffusion process. Axioms 2016, 5, 6. [Google Scholar] [CrossRef]
- Beck, C. Generalized information and entropy measures in physics. Contemp. Phys. 2009, 50, 495–510. [Google Scholar] [CrossRef]
- Mathai, A.M.; Haubold, H.J. On generalized entropy measures and pathways. Physica A 2007, 385, 493–500. [Google Scholar] [CrossRef]
- Prehi, J.; Essex, C.; Hoffmann, K.H. Tsallis relative entropy and anomalous diffusion. Entopy 2012, 14, 701–716. [Google Scholar]
- Podlubny, I. Fractional Differential Equations, 1st ed.; Academic Press: San Diego, CA, USA, 1999; ISBN 978-0125588409. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to Fractional Calculus and Fractional Differential Equations; John Wiley and Sons Inc.: New York, NY, USA, 1993; ISBN 047-1588849. [Google Scholar]
- Oldham, K.B.; Spanier, J. The Fractional Calculus: Theory and Application of Differentiation and Integration to Arbitrary Order, 1st ed.; Academic Press Inc.: New York, NY, USA, 1974; ISBN 978-0125255509. [Google Scholar]
- Zafar, A.A.; Riaz, M.B.; Shah, N.A.; Imran, M.A. Influence of non-integer order derivatives on unsteady unidirectionalmotions of an Oldroyd-B fluid with generalized boundary conditions. Eur. Phys. J. Plus 2018, 133, 127. [Google Scholar] [CrossRef]
- Atanackovic, T.M.; Stankovic, B. Dynamics of a viscoelastic rod of fractional derivative type. Z. Angew. Math. Mech. 2002, 82, 377–386. [Google Scholar] [CrossRef]
- Fa, K.S. A falling body problem through the air in view of the fractional derivative approach. Physica A 2005, 350, 199–206. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. Fractional Calculus-A different approach to the analysis of viscoelastically damped structures. AIAA J. 1983, 21, 741–748. [Google Scholar] [CrossRef]
- Torvik, P.J.; Bagley, R.L. On the appearance of the fractional derivative in the behavior of real materials. J. Appl. Mech. 1984, 51, 294–298. [Google Scholar] [CrossRef]
- Makris, N.; Dargush, G.F.; Constantinou, M.C. Dynamic analysis of generalized viscoerlastic fluids. J. Eng. Mech. 1993, 119, 1663–1679. [Google Scholar] [CrossRef]
- Heibig, A.; Plade, L.I. On the rest state stability of an objective fractional derivative viscoelastic fluid model. J. Math. Phys. 2008, 49, 043101. [Google Scholar] [CrossRef]
- Lazopoulos, K.A.; Lazopoulos, A.K. Fractional vector calculus and fractional continuum mechanics. Prog. Fract. Differ. Appl. 2016, 2, 67–86. [Google Scholar] [CrossRef]
- Carpinteri, A.; Cornetti, P.; Sapora, A. A fractional calculus approach to non-local elasticity. Eur. Phys. J. Spec. Top. 2011, 193, 193–204. [Google Scholar] [CrossRef]
- Lazopoulos, K.A.; Lazopoulos, A.K. On the mathematical formulation of fractional derivatives. Prog. Fract. Differ. Appl. 2019, 5, 261–267. [Google Scholar]
- Lazopoulos, K.A.; Lazopoulos, A.K. On fractional bending of beams with ∧-fractional derivative. Arch. Appl. Mech. 2019. [Google Scholar] [CrossRef]
- Ray, S.S.; Bera, R.K. Analytical solution of the Bagley-Torvik equation by Adomian decomposition method. Appl. Math. Comput. 2005, 168, 398–410. [Google Scholar] [CrossRef]
- El-Sayed, A.M.A.; El-Kalla, I.L.; Ziada, E.A.A. Analytical and numerical solutions of multiterm nonlinear fractional orders differential equations. Appl. Numer. Math. 2010, 60, 788–797. [Google Scholar] [CrossRef]
- Hu, Y.; Luo, Y.; Lu, Z. Analytical solution of the linear fractional differential equation by Adomian decomposition method. J. Comput. Appl. Math. 2008, 215, 220–229. [Google Scholar] [CrossRef]
- Karaaslan, M.F.; Celiker, F.; Kurulay, M. Approximate solution of the Bagley-Torvik equation by hybridisable discontinuous Galerkin methods. Appl. Math. Comput. 2013, 219, 6328–6343. [Google Scholar]
- Enesiz, Y.C.; Keskin, Y.; Kurnaz, A. The solution of the Bagley-Torvik equation with the generalized Taylor collocation method. J. Franklin I 2010, 347, 452–466. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J. Numerical solution of the Bagley-Torvik equation. BIT Numer. Math. 2002, 43, 490–507. [Google Scholar]
- Wang, Z.H.; Wang, X. General solution of the Bagley-Torvik equation with fractional-order derivative. Commun. Nonlinear Sci. Numer. Simulat. 2010, 15, 1279–1285. [Google Scholar] [CrossRef]
- Ghorbani, A.; Alavi, A. Application of He’s variational iteration method to solve semi differential equations of nth order. Math. Probl. Eng. 2008, 1–9. [Google Scholar] [CrossRef]
- Bansal, M.K.; Jain, R. Analytical solution of Bagley Torvik equation by generalize differential transform. Int. J. Pure Appl. Math. 2016, 110, 265–273. [Google Scholar] [CrossRef]
- Anjara, F.; Solofoniaina, J. Solution of General Fractional Oscillation Relaxation Equation by Adomians Method. Gen. Math. Notes 2014, 20, 1–11. [Google Scholar]
- Fazli, H.; Nieto, J.J. An investigation of fractional Bagley-Torvik equation. Open Math 2019, 17, 499–512. [Google Scholar] [CrossRef]
- Gamel, M.; Abd-El-Hady, M.; El-Azab, M. Chelyshkov-Tau Approach for Solving Bagley-Torvik Equation. Appl. Math. 2017, 8, 1795–1807. [Google Scholar] [CrossRef]
- Uddin, M.; Ahmad, S. On the numerical solution of Bagley-Torvik equation via the Laplace transform. Tbilisi Math. J. 2017, 10, 279–284. [Google Scholar] [CrossRef]
- Setia, A.; Liu, Y.; Vatsala, A.S. The solution of the Bagley-Torvik equation by using second kind Chebyshev wavelet. In Proceedings of the 2014 11th International Conference on Information Technology: New Generations, Las Vegas, NV, USA, 7–9 April 2014; pp. 443–446. [Google Scholar]
- Lorenzo, C.F.; Hartley, T.T. Generalized Functions for Fractional Calculus. NASA/TP-1999-209424/Rev1. 1999. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19990110709.pdf (accessed on 18 November 2019).
- Debnath, L.; Bhatta, D. Integral Transforms and Their Applications, 2nd ed.; Chapman and Hall/CRC Press: Boca-Raton, FL, USA, 2007. [Google Scholar]
- Skurativskyi, S.; Kudra, G.; Wasilewski, G.; Awrejcewicz, J. Properties of impact events in the model of forced impacting oscillator: Experimental and numerical investigations. Commun. Nonlinear Sci. Numer. Simulat. 2019, 113, 55–61. [Google Scholar] [CrossRef]
- Witkowski, K.; Kudra, G.; Wasilewski, G.; Awrejcewicz, J. Modelling and experimental validation of 1-degree-of-freedom impacting oscillator. J. Syst. Control Eng. 2019, 233, 418–430. [Google Scholar] [CrossRef]



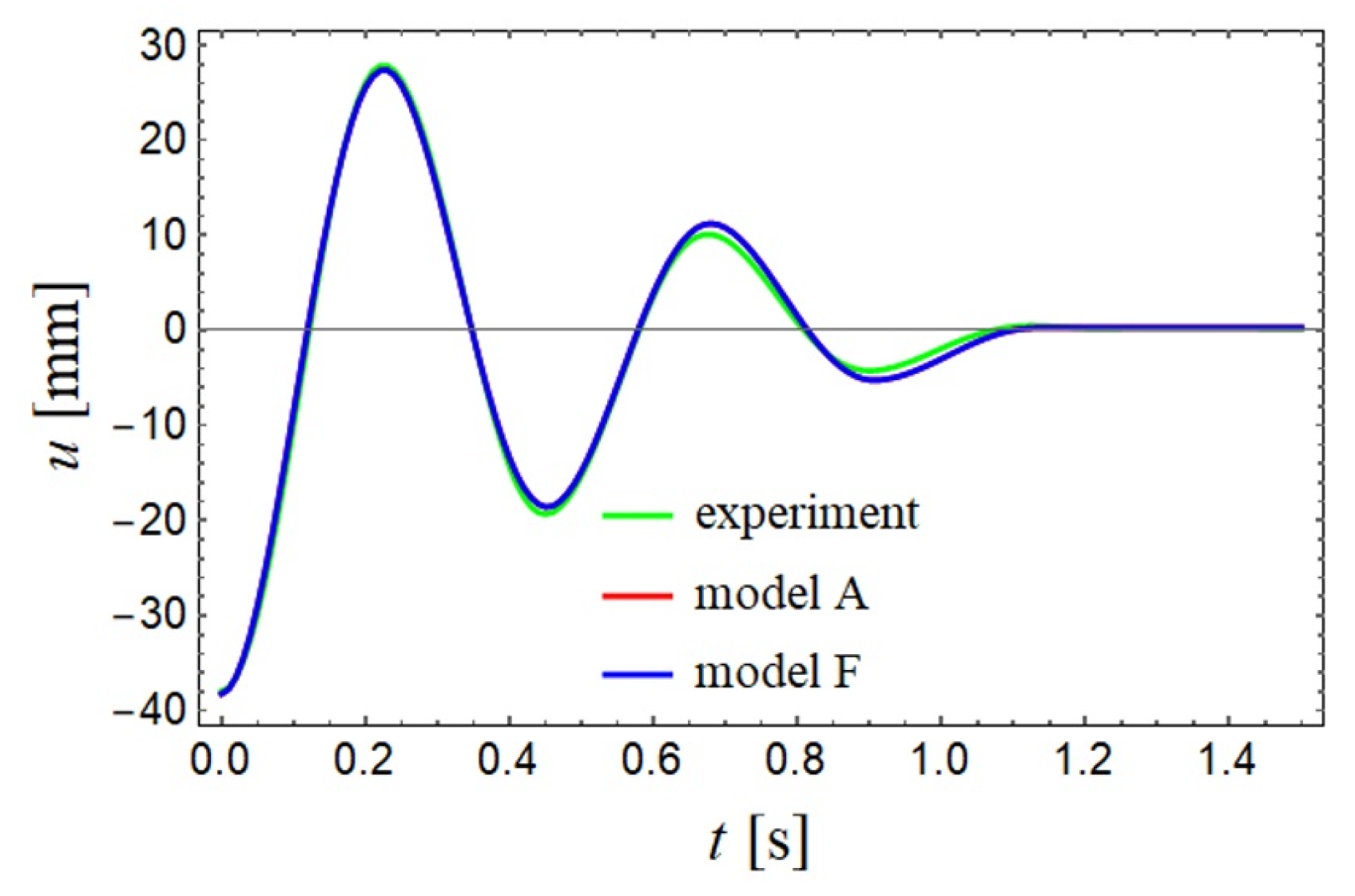
| Model | ||||||
|---|---|---|---|---|---|---|
| A | 0 | 2 | 196.359 | 1.73345 | 0.436005 | 0.328796 |
| B | 0.9999946 | 1.99999 | 196.394 | 1.73192 | 0.436556 | 0.328778 |
| C | 0.5 | 2 | 224.652 | 092534 | 0.500898 | 0.361783 |
| D | 0.9 | 2 | 3761.75 | 25.1388 | 8.53502 | 0.420043 |
| E | 0 | 1.95 | 167.157 | 0.74288 | 0.370936 | 0.361385 |
| F | 0 | 1.85 | 120.003 | 0.60625 | 0.265951 | 0.51812 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zafar, A.A.; Kudra, G.; Awrejcewicz, J. An Investigation of Fractional Bagley–Torvik Equation. Entropy 2020, 22, 28. https://doi.org/10.3390/e22010028
Zafar AA, Kudra G, Awrejcewicz J. An Investigation of Fractional Bagley–Torvik Equation. Entropy. 2020; 22(1):28. https://doi.org/10.3390/e22010028
Chicago/Turabian StyleZafar, Azhar Ali, Grzegorz Kudra, and Jan Awrejcewicz. 2020. "An Investigation of Fractional Bagley–Torvik Equation" Entropy 22, no. 1: 28. https://doi.org/10.3390/e22010028
APA StyleZafar, A. A., Kudra, G., & Awrejcewicz, J. (2020). An Investigation of Fractional Bagley–Torvik Equation. Entropy, 22(1), 28. https://doi.org/10.3390/e22010028









