Many-Body Dynamics and Decoherence of the XXZ Central Spin Model in External Magnetic Field
Abstract
1. Introduction
2. Model
3. Decoherence Dynamics
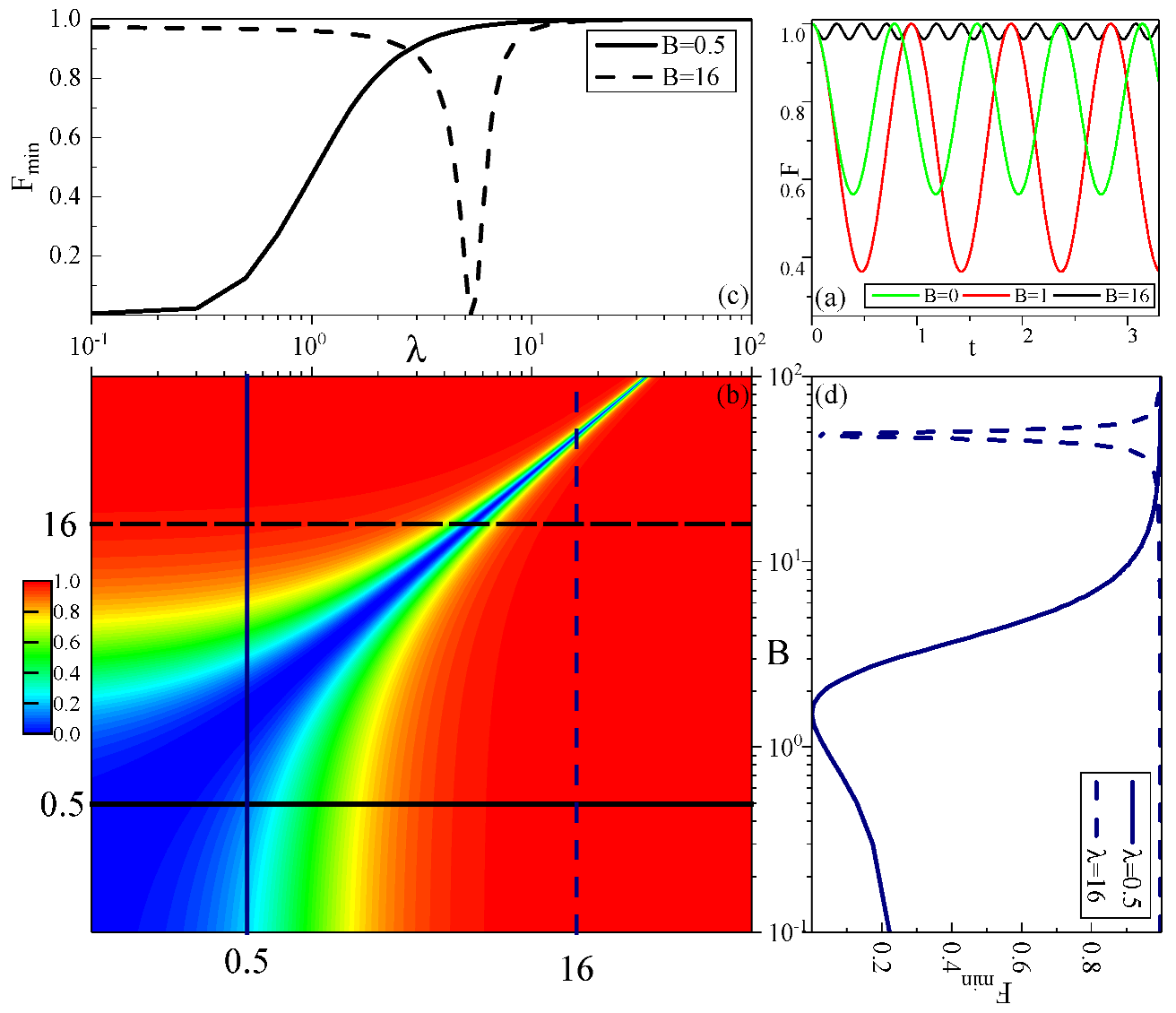
3.1. Constant Magnetic Field
3.2. Disordered Magnetic Field
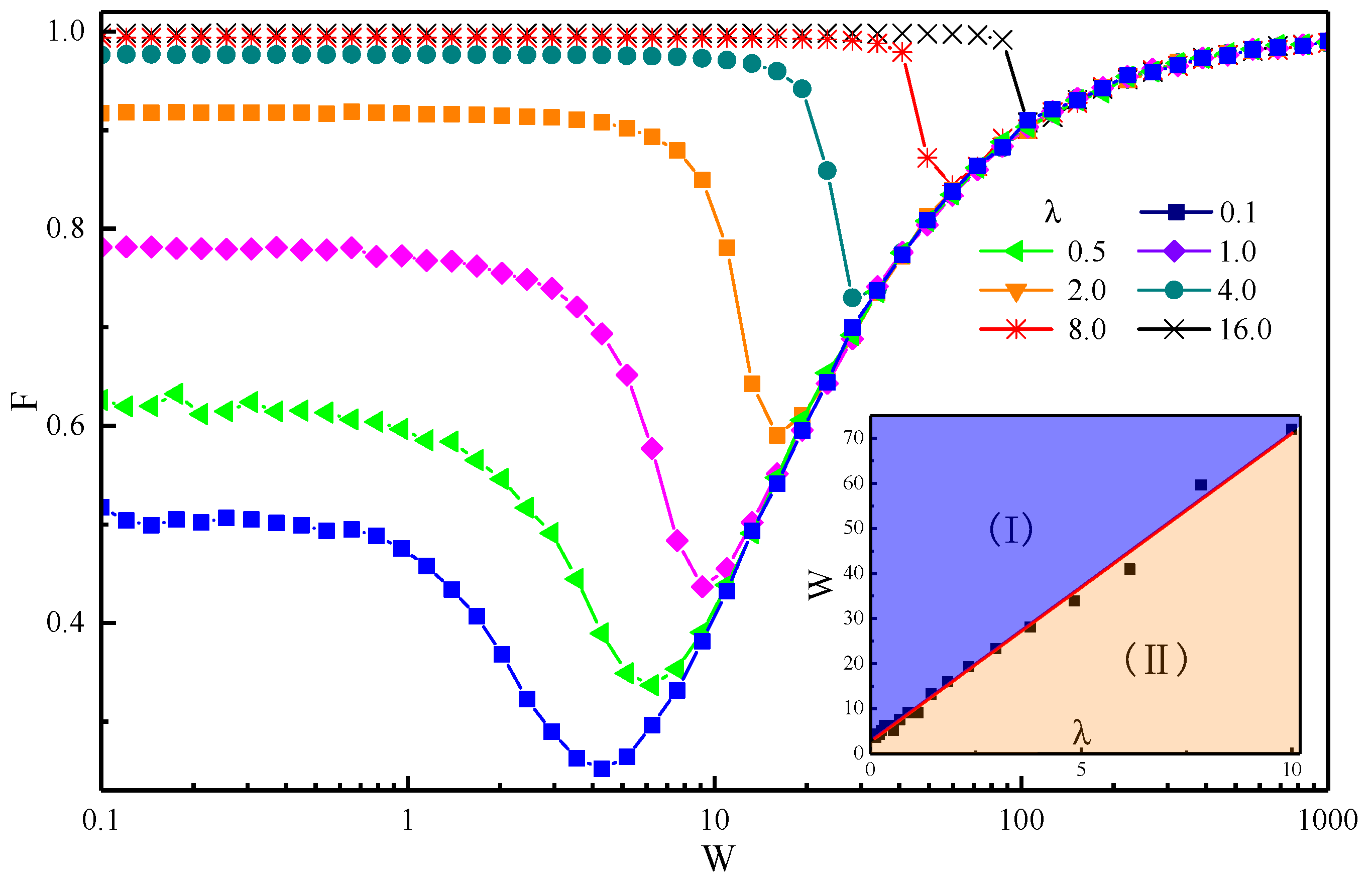
3.2.1. Fidelity
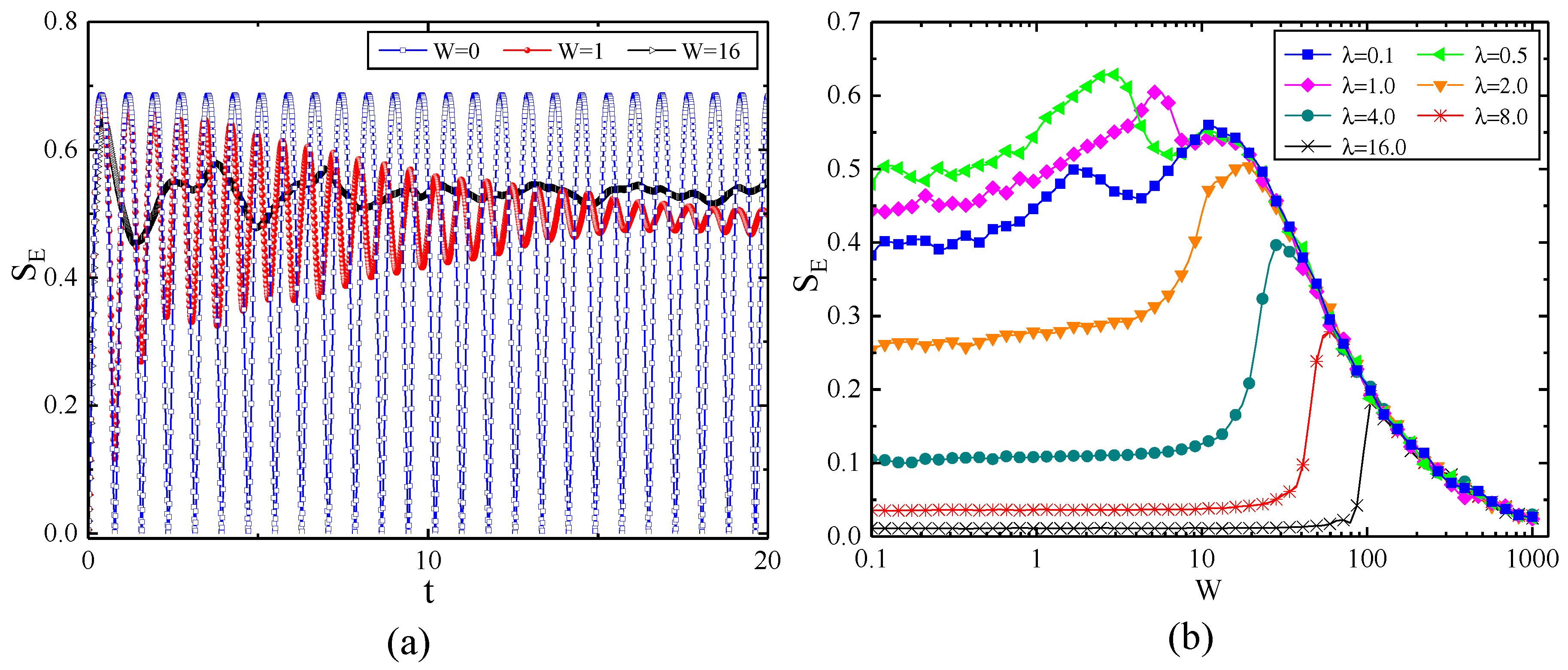
3.2.2. Entanglement Entropy
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- DiVincenzo, D.P. The Physical Implementation of Quantum Computation. Fortschritte der Physik 2000, 48, 771–783. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information: 10th Anniversary Edition, 10 anv ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Zurek, W.H. Decoherence and the Transition from Quantum to Classical. Phys. Today 1991, 44, 36. [Google Scholar] [CrossRef]
- Loss, D.; DiVincenzo, D.P. Quantum computation with quantum dots. Phys. Rev. A 1998, 57, 120–126. [Google Scholar] [CrossRef]
- Koppens, F.H.L.; Buizert, C.; Tielrooij, K.J.; Vink, I.T.; Nowack, K.C.; Meunier, T.; Kouwenhoven, L.P.; Vandersypen, L.M.K. Driven coherent oscillations of a single electron spin in a quantum dot. Nature 2006, 442, 766–771. [Google Scholar] [CrossRef] [PubMed]
- Hanson, R.; Kouwenhoven, L.P.; Petta, J.R.; Tarucha, S.; Vandersypen, L.M.K. Spins in few-electron quantum dots. Rev. Mod. Phys. 2007, 79, 1217–1265. [Google Scholar] [CrossRef]
- Koppens, F.H.L.; Nowack, K.C.; Vandersypen, L.M.K. Spin Echo of a Single Electron Spin in a Quantum Dot. Phys. Rev. Lett. 2008, 100, 236802. [Google Scholar] [CrossRef]
- Lee, B.; Witzel, W.M.; Das Sarma, S. Universal Pulse Sequence to Minimize Spin Dephasing in the Central Spin Decoherence Problem. Phys. Rev. Lett. 2008, 100, 160505. [Google Scholar] [CrossRef]
- Salamon, T.; Roszak, K. Entanglement generation between a charge qubit and its bosonic environment during pure dephasing: Dependence on the environment size. Phys. Rev. A 2017, 96, 032333. [Google Scholar] [CrossRef]
- Khaetskii, A.V.; Nazarov, Y.V. Spin relaxation in semiconductor quantum dots. Phys. Rev. B 2000, 61, 12639–12642. [Google Scholar] [CrossRef]
- Golovach, V.N.; Khaetskii, A.; Loss, D. Phonon-Induced Decay of the Electron Spin in Quantum Dots. Phys. Rev. Lett. 2004, 93, 016601. [Google Scholar] [CrossRef]
- Gaudin, M. Diagonalisation d’une classe d’hamiltoniens de spin. J. Phys. 1976, 37, 1087–1098. [Google Scholar] [CrossRef]
- Wertz, J.E.; Bolton, J.R. Electron Spin Resonance: Elementary Theory and Practical Applications, 1st ed.; Springer: Haarlem, The Netherlands, 1986. [Google Scholar]
- Al-Hassanieh, K.A.; Dobrovitski, V.V.; Dagotto, E.; Harmon, B.N. Numerical Modeling of the Central Spin Problem Using the Spin-Coherent-State P Representation. Phys. Rev. Lett. 2006, 97, 037204. [Google Scholar] [CrossRef]
- Arenz, C.; Gualdi, G.; Burgarth, D. Control of open quantum systems: case study of the central spin model. New J. Phys. 2014, 16, 065023. [Google Scholar] [CrossRef]
- Claeys, P.W.; De Baerdemacker, S.; Araby, O.E.; Caux, J.S. Spin Polarization through Floquet Resonances in a Driven Central Spin Model. Phys. Rev. Lett. 2018, 121, 080401. [Google Scholar] [CrossRef] [PubMed]
- Guan, X.W.; Foerster, A.; Links, J.; Zhou, H.Q. Exact results for BCS systems. PoS 2002, unesp2002, 016. [Google Scholar]
- Bortz, M.; Stolze, J. Spin and entanglement dynamics in the central-spin model with homogeneous couplings. J. Stat. Mech. Theory Exp. 2007, 2007, P06018. [Google Scholar] [CrossRef][Green Version]
- Bortz, M.; Stolze, J. Exact dynamics in the inhomogeneous central-spin model. Phys. Rev. B 2007, 76, 014304. [Google Scholar] [CrossRef]
- Schliemann, J.; Khaetskii, A.; Loss, D. Electron spin dynamics in quantum dots and related nanostructures due to hyperfine interaction with nuclei. J. Phys. Condens. Matter 2003, 15, R1809–R1833. [Google Scholar] [CrossRef]
- Cywiński, L.; Dobrovitski, V.V.; Das Sarma, S. Spin echo decay at low magnetic fields in a nuclear spin bath. Phys. Rev. B 2010, 82, 035315. [Google Scholar] [CrossRef]
- Dobrovitski, V.V.; De Raedt, H.A. Efficient scheme for numerical simulations of the spin-bath decoherence. Phys. Rev. E 2003, 67, 056702. [Google Scholar] [CrossRef]
- Hackmann, J.; Anders, F.B. Spin noise in the anisotropic central spin model. Phys. Rev. B 2014, 89, 045317. [Google Scholar] [CrossRef]
- Stanek, D.; Raas, C.; Uhrig, G.S. Dynamics and decoherence in the central spin model in the low-field limit. Phys. Rev. B 2013, 88, 155305. [Google Scholar] [CrossRef]
- Gravert, L.B.; Lorenz, P.; Nase, C.; Stolze, J.; Uhrig, G.S. Increased coherence time in narrowed bath states in quantum dots. Phys. Rev. B 2016, 94, 094416. [Google Scholar] [CrossRef]
- Khaetskii, A.V.; Loss, D.; Glazman, L. Electron Spin Decoherence in Quantum Dots due to Interaction with Nuclei. Phys. Rev. Lett. 2002, 88, 186802. [Google Scholar] [CrossRef] [PubMed]
- Barnes, E.; Cywiński, L.; Das Sarma, S. Nonperturbative Master Equation Solution of Central Spin Dephasing Dynamics. Phys. Rev. Lett. 2012, 109, 140403. [Google Scholar] [CrossRef]
- Thacker, H.B. Exact integrability in quantum field theory and statistical systems. Rev. Mod. Phys. 1981, 53, 253–285. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, W.L.; Cao, J.; Shi, K. Off-Diagonal Bethe Ansatz for Exactly Solvable Models; Springer: Berlin, Germany, 2015. [Google Scholar]
- Arraut, I. The Quantum Yang-Baxter Conditions: The Fundamental Relations behind the Nambu-Goldstone Theorem. Symmetry 2019, 11, 803. [Google Scholar] [CrossRef]
- Hetterich, D.; Yao, N.Y.; Serbyn, M.; Pollmann, F.; Trauzettel, B. Detection and characterization of many-body localization in central spin models. Phys. Rev. B 2018, 98, 161122. [Google Scholar] [CrossRef]
- Basko, D.; Aleiner, I.; Altshuler, B. Metal-insulator transition in a weakly interacting many-electron system with localized single-particle states. Ann. Phys. 2006, 321, 1126–1205. [Google Scholar] [CrossRef]
- Srednicki, M. Chaos and quantum thermalization. Phys. Rev. E 1994, 50, 888–901. [Google Scholar] [CrossRef]
- Wiersma, D.S.; Bartolini, P.; Lagendijk, A.; Righini, R. Localization of light in a disordered medium. Nature 1997, 390, 671–673. [Google Scholar] [CrossRef]
- Deutsch, J.M. Quantum statistical mechanics in a closed system. Phys. Rev. A 1991, 43, 2046–2049. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Ganeshan, S.; Pixley, J.H.; Das Sarma, S. Many-Body Localization and Quantum Nonergodicity in a Model with a Single-Particle Mobility Edge. Phys. Rev. Lett. 2015, 115, 186601. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.; Bardarson, J.H.; Pollmann, F. Signatures of the many-body localization transition in the dynamics of entanglement and bipartite fluctuations. New J. Phys. 2016, 18, 023046. [Google Scholar] [CrossRef]
- Gogolin, C.; Eisert, J. Equilibration, thermalisation, and the emergence of statistical mechanics in closed quantum systems. Rep. Prog. Phys. 2016, 79, 056001. [Google Scholar] [CrossRef]
- Friesdorf, M.; Werner, A.H.; Brown, W.; Scholz, V.B.; Eisert, J. Many-Body Localization Implies that Eigenvectors are Matrix-Product States. Phys. Rev. Lett. 2015, 114, 170505. [Google Scholar] [CrossRef]
- Kjäll, J.A.; Bardarson, J.H.; Pollmann, F. Many-Body Localization in a Disordered Quantum Ising Chain. Phys. Rev. Lett. 2014, 113, 107204. [Google Scholar] [CrossRef]
- Vosk, R.; Altman, E. Many-Body Localization in One Dimension as a Dynamical Renormalization Group Fixed Point. Phys. Rev. Lett. 2013, 110, 067204. [Google Scholar] [CrossRef]
- He, W.B.; Chesi, S.; Lin, H.Q.; Guan, X.W. Exact quantum dynamics of XXZ central spin problems. Phys. Rev. B 2019, 99, 174308. [Google Scholar] [CrossRef]
- Mohamed, A.; Eleuch, H. Non-classical effects in cavity QED containing a nonlinear optical medium and a quantum well: Entanglement and non-Gaussanity. Eur. Phys. J. D 2015, 69. [Google Scholar] [CrossRef]
- Sete, E.A.; Eleuch, H.; Das, S. Semiconductor cavity QED with squeezed light: Nonlinear regime. Phys. Rev. A 2011, 84, 053817. [Google Scholar] [CrossRef]
- Berrada, K.; Abdel-Khalek, S.; Eleuch, H.; Hassouni, Y. Beam splitting and entanglement generation: Excited coherent states. Quant. Inf. Process 2013, 12, 69–82. [Google Scholar] [CrossRef]
- Paget, D.; Lampel, G.; Sapoval, B.; Safarov, V.I. Low field electron-nuclear spin coupling in gallium arsenide under optical pumping conditions. Phys. Rev. B 1977, 15, 5780–5796. [Google Scholar] [CrossRef]
- Fischer, J.; Coish, W.A.; Bulaev, D.V.; Loss, D. Spin decoherence of a heavy hole coupled to nuclear spins in a quantum dot. Phys. Rev. B 2008, 78, 155329. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Wan, Q.-K.; Wang, X.-H. Many-Body Dynamics and Decoherence of the XXZ Central Spin Model in External Magnetic Field. Entropy 2020, 22, 23. https://doi.org/10.3390/e22010023
Zhou X, Wan Q-K, Wang X-H. Many-Body Dynamics and Decoherence of the XXZ Central Spin Model in External Magnetic Field. Entropy. 2020; 22(1):23. https://doi.org/10.3390/e22010023
Chicago/Turabian StyleZhou, Xu, Qing-Kun Wan, and Xiao-Hui Wang. 2020. "Many-Body Dynamics and Decoherence of the XXZ Central Spin Model in External Magnetic Field" Entropy 22, no. 1: 23. https://doi.org/10.3390/e22010023
APA StyleZhou, X., Wan, Q.-K., & Wang, X.-H. (2020). Many-Body Dynamics and Decoherence of the XXZ Central Spin Model in External Magnetic Field. Entropy, 22(1), 23. https://doi.org/10.3390/e22010023




