Unsupervised Indoor Positioning System Based on Environmental Signatures
Abstract
1. Introduction
2. Related Work
- The paper uses multi-domain sensors to make up for the single signal to be easily affected by the environment, and the positioning accuracy is insufficient. For example, Horus system is susceptible to noise in the channel.
- The paper proposes global landmarks, which has not been seen in past positioning systems. Global landmarks enable the system to obtain certain environmental information in advance, which helps to improve positioning accuracy.
- This paper makes use of the simultaneous localization and mapping (SLAM) architecture and framework that leverages smart phone sensors to both dead-reckon the user location and identify semantic landmarks. These landmarks are used in a SLAM probabilistic framework to reset the accumulated localization error. It makes the UIP system have high positioning accuracy without initial manual calibration.
3. Mobile Sensor Positioning
3.1. Dead Reckoning
- (1)
- Displacement: It can be calculated simply by the direct integral of the accelerometer reading which can be obtained by acceleratometer. However, it has a bad positioning error. As shown in Figure 1, after the actual displacement of 30 m, the deviation of the estimated value exceeds 100 m; this is due to the noise and low sampling rate of the accelerometer and the jitter of the phone when the user is walking. The paper uses another effective method.It is identifying the feature of the user’s walking [18,24]. The feature comes from the natural upward/downward rebound of the body at every step. To capture it, the accelerometer signal is processed by a low-pass filter, and the system identifies two consecutive local minimum, if the difference value between maximum and minimum is larger than the given threshold, it will be considered as a step of the user, and the displacement is calculated by multiplying the steps by the step size.
- (2)
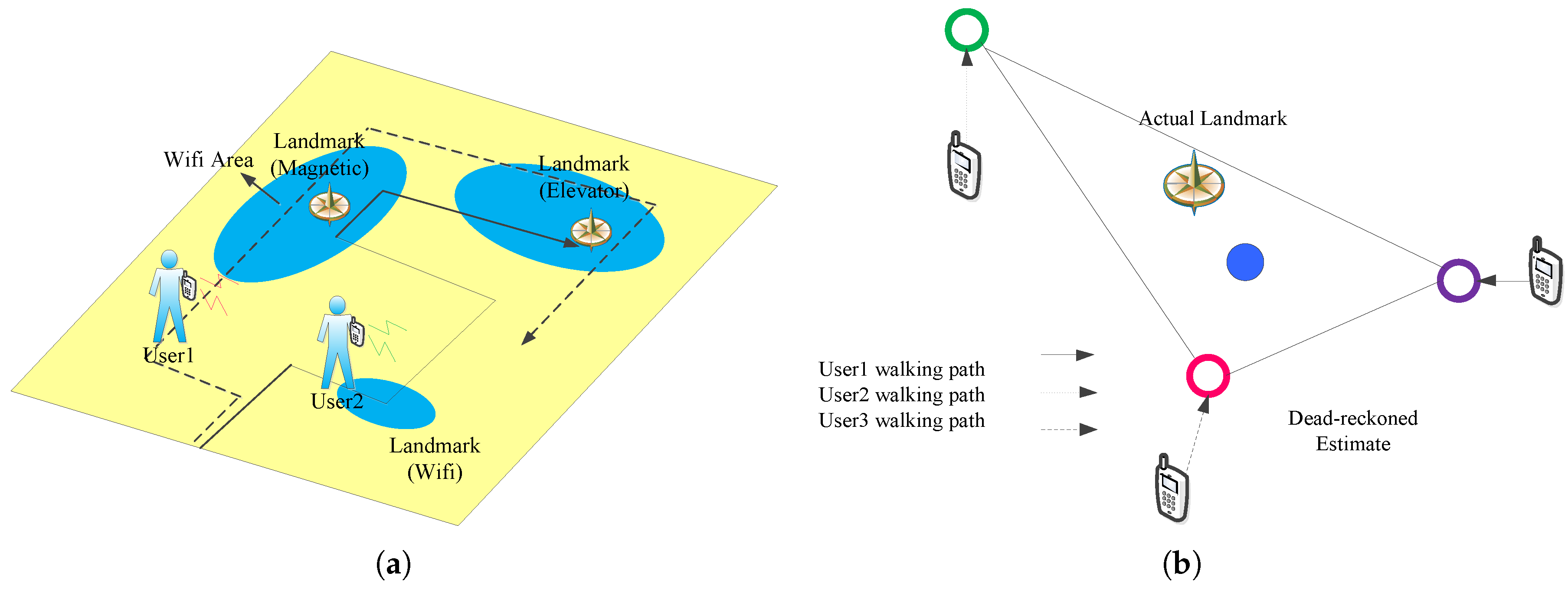
- Orientation: Traditional approaches rely on the compass, which can indicate the orientation by the magnetic field. However, it is noisy and seriously impacts positioning results. Gyroscope is also used in the paper, and it can measure relative palstance, which is a three-dimensional rotation matrix, and the relative angular displacement (RAD) can be obtained when the matrix is multiplied by a time interval. The path structure of the user can be tracked by the gyroscope; however, the estimated path has an error in the initial orientation. As shown in Figure 2a, all of these paths are rotated versions of the real path.Landmarks can correct the deviation. As shown in Figure 2b, the position X of the user at time is known, dead reckoning with initial bias estimates that the position is X at time , and the real position is X. Assuming that the user encounters the landmark L at time and the location of L is X, which is known, the algorithm thus considers that the the location of the user is X, which is an accuracy position.
3.2. Landmark Introduction
3.2.1. Landmark Density Indoors
3.2.2. Location Estimate
3.2.3. The Effect of Regular Error Compensation
4. Landmark Design
4.1. Local Landmark
4.2. Global Landmark
5. Simultaneous Localization and Mapping
5.1. Background
5.1.1. EKF-SLAM
5.1.2. FastSLAM
5.2. SLAM Algorithm
5.2.1. Pose Estimation
5.2.2. Map Update
5.2.3. Resampling
6. Results and Discussion
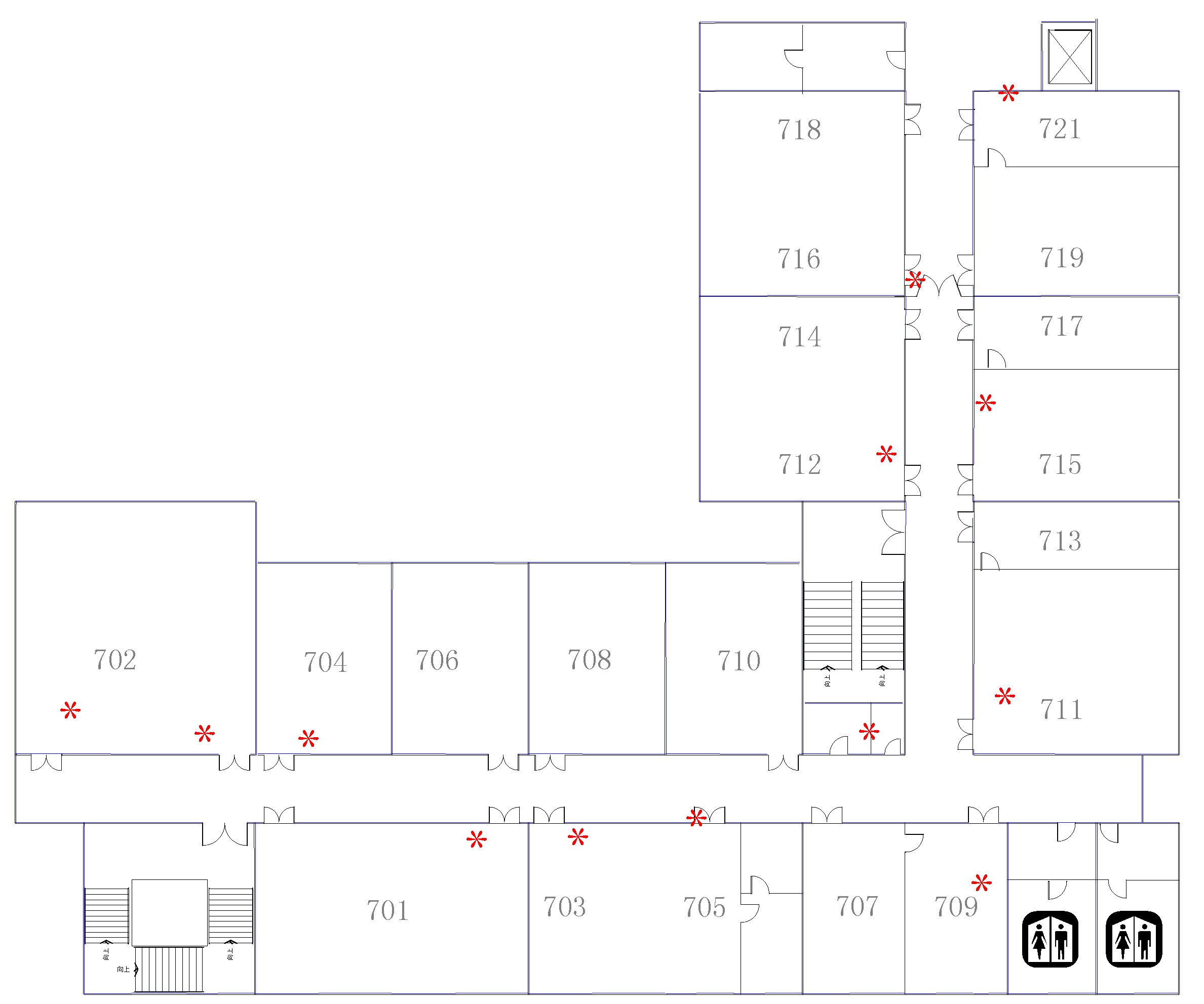
6.1. Experiment Introduction
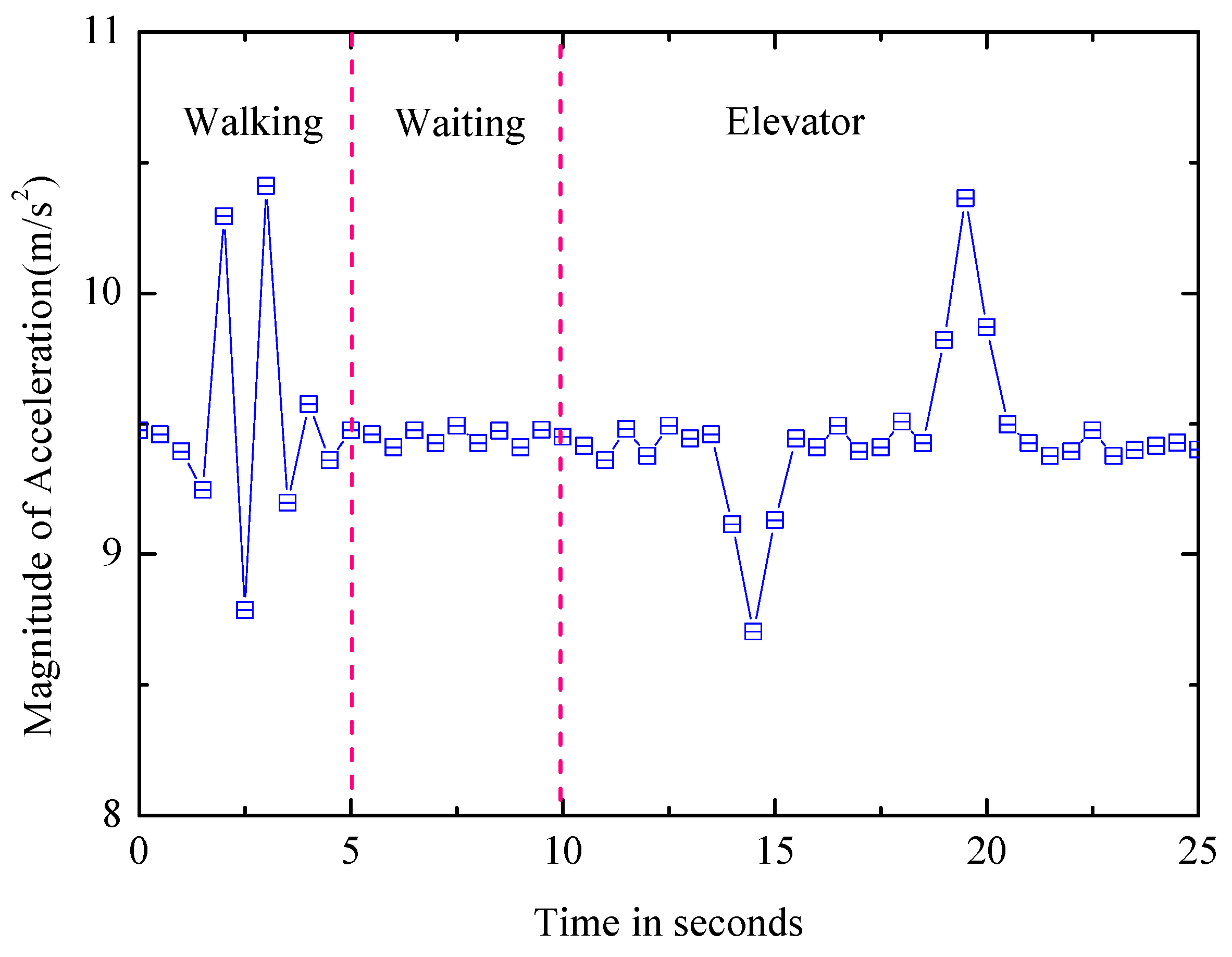
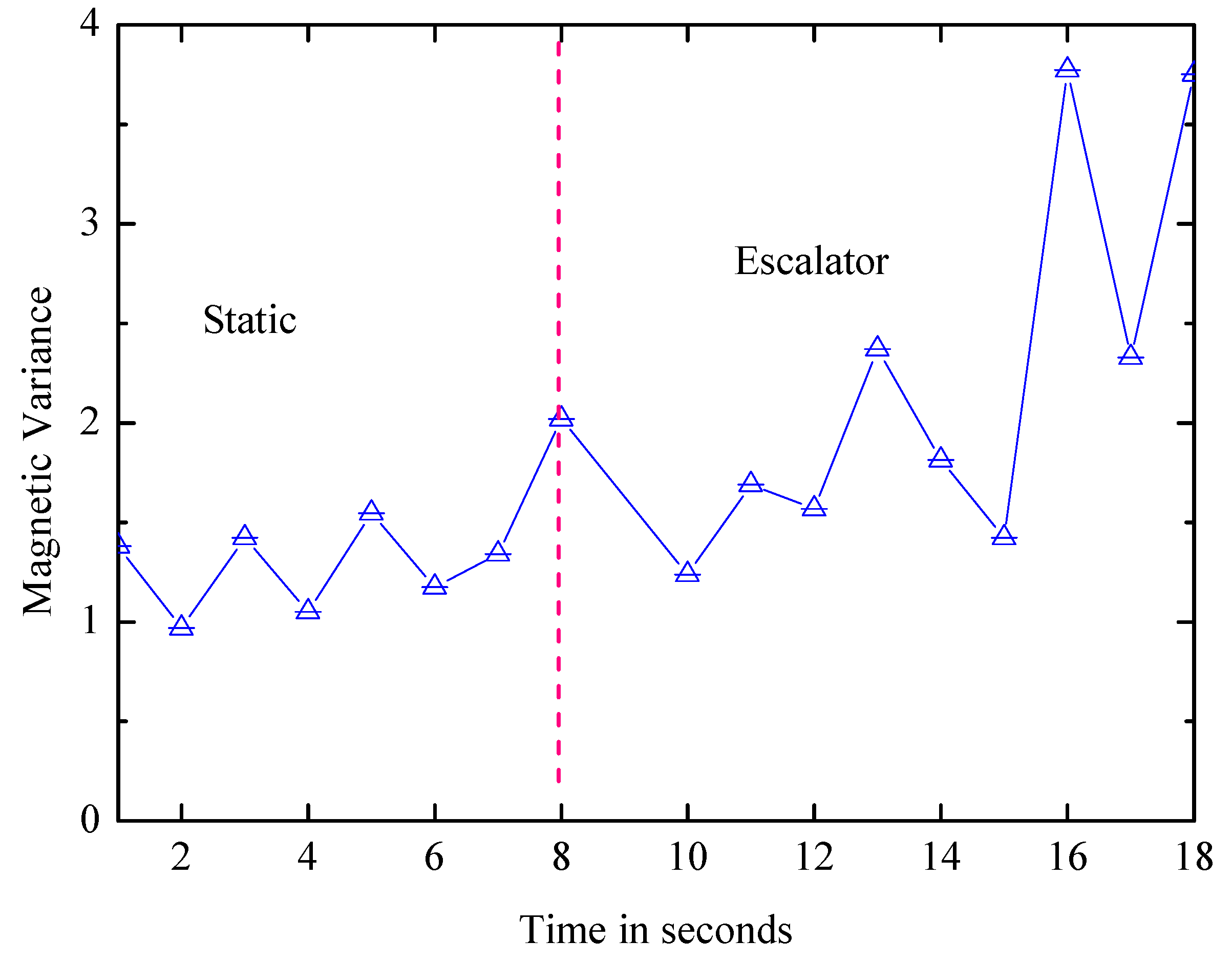
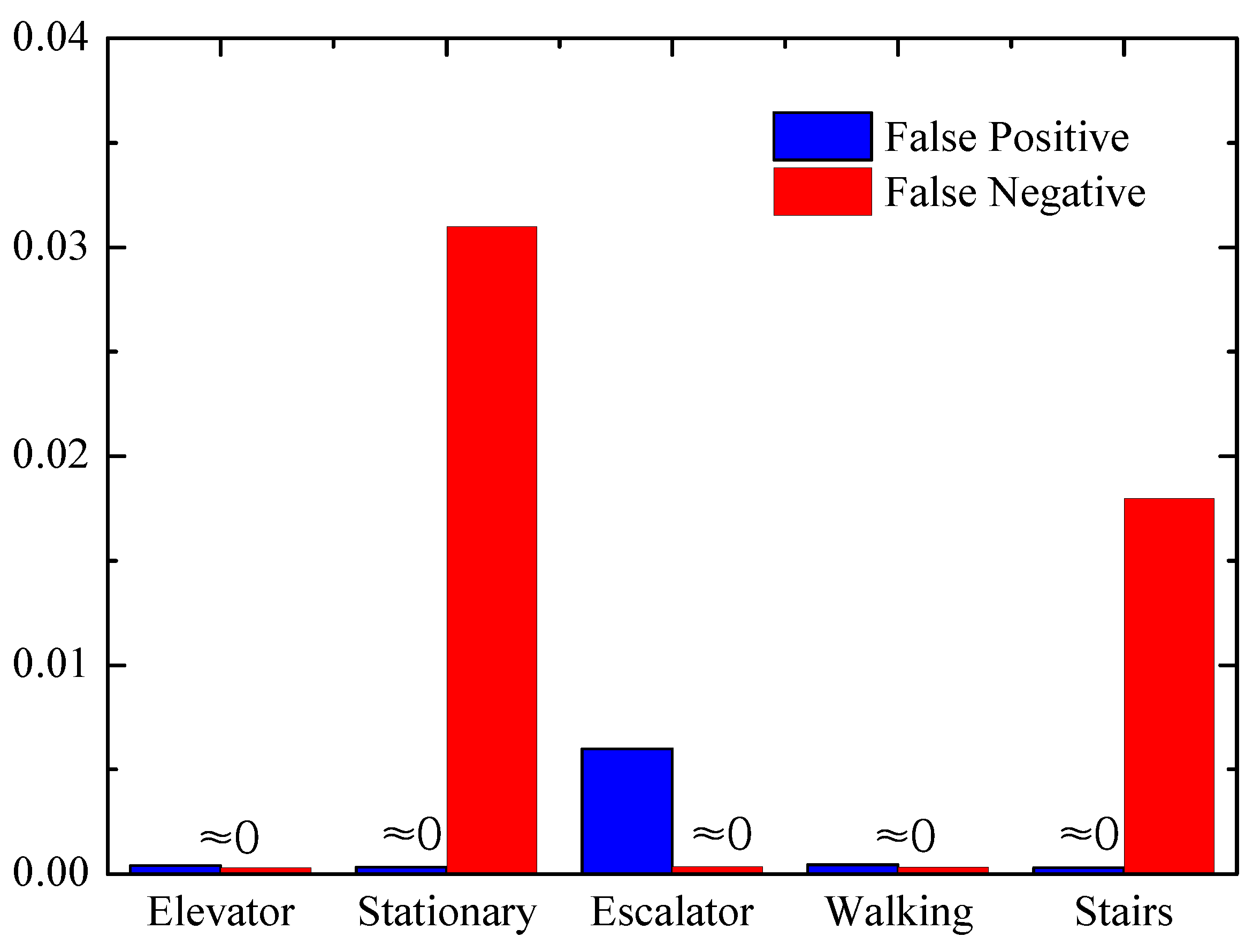
6.2. Landmark Detection
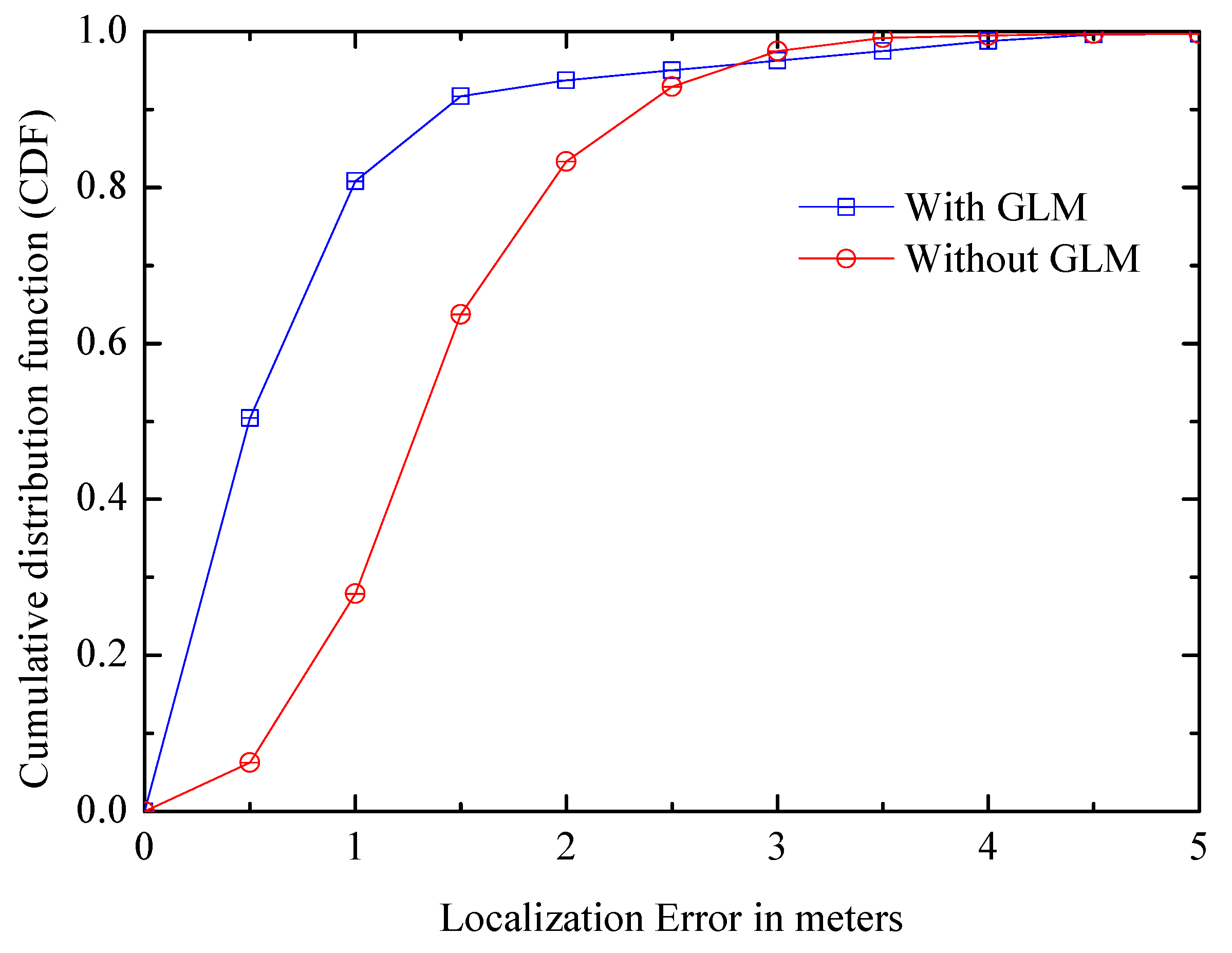
6.2.1. Global Landmark
6.2.2. Local Landmark
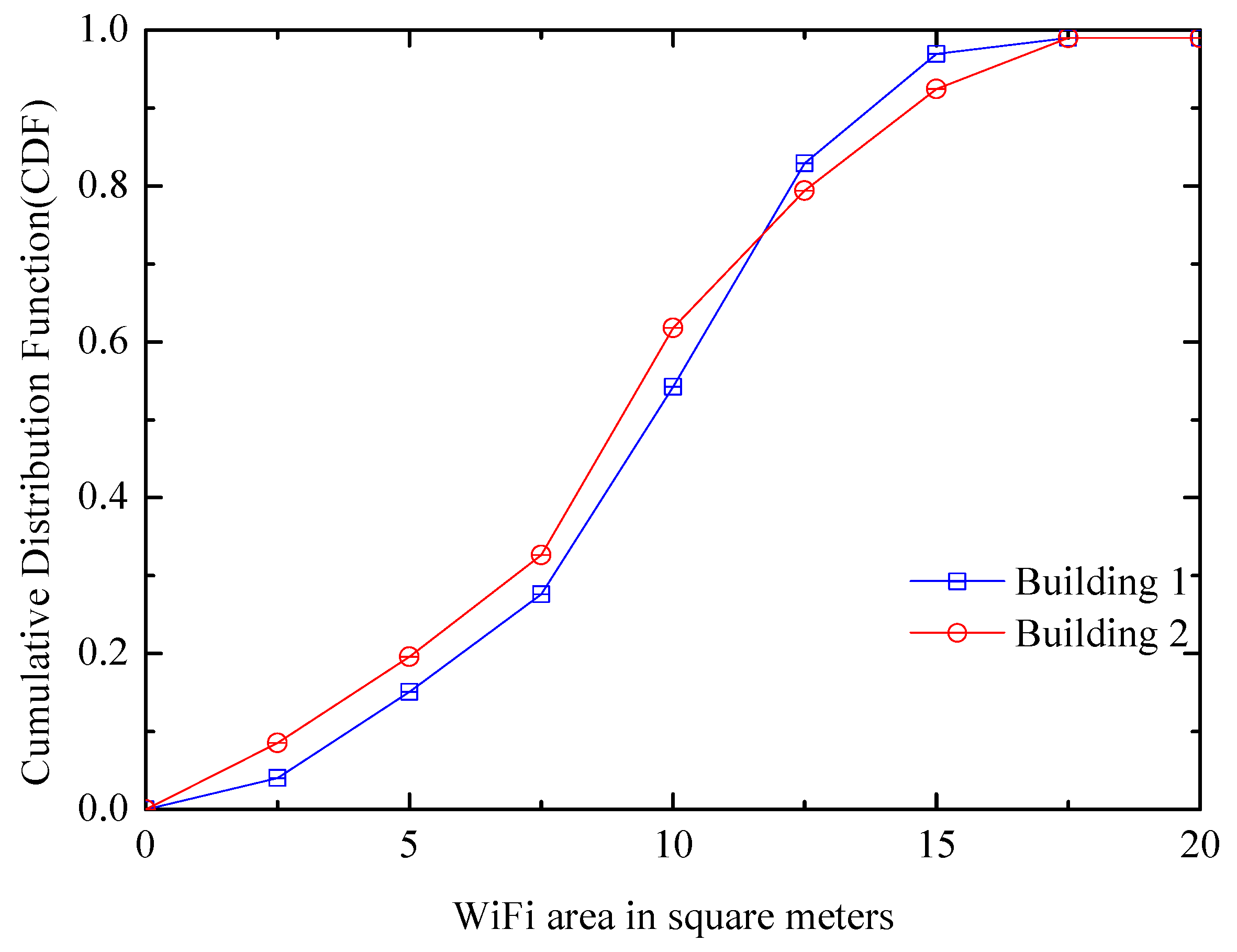
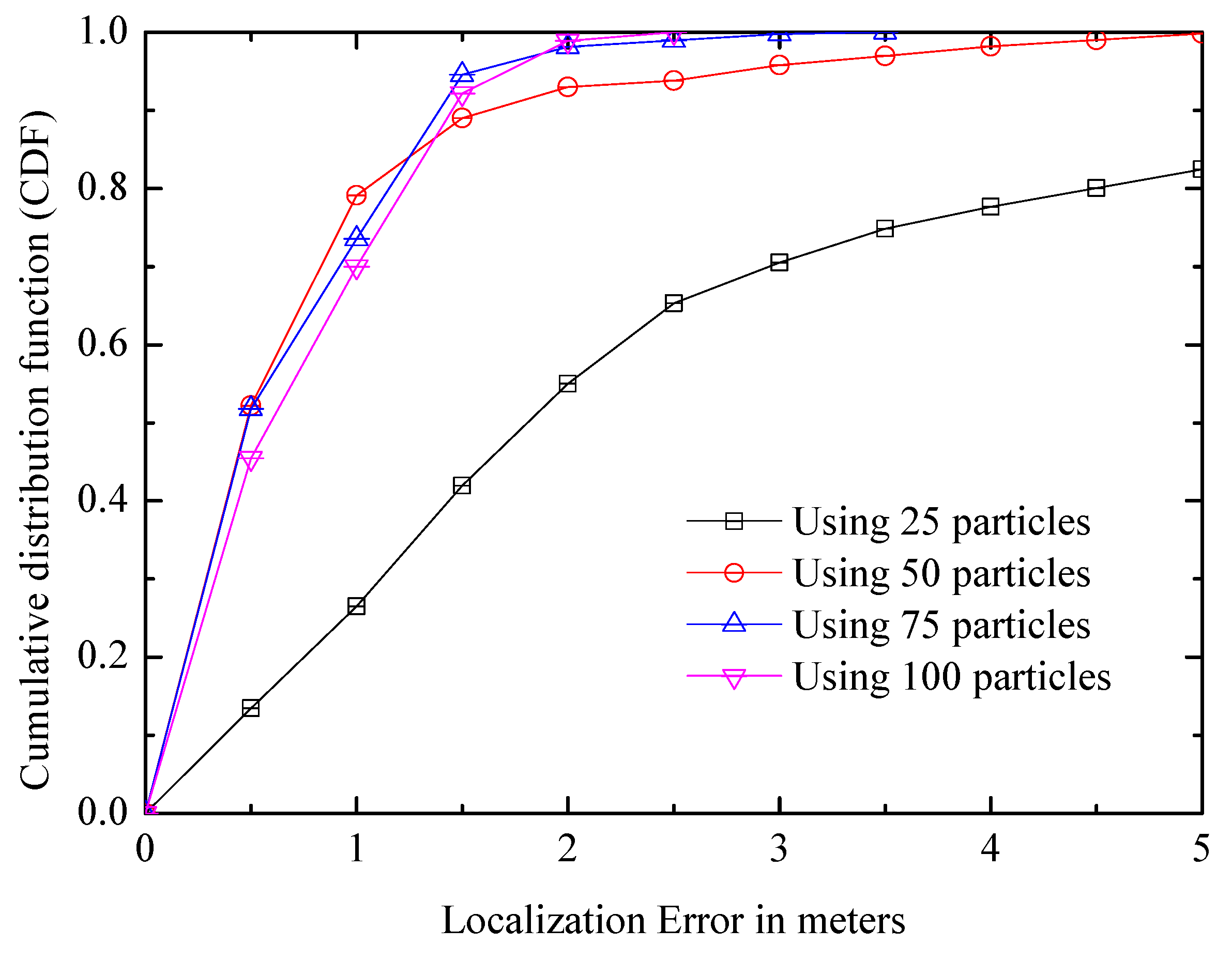
6.2.3. Landmark Quantity
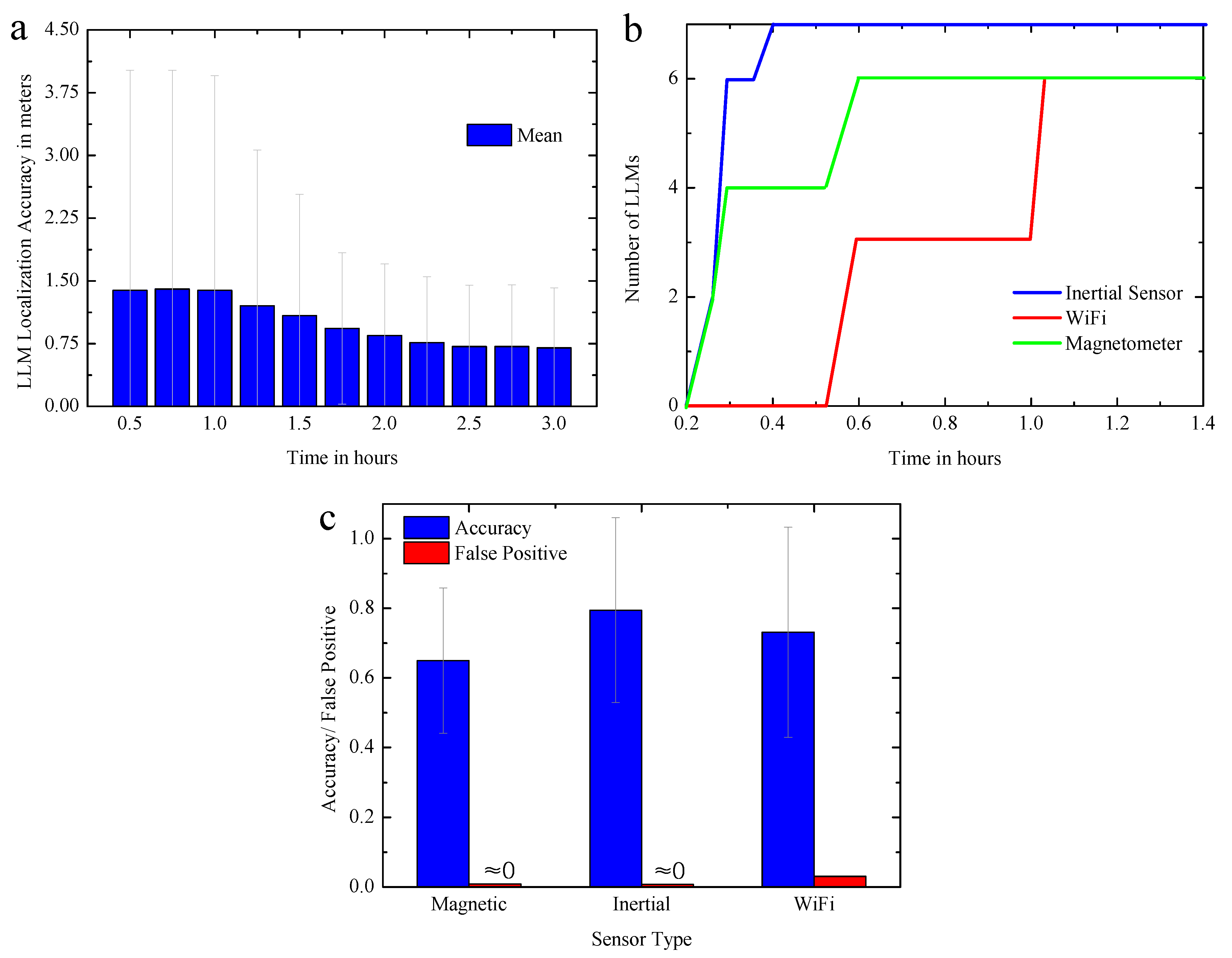
6.3. UIP Positioning Assessment
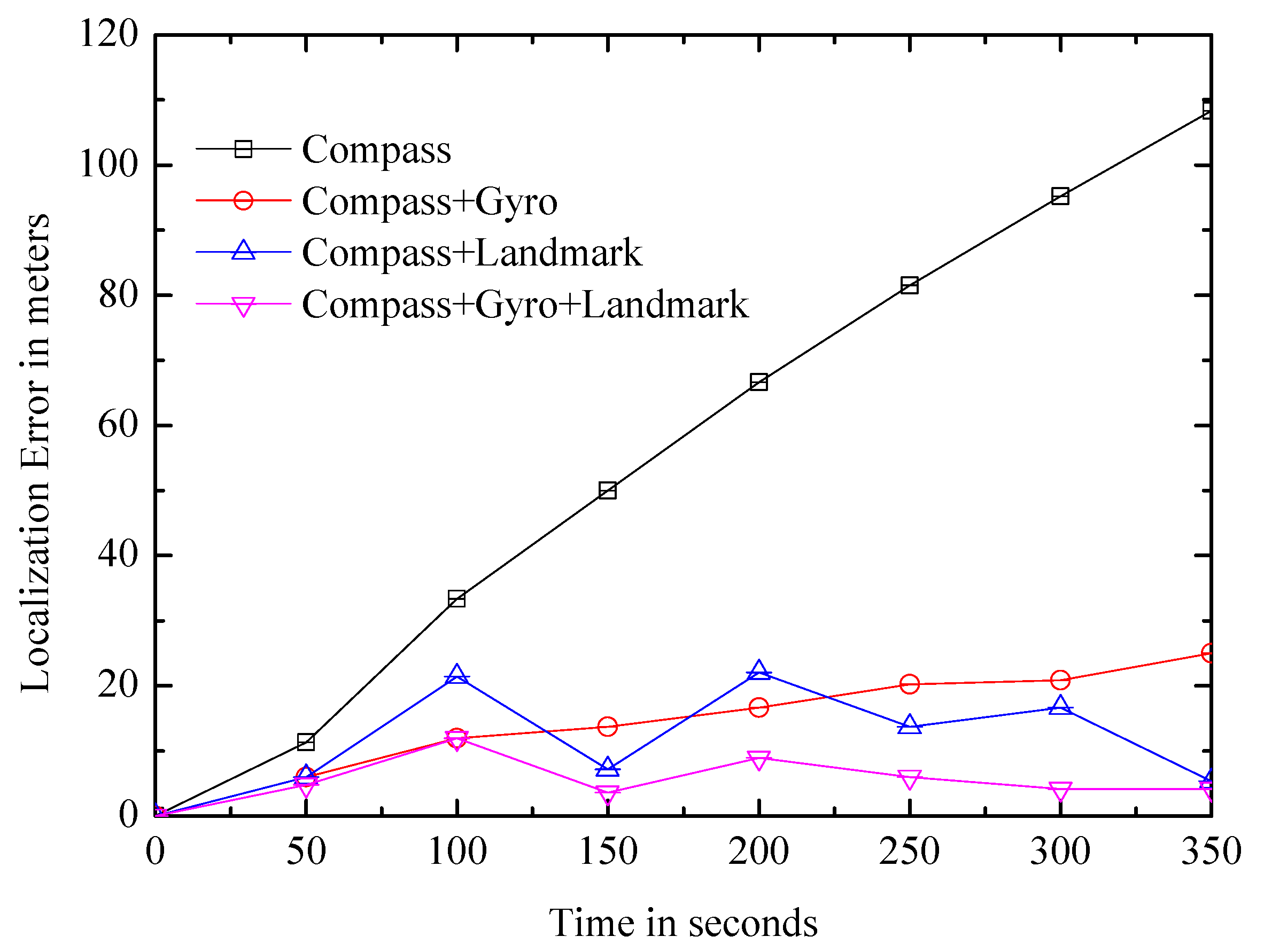
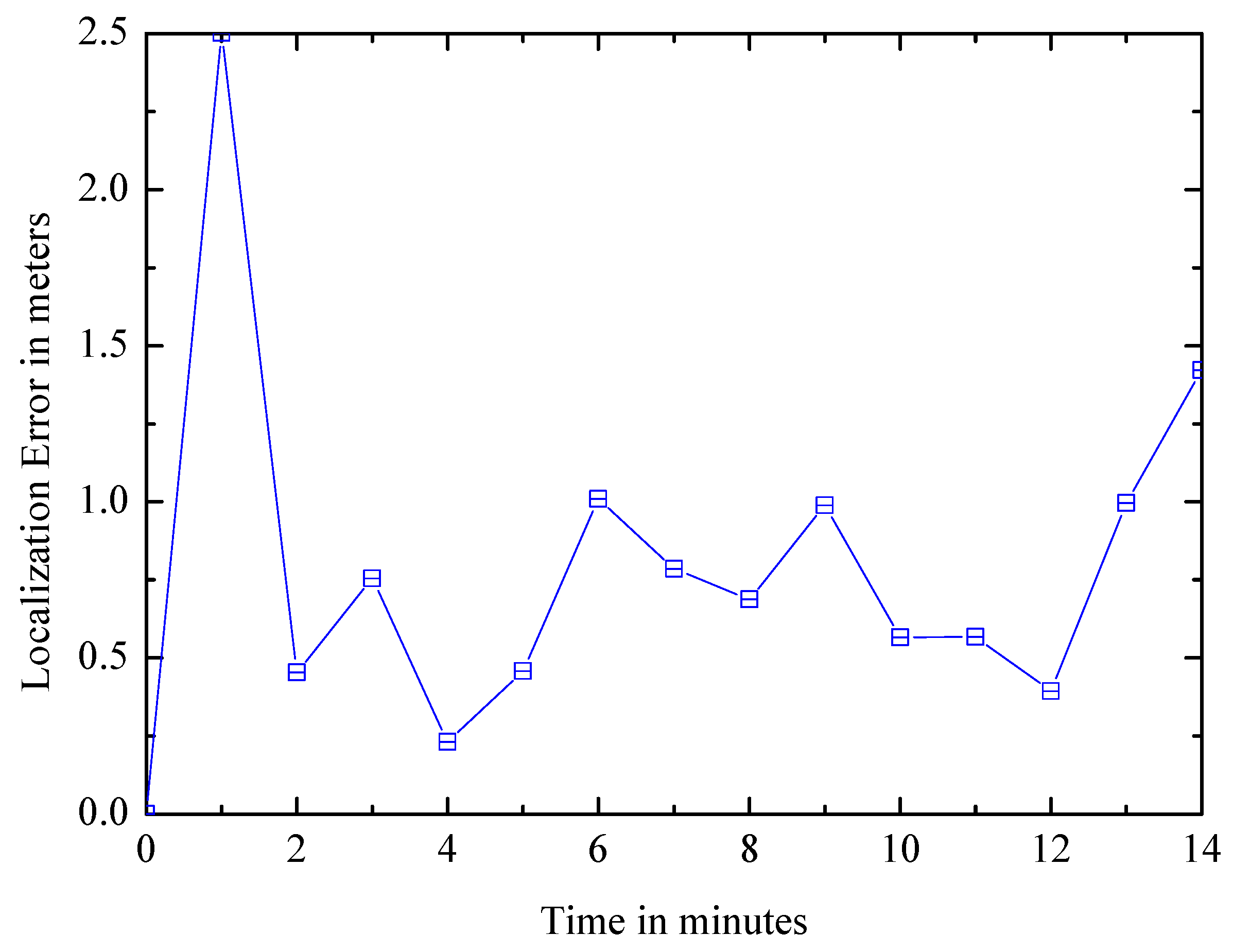
6.3.1. Factors Affecting Performance
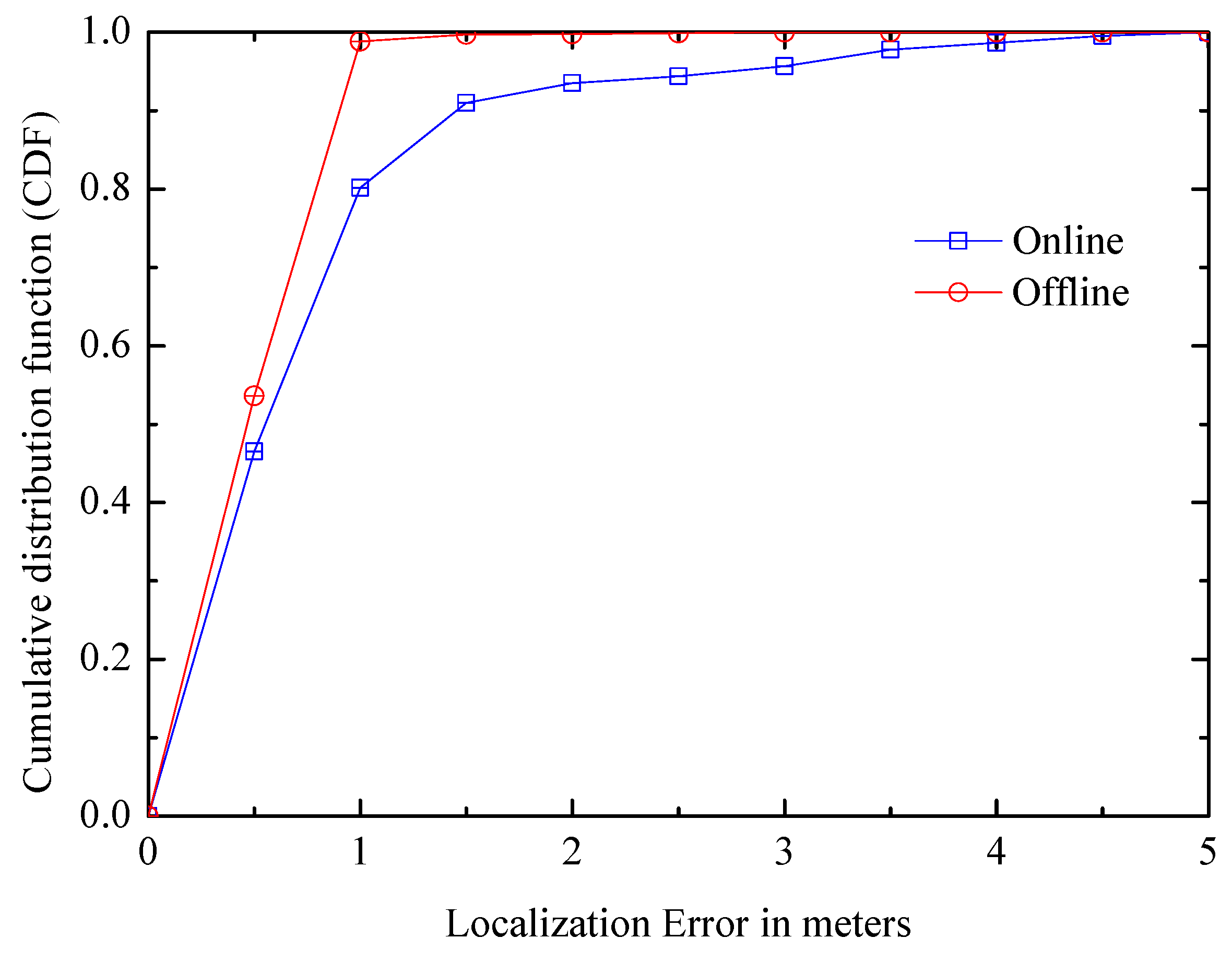
6.3.2. SLAM Framework
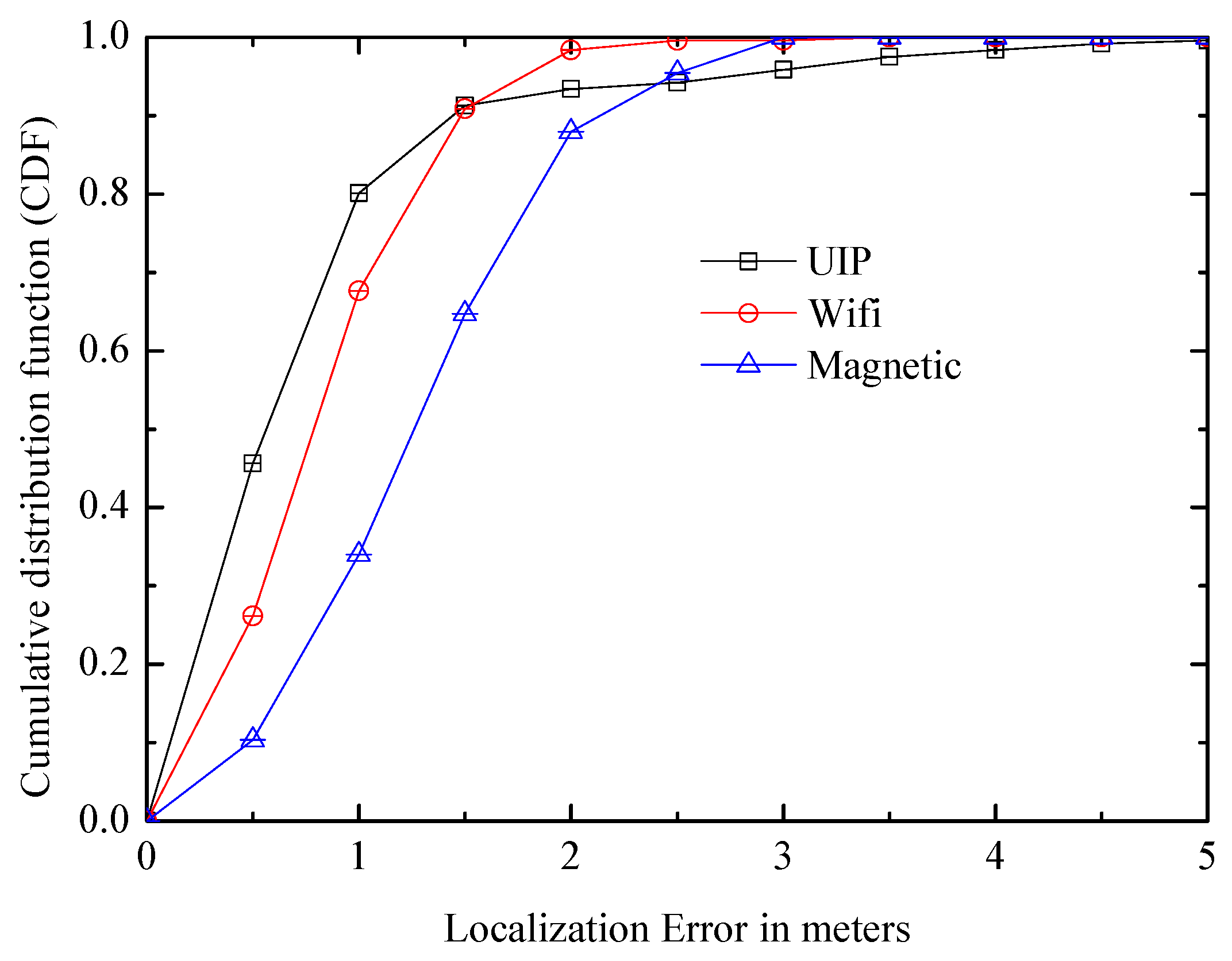
6.3.3. Other Systems
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| UIP | Unsupervised Indoor Positioning |
| SLAM | Simultaneous Localization and Mapping |
| GNSS | Global Navigation Satellite System |
| AP | Access Point |
| CSI | Channel State Information |
| RSSI | Received Signal Strength Indication |
| CDF | Cumulative Distribution Function |
References
- Hou, X.; Arslan, T. Monte Carlo localization algorithm for indoor positioning using Bluetooth low energy devices. In Proceedings of the International Conference on Localization and GNSS (ICL-GNSS), Nottingham, UK, 27–29 June 2017; pp. 1–6. [Google Scholar]
- Song, J.; Jeong, H.; Hui, S.; Park, Y. Improved indoor position estimation algorithm based on geo-magnetism intensity. In Proceedings of the 2014 International Conference on Indoor Positioning and Indoor Navigation(IPIN), Busan, Korea, 27–30 October 2014; pp. 741–744. [Google Scholar]
- Zhang, Y.; Deng, L.; Yang, Z. Indoor positioning based on FM radio signals strength. In Proceedings of the 2017 First International Conference on Electronics Instrumentation & Information Systems (EIIS), Harbin, China, 3–5 June 2017; pp. 1–5. [Google Scholar]
- Ding, H.; Zheng, Z.; Zhang, Y. AP weighted multiple matching nearest neighbors approach for fingerprint-based indoor localization. In Proceedings of the International Conference on Ubiquitous Positioning, Indoor Navigation and Location Based Services (UPINLBS), Shanghai, China, 3–4 November 2016; pp. 218–222. [Google Scholar]
- Kui, W.; Mao, S.; Hei, X.; Li, F. Towards accurate indoor localization using channel state information. In Proceedings of the International Conference on Consumer Electronics-Taiwan (ICCE-TW), Taichung, Taiwan, 19–21 May 2018; pp. 1–2. [Google Scholar]
- Zayets, A.; Steinbach, E. Robust WiFi-based indoor localization using multipath component analysis. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation (IPIN), Sapporo, Japan, 18–21 September 2017; pp. 1–8. [Google Scholar]
- Jung, S.-H.; Han, D. Automated Construction and Maintenance of Wi-Fi Radio Maps for Crowdsourcing-Based Indoor Positioning Systems. IEEE Access 2018, 6, 1764–1777. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, J.; Xue, W. Unsupervised indoor localization based on Smartphone Sensors, iBeacon and Wi-Fi. In Proceedings of the 2018 Ubiquitous Positioning, Indoor Navigation and Location-Based Services (UPINLBS), Wuhan, China, 22–23 March 2018; pp. 1–8. [Google Scholar]
- Szabo, A.; Weiherer, T.; Bamberger, J. Unsupervised Learning of Propagation Time for Indoor Localization. In Proceedings of the 2011 IEEE 73rd Vehicular Technology Conference (VTC Spring), Yokohama, Japan, 15–18 May 2011; pp. 1–5. [Google Scholar]
- Want, R.; Hopper, A.; Falcao, V.; Gibbons, J. The active badge location system. ACM Trans. Inf. Syst. 1992, 10, 91–102. [Google Scholar] [CrossRef]
- Niculescu, D.; Nath, B. VOR base stations for indoor 802.11 positioning. In Proceedings of the 10th Annual International Conference on Mobile Computing and Networking, Philadelphia, PA, USA, 26 September–1 October 2004; pp. 58–69. [Google Scholar]
- Bahl, P.; Padmanabhan, V.N. RADAR: An in-building RF-based user location and tracking system. In Proceedings of the 19th Annual Joint Conference of the IEEE Computer and Communications Societies, Tel Aviv, Israel, 26–30 March 2000; pp. 775–782. [Google Scholar]
- Youssef, M.; Youssef, A.; Rieger, C. Pinpoint: An asynchronous time-based location determination system. In Proceedings of the 19th Annual Joint Conference of the IEEE Computer and Communications Societies, New York, NY, USA, 23–29 April 2006; pp. 165–176. [Google Scholar]
- Krishnan, P.; Krishnakumar, A.S.; Ju, W.H.; Mallows, C.; Gamt, S.N. A system for LEASE: Location estimation assisted by stationary emitters for indoor RF wireless networks. In Proceedings of the International Conference on Computer Communicat, Hong Kong, China, 7–11 March 2004; pp. 1001–1011. [Google Scholar]
- Cheng, Y.C.; Chawathe, Y.; LaMarca, A.; Krumm, J. Accuracy characterization for metropolitan-scale Wi-Fi localization. In Proceedings of the 3rd International Conference on Mobile Systems, Applications, and Services, Seattle, WA, USA, 6–8 June 2005; pp. 233–245. [Google Scholar]
- Chintalapudi, K.; Padmanabha, I.A.; Padmanabhan, V.N. Indoor localization without the pain. In Proceedings of the Sixteenth Annual International Conference on Mobile Computing and Networking, New York, NY, USA, 20–24 September 2010; pp. 173–184. [Google Scholar]
- Youssef, M.; Yosef, M.A.; El-Derini, M. GAC: Energy-efficient hybrid GPS-accelerometer-compass GSM localization. In Proceedings of the IEEE Global Telecommunication Conference, Miami, FL, USA, 6–10 December 2010; pp. 1–5. [Google Scholar]
- Constandache, I.; Choudhury, R.R.; Rhee, I. Towards mobile phone localization without war-driving. In Proceedings of the International Conference on Computer Communications, San Diego, CA, USA, 15–19 March 2010; pp. 1–9. [Google Scholar]
- PanyovA, A.; Golovan, A.A.; Smirnov, A.S. Indoor positioning using Wi-Fi fingerprinting pedestrian dead reckoning and aided INS. In Proceedings of the 2014 International Symposium on Inertial Sensors and Systems(ISISS), Laguna Beach, CA, USA, 25–26 February 2014; pp. 1–2. [Google Scholar]
- Kim, Y.; Eyobu, O.S.; Han, D.S. ANN-based stride detection using smartphones for Pedestrian dead reckoning. In Proceedings of the 2018 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 12–15 January 2018; pp. 1–2. [Google Scholar]
- Alzantot, M.; Youssef, M. Crowdinside: Automatic construction of indoor floorplans. In Proceedings of the 20th International Conference on Advances in Geographic Information Systems, New York, USA, 7–9 November 2012; pp. 99–108. [Google Scholar]
- Elhamshary, M.; Youssef, M. CheckInside: A fine-grained indoor location-based social network. In Proceedings of the 2014 ACM International Joint Conference on Pervasive and Ubiquitous Computing, Seattle, WA, USA, 13–17 September 2014; pp. 607–618. [Google Scholar]
- Elhamshary, M.; Youssef, M. SemSense: Automatic construction of semantic indoor floorplans. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation (IPIN), Banff, AB, Canada, 13–16 October 2015; pp. 1–11. [Google Scholar]
- Evennou, F.; Marx, F. Advanced integration of WiFi and inertial navigation systems for indoor mobile positioning. EURASIP J. Appl. Signal Process. 2006, 2006, 164. [Google Scholar] [CrossRef]
- Durrant-Whyte, H.; Bailey, T. Simultaneous localization and mapping: Part I. IEEE Robot. Autom. Mag. 2006, 13, 99–110. [Google Scholar] [CrossRef]
- Moutarlier, P.; Chatila, R. An experimental system for incremental environment modelling by an autonomous mobile robot. In Proceedings of the International Symposium on Experimental Robotics, Québec City, QC, Canada, 18–21 June 2012; pp. 327–346. [Google Scholar]
- Moutarilier, P. Stochastic multisensory data fusion for mobile robot location and environment modeling. In Proceedings of the 5th International Symposium on Robotics Research, Tokyo, Japan, 28–31 August 1989. [Google Scholar]
- Doucet, A.; De Freitas, N.; Gordon, N. An introduction to sequential Monte Carlo methods. In Sequential Monte Carlo Methods in Practice; Doucet, A., De Freitas, N., Gordon, N., Eds.; Publishing House: New York, NY, USA, 2001; pp. 3–14. [Google Scholar]
- Liu, J.S. Chen R.Sequential Monte Carlo methods for dynamic systems. J. Am. Stat. Assoc. 1998, 93, 1032–1044. [Google Scholar] [CrossRef]
- Montemerlo, M.; Thrun, S.; Koller, D. FastSLAM: A factored solution to the simultaneous localization and mapping problem. In Proceedings of the 8th National Conference on Artificial Intelligence (AAAI-02), Edmonton, AB, Canada, 28 July–1 August 2002; pp. 1032–1044. [Google Scholar]
- Michael, M.; Sebastian, T.; Daphne, K. Fastslam 2.0: An improved particle filtering algorithm for simultaneous localization and mapping that provably converges. In Proceedings of the Sixteenth International Joint Conference on Artificial Intelligence (IJCAI), Edmonton, AB, Canada, 28 July–1 August 2002. [Google Scholar]
- Youssef, M.; Agrawala, A. The Horus WLAN location determination system. In Proceedings of the 3rd International Conference on Mobile Systems, Applications, and Services, Seattle, WA, USA, 6–8 June 2005; pp. 205–218. [Google Scholar]
- Xie, H.; Gu, T.; Tao, X.; Ye, H.; Lv, J. Maloc: A practical magnetic fingerprinting approach to indoor localization using smartphones. In Proceedings of the 2014 ACM International Joint Conference on Pervasive and Ubiquitous Computing, Seattle, WA, USA, 13–17 September 2014; pp. 243–253. [Google Scholar]







© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, P.; Qin, D.; Zhao, M.; Guo, R.; Berhane, T.M. Unsupervised Indoor Positioning System Based on Environmental Signatures. Entropy 2019, 21, 327. https://doi.org/10.3390/e21030327
Feng P, Qin D, Zhao M, Guo R, Berhane TM. Unsupervised Indoor Positioning System Based on Environmental Signatures. Entropy. 2019; 21(3):327. https://doi.org/10.3390/e21030327
Chicago/Turabian StyleFeng, Pan, Danyang Qin, Min Zhao, Ruolin Guo, and Teklu Merhawit Berhane. 2019. "Unsupervised Indoor Positioning System Based on Environmental Signatures" Entropy 21, no. 3: 327. https://doi.org/10.3390/e21030327
APA StyleFeng, P., Qin, D., Zhao, M., Guo, R., & Berhane, T. M. (2019). Unsupervised Indoor Positioning System Based on Environmental Signatures. Entropy, 21(3), 327. https://doi.org/10.3390/e21030327




