Efficient Algorithms for Coded Multicasting in Heterogeneous Caching Networks
Abstract
:1. Introduction
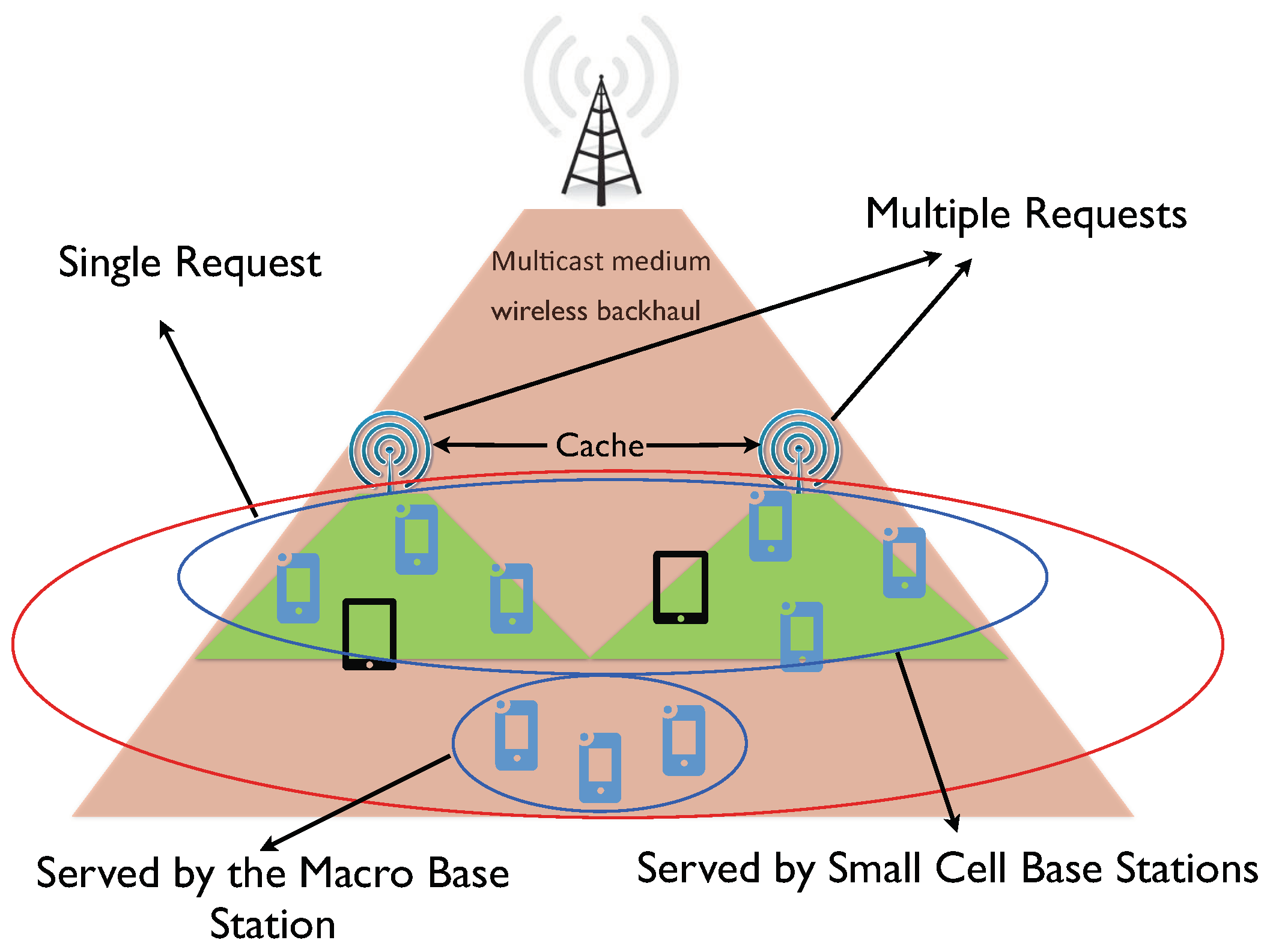
- We provide a generalized model for heterogeneous shared link caching networks, in which users can have different cache sizes and make different number of requests according to different demand distributions.
- We design two novel coded multicast algorithms based on local graph coloring, referred to as Greedy Local Coloring (GLC) and Hierarchical Greedy Local Coloring (HgLC) that exhibit polynomial-time complexity in both the number of caches and the packetization order. In combination with the Random Aggregate Popularity (RAP) placement policy of [10,12], we show that the overall schemes RAP-GLC and RAP-HgLC are order-optimal in the asymptotic file-length regime.
- Focusing on the finite-length regime, in which content items can be partitioned into a finite number of packets, we show how the general advantage of local graph coloring is especially relevant when the number of per-user requests grow. We validate via simulations the superiority of RAP-GLC, especially with high number of per-user requests. We then show how RAP-HgLC, with a slight increase in the polynomial complexity order, further improves the caching gain of RAP-GLC, remarkably approaching the multiplicative gain that existing schemes can only guarantee in the asymptotic file-length regime.
- We demonstrate that there is a tradeoff between the required packetization order and the number of requested files per user. In particular, for a given target gain, if the number of requests increases, then the number of packets per file can be reduced, while preserving the target gain. We further quantify the regime of per-user requests for which a caching scheme with unit packetization order (i.e., a scheme that treats only whole files) is order-optimal. Our analysis illustrates the key impact of content request aggregation in time and space on caching performance. That is, if edge caches can wait for collecting multiple requests over time and/or aggregate requests from multiple users, the same performance can be achieved with lower packetization order, and hence lower computational complexity.
2. Network Model and Problem Formulation
- Placement phase, which operates at a large time-scale and determines the content to be placed at the caching nodes,
- Delivery phase, during which users requests are served from the content caches and sources in the network.
2.1. Random Fractional Cache Placement
- Packetization: Each file is partitioned into B packets of equal-size bits, where the integer B is referred to as the packetization order. Each packet is represented by a symbol in finite field , where we assume that is large enough.
- Random Placement: Each user u caches packets independently at random from each file f, where is the probability that file f is cached at user u, and satisfies such that .
2.2. Random Multiple Requests
2.3. Performance Metric
3. Graph-Coloring-Based Coded Multicast Delivery
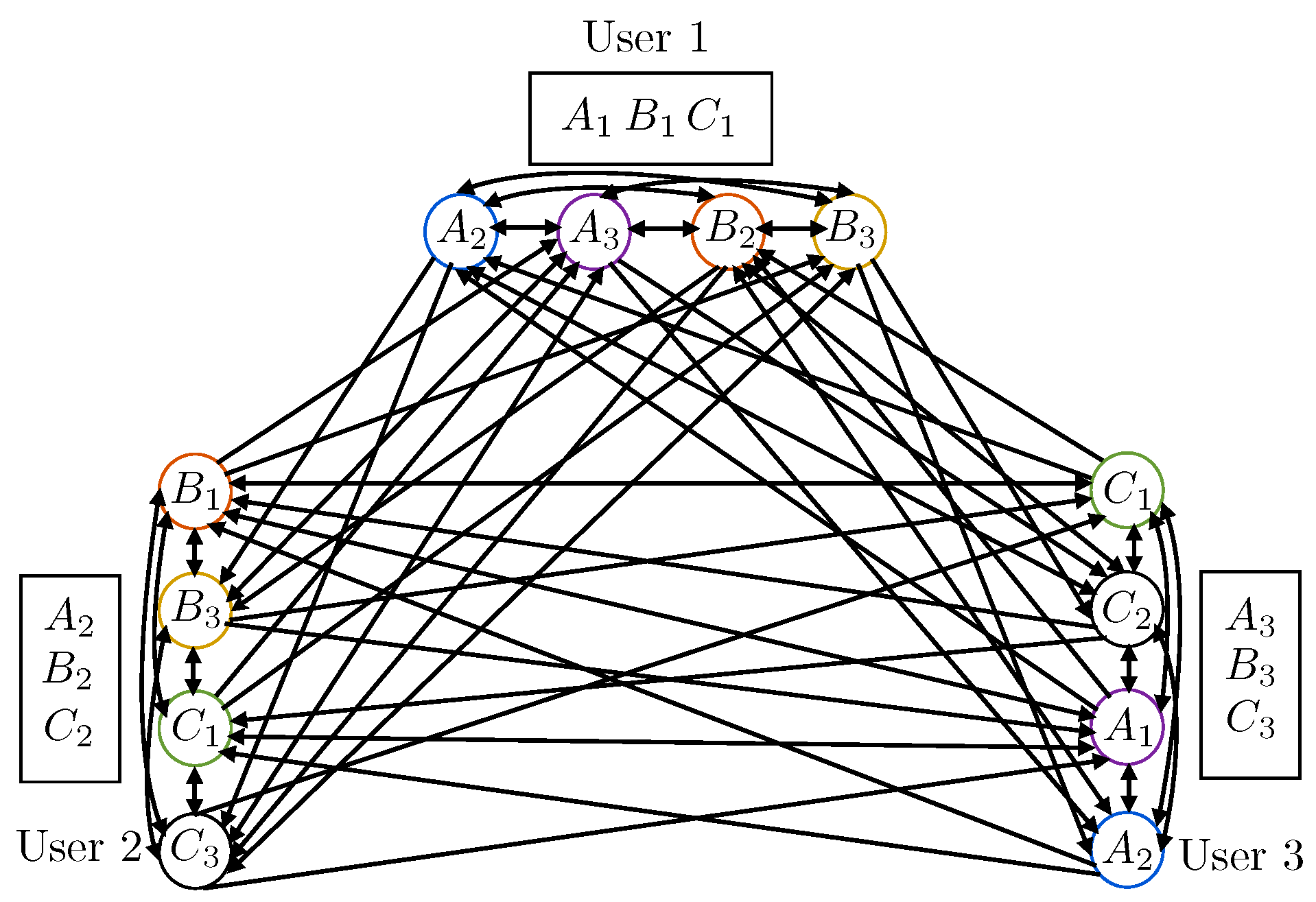
3.1. Conflict Graph Construction
- Vertices: For each packet request in , there is a vertex in . Each vertex is uniquely identified or labeled by a packet-user pair , where denotes the identity of the packet, and the user requesting it. Hence, if a packet is requested by multiple users, such a packet is represented in as many vertices as the number of users requesting it. Such vertices have the same packet label , but different user label .
- Arcs: For any , there is an edge with direction from to if and only if and packet is not in the cache of user .
- and : This indicates that two different packets are requested by the same user. Then, and are mutually conflicting, in the sense that if sent within the same time-frequency resource they interfere with each other. Hence, in the conflict graph, they are connected with two directed edges, and ;
- and : This indicates that the same packet is requested by two different users. Then, and are not conflicting, and hence not connected in the conflict graph; i.e., and ;
- and : This indicates that two different packets are requested by two different users. In this case, if packet is in the cache of user , then, even if and are sent within the same time-frequency resource, user will not suffer from interference, since, using its cache information, it can cancel out the undesired packet from the received signal. On the other hand, if packet is not in the cache of user , then conflicts with , and a directed edge is drawn from to . Similarly, if and only if .
3.2. Code Construction
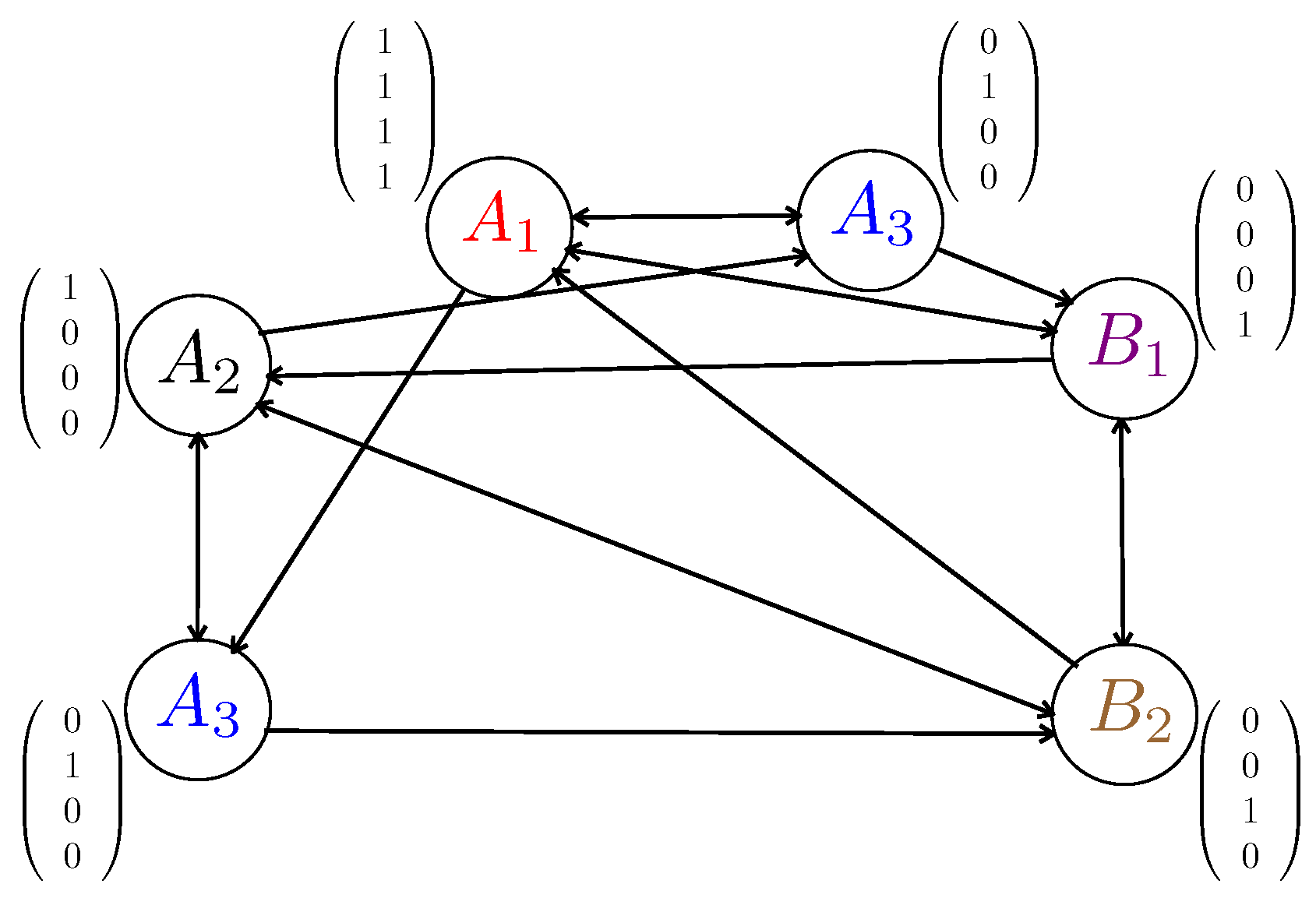
3.2.1. Graph Coloring and Chromatic Number
3.2.2. Local Graph Coloring and Local Chromatic Number
3.3. Benefits of Local Coloring
4. Proposed Algorithms and Performance Analysis
- Given a realization of the cache placement () and of the user requests (), build the conflict graph as in Section 3.1.
- Use any of the above algorithms (GLC or HgLC) to compute a proper coloring. Let denote the number of colors used by either of the above algorithms to color . Let be the associated local coloring number.
- Consider a MDS code and compute the corresponding coded multicast scheme as described in Section 3.2.2.
4.1. Randomized Aggregate Popularity-Greedy Local Coloring (RAP-GLC)
4.1.1. RAP-GLC Algorithm Description
| Algorithm 1 RAP-GLC |
| 1: Let ; 2: Let ; 3: while do 4: Pick an arbitrary vertex v in ; Let ; 5: Let ; 6: if { } then 7: for all with do 8: ; 9: end for 10: Color all the vertices in by ; 11: Let ; 12: . 13: else 14: for all with do 15: if {There is no edge between and } then 16: ; 17: end if 18: end for 19: Color all the vertices in by ; 20: Let ; 21: . 22: end if 23: end while 24: return the local coloring number and the corresponding color assignment for each v; |
4.1.2. RAP-GLC Performance Analysis
4.2. Randomized Aggregate Popularity-Hierarchical Greedy Local Coloring (RAP-HgLC) for Finite-Length Packetization
4.2.1. RAP-HgLC Algorithm Description
- : The i-th layer, is initialized with the set of vertices and at any point in the algorithm contains only vertices with . is updated continuously in the algorithm. Therefore, higher numbered layers contain vertices with greater popularity.
- : a subset of consists of all the vertices with as well as a certain number of vertices with higher popularity (if available at any iteration), defined aswhere is a design parameter and is updated with every iteration.
- (see Algorithm 2): another subset of that is updated every iteration.
- : a subset of vertices in defined as:where is another design parameter.
- Step I: The first step is similar to that in RAP-GLC algorithm. Given a vertex v, the algorithm first checks if the cardinality of is higher than t, i.e., then all the vertices such that are colored with the same color. If then the algorithm greedily finds independent sets of size i, where every vertex v in the independent set (Algorithm 2, Line 20) has the same (Algorithm 2, Line 19). After removing these vertices, the rest of the vertices in are left for the second step.
- Step II: A candidate pool of vertices is created. This set contains vertices v such that being close to the smallest available ’s. We randomly pick a vertex v from (Algorithm 2, Line 31). The design parameter a determines how close is the picked to the smallest available ones. We gradually form an independent set of size i with v included as follows: Form another set (Algorithm 2, Line 34), excluding v, whose vertices have that is bigger but closer to that of v determined by b, sample repeatedly with replacement from it to grow the independent set. If an independent set of size at least i cannot be formed, we drop the vertex v to the lower layer , and take it into account in the next layer iteration. Otherwise, we assign a color to the independent set. is repeatedly formed and random sampling from repeated till every vertex in is dropped or colored.
| Algorithm 2 HgLC |
| 1: ; 2: ; 3: choose 4: choose 5: for all do 6: for all and do 7: ; 8: Let ; 9: if { } then 10: for all with do 11: ; 12: end for 13: Color all the vertices in by ; 14: Let ; 15: for all do 16: ; 17: end for 18: else 19: for all with do 20: if {There is no edge between and } then 21: ; 22: end if 23: end for 24: if then 25: Color all the vertices in by ; 26: , ; 27: ; 28: end if 29: end if 30: end for 31: for all with v randomly picked from do 32: ; 33: ; 34: for all with randomly picked from . do 35: if { } ∩ {No edge between and } then 36: ; 37: ; 38: else 39: ; 40: end if 41: end for 42: if then 43: Color all the vertices in by ; 44: , ; 45: ; 46: else 47: , ; 48: end if 49: end for 50: end for 51: LocalSearch(); 52: return the local coloring number and the corresponding color assignment for each v; |
- For each vertex , if there is a color , that is not assigned to any adjacent vertex , then assign vertex i with color ;
- Color c is removed from the set if and only if in the previous step it has been possible to replace c with some color for all vertices in .
| Algorithm 3 LocalSearch() |
| 1: for all do 2: Let be the set of vertices whose color is c; 3: Let ; 4: Let ; 5: for all do 6: ; 7: for all do 8: ; 9: if then 10: is chosen uniformly at random from ; 11: ; 12: ; 13: end if 14: end for 15: if then 16: ; 17: ; 18: end if 19: end for 20: end for 21: return ; |
4.2.2. RAP-HgLC Performance Analysis
5. Tradeoff between Number of Requests and Code Length
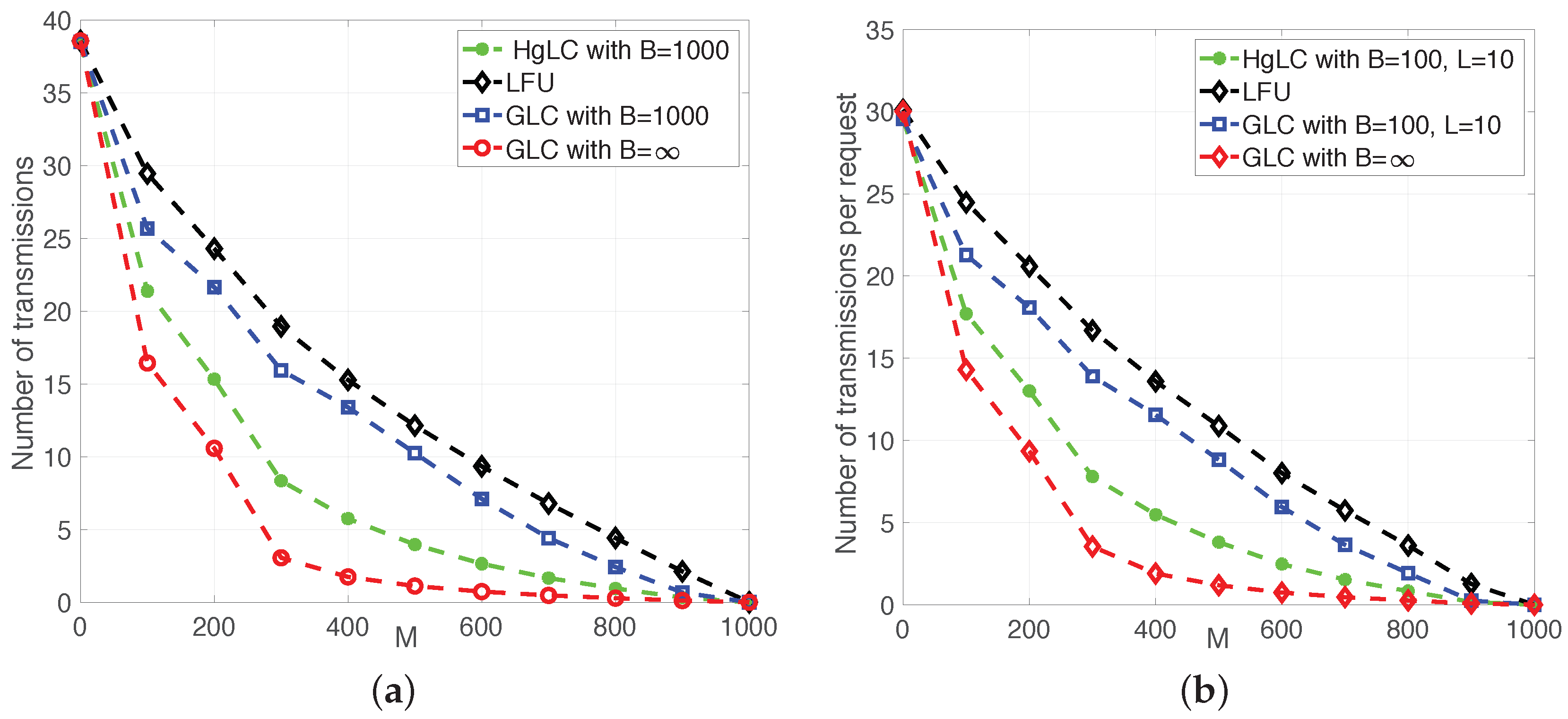
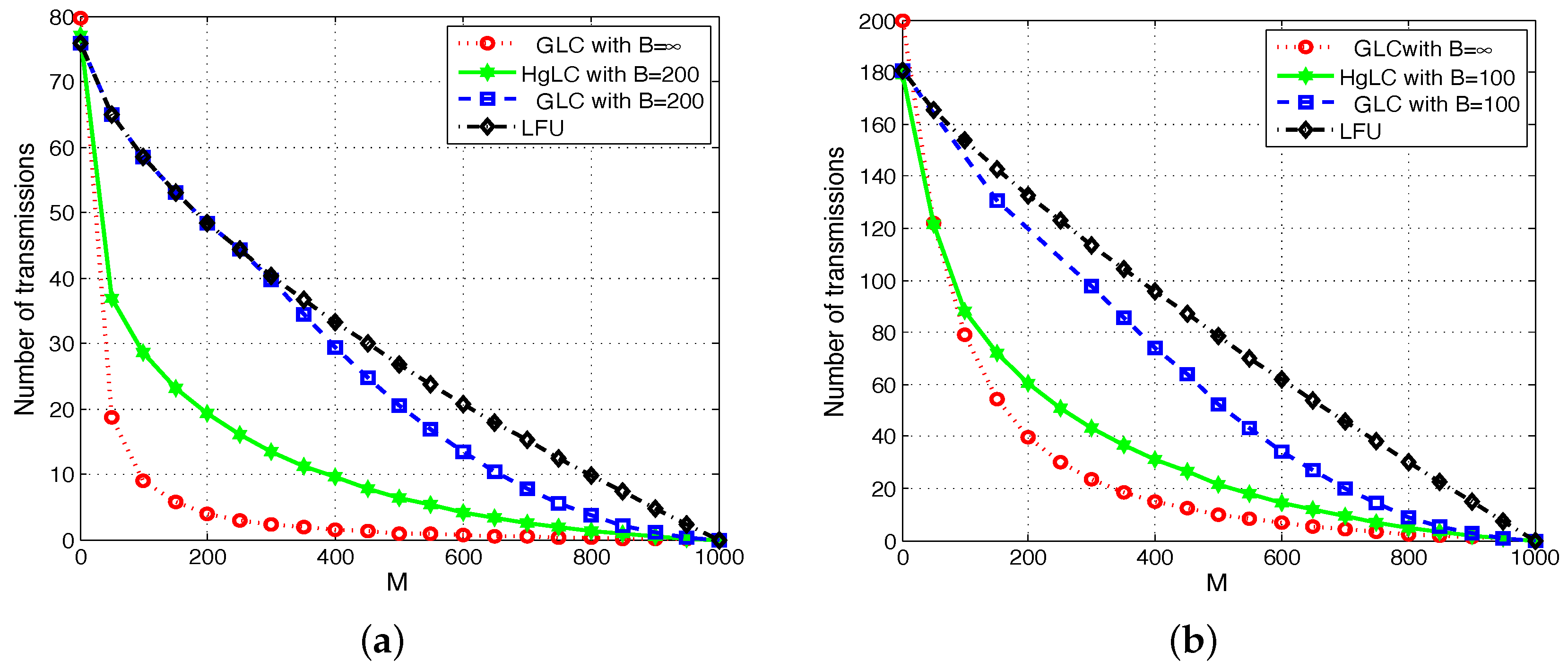
6. Simulations and Discussions
- LFU, which has been shown to be optimal in single cache networks;
- RLFU-GLC with infinite file packetization (), whose performance guarantee is given in Theorem 1, and it is shown to be order optimal.
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof of Theorem 1
Appendix A.1. Average Total Number of Colors for RAP-GLC1
Appendix A.2. Average Total Number of Colors for RAP-GLC2
Appendix B. Proof of Theorem 2
- When , then we have . Hence, is a decreasing function such that the minimum value of take place when . Thus, by using (A15), we obtain the sufficient condition is given by
- When , then we have . Hence, is an increasing function such that the minimum value of take place when . Thus, by using (A15) we obtain the sufficient condition is given byThus, we finished the proof of Theorem 2.
Appendix C. Proof of Theorem 3
References
- Shanmugam, K.; Golrezaei, N.; Dimakis, A.; Molisch, A.; Caire, G. FemtoCaching: Wireless Video Content Delivery through Distributed Caching Helpers. IEEE Trans. Inf. Theory 2013, 59, 8402–8413. [Google Scholar] [CrossRef]
- Llorca, J.; Tulino, A.; Guan, K.; Kilper, D. Network-Coded Caching-Aided Multicast for Efficient Content Delivery. In Proceedings of the 2013 IEEE International Conference on Communications (ICC), Budapest, Hungary, 9–13 June 2013. [Google Scholar]
- Fadlallah, Y.; Tulino, A.M.; Barone, D.; Vettigli, G.; Llorca, J.; Gorce, J. Coding for Caching in 5G Networks. IEEE Commun. Mag. 2017, 55, 106–113. [Google Scholar] [CrossRef]
- Liu, D.; Chen, B.; Yang, C.; Molisch, A.F. Caching at the wireless edge: Design aspects, challenges, and future directions. IEEE Commun. Mag. 2016, 54, 22–28. [Google Scholar] [CrossRef]
- Tandon, R.; Simeone, O. Harnessing cloud and edge synergies: Toward an information theory of fog radio access networks. IEEE Commun. Mag. 2016, 54, 44–50. [Google Scholar] [CrossRef]
- Maddah-Ali, M.A.; Niesen, U. Coding for caching: Fundamental limits and practical challenges. IEEE Commun. Mag. 2016, 54, 23–29. [Google Scholar] [CrossRef]
- Paschos, G.; Bastug, E.; Land, I.; Caire, G.; Debbah, M. Wireless caching: Technical misconceptions and business barriers. IEEE Commun. Mag. 2016, 54, 16–22. [Google Scholar] [CrossRef]
- Maddah-Ali, M.; Niesen, U. Fundamental Limits of Caching. IEEE Trans. Inf. Theory 2014, 60, 2856–2867. [Google Scholar] [CrossRef]
- Maddah-Ali, M.; Niesen, U. Decentralized Coded Caching Attains Order-Optimal Memory-Rate Tradeoff. IEEE/ACM Trans. Netw. 2014. [Google Scholar] [CrossRef]
- Ji, M.; Tulino, A.; Llorca, J.; Caire, G. On the average performance of caching and coded multicasting with random demands. In Proceedings of the 2014 11th International Symposium on Wireless Communications Systems (ISWCS), Barcelona, Spain, 26–29 August 2014; pp. 922–926. [Google Scholar]
- Niesen, U.; Maddah-Ali, M.A. Coded Caching With Nonuniform Demands. IEEE Trans. Inf. Theory 2017, 63, 1146–1158. [Google Scholar] [CrossRef]
- Ji, M.; Tulino, A.M.; Llorca, J.; Caire, G. Order-Optimal Rate of Caching and Coded Multicasting with Random Demands. IEEE Trans. Inf. Theory 2017, 63, 3923–3949. [Google Scholar] [CrossRef]
- Ji, M.; Tulino, A.; Llorca, J.; Caire, G. Caching and Coded Multicasting: Multiple Groupcast Index Coding. In Proceedings of the 2014 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Atlanta, GA, USA, 3–5 December 2014; pp. 881–885. [Google Scholar]
- Ji, M.; Tulino, A.M.; Llorca, J.; Caire, G. Caching-Aided Coded Multicasting with Multiple Random Requests. In Proceedings of the 2015 IEEE Information Theory Workshop (ITW), Jerusalem, Israel, 26 April–1 May 2015; pp. 1–5. [Google Scholar]
- Wan, K.; Tuninetti, D.; Piantanida, P. On caching with more users than files. In Proceedings of the 2016 IEEE International Symposium on Information Theory (ISIT), Barcelona, Spain, 10–15 July 2016; pp. 135–139. [Google Scholar] [CrossRef]
- Wan, K.; Tuninetti, D.; Piantanida, P. On the optimality of uncoded cache placement. In Proceedings of the 2016 IEEE Information Theory Workshop (ITW), Cambridge, UK, 11–14 September 2016; pp. 161–165. [Google Scholar] [CrossRef]
- Ji, M.; Caire, G.; Molisch, A.F. The Throughput-Outage Tradeoff of Wireless One-Hop Caching Networks. IEEE Trans. Inf. Theory 2015, 61, 6833–6859. [Google Scholar] [CrossRef]
- Ji, M.; Caire, G.; Molisch, A.F. Fundamental Limits of Caching in Wireless D2D Networks. IEEE Trans. Inf. Theory 2016, 62, 849–869. [Google Scholar] [CrossRef]
- Ji, M.; Caire, G.; Molisch, A.F. Wireless Device-to-Device Caching Networks: Basic Principles and System Performance. IEEE J. Sel. Areas Commun. 2016, 34, 176–189. [Google Scholar] [CrossRef]
- Cacciapuoti, A.S.; Caleffi, M.; Ji, M.; Llorca, J.; Tulino, A.M. Speeding Up Future Video Distribution via Channel-Aware Caching-Aided Coded Multicast. IEEE J. Sel. Areas Commun. 2016, 34, 2207–2218. [Google Scholar] [CrossRef]
- Shanmugam, K.; Ji, M.; Tulino, A.M.; Llorca, J.; Dimakis, A.G. Finite-Length Analysis of Caching-Aided Coded Multicasting. IEEE Trans. Inf. Theory 2016, 62, 5524–5537. [Google Scholar] [CrossRef]
- Shangguan, C.; Zhang, Y.; Ge, G. Centralized Coded Caching Schemes: A Hypergraph Theoretical Approach. IEEE Trans. Inf. Theory 2018, 64, 5755–5766. [Google Scholar] [CrossRef]
- Chen, Z. Fundamental limits of caching: Improved bounds for users with small buffers. IET Commun. 2016, 10, 2315–2318. [Google Scholar] [CrossRef]
- Karamchandani, N.; Niesen, U.; Maddah-Ali, M.A.; Diggavi, S.N. Hierarchical Coded Caching. IEEE Trans. Inf. Theory 2016, 62, 3212–3229. [Google Scholar] [CrossRef]
- Pedarsani, R.; Maddah-Ali, M.A.; Niesen, U. Online Coded Caching. IEEE/ACM Trans. Netw. 2016, 24, 836–845. [Google Scholar] [CrossRef]
- Sahraei, S.; Gastpar, M. K users caching two files: An improved achievable rate. In Proceedings of the 2016 Annual Conference on Information Science and Systems (CISS), Princeton, NJ, USA, 16–18 March 2016; pp. 620–624. [Google Scholar] [CrossRef]
- Wang, C.; Lim, S.H.; Gastpar, M. Information-Theoretic Caching: Sequential Coding for Computing. IEEE Trans. Inf. Theory 2016, 62, 6393–6406. [Google Scholar] [CrossRef]
- Gómez-Vilardebó, J. Fundamental limits of caching: Improved bounds with coded prefetching. arXiv, 2016; arXiv:1612.09071. [Google Scholar]
- Shariatpanahi, S.P.; Motahari, S.A.; Khalaj, B.H. Multi-Server Coded Caching. IEEE Trans. Inf. Theory 2016, 62, 7253–7271. [Google Scholar] [CrossRef]
- Shanmugam, K.; Tulino, A.M.; Dimakis, A.G. Coded caching with linear subpacketization is possible using Ruzsa-Szeméredi graphs. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 1237–1241. [Google Scholar] [CrossRef]
- Ghasemi, H.; Ramamoorthy, A. Improved Lower Bounds for Coded Caching. IEEE Trans. Inf. Theory 2017, 63, 4388–4413. [Google Scholar] [CrossRef]
- Lim, S.H.; Wang, C.; Gastpar, M. Information-Theoretic Caching: The Multi-User Case. IEEE Trans. Inf. Theory 2017, 63, 7018–7037. [Google Scholar] [CrossRef]
- Jeon, S.; Hong, S.; Ji, M.; Caire, G.; Molisch, A.F. Wireless Multihop Device-to-Device Caching Networks. IEEE Trans. Inf. Theory 2017, 63, 1662–1676. [Google Scholar] [CrossRef]
- Sengupta, A.; Tandon, R. Improved Approximation of Storage-Rate Tradeoff for Caching With Multiple Demands. IEEE Trans. Commun. 2017, 65, 1940–1955. [Google Scholar] [CrossRef]
- Hachem, J.; Karamchandani, N.; Diggavi, S.N. Coded Caching for Multi-level Popularity and Access. IEEE Trans. Inf. Theory 2017, 63, 3108–3141. [Google Scholar] [CrossRef]
- Ji, M.; Wong, M.F.; Tulino, A.M.; Llorca, J.; Caire, G.; Effros, M.; Langberg, M. On the fundamental limits of caching in combination networks. In Proceedings of the 2015 IEEE 16th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Stockholm, Sweden, 28 June–1 July 2015; pp. 695–699. [Google Scholar] [CrossRef]
- Ji, M.; Tulino, A.M.; Llorca, J.; Caire, G. Caching in combination networks. In Proceedings of the 2015 49th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 8 November 2015; pp. 1269–1273. [Google Scholar] [CrossRef]
- Wan, K.; Ji, M.; Piantanida, P.; Tuninetti, D. Novel outer bounds for combination networks with end-user-caches. In Proceedings of the 2017 IEEE Information Theory Workshop (ITW), Kaohsiung, Taiwan, 6–10 November 2017; pp. 444–448. [Google Scholar] [CrossRef]
- Wan, K.; Tuninetti, D.; Ji, M.; Piantanida, P. State-of-the-art in cache-aided combination networks. In Proceedings of the 2017 51st Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 29 October–1 November 2017; pp. 641–645. [Google Scholar] [CrossRef]
- Wan, K.; Ji, M.; Piantanida, P.; Tuninetti, D. Caching in Combination Networks: Novel Multicast Message Generation and Delivery by Leveraging the Network Topology. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Wan, K.; Jit, M.; Piantanida, P.; Tuninetti, D. On the Benefits of Asymmetric Coded Cache Placement in Combination Networks with End-User Caches. In Proceedings of the 2018 IEEE International Symposium on Information Theory (ISIT), Vail, CO, USA, 17–22 June 2018; pp. 1550–1554. [Google Scholar] [CrossRef]
- Wan, K.; Tuninetti, D.; Ji, M.; Piantanida, P. A Novel Asymmetric Coded Placement in Combination Networks with End-User Caches. In Proceedings of the 2018 Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 11–16 February 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Tian, C.; Chen, J. Caching and Delivery via Interference Elimination. IEEE Trans. Inf. Theory 2018, 64, 1548–1560. [Google Scholar] [CrossRef]
- Yu, Q.; Maddah-Ali, M.A.; Avestimehr, A.S. The Exact Rate-Memory Tradeoff for Caching With Uncoded Prefetching. IEEE Trans. Inf. Theory 2018, 64, 1281–1296. [Google Scholar] [CrossRef]
- Zhang, K.; Tian, C. Fundamental Limits of Coded Caching: From Uncoded Prefetching to Coded Prefetching. IEEE J. Sel. Areas Commun. 2018, 36, 1153–1164. [Google Scholar] [CrossRef]
- Wang, C.; Bidokhti, S.S.; Wigger, M. Improved Converses and Gap Results for Coded Caching. IEEE Trans. Inf. Theory 2018, 64, 7051–7062. [Google Scholar] [CrossRef]
- Yu, Q.; Maddah-Ali, M.A.; Avestimehr, A.S. Characterizing the Rate-Memory Tradeoff in Cache Networks Within a Factor of 2. IEEE Trans. Inf. Theory 2019, 65, 647–663. [Google Scholar] [CrossRef]
- Karat, N.S.; Thomas, A.; Rajan, B.S. Optimal Error Correcting Delivery Scheme for an Optimal Coded Caching Scheme with Small Buffers. In Proceedings of the 2018 IEEE International Symposium on Information Theory (ISIT), Vail, CO, USA, 17–22 June 2018; pp. 1710–1714. [Google Scholar] [CrossRef]
- Tian, C. Symmetry, Outer Bounds, and Code Constructions: A Computer-Aided Investigation on the Fundamental Limits of Caching. Entropy 2018, 20, 603. [Google Scholar] [CrossRef]
- Cisco. The Zettabyte Era-Trends and Analysis; Cisco White Paper; Cisco: San Jose, CA, USA, 2013. [Google Scholar]
- Birk, Y.; Kol, T. Informed-source coding-on-demand (ISCOD) over broadcast channels. In Proceedings of the Conference on Computer Communications, Seventeenth Annual Joint Conference of the IEEE Computer and Communications Societies, Gateway to the 21st Century, San Francisco, CA, USA, 29 March–2 April 1998. [Google Scholar]
- Breslau, L.; Cao, P.; Fan, L.; Phillips, G.; Shenker, S. Web caching and Zipf-like distributions: Evidence and implications. In Proceedings of the INFOCOM’99: Conference on Computer Communications, New York, NY, USA, 21–25 March 1999; Volume 1, pp. 126–134. [Google Scholar]
- Tang, L.; Ramamoorthy, A. Coded Caching Schemes With Reduced Subpacketization From Linear Block Codes. IEEE Trans. Inf. Theory 2018, 64, 3099–3120. [Google Scholar] [CrossRef]
- Yan, Q.; Cheng, M.; Tang, X.; Chen, Q. On the Placement Delivery Array Design for Centralized Coded Caching Scheme. IEEE Trans. Inf. Theory 2017, 63, 5821–5833. [Google Scholar] [CrossRef]
- Vettigli, G.; Ji, M.; Tulino, A.M.; Llorca, J.; Festa, P. An efficient coded multicasting scheme preserving the multiplicative caching gain. In Proceedings of the 2015 IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Hong Kong, China, 26 April–1 May 2015; pp. 251–256. [Google Scholar] [CrossRef]
- Ji, M.; Shanmugam, K.; Vettigli, G.; Llorca, J.; Tulino, A.M.; Caire, G. An efficient multiple-groupcast coded multicasting scheme for finite fractional caching. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 3801–3806. [Google Scholar] [CrossRef]
- Ramakrishnan, A.; Westphal, C.; Markopoulou, A. An Efficient Delivery Scheme for Coded Caching. In Proceedings of the 2015 27th International Teletraffic Congress, Ghent, Belgium, 8–10 September 2015; pp. 46–54. [Google Scholar] [CrossRef]
- Jin, S.; Cui, Y.; Liu, H.; Caire, G. Order-Optimal Decentralized Coded Caching Schemes with Good Performance in Finite File Size Regime. In Proceedings of the 2016 IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–7. [Google Scholar] [CrossRef]
- Wan, K.; Tuninetti, D.; Piantanida, P. Novel delivery schemes for decentralized coded caching in the finite file size regime. In Proceedings of the 2017 IEEE International Conference on Communications Workshops (ICC Workshops), Paris, France, 21–25 May 2017; pp. 1183–1188. [Google Scholar] [CrossRef]
- Asghari, S.M.; Ouyang, Y.; Nayyar, A.; Avestimehr, A.S. Optimal Coded Multicast in Cache Networks with Arbitrary Content Placement. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Amiri, M.M.; Yang, Q.; Gündüz, D. Decentralized coded caching with distinct cache capacities. In Proceedings of the 2016 50th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 6–9 November 2016; pp. 734–738. [Google Scholar] [CrossRef]
- Amiri, M.M.; Yang, Q.; Gündüz, D. Decentralized Caching and Coded Delivery With Distinct Cache Capacities. IEEE Trans. Commun. 2017, 65, 4657–4669. [Google Scholar] [CrossRef]
- Ibrahim, A.M.; Zewail, A.A.; Yener, A. Centralized Coded Caching with Heterogeneous Cache Sizes. In Proceedings of the 2017 IEEE Wireless Communications and Networking Conference (WCNC), San Francisco, CA, USA, 19–22 March 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Wei, Y.; Ulukus, S. Coded caching with multiple file requests. In Proceedings of the 2017 55th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 3–6 October 2017; pp. 437–442. [Google Scholar] [CrossRef]
- Parrinello, E.; Unsal, A.; Elia, P. Fundamental Limits of Caching in Heterogeneous Networks with Uncoded Prefetching. arXiv, 2018; arXiv:1811.06247. [Google Scholar]
- Shanmugam, K.; Dimakis, A.G.; Langberg, M. Local graph coloring and index coding. In Proceedings of the 2013 IEEE International Symposium on Information Theory, Istanbul, Turkey, 7–12 July 2013; pp. 1152–1156. [Google Scholar] [CrossRef]
- Lin, S.; Costello, D.J. Error Control Coding; Prentice-hall Englewood Cliffs: Upper Saddle River, NJ, USA, 2004; Volume 123. [Google Scholar]
- Bar-Yossef, Z.; Birk, Y.; Jayram, T.; Kol, T. Index coding with side information. IEEE Trans. Inf. Theory 2011, 57, 1479–1494. [Google Scholar] [CrossRef]
- Lee, D.; Noh, S.; Min, S.; Choi, J.; Kim, J.; Cho, Y.; Kim, C. LRFU: A spectrum of policies that subsumes the least recently used and least frequently used policies. IEEE Trans. Comput. 2001, 50, 1352–1361. [Google Scholar]
- Boucheron, S.; Lugosi, G.; Massart, P. Concentration Inequalities: A Nonasymptotic Theory of Independence; Oxford University Press: Oxford, UK, 2013. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vettigli, G.; Ji, M.; Shanmugam, K.; Llorca, J.; Tulino, A.M.; Caire, G. Efficient Algorithms for Coded Multicasting in Heterogeneous Caching Networks. Entropy 2019, 21, 324. https://doi.org/10.3390/e21030324
Vettigli G, Ji M, Shanmugam K, Llorca J, Tulino AM, Caire G. Efficient Algorithms for Coded Multicasting in Heterogeneous Caching Networks. Entropy. 2019; 21(3):324. https://doi.org/10.3390/e21030324
Chicago/Turabian StyleVettigli, Giuseppe, Mingyue Ji, Karthikeyan Shanmugam, Jaime Llorca, Antonia M. Tulino, and Giuseppe Caire. 2019. "Efficient Algorithms for Coded Multicasting in Heterogeneous Caching Networks" Entropy 21, no. 3: 324. https://doi.org/10.3390/e21030324
APA StyleVettigli, G., Ji, M., Shanmugam, K., Llorca, J., Tulino, A. M., & Caire, G. (2019). Efficient Algorithms for Coded Multicasting in Heterogeneous Caching Networks. Entropy, 21(3), 324. https://doi.org/10.3390/e21030324





