1. Introduction
Auxiliary variables are often observed along with primary variables. Here, the primary variables are random variables of interest, and our purpose is to estimate their predictive distribution, i.e., a probability distribution of the primary variables in future test data, while the auxiliary variables are random variables that are observed in training data but not included in the primary variables. We assume that the auxiliary variables are not observed in the test data, or we do not use them even if they are observed in the test data. When the auxiliary variables have a close relation with the primary variables, we expect to improve the accuracy of predictive distribution of the primary variables by considering a joint modeling of the primary and auxiliary variables.
The notion of auxiliary variables has been considered in statistics and machine learning literature. For example, the “curds and whey” method [
1] and the “coaching variables” method [
2] are based on a similar idea for improving prediction accuracy of primary variables by using auxiliary variables. In multitask learning, Caruana [
3] improved generalization accuracy of a main task by exploiting extra tasks. Auxiliary variables are also considered in incomplete data analysis, i.e., a part of primary variables are not observed; Mercatanti et al. [
4] showed some theoretical results to make parameter estimation better by utilizing auxiliary variables in Gaussian mixture model (GMM).
Although auxiliary variables are expected to be useful for modeling primary variables, they can actually be harmful. As mentioned in Mercatanti et al. [
4], using auxiliary variables may affect modeling results adversely because the number of parameters to be estimated increases and a candidate model of the auxiliary variables can be misspecified. Hence, it is important to select useful auxiliary variables. This is formulated as model selection by considering parametric models with auxiliary variables. In this paper, usefulness of auxiliary variables for estimating predictive distribution of primary variables is measured by a risk function based on the Kullback–Leibler (KL) divergence [
5] that is often used for model selection. Because the KL risk function includes unknown parameters, we have to estimate it in actual use. Akaike Information Criterion (AIC) proposed by Akaike [
6] is one of the most famous criteria, which is known as an asymptotically unbiased estimator of the KL risk function. AIC is a good criterion from the perspective of prediction due to the asymptotic efficiency; see Shibata [
7,
8]. Takeuchi [
9] proposed a modified version of AIC, called Takeuchi Information Criterion (TIC), which relaxes an assumption for deriving AIC, that is, correct specification of candidate model. However, AIC and TIC are derived for primary variables without considering auxiliary variables in the setting of complete data analysis, and therefore, they are not suitable for auxiliary variable selection nor incomplete data analysis.
Incomplete data analysis is widely used in a broad range of statistical problems by regarding a part of primary variables as latent variables that are not observed. This setting also includes complete data analysis as a special case, where all the primary variables are observed. Information criteria for incomplete data analysis have been proposed in previous studies. Shimodaira [
10] developed an information criterion based on the KL divergence for complete data when the data are only partially observed. Cavanaugh and Shumway [
11] modified the first term of the information criterion of Shimodaira [
10] by the objective function of the EM algorithm [
12]. Recently, Shimodaira and Maeda [
13] proposed an information criterion, which is derived by mitigating a condition assumed in Shimodaira [
10] and Cavanaugh and Shumway [
11].
However, any of these previously proposed criteria are not derived by taking auxiliary variables into account. Thus, we propose a new information criterion by considering not only primary variable but also auxiliary variables in the setting of incomplete data analysis. The proposed criterion is a generalization of AIC, TIC, and the criterion of Shimodaira and Maeda [
13]. To the best of our knowledge, this is the first attempt to derive an information criterion by considering auxiliary variables. Moreover, we show an asymptotic equivalence between the proposed criterion and a variant of leave-one-out cross validation (LOOCV); this result is a generalization of the relationship between TIC and LOOCV [
14].
Note that “auxiliary variables” may also be used in other contexts in literature. For example, Ibrahim et al. [
15] considered to use auxiliary variables in missing data analysis, which is similar to our usage in the sense that auxiliary variables are highly correlated with missing data. However, they use the auxiliary variables in order to avoid specifying a missing data mechanism; this goal is different from ours, because no missing data mechanism is considered in our study.
The reminder of this paper is organized as follows. Notations as well as the setting of this paper are introduced in
Section 2. Illustrative examples of useful and useless auxiliary variables are given in
Section 3. The information criterion for selecting useful auxiliary variables in incomplete data analysis is derived in
Section 4, and the asymptotic equivalence between the proposed criterion and a variant of LOOCV is shown in
Section 5. Performance of our method is examined via a simulation study and a real data analysis in
Section 6 and
Section 7, respectively. Finally, we conclude this paper in
Section 8. All proofs are shown in
Appendix A.
5. Leave-One-Out Cross Validation
Variable selection by cross-validatory (CV) choice [
18] is often applied to real data analysis due to its simplicity, although its computational burden is larger than that of information criteria; see Arlot and Celisse [
19] for a recent review of cross-validation methods. As shown in Stone [
14], leave-one-out cross validation (LOOCV) is asymptotically equivalent to TIC. Because LOOCV does not require calculation of the information matrices of TIC, LOOCV is easier to use than TIC. There are also some literature for improving LOOCV such as Yanagihara et al. [
20], which gives a modification of LOOCV to reduce its bias by considering maximum weighted log-likelihood estimation. However, we focus on the result of Stone [
14] and extend it to our setting.
In incomplete data analysis, LOOCV cannot be directly used because the loss function with respect to the complete data includes latent variables. Thus, we transform the loss function as follows:
where
and
Note that
when
. Using the function
, we then obtain the following LOOCV estimator of the risk function
.
where
is the leave-out-out estimate of
defined as
We will show below in this section that
is asymptotically equivalent to
. For implementing the LOOCV procedure with latent variables, however, we have to estimate
by
in
. This introduces a bias to
, and hence, information criteria are preferable to the LOOCV in incomplete data analysis.
Let us show the asymptotic equivalence of
and
by assuming that we know the functional form of
. Noting that
is a critical point of
, we have
By applying Taylor expansion to
around
, it follows from
that
where
lies between
and
. We can see from (
14) that
. Next, we regard
as a function of
and apply Taylor expansion to it around
. Therefore,
can be expressed as follows:
where
lies between
and
(
does not corresponding to
). Then we assume that
By noting
, we have
and
, and thus (
16) holds at least formally. With the above setup, we show the following theorem. The proof is given in
Appendix A.4.
Theorem 3. Supposing the same assumptions of Theorem 1 and (16), we have Because the second term on the right-hand side of (
17) does not depend on candidate models under condition (
6), this theorem implies that
is asymptotically equivalent to
except for the scaling and the constant term. However, someone may wonder why
is included in
for comparing models of
. By assuming that
is correctly specified for
,
does not depend on the model anymore, so we may simply exclude
from
, leading to the loss
instead. The reason for including
in
is explained as follows.
, as well as
(and
), include the additional penalty for estimating
in
, which depends on the candidate models even if
is correctly specified.
6. Experiments with Simulated Datasets
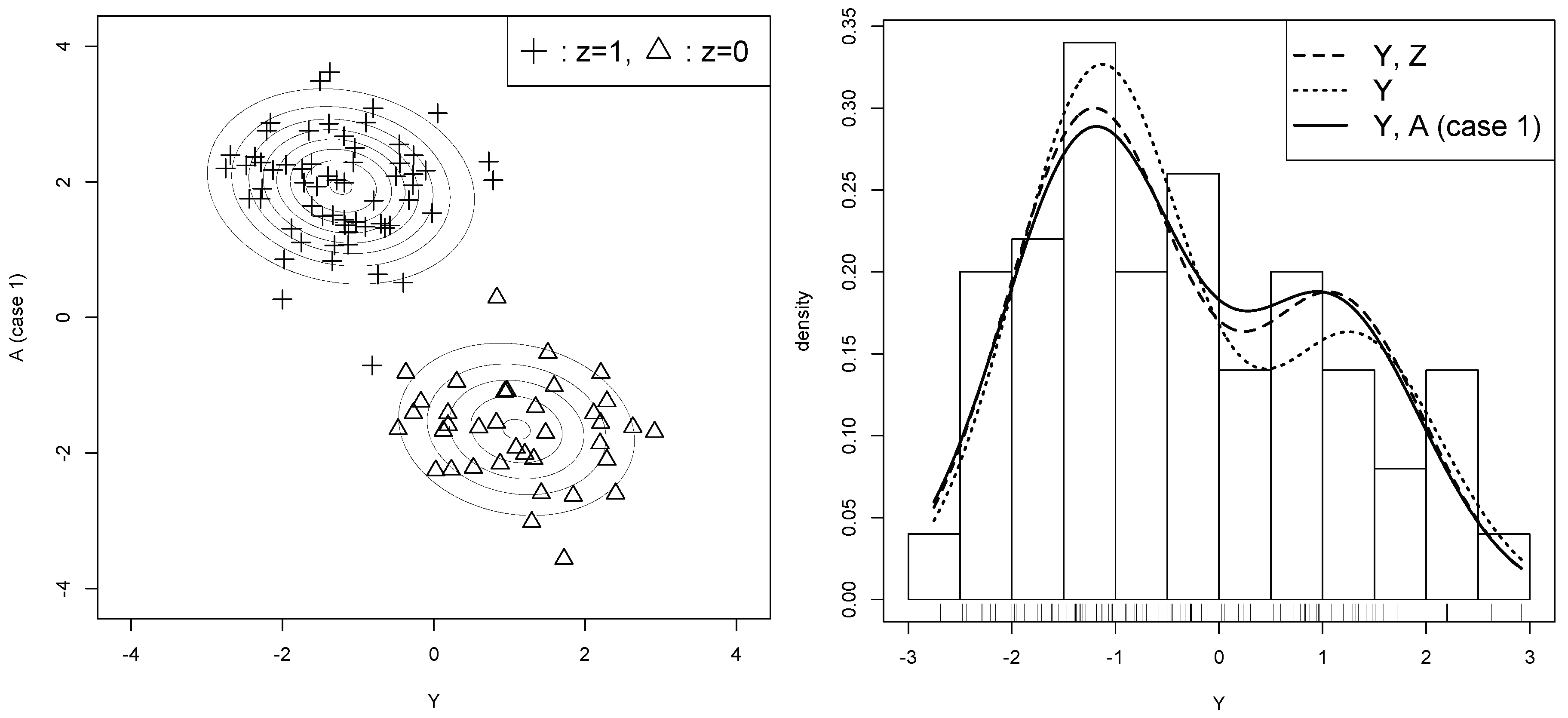
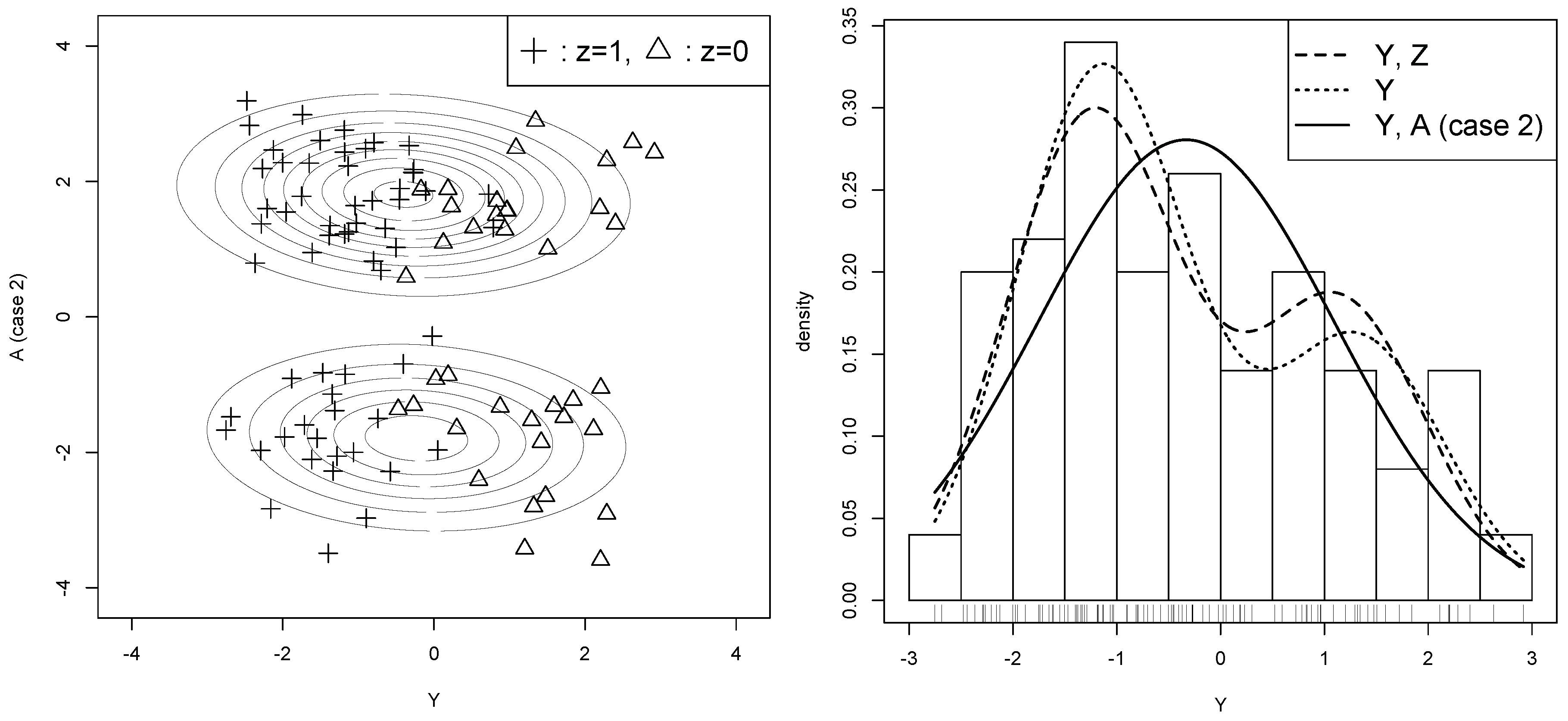
This section shows the usefulness of auxiliary variables and the proposed information criteria via a simulation study. The models illustrated in
Section 3 are used for confirming the asymptotic unbiasedness of the information criterion and the validity of auxiliary variable selection.
6.1. Unbiasedness
At first, we confirm the asymptotic unbiasedness of
for estimating
except for the constant term,
. The simulation setting is the same as Case 1 in
Section 3, thus the data generating model is given by
where
and
. We generated
independent replicates of the dataset
from this model; in fact, we used
generated in
Section 6.2. The candidate model is given by (
4), which is correctly specified for the above data generating model. Because
is derived by ignoring
, we compare
with
. The computation of the expectation is approximated by the simulation average as
where
,
,
, and
are those computed for the
t-th dataset (
).
Here, we remark about calculation of the loss function in two-component GMM. Let be an estimator of . We expect that the components of GMM corresponding to and consist of and , respectively. However, we cannot determine the assignment of the estimated parameters in reality, i.e., and may correspond to and , respectively, because the labels are missing. The assignment is required to calculate whereas it is not used for and the proposed information criteria. Hence, in this paper, we define as the minimum value between and , where .
Table 3 shows the result of the simulation for
, and 5000. For all
n, we observe that
is very close to
, indicating the unbiasedness of
.
6.2. Auxiliary Variable Selection
Next, we demonstrate that the proposed AIC selects a useful auxiliary variable (Case 1), while it does not select a useless auxiliary variable (Case 2). In each case, we generated
independent replicates of the dataset
from the model. In fact, the values of
are shared in both cases, so we generated replicates of
, where
and
are auxiliary variables for Case 1 and Case 2, respectively. In each case, we compute
and
, then we select
(i.e., selecting the auxiliary variable
A) if
and select
(i.e., not selecting the auxiliary variable
A) otherwise. The selected estimator is denoted as
. This experiment was repeated for
times. Note that the typical dataset in
Section 3 was picked from the generated datasets so that it has around the median value in each of
,
,
, and
in both cases.
The selection frequencies are shown in
Table 4 and
Table 5. We observe that, as expected, the useful auxiliary variable tends to be selected in Case 1, while the useless auxiliary variable tends to be not selected in Case 2.
For verifying the usefulness of the auxiliary variable in both cases, we computed the risk value
for
,
, and
. They are approximated by the simulation average as
The results are shown in
Table 6 and
Table 7. For easier comparisons, the values are the differences from
with the true value
. For all
n, we observe that, as expected,
in Case 1, and
in Case 2. In both cases,
is close to
, indicating that the variable selection is working well.
7. Experiments with Real Datasets
We show an example of auxiliary variable selection using Wine Data Set available at UCI Machine Learning Repository [
21], which consists of 1 categorical variable (3 categories) and 13 continuous variables, denoted as
. For simplicity, we only use the first two categories and regard them as a latent variable
; the experiment results were similar to the other combinations. The sample size is then
and all variables except for
Z are standardized. We set one of the 13 continuous variables as the observed primary variable
Y, and set the rest of 12 variables as auxiliary variables
. For example, if
Y is
, then
are
. The dataset is now
, which is randomly divided into the training set with sample size
(
is not used) and the test set with sample size
(
are not used).
In the experiment, we compute
for
,
, and
for
Y from the training dataset using the model (
4). We select
from
and
by finding the minimum of the 13 AIC values. Thus we are selecting one of the auxiliary variables
or not selecting any of them. It is possible to select a combination of the auxiliary variables, but we did not attempt such an experiment. For measuring the generalization error, we compute
from the test set as
where
represents the test set. The assignment problem of
mentioned in
Section 6 is avoided by a similar manner.
For each case of
,
, the above experiment was repeated 100 times, and the experiment average of the generalization error was computed. The result is shown in
Table 8. A positive value indicates that
performed better than
. We observe that
is better than or almost the same as
for all cases
, suggesting that AIC works well to select a useful auxiliary variable.
8. Conclusions
We often encounter a dataset composed of various variables. If only some of the variables are of interest, then the rest of the variables can be interpreted as auxiliary variables. Auxiliary variables may be able to improve estimation accuracy of unknown parameters but they could also be harmful. Hence, it is important to select useful auxiliary variables.
In this paper, we focused on exploiting auxiliary variables in incomplete data analysis. The usefulness of auxiliary variables is measured by a risk function based on the KL divergence for complete data. We derived an information criterion which is an asymptotically unbiased estimator of the risk function except for a constant term. Moreover, we extended a result of Stone [
14] to our setting and proved asymptotic equivalence between a variant of LOOCV and the proposed criteria. Since LOOCV requires an additional condition for its justification, the proposed criteria are preferable to LOOCV.
This study assumes that variables are different between training set and test set. There are other settings, such as covariate shift [
17] and transfer learning [
22], where distributions are different between the training set and test set. It will be possible to combine these settings to construct a generalized framework. It is also possible to extend our study for taking account of a missing mechanism. We will leave these extensions as future works.