Approximations of Shannon Mutual Information for Discrete Variables with Applications to Neural Population Coding
Abstract
1. Introduction
2. Theory and Methods
2.1. Notations and Definitions
2.2. Theorems
2.3. Approximations for Mutual Information
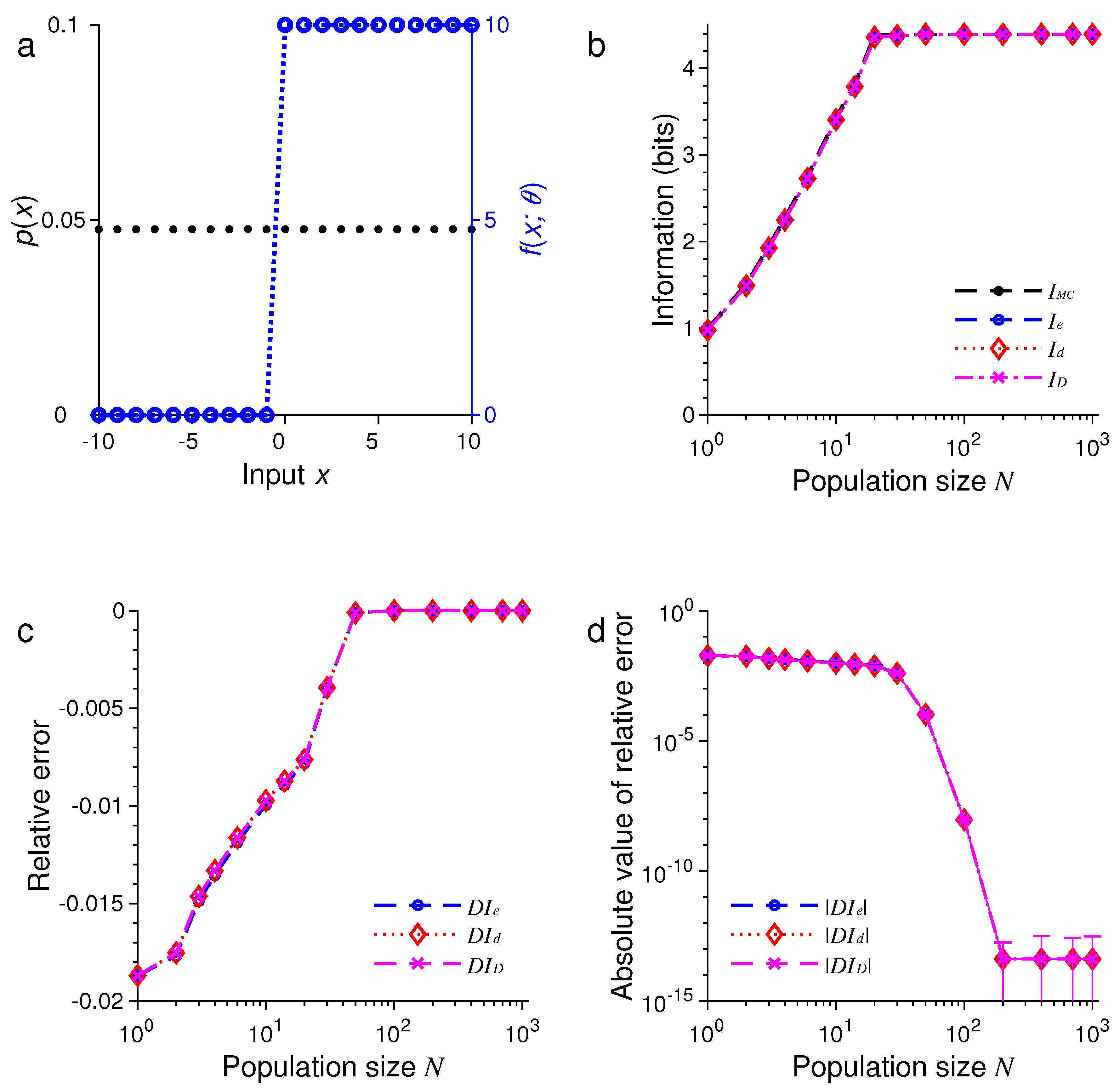
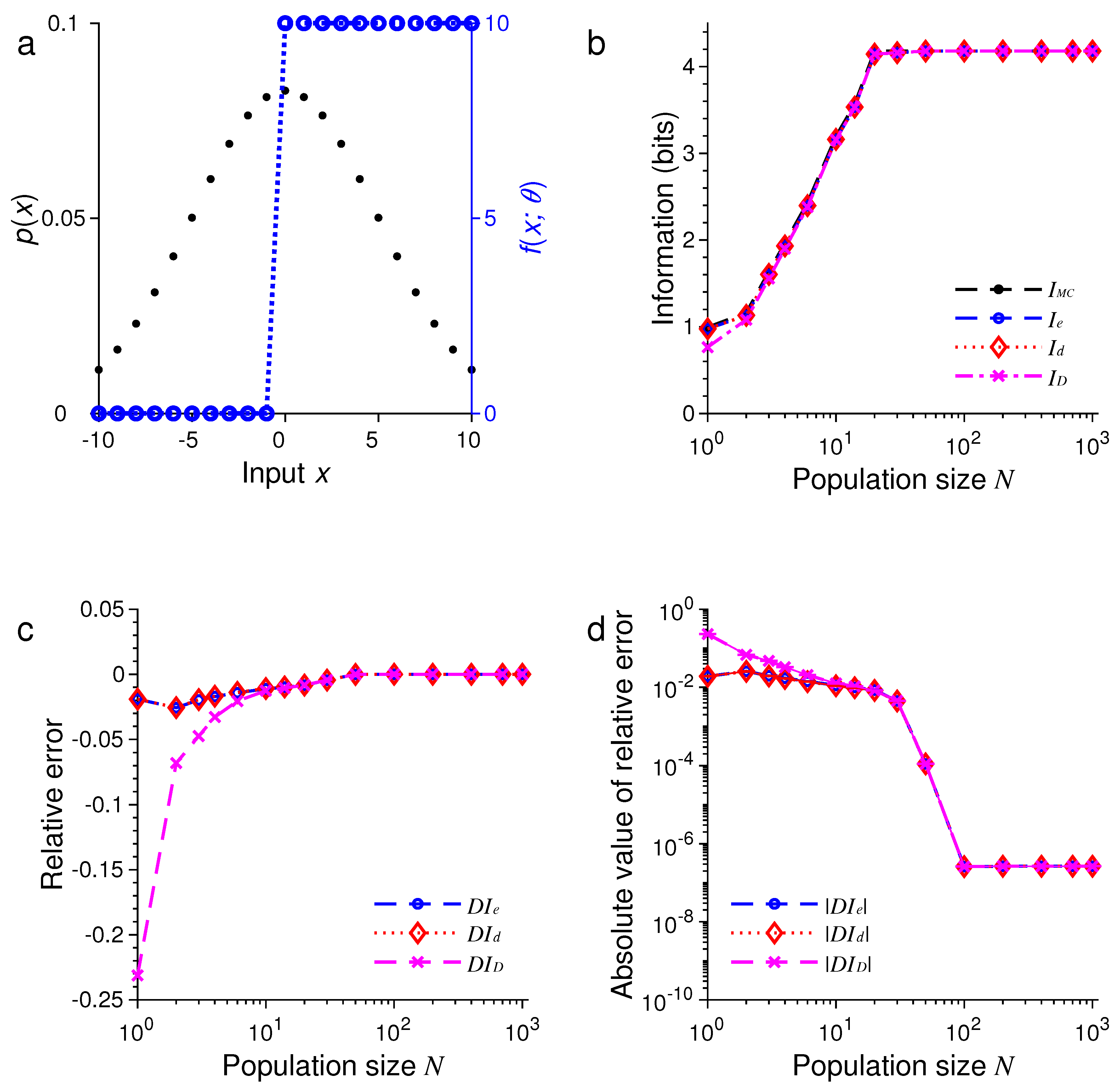
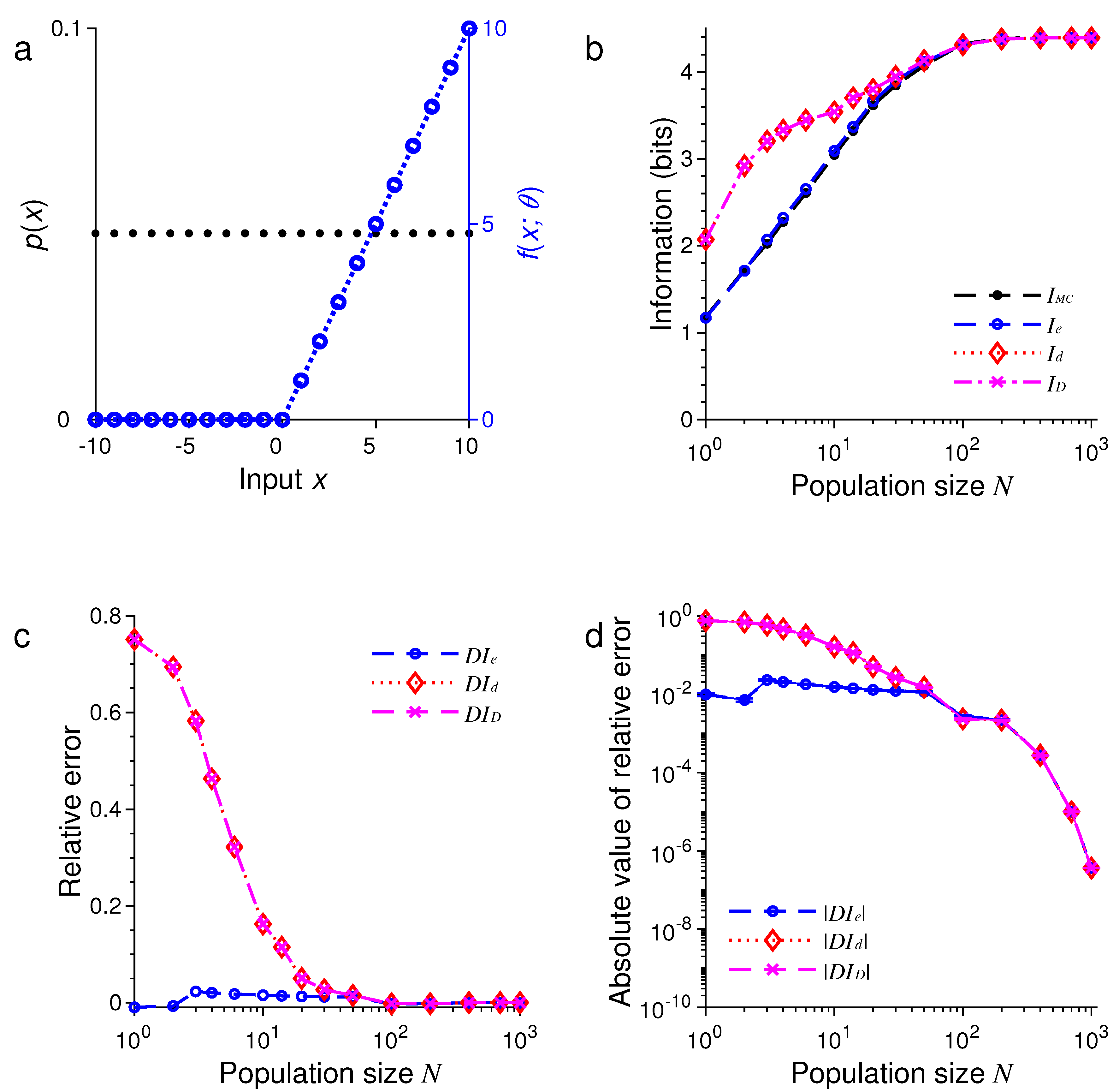
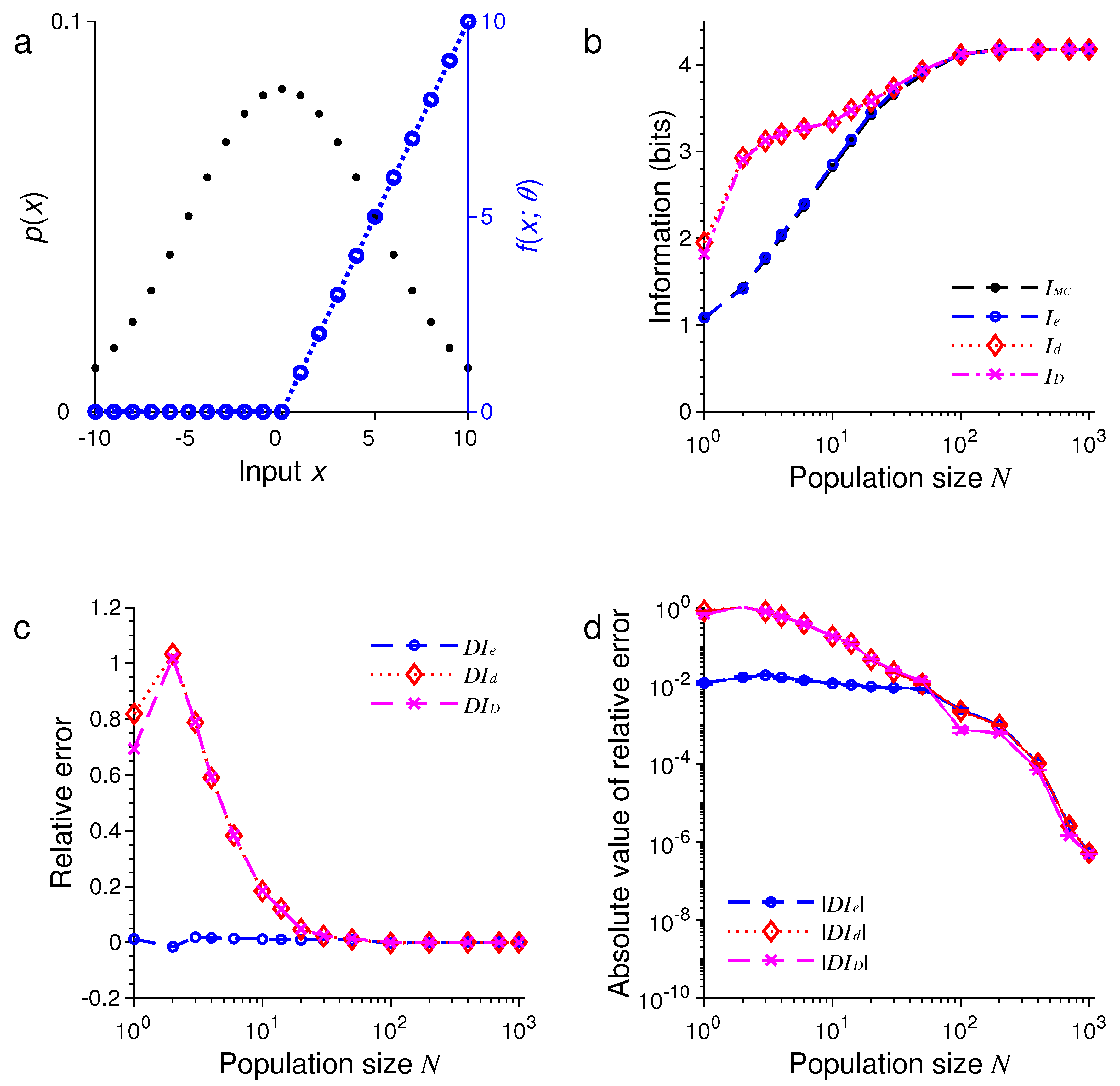
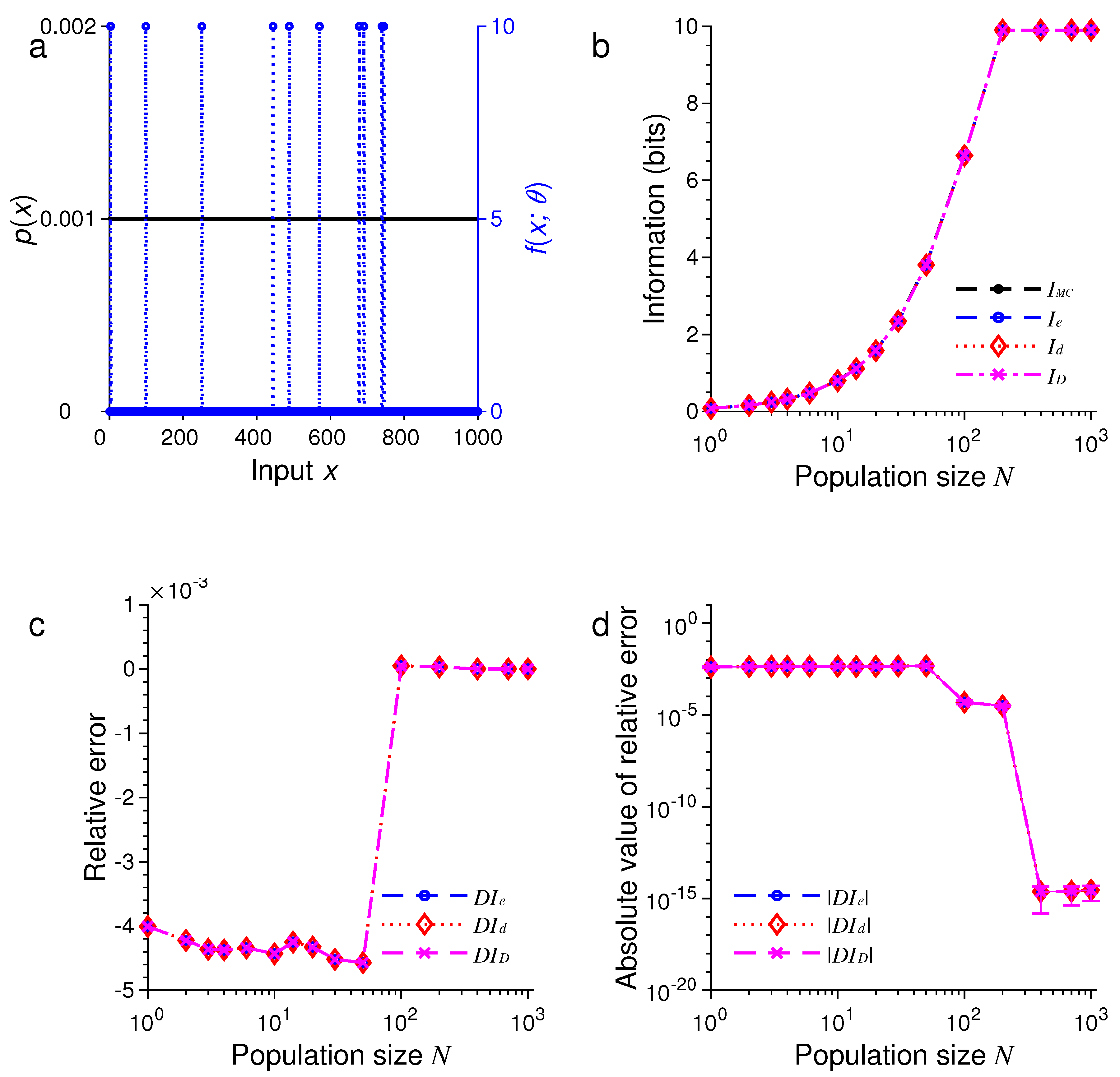
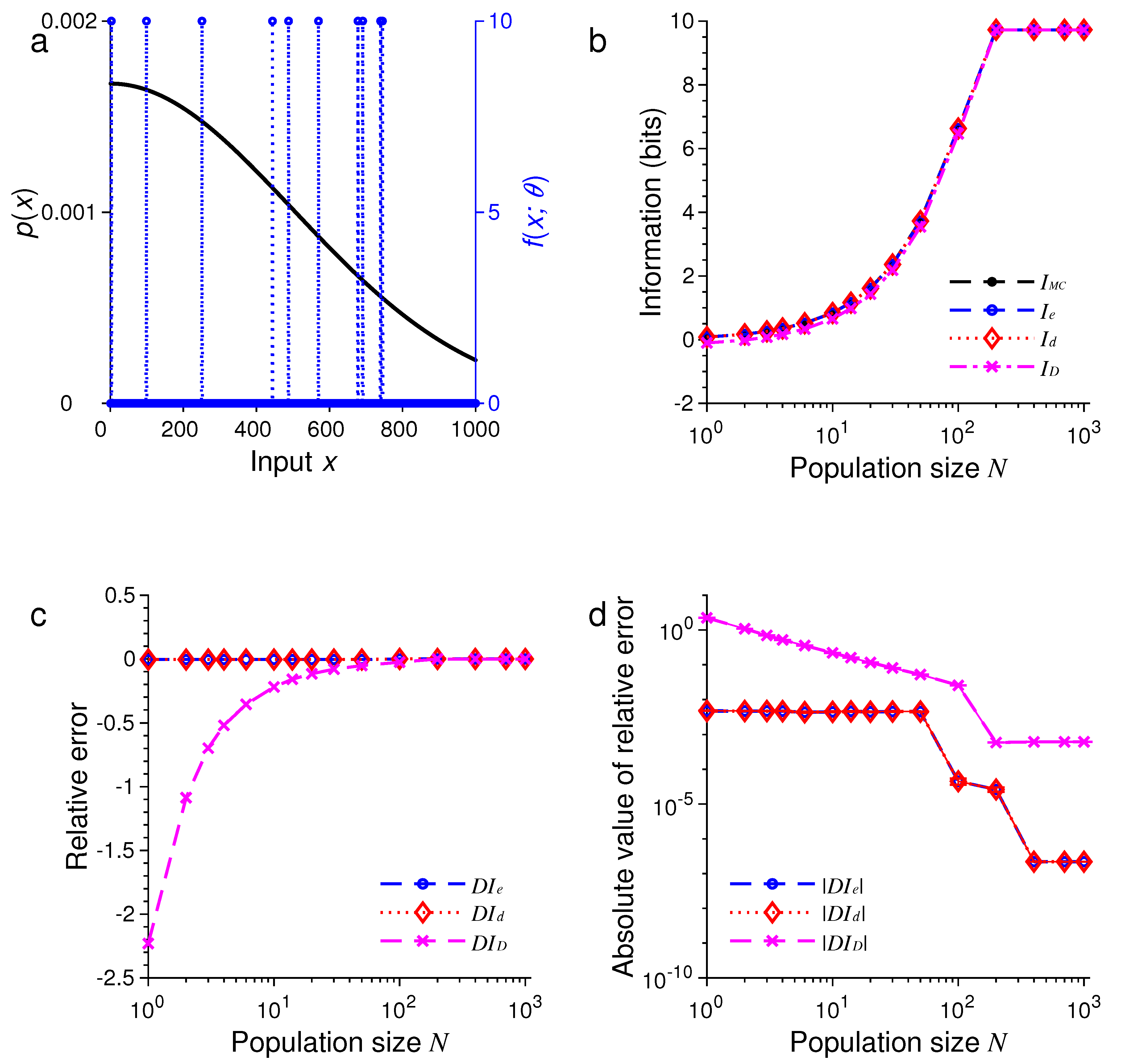
3. Results of Numerical Simulations
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A. The Proofs
Appendix A.1. Proof of Theorem 1
Appendix A.2. Proof of Theorem 2
Appendix A.3. Proof of Theorem 3
Appendix A.4. Proof of Theorem 4
References
- Borst, A.; Theunissen, F.E. Information theory and neural coding. Nat. Neurosci. 1999, 2, 947–957. [Google Scholar] [CrossRef] [PubMed]
- Pouget, A.; Dayan, P.; Zemel, R. Information processing with population codes. Nat. Rev. Neurosci. 2000, 1, 125–132. [Google Scholar] [CrossRef] [PubMed]
- Laughlin, S.B.; Sejnowski, T.J. Communication in neuronal networks. Science 2003, 301, 1870–1874. [Google Scholar] [CrossRef] [PubMed]
- Brown, E.N.; Kass, R.E.; Mitra, P.P. Multiple neural spike train data analysis: State-of-the-art and future challenges. Nat. Neurosci. 2004, 7, 456–461. [Google Scholar] [CrossRef] [PubMed]
- Bell, A.J.; Sejnowski, T.J. The “independent components” of natural scenes are edge filters. Vision Res. 1997, 37, 3327–3338. [Google Scholar] [CrossRef]
- Huang, W.; Zhang, K. An Information-Theoretic Framework for Fast and Robust Unsupervised Learning via Neural Population Infomax. In Proceedings of the 5th International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Huang, W.; Huang, X.; Zhang, K. Information-theoretic interpretation of tuning curves for multiple motion directions. In Proceedings of the 2017 51st Annual Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 22–24 March 2017. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information, 2nd ed.; Wiley-Interscience: New York, NY, USA, 2006. [Google Scholar]
- Miller, G.A. Note on the bias of information estimates. Inf. Theory Psychol. Probl. Methods 1955, 2, 100. [Google Scholar]
- Carlton, A. On the bias of information estimates. Psychol. Bull. 1969, 71, 108. [Google Scholar] [CrossRef]
- Treves, A.; Panzeri, S. The upward bias in measures of information derived from limited data samples. Neural Comput. 1995, 7, 399–407. [Google Scholar] [CrossRef]
- Victor, J.D. Asymptotic bias in information estimates and the exponential (Bell) polynomials. Neural Comput. 2000, 12, 2797–2804. [Google Scholar] [CrossRef] [PubMed]
- Paninski, L. Estimation of entropy and mutual information. Neural Comput. 2003, 15, 1191–1253. [Google Scholar] [CrossRef]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef] [PubMed]
- Khan, S.; Bandyopadhyay, S.; Ganguly, A.R.; Saigal, S.; Erickson, D.J., III; Protopopescu, V.; Ostrouchov, G. Relative performance of mutual information estimation methods for quantifying the dependence among short and noisy data. Phys. Rev. E 2007, 76, 026209. [Google Scholar] [CrossRef] [PubMed]
- Safaai, H.; Onken, A.; Harvey, C.D.; Panzeri, S. Information estimation using nonparametric copulas. Phys. Rev. E 2018, 98, 053302. [Google Scholar] [CrossRef]
- Rao, C.R. Information and accuracy attainable in the estimation of statistical parameters. Bull. Calcutta Math. Soc. 1945, 37, 81–91. [Google Scholar]
- Van Trees, H.L.; Bell, K.L. Bayesian Bounds for Parameter Estimation and Nonlinear Filtering/Tracking; John Wiley: Piscataway, NJ, USA, 2007. [Google Scholar]
- Clarke, B.S.; Barron, A.R. Information-theoretic asymptotics of Bayes methods. IEEE Trans. Inform. Theory 1990, 36, 453–471. [Google Scholar] [CrossRef]
- Rissanen, J.J. Fisher information and stochastic complexity. IEEE Trans. Inform. Theory 1996, 42, 40–47. [Google Scholar] [CrossRef]
- Brunel, N.; Nadal, J.P. Mutual information, Fisher information, and population coding. Neural Comput. 1998, 10, 1731–1757. [Google Scholar] [CrossRef] [PubMed]
- Sompolinsky, H.; Yoon, H.; Kang, K.J.; Shamir, M. Population coding in neuronal systems with correlated noise. Phys. Rev. E 2001, 64, 051904. [Google Scholar] [CrossRef] [PubMed]
- Kang, K.; Sompolinsky, H. Mutual information of population codes and distance measures in probability space. Phys. Rev. Lett. 2001, 86, 4958–4961. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Zhang, K. Information-theoretic bounds and approximations in neural population coding. Neural Comput. 2018, 30, 885–944. [Google Scholar] [CrossRef] [PubMed]
- Strong, S.P.; Koberle, R.; van Steveninck, R.R.D.R.; Bialek, W. Entropy and information in neural spike trains. Phys. Rev. Lett. 1998, 80, 197. [Google Scholar] [CrossRef]
- Nemenman, I.; Bialek, W.; van Steveninck, R.D.R. Entropy and information in neural spike trains: Progress on the sampling problem. Phys. Rev. E 2004, 69, 056111. [Google Scholar] [CrossRef] [PubMed]
- Panzeri, S.; Senatore, R.; Montemurro, M.A.; Petersen, R.S. Correcting for the sampling bias problem in spike train information measures. J. Neurophysiol. 2017, 98, 1064–1072. [Google Scholar] [CrossRef] [PubMed]
- Houghton, C. Calculating the Mutual Information Between Two Spike Trains. Neural Comput. 2019, 31, 330–343. [Google Scholar] [CrossRef] [PubMed]
- Rényi, A. On measures of entropy and information. In Fourth Berkeley Symposium on Mathematical Statistics and Probability; The Regents of the University of California, University of California Press: Berkeley, CA, USA, 1961; pp. 547–561. [Google Scholar]
- Chernoff, H. A measure of asymptotic efficiency for tests of a hypothesis based on the sum of observations. Ann. Math. Stat. 1952, 23, 493–507. [Google Scholar] [CrossRef]
- Bhattacharyya, A. On a measure of divergence between two statistical populations defined by their probability distributions. Bull. Calcutta Math. Soc. 1943, 35, 99–109. [Google Scholar]
- Beran, R. Minimum Hellinger distance estimates for parametric models. Ann. Stat. 1977, 5, 445–463. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, W.; Zhang, K. Approximations of Shannon Mutual Information for Discrete Variables with Applications to Neural Population Coding. Entropy 2019, 21, 243. https://doi.org/10.3390/e21030243
Huang W, Zhang K. Approximations of Shannon Mutual Information for Discrete Variables with Applications to Neural Population Coding. Entropy. 2019; 21(3):243. https://doi.org/10.3390/e21030243
Chicago/Turabian StyleHuang, Wentao, and Kechen Zhang. 2019. "Approximations of Shannon Mutual Information for Discrete Variables with Applications to Neural Population Coding" Entropy 21, no. 3: 243. https://doi.org/10.3390/e21030243
APA StyleHuang, W., & Zhang, K. (2019). Approximations of Shannon Mutual Information for Discrete Variables with Applications to Neural Population Coding. Entropy, 21(3), 243. https://doi.org/10.3390/e21030243




