Bounding the Plausibility of Physical Theories in a Device-Independent Setting via Hypothesis Testing
Abstract
:1. Introduction
2. Methods
2.1. Preliminaries
2.2. Finite Statistics and the Prediction-Based-Ratio Method
2.3. Generalization for Hypothesis Testing Beyond LHV Theories
3. Results
3.1. Modeling a Bell Test
with the same level of confidence. Inspired by the experiments of Ref. [72] where ∼, we set in our simulations . Note also that instead of , we can equally well choose another set of correlations that admits a semidefinite programming characterization, such as those described in Refs. [59,62].“The observed data is compatible with a physical theory that is constrained to produce only the almost-quantum set of correlations.”
3.2. Simulations of Bell Tests with an i.i.d. Nonlocal Source
3.3. Simulations of Bell tests with a non-i.i.d. Nonlocal Source
3.4. Application to Some Real Experimental Data
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Acín, A.; Gisin, N.; Masanes, L. From Bell’s Theorem to Secure Quantum Key Distribution. Phys. Rev. Lett. 2006, 97, 120405. [Google Scholar] [CrossRef]
- Bell, J.S. On the Einstein-Podolsky-Rosen paradox. Physics 1964, 1, 195. [Google Scholar] [CrossRef]
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145–195. [Google Scholar] [CrossRef]
- Barrett, J.; Hardy, L.; Kent, A. No Signaling and Quantum Key Distribution. Phys. Rev. Lett. 2005, 95, 010503. [Google Scholar] [CrossRef]
- Acín, A.; Brunner, N.; Gisin, N.; Massar, S.; Pironio, S.; Scarani, V. Device-Independent Security of Quantum Cryptography against Collective Attacks. Phys. Rev. Lett. 2007, 98, 230501. [Google Scholar] [CrossRef] [PubMed]
- Vazirani, U.; Vidick, T. Fully Device-Independent Quantum Key Distribution. Phys. Rev. Lett. 2014, 113, 140501. [Google Scholar] [CrossRef] [PubMed]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar] [CrossRef]
- Colbeck, R. Quantum and Relativistic Protocols for Secure Multi-Party Computation. arXiv, 2009; arXiv:0911.3814. [Google Scholar]
- Pironio, S.; Acín, A.; Massar, S.; de La Giroday, A.B.; Matsukevich, D.N.; Maunz, P.; Olmschenk, S.; Hayes, D.; Luo, L.; Manning, T.A.; Monroe, C. Random numbers certified by Bell’s theorems theorem. Nature (London) 2010, 464, 1021. [Google Scholar] [CrossRef]
- Colbeck, R.; Kent, A. Private randomness expansion with untrusted devices. J. Phys. A Math. Theor. 2011, 44, 095305. [Google Scholar] [CrossRef]
- Mayers, D.; Yao, A. Self Testing Quantum Apparatus. Quantum Inf. Comput. 2004, 4, 273. [Google Scholar]
- Brunner, N.; Pironio, S.; Acín, A.; Gisin, N.; Méthot, A.A.; Scarani, V. Testing the Dimension of Hilbert Spaces. Phys. Rev. Lett. 2008, 100, 210503. [Google Scholar] [CrossRef] [PubMed]
- Reichardt, B.W.; Unger, F.; Vazirani, U. Classical command of quantum systems. Nature (London) 2013, 496, 456. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.H.; Vértesi, T.; Bancal, J.D.; Scarani, V.; Navascués, M. Robust and Versatile Black-Box Certification of Quantum Devices. Phys. Rev. Lett. 2014, 113, 040401. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.C.; Rosset, D.; Bancal, J.D.; Pütz, G.; Barnea, T.J.; Gisin, N. Family of Bell-like Inequalities as Device-Independent Witnesses for Entanglement Depth. Phys. Rev. Lett. 2015, 114, 190401. [Google Scholar] [CrossRef] [PubMed]
- Coladangelo, A.; Goh, K.T.; Scarani, V. All pure bipartite entangled states can be self-tested. Nat. Comm. 2017, 8, 15485. [Google Scholar] [CrossRef] [PubMed]
- Sekatski, P.; Bancal, J.D.; Wagner, S.; Sangouard, N. Certifying the Building Blocks of Quantum Computers from Bell’s Theorem. Phys. Rev. Lett. 2018, 121, 180505. [Google Scholar] [CrossRef]
- Scarani, V. The device-independent outlook on quantum physics. Acta Phys. Slovaca 2012, 62, 347. [Google Scholar]
- Brunner, N.; Cavalcanti, D.; Pironio, S.; Scarani, V.; Wehner, S. Bell nonlocality. Rev. Mod. Phys. 2014, 86, 419–478. [Google Scholar] [CrossRef]
- Bell, J.S. Speakable and Unspeakable in Quantum Mechanics: Collected Papers on Quantum Philosophy, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Hensen, B.; Bernien, H.; Dreau, A.E.; Reiserer, A.; Kalb, N.; Blok, M.S.; Ruitenberg, J.; Vermeulen, R.F.L.; Schouten, R.N.; Abellan, C.; et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 2015, 526, 682–686. [Google Scholar] [CrossRef]
- Shalm, L.K.; Meyer-Scott, E.; Christensen, B.G.; Bierhorst, P.; Wayne, M.A.; Stevens, M.J.; Gerrits, T.; Glancy, S.; Hamel, D.R.; Allman, M.S.; et al. Strong Loophole-Free Test of Local Realism. Phys. Rev. Lett. 2015, 115, 250402. [Google Scholar] [CrossRef] [PubMed]
- Giustina, M.; Versteegh, M.A.M.; Wengerowsky, S.; Handsteiner, J.; Hochrainer, A.; Phelan, K.; Steinlechner, F.; Kofler, J.; Larsson, J.A.; Abellán, C.; et al. Significant-Loophole-Free Test of Bell’s Theorem with Entangled Photons. Phys. Rev. Lett. 2015, 115, 250401. [Google Scholar] [CrossRef] [PubMed]
- Rosenfeld, W.; Burchardt, D.; Garthoff, R.; Redeker, K.; Ortegel, N.; Rau, M.; Weinfurter, H. Event-Ready Bell Test Using Entangled Atoms Simultaneously Closing Detection and Locality Loopholes. Phys. Rev. Lett. 2017, 119, 010402. [Google Scholar] [CrossRef] [PubMed]
- Li, M.H.; Wu, C.; Zhang, Y.; Liu, W.Z.; Bai, B.; Liu, Y.; Zhang, W.; Zhao, Q.; Li, H.; Wang, Z.; et al. Test of Local Realism into the Past without Detection and Locality Loopholes. Phys. Rev. Lett. 2018, 121, 080404. [Google Scholar] [CrossRef] [PubMed]
- Schwarz, S.; Bessire, B.; Stefanov, A.; Liang, Y.C. Bipartite Bell inequalities with three ternary-outcome measurements - from theory to experiments. New J. Phys. 2016, 18, 035001. [Google Scholar] [CrossRef]
- Lin, P.S.; Rosset, D.; Zhang, Y.; Bancal, J.D.; Liang, Y.C. Device-independent point estimation from finite data and its application to device-independent property estimation. Phys. Rev. A 2018, 97, 032309. [Google Scholar] [CrossRef]
- Popescu, S.; Rohrlich, D. Quantum nonlocality as an axiom. Found. Phys. 1994, 24, 379–385. [Google Scholar] [CrossRef]
- Barrett, J.; Linden, N.; Massar, S.; Pironio, S.; Popescu, S.; Roberts, D. Nonlocal correlations as an information-theoretic resource. Phys. Rev. A 2005, 71, 022101. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, Q.; Li, M.H.; Guan, J.Y.; Zhang, Y.; Bai, B.; Zhang, W.; Liu, W.Z.; Wu, C.; Yuan, X.; et al. Device-independent quantum random-number generation. Nature 2018, 562, 548–551. [Google Scholar] [CrossRef]
- Adenier, G.; Khrennikov, A.Y. Test of the no-signaling principle in the Hensen loophole-free CHSH experiment. Fortschr. Phys. 2017, 65, 1600096. [Google Scholar] [CrossRef]
- Bednorz, A. Analysis of assumptions of recent tests of local realism. Phys. Rev. A 2017, 95, 042118. [Google Scholar] [CrossRef]
- Kupczynski, M. Is Einsteinian no-signalling violated in Bell tests? Open Phys. 2017, 15, 739. [Google Scholar] [CrossRef]
- Aspect, A.; Dalibard, J.; Roger, G. Experimental Test of Bell’s Inequalities Using Time-Varying Analyzers. Phys. Rev. Lett. 1982, 49, 1804–1807. [Google Scholar] [CrossRef]
- Tittel, W.; Brendel, J.; Zbinden, H.; Gisin, N. Violation of Bell Inequalities by Photons More Than 10 km Apart. Phys. Rev. Lett. 1998, 81, 3563–3566. [Google Scholar] [CrossRef]
- Weihs, G.; Jennewein, T.; Simon, C.; Weinfurter, H.; Zeilinger, A. Violation of Bell’s Inequality under Strict Einstein Locality Conditions. Phys. Rev. Lett. 1998, 81, 5039–5043. [Google Scholar] [CrossRef]
- Rowe, M.A.; Kielpinski, D.; Meyer, V.; Sackett, C.A.; Itano, W.M.; Monroe, C.; Wineland, D.J. Experimental violation of a Bell’s inequality with efficient detection. Nature 2001, 409, 791–794. [Google Scholar] [CrossRef] [PubMed]
- Giustina, M.; Mech, A.; Ramelow, S.; Wittmann, B.; Kofler, J.; Beyer, J.; Lita, A.; Calkins, B.; Gerrits, T.; Nam, S.W.; et al. Bell violation using entangled photons without the fair-sampling assumption. Nature 2013, 497, 227. [Google Scholar] [CrossRef]
- Christensen, B.G.; McCusker, K.T.; Altepeter, J.B.; Calkins, B.; Gerrits, T.; Lita, A.E.; Miller, A.; Shalm, L.K.; Zhang, Y.; Nam, S.W.; et al. Detection-Loophole-Free Test of Quantum Nonlocality, and Applications. Phys. Rev. Lett. 2013, 111, 130406. [Google Scholar] [CrossRef]
- Erven, C.; Meyer-Scott, E.; Fisher, K.; Lavoie, J.; Higgins, B.L.; Yan, Z.; Pugh, C.J.; Bourgoin, J.P.; Prevedel, R.; Shalm, L.K.; et al. Experimental three-photon quantum nonlocality under strict locality conditions. Nature Photonics 2014, 8, 292. [Google Scholar] [CrossRef]
- Lanyon, B.P.; Zwerger, M.; Jurcevic, P.; Hempel, C.; Dür, W.; Briegel, H.J.; Blatt, R.; Roos, C.F. Experimental Violation of Multipartite Bell Inequalities with Trapped Ions. Phys. Rev. Lett. 2014, 112, 100403. [Google Scholar] [CrossRef]
- Shen, L.; Lee, J.; Thinh, L.P.; Bancal, J.D.; Cerè, A.; Lamas-Linares, A.; Lita, A.; Gerrits, T.; Nam, S.W.; Scarani, V.; et al. Randomness Extraction from Bell Violation with Continuous Parametric Down-Conversion. Phys. Rev. Lett. 2018, 121, 150402. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Glancy, S.; Knill, E. Asymptotically optimal data analysis for rejecting local realism. Phys. Rev. A 2011, 84, 062118. [Google Scholar] [CrossRef]
- Gill, R.D. Time, Finite Statistics, and Bell’s Fifth Position. arXiv, 2003; arXiv:quant-ph/0301059. [Google Scholar]
- Clauser, J.F.; Horne, M.A.; Shimony, A.; Holt, R.A. Proposed Experiment to Test Local Hidden-Variable Theories. Phys. Rev. Lett. 1969, 23, 880–884. [Google Scholar] [CrossRef]
- Zhang, Y.; Glancy, S.; Knill, E. Efficient quantification of experimental evidence against local realism. Phys. Rev. A 2013, 88, 052119. [Google Scholar] [CrossRef]
- Cavalcanti, D.; Salles, A.; Scarani, V. Macroscopically local correlations can violate information causality. Nat. Commun. 2010, 1, 136. [Google Scholar] [CrossRef] [PubMed]
- Fritz, T.; Sainz, A.B.; Augusiak, R.; Brask, J.B.; Chaves, R.; Leverrier, A.; Acín, A. Local orthogonality as a multipartite principle for quantum correlations. Nat. Commun. 2013, 4, 2263. [Google Scholar] [CrossRef] [PubMed]
- Amaral, B.; Cunha, M.T.; Cabello, A. Exclusivity principle forbids sets of correlations larger than the quantum set. Phys. Rev. A 2014, 89, 030101. [Google Scholar] [CrossRef]
- Navascués, M.; Guryanova, Y.; Hoban, M.J.; Acín, A. Almost quantum correlations. Nat. Commun. 2015, 6, 6288. [Google Scholar] [CrossRef]
- Navascués, M.; Wunderlich, H. A glance beyond the quantum model. Proc. R. Soc. A 2010, 466, 881. [Google Scholar] [CrossRef]
- Rohrlich, D. PR-Box Correlations Have No Classical Limit. In Quantum Theory: A Two-Time Success Story; Struppa, D.C., Tollaksen, J.M., Eds.; Springer Milan: Milano, Italy, 2014; pp. 205–211. [Google Scholar]
- Van Dam, W. Implausible consequences of superstrong nonlocality. Nat. Comput. 2013, 12, 9–12. [Google Scholar] [CrossRef]
- Brassard, G.; Buhrman, H.; Linden, N.; Méthot, A.A.; Tapp, A.; Unger, F. Limit on Nonlocality in Any World in Which Communication Complexity Is Not Trivial. Phys. Rev. Lett. 2006, 96, 250401. [Google Scholar] [CrossRef]
- Linden, N.; Popescu, S.; Short, A.J.; Winter, A. Quantum Nonlocality and Beyond: Limits from Nonlocal Computation. Phys. Rev. Lett. 2007, 99, 180502. [Google Scholar] [CrossRef] [PubMed]
- Pawłowski, M.; Paterek, T.; Kaszlikowski, D.; Scarani, V.; Winter, A.; Żukowski, M. Information causality as a physical principle. Nature 2009, 461, 1101. [Google Scholar] [CrossRef] [PubMed]
- Goh, K.T.; Kaniewski, J.; Wolfe, E.; Vértesi, T.; Wu, X.; Cai, Y.; Liang, Y.C.; Scarani, V. Geometry of the set of quantum correlations. Phys. Rev. A 2018, 97, 022104. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization, 1st ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Navascués, M.; Pironio, S.; Acín, A. Bounding the Set of Quantum Correlations. Phys. Rev. Lett. 2007, 98, 010401. [Google Scholar] [CrossRef] [PubMed]
- Navascués, M.; Pironio, S.; Acín, A. A convergent hierarchy of semidefinite programs characterizing the set of quantum correlations. New J. Phys. 2008, 10, 073013. [Google Scholar] [CrossRef]
- Doherty, A.C.; Liang, Y.C.; Toner, B.; Wehner, S. The Quantum Moment Problem and Bounds on Entangled Multi-prover Games. In Proceedings of the 2008 23rd Annual IEEE Conference on Computational Complexity, College Park, MD, USA, 23–26 June 2008; pp. 199–210. [Google Scholar]
- Moroder, T.; Bancal, J.D.; Liang, Y.C.; Hofmann, M.; Gühne, O. Device-Independent Entanglement Quantification and Related Applications. Phys. Rev. Lett. 2013, 111, 030501. [Google Scholar] [CrossRef] [PubMed]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Statist. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Van Dam, W.; Gill, R.D.; Grunwald, P.D. The statistical strength of nonlocality proofs. IEEE Trans. Inf. Theor. 2005, 51, 2812–2835. [Google Scholar] [CrossRef]
- Acín, A.; Gill, R.; Gisin, N. Optimal Bell Tests Do Not Require Maximally Entangled States. Phys. Rev. Lett. 2005, 95, 210402. [Google Scholar] [CrossRef]
- Zhang, Y.; Knill, E.; Glancy, S. Statistical strength of experiments to reject local realism with photon pairs and inefficient detectors. Phys. Rev. A 2010, 81, 032117. [Google Scholar] [CrossRef]
- Bancal, J.D.; Pironio, S.; Acin, A.; Liang, Y.C.; Scarani, V.; Gisin, N. Quantum non-locality based on finite-speed causal influences leads to superluminal signalling. Nat. Phys. 2012, 8, 867–870. [Google Scholar] [CrossRef]
- Barnea, T.J.; Bancal, J.D.; Liang, Y.C.; Gisin, N. Tripartite quantum state violating the hidden-influence constraints. Phys. Rev. A 2013, 88, 022123. [Google Scholar] [CrossRef]
- Chen, S.L.; Budroni, C.; Liang, Y.C.; Chen, Y.N. Natural Framework for Device-Independent Quantification of Quantum Steerability, Measurement Incompatibility, and Self-Testing. Phys. Rev. Lett. 2016, 116, 240401. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.L.; Budroni, C.; Liang, Y.C.; Chen, Y.N. Exploring the framework of assemblage moment matrices and its applications in device-independent characterizations. Phys. Rev. A 2018, 98, 042127. [Google Scholar] [CrossRef]
- Fiala, J.; Kočvara, M.; Stingl, M. PENLAB: A MATLAB solver for nonlinear semidefinite optimization. arXiv, 2013; arXiv:1311.5240. [Google Scholar]
- Christensen, B.G.; Liang, Y.C.; Brunner, N.; Gisin, N.; Kwiat, P.G. Exploring the Limits of Quantum Nonlocality with Entangled Photons. Phys. Rev. X 2015, 5, 041052. [Google Scholar] [CrossRef]
- Poh, H.S.; Joshi, S.K.; Cerè, A.; Cabello, A.; Kurtsiefer, C. Approaching Tsirelson’s Bound in a Photon Pair Experiment. Phys. Rev. Lett. 2015, 115, 180408. [Google Scholar] [CrossRef]
- Minka, T. The Lightspeed Matlab Toolbox. Available online: https://github.com/tminka/lightspeed (accessed on 18 June 2017).
- Christensen, B.G.; (University of Wisconsin-Madison, Madison, WI, USA). Personal communication, 2017.
- Pütz, G.; Rosset, D.; Barnea, T.J.; Liang, Y.-C.; Gisin, N. Arbitrarily Small Amount of Measurement Independence Is Sufficient to Manifest Quantum Nonlocality. Phys. Rev. Lett. 2014, 113, 190402. [Google Scholar] [CrossRef]
- Nuzzo, R. Statistical errors: P values, the ’gold standard’ of statistical validity, are not as reliable as many scientists assume. Nature 2014, 506, 150. [Google Scholar] [CrossRef]
- Leek, J.T.; Peng, R.D. P values are just the tip of the iceberg. Nature 2015, 520, 612. [Google Scholar] [CrossRef] [PubMed]
- Wasserstein, R.L.; Lazar, N.A. The ASA’s Statement on p-Values: Context, Process, and Purpose. Am. Stat. 2016, 70, 129–133. [Google Scholar] [CrossRef]
- Smania, M.; Kleinmann, M.; Cabello, A.; Bourennane, M. Avoiding apparent signaling in Bell tests for quantitative applications. arXiv, 2018; arXiv:1801.05739. [Google Scholar]
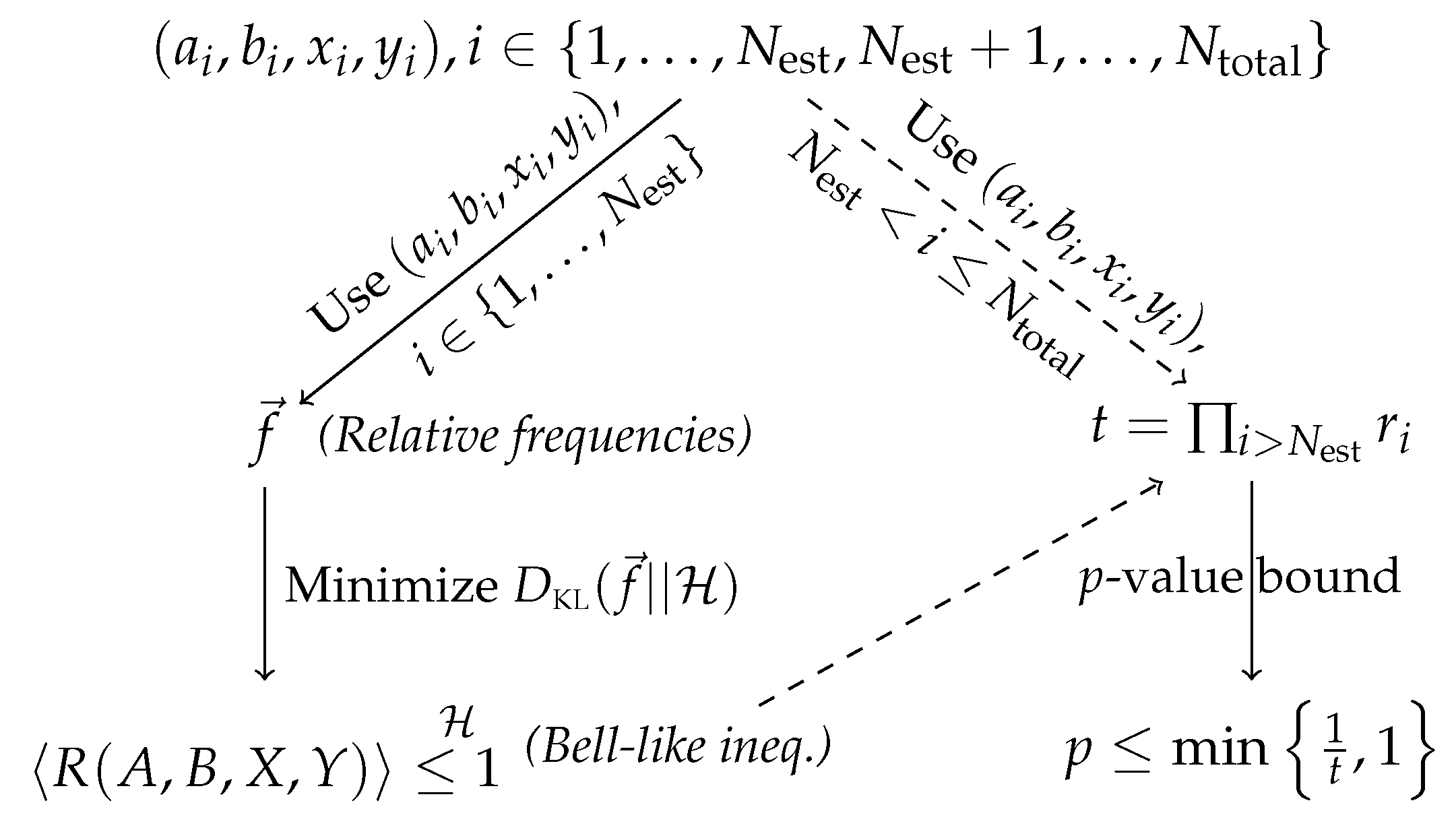
| p-Value Bound | ≤ | ≤ | ≤ | ≤ | Trivial |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 97% | |
| 58% | 85% | 90% | 93% | 5.8% |
| p-Value Bound | Trivial | ||||
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 97% | |
| 17 | 59% | 69% | 72 | 24% |
| p-Value Bound | Trivial | ||||
|---|---|---|---|---|---|
| 38% | 45% | 48% | 51% | 48% | |
| 35% | 44% | 47% | 49% | 49% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Y.-C.; Zhang, Y. Bounding the Plausibility of Physical Theories in a Device-Independent Setting via Hypothesis Testing. Entropy 2019, 21, 185. https://doi.org/10.3390/e21020185
Liang Y-C, Zhang Y. Bounding the Plausibility of Physical Theories in a Device-Independent Setting via Hypothesis Testing. Entropy. 2019; 21(2):185. https://doi.org/10.3390/e21020185
Chicago/Turabian StyleLiang, Yeong-Cherng, and Yanbao Zhang. 2019. "Bounding the Plausibility of Physical Theories in a Device-Independent Setting via Hypothesis Testing" Entropy 21, no. 2: 185. https://doi.org/10.3390/e21020185
APA StyleLiang, Y.-C., & Zhang, Y. (2019). Bounding the Plausibility of Physical Theories in a Device-Independent Setting via Hypothesis Testing. Entropy, 21(2), 185. https://doi.org/10.3390/e21020185





