An Optimal Resonant Frequency Band Feature Extraction Method Based on Empirical Wavelet Transform
Abstract
:1. Introduction
2. Theoretical Background
2.1. Empirical Wavelet Transform
2.2. Scale Space Histogram
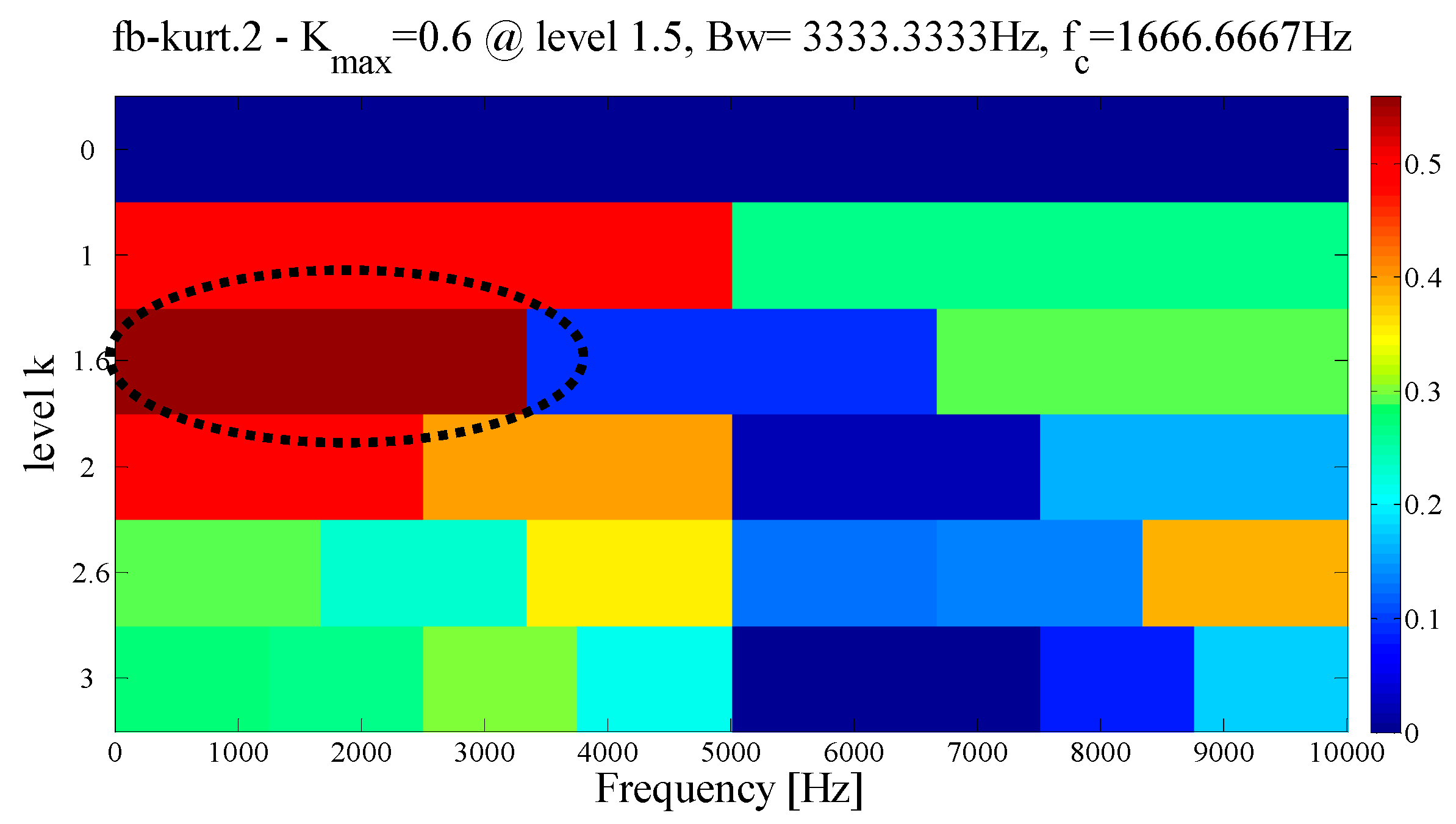
3. Optimal Resonant Frequency Band is Established Based on the EWT
3.1. Average Spectral Negentropy Operator
3.2. ASN Modified by Correlation Coefficient
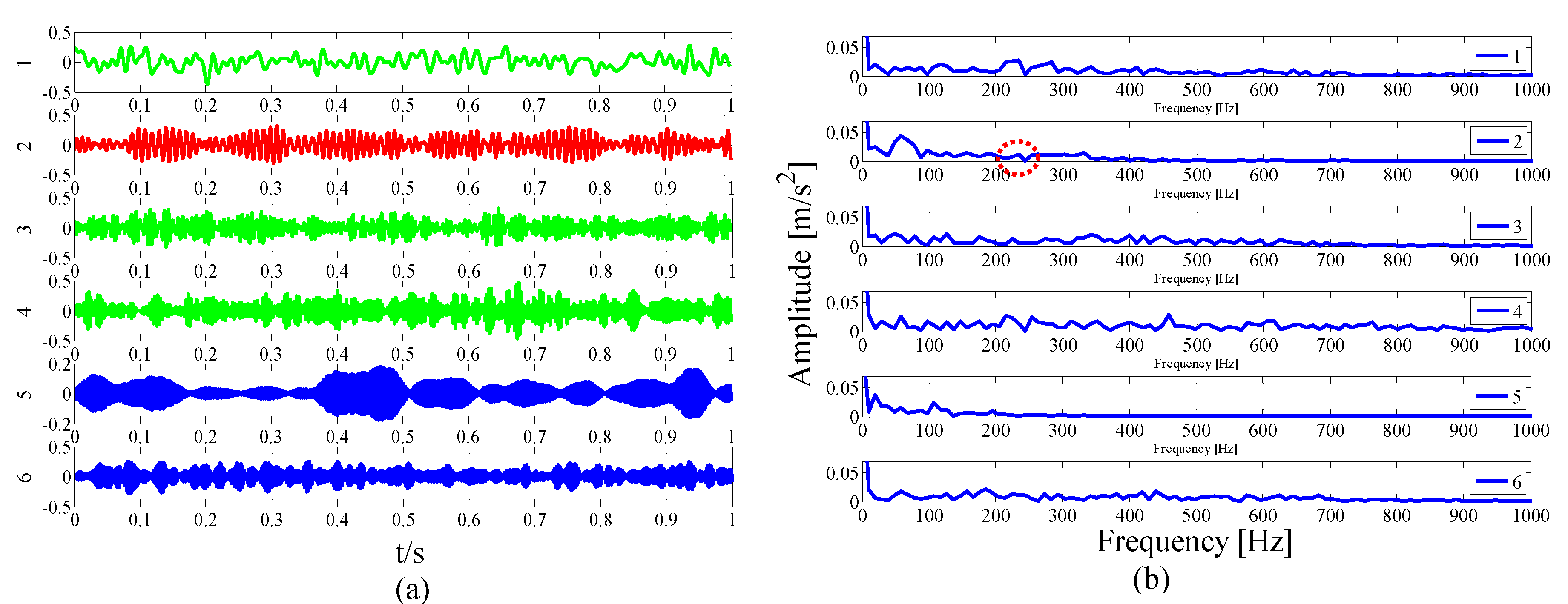
3.3. Fault Feature Extraction Based on the AEWT
- Step 1:
- Fourier spectrum X(f) is obtained by performing the DFT on the input signal x(t).
- Step 2:
- Apply a parameterless clustering scale-space histogram segmentation boundary to X(f).
- Step 3:
- Application EWT is used to decompose the input signal into a set of empirical modes.
- Step 4:
- Calculate the ASN and correlation coefficient values on each mode.
- Step 5:
- The AASN is calculated according to Equation (15). The mode corresponding to the highest value is selected as the center band.
- Step 6:
- Determine whether the correlation coefficient of the adjacent mode is greater than 0.25, and if the requirement is met, the reconstruction signal is composed.
- Step 7:
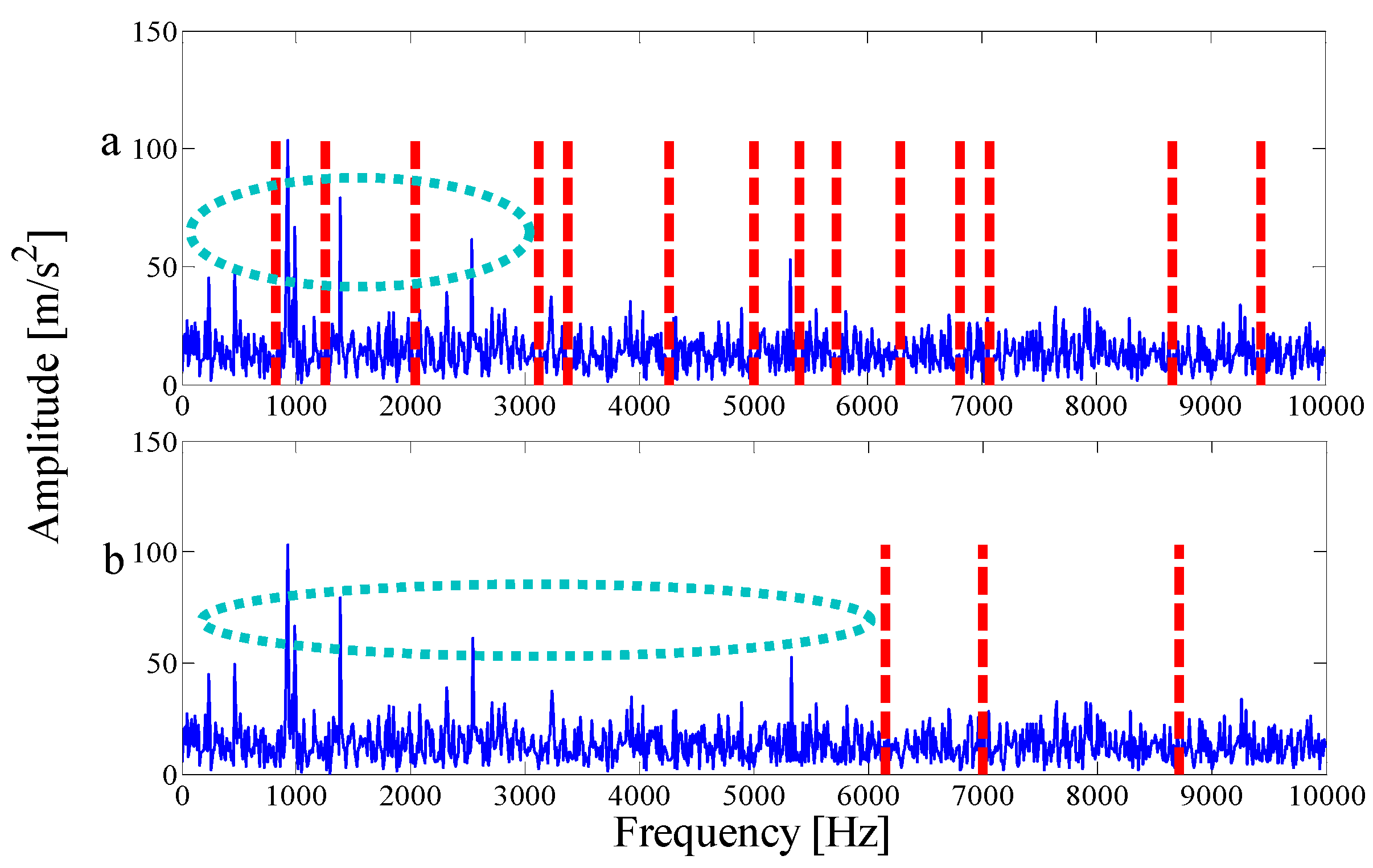
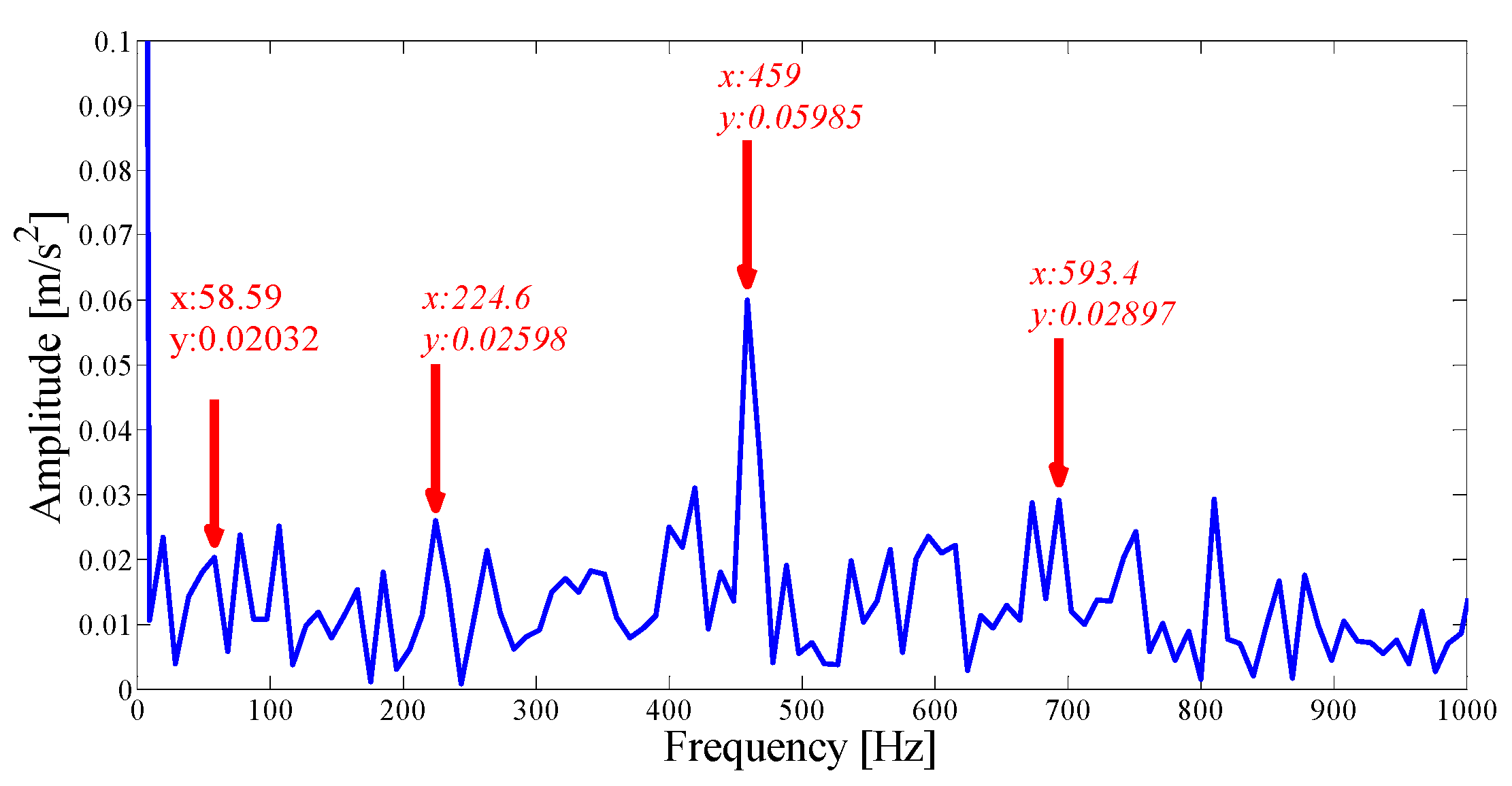
- Fault types are diagnosed by observing Hilbert envelope spectrum.
4. Simulations and Comparative Analysis
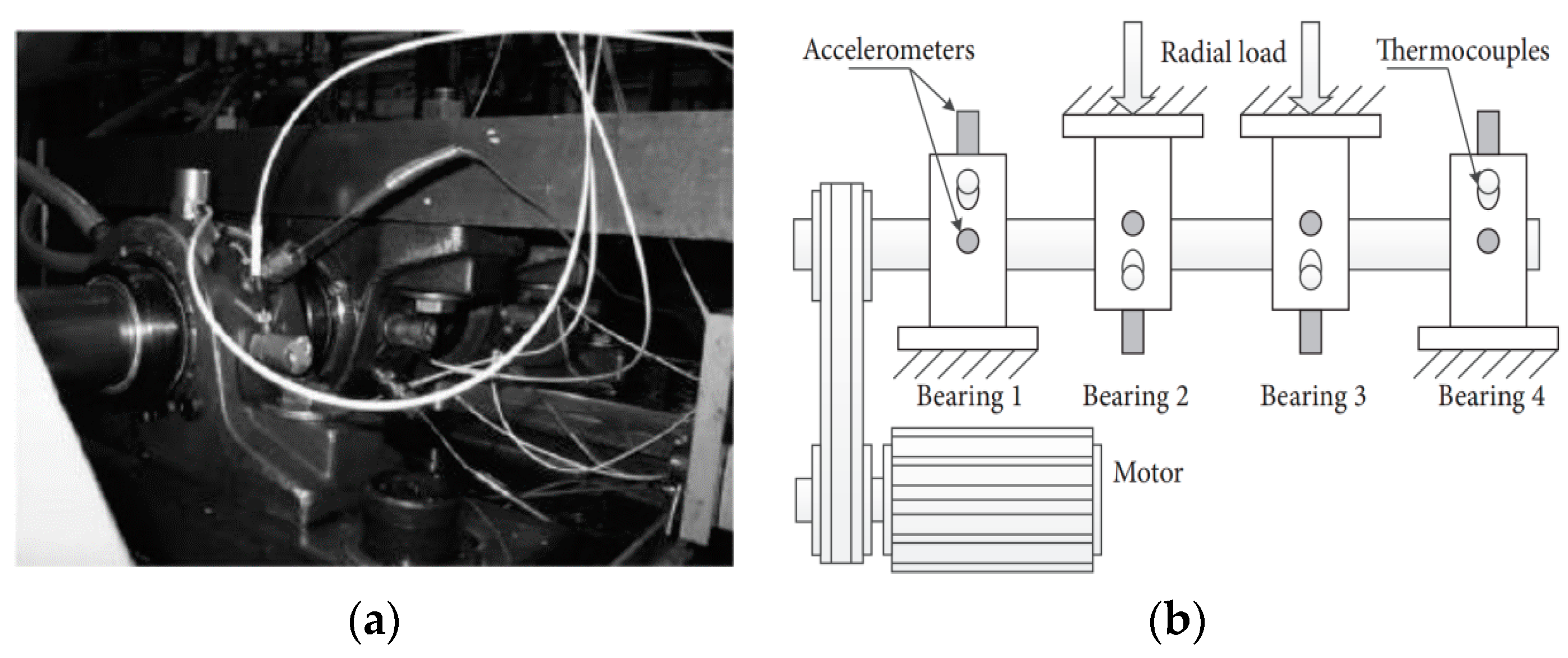
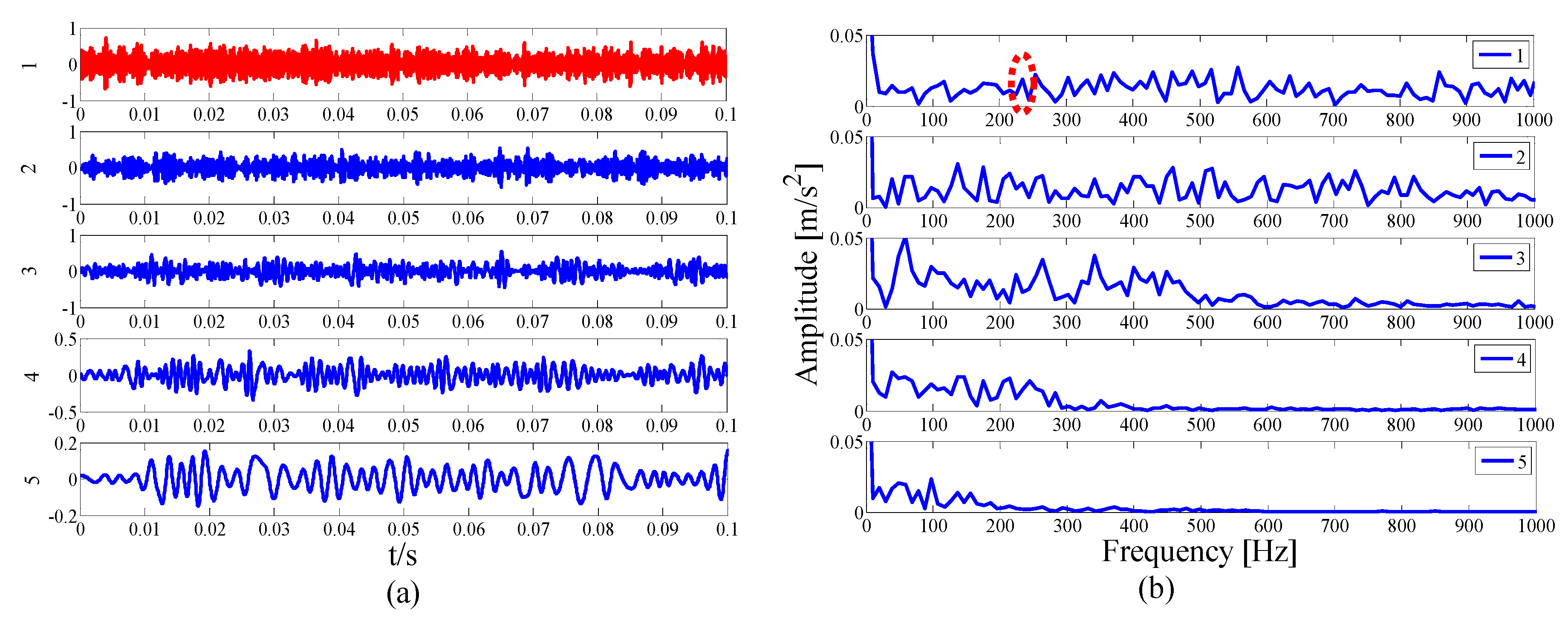
5. Application to Roller Bearings Testing
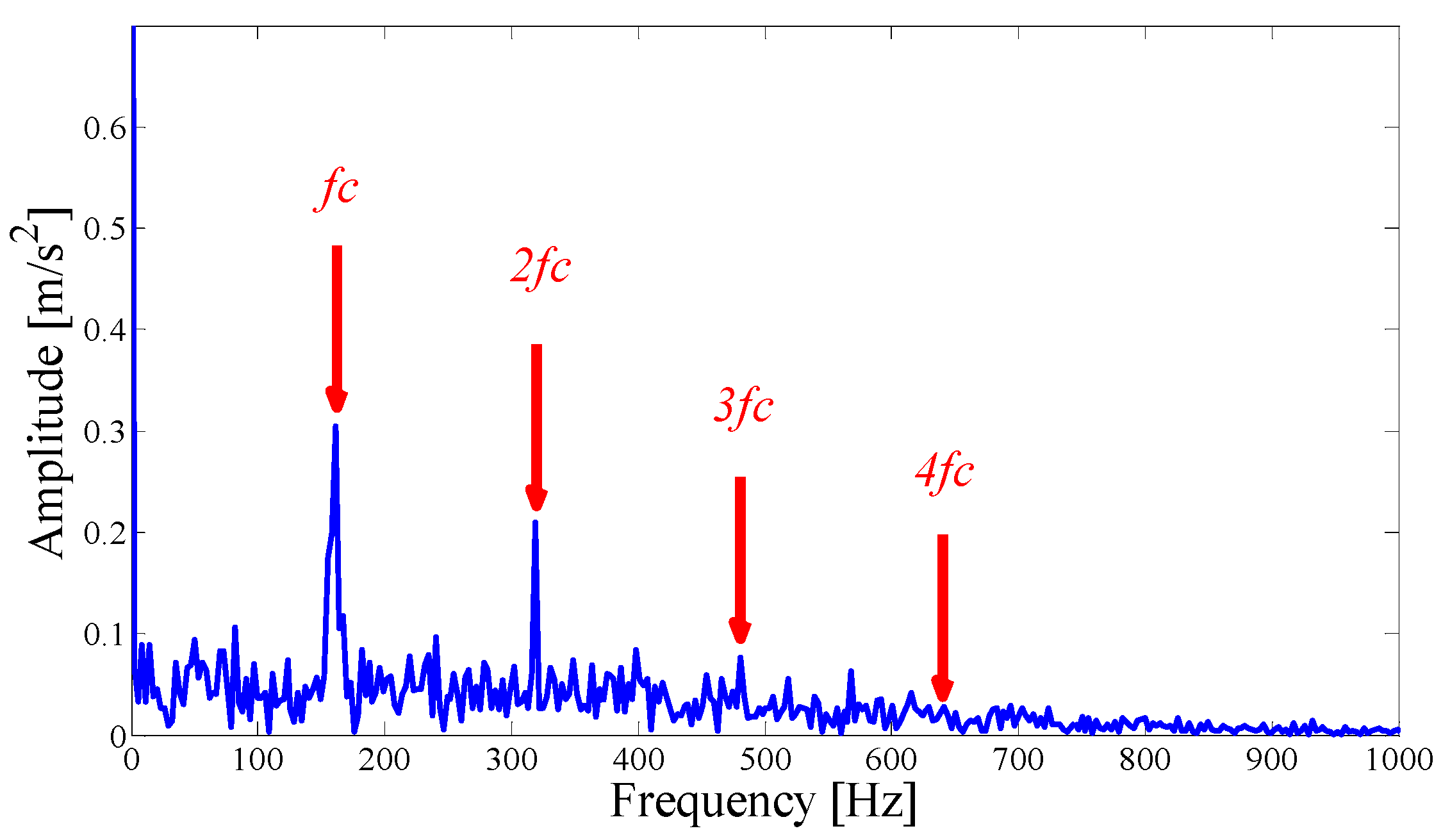
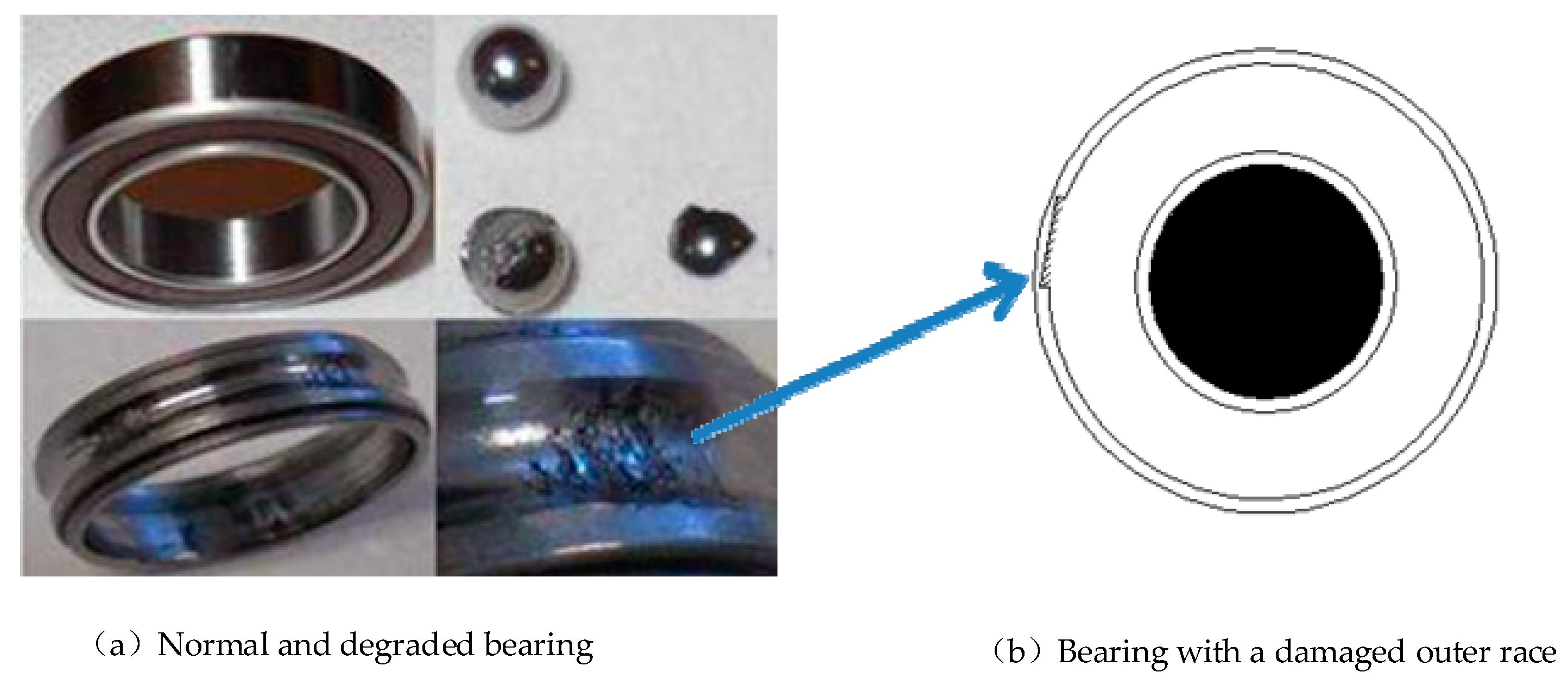
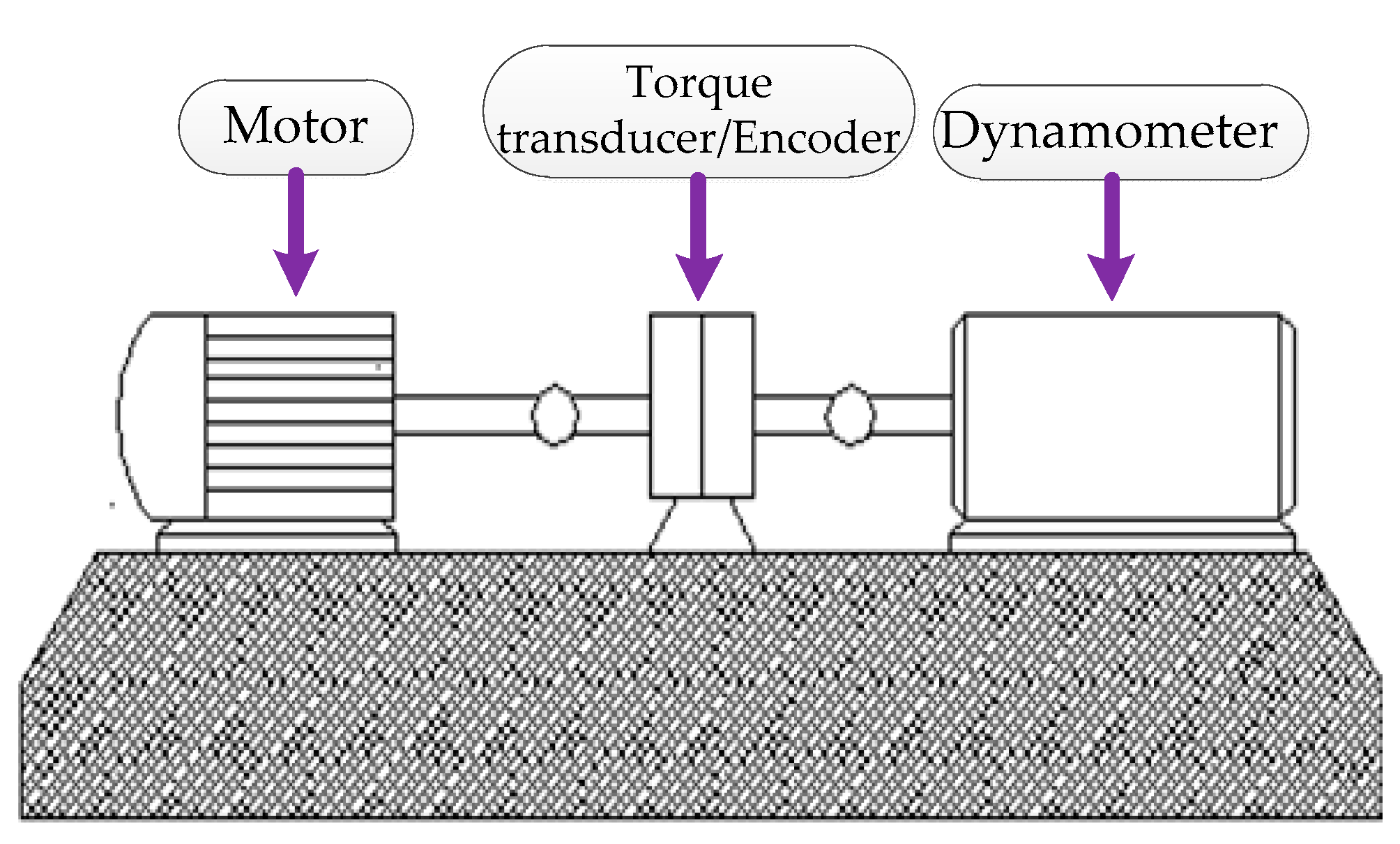
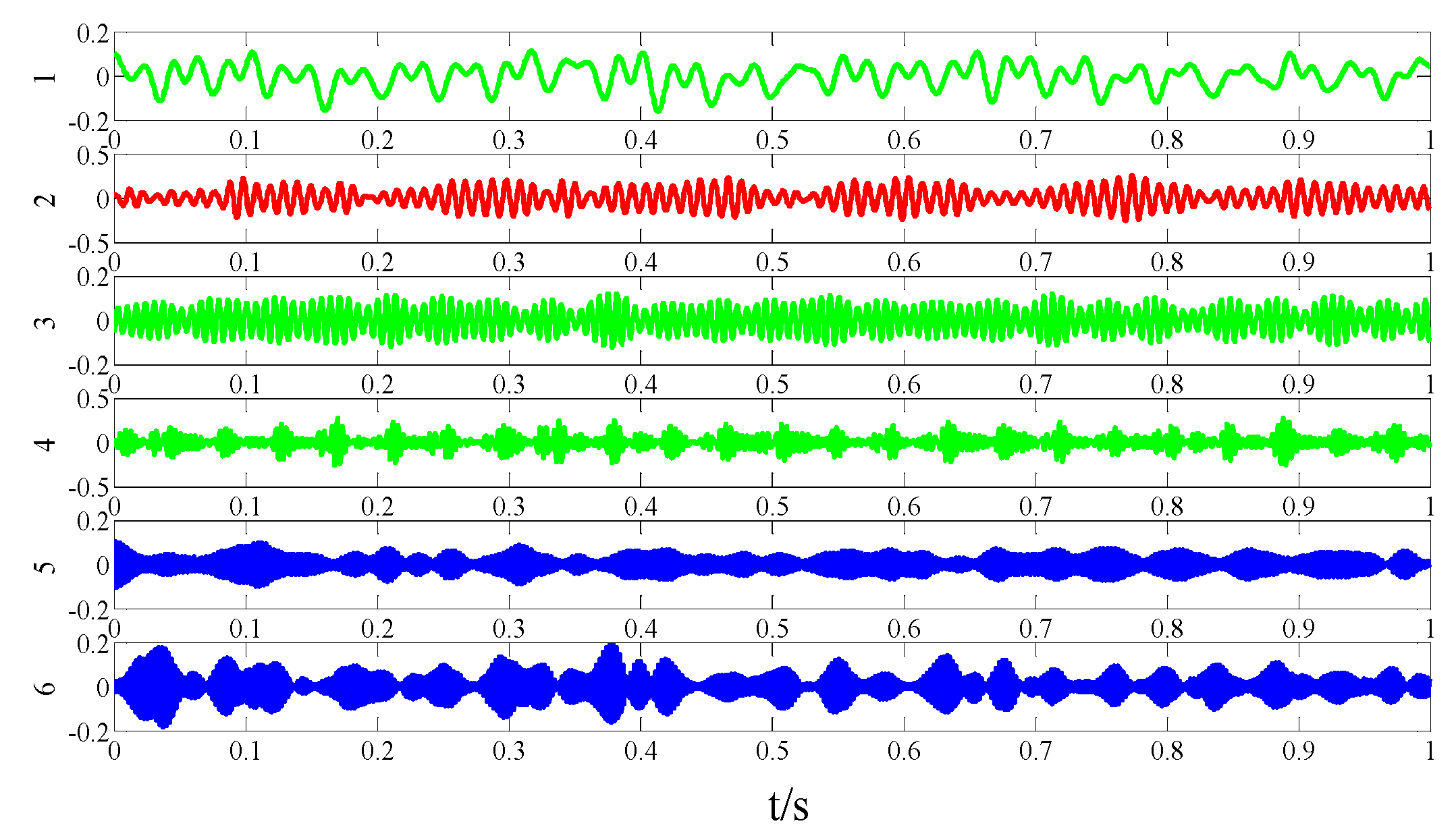
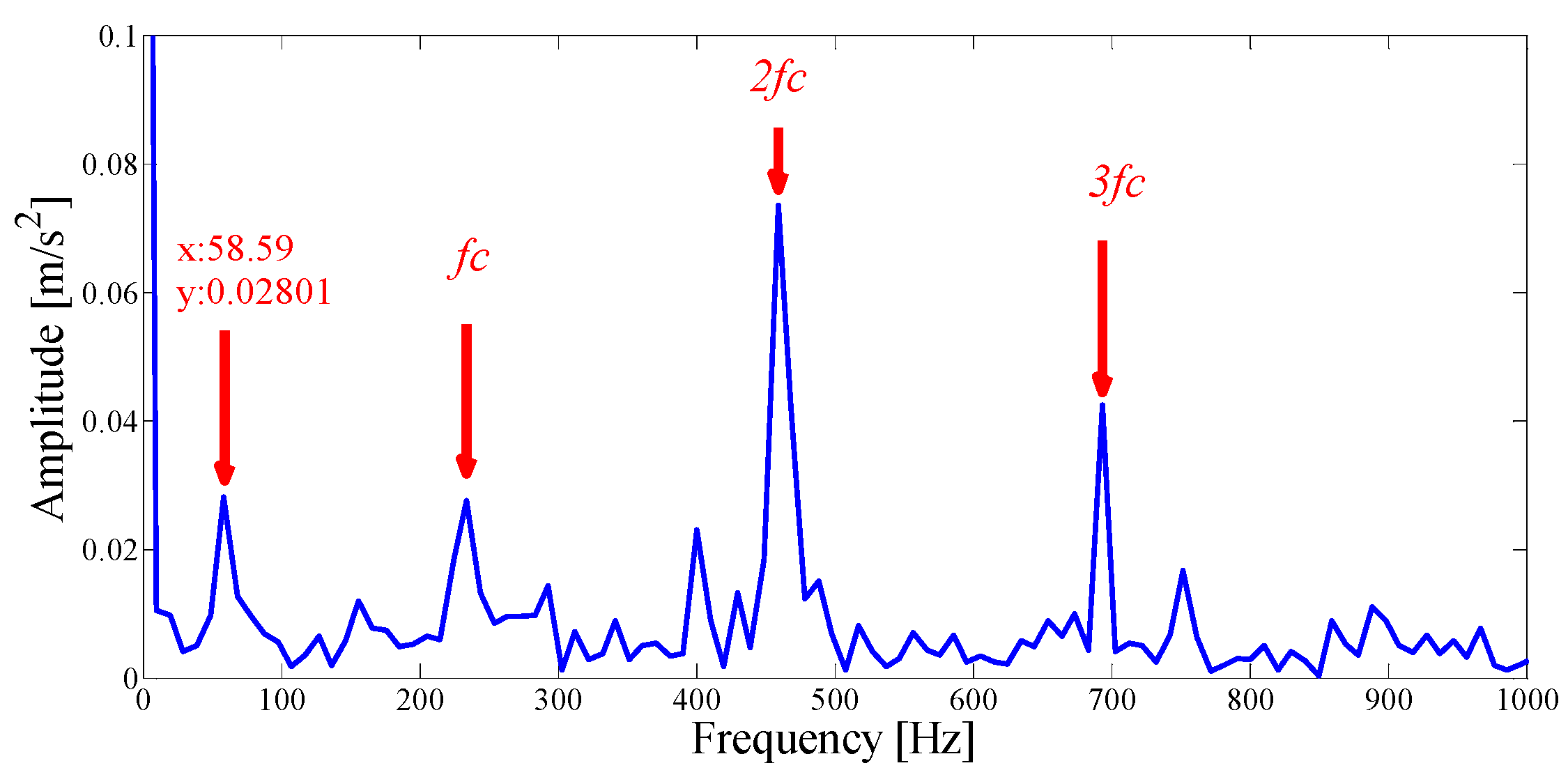
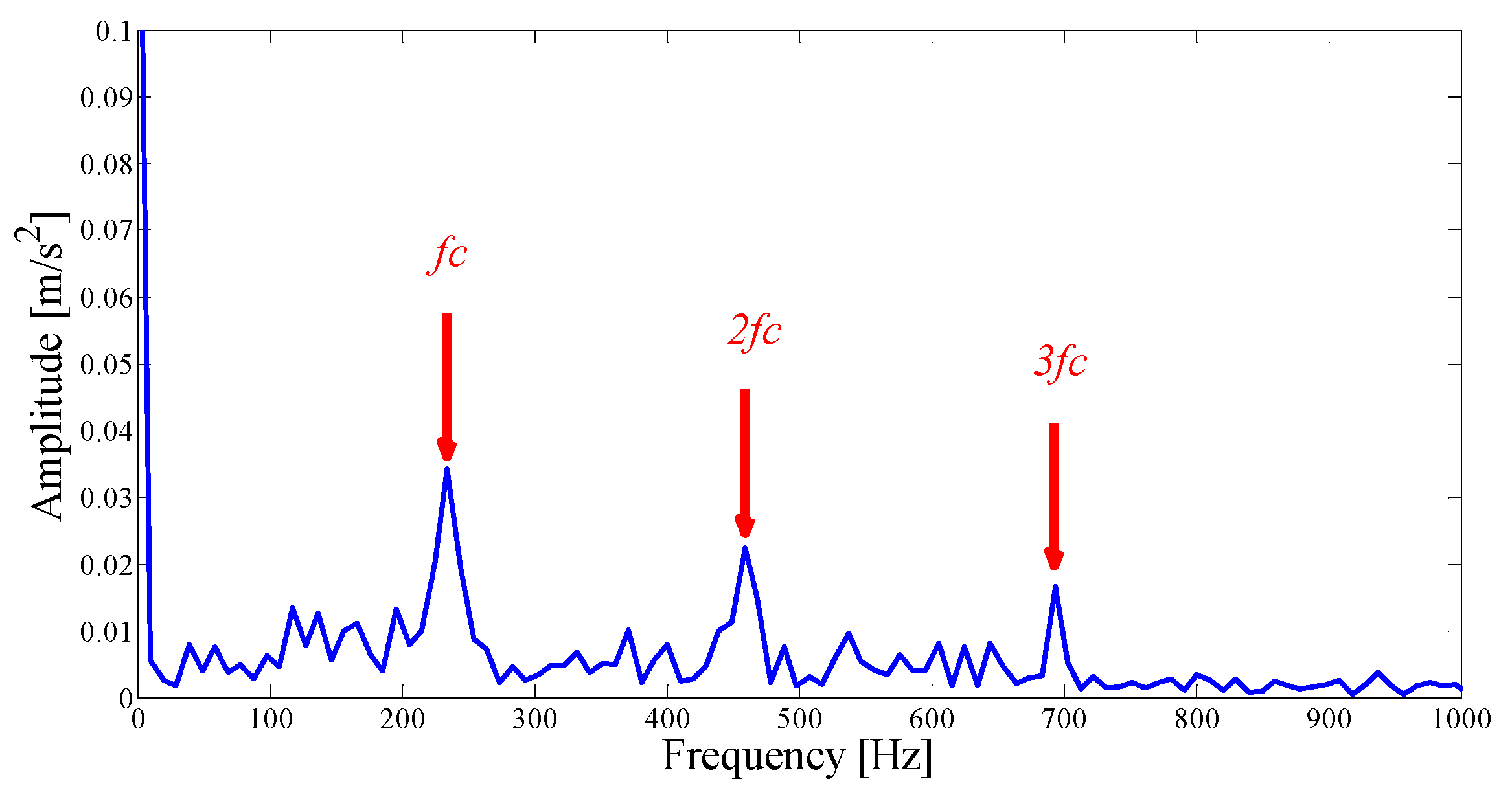
5.1. Case 1: Analysis of CWRU Outer Ring Fault Vibration Signal
5.2. Case 2: Analysis of NASA Outer Ring Fault Vibration Signal
5.2.1. Original Fault Vibration Signal Analysis
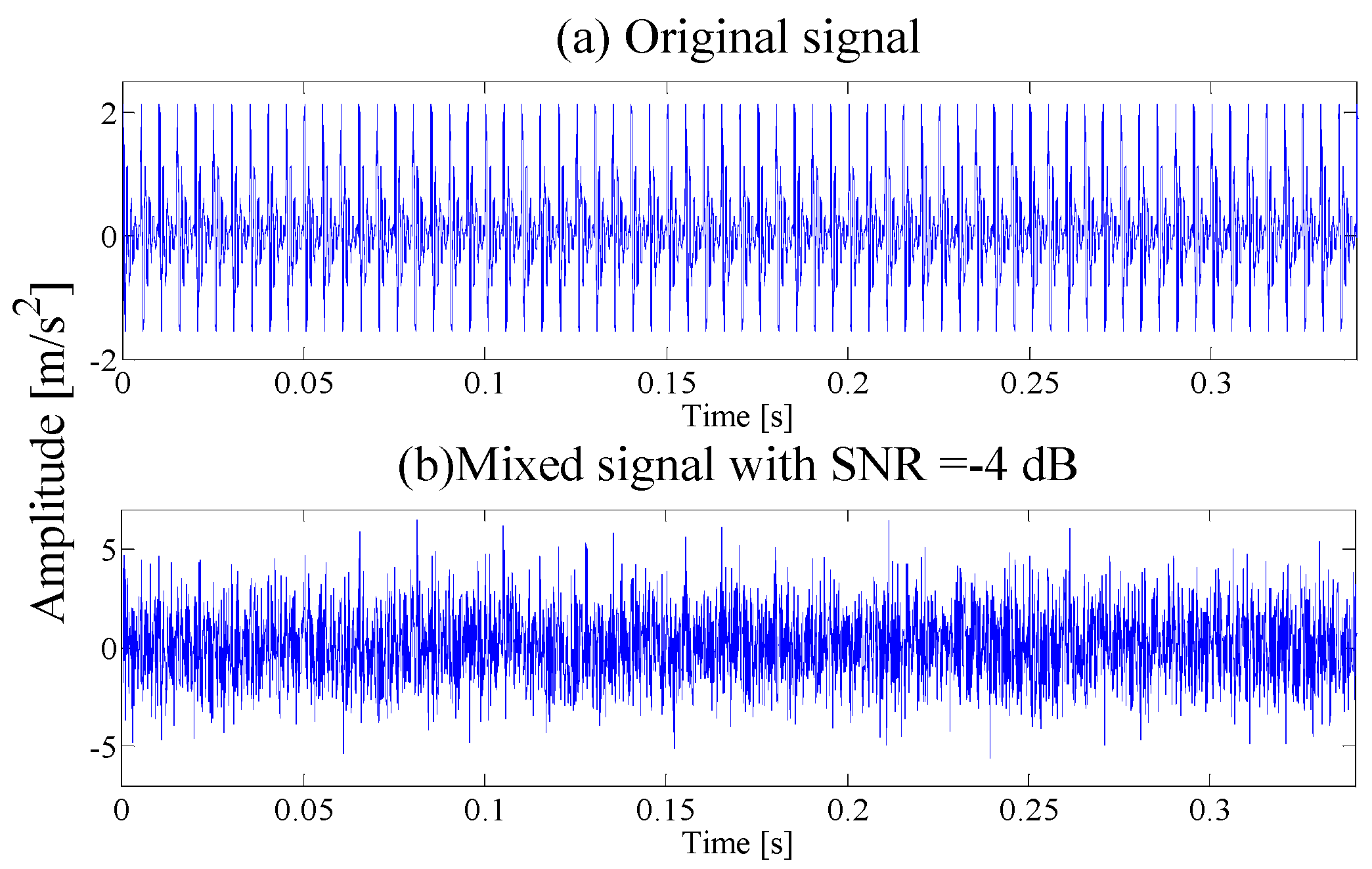
5.2.2. Analysis of Noise-Adding Fault Vibration Signal
6. Discussion and Conclusions
6.1. Discussion
6.2. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Caesarendra, W.; Tjahjowidodo, T. A review of feature extraction methods in vibration-based condition monitoring and its application for degradation trend estimation of low-speed slew bearing. Machines 2017, 5, 21. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, Y.; Guo, Q.; Hu, C.; Peng, Z. Multi-dimensional variational mode decomposition for bearing-crack detection in wind turbines with large driving-speed variations. Renew. Energy 2016, 116, 55–73. [Google Scholar] [CrossRef]
- Wahyu, C.; Tegoeh, T.; Buyung, K. Integrated Condition Monitoring and Prognosis Method for Incipient Defect Detection and Remaining Life Prediction of Low Speed Slew Bearings. Machine 2017, 5, 11. [Google Scholar]
- Jian, X.; Li, W.; Guo, X.; Wang, R. Fault Diagnosis of Motor Bearings Based on a One-Dimensional Fusion Neural Network. Sensors 2019, 19, 122. [Google Scholar] [CrossRef] [PubMed]
- Glowacz, A. Recognition of Acoustic Signals of Commutator Motors. Appl. Sci. 2018, 8, 2630. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Z.; Chen, S.; Wang, J.; Zhang, X. Optimised ensemble empirical mode decomposition with optimised noise parameters and its application to rolling element bearing fault diagnosis. Insight-Non-Destr. Test. Cond. Monit. 2016, 58, 494–501. [Google Scholar] [CrossRef]
- Hoseinzadeh, M.S.; Khadem, S.E.; Sadooghi, M.S. Quantitative diagnosis for bearing faults by improving ensemble empirical mode decomposition. ISA Trans. 2018, 83, 261–275. [Google Scholar] [CrossRef]
- Fan, G.F.; Peng, L.L.; Hong, W.C.; Sun, F. Electric load forecasting by the SVR model with differential empirical mode decomposition and auto regression. Neurocomputing 2016, 173, 958–970. [Google Scholar] [CrossRef]
- Nava, N.; Di Matteo, T.; Aste, T. Dynamic correlations at different time-scales with empirical mode decomposition. Phys. A Stat. Mech. Its Appl. 2018, 502, 534–544. [Google Scholar] [CrossRef]
- Flandrin, P.; Rilling, G.; Goncalves, P. Empirical mode decomposition as a filter bank. IEEE Signal Process. Lett. 2004, 11, 112–114. [Google Scholar] [CrossRef]
- Gilles, J. Empirical wavelet transform. IEEE Trans. Signal Process. 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Wang, D.; Zhao, Y.; Yi, C.; Tsui, K.L.; Lin, J. Sparsity guided empirical wavelet transform for fault diagnosis of rolling element bearings. Mech. Syst. Signal Process. 2018, 101, 292–308. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, K.; Ma, C. An Improved Empirical Wavelet Transform and Its Applications in Rolling Bearing Fault Diagnosis. Appl. Sci. 2018, 8, 2352. [Google Scholar] [CrossRef]
- Yu, K.; Lin, T.R.; Tan, J.; Ma, H. An adaptive sensitive frequency band selection method for empirical wavelet transform and its application in bearing fault diagnosis. Measurement 2019, 134, 375–384. [Google Scholar] [CrossRef]
- Gilles, J.; Heal, K. A parameterless scale-space approach to find meaningful modes in histogram—Application to image and spectrum segmentation. Int. J. Wavelets Multiresolut. Inf. Process. 2014, 12, 1450044. [Google Scholar] [CrossRef]
- Pan, J.; Chen, J.; Zi, Y. Mono-component feature extraction for mechanical fault diagnosis using modified empirical wavelet transform via data-driven adaptive Fourier spectrum segment. Mech. Syst. Signal Process. 2016, 72, 160–183. [Google Scholar] [CrossRef]
- Bernstein, S. Fractional Riesz–Hilbert-Type Transforms and Associated Monogenic Signals. Complex Anal. Oper. Theory 2017, 11, 995–1015. [Google Scholar] [CrossRef]
- Antoni, J. The spectral kurtosis: A useful tool for characterising non-stationary signals. Mech. Syst. Signal Process. 2006, 20, 282–307. [Google Scholar] [CrossRef]
- Antoni, J. Fast computation of the kurtogram for the detection of transient faults. Mech. Syst. Signal Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]
- Antoni, J. Cyclic spectral analysis of rolling-element bearing signals: Facts and fictions. J. Sound Vib. 2007, 304, 497–529. [Google Scholar] [CrossRef]
- Li, Y.B.; Xu, M.Q.; Zhao, H.Y.; Huang, W.H. A study on rolling bearing fault diagnosis method based on hierarchical fuzzy entropy and ISVM-BT. J. Vib. Eng. 2016, 29, 184–192. [Google Scholar]
- Miao, Y.; Zhao, M.; Lin, J. Periodicity-Impulsiveness Spectrum Based on Singular Value Negentropy and Its Application for Identification of Optimal Frequency Band. IEEE Trans. Ind. Electron. 2019, 66, 3127–3138. [Google Scholar] [CrossRef]
- Abboud, D.; Antoni, J.; Eltabach, M.; Sieg-Zieba, S. Angle\time cyclostationarity for the analysis of rolling element bearing vibrations. Measurement 2015, 75, 29–39. [Google Scholar] [CrossRef]
- Barszcz, T.; JabŁoński, A. A novel method for the optimal band selection for vibration signal demodulation and comparison with the Kurtogram. Mech. Syst. Signal Process. 2011, 25, 431–451. [Google Scholar] [CrossRef]
- Kruczek, P.; Obuchowski, J. Modified protrugram method for damage detection in bearing operating under impulsive load. In Cyclostationarity: Theory and Methods III; Springer: Cham, Switzerland, 2017; pp. 229–240. [Google Scholar]
- Antoni, J. The infogram: Entropic evidence of the signature of repetitive transients. Mech. Syst. Signal Process. 2016, 74, 73–94. [Google Scholar] [CrossRef]
- An, X.; Yang, J. Denoising of hydropower unit vibration signal based on variational mode decomposition and approximate entropy. Trans. Inst. Meas. Control 2016, 38, 282–292. [Google Scholar] [CrossRef]
- Xu, X.; Qiao, Z.; Lei, Y. Repetitive transient extraction for machinery fault diagnosis using multiscale fractional order entropy infogram. Mech. Syst. Signal Process. 2018, 103, 312–326. [Google Scholar] [CrossRef]
- Witkin, A. Scale-space filtering: A new approach to multi-scale description. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, ICASSP’84, San Diego, CA, USA, 19–21 March 1984; Volume 9, pp. 150–153. [Google Scholar]
- Lindeberg, T. Scale-space for discrete signals. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 234–254. [Google Scholar] [CrossRef]
- Ma, J.; Wu, J.; Wang, X. Incipient fault feature extraction of rolling bearings based on the MVMD and Teager energy operator. ISA Trans. 2018, 80, 297–311. [Google Scholar] [CrossRef]
- Smith, W.A.; Randall, R.B. Rolling element bearing diagnostics using the Case Western Reserve University date:A benchmark study. Mech. Syst. Signal Process. 2015, 64–65, 100–131. [Google Scholar]
- Lee, J.; Qiu, H.; Yu, G.; Lin, J. Rexnord Technical Services; IMS.; University of Cincinnati; “Bearing Data Set”. In NASA Ames Prognostics Data Repository; NASA Ames Research Center: Moffett Field, CA, USA. Available online: http://ti. arc. nasa. gov/project/prognostic-data-repository (accessed on 8 February 2018).
- Nectoux, P.; Gouriveau, R.; Medjaher, K.; Ramasso, E.; Chebel-Morello, B.; Zerhouni, N.; Varnier, C. PRONOSTIA: An experimental platform for bearings accelerated degradation tests. In Proceedings of the IEEE International Conference on Prognostics and Health Management, Denver, Colorado, USA, June 2012; pp. 1–8. [Google Scholar]
- Qiu, H.; Lee, J.; Lin, J.; Yu, G. Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics. J. Sound Vib. 2006, 289(4), 1066–1090. [Google Scholar]





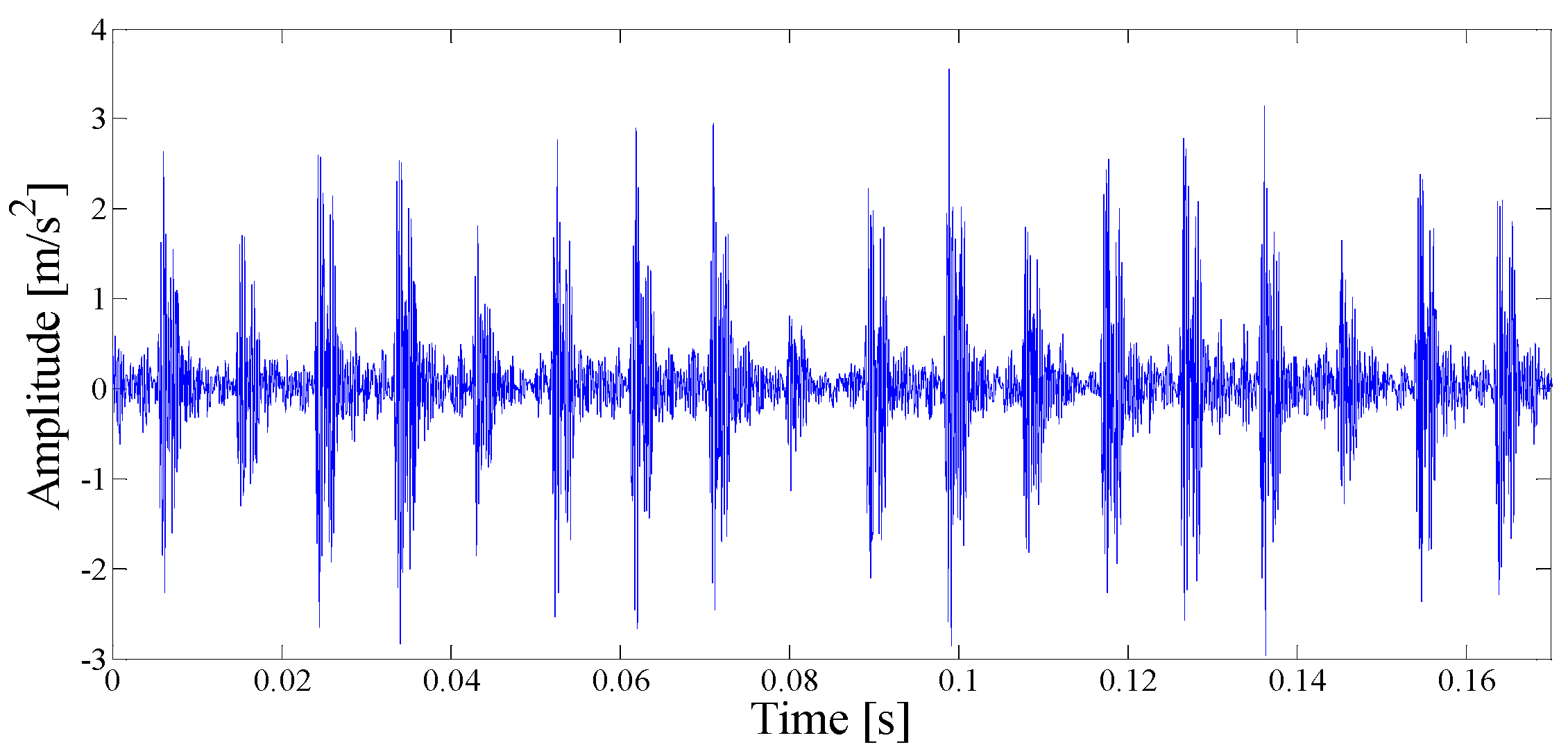

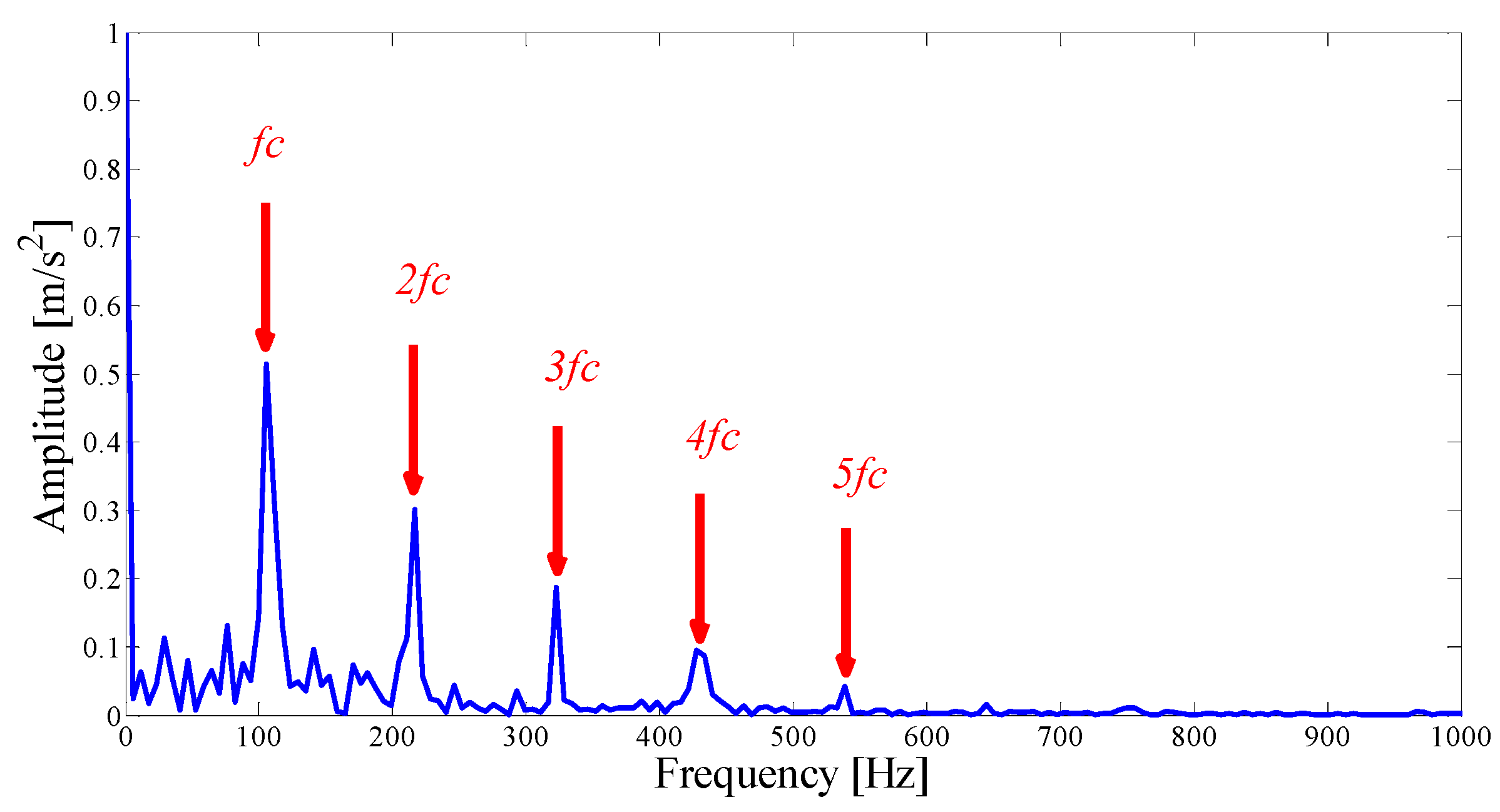
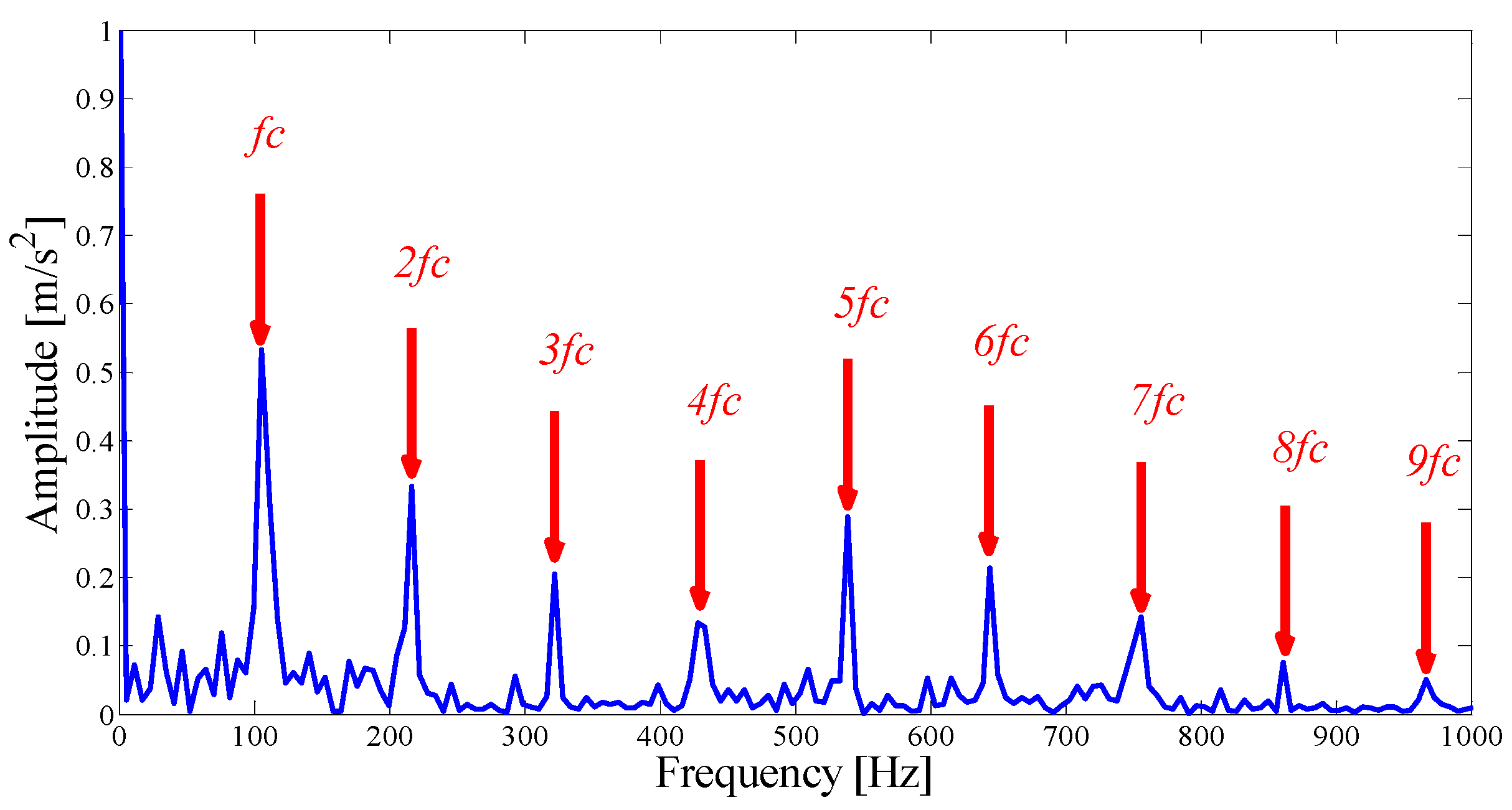

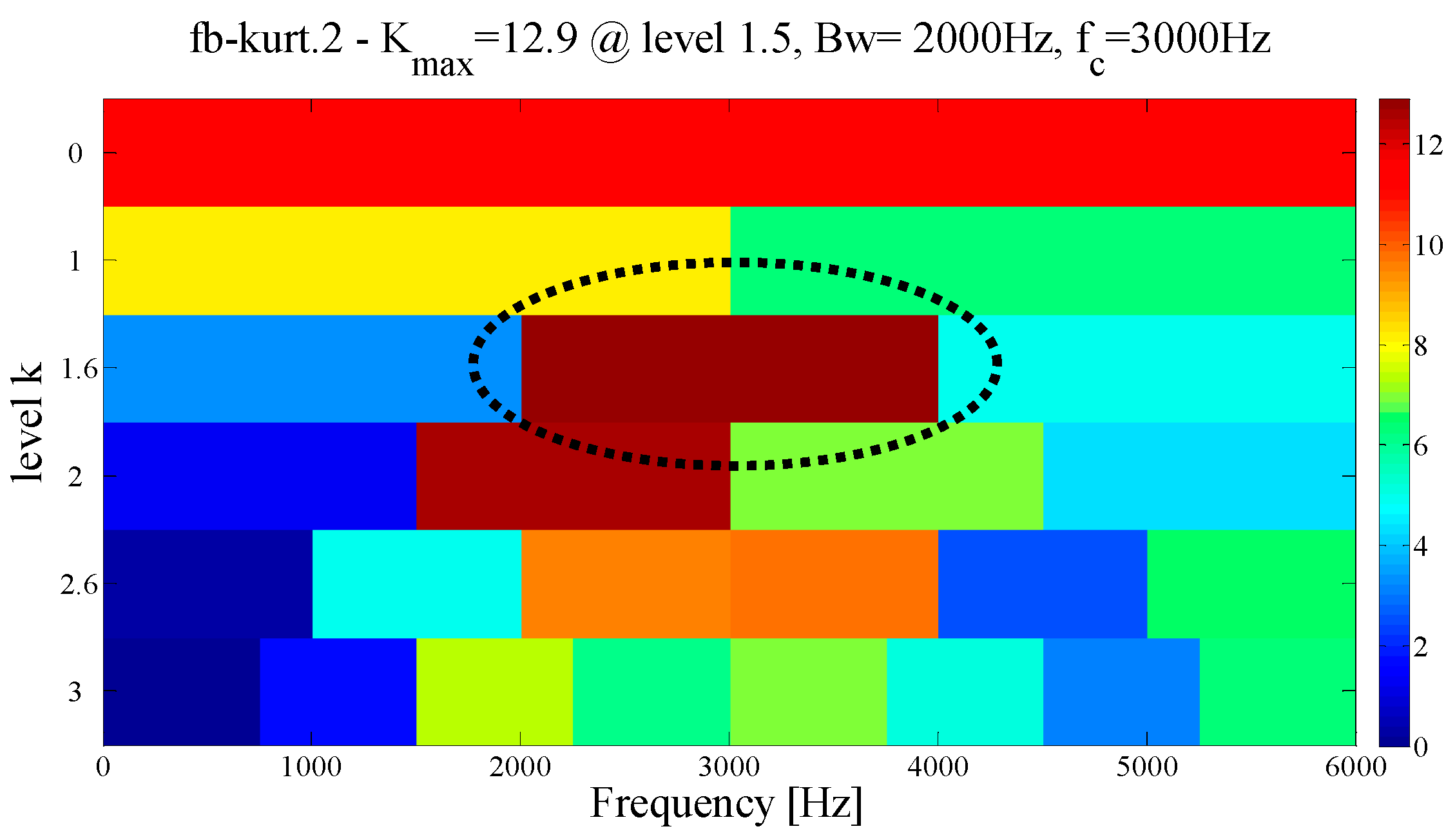





| IMF | ∆I1/2 | ρX,Y | ∆IC | IMF | ∆I1/2 | ρX,Y | ∆IC |
|---|---|---|---|---|---|---|---|
| 1 | 5.7755 | 0.2936 | 1.6954 | 11 | 6.4204 | 0.1561 | 1.0022 |
| 2 | 7.3191 | 0.2682 | 1.8896 | 12 | 6.1135 | 0.1918 | 1.1728 |
| 3 | 7.6186 | 0.2883 | 2.1966 | 13 | 6.2320 | 0.1742 | 1.0858 |
| 4 | 6.7521 | 0.2960 | 1.9989 | 14 | 5.9637 | 0.2477 | 1.4773 |
| 5 | 5.9245 | 0.2467 | 1.4795 | 15 | 5.8851 | 0.3126 | 1.8399 |
| 6 | 6.3692 | 0.1491 | 0.9499 | 16 | 6.3084 | 0.1737 | 1.0958 |
| 7 | 5.6528 | 0.3050 | 1.7238 | 17 | 6.4203 | 0.1740 | 1.1174 |
| 8 | 6.3221 | 0.1700 | 1.0747 | 18 | 6.3126 | 0.2104 | 1.3284 |
| 9 | 6.2089 | 0.2121 | 1.3168 | 19 | 6.4710 | 0.1717 | 1.1113 |
| 10 | 6.6168 | 0.1734 | 1.1472 | 20 | 6.0843 | 0.2624 | 1.5964 |
| IMF | ∆I1/2 | ρX,Y | ∆IC | IMF | ∆I1/2 | ρX,Y | ∆IC |
|---|---|---|---|---|---|---|---|
| 1 | 7.6090 | 0.0204 | 0.1551 | 6 | 6.2622 | 0.5325 | 3.3348 |
| 2 | 6.3599 | 0.0788 | 0.5012 | 7 | 6.1155 | 0.8502 | 5.1992 |
| 3 | 6.3114 | 0.0284 | 0.1789 | 8 | 5.7584 | 0.0442 | 0.2548 |
| 4 | 6.2948 | 0.0444 | 0.2797 | 9 | 5.7374 | 0.0814 | 0.1668 |
| 5 | 6.1204 | 0.0278 | 0.1702 |
| IMF | ∆I1/2 | ρX,Y | ∆IC | IMF | ∆I1/2 | ρX,Y | ∆IC |
|---|---|---|---|---|---|---|---|
| 1 | 6.4651 | 0.3079 | 1.9903 | 8 | 6.0680 | 0.2747 | 1.6668 |
| 2 | 6.7327 | 0.5824 | 3.9212 | 9 | 5.6489 | 0.1038 | 0.5865 |
| 3 | 7.1859 | 0.3234 | 2.3240 | 10 | 5.6357 | 0.1090 | 0.6140 |
| 4 | 6.3065 | 0.4246 | 2.6780 | 11 | 5.4719 | 0.0934 | 0.5111 |
| 5 | 6.4987 | 0.2032 | 1.3207 | 12 | 5.6168 | 0.1023 | 0.5745 |
| 6 | 6.0117 | 0.3014 | 1.8122 | 13 | 6.8529 | 0.0778 | 0.5329 |
| 7 | 5.9508 | 0.1887 | 1.1230 | 14 | 5.6431 | 0.0555 | 0.3131 |
| IMF | ∆I1/2 | ρX,Y | ∆IC | IMF | ∆I1/2 | ρX,Y | ∆IC |
|---|---|---|---|---|---|---|---|
| 1 | 5.8326 | 0.2946 | 1.7182 | 9 | 5.9337 | 0.1796 | 1.0656 |
| 2 | 6.5265 | 0.3609 | 2.3557 | 10 | 5.6078 | 0.2080 | 1.1664 |
| 3 | 6.4852 | 0.3098 | 2.0091 | 11 | 5.6867 | 0.2146 | 1.2206 |
| 4 | 5.7762 | 0.3534 | 2.0411 | 12 | 5.9589 | 0.1649 | 0.9827 |
| 5 | 6.3258 | 0.1686 | 1.0668 | 13 | 5.2600 | 0.3758 | 1.9768 |
| 6 | 5.4575 | 0.2721 | 1.4849 | 14 | 5.5263 | 0.2492 | 1.3771 |
| 7 | 5.4696 | 0.2451 | 1.3407 | 15 | 5.8034 | 0.2059 | 1.1947 |
| 8 | 6.3494 | 0.2085 | 1.3238 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Z.; Ma, J.; Wang, X.; Wu, J.; Zhou, C. An Optimal Resonant Frequency Band Feature Extraction Method Based on Empirical Wavelet Transform. Entropy 2019, 21, 135. https://doi.org/10.3390/e21020135
Feng Z, Ma J, Wang X, Wu J, Zhou C. An Optimal Resonant Frequency Band Feature Extraction Method Based on Empirical Wavelet Transform. Entropy. 2019; 21(2):135. https://doi.org/10.3390/e21020135
Chicago/Turabian StyleFeng, Zezhong, Jun Ma, Xiaodong Wang, Jiande Wu, and Chengjiang Zhou. 2019. "An Optimal Resonant Frequency Band Feature Extraction Method Based on Empirical Wavelet Transform" Entropy 21, no. 2: 135. https://doi.org/10.3390/e21020135
APA StyleFeng, Z., Ma, J., Wang, X., Wu, J., & Zhou, C. (2019). An Optimal Resonant Frequency Band Feature Extraction Method Based on Empirical Wavelet Transform. Entropy, 21(2), 135. https://doi.org/10.3390/e21020135




