Probabilistic Modeling with Matrix Product States
Abstract
1. Introduction
2. The Problem Formulation
3. Outline of Our Approach to Solving the Problem
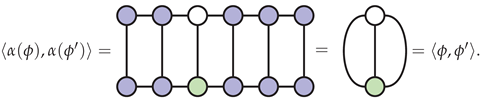
4. Effective Versions of the Problem
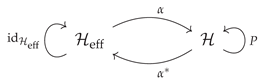
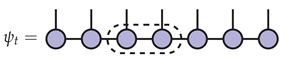
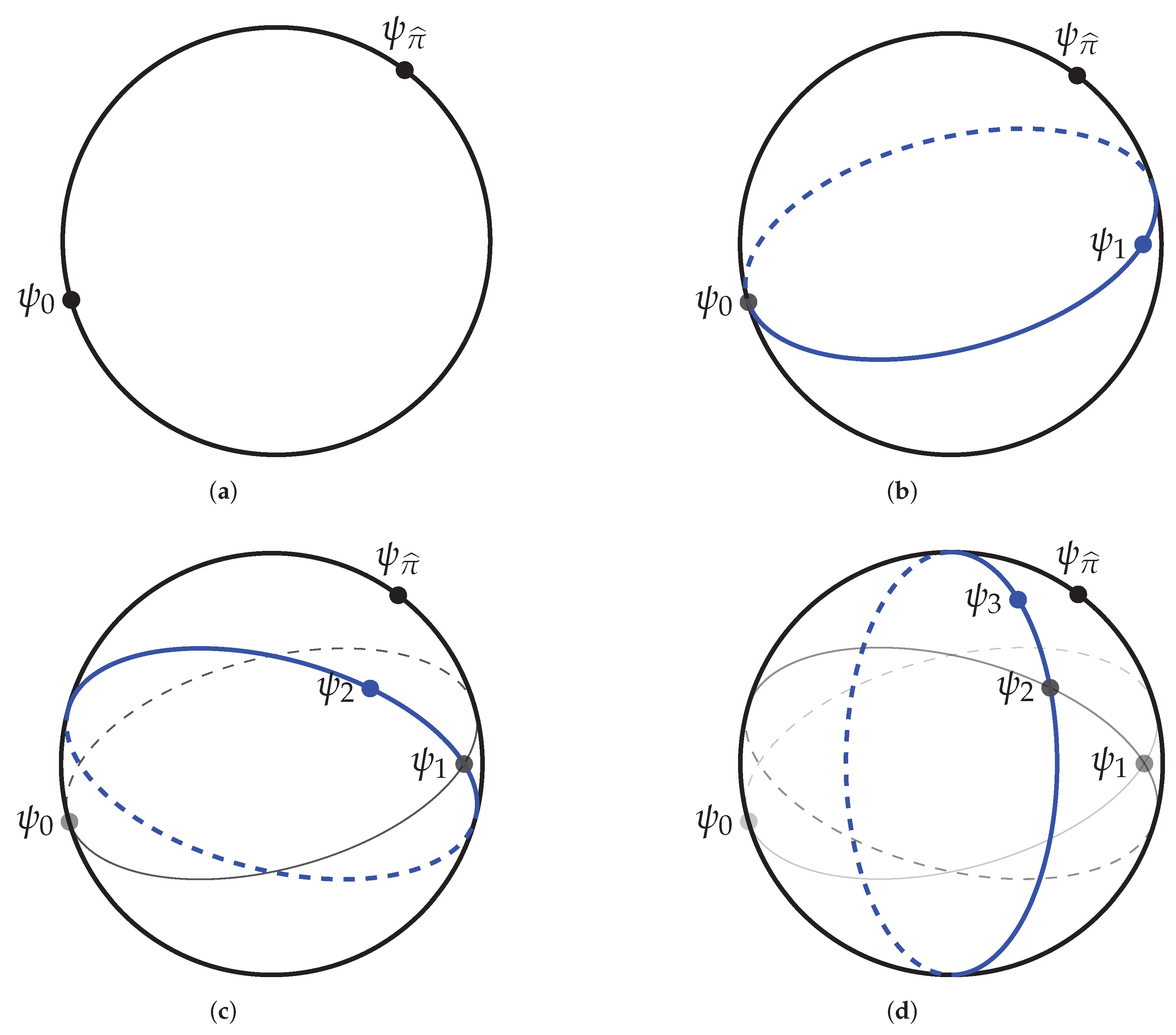
5. The Exact Single-Site DMRG Algorithm
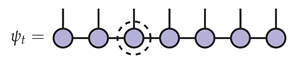






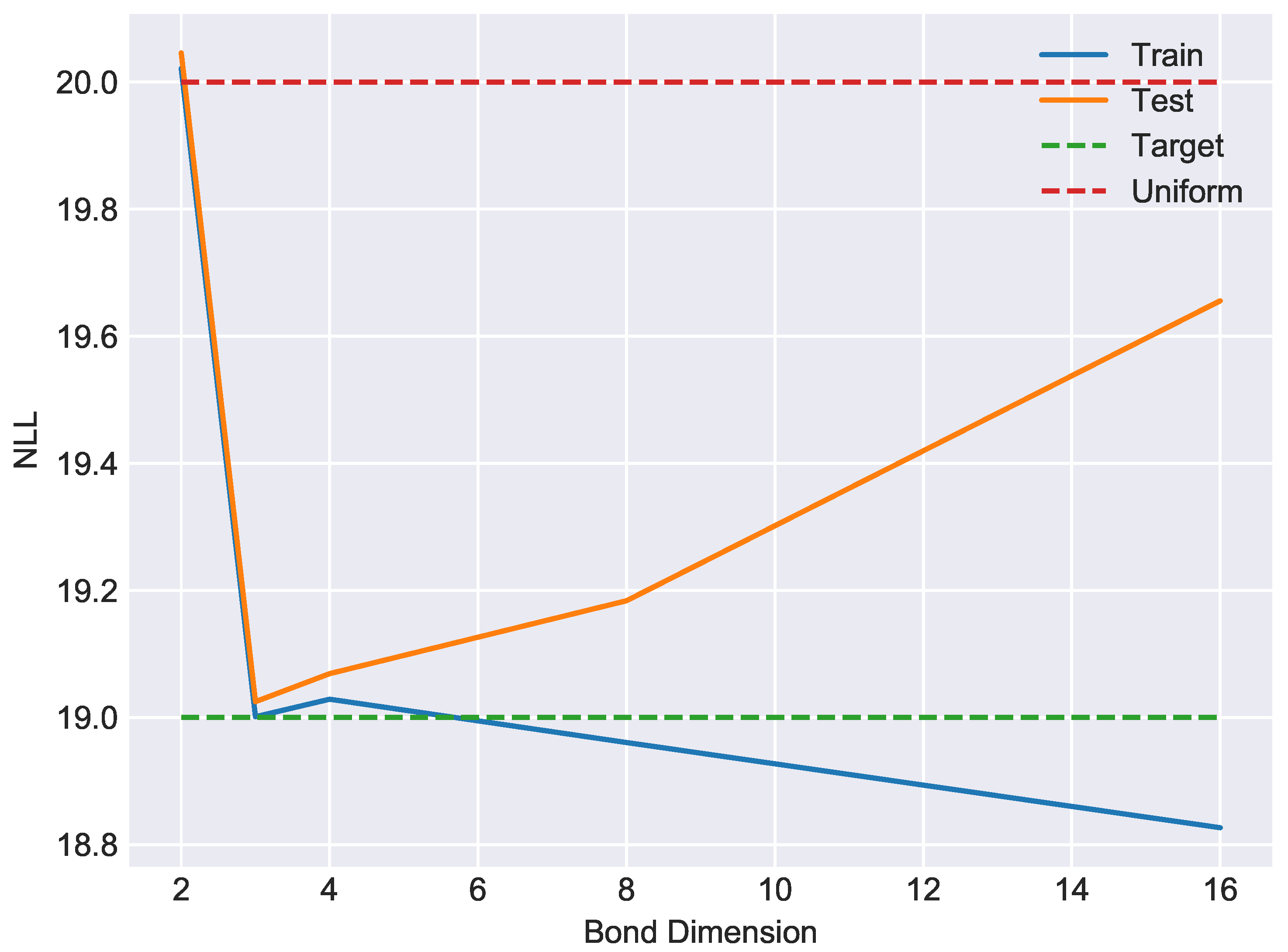
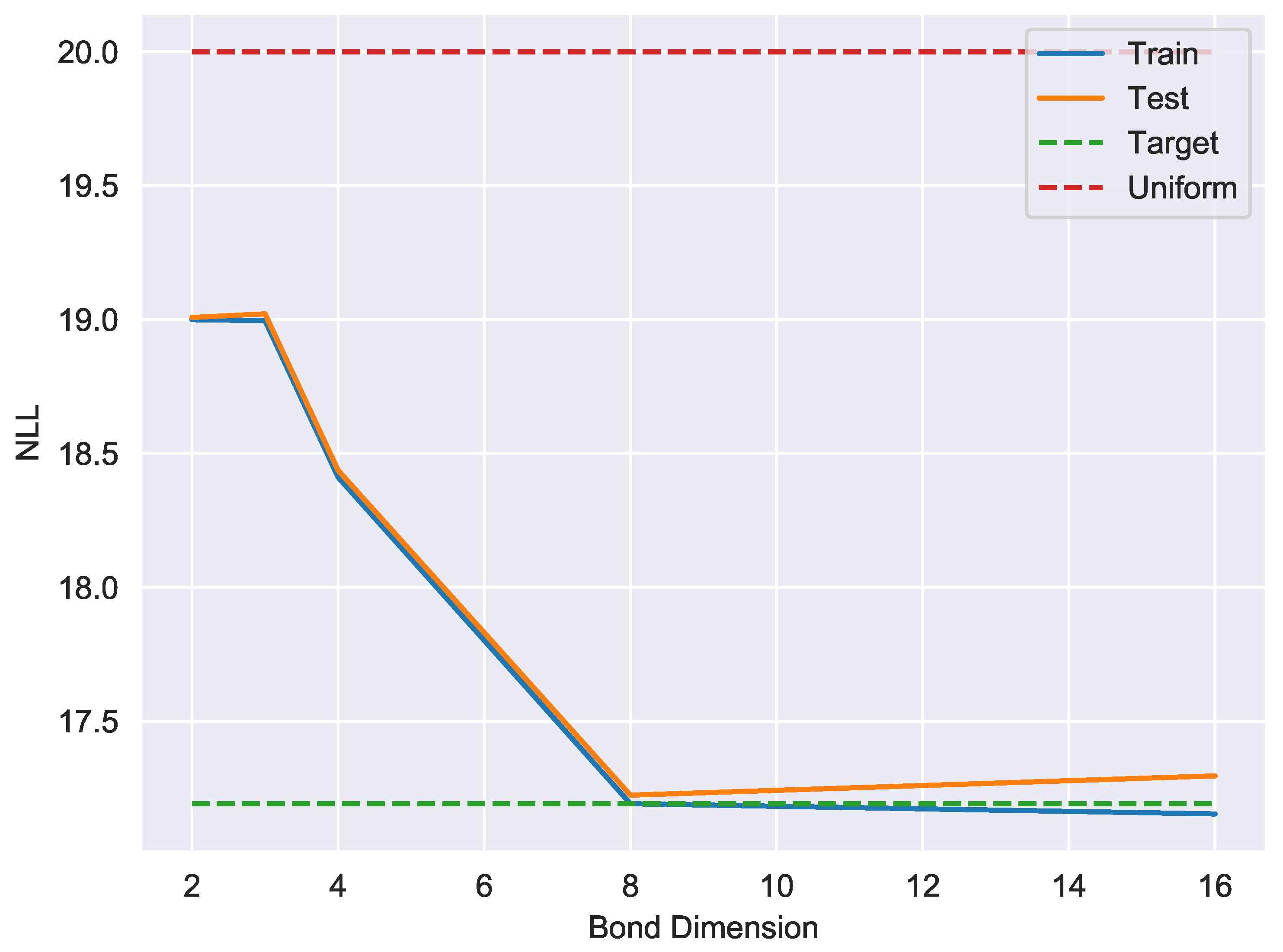
6. Experiments
7. Discussion
8. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
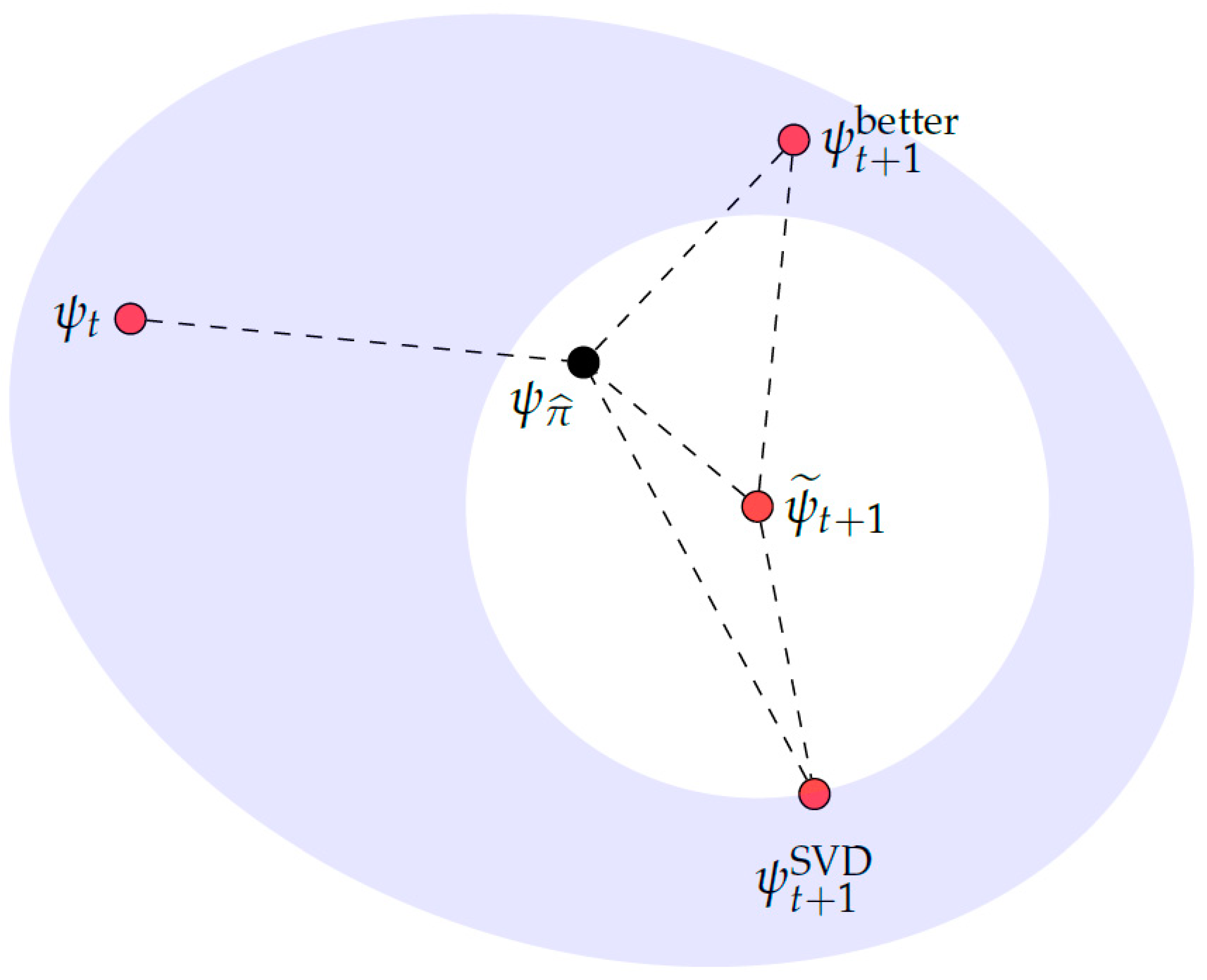
Appendix A. Multi-Site DMRG
- Use to define an isometric embedding with
- Let be the unit vector in closest to .
- Perform a model repair of to obtain a vector There are multiple ways to do the model repair.


References
- Biamonte, J.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum machine learning. Nature 2017, 549, 195. [Google Scholar] [CrossRef]
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Peruzzo, A.; McClean, J.; Shadbolt, P.; Yung, M.H.; Zhou, X.Q.; Love, P.J.; Aspuru-Guzik, A.; O’brien, J.L. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 2014, 5, 4213. [Google Scholar] [CrossRef]
- Farhi, E.; Goldstone, J.; Gutmann, S. A quantum approximate optimization algorithm. arXiv 2014, arXiv:1411.4028. [Google Scholar]
- Huggins, W.; Patil, P.; Mitchell, B.; Whaley, K.B.; Stoudenmire, E.M. Towards quantum machine learning with tensor networks. Quantum Sci. Technol. 2019, 4, 024001. [Google Scholar] [CrossRef]
- Liu, J.G.; Wang, L. Differentiable learning of quantum circuit Born machines. Phys. Rev. A 2018, 98, 062324. [Google Scholar] [CrossRef]
- Benedetti, M.; Garcia-Pintos, D.; Perdomo, O.; Leyton-Ortega, V.; Nam, Y.; Perdomo-Ortiz, A. A generative modeling approach for benchmarking and training shallow quantum circuits. npj Quantum Inf. 2019, 5, 45. [Google Scholar] [CrossRef]
- Du, Y.; Hsieh, M.H.; Liu, T.; Tao, D. The expressive power of parameterized quantum circuits. arXiv 2018, arXiv:1810.11922. [Google Scholar]
- Killoran, N.; Bromley, T.R.; Arrazola, J.M.; Schuld, M.; Quesada, N.; Lloyd, S. Continuous-variable quantum neural networks. Phys. Rev. Res. 2019, 1, 033063. [Google Scholar] [CrossRef]
- Shepherd, D.; Bremner, M.J. Temporally unstructured quantum computation. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 465. [Google Scholar] [CrossRef]
- Romero, E.; Mazzanti Castrillejo, F.; Delgado, J.; Buchaca, D. Weighted Contrastive Divergence. Neural Netw. 2018. [Google Scholar] [CrossRef] [PubMed]
- Shalev-Shwartz, S.; Shamir, O.; Shammah, S. Failures of Gradient-Based Deep Learning. In Proceedings of the 34th International Conference on Machine Learning (ICML 2017), Sydney, Australia, 6–11 August 2017; pp. 3067–3075. [Google Scholar]
- Han, Z.Y.; Wang, J.; Fan, H.; Wang, L.; Zhang, P. Unsupervised generative modeling using matrix product states. Phys. Rev. X 2018, 8, 031012. [Google Scholar] [CrossRef]
- Cheng, S.; Wang, L.; Xiang, T.; Zhang, P. Tree tensor networks for generative modeling. Phys. Rev. B 2019, 99, 155131. [Google Scholar] [CrossRef]
- Farhi, E.; Neven, H. Classification with quantum neural networks on near term processors. arXiv 2018, arXiv:1802.06002. [Google Scholar]
- Stoudenmire, E.M. The Tensor Network. 2019. Available online: https://tensornetwork.org (accessed on 13 February 2019).
- Schollwöck, U. The density-matrix renormalization group in the age of matrix product states. Ann. Phys. 2011, 326, 96–192. [Google Scholar] [CrossRef]
- Bridgeman, J.C.; Chubb, C.T. Hand-waving and interpretive dance: An introductory course on tensor networks. J. Phys. A Math. Theor. 2017, 50, 223001. [Google Scholar] [CrossRef]
- Orús, R. A practical introduction to tensor networks: Matrix product states and projected entangled pair states. Ann. Phys. 2014, 349, 117–158. [Google Scholar] [CrossRef]
- Glasser, I.; Sweke, R.; Pancotti, N.; Eisert, J.; Cirac, J.I. Expressive power of tensor-network factorizations for probabilistic modeling, with applications from hidden Markov models to quantum machine learning. arXiv 2019, arXiv:1907.03741. [Google Scholar]
- Montúfar, G.F.; Rauh, J.; Ay, N. Expressive Power and Approximation Errors of Restricted Boltzmann Machines. In Proceedings of the 24th International Conference on Neural Information Processing Systems (NIPS’11), Granada, Spain, 12–15 December 2011; Curran Associates Inc.: Red Hook, NY, USA, 2011; pp. 415–423. [Google Scholar]
- Amin, M.H.; Andriyash, E.; Rolfe, J.; Kulchytskyy, B.; Melko, R. Quantum boltzmann machine. Phys. Rev. X 2018, 8, 021050. [Google Scholar] [CrossRef]
- Kappen, H.J. Learning quantum models from quantum or classical data. arXiv 2018, arXiv:1803.11278. [Google Scholar]
- Bradley, T.D.; Stoudenmire, E.M.; Terilla, J. Modeling Sequences with Quantum States: A Look Under the Hood. arXiv 2019, arXiv:1910.07425. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stokes, J.; Terilla, J. Probabilistic Modeling with Matrix Product States. Entropy 2019, 21, 1236. https://doi.org/10.3390/e21121236
Stokes J, Terilla J. Probabilistic Modeling with Matrix Product States. Entropy. 2019; 21(12):1236. https://doi.org/10.3390/e21121236
Chicago/Turabian StyleStokes, James, and John Terilla. 2019. "Probabilistic Modeling with Matrix Product States" Entropy 21, no. 12: 1236. https://doi.org/10.3390/e21121236
APA StyleStokes, J., & Terilla, J. (2019). Probabilistic Modeling with Matrix Product States. Entropy, 21(12), 1236. https://doi.org/10.3390/e21121236



