Detecting Causality in Multivariate Time Series via Non-Uniform Embedding
Abstract
1. Introduction
2. Method
2.1. PMIME Method
- An empty embedding vector is initialized.
- At the first iteration k = 1, the embedding vector is selected most related to :where represents mutual information. Mutual information is estimated by the k-nearest neighbors (k-NNs) method. Then we have . At the same time, is removed from .
- At the iteration , the mixed embedding vector is augmented by the component of , giving most information about additionally to the information already contained in . will be selected by a standard through calculating the maximum value of the conditional mutual information, , i.e., at the iteration , , where the CMI is calculated by the k-NNs estimator, and the mixed embedding vector is . By using greedy forward method, each will be embedded in the already embedded vector until the process stops. The termination criterion is quantified as:where the threshold and the general value of A is 0.95 or 0.97 in [15,16]. That is, the additional information of selected at the iteration k is not large enough. The embedding process will stop and we have the mixed embedding vector . Any combination of the lagged variables may be included in .
- To calculate the causality strength of X on Y conditioned by the other variables in Z, the index is defined aswhere represents the component of X in . It is the same with and . The causal effect of X to Y depends on the components of X in .
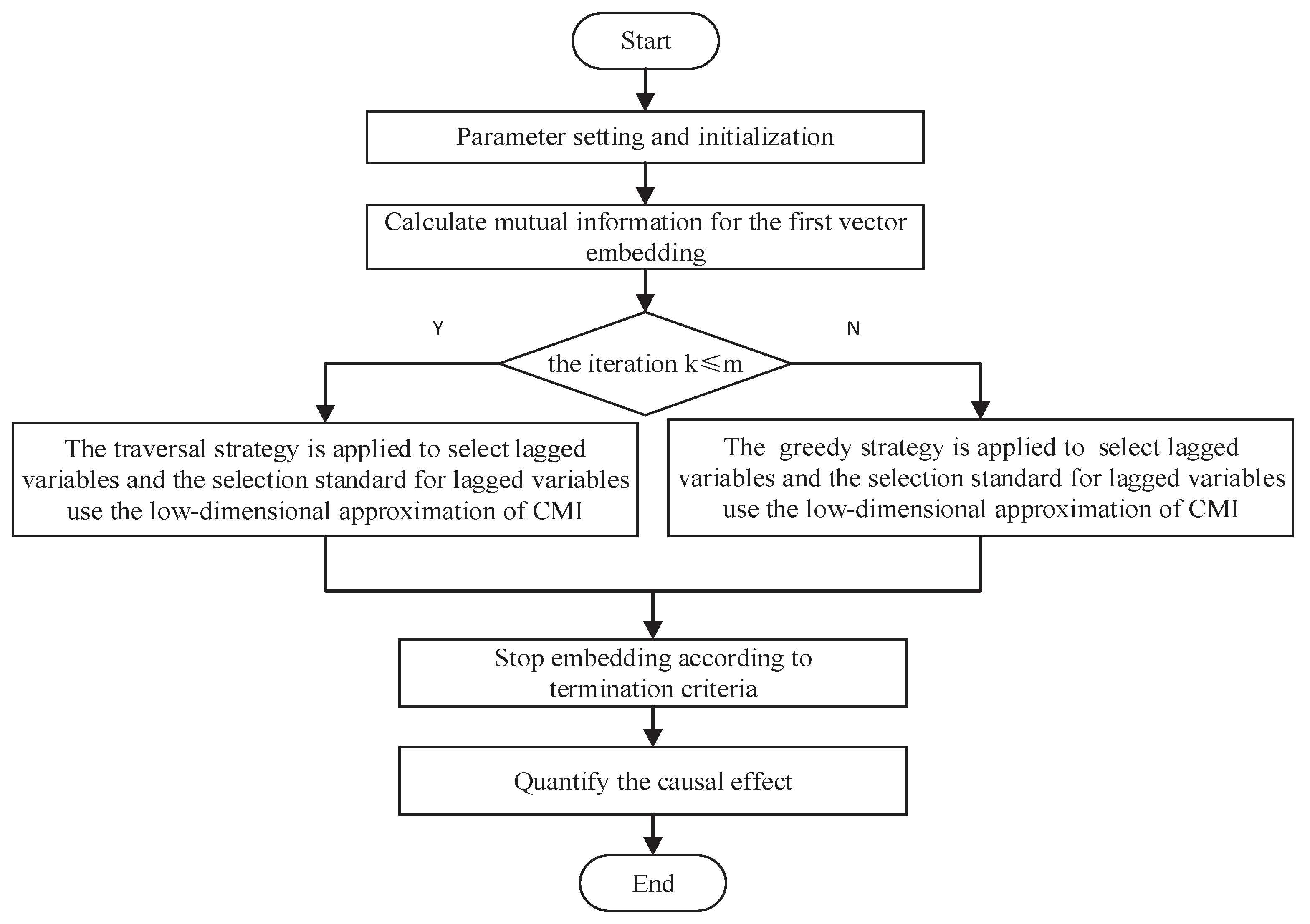
2.2. The Proposed Method
2.2.1. Low Dimensional Approximation of CMI
2.2.2. Mixed Search Strategy
2.2.3. LM-PMIME Method
- Initialize an empty embedding vector .
- At the first iteration k = 1, the embedding vector is selected most related to :Then we have .
- At the iteration , will be selected by a standard through calculating the maximum value of the low dimensional approximation of CMI.where and . The traversal strategy is applied to select , i.e., at the iteration and , needs to be selected. First, clear the already embedded vector and calculate combinations in total. Then select the combination of largest conditional mutual information as of the current step. Finally, .
- At the iteration , greedy strategy is used. Each will be embedded in the already embedded vector until the process stops. The standard of low dimensional approximation is still used before stopping.
- The termination criterion is quantified as:where the threshold and threshold A near 1, e.g., , allows the inclusion of a new component in the mixed embedding vector even if the augmented vector explains very little of the information on that was not explained at the previous step. Although the statistical significance threshold is widely used [32,33], the accuracy of causal analysis is lower than the threshold A and the amount of calculation is large [15,16]. Therefore, we employ the threshold A for non-uniform embedding. The general value of A is 0.95 or 0.97 in [15,16]. That is, the additional information of selected at the iteration k is not large enough. The embedding process will stop and we have the mixed embedding vector . In addition, any combination of the lagged variables may be included in .
- To calculate the causality strength of X on Y conditioned by the other variables in Z, the index is defined as:where represents the component of X in . It is the same with and . The causality strength of X to Y depends on the components of X in . The presence of components of X in the mixed embedding vector shows that X has effect on Y and then the derived causality strength is positive, whereas the absence shows no effect and causality strength is exactly zero. In addition, the is considered significant if it is positive in the PMIME method and proposed method.
3. Simulation Study
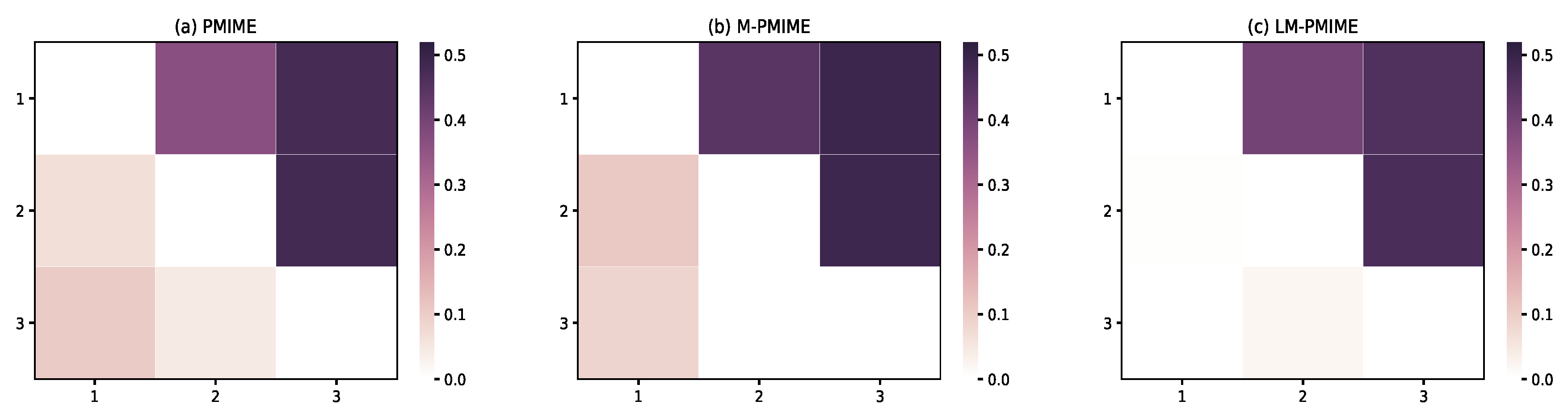
3.1. Linear Multivariate Stochastic Process
3.2. Nonlinear Multivariate Stochastic Process
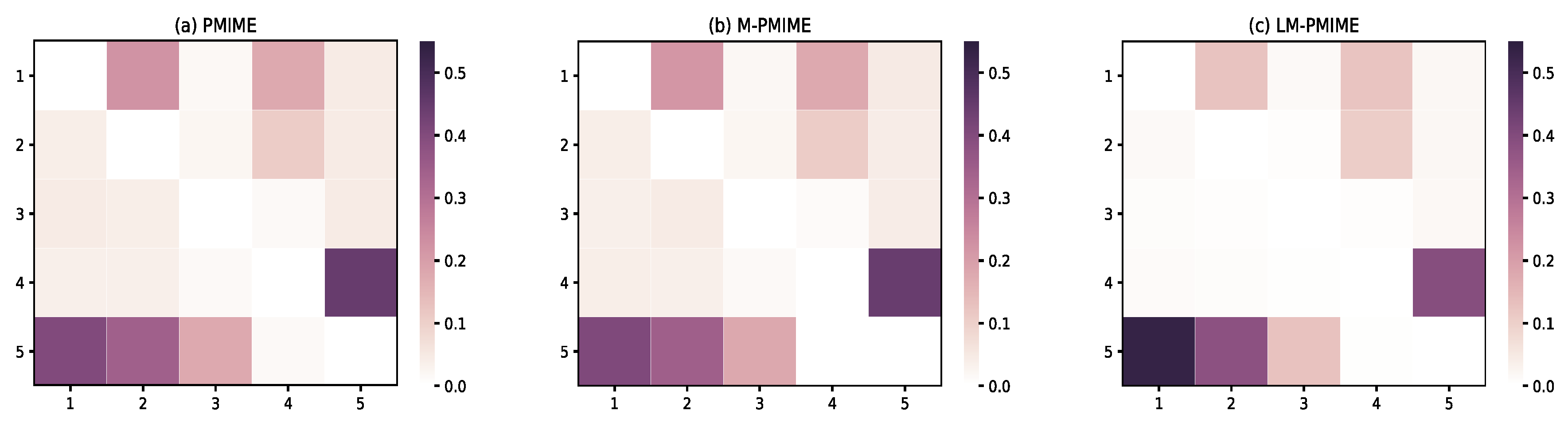
3.3. Coupled Henon Maps
3.4. Coupled Lorenz System
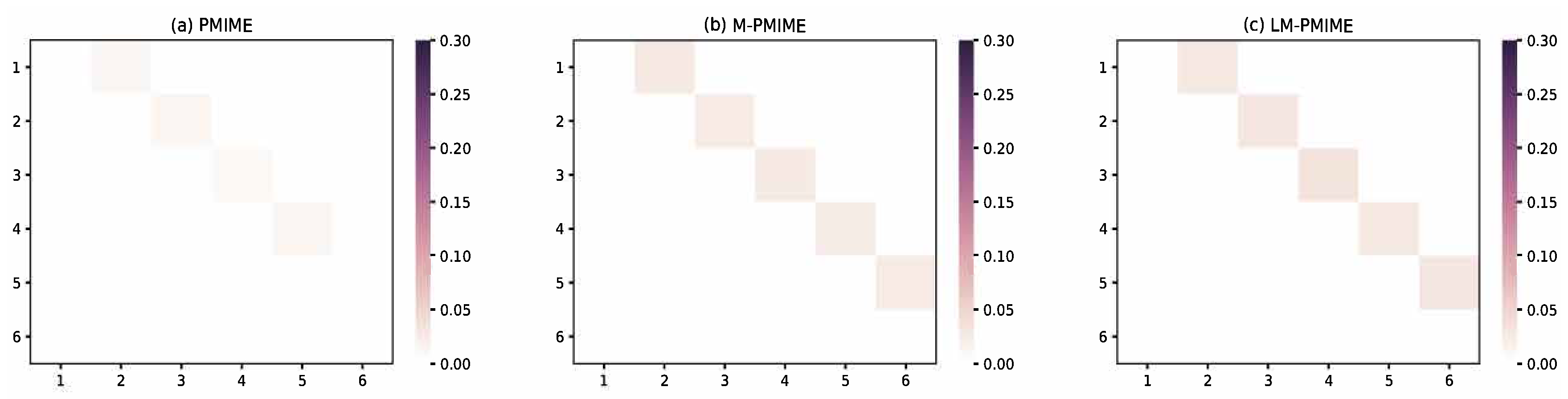
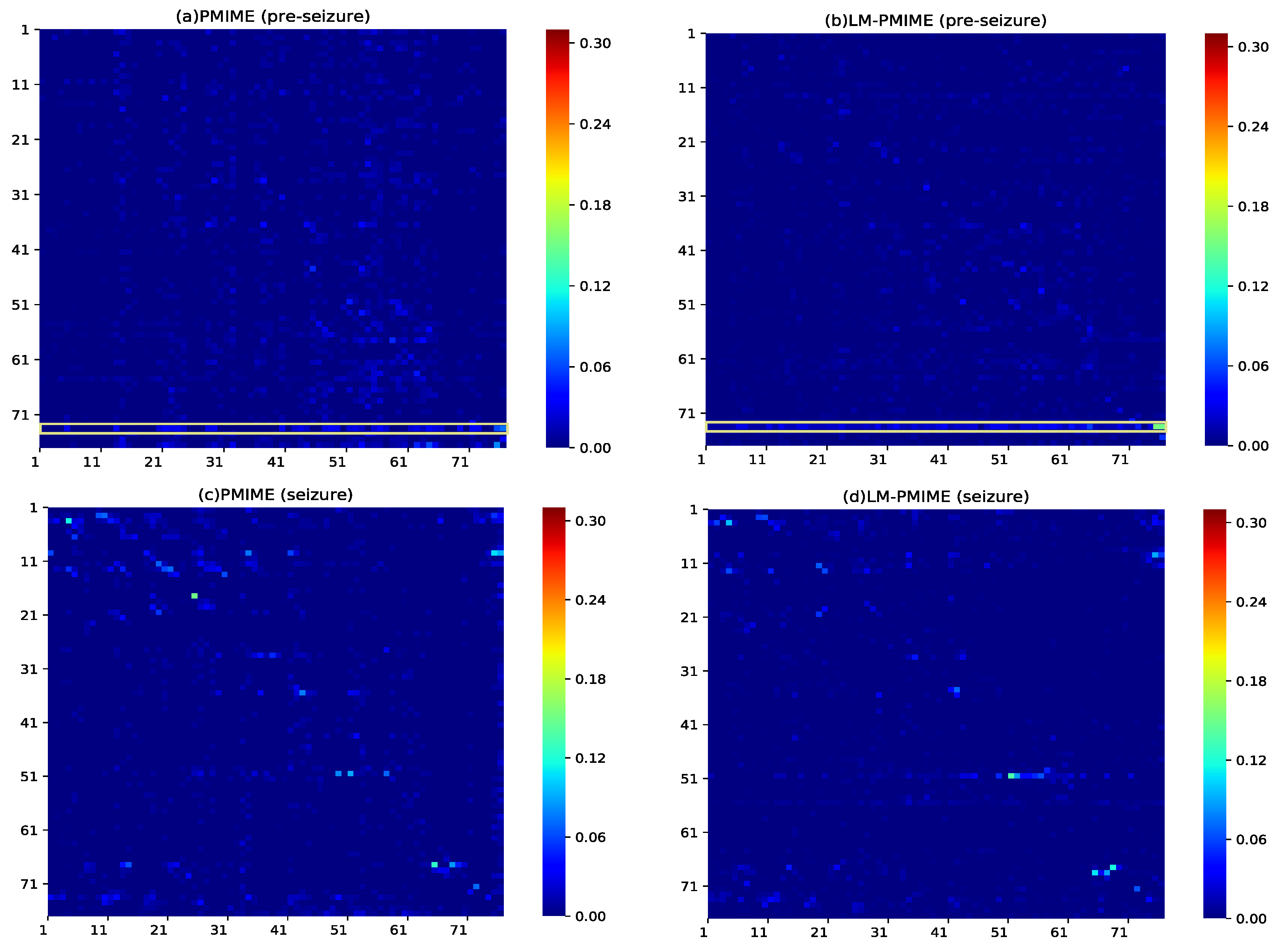
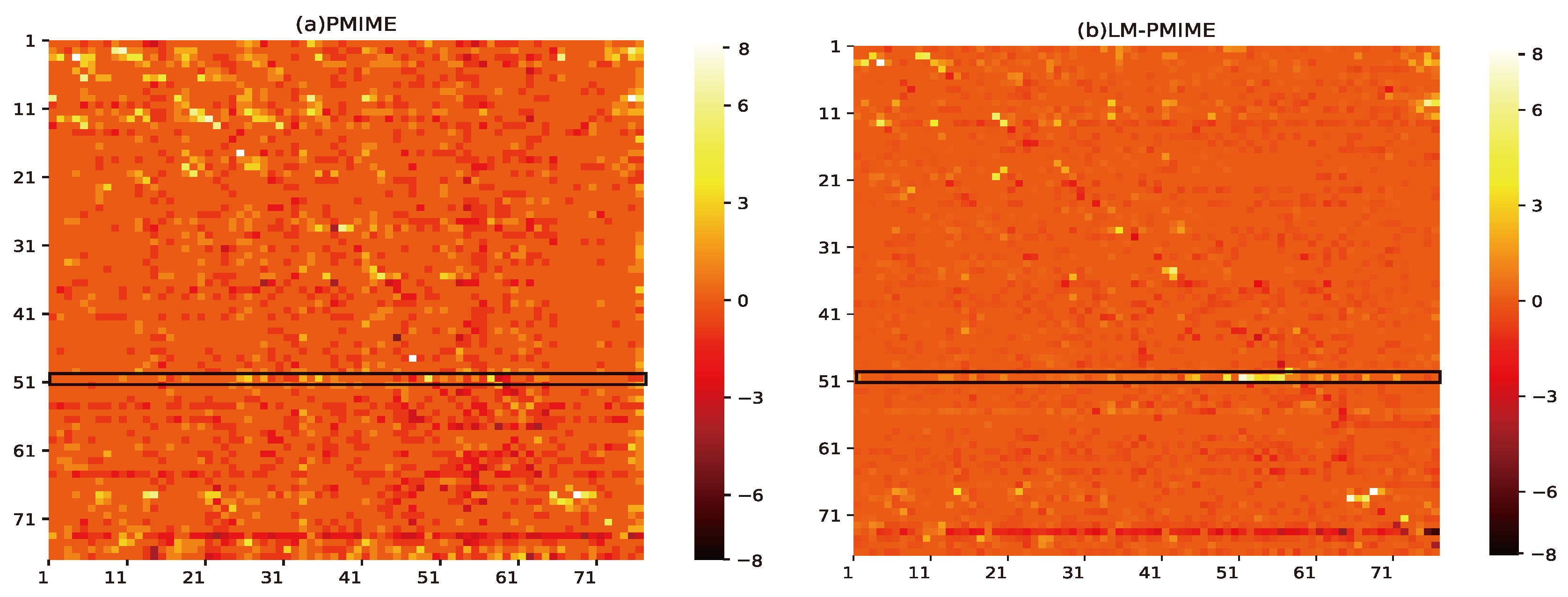
4. Application to Epilespy ECoG Signals
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Paluš, M.; Krakovská, A.; Jakubík, J.; Chvosteková, M. Causality, dynamical systems and the arrow of time. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 075307. [Google Scholar] [CrossRef] [PubMed]
- Krakovská, A.; Jakubík, J.; Chvosteková, M.; Coufal, D.; Jajcay, N.; Paluš, M. Comparison of six methods for the detection of causality in a bivariate time series. Phys. Rev. E 2018, 97, 042207. [Google Scholar] [CrossRef] [PubMed]
- Paluš, M.; Komárek, V.; Hrnčíř, Z.; Štěrbová, K. Synchronization as adjustment of information rates: Detection from bivariate time series. Phys. Rev. E 2001, 63, 046211. [Google Scholar] [CrossRef] [PubMed]
- Granger, C.W.J. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 1969, 424–438. [Google Scholar] [CrossRef]
- Marko, H. The bidirectional communication theory–a generalization of information theory. IEEE Trans. Commun. 1973, 21, 1345–1351. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461. [Google Scholar] [CrossRef]
- Barnett, L.; Barrett, A.B.; Seth, A.K. Granger causality and transfer entropy are equivalent for Gaussian variables. Phys. Rev. Lett. 2009, 103, 238701. [Google Scholar] [CrossRef]
- Schindlerova, K. Equivalence of Granger Causality and Transfer Entropy: A Generalization. Appl. Mathem. Sci. 2011, 5, 3637–3648. [Google Scholar]
- Mao, X.; Shang, P. Transfer entropy between multivariate time series. Commun. Nonlinear Sci. Numer. Simul. 2017, 47, 338–347. [Google Scholar] [CrossRef]
- Montalto, A.; Stramaglia, S.; Faes, L.; Tessitore, G.; Prevete, R.; Marinazzo, D. Neural networks with non-uniform embedding and explicit validation phase to assess Granger causality. Neural Netw. 2015, 71, 159–171. [Google Scholar] [CrossRef]
- Faes, L.; Nollo, G.; Porta, A. Information-based detection of nonlinear Granger causality in multivariate processes via a nonuniform embedding technique. Phys. Rev. E 2011, 83, 051112. [Google Scholar] [CrossRef] [PubMed]
- Runge, J. Causal network reconstruction from time series: From theoretical assumptions to practical estimation. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 075310. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Sun, Y.; Li, X.; Shang, P. Multiscale transfer entropy: Measuring information transfer on multiple time scales. Commun. Nonlinear Sci. Numer. Simul. 2018, 62, 202–212. [Google Scholar] [CrossRef]
- Sysoev, I.V.; Ponomarenko, V.I.; Pikovsky, A. Reconstruction of coupling architecture of neural field networks from vector time series. Commun. Nonlinear Sci. Numer. Simul. 2018, 57, 342–351. [Google Scholar] [CrossRef]
- Vlachos, I.; Kugiumtzis, D. Nonuniform state-space reconstruction and coupling detection. Phys. Rev. E 2010, 82, 016207. [Google Scholar] [CrossRef]
- Kugiumtzis, D. Direct-coupling information measure from nonuniform embedding. Phys. Rev. E 2013, 87, 062918. [Google Scholar] [CrossRef]
- Kugiumtzis, D.; Koutlis, C.; Tsimpiris, A.; Kimiskidis, V.K. Dynamics of epileptiform discharges induced by transcranial magnetic stimulation in genetic generalized epilepsy. Int. J. Neural Syst. 2017, 27, 1750037. [Google Scholar] [CrossRef]
- Kugiumtzis, D.; Kimiskidis, V.K. Direct causal networks for the study of transcranial magnetic stimulation effects on focal epileptiform discharges. Int. J. Neural Syst. 2015, 25, 1550006. [Google Scholar] [CrossRef]
- Papana, A.; Kyrtsou, C.; Kugiumtzis, D.; Diks, C. Financial networks based on Granger causality: A case study. Physica A 2017, 482, 65–73. [Google Scholar] [CrossRef]
- Papana, A.; Kyrtsou, C.; Kugiumtzis, D.; Diks, C. Assessment of resampling methods for causality testing: A note on the US inflation behavior. PLoS ONE 2017, 12, e0180852. [Google Scholar] [CrossRef]
- Runge, J.; Heitzig, J.; Petoukhov, V.; Kurths, J. Escaping the curse of dimensionality in estimating multivariate transfer entropy. Phys. Rev. Lett. 2012, 108, 258701. [Google Scholar] [CrossRef] [PubMed]
- Runge, J.; Donner, R.V.; Kurths, J. Optimal model-free prediction from multivariate time series. Phys. Rev. E 2015, 91, 052909. [Google Scholar] [CrossRef] [PubMed]
- Brown, G.; Pocock, A.; Zhao, M.J.; Luján, M. Conditional likelihood maximisation: A unifying framework for information theoretic feature selection. J. Mach. Learn. Res. 2012, 13, 27–66. [Google Scholar]
- Vinh, N.X.; Zhou, S.; Chan, J.; Bailey, J. Can high-order dependencies improve mutual information based feature selection? Pattern Recognit. 2016, 53, 46–58. [Google Scholar] [CrossRef]
- Battiti, R. Using mutual information for selecting features in supervised neural net learning. IEEE Trans. Neural Netw. Learn. Syst. 1994, 5, 537–550. [Google Scholar] [CrossRef]
- Yang, H.H.; Moody, J. Data visualization and feature selection: New algorithms for nongaussian data. NIPS 2000, 687–693. [Google Scholar]
- Fleuret, F. Fast binary feature selection with conditional mutual information. J. Mach. Learn. Res. 2004, 5, 1531–1555. [Google Scholar]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef]
- Lin, D.; Tang, X. Conditional infomax learning: An integrated framework for feature extraction and fusion. ECCV 2006, 68–82. [Google Scholar]
- Runge, J.; Nowack, P.; Kretschmer, M.; Flaxman, S.; Sejdinovic, D. Detecting causal associations in large nonlinear time series datasets. arXiv 2017, arXiv:1702.07007. [Google Scholar] [CrossRef]
- Meyer, P.E.; Bontempi, G. On the use of variable complementarity for feature selection in cancer classification. ECCV 2006, 91–102. [Google Scholar]
- Montalto, A.; Faes, L.; Marinazzo, D. MuTE: A MATLAB toolbox to compare established and novel estimators of the multivariate transfer entropy. PLoS ONE 2014, 9, e109462. [Google Scholar] [CrossRef] [PubMed]
- Faes, L.; Kugiumtzis, D.; Nollo, G.; Jurysta, F.; Marinazzo, D. Estimating the decomposition of predictive information in multivariate systems. Phys. Rev. E 2015, 91, 032904. [Google Scholar] [CrossRef]
- Hacine-Gharbi, A.; Ravier, P.; Harba, R.; Mohamadi, T. Low bias histogram-based estimation of mutual information for feature selection. Pattern Recognit. Lett. 2012, 33, 1302–1308. [Google Scholar] [CrossRef]
- Kwak, N.; Choi, C.H. Input feature selection by mutual information based on Parzen window. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 12, 1667–1671. [Google Scholar] [CrossRef]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef]
- Schelter, B.; Winterhalder, M.; Hellwig, B.; Guschlbauer, B.; Lücking, C.H.; Timmer, J. Direct or indirect? Graphical models for neural oscillators. J. Physiol. Paris 2006, 99, 37–46. [Google Scholar] [CrossRef]
- Gourévitch, B.; Le Bouquin-Jeannès, R.; Faucon, G. Linear and nonlinear causality between signals: Methods, examples and neurophysiological applications. Biol. Cybern. 2006, 95, 349–369. [Google Scholar] [CrossRef]
- Kramer, M.A.; Kolaczyk, E.D.; Kirsch, H.E. Emergent network topology at seizure onset in humans. Epilepsy Res. 2008, 79, 173–186. [Google Scholar] [CrossRef]
- Marinazzo, D.; Pellicoro, M.; Stramaglia, S. Kernel method for nonlinear Granger causality. Phys. Rev. Lett. 2008, 100, 144103. [Google Scholar] [CrossRef]
- Faes, L.; Marinazzo, D.; Stramaglia, S. Multiscale information decomposition: Exact computation for multivariate Gaussian processes. Entropy 2017, 19, 408. [Google Scholar] [CrossRef]
- Porta, A.; Faes, L. Wiener–Granger causality in network physiology with applications to cardiovascular control and neuroscience. Proc. IEEE 2016, 104, 282–309. [Google Scholar] [CrossRef]
- Sun, J.; Taylor, D.; Bollt, E.M. Causal network inference by optimal causation entropy. SIAM J. Appl. Dyn. Syst. 2015, 14, 73–106. [Google Scholar] [CrossRef]
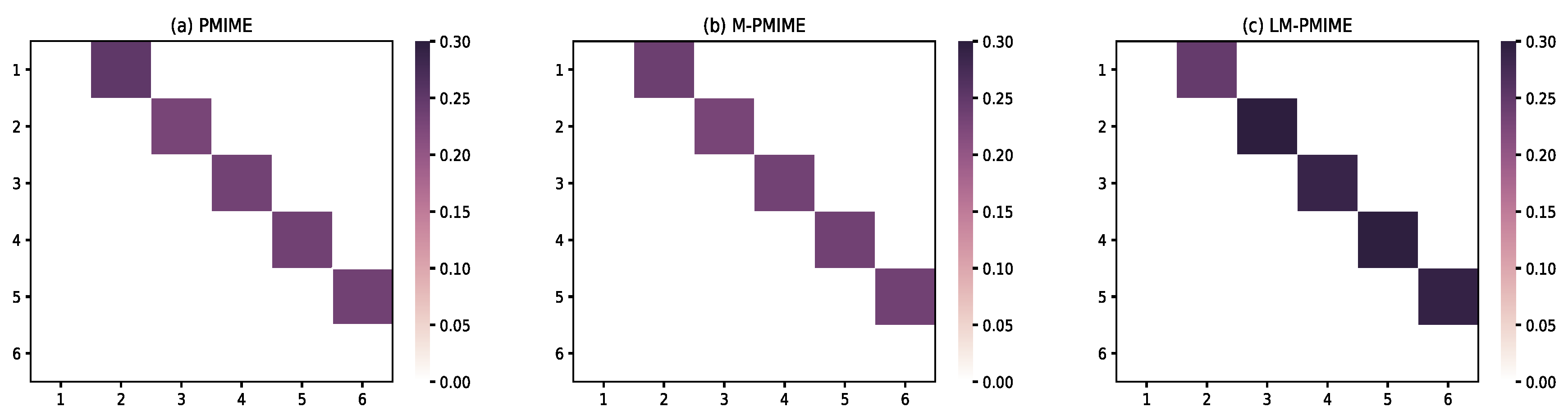
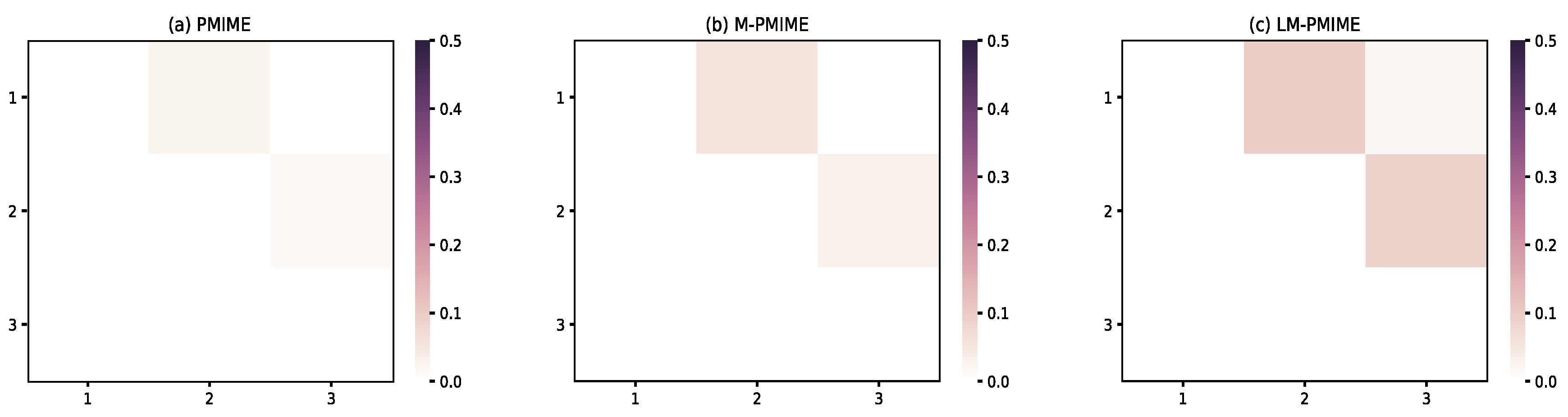
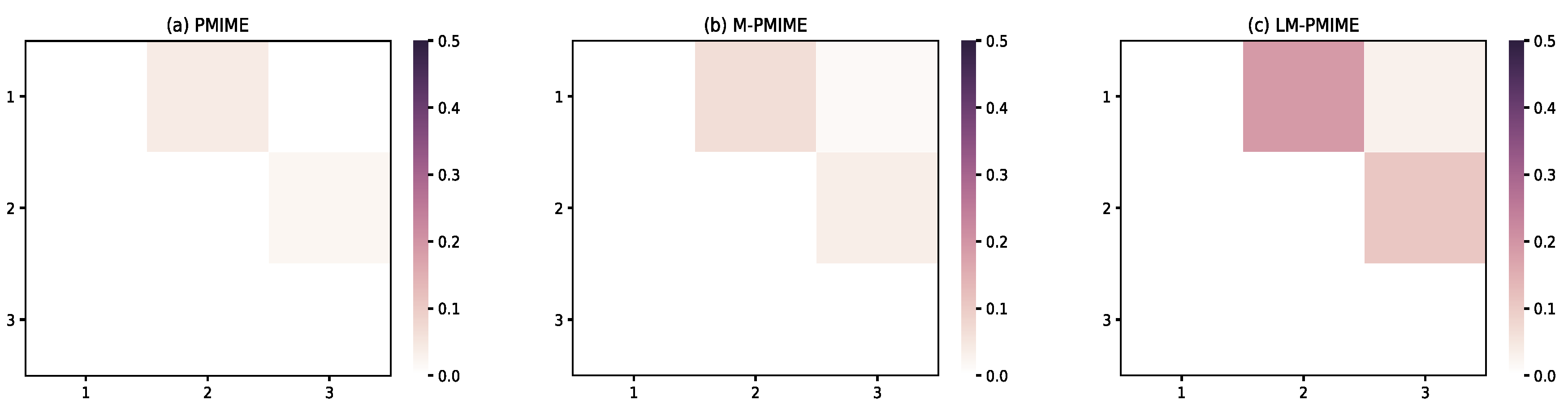
| Sensitivity | Specificity | F1 Score | |
|---|---|---|---|
| PMIME | |||
| M-PMIME | |||
| LM-PMIME | |||
| PMIME | |||
| M-PMIME | |||
| LM-PMIME | |||
| PMIME | |||
| M-PMIME | |||
| LM-PMIME |
| Sensitivity | Specificity | F1 Score | |
|---|---|---|---|
| PMIME | |||
| M-PMIME | |||
| LM-PMIME | |||
| PMIME | |||
| M-PMIME | |||
| LM-PMIME | |||
| PMIME | |||
| M-PMIME | |||
| LM-PMIME |
| Sensitivity | Specificity | F1 Score | |
|---|---|---|---|
| PMIME | |||
| M-PMIME | |||
| LM-PMIME | |||
| PMIME | |||
| M-PMIME | |||
| LM-PMIME | |||
| PMIME | |||
| M-PMIME | |||
| LM-PMIME |
| Sensitivity | Specificity | F1 Score | |
|---|---|---|---|
| PMIME | |||
| M-PMIME | |||
| LM-PMIME | |||
| PMIME | |||
| M-PMIME | |||
| LM-PMIME | |||
| PMIME | |||
| M-PMIME | |||
| LM-PMIME |
| Sensitivity | Specificity | F1 Score | |
|---|---|---|---|
| PMIME | |||
| M-PMIME | |||
| LM-PMIME | |||
| PMIME | |||
| M-PMIME | |||
| LM-PMIME | |||
| PMIME | |||
| M-PMIME | |||
| LM-PMIME |
| Sensitivity | Specificity | F1 Score | |
|---|---|---|---|
| PMIME | |||
| M-PMIME | |||
| LM-PMIME | |||
| PMIME | |||
| M-PMIME | |||
| LM-PMIME | |||
| PMIME | |||
| M-PMIME | |||
| LM-PMIME | |||
| PMIME | |||
| M-PMIME | |||
| LM-PMIME | |||
| PMIME | |||
| M-PMIME | |||
| LM-PMIME |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, Z.; Lin, Y.; Jiao, Z.; Ma, Y.; Wang, J. Detecting Causality in Multivariate Time Series via Non-Uniform Embedding. Entropy 2019, 21, 1233. https://doi.org/10.3390/e21121233
Jia Z, Lin Y, Jiao Z, Ma Y, Wang J. Detecting Causality in Multivariate Time Series via Non-Uniform Embedding. Entropy. 2019; 21(12):1233. https://doi.org/10.3390/e21121233
Chicago/Turabian StyleJia, Ziyu, Youfang Lin, Zehui Jiao, Yan Ma, and Jing Wang. 2019. "Detecting Causality in Multivariate Time Series via Non-Uniform Embedding" Entropy 21, no. 12: 1233. https://doi.org/10.3390/e21121233
APA StyleJia, Z., Lin, Y., Jiao, Z., Ma, Y., & Wang, J. (2019). Detecting Causality in Multivariate Time Series via Non-Uniform Embedding. Entropy, 21(12), 1233. https://doi.org/10.3390/e21121233







