Application of Data Mining for the Prediction of Mortality and Occurrence of Complications for Gastric Cancer Patients
Abstract
1. Introduction
2. State of Art
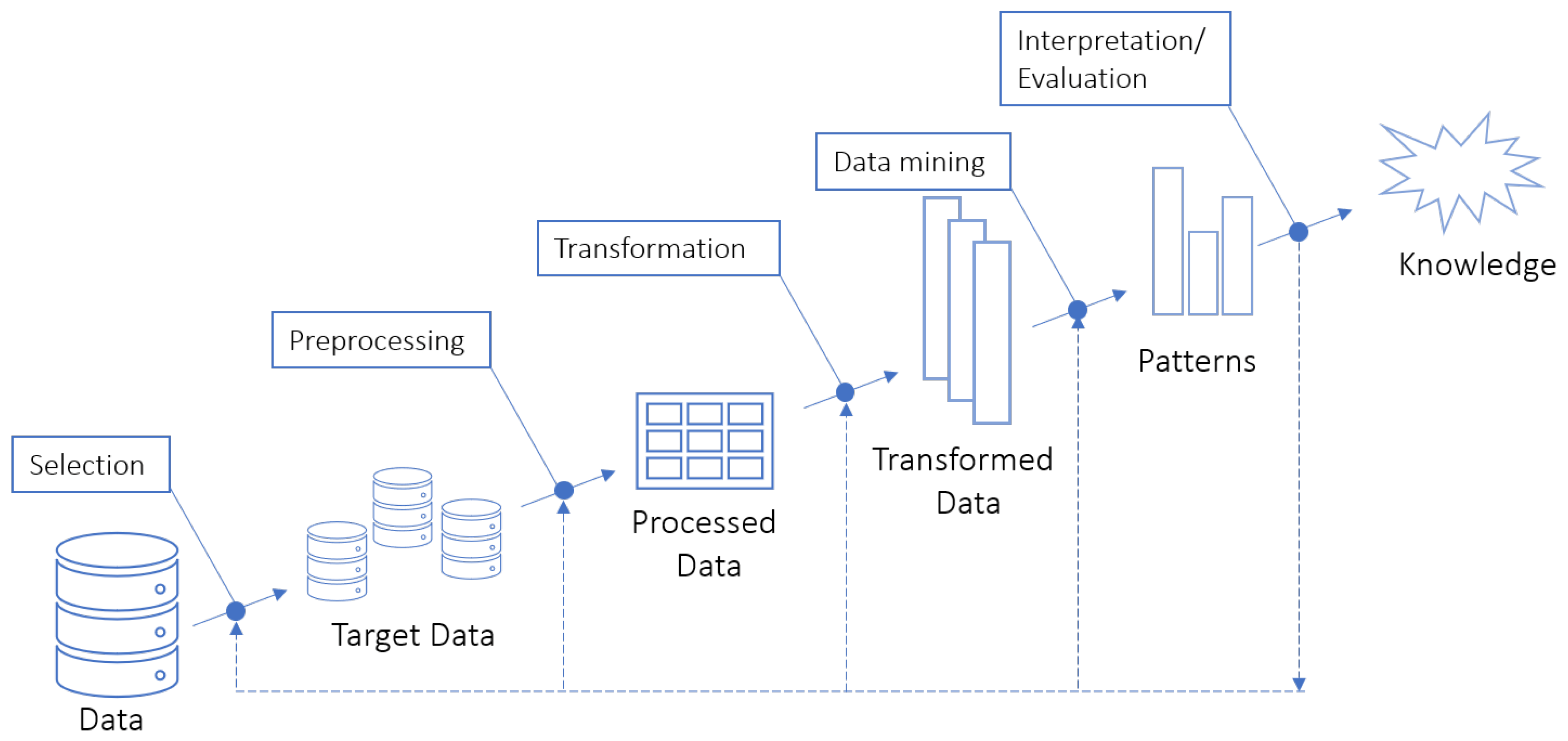
2.1. Knowledge Discovery in Databases
2.2. Data Mining
2.3. Clinical Decision Support Systems
3. Related Work
4. Methodology and Methods
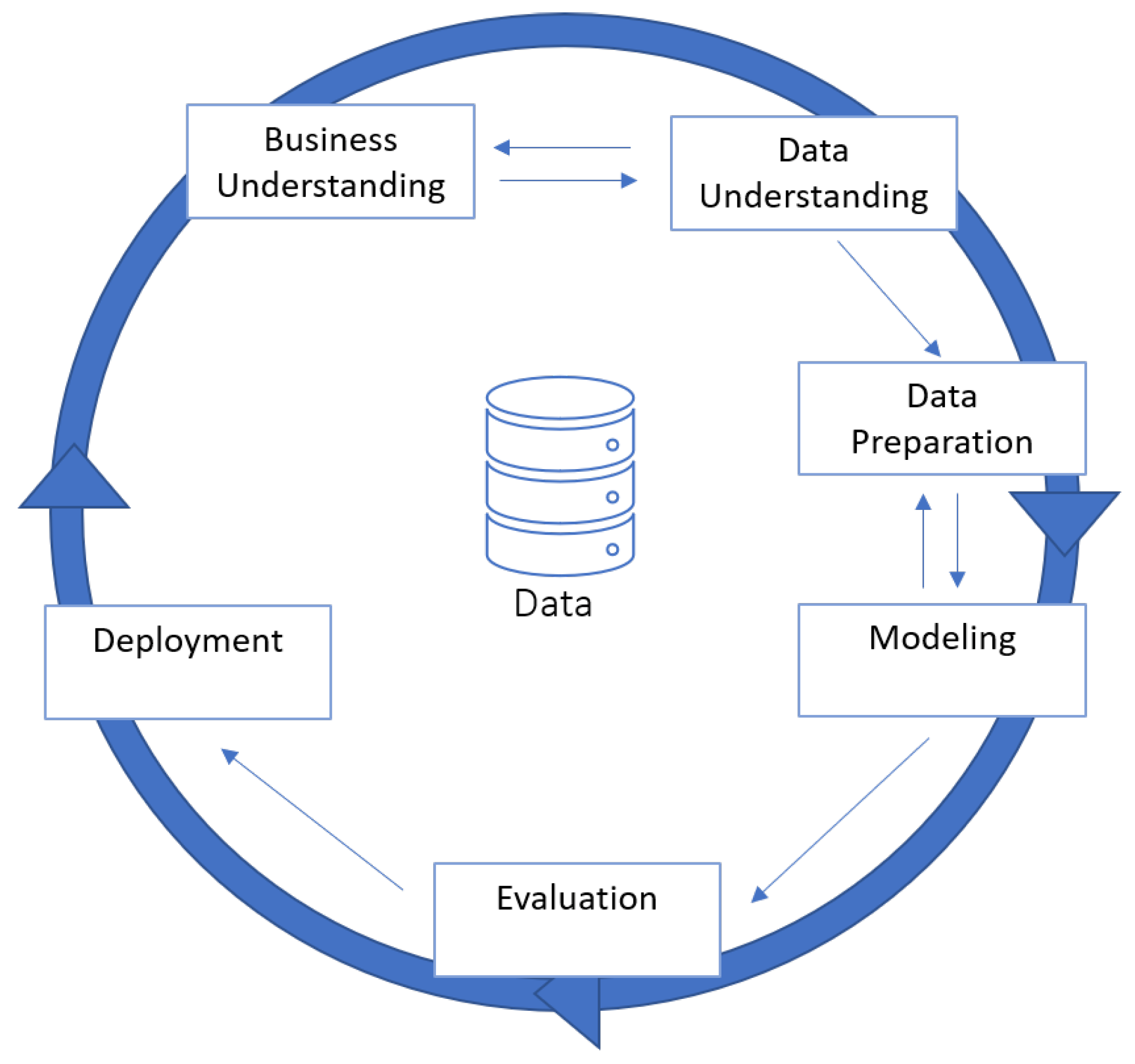
4.1. Methodology
4.2. Methods
4.2.1. Random Forest
4.2.2. J48
4.2.3. Simple Logistic
4.2.4. Bayes Net
4.2.5. PART
4.2.6. Bagging
4.2.7. AdaBoost
4.2.8. Sythetic Minority Oversampling (SMOTE)
5. Data Mining Process
5.1. Business Understanding
- Promote early examinations among the general population in order to avoid late gastric cancer diagnoses that often lead to the patient’s death
- Predict the probability of mortality after the surgery
- Predict the occurrence of complications after in-hospital stays for gastric cancer patients
5.2. Data Understanding
5.3. Data Preparation
5.4. Modeling
- T = {Mortality}
- S = {S1, S2, S3, S4}
- DMT = {RF, J48, J48 using Laplace correction, SL, BN, PART, AdaBoost + RF, AdaBoost + J48, AdaBoost + J48 using Laplace correction, AdaBoost + SL, Bagging + RF, Bagging + J48, Bagging + J48a using Laplace correction, Bagging + SL}
- DA = {With oversampling, without oversampling}
- SM = {Cross-validation 10 Folds}
- S1 = {all attributes (Use Case 1)}
- S2 = {19 attributes selected by the OneR algorithm (Use Case 2)}
- S3 = {20 attributes selected by the Relief algorithm (Use Case 3)}
- S4 = {21 attributes selected by the Pearson’s correlation method (Use Case 4)}
- T = {Surgery complications}
- S = {S1}
- DMT = {RF, J48, J48 using Laplace correction, SL, BN, PART, AdaBoost + RF, AdaBoost + J48, AdaBoost + J48 using Laplace correction, AdaBoost + SL, Bagging + RF, Bagging + J48, Bagging + J48a using Laplace correction, Bagging + SL}
- DA = {Without oversampling}
- SM = {Cross validation 10 Folds}
- S1 = {22 attributes (without bias attributes)}
5.5. Evaluation
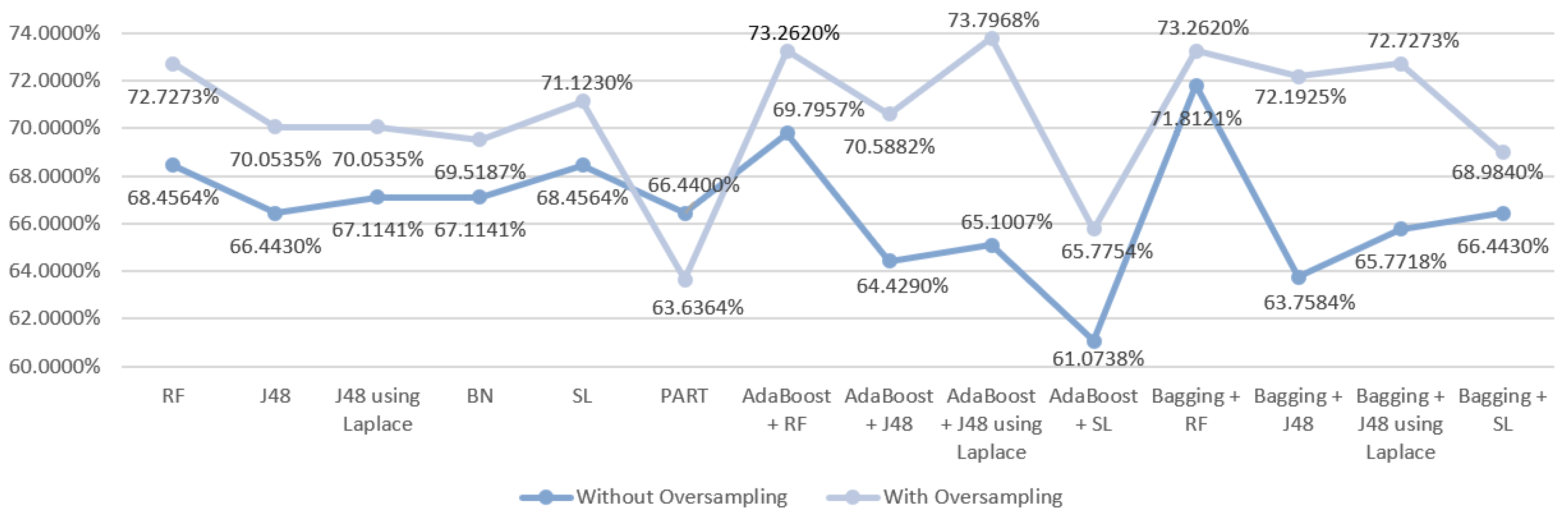
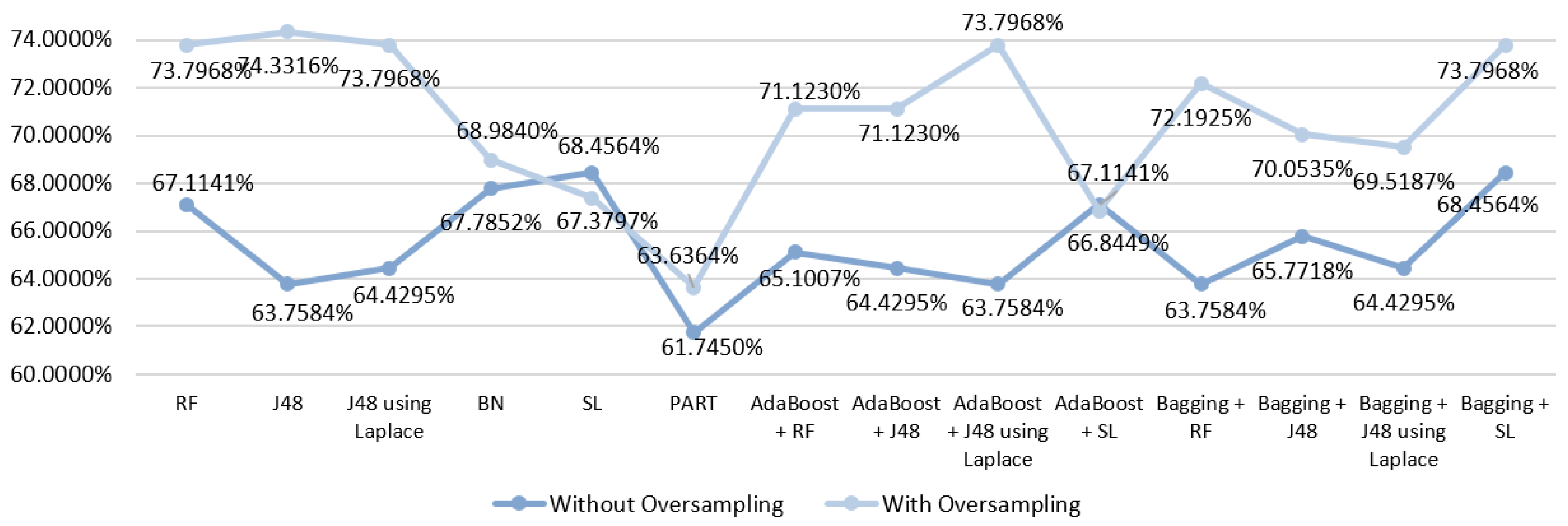
5.5.1. Mortality Prediction Results
5.5.2. Prediction Results for the Occurrence of Complications
6. Discussion
6.1. Predict the Mortality of Gastric Cancer Patients
6.2. Predict the Occurrence of Complications after In-Hospital Stays for Gastric Cancer Patients
6.3. Summary
7. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Archenaa, J.; Anita, E.A. A survey of big data analytics in healthcare and government. Procedia Comput. Sci. 2015, 50, 408–413. [Google Scholar] [CrossRef]
- Raghupathi, W.; Raghupathi, V. Big data analytics in healthcare: Promise and potential. Health Inf. Sci. Syst. 2014, 2, 3. [Google Scholar] [CrossRef] [PubMed]
- Fatt, Q.K.; Ramadas, A. The Usefulness and Challenges of Big Data in Healthcare. J. Healthc. Commun. 2018, 3, 21. [Google Scholar] [CrossRef]
- Neto, C.; Peixoto, H.; Abelha, V.; Abelha, A.; Machado, J. Knowledge Discovery from Surgical Waiting lists. Procedia Comput. Sci. 2017. [Google Scholar] [CrossRef]
- Li, Y.; Beaubouef, T. Data Mining: Concepts, Background and Methods of Integrating Uncertainty in Data Mining. CCSC SC Stud. E-J. 2010, 3, 2–7. [Google Scholar]
- Stomach Cancer Statistics; World Cancer Research Fund. Available online: https://www.wcrf.org/dietandcancer/cancer-trends/stomach-cancer-statistics (accessed on 13 November 2019).
- Bray, F.; Ferlay, J.; Soerjomataram, I.; Siegel, R.L.; Torre, L.A.; Jemal, A. Global cancer statistics 2018: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2018. [Google Scholar] [CrossRef]
- Maconi, G.; Manes, G.; Porro, G.B. Role of symptoms in diagnosis and outcome of gastric cancer. World J. Gastroenterol. WJG 2008, 14, 1149. [Google Scholar] [CrossRef]
- Lin, Y.; Ueda, J.; Kikuchi, S.; Totsuka, Y.; Wei, W.Q.; Qiao, Y.L.; Inoue, M. Comparative epidemiology of gastric cancer between Japan and China. World J. Gastroenterol. WJG 2011, 17, 4421. [Google Scholar] [CrossRef]
- Ferreira, D.; Peixoto, H.; Machado, J.; Abelha, A. Predictive Data Mining in Nutrition Therapy. In Proceedings of the IEEE 2018 13th APCA International Conference on Automatic Control and Soft Computing (CONTROLO), Ponta Delgada, Portugal, 4–6 June 2018; pp. 137–142. [Google Scholar] [CrossRef]
- Silwattananusarn, T.; Tuamsuk, K. Data Mining and Its Applications for Knowledge Management: A Literature Review from 2007 to 2012. Int. J. Data Min. Knowl. Manag. Process. 2012, 2. [Google Scholar] [CrossRef]
- Fayyad, U.M.; Piatetsky-Shapiro, G.; Smyth, P.; Uthurusamy, R. Advances in Knowledge Discovery and Data Mining; AAAI Press: Menlo Park, CA, USA, 1996; Volume 21. [Google Scholar]
- Kavakiotis, I.; Tsave, O.; Salifoglou, A.; Maglaveras, N.; Vlahavas, I.; Chouvarda, I. Machine Learning and Data Mining Methods in Diabetes Research. Comput. Struct. Biotechnol. J. 2017, 15, 104–116. [Google Scholar] [CrossRef]
- Obenshain, M.K. Application of Data Mining Techniques to Healthcare Data. Infect. Control. Hosp. Epidemiol. 2004, 25, 690–695. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.C. Mining the Complication Pattern of Gastric Cancer Patients by Using Artificial Neural Networks and Logistic Regression. J. Hum. Resour. Adult Learn. 2006, 2, 150–155. [Google Scholar]
- Polaka, I.; Gašenko, E.; Barash, O.; Haick, H.; Leja, M. Constructing Interpretable Classifiers to Diagnose Gastric Cancer Based on Breath Tests. Procedia Comput. Sci. 2016. [Google Scholar] [CrossRef]
- Hosein Zadeh, R.; Goshayeshi, L.; Khooie, A.; Etminani, K.; Yousefli, Z.; Nastarani, S.; Farhang Nezhad, N.; Golabpoor, A. Predictive Model for Survival in Patients With Gastric Cancer. Acta Healthmed. 2017. [Google Scholar] [CrossRef][Green Version]
- Berner, E.S. Clinical Decision Support Systems; Springer: Cham, Switzerland, 2007; Volume 233. [Google Scholar]
- Mohammadzadeh, F.; Noorkojuri, H.; Pourhoseingholi, M.A.; Saadat, S.; Baghestani, A.R. Predicting the probability of mortality of gastric cancer patients using decision tree. Ir. J. Med. Sci. 2015, 184, 277–284. [Google Scholar] [CrossRef]
- Silva, E.; Cardoso, L.; Portela, F.; Abelha, A.; Santos, M.F.; Machado, J. Predicting nosocomial infection by using data mining technologies. In New Contributions in Information Systems and Technologies; Springer: Cham, Switzerland, 2015; pp. 189–198. [Google Scholar] [CrossRef]
- Chapman, P. CRISP-DM 1.0: Step-by-Step Data Mining Guide; SPSS: River Edge, NJ, USA, 2000. [Google Scholar]
- Tapak, L.; Mahjub, H.; Hamidi, O.; Poorolajal, J. Real-data comparison of data mining methods in prediction of diabetes in Iran. Healthc. Inform. Res. 2013, 19. [Google Scholar] [CrossRef]
- Kandhasamy, J.P.; Balamurali, S. Performance Analysis of Classifier Models to Predict Diabetes Mellitus. Procedia Comput. Sci. 2015, 47, 45–51. [Google Scholar] [CrossRef]
- Rokach, L.; Maimon, O. Data Mining with Decision Trees: Theory and Applications, 2nd ed.; World Scientific Publishing Co., Inc.: River Edge, NJ, USA, 2014. [Google Scholar]
- Yang, X.S.; Nagar, A.K.; Joshi, A. Smart Trends in Systems, Security and Sustainability: Proceedings of WS4 2017; Springer: Singapore, 2017; Volume 18. [Google Scholar]
- Iyer, A.; Jeyalatha, S.; Sumbaly, R. Diagnosis of Diabetes Using Classification Mining Techniques. Int. J. Data Min. Knowl. Manag. Process. 2015, 5, 1–14. [Google Scholar] [CrossRef]
- Landwehr, N.; Hall, M.; Frank, E. Logistic Model Trees. Machine Learning; Springer: Berlin, Germany, 2005; Volume 95, pp. 161–205. [Google Scholar]
- Sumner, M.; Frank, E.; Hall, M. Speeding up Logistic Model Tree Induction. In Proceedings of the 9th European Conference on Principles and Practice of Knowledge Discovery in Databases, Porto, Portugal, 3–7 October 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 675–683. [Google Scholar] [CrossRef]
- Area, S.; Mesra, R. Analysis of Bayes, Neural Network and Tree Classifier of Classification Technique in Data Mining Using WEKA. In Computer Science & Information Technology; AIRCC Publishing Corporation: Chennai, India, 2012. [Google Scholar]
- Kulczycki, P.; Kacprzyk, J.; Kóczy, L.T.; Mesiar, R.; Wisniewski, R. Information Technology, Systems Research, and Computational Physics; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Frank, E.; Witten, I.H. Generating Accurate Rule Sets without Global Optimization; Morgan Kaufmann Publishers: San Francisco, CA, USA, 1998. [Google Scholar]
- Ryżko, D.; Gawrysiak, P.; Rybinski, H.; Kryszkiewicz, M. Emerging Intelligent Technologies in Industry; Springer: Berlin/Heidelberg, Germany, 2011; Volume 369. [Google Scholar]
- Freund, Y.; Schapire, R.E. Experiments with a new boosting algorithm. In Proceedings of the Thirteenth International Conference on International Conference on Machine Learning, Bari, Italy, 3–6 July 1996; Volume 96, pp. 148–156. [Google Scholar]
- Perveen, S.; Shahbaz, M.; Guergachi, A.; Keshavjee, K. Performance Analysis of Data Mining Classification Techniques to Predict Diabetes. Procedia Comput. Sci. 2016, 82, 115–121. [Google Scholar] [CrossRef]
- Skurichina, M.; Duin, R.P. Bagging, boosting and the random subspace method for linear classifiers. Pattern Anal. Appl. 2002, 5, 121–135. [Google Scholar] [CrossRef]
- Cornelis, C.; Kryszkiewicz, M.; Ciucci, D.; Medina-Moreno, J.; Motoda, H.; Ras, Z.W. Rough Sets and Intelligent Systems Paradigms; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Sitarz, R.; Skierucha, M.; Mielko, J.; Offerhaus, G.J.A.; Maciejewski, R.; Polkowski, W.P. Gastric cancer: Epidemiology, prevention, classification, and treatment. Cancer Manag. Res. 2018, 10, 239–248. [Google Scholar] [CrossRef] [PubMed]
- Correa, P. Gastric Cancer. Overview. Gastroenterol. Clin. N. Am. 2013, 42, 211–217. [Google Scholar] [CrossRef] [PubMed]
- Waddell, T.; Verheij, M.; Allum, W.; Cunningham, D.; Cervantes, A.; Arnold, D. Gastric cancer: ESMO–ESSO–ESTRO Clinical Practice Guidelines for diagnosis, treatment and follow-up. Ann. Oncol. 2013, 24, vi57–vi63. [Google Scholar] [CrossRef] [PubMed]
- Schatz, R.A.; Rockey, D.C. Gastrointestinal bleeding due to gastrointestinal tract malignancy: Natural history, management, and outcomes. Dig. Dis. Sci. 2017, 62, 491–501. [Google Scholar] [CrossRef]
- Biskup, E.; Cai, F.; Vetter, M.; Marsch, S. Oncological patients in the intensive care unit: Prognosis, decision-making, therapies and end-of-life care. Swiss Med. Wkly. 2017, 147. [Google Scholar] [CrossRef]
| Use Case | # Attr | # Numeric Attr | # Categorical Attr |
|---|---|---|---|
| 1 | 33 | 4 | 29 |
| 2 | 19 | 1 | 18 |
| 3 | 20 | 1 | 19 |
| 4 | 21 | 2 | 19 |
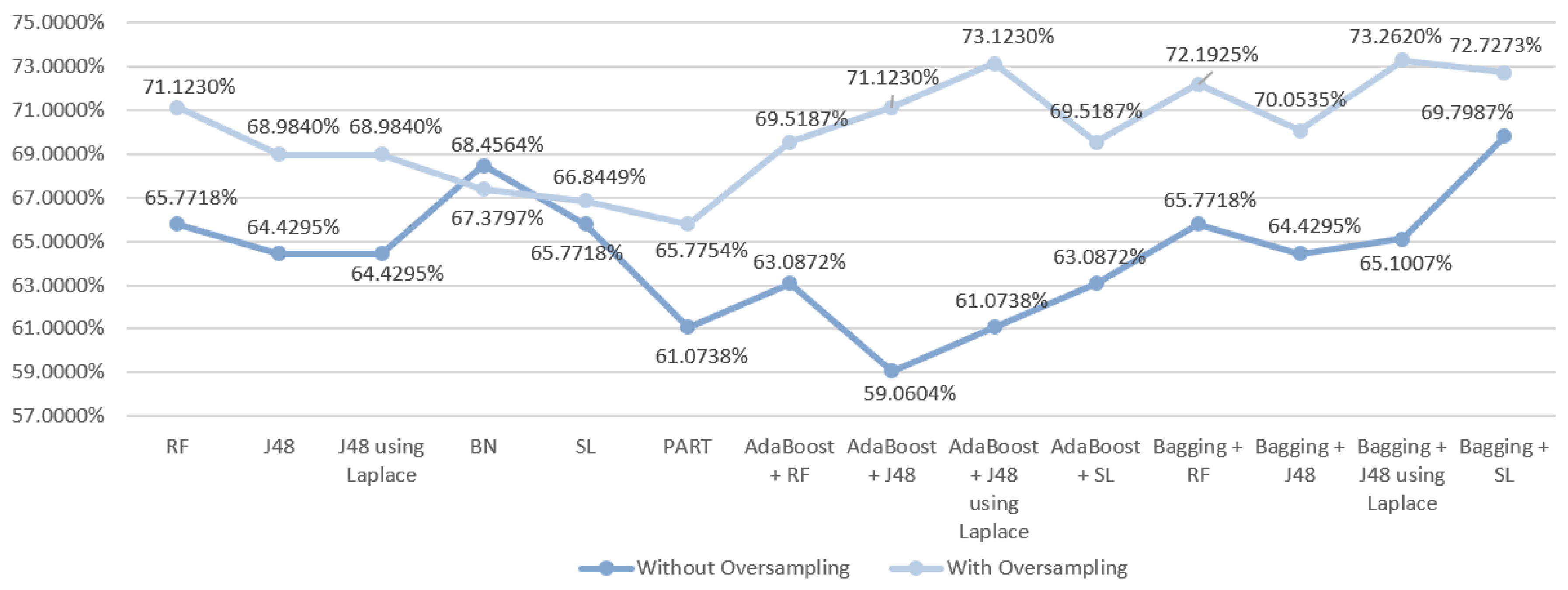
| DM Technique | Scenario | Data Approach | Accuracy (%) | Precision | F-Measure | Recall | AUC |
|---|---|---|---|---|---|---|---|
| RF | S1 | Without oversampling | 68.4564 | 0.670 | 0.674 | 0.685 | 0.815 |
| With oversampling | 72.7273 | 0.723 | 0.717 | 0.727 | 0.859 | ||
| J48 | S1 | Without oversampling | 66.443 | 0.640 | 0.647 | 0.664 | 0.770 |
| With oversampling | 70.0535 | 0.699 | 0.694 | 0.701 | 0.772 | ||
| J48 | S1 | Without oversampling | 67.1141 | 0.645 | 0.652 | 0.671 | 0.755 |
| With oversampling | 70.0535 | 0.699 | 0.694 | 0.701 | 0.801 | ||
| BN | S1 | Without oversampling | 67.1141 | 0.676 | 0.672 | 0.761 | 0.808 |
| With oversampling | 69.5187 | 0.693 | 0.694 | 0.695 | 0.837 | ||
| SL | S1 | Without oversampling | 68.4564 | 0.683 | 0.681 | 0.685 | 0.792 |
| With oversampling | 71.1230 | 0.706 | 0.707 | 0.711 | 0.821 | ||
| PART | S1 | Without oversampling | 66.443 | 0.662 | 0.658 | 0.664 | 0.777 |
| With oversampling | 63.6364 | 0.629 | 0.631 | 0.636 | 0.748 | ||
| AdaBoost + RF | S1 | Without oversampling | 69.7957 | 0.686 | 0.688 | 0.698 | 0.821 |
| With oversampling | 73.2620 | 0.726 | 0.725 | 0.733 | 0.862 | ||
| AdaBoost + J48 | S1 | Without oversampling | 64.4295 | 0.640 | 0.642 | 0.644 | 0.790 |
| With oversampling | 70.5882 | 0.701 | 0.701 | 0.706 | 0.848 | ||
| AdaBoost + J48 | S1 | Without oversampling | 65.1007 | 0.659 | 0.655 | 0.651 | 0.794 |
| With oversampling | 73.7968 | 0.738 | 0.731 | 0.738 | 0.850 | ||
| AdaBoost + SL | S1 | Without oversampling | 61.0738 | 0.619 | 0.614 | 0.611 | 0.693 |
| With oversampling | 65.7754 | 0.662 | 0.659 | 0.658 | 0.783 | ||
| Bagging + RF | S1 | Without oversampling | 71.8121 | 0.702 | 0.705 | 0.718 | 0.810 |
| With oversampling | 73.2620 | 0.724 | 0.718 | 0.733 | 0.859 | ||
| Bagging + J48 | S1 | Without oversampling | 63.7584 | 0.605 | 0.616 | 0.638 | 0.800 |
| With oversampling | 72.1925 | 0.716 | 0.718 | 0.722 | 0.840 | ||
| Bagging + J48 | S1 | Without oversampling | 65.7718 | 0.637 | 0.643 | 0.658 | 0.801 |
| With oversampling | 72.7273 | 0.722 | 0.723 | 0.727 | 0.840 | ||
| Bagging + SL | S1 | Without oversampling | 66.443 | 0.656 | 0.660 | 0.664 | 0.780 |
| With oversampling | 68.9840 | 0.690 | 0.689 | 0.690 | 0.834 |
| DM Technique | Scenario | Data Approach | Accuracy (%) | Precision | F-Measure | Recall | AUC |
|---|---|---|---|---|---|---|---|
| RF | S2 | Without oversampling | 67.1141 | 0.656 | 0.659 | 0.671 | 0.811 |
| With oversampling | 73.7968 | 0.735 | 0.736 | 0.738 | 0.873 | ||
| J48 | S2 | Without oversampling | 63.7584 | 0.625 | 0.629 | 0.638 | 0.789 |
| With oversampling | 74.3316 | 0.744 | 0.743 | 0.743 | 0.826 | ||
| J48 | S2 | Without oversampling | 64.4295 | 0.629 | 0.634 | 0.644 | 0.761 |
| With oversampling | 73.7968 | 0.738 | 0.738 | 0.738 | 0.821 | ||
| BN | S2 | Without oversampling | 67.7852 | 0.675 | 0.676 | 0.678 | 0.820 |
| With oversampling | 68.9840 | 0.687 | 0.687 | 0.690 | 0.836 | ||
| SL | S2 | Without oversampling | 68.4564 | 0.682 | 0.682 | 0.685 | 0.793 |
| With oversampling | 67.3797 | 0.667 | 0.669 | 0.674 | 0.804 | ||
| PART | S2 | Without oversampling | 61.7450 | 0.603 | 0.604 | 0.617 | 0.754 |
| With oversampling | 63.6364 | 0.632 | 0.633 | 0.636 | 0.776 | ||
| AdaBoost + RF | S2 | Without oversampling | 65.1007 | 0.643 | 0.646 | 0.651 | 0.760 |
| With oversampling | 71.1230 | 0.710 | 0.711 | 0.711 | 0.829 | ||
| AdaBoost + J48 | S2 | Without oversampling | 64.4295 | 0.643 | 0.643 | 0.644 | 0.779 |
| With oversampling | 71.1230 | 0.709 | 0.710 | 0.711 | 0.868 | ||
| AdaBoost + J48 | S2 | Without oversampling | 63.7584 | 0.634 | 0.636 | 0.638 | 0.778 |
| With oversampling | 73.7968 | 0.733 | 0.734 | 0.738 | 0.878 | ||
| AdaBoost + SL | S2 | Without oversampling | 67.1141 | 0.670 | 0.671 | 0.671 | 0.791 |
| With oversampling | 66.8449 | 0.666 | 0.667 | 0.668 | 0.802 | ||
| Bagging + RF | S2 | Without oversampling | 63.7584 | 0.616 | 0.623 | 0.638 | 0.804 |
| With oversampling | 72.1925 | 0.718 | 0.719 | 0.722 | 0.879 | ||
| Bagging + J48 | S2 | Without oversampling | 65.7718 | 0.629 | 0.639 | 0.658 | 0.801 |
| With oversampling | 70.0535 | 0.697 | 0.697 | 0.701 | 0.842 | ||
| Bagging + J48 | S2 | Without oversampling | 64.4295 | 0.617 | 0.628 | 0.644 | 0.798 |
| With oversampling | 69.5187 | 0.690 | 0.691 | 0.695 | 0.835 | ||
| Bagging + SL | S2 | Without oversampling | 68.4564 | 0.672 | 0.676 | 0.685 | 0.806 |
| With oversampling | 73.7968 | 0.734 | 0.733 | 0.738 | 0.848 |
| DM Technique | Scenario | Data Approach | Accuracy (%) | Precision | F-Measure | Recall | AUC |
|---|---|---|---|---|---|---|---|
| RF | S3 | Without oversampling | 65.7718 | 0.644 | 0.646 | 0.658 | 0.805 |
| With oversampling | 71.1230 | 0.699 | 0.700 | 0.711 | 0.863 | ||
| J48 | S3 | Without oversampling | 64.4295 | 0.625 | 0.632 | 0.644 | 0.781 |
| With oversampling | 68.9840 | 0.682 | 0.683 | 0.690 | 0.795 | ||
| J48 | S3 | Without oversampling | 64.4295 | 0.625 | 0.632 | 0.644 | 0.754 |
| With oversampling | 68.9840 | 0.682 | 0.683 | 0.690 | 0.793 | ||
| BN | S3 | Without oversampling | 68.4564 | 0.682 | 0.683 | 0.685 | 0.820 |
| With oversampling | 67.3797 | 0.682 | 0.674 | 0.674 | 0.836 | ||
| SL | S3 | Without oversampling | 65.7718 | 0.651 | 0.652 | 0.658 | 0.790 |
| With oversampling | 66.8449 | 0.663 | 0.664 | 0.668 | 0.825 | ||
| PART | S3 | Without oversampling | 61.0738 | 0.600 | 0.604 | 0.611 | 0.756 |
| With oversampling | 65.7754 | 0.648 | 0.650 | 0.658 | 0.770 | ||
| AdaBoost + RF | S3 | Without oversampling | 63.0872 | 0.614 | 0.621 | 0.631 | 0.789 |
| With oversampling | 69.5187 | 0.688 | 0.691 | 0.695 | 0.830 | ||
| AdaBoost + J48 | S3 | Without oversampling | 59.0604 | 0.604 | 0.597 | 0.591 | 0.778 |
| With oversampling | 71.1230 | 0.711 | 0.711 | 0.711 | 0.861 | ||
| AdaBoost + J48 | S3 | Without oversampling | 61.0738 | 0.619 | 0.614 | 0.611 | 0.780 |
| With oversampling | 73.1230 | 0.708 | 0.709 | 0.711 | 0.859 | ||
| AdaBoost + SL | S3 | Without oversampling | 63.0872 | 0.617 | 0.623 | 0.631 | 0.766 |
| With oversampling | 69.5187 | 0.692 | 0.693 | 0.665 | 0.815 | ||
| Bagging + RF | S3 | Without oversampling | 65.7718 | 0.640 | 0.658 | 0.644 | 0.805 |
| With oversampling | 72.1925 | 0.718 | 0.719 | 0.722 | 0.862 | ||
| Bagging + J48 | S3 | Without oversampling | 64.4295 | 0.611 | 0.624 | 0.644 | 0.800 |
| With oversampling | 70.0535 | 0.697 | 0.697 | 0.701 | 0.845 | ||
| Bagging + J48 | S3 | Without oversampling | 65.1007 | 0.623 | 0.633 | 0.651 | 0.801 |
| With oversampling | 73.2620 | 0.728 | 0.729 | 0.733 | 0.841 | ||
| Bagging + SL | S3 | Without oversampling | 69.7987 | 0.683 | 0.688 | 0.698 | 0.799 |
| With oversampling | 72.7273 | 0.727 | 0.726 | 0.727 | 0.857 |
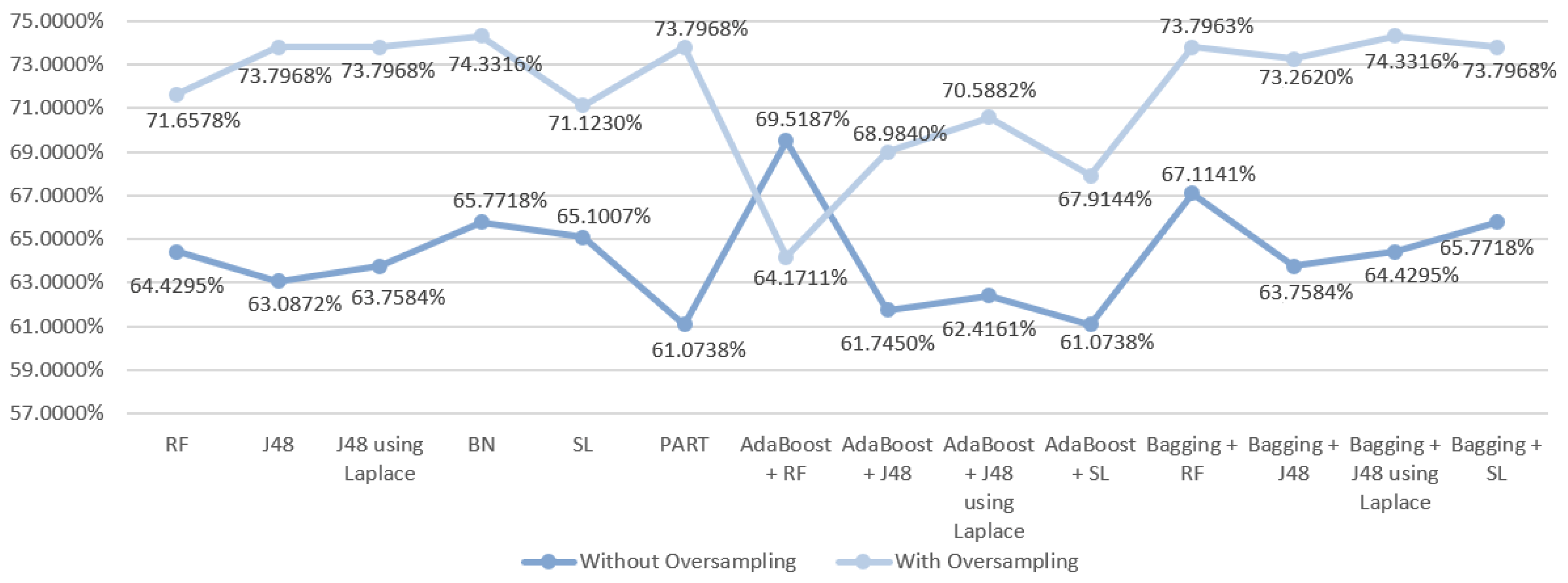
| DM Technique | Scenario | Data Approach | Accuracy (%) | Precision | F-Measure | Recall | AUC |
|---|---|---|---|---|---|---|---|
| RF | S3 | Without oversampling | 64.4295 | 0.632 | 0.636 | 0.644 | 0.801 |
| With oversampling | 71.6578 | 0.712 | 0.714 | 0.717 | 0.859 | ||
| J48 | S3 | Without oversampling | 63.0872 | 0.602 | 0.614 | 0.631 | 0.753 |
| With oversampling | 73.7968 | 0.735 | 0.735 | 0.738 | 0.792 | ||
| J48 | S3 | Without oversampling | 63.7584 | 0.606 | 0.619 | 0.638 | 0.734 |
| With oversampling | 73.7968 | 0.735 | 0.735 | 0.738 | 0.797 | ||
| BN | S3 | Without oversampling | 65.7718 | 0.653 | 0.655 | 0.658 | 0.812 |
| With oversampling | 74.3316 | 0.740 | 0.741 | 0.743 | 0.842 | ||
| SL | S3 | Without oversampling | 65.1007 | 0.653 | 0.655 | 0.658 | 0.795 |
| With oversampling | 71.1230 | 0.709 | 0.708 | 0.711 | 0.809 | ||
| PART | S3 | Without oversampling | 61.0738 | 0.603 | 0.606 | 0.611 | 0.735 |
| With oversampling | 73.7968 | 0.735 | 0.735 | 0.738 | 0.782 | ||
| AdaBoost + RF | S3 | Without oversampling | 69.5187 | 0.688 | 0.691 | 0.695 | 0.740 |
| With oversampling | 64.1711 | 0.640 | 0.641 | 0.642 | 0.807 | ||
| AdaBoost + J48 | S3 | Without oversampling | 61.7450 | 0.609 | 0.613 | 0.617 | 0.790 |
| With oversampling | 68.9840 | 0.687 | 0.688 | 0.690 | 0.854 | ||
| AdaBoost + J48 | S3 | Without oversampling | 62.4161 | 0.622 | 0.621 | 0.624 | 0.787 |
| With oversampling | 70.5882 | 0.705 | 0.706 | 0.706 | 0.859 | ||
| AdaBoost + SL | S3 | Without oversampling | 61.0738 | 0.622 | 0.616 | 0.611 | 0.776 |
| With oversampling | 67.9144 | 0.684 | 0.681 | 0.679 | 0.802 | ||
| Bagging + RF | S3 | Without oversampling | 67.1141 | 0.653 | 0.658 | 0.671 | 0.803 |
| With oversampling | 73.7963 | 0.732 | 0.734 | 0.738 | 0.864 | ||
| Bagging + J48 | S3 | Without oversampling | 63.7584 | 0.617 | 0.624 | 0.638 | 0.794 |
| With oversampling | 73.2620 | 0.732 | 0.732 | 0.733 | 0.836 | ||
| Bagging + J48 | S3 | Without oversampling | 64.4295 | 0.608 | 0.621 | 0.644 | 0.795 |
| With oversampling | 74.3316 | 0.742 | 0.742 | 0.743 | 0.832 | ||
| Bagging + SL | S3 | Without oversampling | 65.7718 | 0.648 | 0.652 | 0.658 | 0.800 |
| With oversampling | 73.7968 | 0.733 | 0.735 | 0.738 | 0.856 |
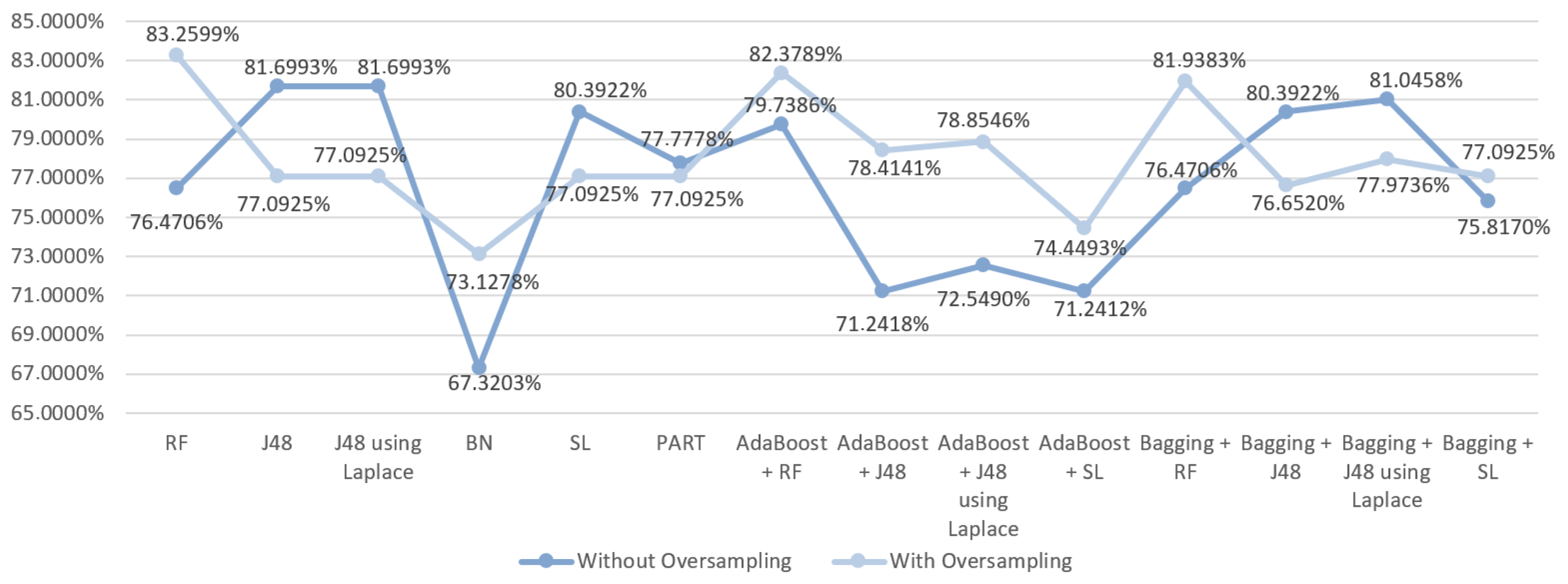
| DM Technique | Scenario | Data Approach | Accuracy (%) | Precision | F-Measure | Recall | AUC |
|---|---|---|---|---|---|---|---|
| RF | S3 | Without oversampling | 76.4706 | 0.730 | 0.730 | 0.765 | 0.654 |
| With oversampling | 83.2599 | 0.833 | 0.833 | 0.833 | 0.909 | ||
| J48 | S3 | Without oversampling | 81.6993 | 0.834 | 0.777 | 0.817 | 0.580 |
| With oversampling | 77.0925 | 0.773 | 0.770 | 0.771 | 0.806 | ||
| J48 | S3 | Without oversampling | 81.6993 | 0.834 | 0.777 | 0.817 | 0.580 |
| With oversampling | 77.0925 | 0.773 | 0.770 | 0.771 | 0.825 | ||
| BN | S3 | Without oversampling | 67.3203 | 0.708 | 0.687 | 0.673 | 0.690 |
| With oversampling | 73.1278 | 0.733 | 0.731 | 0.731 | 0.822 | ||
| SL | S3 | Without oversampling | 80.3922 | 0.807 | 0.761 | 0.804 | 0.662 |
| With oversampling | 77.0925 | 0.771 | 0.771 | 0.771 | 0.826 | ||
| PART | S3 | Without oversampling | 77.7778 | 0.753 | 0.754 | 0.778 | 0.655 |
| With oversampling | 77.0925 | 0.775 | 0.770 | 0.771 | 0.794 | ||
| AdaBoost + RF | S3 | Without oversampling | 79.7386 | 0.798 | 0.750 | 0.797 | 0.662 |
| With oversampling | 82.3789 | 0.824 | 0.824 | 0.824 | 0.914 | ||
| AdaBoost + J48 | S3 | Without oversampling | 71.2418 | 0.696 | 0.703 | 0.712 | 0.640 |
| With oversampling | 78.4141 | 0.785 | 0.784 | 0.784 | 0.868 | ||
| AdaBoost + J48 | S3 | Without oversampling | 72.5490 | 0.705 | 0.713 | 0.725 | 0.635 |
| With oversampling | 78.8546 | 0.794 | 0.788 | 0.789 | 0.868 | ||
| AdaBoost + SL | S3 | Without oversampling | 71.2412 | 0.702 | 0.707 | 0.712 | 0.599 |
| With oversampling | 74.4493 | 0.745 | 0.745 | 0.744 | 0.770 | ||
| Bagging + RF | S3 | Without oversampling | 76.4706 | 0.725 | 0.698 | 0.765 | 0.681 |
| With oversampling | 81.9383 | 0.819 | 0.819 | 0.819 | 0.908 | ||
| Bagging + J48 | S3 | Without oversampling | 80.3922 | 0.793 | 0.771 | 0.804 | 0.643 |
| With oversampling | 76.6520 | 0.767 | 0.767 | 0.767 | 0.872 | ||
| Bagging + J48 | S3 | Without oversampling | 81.0458 | 0.806 | 0.776 | 0.810 | 0.660 |
| With oversampling | 77.9736 | 0.781 | 0.780 | 0.780 | 0.879 | ||
| Bagging + SL | S3 | Without oversampling | 75.8170 | 0.736 | 0.743 | 0.758 | 0.641 |
| With oversampling | 77.0925 | 0.771 | 0.771 | 0.771 | 0.852 |
| Scenario | Data Technique | Classifier | Accuracy (%) |
|---|---|---|---|
| S1 | Without oversampling | Bagging with RF | 71.8121 |
| With oversampling | Boosting with J48 using Laplace | 73.7968 | |
| S2 | Without oversampling | SL and Bagging with SL | 68.4564 |
| With oversampling | J48 | 74.3316 | |
| S3 | Without oversampling | Boosting with SL | 69.7987 |
| With oversampling | Boosting with J48 using Laplace | 73.2620 | |
| S4 | Without oversampling | Boosting with RF | 69.5187 |
| With oversampling | Bagging with J48 using Laplace | 74.3316 |
| Scenario | Data Aproach | Classifier | Precision | F-Measure | Recall |
|---|---|---|---|---|---|
| S1 | Without oversampling | Bagging with RF | 0.702 | 0.705 | 0.718 |
| With oversampling | Boosting with J48 using Laplace | 0.738 | 0.731 | 0.738 | |
| S2 | Without oversampling | SL | 0.682 | 0.682 | 0.685 |
| With oversampling | J48 | 0.744 | 0.743 | 0.743 | |
| S3 | Without oversampling | Bagging with SL | 0.683 | 0.688 | 0.698 |
| With oversampling | Bagging with SL | 0.727 | 0.726 | 0.727 | |
| S4 | Without oversampling | AdaBoost + RF | 0.688 | 0.691 | 0.695 |
| With oversampling | Bagging with J48 using Laplace | 0.742 | 0.742 | 0.743 |
| Scenario | Data Approach | Classifier | AUC |
|---|---|---|---|
| S1 | Without oversampling | AdaBoost with RF | 0.821 |
| With oversampling | AdaBoost with RF | 0.862 | |
| S2 | Without oversampling | BN | 0.820 |
| With oversampling | Bagging with RF | 0.879 | |
| S3 | Without oversampling | BN | 0.820 |
| With oversampling | RF | 0.805 | |
| S4 | Without oversampling | BN | 0.812 |
| With oversampling | Bagging with RF | 0.864 |
| Data Mining Models | Scenario | Data Approach | Classifier | Accuracy (%) | Precision | F-Measure | Recall |
|---|---|---|---|---|---|---|---|
| DMM1 | S2 | With oversampling | J48 | 74.3316 | 0.744 | 0.743 | 0.743 |
| DMM2 | S1 | With oversampling | RF | 83.2599 | 0.833 | 0.833 | 0.833 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neto, C.; Brito, M.; Lopes, V.; Peixoto, H.; Abelha, A.; Machado, J. Application of Data Mining for the Prediction of Mortality and Occurrence of Complications for Gastric Cancer Patients. Entropy 2019, 21, 1163. https://doi.org/10.3390/e21121163
Neto C, Brito M, Lopes V, Peixoto H, Abelha A, Machado J. Application of Data Mining for the Prediction of Mortality and Occurrence of Complications for Gastric Cancer Patients. Entropy. 2019; 21(12):1163. https://doi.org/10.3390/e21121163
Chicago/Turabian StyleNeto, Cristiana, Maria Brito, Vítor Lopes, Hugo Peixoto, António Abelha, and José Machado. 2019. "Application of Data Mining for the Prediction of Mortality and Occurrence of Complications for Gastric Cancer Patients" Entropy 21, no. 12: 1163. https://doi.org/10.3390/e21121163
APA StyleNeto, C., Brito, M., Lopes, V., Peixoto, H., Abelha, A., & Machado, J. (2019). Application of Data Mining for the Prediction of Mortality and Occurrence of Complications for Gastric Cancer Patients. Entropy, 21(12), 1163. https://doi.org/10.3390/e21121163







