Abstract
Bounding the best achievable error probability for binary classification problems is relevant to many applications including machine learning, signal processing, and information theory. Many bounds on the Bayes binary classification error rate depend on information divergences between the pair of class distributions. Recently, the Henze–Penrose (HP) divergence has been proposed for bounding classification error probability. We consider the problem of empirically estimating the HP-divergence from random samples. We derive a bound on the convergence rate for the Friedman–Rafsky (FR) estimator of the HP-divergence, which is related to a multivariate runs statistic for testing between two distributions. The FR estimator is derived from a multicolored Euclidean minimal spanning tree (MST) that spans the merged samples. We obtain a concentration inequality for the Friedman–Rafsky estimator of the Henze–Penrose divergence. We validate our results experimentally and illustrate their application to real datasets.
1. Introduction
Divergence measures between probability density functions are used in many signal processing applications including classification, segmentation, source separation, and clustering (see [1,2,3]). For more applications of divergence measures, we refer to [4].
In classification problems, the Bayes error rate is the expected risk for the Bayes classifier, which assigns a given feature vector to the class with the highest posterior probability. The Bayes error rate is the lowest possible error rate of any classifier for a particular joint distribution. Mathematically, let be realizations of random vector and class labels , with prior probabilities and , such that . Given conditional probability densities and , the Bayes error rate is given by
The Bayes error rate provides a measure of classification difficulty. Thus, when known, the Bayes error rate can be used to guide the user in the choice of classifier and tuning parameter selection. In practice, the Bayes error is rarely known and must be estimated from data. Estimation of the Bayes error rate is difficult due to the nonsmooth min function within the integral in (1). Thus, research has focused on deriving tight bounds on the Bayes error rate based on smooth relaxations of the min function. Many of these bounds can be expressed in terms of divergence measures such as the Bhattacharyya [5] and Jensen–Shannon [6]. Tighter bounds on the Bayes error rate can be obtained using an important divergence measure known as the Henze–Penrose (HP) divergence [7,8].
Many techniques have been developed for estimating divergence measures. These methods can be broadly classified into two categories: (i) plug-in estimators in which we estimate the probability densities and then plug them in the divergence function [9,10,11,12], (ii) entropic graph approaches, in which the relationship between the divergence function and a graph functional in Euclidean space is derived [8,13]. Examples of plug-in methods include k-nearest neighbor (K-NN) and Kernel density estimator (KDE) divergence estimators. Examples of entropic graph approaches include methods based on minimal spanning trees (MST), K-nearest neighbors graphs (K-NNG), minimal matching graphs (MMG), traveling salesman problem (TSP), and their power-weighted variants.
Disadvantages of plug-in estimators are that these methods often require assumptions on the support set boundary and are more computationally complex than direct graph-based approaches. Thus, for practical and computational reasons, the asymptotic behavior of entropic graph approaches has been of great interest. Asymptotic analysis has been used to justify graph based approaches. For instance, in [14], the authors showed that a cross match statistic based on optimal weighted matching converges to the the HP-divergence. In [15], a more complex approach based on the K-NNG was proposed that also converges to the HP-divergence.
The first contribution of our paper is that we obtain a bound on the convergence rates for the Friedman and Rafsky (FR) estimator of the HP-divergence, which is based on a multivariate extension of the non-parametric run length test of equality of distributions. This estimator is constructed using a multicolored MST on the labeled training set where MST edges connecting samples with dichotomous labels are colored differently from edges connecting identically labeled samples. While previous works have investigated the FR test statistic in the context of estimating the HP-divergence (see [8,16]), to the best of our knowledge, its minimax MSE convergence rate has not been previously derived. The bound on convergence rate is established by using the umbrella theorem of [17], for which we define a dual version of the multicolor MST. The proposed dual MST in this work is different than the standard dual MST introduced by Yukich in [17]. We show that the bias rate of the FR estimator is bounded by a function of N, and d, as , where N is the total sample size, d is the dimension of the data samples , and is the Hölder smoothness parameter . We also obtain the variance rate bound as .
The second contribution of our paper is a new concentration bound for the FR test statistic. The bound is obtained by establishing a growth bound and a smoothness condition for the multicolored MST. Since the FR test statistic is not a Euclidean functional, we cannot use the standard subadditivity and superadditivity approaches of [17,18,19]. Our concentration inequality is derived using a different Hamming distance approach and a dual graph to the multicolored MST.
We experimentally validate our theoretic results. We compare the MSE theory and simulation in three experiments with various dimensions . We observe that, in all three experiments, as sample size increases, the MSE rate decreases and, for higher dimensions, the rate is slower. In all sets of experiments, our theory matches the experimental results. Furthermore, we illustrate the application of our results on estimation of the Bayes error rate on three real datasets.
1.1. Related Work
Much research on minimal graphs has focused on the use of Euclidean functionals for signal processing and statistics applications such as image registration [20,21], pattern matching [22], and non-parametric divergence estimation [23]. A K-NNG-based estimator of Rényi and f-divergence measures has been proposed in [13]. Additional examples of direct estimators of divergence measures include statistic based on the nonparametric two sample problem, the Smirnov maximum deviation test [24], and the Wald–Wolfowitz [25] runs test, which have been studied in [26].
Many entropic graph estimators such as MST, K-NNG, MMG, and TSP have been considered for multivariate data from a single probability density f. In particular, the normalized weight function of graph constructions all converge almost surely to the Rényi entropy of f [17,27]. For N uniformly distributed points, the MSE is [28,29]. Later, Hero et al. [30,31] reported bounds on -norm bias convergence rates of power-weighted Euclidean weight functionals of order for densities f belonging to the space of Hölder continuous functions as , where , , , and . In this work, we derive a bound on convergence rate of FR estimator for the HP-divergence when the density functions belong to the Hölder class, , for , [32]. Note that throughout the paper we assume the density functions are absolutely continuous and bounded with support on the unit cube .
In [28], Yukich introduced the general framework of continuous and quasi-additive Euclidean functionals. This has led to many convergence rate bounds of entropic graph divergence estimators.
The framework of [28] is as follows: Let F be finite subset of points in , , drawn from an underlying density. A real-valued function defined on F is called a Euclidean functional of order if it is of the form , where is a set of graphs, e is an edge in the graph E, is the Euclidean length of e, and is called the edge exponent or power-weighting constant. The MST, TSP, and MMG are some examples for which .
Following this framework, we show that the FR test statistic satisfies the required continuity and quasi-additivity properties to obtain similar convergence rates to those predicted in [28]. What distinguishes our work from previous work is that the count of dichotomous edges in the multicolored MST is not Euclidean. Therefore, the results in [17,27,30,31] are not directly applicable.
Using the isoperimetric approach, Talagrand [33] showed that, when the Euclidean functional is based on the MST or TSP, then the functional for derived random vertices uniformly distributed in a hypercube is concentrated around its mean. Namely, with high probability, the functional and its mean do not differ by more than . In this paper, we establish concentration bounds for the FR statistic: with high probability , the FR statistic differs from its mean by not more than , where C is a function of N and d.
1.2. Organization
This paper is organized as follows. In Section 2, we first introduce the HP-divergence and the FR multivariate test statistic. We then present the bias and variance rates of the FR-based estimator of HP-divergence followed by the concentration bounds and the minimax MSE convergence rate. Section 3 provides simulations that validate the theory. All proofs and relevant lemmas are given in the Appendix A, Appendix B, Appendix C, Appendix D and Appendix E.
Throughout the paper, we denote expectation by and variance by abbreviation . Bold face type indicates random variables. In this paper, when we say number of samples we mean number of observations.
2. The Henze–Penrose Divergence Measure
Consider parameters and . We focus on estimating the HP-divergence measure between distributions and with domain defined by
It can be verified that this measure is bounded between 0 and 1 and, if , then . In contrast with some other divergences such as the Kullback–Liebler [34] and Rényi divergences [35], the HP-divergence is symmetrical, i.e., . By invoking relation (3) in [8],
where
one can rewrite in the alternative form:
Throughout the paper, we refer to as the HP-integral. The HP-divergence measure belongs to the class of -divergences [36]. For the special case , the divergence (2) becomes the symmetric -divergence and is similar to the Rukhin f-divergence. See [37,38].
2.1. The Multivariate Runs Test Statistic
The MST is a graph of minimum weight among all graphs that span n vertices. The MST has many applications including pattern recognition [39], clustering [40], nonparametric regression [41], and testing of randomness [42]. In this section, we focus on the FR multivariate two sample test statistic constructed from the MST.
Assume that sample realizations from and , denoted by and , respectively, are available. Construct an MST spanning the samples from both and and color the edges in the MST that connect dichotomous samples green and color the remaining edges black. The FR test statistic is the number of green edges in the MST. Note that the test assumes a unique MST, therefore all inter point distances between data points must be distinct. We recall the following theorem from [7,8]:
Theorem 1.
As and such that and ,
In the next section, we obtain bounds on the MSE convergence rates of the FR approximation for HP-divergence between densities that belong to , the class of Hölder continuous functions with Lipschitz constant K and smoothness parameter [32]:
Definition 1
(Hölder class). Let be a compact space. The Hölder class , with η-Hölder parameter, of functions with the -norm, consists of the functions g that satisfy
where is the Taylor polynomial (multinomial) of g of order k expanded about the point and is defined as the greatest integer strictly less than η.
In what follows, we will use both notations and for the FR statistic over the combined samples.
2.2. Convergence Rates
In this subsection, we obtain the mean convergence rate bounds for general non-uniform Lebesgue densities and belonging to the Hölder class . Since the expectation of can be closely approximated by the sum of the expectation of the FR statistic constructed on a dense partition of , is a quasi-additive functional in mean. The family of bounds (A16) in Appendix B enables us to achieve the minimax convergence rate for the mean under the Hölder class assumption with smoothness parameter , :
Theorem 2
(Convergence Rate of the Mean). Let , and be the FR statistic for samples drawn from Hölder continuous and bounded density functions and in . Then, for ,
This bound holds over the class of Lebesgue densities , . Note that this assumption can be relaxed to and that is Lebesgue densities and belong to the Strong Hölder class with the same Hölder parameter and different constants and , respectively.
The following variance bound uses the Efron–Stein inequality [43]. Note that in Theorem 3 we do not impose any strict assumptions. We only assume that the density functions are absolutely continuous and bounded with support on the unit cube . Appendix C contains the proof.
Theorem 3.
The variance of the HP-integral estimator based on the FR statistic, is bounded by
where the constant depends only on d.
By combining Theorems 2 and 3, we obtain the MSE rate of the form . Figure 1 indicates a heat map showing the MSE rate as a function of d and . The heat map shows that the MSE rate of the FR test statistic-based estimator given in (3) is small for large sample size N.

Figure 1.
Heat map of the theoretical MSE rate of the FR estimator of the HP-divergence based on Theorems 2 and 3 as a function of dimension and sample size when . Note the color transition (MSE) as sample size increases for high dimension. For fixed sample size N, the MSE rate degrades in higher dimensions.
2.3. Proof Sketch of Theorem 2
In this subsection, we first establish subadditivity and superadditivity properties of the FR statistic, which will be employed to derive the MSE convergence rate bound. This will establish that the mean of the FR test statistic is a quasi-additive functional:
Theorem 4.
Let be the number of edges that link nodes from differently labeled samples and in . Partition into equal volume subcubes such that and are the number of samples from and , respectively, that fall into the partition . Then, there exists a constant such that
Here, is the number of dichotomous edges in partition . Conversely, for the same conditions as above on partitions , there exists a constant such that
The inequalities (7) and (8) are inspired by corresponding inequalities in [30,31]. The full proof is given in Appendix A. The key result in the proof is the inequality:
where indicates the number of all edges of the MST which intersect two different partitions.
Furthermore, we adapt the theory developed in [17,30] to derive the MSE convergence rate of the FR statistic-based estimator by defining a dual MST and dual FR statistic, denoted by and respectively (see Figure 2):
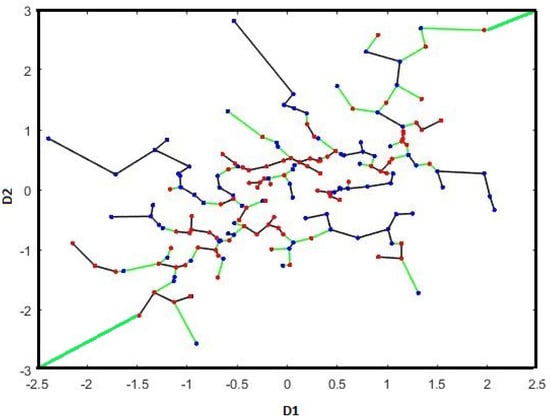
Figure 2.
The dual MST spanning the merged set (blue points) and (red points) drawn from two Gaussian distributions. The dual FR statistic () is the number of edges in the (contains nodes in ) that connect samples from different color nodes and corners (denoted in green). Black edges are the non-dichotomous edges in the .
Definition 2
(Dual MST, MST and dual FR statistic ). Let be the set of corner points of the subsection for . Then, we define as the boundary MST graph of partition [17], which contains and points falling inside the section and those corner points in which minimize total MST length. Notice it is allowed to connect the MSTs in and through points strictly contained in and and corner points are taken into account under condition of minimizing total MST length. Another word, the dual MST can connect the points in by direct edges to pair to another point in or the corner the corner points (we assume that all corner points are connected) in order to minimize the total length. To clarify this, assume that there are two points in , then the dual MST consists of the two edges connecting these points to the corner if they are closed to a corner point; otherwise, dual MST consists of an edge connecting one to another. Furthermore, we define as the number of edges in an graph connecting nodes from different samples and number of edges connecting to the corner points. Note that the edges connected to the corner nodes (regardless of the type of points) are always counted in dual FR test statistic .
In Appendix B, we show that the dual FR test statistic is a quasi-additive functional in mean and . This property holds true since and graphs can only be different in the edges connected to the corner nodes, and in we take all of the edges between these nodes and corner nodes into account.
To prove Theorem 2, we partition into subcubes. Then, by applying Theorem 4 and the dual MST, we derive the bias rate in terms of partition parameter l (see (A16) in Theorem A1). See Appendix B and Appendix E for details. According to (A16), for , and , the slowest rates as a function of l are and . Therefore, we obtain an l-independent bound by letting l be a function of that minimizes the maximum of these rates i.e.,
The full proof of the bound in (2) is given in Appendix B.
2.4. Concentration Bounds
Another main contribution of our work in this part is to provide an exponential inequality convergence bound derived for the FR estimator of the HP-divergence. The error of this estimator can be decomposed into a bias term and a variance-like term via the triangle inequality:
The bias bound was given in Theorem 2. Therefore, we focus on an exponential concentration bound for the variance-like term. One application of concentration bounds is to employ these bounds to compare confidence intervals on the HP-divergence measure in terms of the FR estimator. In [44,45], the authors provided an exponential inequality convergence bound for an estimator of Rény divergence for a smooth Hölder class of densities on the d-dimensional unite cube . We show that if and are the set of m and n points drawn from any two distributions and , respectively, the FR criteria is tightly concentrated. Namely, we establish that, with high probability, is within
of its expected value, where is the solution of the following convex optimization problem:
where and
Note that, under the assumption , becomes a constant depending only on by , where c is a constant. This is inferred from Theorems 5 and 6 below as . See Appendix D, specifically Lemmas A8–A12 for more detail. Indeed, we first show the concentration around the median. A median is by definition any real number that satisfies the inequalities and . To derive the concentration results, the properties of growth bounds and smoothness for , given in Appendix D, are exploited.
Theorem 5
(Concentration around the median). Let be a median of which implies that . Recall from (9) then we have
where .
Theorem 6
(Concentration of around the mean). Let be the FR statistic. Then,
Here, and the explicit form for is given by (10) when .
See Appendix D for full proofs of Theorems 5 and 6. Here, we sketch the proofs. The proof of the concentration inequality for , Theorem 6, requires involving the median , where , inside the probability term by using
To prove the expressions for the concentration around the median, Theorem 5, we first consider the uniform partitions of , with edges parallel to the coordinate axes having edge lengths and volumes . Then, by applying the Markov inequality, we show that with at least probability , where , the FR statistic is subadditive with threshold. Afterward, owing to the induction method [17], the growth bound can be derived with at least probability . The growth bound explains that with high probability there exists a constant depending on and h, , such that . Applying the law of total probability and semi-isoperimetric inequality (A108) in Lemma A11 gives us (A35). By considering the solution to convex optimization problem (9), i.e., and optimal the claimed results (11) and (12) are derived. The only constraint here is that is lower bounded by a function of .
Next, we provide a bound for the variance-like term with high probability at least . According to the previous results, we expect that this bound depends on , d, m and n. The proof is short and is given in Appendix D.
Theorem 7
(Variance-like bound for ). Let be the FR statistic. With at least probability , we have
or, equivalently,
where depends on , and d is given in (10) when .
3. Numerical Experiments
3.1. Simulation Study
In this section, we apply the FR statistic estimate of the HP-divergence to both simulated and real data sets. We present results of a simulation study that evaluates the proposed bound on the MSE. We numerically validate the theory stated in Section 2.2 and Section 2.4 using multiple simulations. In the first set of simulations, we consider two multivariate Normal random vectors , and perform three experiments , to analyze the FR test statistic-based estimator performance as the sample sizes m, n increase. For the three dimensions , we generate samples from two normal distributions with identity covariance and shifted means: , and , and , when , and , respectively. For all of the following experiments, the sample sizes for each class are equal ().
We vary up to 800. From Figure 3, we deduce that, when the sample size increases, the MSE decreases such that for higher dimensions the rate is slower. Furthermore, we compare the experiments with the theory in Figure 3. Our theory generally matches the experimental results. However, the MSE for the experiments tends to decrease to zero faster than the theoretical bound. Since the Gaussian distribution has a smooth density, this suggests that a tighter bound on the MSE may be possible by imposing stricter assumptions on the density smoothness as in [12].

Figure 3.
Comparison of the bound on the MSE theory and experiments for standard Gaussian random vectors versus sample size from 100 trials.
In our next simulation, we compare three bivariate cases: first, we generate samples from a standard Normal distribution. Second, we consider a distinct smooth class of distributions i.e., binomial Gamma density with standard parameters and dependency coefficient . Third, we generate samples from Standard t-student distributions. Our goal in this experiment is to compare the MSE of the HP-divergence estimator between two identical distributions, , when is one of the Gamma, Normal, and t-student density function. In Figure 4, we observe that the MSE decreases as N increases for all three distributions.
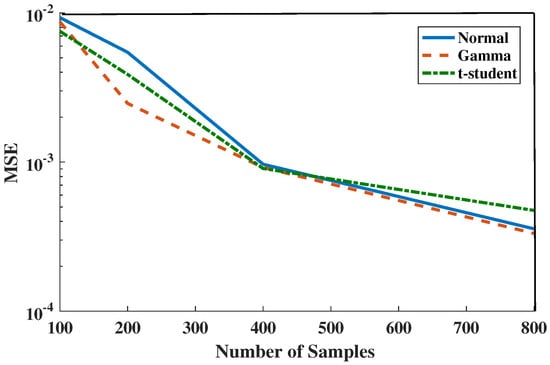
Figure 4.
Comparison of experimentally predicted MSE of the FR-statistic as a function of sample size in various distributions Standard Normal, Gamma () and Standard t-Student.
3.2. Real Datasets
We now show the results of applying the FR test statistic to estimate the HP-divergence using three different real datasets [46]:
- Human Activity Recognition (HAR), Wearable Computing, Classification of Body Postures and Movements (PUC-Rio): This dataset contains five classes (sitting-down, standing-up, standing, walking, and sitting) collected on eight hours of activities of four healthy subjects.
- Skin Segmentation dataset (SKIN): The skin dataset is collected by randomly sampling B,G,R values from face images of various age groups (young, middle, and old), race groups (white, black, and asian), and genders obtained from the FERET and PAL databases [47].
- Sensorless Drive Diagnosis (ENGIN) dataset: In this dataset, features are extracted from electric current drive signals. The drive has intact and defective components. The dataset contains 11 different classes with different conditions. Each condition has been measured several times under 12 different operating conditions, e.g., different speeds, load moments, and load forces.
We focus on two classes from each of the HAR, SKIN, and ENGIN datasets, specifically, for HAR dataset two classes “sitting” and “standing” and for SKIN dataset the classes “Skin” and “Non-skin” are considered. In the ENGIN dataset, the drive has intact and defective components, which results in 11 different classes with different conditions. We choose conditions 1 and 2.
In the first experiment, we computed the HP-divergence using KDE plug-in estimator and then the MSE for the FR test statistic estimator is derived as the sample size increases. We used 95% confidence interval as the error bars. We observe in Figure 5 that the estimated HP-divergence ranges in , which is one of the HP-divergence properties [8]. Interestingly, when N increases the HP-divergence tends to 1 for all HAR, SKIN, and ENGIN datasets. Note that in this set of experiments we have repeated the experiments on independent parts of the datasets to obtain the error bars. Figure 6 shows that the MSE expectedly decreases as the sample size grows for all three datasets. Here, we have used the KDE plug-in estimator [12], implemented on the all available samples, to determine the true HP-divergence. Furthermore, according to Figure 6, the FR test statistic-based estimator suggests that the Bayes error rate is larger for the SKIN dataset compared to the HAR and ENGIN datasets.
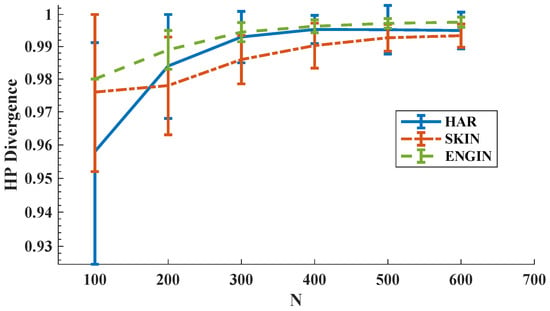
Figure 5.
HP-divergence vs. sample size for three real datasets HAR, SKIN, and ENGIN.

Figure 6.
The empirical MSE vs. sample size. The empirical MSE of the FR estimator for all three datasets HAR, SKIN, and ENGIN decreases for larger sample size N.
In our next experiment, we add the first six features (dimensions) in order to our datasets and evaluate the FR test statistic’s performance as the HP-divergence estimator. Surprisingly, the estimated HP-divergence doesn’t change for the HAR sample; however, big changes are observed for the SKIN and ENGIN samples (see Figure 7).

Figure 7.
HP-divergence vs. dimension for three datasets HAR, SKIN, and ENGIN.
Finally, we apply the concentration bounds on the FR test statistic (i.e., Theorems 6 and 7) and compute theoretical implicit variance-like bound for the FR criteria with error for the real datasets ENGIN, HAR, and SKIN. Since datasets ENGIN, HAR, and SKIN have the equal total sample size and different dimensions , respectively; here, we first intend to compare the concentration bound (13) on the FR statistic in terms of dimension d when . For real datasets ENGIN, HAR, and SKIN, we obtain
where , respectively, and is a constant not dependent on d. One observes that as the dimension decreases the interval becomes significantly tighter. However, this could not be generally correct and computing bound (13) precisely requires the knowledge of distributions and unknown constants. In Table 1, we compute the standard variance-like bound by applying the percentiles technique and observe that the bound threshold is not monotonic in terms of dimension d. Table 1 shows the FR test statistic, HP-divergence estimate (denoted by , , respectively), and standard variance-like interval for the FR statistic using the three real datasets HAR, SKIN, and ENGIN.

Table 1.
, , m, and n are the FR test statistic, HP-divergence estimates using , and sample sizes for two classes, respectively.
4. Conclusions
We derived a bound on the MSE convergence rate for the Friedman–Rafsky estimator of the Henze–Penrose divergence assuming the densities are sufficiently smooth. We employed a partitioning strategy to derive the bias rate which depends on the number of partitions, the sample size , the Hölder smoothness parameter , and the dimension d. However, by using the optimal partition number, we derived the MSE convergence rate only in terms of , , and d. We validated our proposed MSE convergence rate using simulations and illustrated the approach for the meta-learning problem of estimating the HP-divergence for three real-world data sets. We also provided concentration bounds around the median and mean of the estimator. These bounds explicitly provide the rate that the FR statistic approaches its median/mean with high probability, not only as a function of the number of samples, m, n, but also in terms of the dimension of the space d. By using these results, we explored the asymptotic behavior of a variance-like rate in terms of m, n, and d.
Author Contributions
Conceptualization, S.Y.S., M.N. and A.O.H.; methodology, S.Y.S. and M.N.; software, S.Y.S. and M.N.; validation, S.Y.S., M.N., K.R.M. and A.O.H.; formal analysis, S.Y.S., M.N. and K.R.M.; investigation, S.Y.S. and M.N.; resources, S.Y.S. and M.N.; data curation, M.N.; writing—original draft preparation, S.Y.S.; writing—review and editing, M.N., K.R.M. and A.O.H.; supervision, A.O.H.; project administration, A.O.H.; funding acquisition, A.O.H.
Funding
The work presented in this paper was partially supported by ARO grant W911NF-15-1-0479 and DOE grants DE-NA0002534 and DE-NA0003921.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Abbreviations
| HP | Henze-Penrose |
| BER | Bayes error rate |
| MST | Minimal Spanning Tree |
| FR | Friedman-Rafsky |
| MSE | Mean squared error |
Appendix A. Proof of Theorem 4
In this section, we prove the subadditivity and superadditivity for the mean of FR test statistic. For this, first we need to illustrate the following lemma.
Lemma A1.
Let be a uniform partition of into subcubes with edges parallel to the coordinate axes having edge lengths and volumes . Let be the set of edges of MST graph between and with cardinality , then for defined as the sum of for all , , we have , or more explicitly
where is the Hölder smoothness parameter and
Here, and in what follows, denote the length of the shortest spanning tree on , namely
where the minimum is over all spanning trees T of the vertex set . Using the subadditivity relation for in [17], with the uniform partition of into subcubes with edges parallel to the coordinate axes having edge lengths and volumes , we have
where C is constant. Denote D the set of all edges of that intersect two different subcubes and with cardinality . Let be the length of i-th edge in set D. We can write
also we know that
Note that using the result from ([31], Proposition 3), for some constants and , we have
To aim toward the goal (7), we partition into subcubes of side . Recalling Lemma 2.1 in [48], we therefore have the set inclusion:
where D is defined as in Lemma A1. Let and be the number of sample and respectively falling into the partition , such that and . Introduce sets A and B as
Since set B has fewer edges than set A, thus (A5) implies that the difference set of B and A contains at most edges, where is the number of edges in D. On the other word,
The number of edge linked nodes from different samples in set A is bounded by the number of edge linked nodes from different samples in set B plus :
Here, stands with the number edge linked nodes from different samples in partition , M. Next, we address the reader to Lemma A1, where it has been shown that there is a constant c such that . This concludes the claimed assertion (7). Now, to accomplish the proof, the lower bound term in (8) is obtained with similar methodology and the set inclusion:
This completes the proof.
Appendix B. Proof of Theorem 2
As many of continuous subadditive functionals on , in the case of the FR statistic, there exists a dual superadditive functional based on dual MST, , proposed in Definition 2. Note that, in the MST* graph, the degrees of the corner points are bounded by , where it only depends on dimension d, and is the bound for degree of every node in MST graph. The following properties hold true for dual FR test statistic, :
Lemma A2.
Given samples and , the following inequalities hold true:
- (i)
- For constant which depends on d:
- (ii)
- (Subadditivity on and Superadditivity) Partition into subcubes such that , be the number of sample and respectively falling into the partition with dual . Then, we havewhere c is a constant.
(i) Consider the nodes connected to the corner points. Since and can only be different in the edges connected to these nodes, and in we take all of the edges between these nodes and corner nodes into account, so we obviously have the second relation in (A8). In addition, for the first inequality in (A8), it is enough to say that the total number of edges connected to the corner nodes is upper bounded by .
(ii) Let be the set of edges of the graph which intersect two different partitions. Since MST and are only different in edges of points connected to the corners and edges crossing different partitions. Therefore, . By eliminating one edge in set D in the worse scenario we would face two possibilities: either the corresponding node is connected to the corner which is counted anyways or any other point in MST graph which wouldn’t change the FR test statistic. This implies the following subadditivity relation:
Further from Lemma A1, we know that there is a constant c such that . Hence, the first inequality in (A9) is obtained. Next, consider which represents the total number of edges from both samples only connected to the all corners points in graph. Therefore, one can easily claim:
In addition, we know that where stands with the largest possible degree of any vertex. One can write
The following list of Lemmas A3, A4 and A6 are inspired from [49] and are required to prove Theorem A1. See Appendix E for their proofs.
Lemma A3.
Let be a density function with support and belong to the Hölder class , , stated in Definition 1. In addition, assume that is a η-Hölder smooth function, such that its absolute value is bounded from above by a constant. Define the quantized density function with parameter l and constants as
Let and . Then,
Lemma A4.
Denote the degree of vertex in the over set with the n number of vertices. For given function , one obtains
where, for constant ,
Lemma A5.
Assume that, for given k, is a bounded function belong to . Let be a symmetric, smooth, jointly measurable function, such that, given k, for almost every , is measurable with a Lebesgue point of the function . Assume that the first derivative P is bounded. For each k, let be an independent d-dimensional variable with common density function . Set and . Then,
Lemma A6.
Consider the notations and assumptions in Lemma A5. Then,
Here, denotes the MST graph over nice and finite set and η is the smoothness Hölder parameter. Note that is given as before in Lemma A4 (A13).
Theorem A1.
Assume denotes the FR test statistic and densities and belong to the Hölder class , . Then, the rate for the bias of the estimator for is of the form:
The proof and a more explicit form for the bound (A16) are given in Appendix E.
Now, we are at the position to prove the assertion in (5). Without loss of generality, assume that . In the range and , we select l as a function of to be the sequence increasing in which minimizes the maximum of these rates:
Appendix C. Proof of Theorems 3
To bound the variance, we will apply one of the first concentration inequalities which was proved by Efron and Stein [43] and further was improved by Steele [18].
Lemma A7
(The Efron–Stein Inequality). Let be a random vector on the space . Let be the copy of random vector . Then, if , we have
Consider two set of nodes , and for . Without loss of generality, assume that . Then, consider the virtual random points with the same distribution as , and define . Now, for using the Efron–Stein inequality on set , we involve another independent copy of as , and define , then becomes where is independent copy of . Next, define the function , which means that we discard the random samples , and find the previously defined function on the nodes , and for , and multiply by some coefficient to normalize it. Then, according to the Efron–Stein inequality, we have
Now, we can divide the RHS as
The first summand becomes
which can also be upper bounded as follows:
For deriving an upper bound on the second line in (A19), we should observe how much changing a point’s position modifies the amount of . We consider two steps of changing ’s position: we first remove it from the graph, and then add it to the new position. Removing it would change at most by because has a degree of at most , and edges will be removed from the MST graph, and edges will be added to it. Similarly, adding to the new position will affect at most by . Thus, we have
and we can also similarly reason that
Therefore, totally we would have
Furthermore, the second summand in (A18) becomes
where . Since, in , the point is a copy of virtual random point , therefore this point doesn’t change the FR test statistic . In addition, following the above arguments, we have
Hence, we can bound the variance as below:
Combining all results with the fact that concludes the proof.
Appendix D. Proof of Theorems 5–7
We will need the following prominent results for the proofs.
Lemma A8.
For , let be the function , where c is a constant. Then, for , we have
Note that, in the case , the above claimed inequality becomes trivial.
The subadditivity property for FR test statistic in Lemma A8, as well as Euclidean functionals, leads to several non-trivial consequences. The growth bound was first explored by Rhee (1993b) [50], and as is illustrated in [17,27] has a wide range of applications. In this paper, we investigate the probabilistic growth bound for . This observation will lead us to our main goal in this appendix that is providing the proof of Theorem 6. For what follows, we will use notation for the expression .
Lemma A9
(Growth bounds for ). Let be the FR test statistic. Then, for given non-negative ϵ, such that , with at least probability , , we have
Here, depending only on ϵ and h.
The complexity of ’s behavior and the need to pursue the proof encouraged us to explore the smoothness condition for . In fact, this is where both subadditivity and superadditivity for the FR statistic are used together and become more important.
Lemma A10
(Smoothness for ). Given observations of
where and , where , denote as before, the number of edges of which connect a point of to a point of . Then, for given integer , for all , where , we have
where .
Remark: Using Lemma A10, we can imply the continuty property, i.e., for all observations and , with at least probability , one obtains
for given , , . Here, denotes symmetric difference of observations and .
The path to approach the assertions (11) and (12) proceeds via semi-isoperimentic inequality for the involving the Hamming distance.
Lemma A11
(Semi-Isoperimetry). Let μ be a measure on ; denotes the product measure on space . In addition, let denotes a median of . Set
Following the notations in [17], and and . Then,
Now, we continue by providing the proof of Theorem 5. Recall (A25) and denote
In addition, for given integer h, define events , by
where is a constant. By virtue of smoothness property, Lemma A10, for , we know and . On the other hand, we have
Moreover, . Therefore, we can write
Thus, we obtain
Note that . Now, we easily claim that
Thus,
On the other word, calling and in Lemma A11, we get
Furthermore, denote event
Then, we have
Define set , so
Since
and
Consequently, from (A30), one can write
The last inequality implies by owing to (A29) and . For , we have
or equivalently this holds true when . Furthermore, for , we have
therefore is less than and equal to
By virtue of Lemma A11, finally we obtain
Similarly, we can derive the same bound on , so we obtain
where
We will analyze (A35) together with Theorem 6. The next lemma will be employed in Theorem 6’s proof.
Lemma A12
(Deviation of the Mean and Median). Consider as a median of . Then, for and given , we have
where is a constant depending on ϵ, h, m, and n by
where C is a constant and
We conclude this part by pursuing our primary intension which has been the Theorem 6’s proof. Observe from Theorem 5, (11) that
Note that the last bound is derived by (11). The rest of the proof is as the following: When , we use
Therefore, it turns out that
In other words, there exist constants depending on , , and h such that
where .
To verify the behavior of bound (A40) in terms of , observe (A35) first; it is not hard to see that this function is decreasing in . However, the function
increases in . Therefore, one can not immediately infer that the bound in (12) is monotonic with respect to . For fixed , d, and h, the first and second derivatives of the bound (12) with respect to are quite complicated functions. Thus, deriving an explicit optimal solution for the minimization problem with the objective function (12) is not feasible. However, in the sequel, we discuss that under conditions when t is not much larger than , this bound becomes convex with respect to . Set
where is given in (10) and
By taking the derivative with respect to , we have
where
where . The second derivative with respect to after simplification is given as
where . The first term in (A44) and are non-negative, so is convex if the second term in the second line of (A44) is non-negative. We know that , when , we can parameterize by setting it equal to , where . After simplification, is convex if
This is implied if
such that . One can easily check that, as , then (A46) tends to . This term can be negligible unless we have t that is much larger than with the threshold depending on d. Here, by setting , a rough threshold depending on d, is proposed. Therefore, minimizing (A35) and (A40) with respect to when optimal is a convex optimization problem. Denote the solution of the convex optimization problem (9). By plugging optimal h () and ( in (A35) and (A40), we derive (11) and (12), respectively.
In this appendix, we also analyze the bound numerically. By simulation, we observed that lower h i.e., is the optimal value experimentally. Indeed, this can be verified by Theorem 11’s proof. We address the reader to Lemma A8 in Appendix D and Appendix E where, as h increases, the lower bound for the probability increases too. In other words, for fixed and d, the lowest h implies the maximum bound in (A92). For this, we set in our experiments. We vary the dimension d and sample size in relatively large and small ranges. In Table A1, we solve (9) for various values of d and . We also compute the lower bound for i.e., per experiment. In Table A1, we observe that as we have higher dimension the optimal value equals the lower bound , but this is not true for smaller dimensions with even relatively large sample size.

Table A1.
d, N, are dimension, total sample size , and optimal for the bound in (12). The column represents approximately the lower bound for which is our constraint in the minimization problem and our assumption in Theorems 5 and 6. Here, we set .
Table A1.
d, N, are dimension, total sample size , and optimal for the bound in (12). The column represents approximately the lower bound for which is our constraint in the minimization problem and our assumption in Theorems 5 and 6. Here, we set .
| Concentration Bound (11) | |||||
|---|---|---|---|---|---|
| Optimal (11) | |||||
| 2 | 0.3439 | ||||
| 4 | 168,070 | 0.0895 | |||
| 5 | 550 | 0.9929 | |||
| 6 | 0.1637 | ||||
| 8 | 1200 | 0.7176 | |||
| 10 | 3500 | 0.4795 | |||
| 15 | 0.9042 | ||||
To validate our proposed bound in (12), we again set and for we ran experiments with sample sizes , respectively. Then, we solved the minimization problem to derive optimal bound for t in the range . Note that we chose this range to have a non-trivial bound for all three curves; otherwise, the bounds partly become one. Figure A1 shows that when t increases in the given range, the optimal curves approach zero.
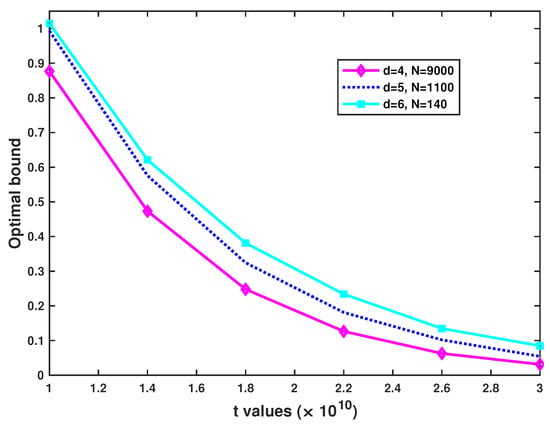
Figure A1.
Optimal bound for (12), when versus . The bound decreases as t grows.
To prove the Theorem 7 in the concentration of , Theorem 6, let
this implies and the proofs are completed.
Appendix E. Additional Proofs
Lemma A3: Let be a density function with support and belong to the Hölder class , , expressed in Definition 1. In addition, assume that is a -Hölder smooth function, such that its absolute value is bounded from above by some constants c. Define the quantized density function with parameter l and constants as
and and . Then,
Proof.
By the mean value theorem, there exist points such that
Using the fact that and is a bounded function, we have
Here, L is the Hölder constant. As , a sub-cube with edge length , then and . This concludes the proof. □
Lemma A4: Let denote the degree of vertex in the over set with the n number of vertices. For given function , one yields
where for constant ,
Proof.
Recall notations in Lemma A3 and
Therefore, by substituting , defined in (A47), into g with considering its error, we have
Here, represents as before in Lemma A3, so the RHS of (A51) becomes
Now, note that is the expectation of over the nodes in , which is equal to , where . Consequently, we have
This gives the assertion (A49). □
Lemma A5: Assume that, for given k, is a bounded function belong to . Let be a symmetric, smooth, jointly measurable function, such that, given k, for almost every , is measurable with a Lebesgue point of the function . Assume that the first derivative P is bounded. For each k, let be independent d-dimensional variable with common density function . Set and . Then,
Proof.
Let . For any positive K, we can obtain:
where is the volume of space which equals . Note that the above inequality appears because and . The first order Taylor series expansion of around is
Then, by recalling the Hölder class, we have
Hence, the RHS of (A55) becomes
The expression in (A54) can be obtained by choice of K. □
Lemma A6: Consider the notations and assumptions in Lemma A5. Then,
Here, denotes the MST graph over nice and finite set and is the smoothness Hölder parameter. Note that is given as before in (A50).
Proof.
Following notations in [49], let denote the degree of vertex in the graph. Moreover, let be a Lebesgue point of with . In addition, let be the point process . Now, by virtue of (A55) in Lemma A5, we can write
On the other hand, it can be seen that
Recalling (A57),
By virtue of Lemma A4, (A49) can be substituted into expression (A59) to obtain (A56). □
Theorem A1: Assume denotes the FR test statistic as before. Then, the rate for the bias of the estimator for , is of the form:
Here, is the Holder smoothness parameter. A more explicit form for the bound on the RHS is given in (A61) below:
Proof.
Assume and be Poisson variables with mean m and n, respectively, one independent of another and of and . Let also and be the Poisson processes and . Set . Applying Lemma 1, and (12) cf. [49], we can write
Here, denotes the largest possible degree of any vertex of the MST graph in . Moreover, by the matter of Poisson variable fact and using Stirling approximation [51], we have
Similarly, . Therefore, by (A62), one yields
Therefore,
Hence, it will suffice to obtain the rate of convergence of in the RHS of (A65). For this, let , denote the number of Poisson process samples and with the FR statistic , falling into partitions with FR statistic . Then, by virtue of Lemma 4, we can write
Note that the Binomial RVs , are independent with marginal distributions , , where , are non-negative constants satisfying, and . Therefore,
Let us first compute the internal expectation given , . For this reason, given , , let be independent variables with common densities , . Moreover, let be an independent Poisson variable with mean . Denote a non-homogeneous Poisson of rate . Let be the non-Poisson point process . Assign a mark from the set to each points of . Let be the sets of points marked 1 with each probability and let be the set points with mark 2. Note that owing to the marking theorem [52], and are independent Poisson processes with the same distribution as and , respectively. Considering as FR statistic over nodes in we have
Again using Lemma 1 and analogous arguments in [49] along with the fact that , we have
Here,
By owing to Lemma A6, we obtain
where
The expression in (A67) equals
Because of Jensen inequality for concave function:
In addition, similarly since , we have
and, for , one yields
Next, we state the following lemma (Lemma 1 from [30,31]), which will be used in the sequel:
Lemma A13.
Let be a continuously differential function of which is convex and monotone decreasing over . Set . Then, for any , we have
Next, continuing the proof of (A60), we attend to find an upper bound for
In order to pursue this aim, in Lemma A13, consider and , therefore as the function is decreasing and convex, one can write
Using the Hölder inequality implies the following inequality:
As random variables , are independent, and because of , , we can claim that the RHS of (A74) becomes less than and equal to
where
Going back to (A66), we have
Finally, owing to and , when , we have
Passing to Definition 2, , and Lemma A2, a similar discussion as above, consider the Poisson processes samples and the FR statistic under the union of samples, denoted by , and superadditivity of dual , we have
the last line is derived from Lemma A2, (ii), inequality (A8). Owing to the Lemma A6, (A69), and (A70), one obtains
Furthermore, by using the Jenson’s inequality, we get
Therefore, since , we can write
Consequently, the RHS of (A79) becomes greater than or equal to
Finally, since and , we have
By definition of the dual and (i) in Lemma A2,
we can imply
Recall , then we obtain
In addition, we have
This implies
Note that the above inequality is derived from (A80) and . Furthermore,
The last line holds because of . Going back to (A73), we can give an upper bound for the RHS of above inequality as
Note that we have assumed and by using Hölder inequality we write
As result, we have
As a consequence, owing to (A85), for , , which implies , we can derive (A61). Thus, the proof can be concluded by giving the summarized bound in (A60). □
Lemma A8: For , let be the function . Then, for , we have
Note that in case the above claimed inequality is trivial.
Proof.
Consider the cardinality of the set of all edges of which intersect two different subcubes and , . Using the Markov inequality, we can write
where . Since , therefore for and :
In addition, if , is a partition of into congruent subcubes of edge length , then
This implies
By subadditivity (A6), we can write
and this along with (A94) establishes (A92). □
Lemma A9: (Growth bounds for ) Let be the FR statistic. Then, for given non-negative , such that , with at least probability , , we have
Here, depending only on , h. Note that, for , the claim is trivial.
Proof.
Without loss of generality, consider the unit cube . For given h, if , is a partition of into congruent subcubes of edge length , then, by Lemma A8, we have
We apply the induction methodology on and . Set which is finite according to assumption. Moreover, set and . Therefore, it is sufficient to show that for all with at least probability
Alternatively, as for the induction hypothesis, we assume the stronger bound
holds whenever and with at least probability . Note that , and , both depend on , h. Hence,
which implies . In addition, we know that ; therefore, the induction hypothesis holds particularly and . Now, consider the partition of ; therefore, for all , we have and and thus, by induction hypothesis, one yields with at least probability
Set the event and stands with the event . From (A96) and since ’s are partitions, which implies
we thus obtain
Equivalently,
In fact, in this stage, we want to show that
Since , therefore it is sufficient to derive that . Indeed, for given , we have hence . Furthermore, we know and since this implies and consequently
or
This implies the fact that for
Now, let and using Hölder inequality gives
Next, we just need to show that in (A100) is less than or equal to , which is equivalent to show
We know that and , so it is sufficient to get
choose t as , then , so (A101) becomes
Note that the function has a minimum at which implies (A101) and subsequently (A95). Hence, the proof is completed. □
Lemma A10: (Smoothness for ) Given observations of
such that and , where , denote as before, the number of edges of which connect a point of to a point of . Then, for integer , for all , , where , we have
where . For the case , this holds trivially.
Proof.
We begin with removing the edges which contain a vertex in and in minimal spanning tree on . Now, since each vertex has bounded degree, say , we can generate a subgraph in which has at most components. Next, choose one vertex from each component and form the minimal spanning tree on these vertices, assuming all of them can be considered in FR test statistic, we can write
with probability at least , where is as in Lemma A9. Note that this expression is obtained from Lemma A9. In this stage, it remains to show that with at least probability
which, again by using the method before, with at least probability , one derives
Letting implies (A105). Thus,
Hence, the smoothness is given with at least probability as in the statement of Lemma A10. □
Lemma A11: (Semi-Isoperimetry) Let be a measure on ; denotes the product measure on space . In addition, let denotes a median of . Set
Then,
Proof.
Lemma A12: (Deviation of the Mean and Median) Consider as a median of . Then, for given , and such that for , , we have
where stands with a form depends on , h, m, n as
where C is a constant.
Proof.
Following the analogous arguments in [17,53], we have
where . The inequality in (A113) is implied from Theorem 5. Hence, the proof is completed. □
References
- Xuan, G.; Chia, P.; Wu, M. Bhattacharyya distance feature selection. In Proceedings of the 13th International Conference on Pattern Recognition, Vienna, Austria, 25–29 August 1996; Volume 2, pp. 195–199. [Google Scholar]
- Hamza, A.; Krim, H. Image registration and segmentation by maximizing the Jensen-Renyi divergence. In Energy Minimization Methods in Computer Vision and Pattern Recognition. EMMCVPR 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 147–163. [Google Scholar]
- Hild, K.E.; Erdogmus, D.; Principe, J. Blind source separation using Renyi’s mutual information. IEEE Signal Process. Lett. 2001, 8, 174–176. [Google Scholar] [CrossRef]
- Basseville, M. Divergence measures for statistical data processing–An annotated bibliography. Signal Process. 2013, 93, 621–633. [Google Scholar] [CrossRef]
- Battacharyya, A. On a measure of divergence between two multinomial populations. Sankhy ā Indian J. Stat. 1946, 7, 401–406. [Google Scholar]
- Lin, J. Divergence Measures Based on the Shannon Entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Berisha, V.; Hero, A. Empirical non-parametric estimation of the Fisher information. IEEE Signal Process. Lett. 2015, 22, 988–992. [Google Scholar] [CrossRef]
- Berisha, V.; Wisler, A.; Hero, A.; Spanias, A. Empirically estimable classification bounds based on a nonparametric divergence measure. IEEE Trans. Signal Process. 2016, 64, 580–591. [Google Scholar] [CrossRef]
- Moon, K.; Hero, A. Multivariate f-divergence estimation with confidence. In Proceedings of the Advances in Neural Information Processing Systems 27 (NIPS 2014), Montreal, QC, Canada, 8–13 December 2014; pp. 2420–2428. [Google Scholar]
- Moon, K.; Hero, A. Ensemble estimation of multivariate f-divergence. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Honolulu, HI, USA, 29 June–4 July 2014; pp. 356–360. [Google Scholar]
- Moon, K.; Sricharan, K.; Greenewald, K.; Hero, A. Improving convergence of divergence functional ensemble estimators. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Barcelona, Spain, 10–15 July 2016; pp. 1133–1137. [Google Scholar]
- Moon, K.; Sricharan, K.; Greenewald, K.; Hero, A. Nonparametric ensemble estimation of distributional functionals. arXiv 2016, arXiv:1601.06884v2. [Google Scholar]
- Noshad, M.; Moon, K.; Yasaei Sekeh, S.; Hero, A. Direct Estimation of Information Divergence Using Nearest Neighbor Ratios. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017. [Google Scholar]
- Yasaei Sekeh, S.; Oselio, B.; Hero, A. A Dimension-Independent discriminant between distributions. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018. [Google Scholar]
- Noshad, M.; Hero, A. Rate-optimal Meta Learning of Classification Error. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018. [Google Scholar]
- Wisler, A.; Berisha, V.; Wei, D.; Ramamurthy, K.; Spanias, A. Empirically-estimable multi-class classification bounds. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016. [Google Scholar]
- Yukich, J. Probability Theory of Classical Euclidean Optimization; Lecture Notes in Mathematics; Springer: Berlin, Germany, 1998; Volume 1675. [Google Scholar]
- Steele, J. An Efron–Stein inequality for nonsymmetric statistics. Ann. Stat. 1986, 14, 753–758. [Google Scholar] [CrossRef]
- Aldous, D.; Steele, J.M. Asymptotic for Euclidean minimal spanning trees on random points. Probab. Theory Relat. Fields 1992, 92, 247–258. [Google Scholar] [CrossRef]
- Ma, B.; Hero, A.; Gorman, J.; Michel, O. Image registration with minimal spanning tree algorithm. In Proceedings of the IEEE International Conference on Image Processing, Vancouver, BC, Canada, 10–13 September 2000; pp. 481–484. [Google Scholar]
- Neemuchwala, H.; Hero, A.; Carson, P. Image registration using entropy measures and entropic graphs. Eur. J. Signal Process. 2005, 85, 277–296. [Google Scholar] [CrossRef]
- Hero, A.; Ma, B.; Michel , O.J.; Gorman, J. Applications of entropic spanning graphs. IEEE Signal Process. Mag. 2002, 19, 85–95. [Google Scholar] [CrossRef]
- Hero, A.; Michel, O. Estimation of Rényi information divergence via pruned minimal spanning trees. In Proceedings of the IEEE Workshop on Higher Order Statistics, Caesarea, Isreal, 16 June 1999. [Google Scholar]
- Smirnov, N. On the estimation of the discrepancy between empirical curves of distribution for two independent samples. Bull. Mosc. Univ. 1939, 2, 3–6. [Google Scholar]
- Wald, A.; Wolfowitz, J. On a test whether two samples are from the same population. Ann. Math. Stat. 1940, 11, 147–162. [Google Scholar] [CrossRef]
- Gibbons, J. Nonparametric Statistical Inference; McGraw-Hill: New York, NY, USA, 1971. [Google Scholar]
- Singh, S.; Póczos, B. Probability Theory and Combinatorial Optimization; CBMF-NSF Regional Conference in Applied Mathematics; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 1997; Volume 69. [Google Scholar]
- Redmond, C.; Yukich, J. Limit theorems and rates of convergence for Euclidean functionals. Ann. Appl. Probab. 1994, 4, 1057–1073. [Google Scholar] [CrossRef]
- Redmond, C.; Yukich, J. Asymptotics for Euclidean functionals with power weighted edges. Stoch. Process. Their Appl. 1996, 6, 289–304. [Google Scholar] [CrossRef][Green Version]
- Hero, A.; Costa, J.; Ma, B. Convergence Rates of Minimal Graphs with Random Vertices. Available online: https://pdfs.semanticscholar.org/7817/308a5065aa0dd44098319eb66f81d4fa7a14.pdf (accessed on 18 November 2019).
- Hero, A.; Costa, J.; Ma, B. Asymptotic Relations between Minimal Graphs and Alpha-Entropy; Tech. Rep.; Communication and Signal Processing Laboratory (CSPL), Department EECS, University of Michigan: Ann Arbor, MI, USA, 2003. [Google Scholar]
- Lorentz, G. Approximation of Functions; Holt, Rinehart and Winston: New York, NY, USA, 1996. [Google Scholar]
- Talagrand, M. Concentration of measure and isoperimetric inequalities in product spaces. Publications Mathématiques de i’I. H. E. S. 1995, 81, 73–205. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, USA, 20 June–30 July 1961; pp. 547–561. [Google Scholar]
- Ali, S.; Silvey, S.D. A general class of coefficients of divergence of one distribution from another. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 28, 131–142. [Google Scholar] [CrossRef]
- Cha, S. Comprehensive survey on distance/similarity measures between probability density functions. Int. J. Math. Models Methods Appl. Sci. 2007, 1, 300–307. [Google Scholar]
- Rukhin, A. Optimal estimator for the mixture parameter by the method of moments and information affinity. In Proceedings of the 12th Prague Conference on Information Theory, Prague, Czech Republic, 29 August–2 September 1994; pp. 214–219. [Google Scholar]
- Toussaint, G. The relative neighborhood graph of a finite planar set. Pattern Recognit. 1980, 12, 261–268. [Google Scholar] [CrossRef]
- Zahn, C. Graph-theoretical methods for detecting and describing Gestalt clusters. IEEE Trans. Comput. 1971, 100, 68–86. [Google Scholar] [CrossRef]
- Banks, D.; Lavine, M.; Newton, H. The minimal spanning tree for nonparametric regression and structure discovery. In Computing Science and Statistics, Proceedings of the 24th Symposium on the Interface; Joseph Newton, H., Ed.; Interface Foundation of North America: Fairfax Station, FA, USA, 1992; pp. 370–374. [Google Scholar]
- Hoffman, R.; Jain, A. A test of randomness based on the minimal spanning tree. Pattern Recognit. Lett. 1983, 1, 175–180. [Google Scholar] [CrossRef]
- Efron, B.; Stein, C. The jackknife estimate of variance. Ann. Stat. 1981, 9, 586–596. [Google Scholar] [CrossRef]
- Singh, S.; Póczos, B. Generalized exponential concentration inequality for Rényi divergence estimation. In Proceedings of the 31st International Conference on Machine Learning (ICML-14), Bejing, China, 22–24 June 2014; pp. 333–341. [Google Scholar]
- Singh, S.; Póczos, B. Exponential concentration of a density functional estimator. In Proceedings of the 27th International Conference on Neural Information Processing Systems (NIPS 2014), Montreal, QC, Canada, 8–13 December 2014; pp. 3032–3040. [Google Scholar]
- Lichman, M. UCI Machine Learning Repository. 2013. Available online: https://www.re3data.org/repository/r3d100010960 (accessed on 18 November 2019).
- Bhatt, R.B.; Sharma, G.; Dhall, A.; Chaudhury, S. Efficient skin region segmentation using low complexity fuzzy decision tree model. In Proceedings of the IEEE-INDICON, Ahmedabad, India, 16–18 December 2009; pp. 1–4. [Google Scholar]
- Steele, J.; Shepp, L.; Eddy, W. On the number of leaves of a euclidean minimal spanning tree. J. Appl. Prob. 1987, 24, 809–826. [Google Scholar] [CrossRef][Green Version]
- Henze, N.; Penrose, M. On the multivarite runs test. Ann. Stat. 1999, 27, 290–298. [Google Scholar]
- Rhee, W. A matching problem and subadditive Euclidean funetionals. Ann. Appl. Prob. 1993, 3, 794–801. [Google Scholar] [CrossRef]
- Whittaker, E.; Watson, G. A Course in Modern Analysis, 4th ed.; Cambridge University Press: New York, NY, USA, 1996. [Google Scholar]
- Kingman, J. Poisson Processes; Oxford Univ. Press: Oxford, UK, 1993. [Google Scholar]
- Pál, D.; Póczos, B.; Szapesvári, C. Estimation of Renyi entropy andmutual information based on generalized nearest-neighbor graphs. In Proceedings of the 23th International Conference on Neural Information Processing Systems (NIPS 2010), Vancouver, BC, Canada, 6–9 December 2010. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).