Performance Comparison between Fountain Codes-Based Secure MIMO Protocols with and without Using Non-Orthogonal Multiple Access
Abstract
:1. Introduction
1.1. Related Work
1.2. Motivations and Contributions
- In contrast to [48,49,50,54], in the proposed protocol, all the nodes including the source, the destination and eavesdropper are equipped with multiple antennas and use the MRC or SC technique to combine the received signals. Although the source nodes in [51,56] have multi-antenna and employ TAS to transmit the encoded packets, the destinations in [51,56] are only single-antenna nodes. Moreover, References [52,53,55] considered single-input-single-output (SISO) relaying protocols where all the terminals are deployed with a single antenna.
- In contrast to [48,49,50,51,52,53,54,55,56], the source in the proposed protocol can employ NOMA to transmit two packets to the destination in each time slot to reduce the number of time slots used. Moreover, reducing the number of time slots also means reducing the delay time and transmit power, which are important metrics of the wireless systems.
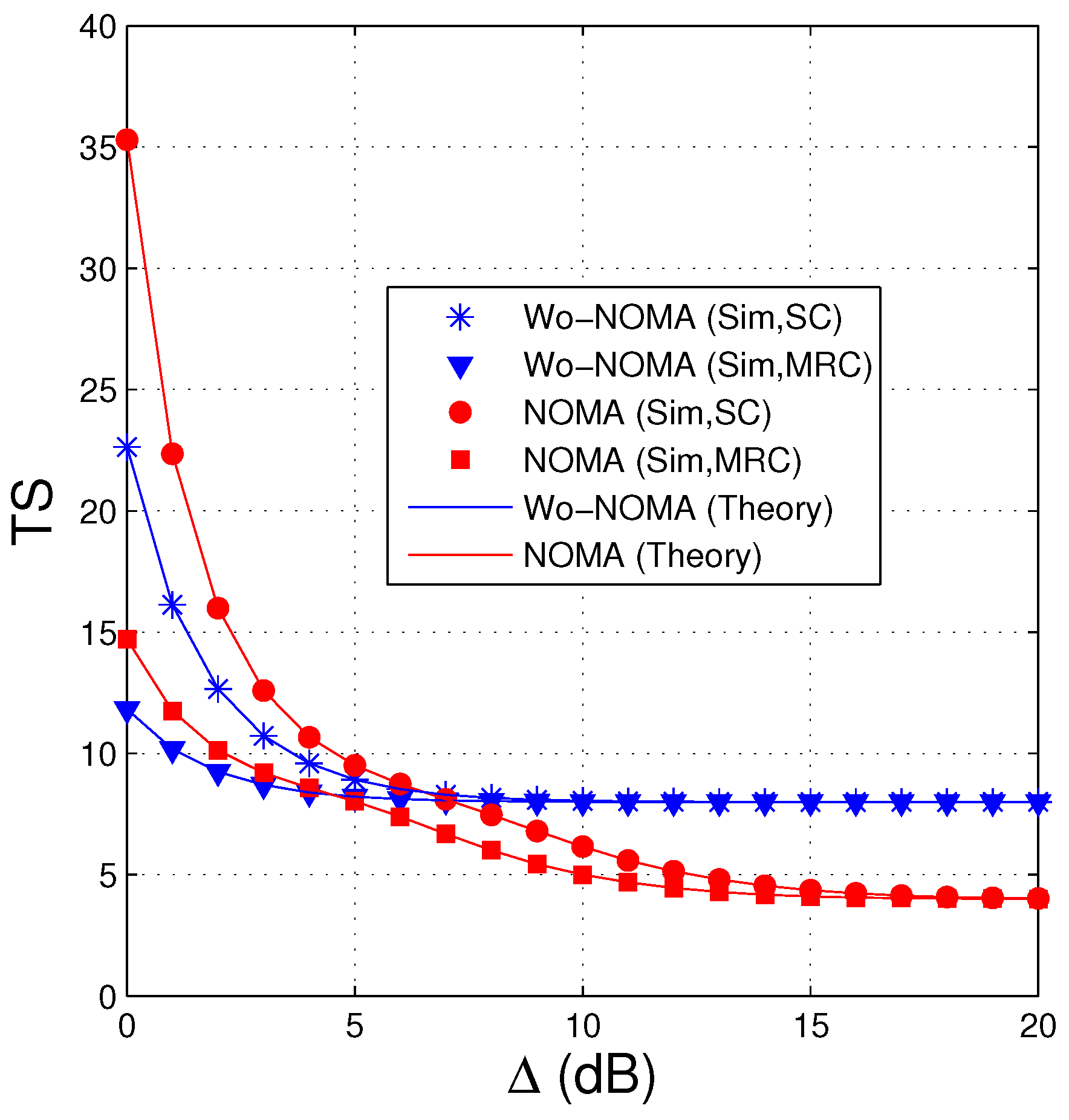
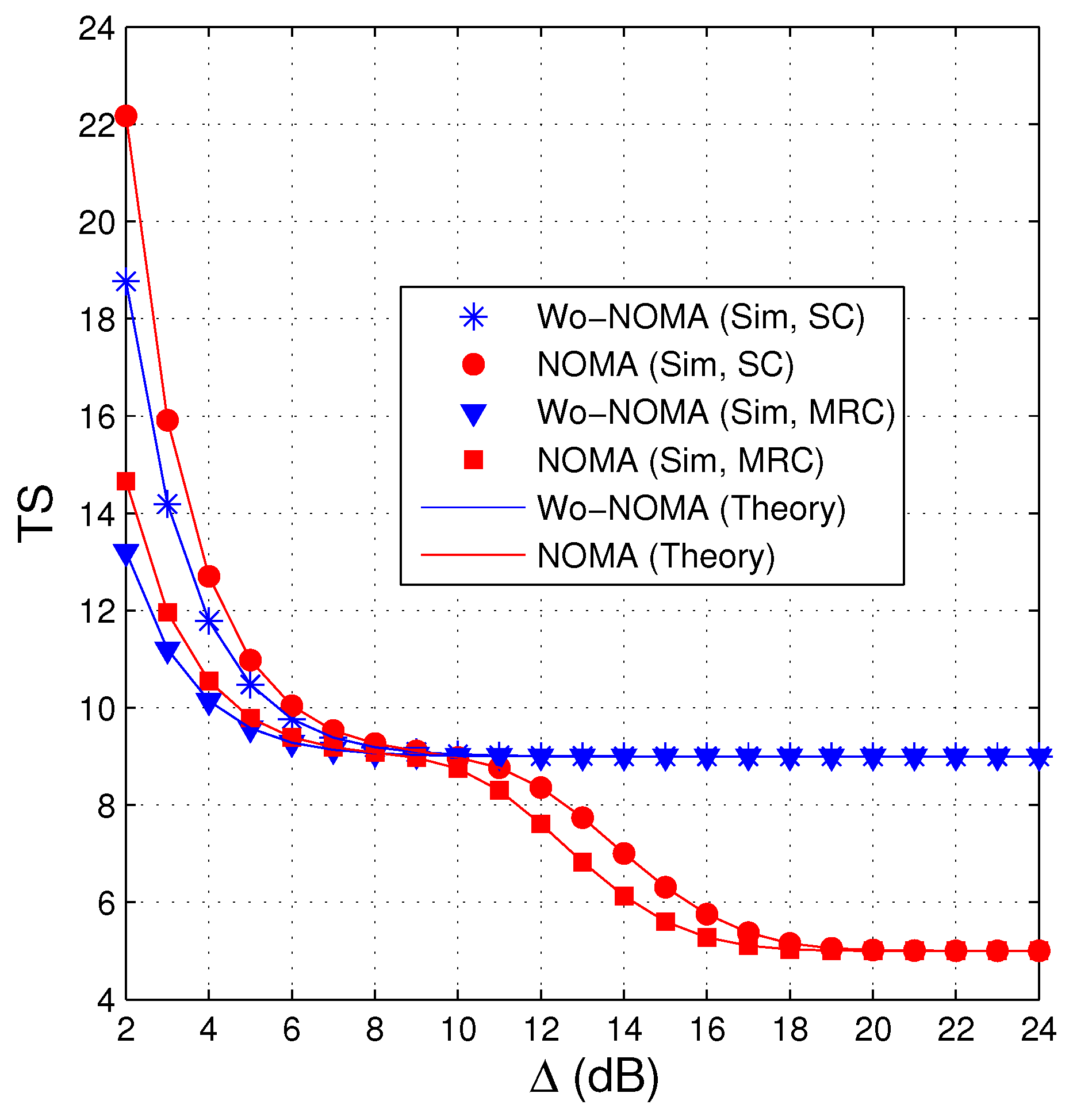
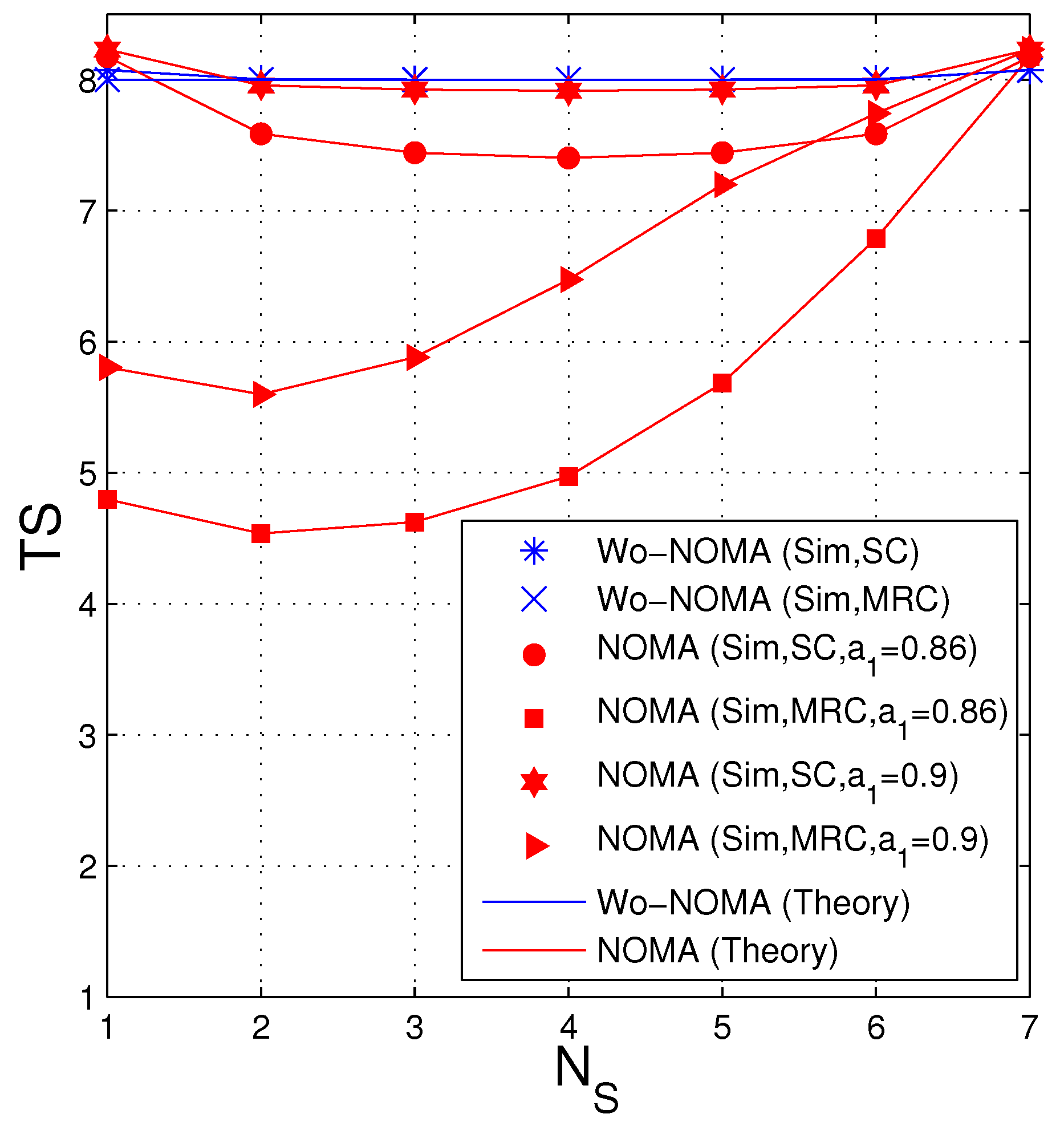
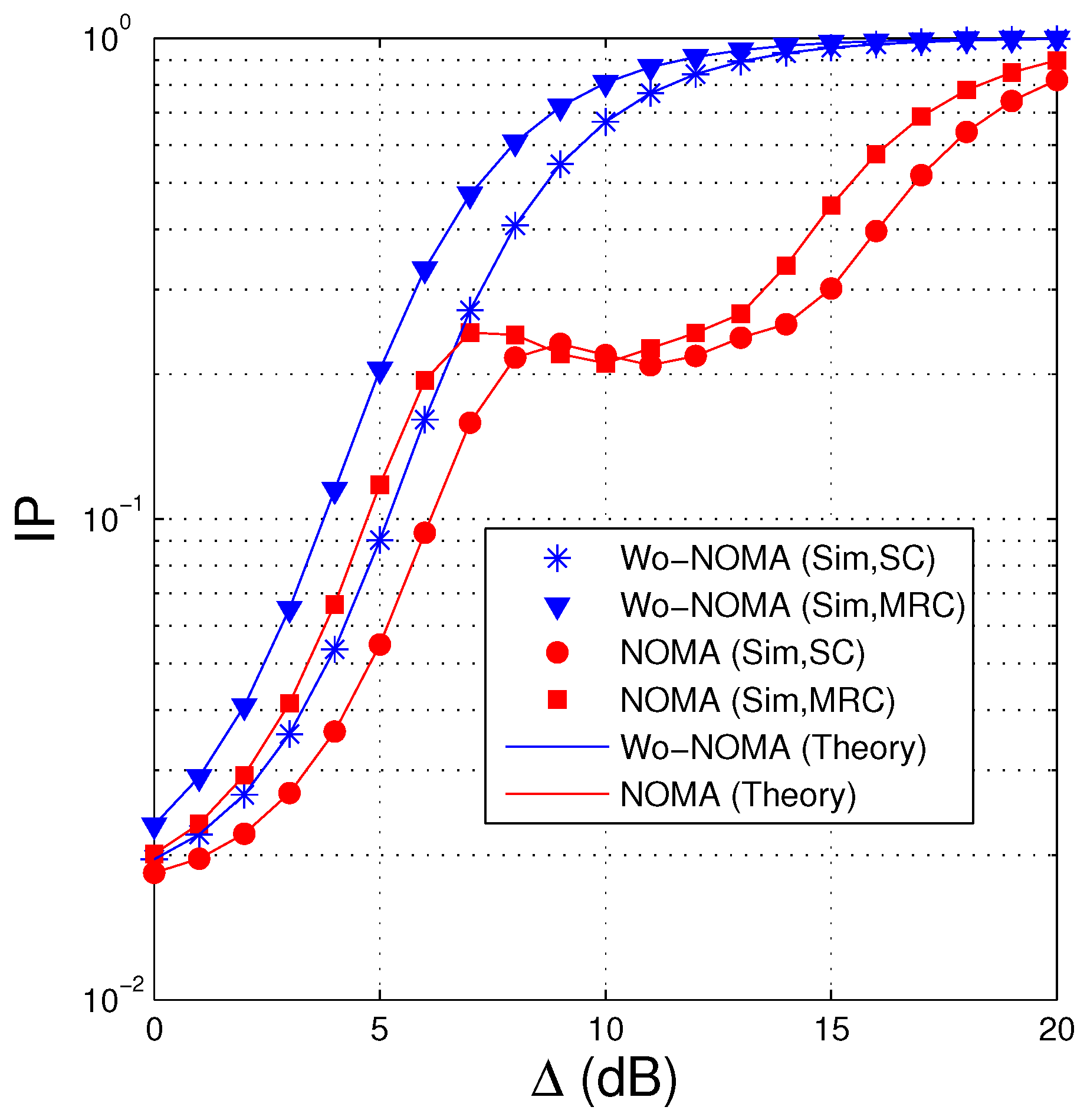
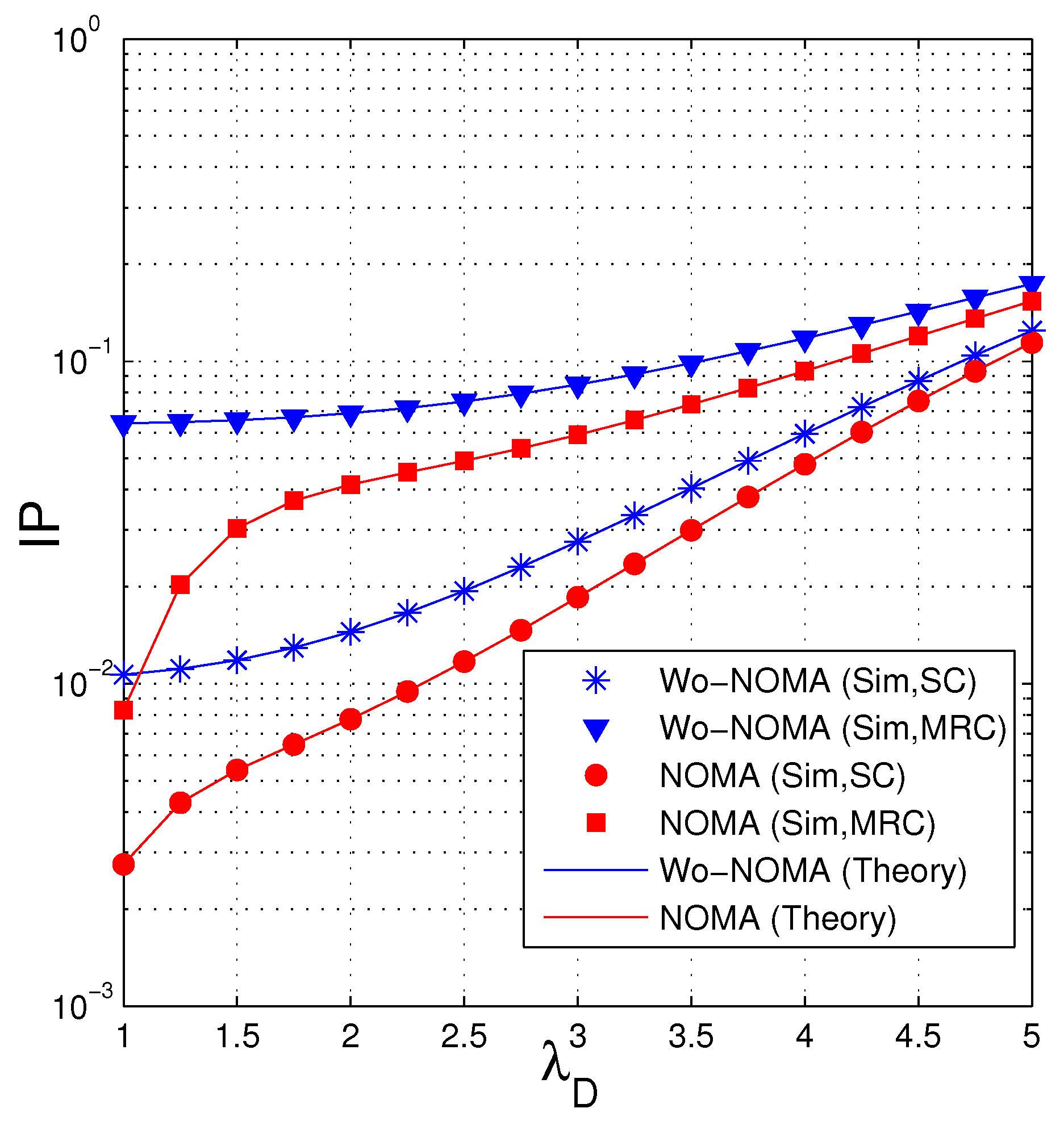
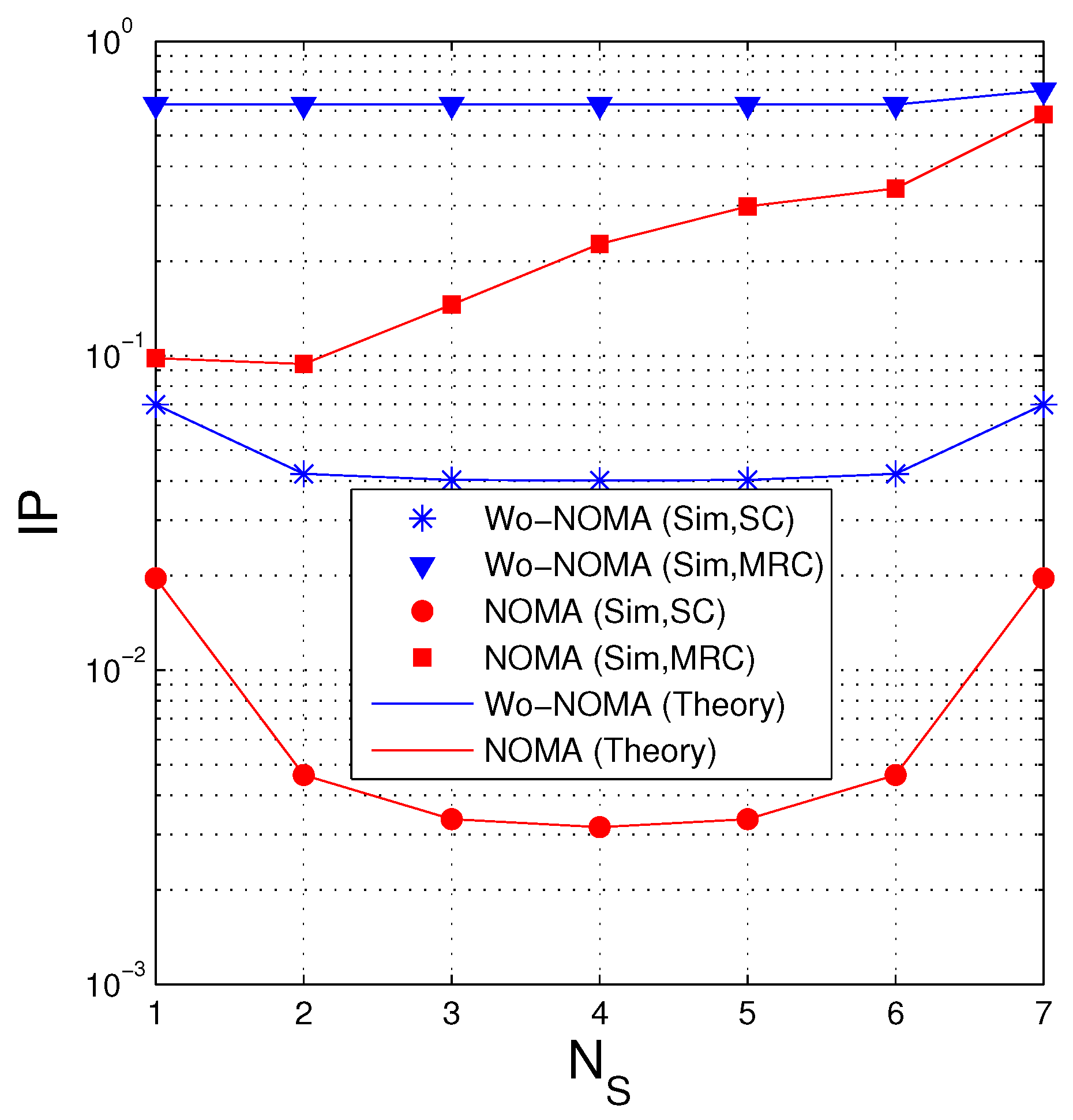
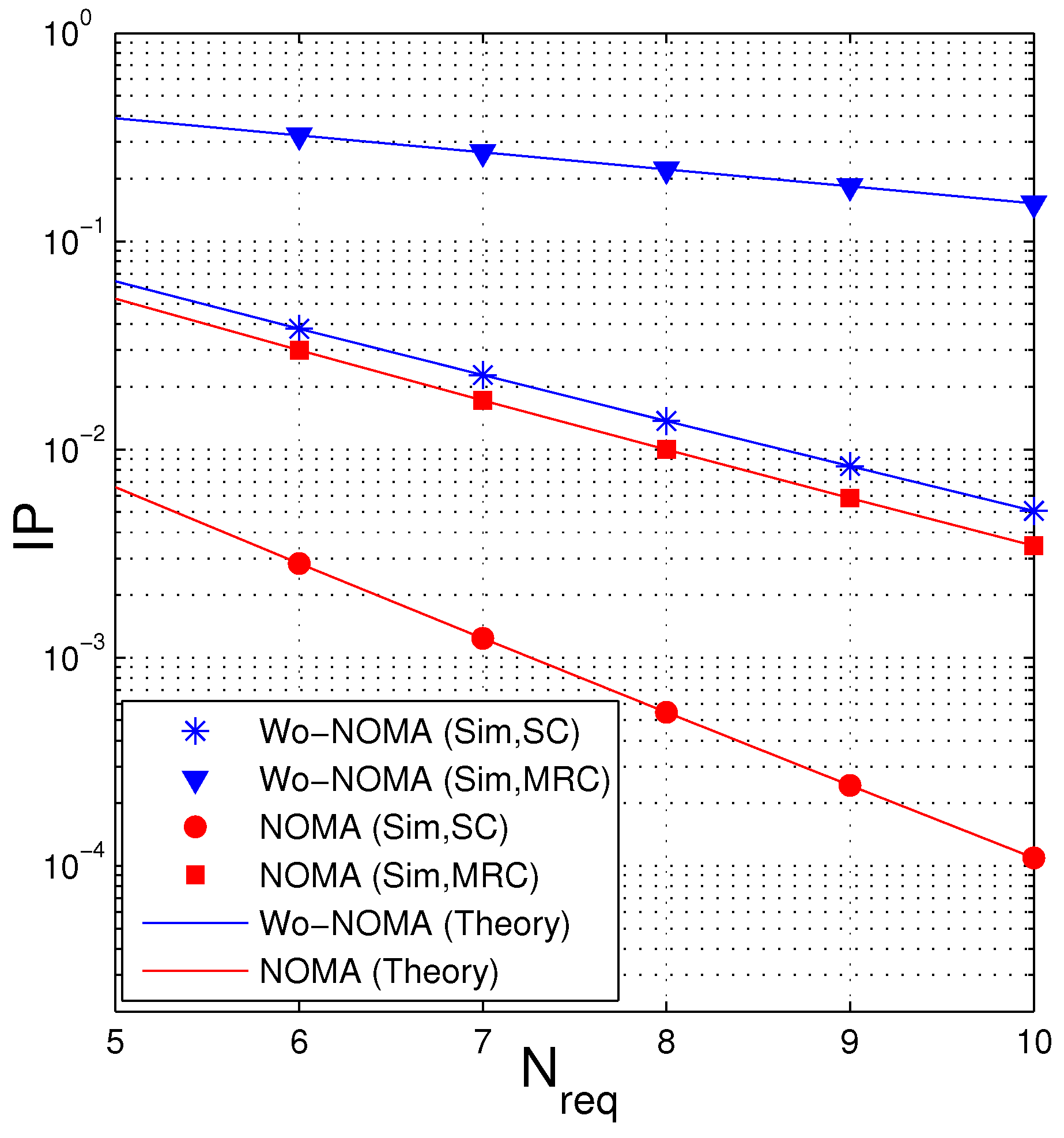
- We compare the performance of the proposed protocols in two cases where the source uses NOMA (named NOMA) and does not use NOMA (named Wo-NOMA), in terms of average number of time slots (TS) and intercept probability (IP). The results shows that the FCs based secure transmission protocol exploiting NOMA can decrease both TS and IP, as compared with the corresponding protocol without using NOMA.
- We derive exact expressions of TS and IP for the NOMA and Wo-NOMA protocols over Rayleigh fading channels and realize computer simulations to verify.
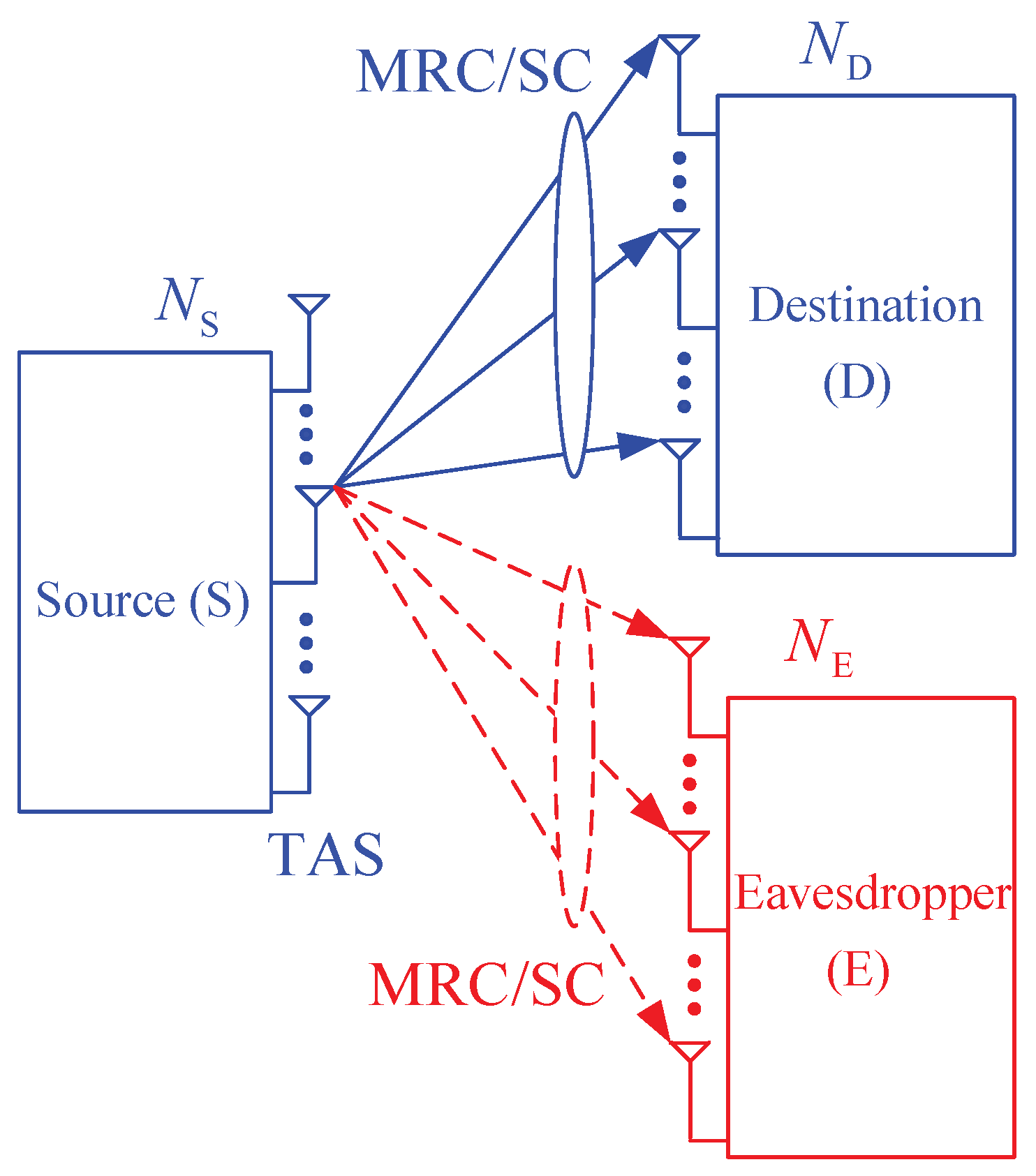
2. System Model
2.1. Without Using NOMA (Wo-NOMA)
2.2. Using NOMA
3. Performance Analysis
3.1. Derivation of and
- Case 1: The SC combiner is used by D and E
- Case 2: The MRC combiner is used by D and E
3.2. Derivation of and
- Case 1: The SC combiner is used by D and E
- Case 2: The MRC combiner is used by D and E
3.3. Average Number of Time Slots (TS)
3.3.1. Without Using NOMA (Wo-NOMA)
3.3.2. Using NOMA
- Case 1: After time slots, the destination obtains encoded packets, and at the last time slot, it obtains two encoded packets.
- Case 2: After time slots, the destination obtains encoded packets, and at the last time slot, it only obtains one encoded packet.
- Case 3: After time slots, the destination obtains encoded packets, and at the last time slot, it obtains two encoded packets.
3.4. Intercept Probability (IP)
3.4.1. Without Using NOMA (Wo-NOMA)
3.4.2. Using NOMA
4. Simulation Results
4.1. Average Number of Time Slots (TS)
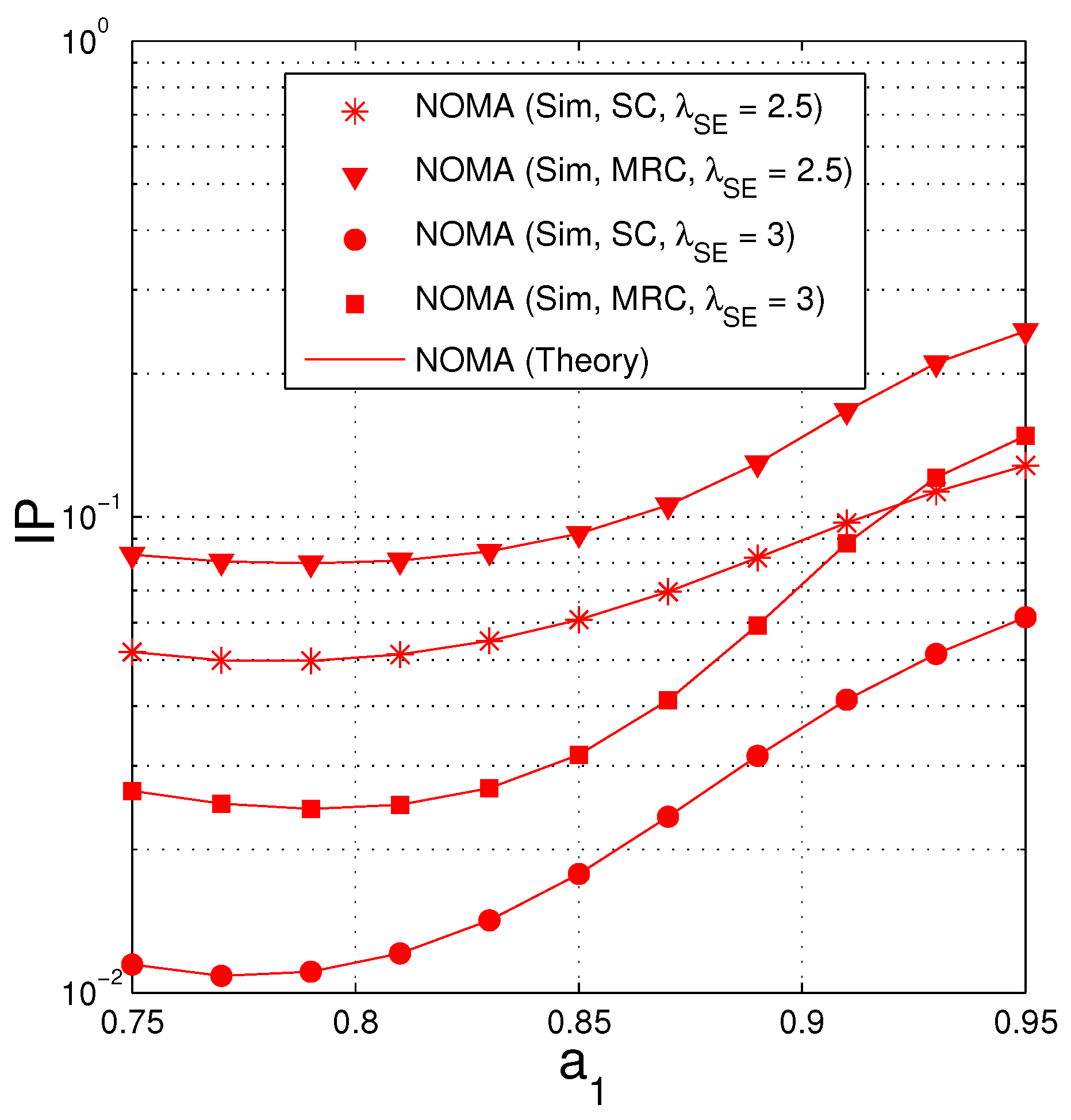
4.2. Intercept Probability (IP)
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wyner, A.D. The Wire-tap Channel. Bell Syst. Tech. J. 1975, 54, 1355–1387. [Google Scholar] [CrossRef]
- Csiszar, I.; Korner, J. Broadcast Channels with Confidential Messages. IEEE Trans. Inf. Theory 1978, 2, 339–348. [Google Scholar] [CrossRef]
- Liu, R.; Maric, I.; Spasojevic, P.; Yates, R.D. Discrete Memoryless Interference and Broadcast Channels with Conffdential Messages: Secrecy Rate Regions. IEEE Trans. Inf. Theory 2008, 2, 2493–2507. [Google Scholar] [CrossRef]
- Gopala, P.K.; Lai, L.; Gamal, H.E. On the Secrecy Capacity of Fading Channels. IEEE Trans. Inf. Theory 2008, 2, 4687–4698. [Google Scholar] [CrossRef]
- Zhang, J.; Duong, T.Q.; Woods, R.; Marshall, A. Securing Wireless Communications of the Internet of Things from the Physical Layer, An Overview. Entropy 2017, 19, 420. [Google Scholar] [CrossRef]
- Li, G.; Sun, C.; Zhang, J.; Jorswieck, E.; Xiao, B.; Hu, A. Physical Layer Key Generation in 5G and Beyond Wireless Communications: Challenges and Opportunities. Entropy 2019, 21, 497. [Google Scholar] [CrossRef]
- Yang, N.; Yeoh, P.L.; Elkashlan, M.; Schober, R.; Collings, I.B. Transmit Antenna Selection for Security Enhancement in MIMO Wiretap Channels. IEEE Trans. Commun. 2013, 61, 144–154. [Google Scholar] [CrossRef]
- Yang, N.; Suraweera, H.A.; Collings, I.B.; Yuen, C. Physical Layer Security of TAS/MRC with Antenna Correlation. IEEE Trans. Inf. Forensics Secur. 2013, 8, 254–259. [Google Scholar] [CrossRef]
- Xiong, J.; Tang, Y.; Ma, D.; Xiao, P.; Wong, K.-K. Secrecy Performance Analysis for TAS-MRC System with Imperfect Feedback. IEEE Trans. Inf. Forensics Secur. 2015, 10, 1617–1629. [Google Scholar] [CrossRef]
- Yang, L.; Hasna, M.O.; Ansari, I.S. Physical Layer Security for TAS/MRC Systems with and without Co-Channel Interference Over η − μ Fading Channels. IEEE Trans. Veh. Technol. 2018, 67, 12421–12426. [Google Scholar] [CrossRef]
- Zhao, H.; Tan, Y.; Pan, G.; Chen, Y.; Yang, N. Secrecy Outage on Transmit Antenna Selection/Maximal Ratio Combining in MIMO Cognitive Radio Networks. IEEE Trans. Veh. Technol. 2016, 65, 10236–10242. [Google Scholar] [CrossRef]
- Li, M.; Huang, Y.; Yin, H.; Wang, Y.; Cai, C. Improving the Security and Spectrum Efficiency in Overlay Cognitive Full-Duplex Wireless Networks. IEEE Access 2019, 7, 68359–68372. [Google Scholar] [CrossRef]
- Pan, G.; Lei, H.; Deng, Y.; Fan, L.; Yang, J.; Chen, Y.; Ding, Z. On Secrecy Performance of MISO SWIPT Systems With TAS and Imperfect CSI. IEEE Commun. 2016, 64, 3831–3843. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Zhang, P.; Wu, Q.; Wang, J. Secrecy Performance of Wireless Powered Communication Networks With Multiple Eavesdroppers and Outdated CSI. IEEE Access 2018, 6, 33774–33788. [Google Scholar] [CrossRef]
- Lei, H.; Zhang, J.; Park, K.H.; Xu, P.; Ansari, I.S.; Pan, G.; Alomair, B.; Alouini, M.S. On Secure NOMA Systems with Transmit Antenna Selection Schemes. IEEE Access 2017, 5, 33774–33788. [Google Scholar] [CrossRef]
- Lei, H.; Zhang, J.; Park, K.H.; Xu, P.; Zhang, Z.; Pan, G.; Alouini, M.S. Secrecy Outage of Max–Min TAS Scheme in MIMO-NOMA Systems. IEEE Trans. Veh. Technol. 2018, 67, 6981–6990. [Google Scholar] [CrossRef]
- Krikidis, I. Opportunistic Relay Selection For Cooperative Networks With Secrecy Constraints. IET Commun. 2010, 4, 1787–1791. [Google Scholar] [CrossRef]
- Zhong, B.; Zhang, Z. Secure Full-Duplex Two-Way Relaying Networks With Optimal Relay Selection. IEEE Commun. Lett. 2017, 21, 1123–1126. [Google Scholar] [CrossRef]
- Kuhestani, A.; Mohammadi, A.; Mohammadi, M. Joint Relay Selection and Power Allocation in Large-Scale MIMO Systems with Untrusted Relays and Passive Eavesdroppers. IEEE Trans. Inf. Forensics Secur. 2018, 13, 341–355. [Google Scholar] [CrossRef]
- Mo, J.; Tao, M.; Liu, Y. Relay Placement for Physical Layer Security: A Secure Connection Perspective. IEEE Commun. Lett. 2012, 16, 878–881. [Google Scholar]
- Yao, J.; Liu, Y. Secrecy Rate Maximization With Outage Constraint in Multihop Relaying Networks. IEEE Commun. Lett. 2018, 22, 304–307. [Google Scholar] [CrossRef]
- Zhao, R.; Lin, H.; He, Y.C.; Chen, D.H.; Huang, Y.; Yang, L. Secrecy Performance of Transmit Antenna Selection for MIMO Relay Systems with Outdated CSI. IEEE Trans. Commun. 2018, 66, 546–559. [Google Scholar] [CrossRef]
- Tang, X.; Cai, Y.; Huang, Y.; Duong, T.Q.; Yang, W.; Yang, W. Secrecy Outage Analysis of Buffer-Aided Cooperative MIMO Relaying Systems. IEEE Trans. Veh. Technol. 2018, 67, 2035–2048. [Google Scholar] [CrossRef]
- Tang, C.; Pan, G.; Li, T. Secrecy Outage Analysis of Underlay Cognitive Radio Unit Over Nakagami-m Fading Channels. IEEE Wirel. Commun. Lett. 2014, 3, 609–612. [Google Scholar] [CrossRef]
- Chakraborty, P.; Prakriya, S. Secrecy Outage Performance of a Cooperative Cognitive Relay Network. IEEE Commun. Lett. 2017, 21, 326–329. [Google Scholar] [CrossRef]
- Tin, P.T.; Hung, D.T.; Tan, N.N.; Duy, T.T.; Voznak, M. Secrecy Performance Enhancement for Underlay Cognitive Radio Networks Employing Cooperative Multi-hop Transmission With and Without Presence of Hardware Impairments. Entropy 2019, 21, 217. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, L.; Tran, T.D.; Elkashlan, M.; Duong, T.Q. Relay Selection for Security Enhancement in Cognitive Relay Networks. IEEE Wirel. Commun. Lett. 2015, 4, 46–49. [Google Scholar] [CrossRef]
- Jia, S.; Zhang, J.; Zhao, H.; Zhang, R. Relay Selection for Improved Security in Cognitive Relay Networks With Jamming. IEEE Wirel. Commun. Lett. 2017, 6, 662–665. [Google Scholar] [CrossRef]
- Sun, C.; Liu, K.; Zheng, D.; Ai, W. Secure Communication for Two-Way Relay Networks with Imperfect CSI. Entropy 2017, 19, 522. [Google Scholar] [CrossRef]
- Chang, S.; Li, J.; Fu, X.; Zhang, L. Energy Harvesting for Physical Layer Security in Cooperative Networks Based on Compressed Sensing. Entropy 2017, 19, 462. [Google Scholar] [CrossRef]
- Kalamkar, S.S.; Banerjee, A. Secure Communication via a Wireless Energy Harvesting Untrusted Relay. IEEE Trans. Veh. Technol. 2017, 66, 2199–2213. [Google Scholar] [CrossRef]
- Yin, C.; Nguyen, H.T.; Kundu, C.; Kaleem, Z.; Emiliano, G.P.; Duong, T.Q. Secure Energy Harvesting Relay Networks with Unreliable Backhaul Connections. IEEE Access 2018, 6, 12074–12084. [Google Scholar] [CrossRef]
- Hoang, T.M.; Duong, T.Q.; Vo, N.S.; Kundu, C. Physical Layer Security in Cooperative Energy Harvesting Networks with a Friendly Jammer. IEEE Wirel. Commun. Lett. 2017, 6, 174–177. [Google Scholar] [CrossRef]
- Zhang, G.; Xu, J.; Wu, Q.; Cui, M.; Li, X.; Lin, F. Wireless Powered Cooperative Jamming for Secure OFDM System. IEEE Trans. Veh. Technol. 2018, 2, 1331–1346. [Google Scholar] [CrossRef]
- Hu, G.; Cai, Y. Analysis and Optimization of Wireless-Powered Cooperative Jamming for Sensor Network Over Nakagami- m Fading Channels. IEEE Commun. Lett. 2019, 23, 926–929. [Google Scholar] [CrossRef]
- Yu, C.; Ko, H.L.; Peng, X.; Xie, W. Secrecy Outage Performance Analysis for Cooperative NOMA Over Nakagami-m Channel. IEEE Access 2019, 7, 79866–79876. [Google Scholar] [CrossRef]
- Wang, Z.; Peng, Z. Secrecy Performance Analysis of Relay Selection in Cooperative NOMA Systems. IEEE Access 2019, 7, 86274–86287. [Google Scholar] [CrossRef]
- Yuan, C.; Tao, X.; Li, N.; Ni, W.; Liu, R.P.; Zhang, P. Analysis on Secrecy Capacity of Cooperative Non-Orthogonal Multiple Access with Proactive Jamming. IEEE Trans. Veh. Technol. 2019, 68, 2682–2696. [Google Scholar] [CrossRef]
- Xiang, Z.; Yang, W.; Pan, G.; Cai, Y.; Song, Y. Physical Layer Security in Cognitive Radio Inspired NOMA Network. IEEE J. Sel. Top. Sig. Process. 2019, 13, 700–714. [Google Scholar] [CrossRef]
- Huynh, T.P.; Son, P.N.; Voznak, M. Secrecy Performance of Underlay Cooperative Cognitive Network Using Non-Orthogonal Multiple Access with Opportunistic Relay Selection. Symmetry 2019, 11, 385. [Google Scholar] [CrossRef]
- Li, B.; Qi, X.; Huang, K.; Fei, Z.; Zhou, F.; Hu, R.Q. Security-Reliability Tradeoff Analysis for Cooperative NOMA in Cognitive Radio Networks. IEEE Trans. Commun. 2018, 67, 83–96. [Google Scholar] [CrossRef]
- MacKay, D. Fountain Codes. IEE Proc. Commun. 2005, 2, 1331–1346. [Google Scholar] [CrossRef]
- Castura, J.; Mao, Y. Rateless Coding over Fading Channels. IEEE Commun. Lett. 2006, 2, 46–48. [Google Scholar] [CrossRef]
- Molisch, A.F.; Mehta, N.B.; Yedidia, J.S.; Zhang, J. Performance of Fountain Codes in Collaborative Relay Networks. IEEE Trans. Wirel. Commun. 2007, 6, 4108–4119. [Google Scholar] [CrossRef]
- Nguyen, H.D.T.; Tran, L.N.; Hong, E.K. On Transmission Efficiency for Wireless Broadcast Using Network Coding and Fountain Codes. IEEE Commun. Lett. 2011, 2, 569–571. [Google Scholar] [CrossRef]
- Duy, T.T.; Kong, H.Y. Secondary Spectrum Access in Cognitive Radio Networks Using Rateless Codes over Rayleigh Fading Channels. Wirel. Pers. Commun. 2014, 2, 963–978. [Google Scholar] [CrossRef]
- Di, X.; Xiong, K.; Fan, P.; Yang, H.C. Simultaneous Wireless Information and Power Transfer in Cooperative Relay Networks With Rateless Codes. IEEE Trans. Veh. Technol. 2017, 66, 2981–2996. [Google Scholar] [CrossRef]
- Niu, H.; Iwai, M.; Sezaki, K.; Sun, L.; Du, Q. Exploiting Fountain Codes for Secure Wireless Delivery. IEEE Commun. Lett. 2014, 2, 777–780. [Google Scholar] [CrossRef]
- Khan, A.S.; Tassi, A.; Chatzigeorgiou, I. Rethinking the Intercept Probability of Random Linear Network Coding. IEEE Commun. Lett. 2015, 19, 1762–1765. [Google Scholar] [CrossRef] [Green Version]
- Du, Q.; Xu, Y.; Li, W.; Song, H. Security Enhancement for Multicast over Internet of Things by Dynamically Constructed Fountain Codes. Wirel. Commun. Mob. Comput. 2018, 2018, 8404219. [Google Scholar] [CrossRef]
- Hung, D.T.; Duy, T.T.; Trinh, D.Q.; Bao, V.N.Q. Secrecy Performance Evaluation of TAS Protocol Exploiting Fountain Codes and Cooperative Jamming under Impact of Hardware Impairments. In Proceedings of the 2018 2nd International Conference on Recent Advances in Signal Processing, Telecommunications & Computing (SigTelCom), Ho Chi Minh City, Vietnam, 29–31 January 2018; pp. 164–169. [Google Scholar]
- Sun, L.; Ren, P.; Du, Q.; Wang, Y. Fountain-coding Aided Strategy for Secure Cooperative Transmission in Industrial Wireless Sensor Networks. IEEE Trans. Ind. Inform. 2016, 2, 291–300. [Google Scholar] [CrossRef]
- Khan, A.S.; Chatzigeorgiou, I. Opportunistic Relaying and Random Linear Network Coding for Secure and Reliable Communication. IEEE Trans. Wirel. Commun. 2018, 17, 223–234. [Google Scholar] [CrossRef]
- Sun, L.; Xu, H. Fountain-Coding-Based Secure Communications Exploiting Outage Prediction and Limited Feedback. IEEE Trans. Veh. Technol. 2019, 68, 740–753. [Google Scholar] [CrossRef]
- Hung, D.T.; Duy, T.T.; Trinh, D.Q. Security-Reliability Analysis of Multi-hop LEACH Protocol with Fountain Codes and Cooperative Jamming. EAI Trans. Ind. Netw. Int. Syst. 2019, 6, 1–7. [Google Scholar] [CrossRef]
- Tin, P.T.; Tan, N.N.; Sang, N.Q.; Duy, T.T.; Phuong, T.T.; Voznak, M. Rateless Codes based Secure Communication Employing Transmit Antenna Selection and Harvest-To-Jam under Joint Effect of Interference and Hardware Impairments. Entropy 2019, 21, 700. [Google Scholar] [CrossRef]
- Papoulis, A.; Pillai, S.U. Probability, Random Variables and Stochastic Processes, 4th ed.; McGraw-Hill Europe: London, UK, 2002. [Google Scholar]
- Qin, D.; Wang, Y.; Zhou, F.; Wong, K.K. Performance Analysis of AF Relaying With Selection Combining in Nakagami-m Fading. IEEE Syst. J. 2019, 13, 2375–2385. [Google Scholar] [CrossRef]
- Amari, S.V.; Misra, R.B. Closed-form Expressions for Distribution of Sum of Exponential Random Variables. IEEE Trans. Reliab. 1997, 46, 519–522. [Google Scholar] [CrossRef]
- Wang, X.; Chen, W.; Cao, Z. A Rateless Coding Based Multi-relay Cooperative Transmission Scheme for Cognitive Radio Networks. In Proceedings of the IEEE Global Telecommunications Conference, Honolulu, HI, USA, 30 November–4 December 2009; pp. 164–169. [Google Scholar]
| System Parameters | Values |
|---|---|
| 0 (dB)–24 (dB) | |
| , | 1–7 |
| 2–4 | |
| 1–5 | |
| 2.5–5 | |
| 5–10 | |
| 1 and 1.5 | |
| , | , |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
The Hung, D.; Trung Duy, T.; Tran, P.T.; Quoc Trinh, D.; Hanh, T. Performance Comparison between Fountain Codes-Based Secure MIMO Protocols with and without Using Non-Orthogonal Multiple Access. Entropy 2019, 21, 982. https://doi.org/10.3390/e21100982
The Hung D, Trung Duy T, Tran PT, Quoc Trinh D, Hanh T. Performance Comparison between Fountain Codes-Based Secure MIMO Protocols with and without Using Non-Orthogonal Multiple Access. Entropy. 2019; 21(10):982. https://doi.org/10.3390/e21100982
Chicago/Turabian StyleThe Hung, Dang, Tran Trung Duy, Phuong T. Tran, Do Quoc Trinh, and Tan Hanh. 2019. "Performance Comparison between Fountain Codes-Based Secure MIMO Protocols with and without Using Non-Orthogonal Multiple Access" Entropy 21, no. 10: 982. https://doi.org/10.3390/e21100982
APA StyleThe Hung, D., Trung Duy, T., Tran, P. T., Quoc Trinh, D., & Hanh, T. (2019). Performance Comparison between Fountain Codes-Based Secure MIMO Protocols with and without Using Non-Orthogonal Multiple Access. Entropy, 21(10), 982. https://doi.org/10.3390/e21100982






