A Nonvolatile Fractional Order Memristor Model and Its Complex Dynamics
Abstract
:1. Introduction
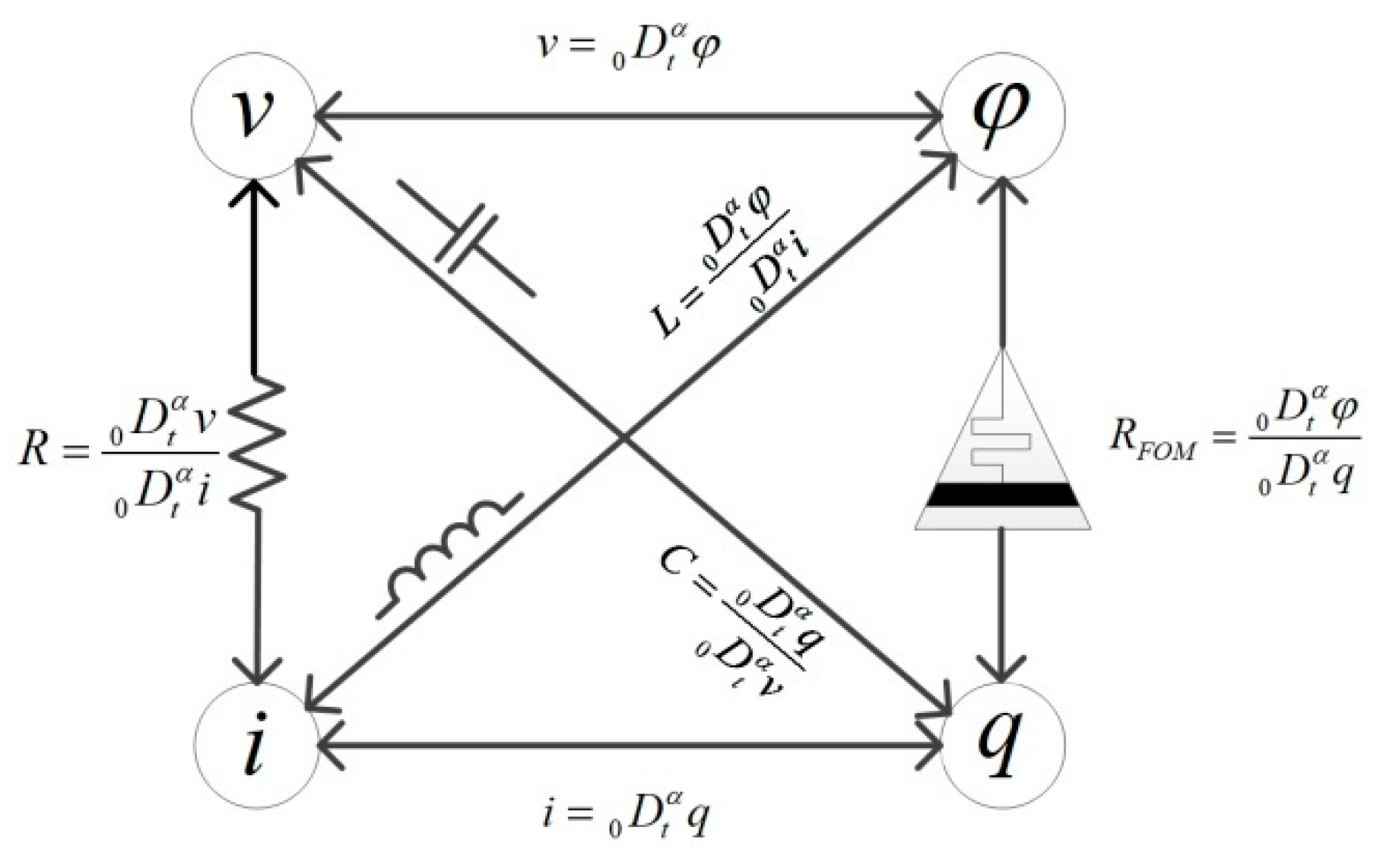
2. Memristor Modeling
2.1. Fractional Order Memristor Model
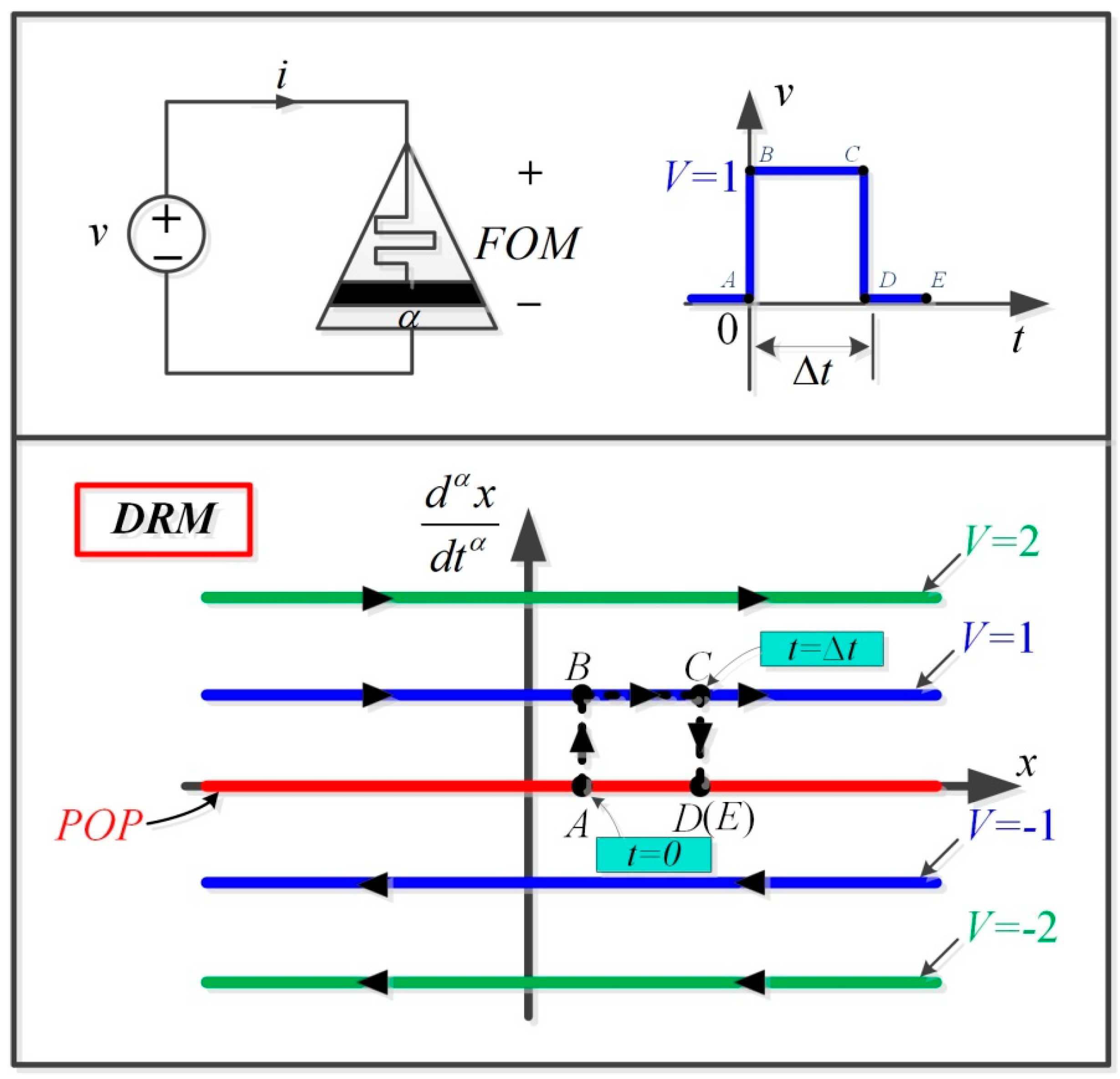
2.2. Nonvolatility Analysis
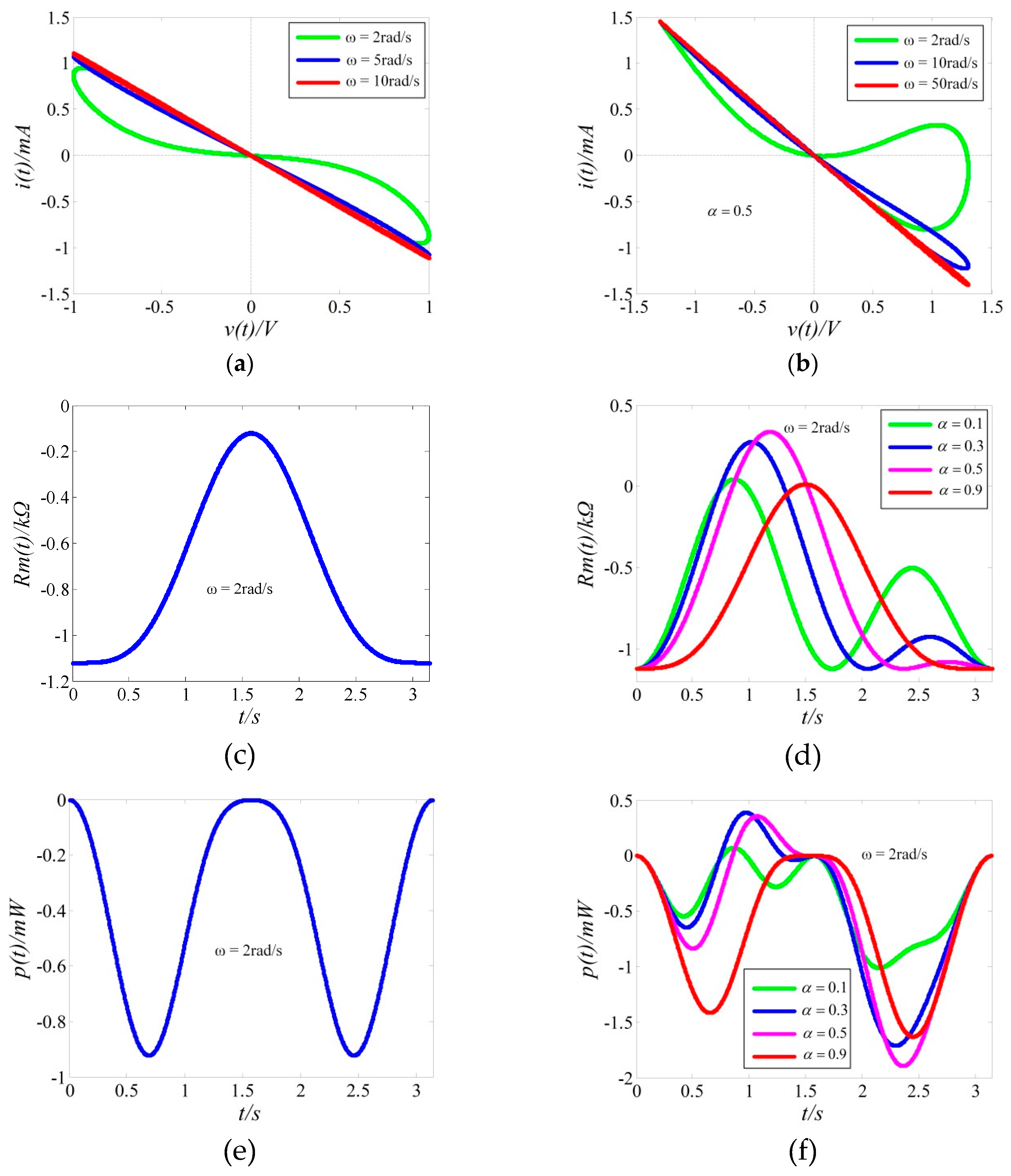
2.3. Numerical Simulations of the Memristor
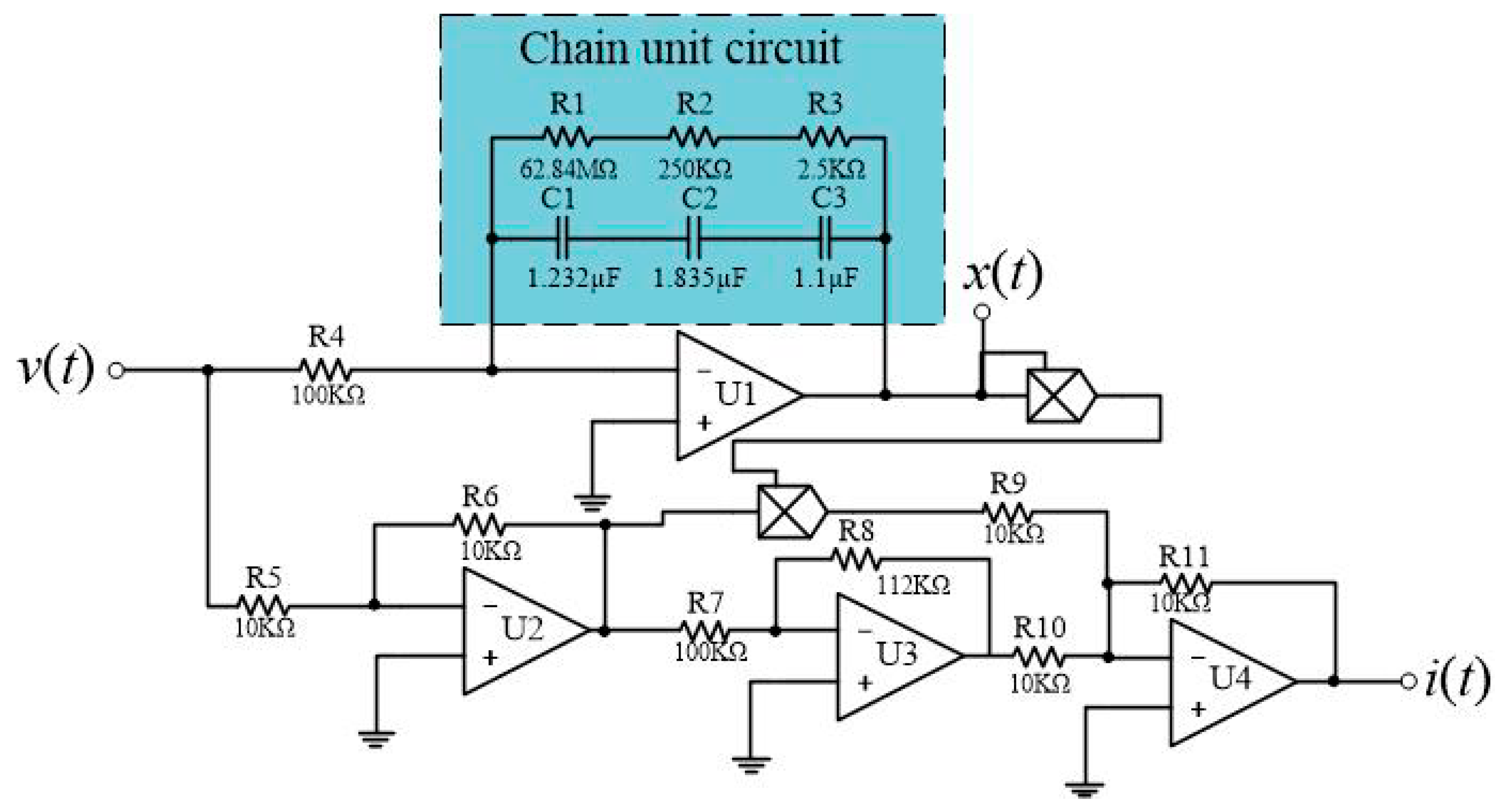
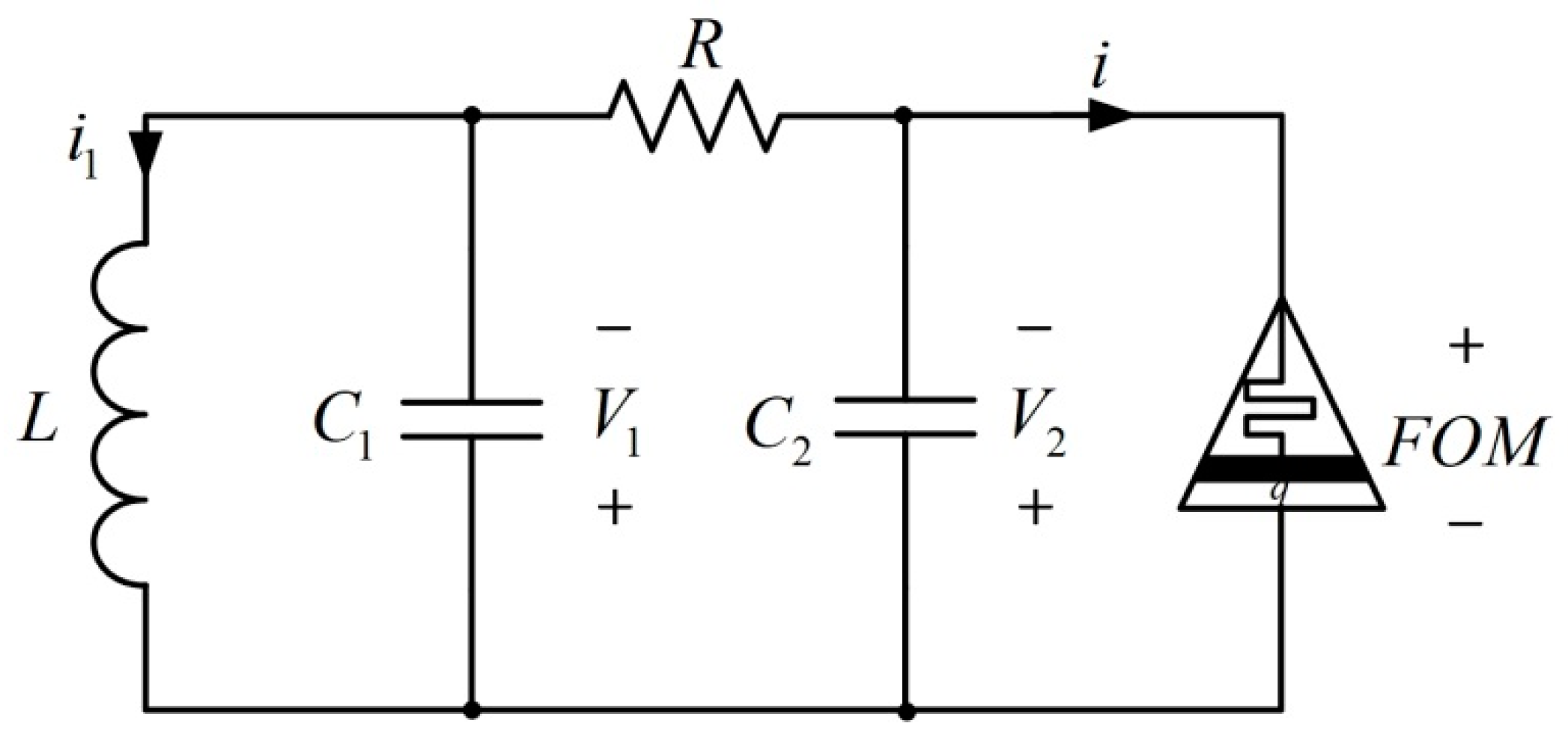
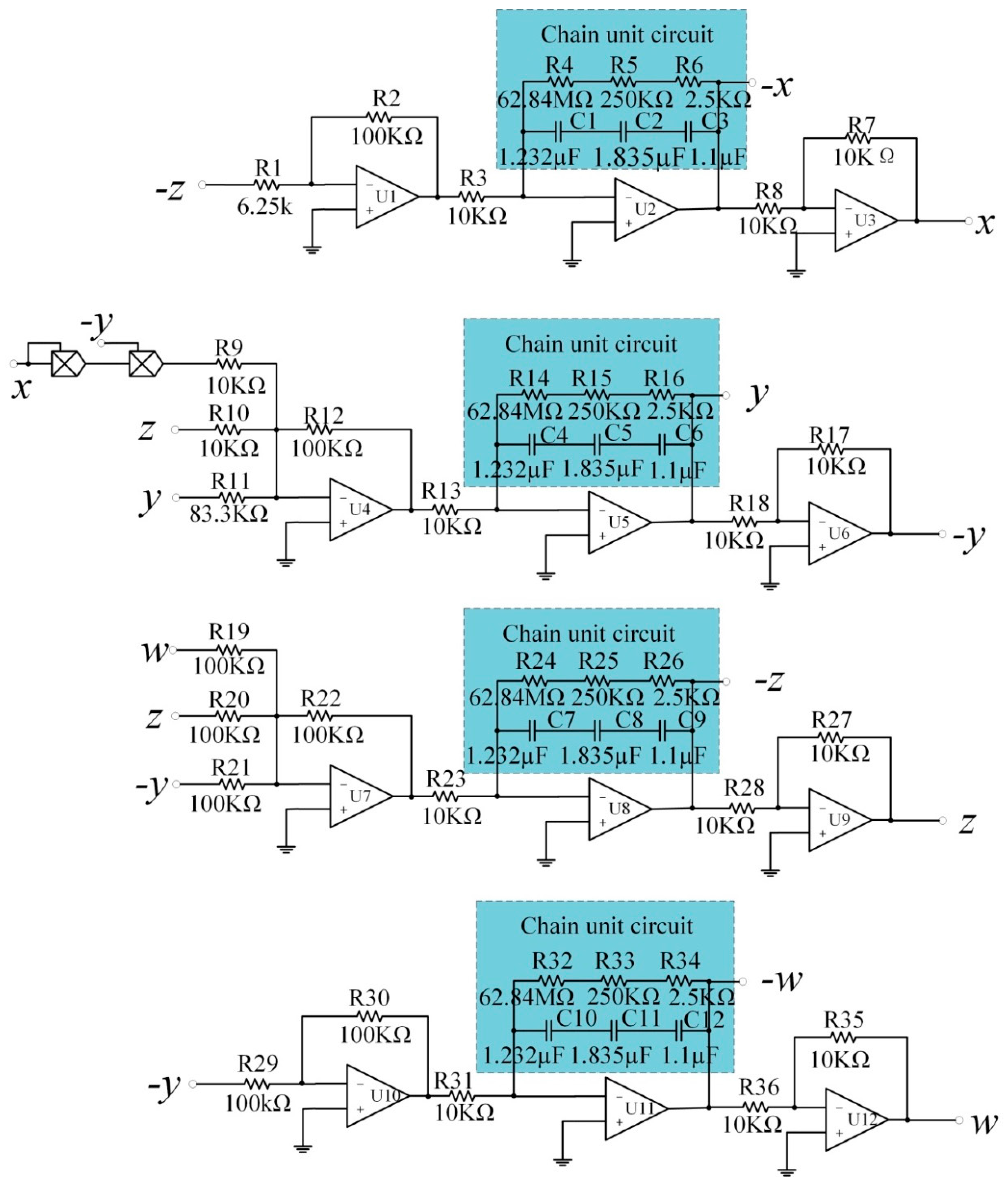
2.4. Equivalent Circuit of the Memristor
3. Fractional Order Memristor Based Chaotic Circuit
3.1. Mathematical Model
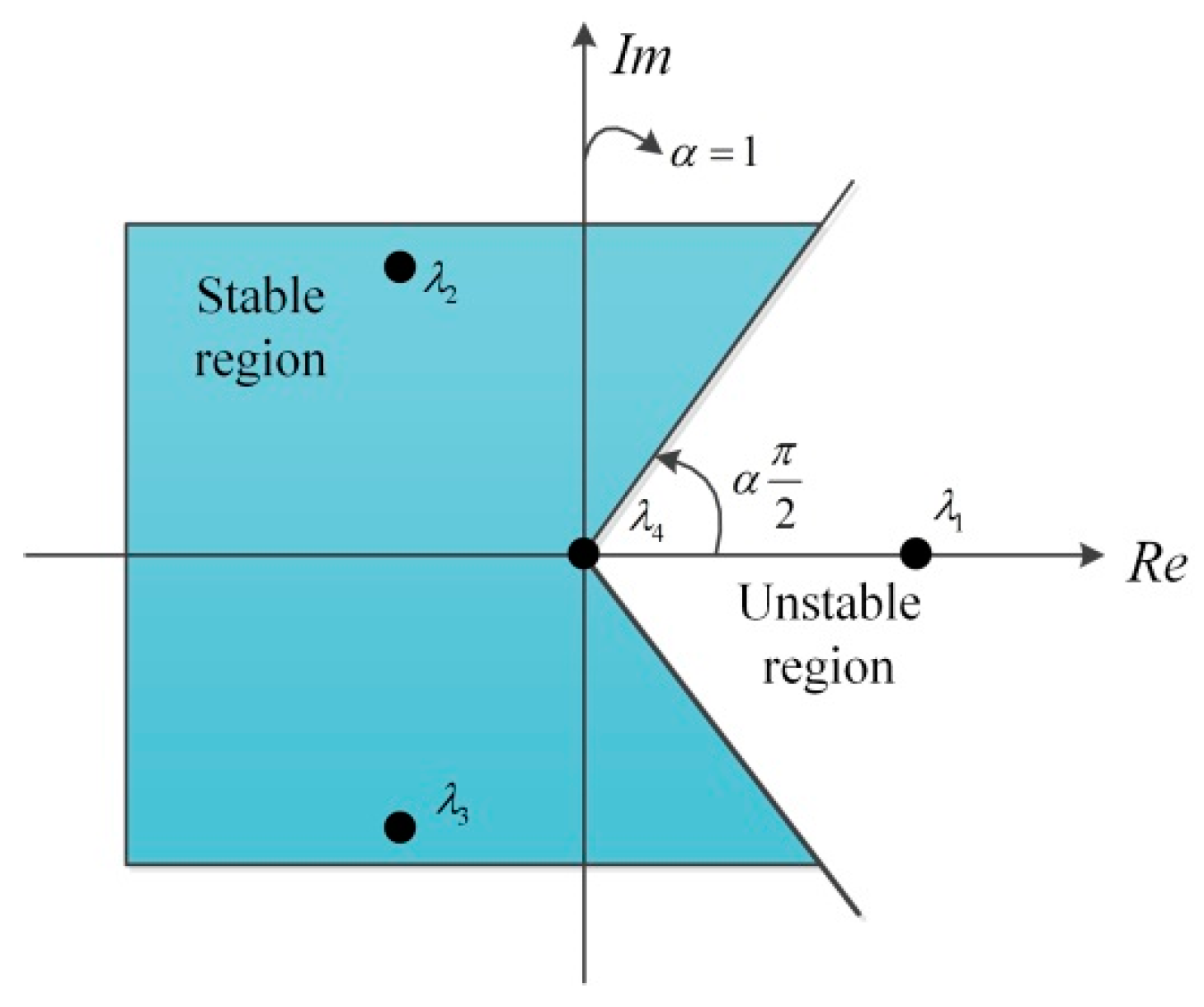
3.2. Equilibrium Points and Stability
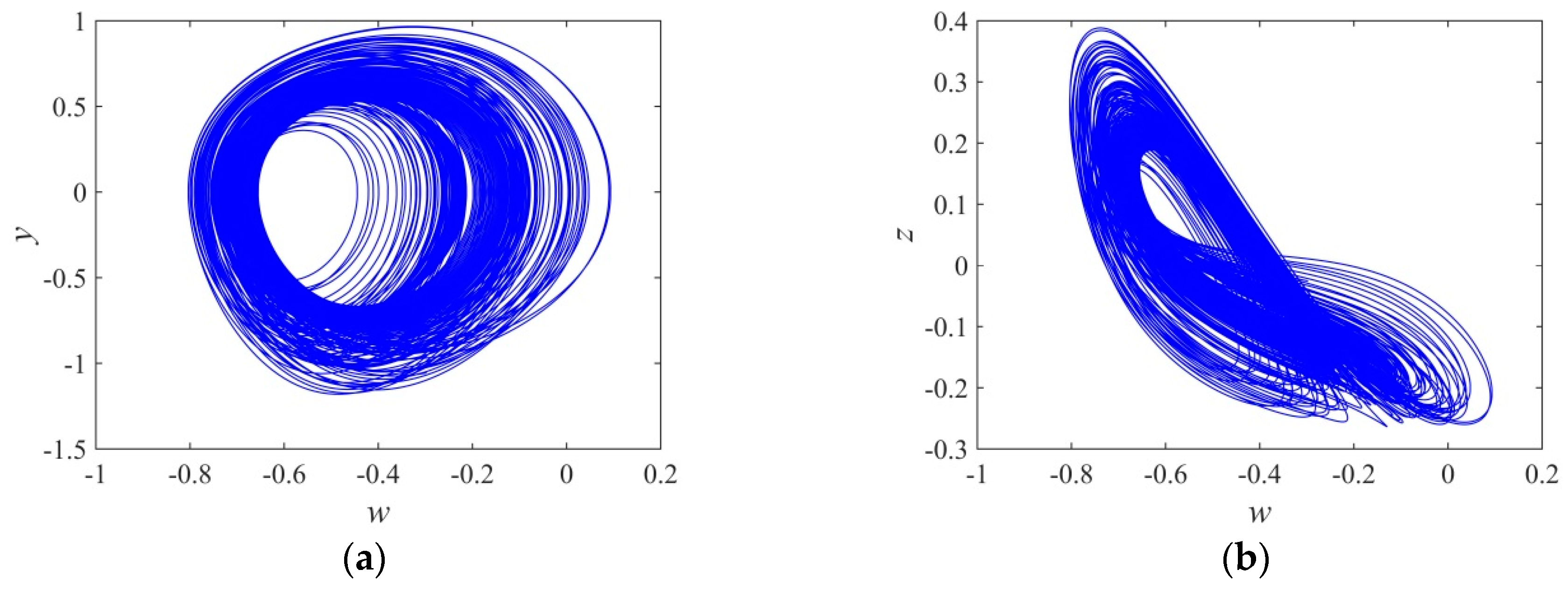
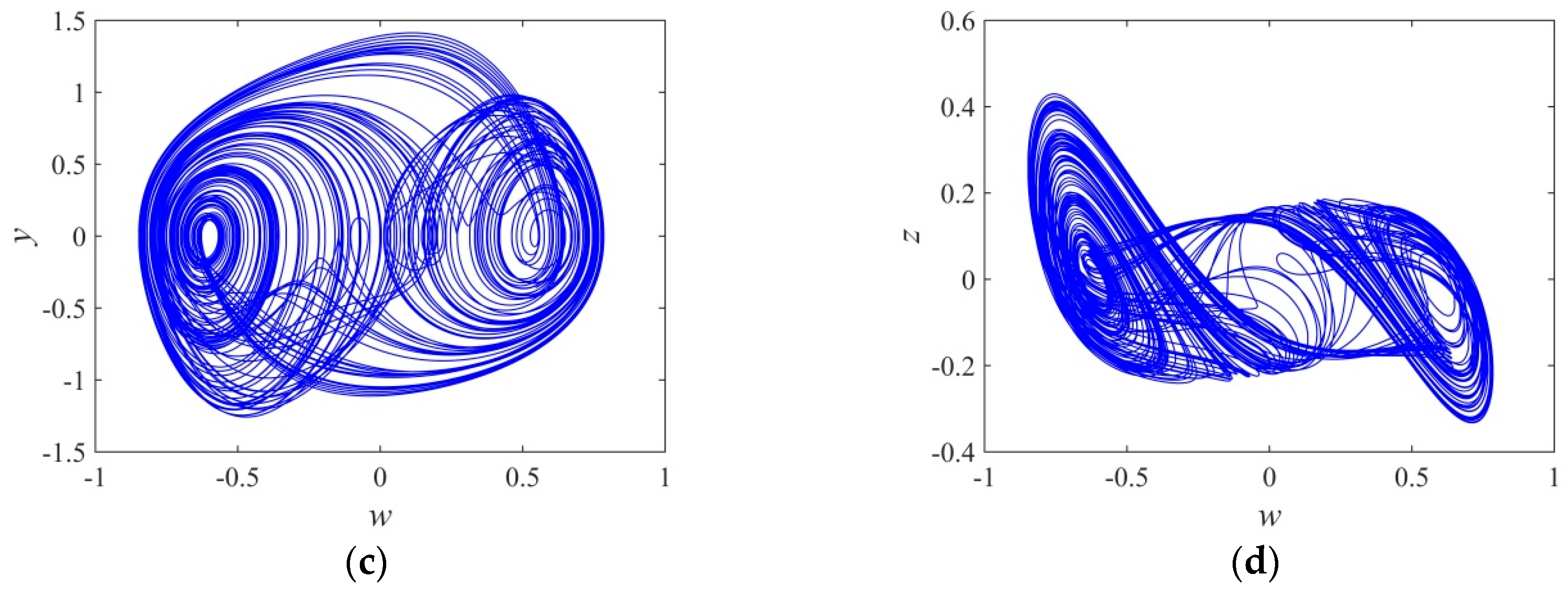
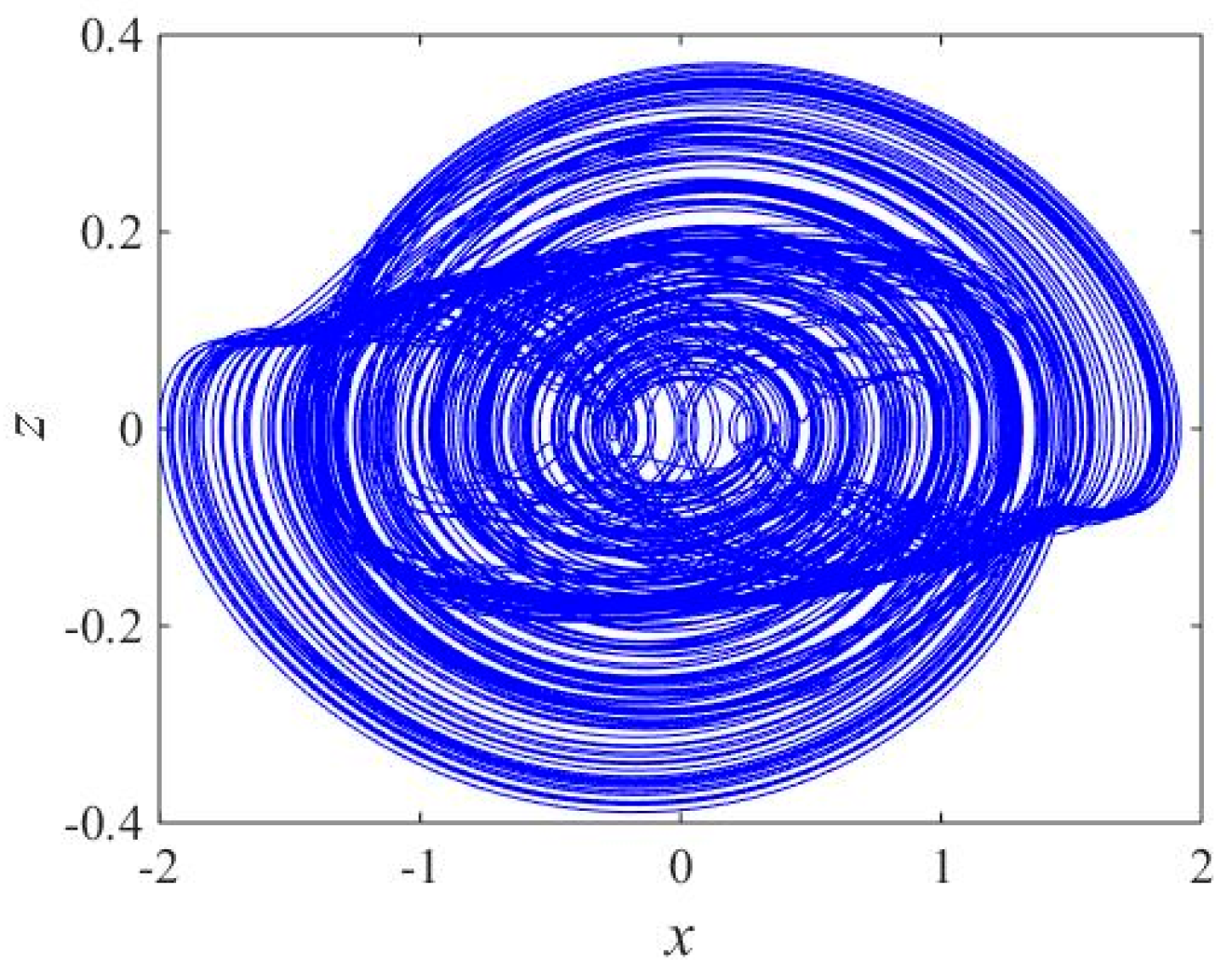
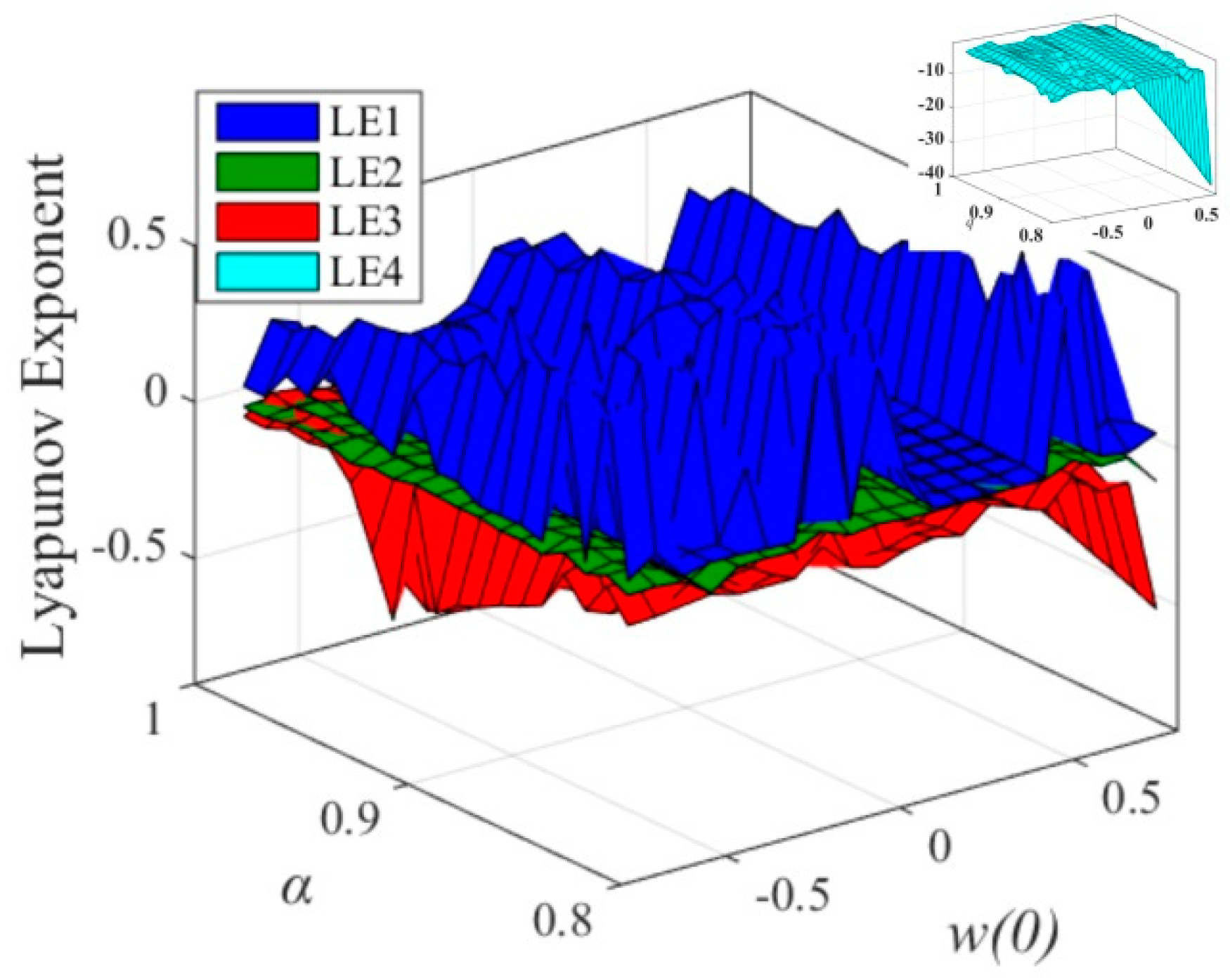
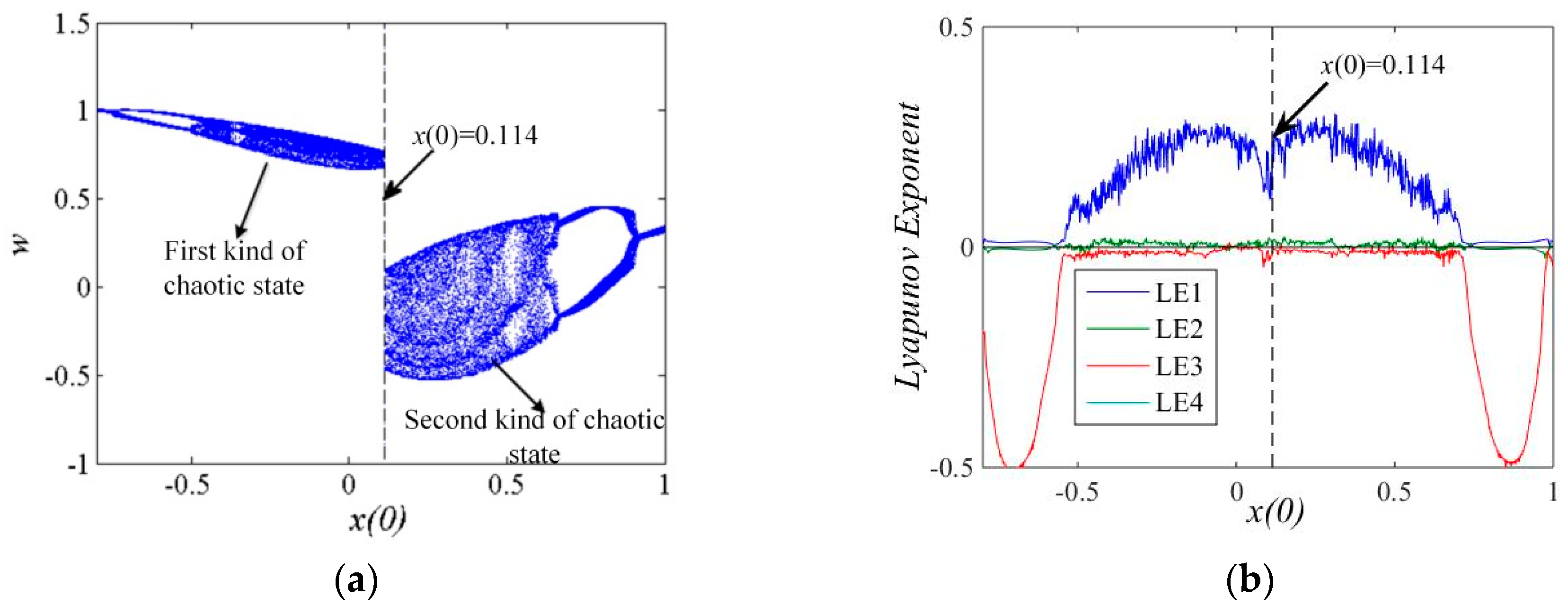
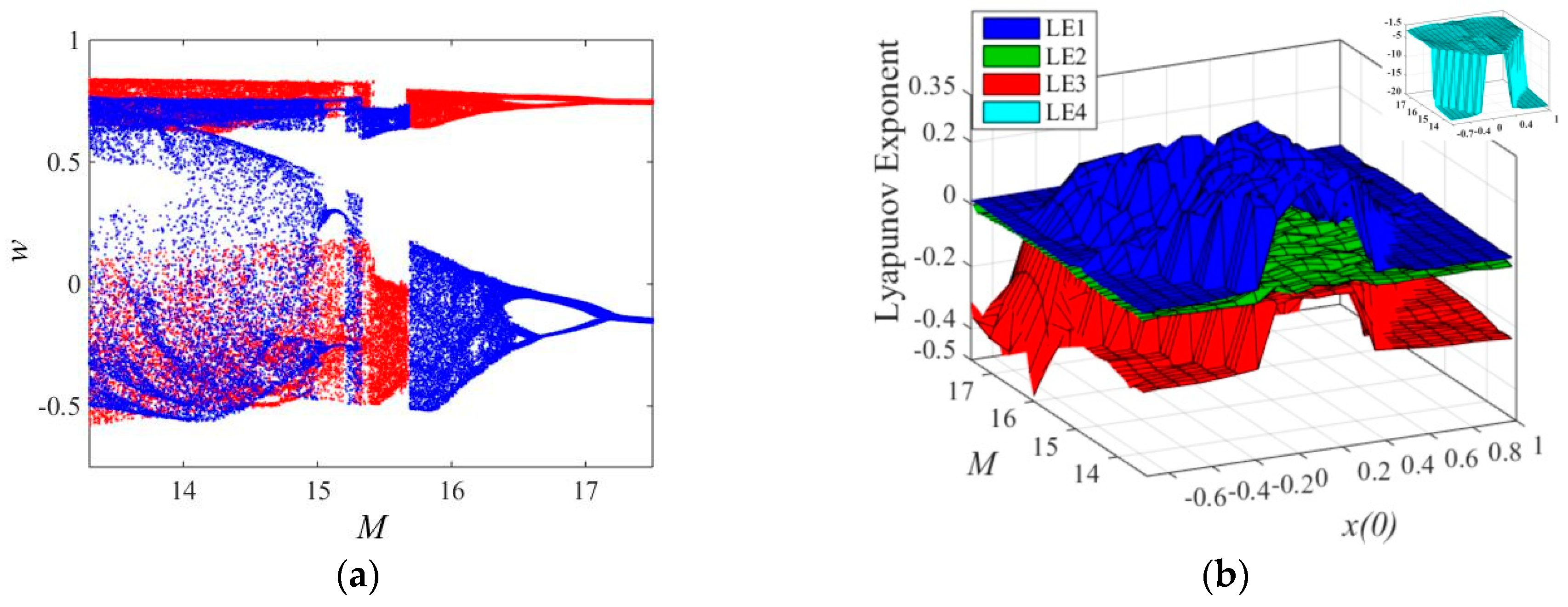
3.3. The Influence of Initial w(0) and Fractional Order α on Dynamics
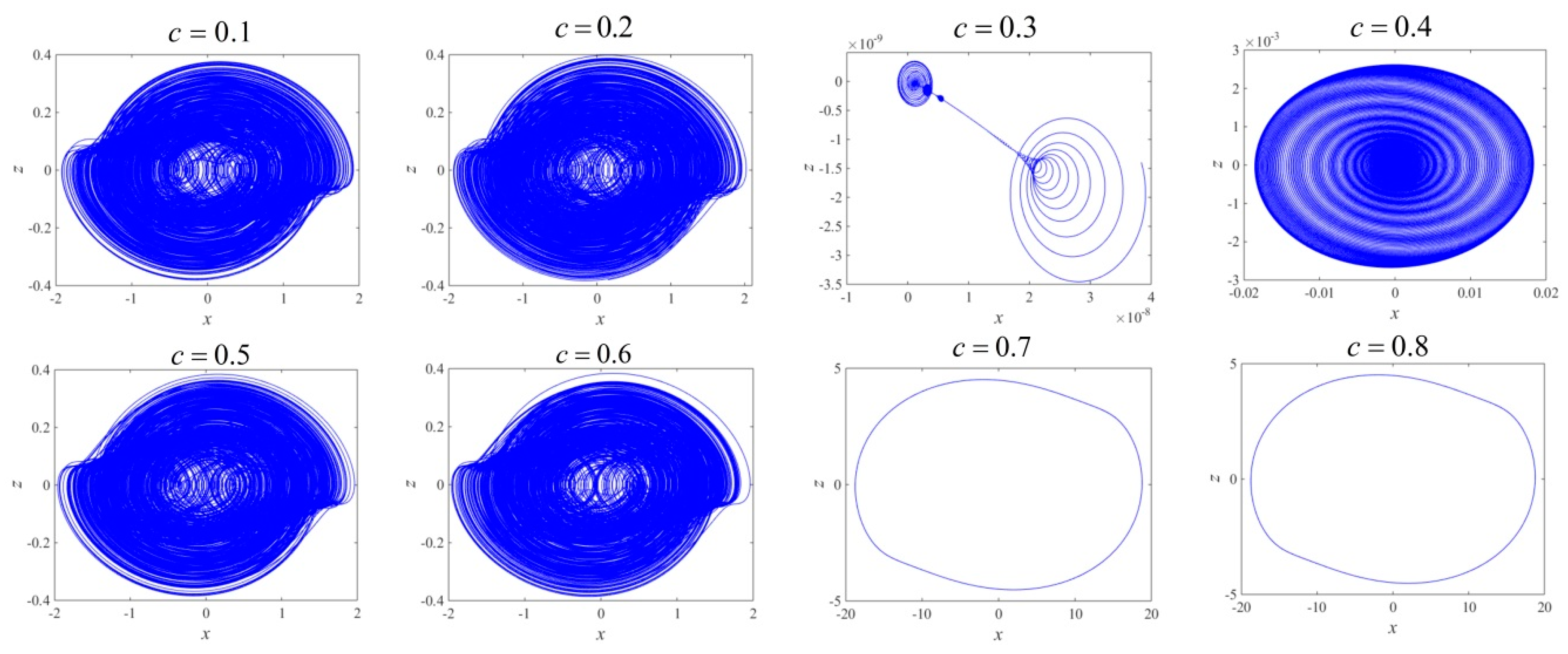
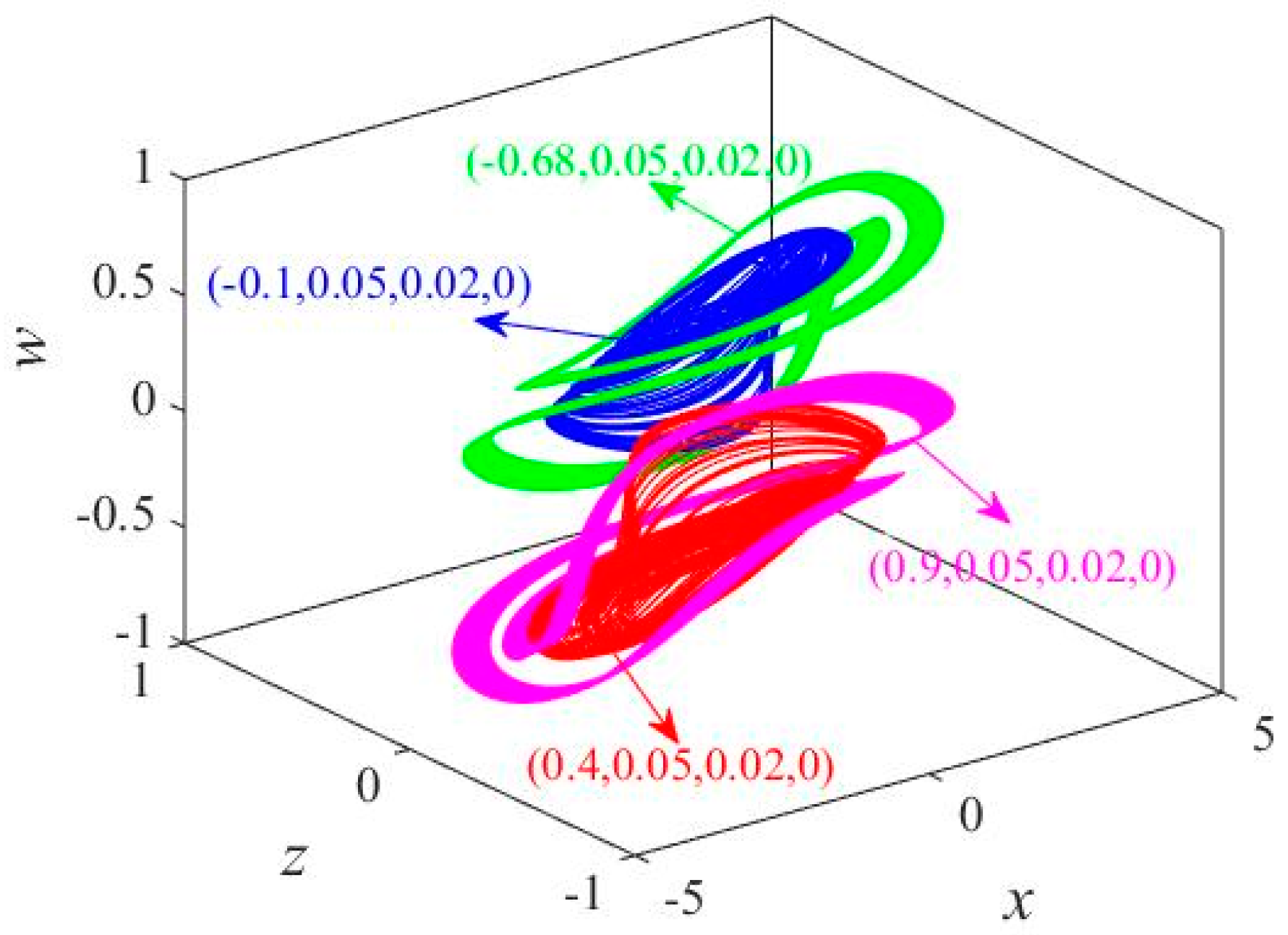
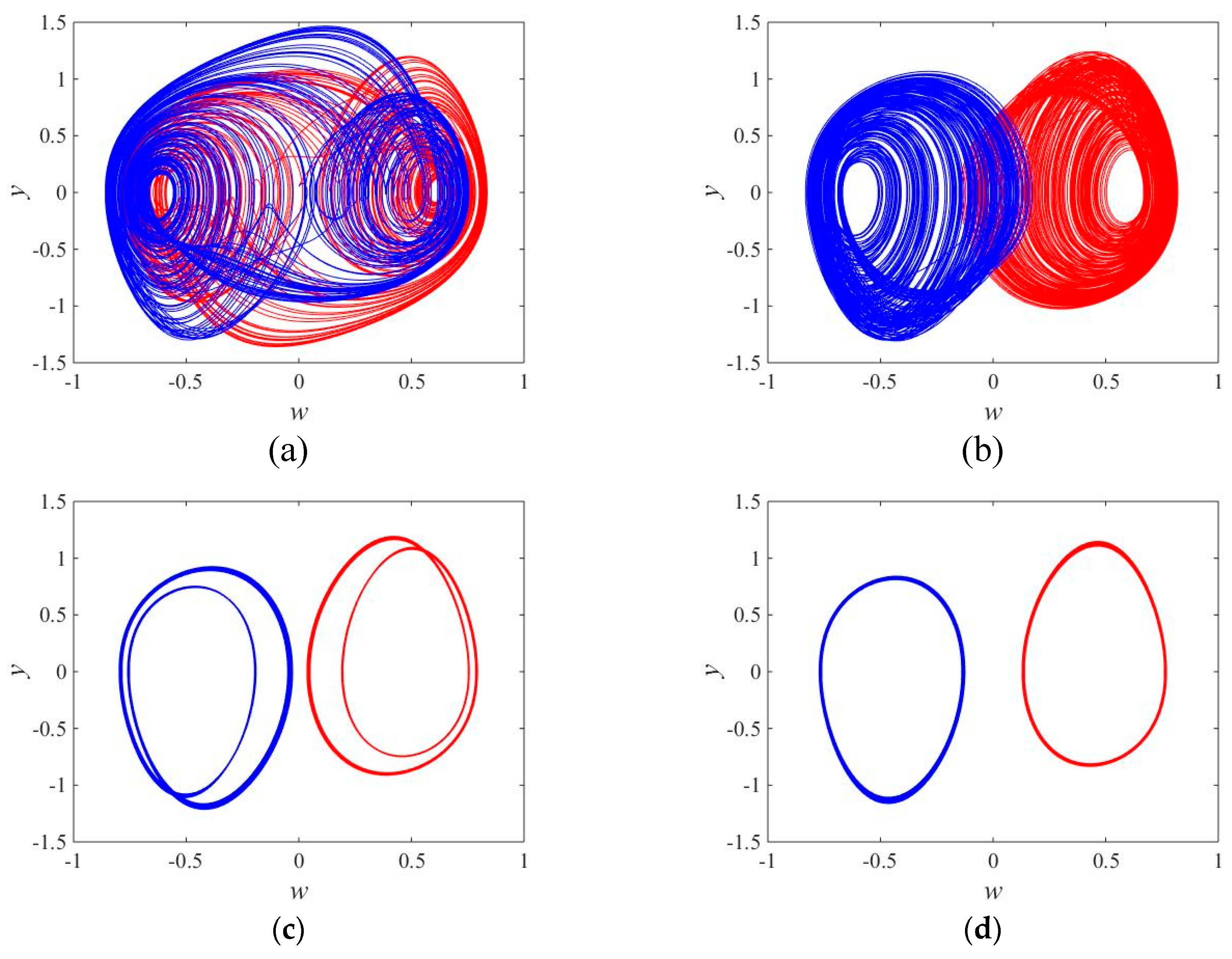
3.4. Coexisting Bifurcation
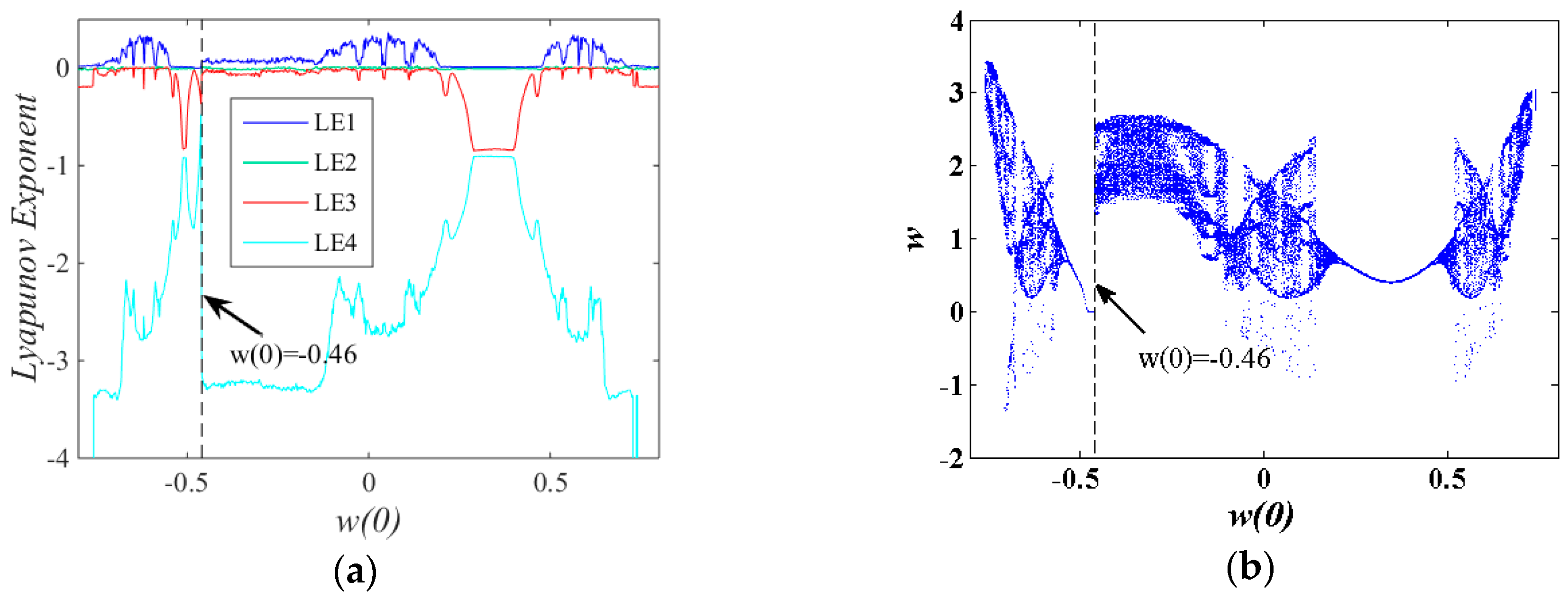
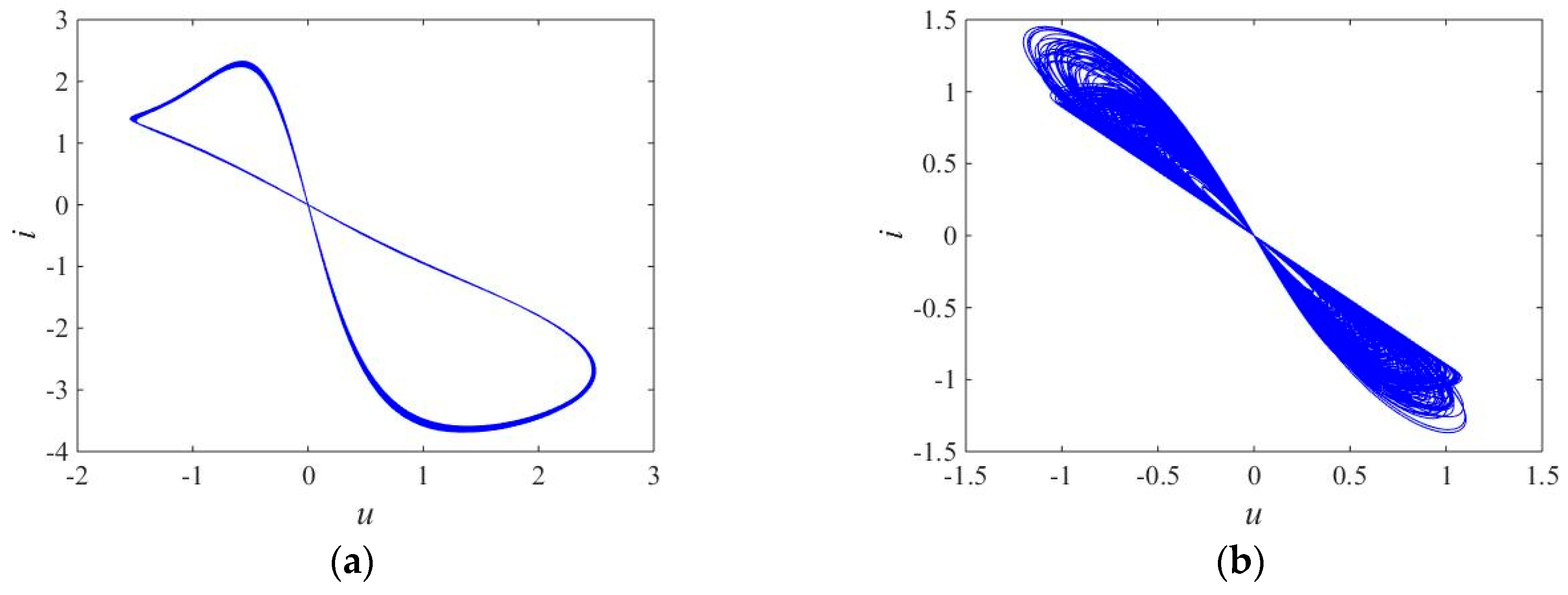
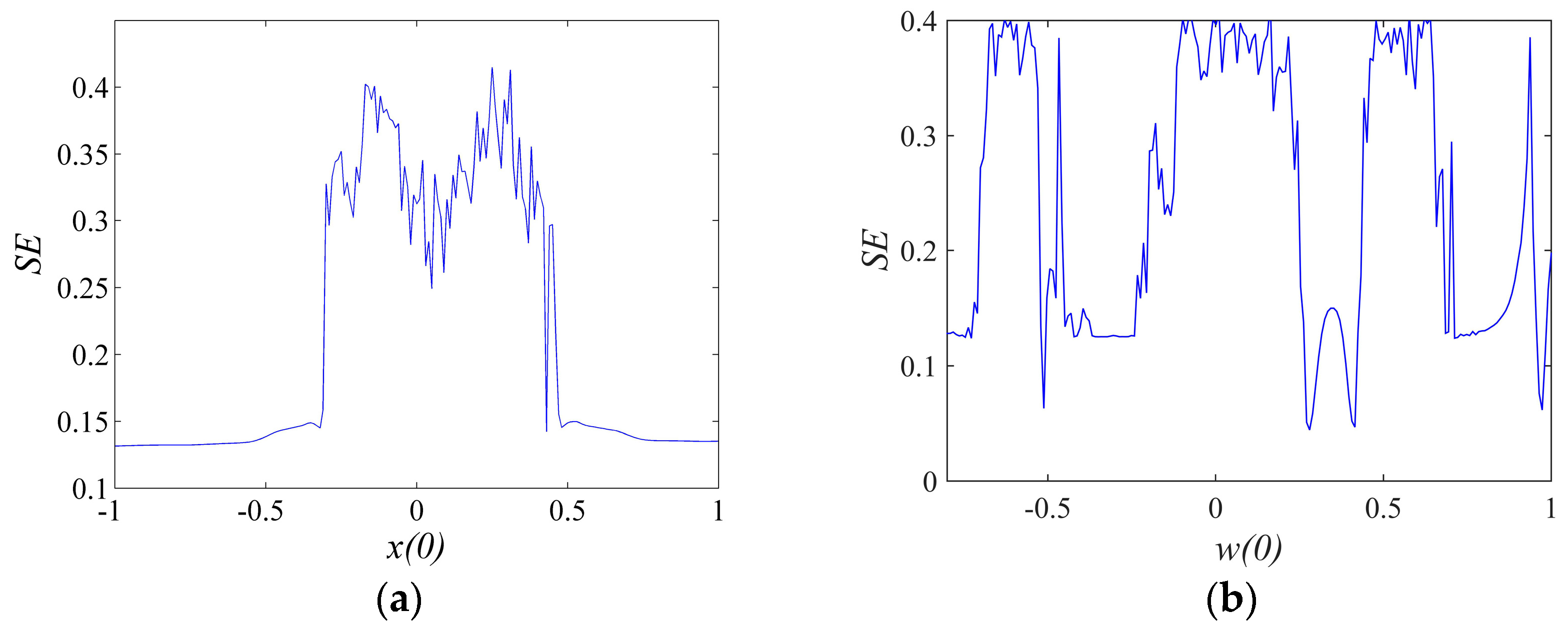
3.5. Spectral Entropy Analysis
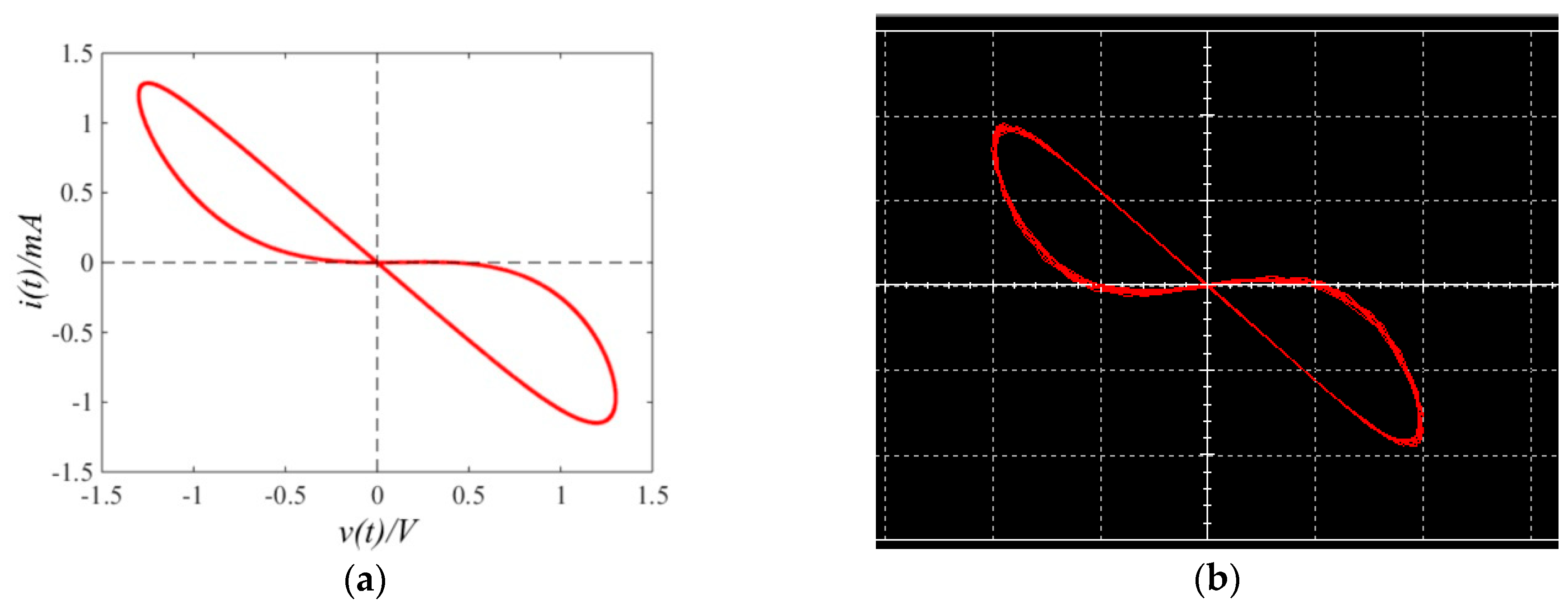
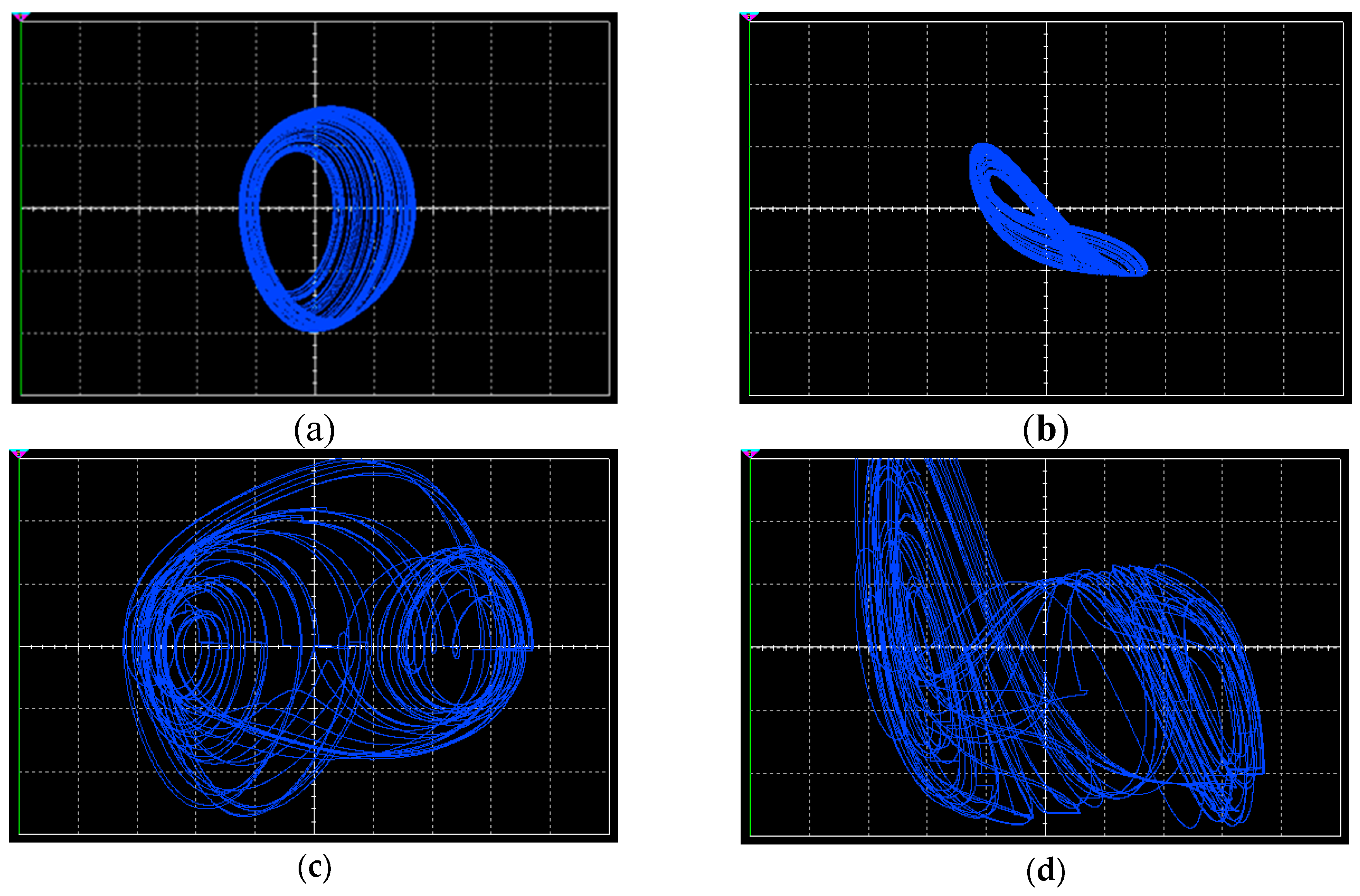
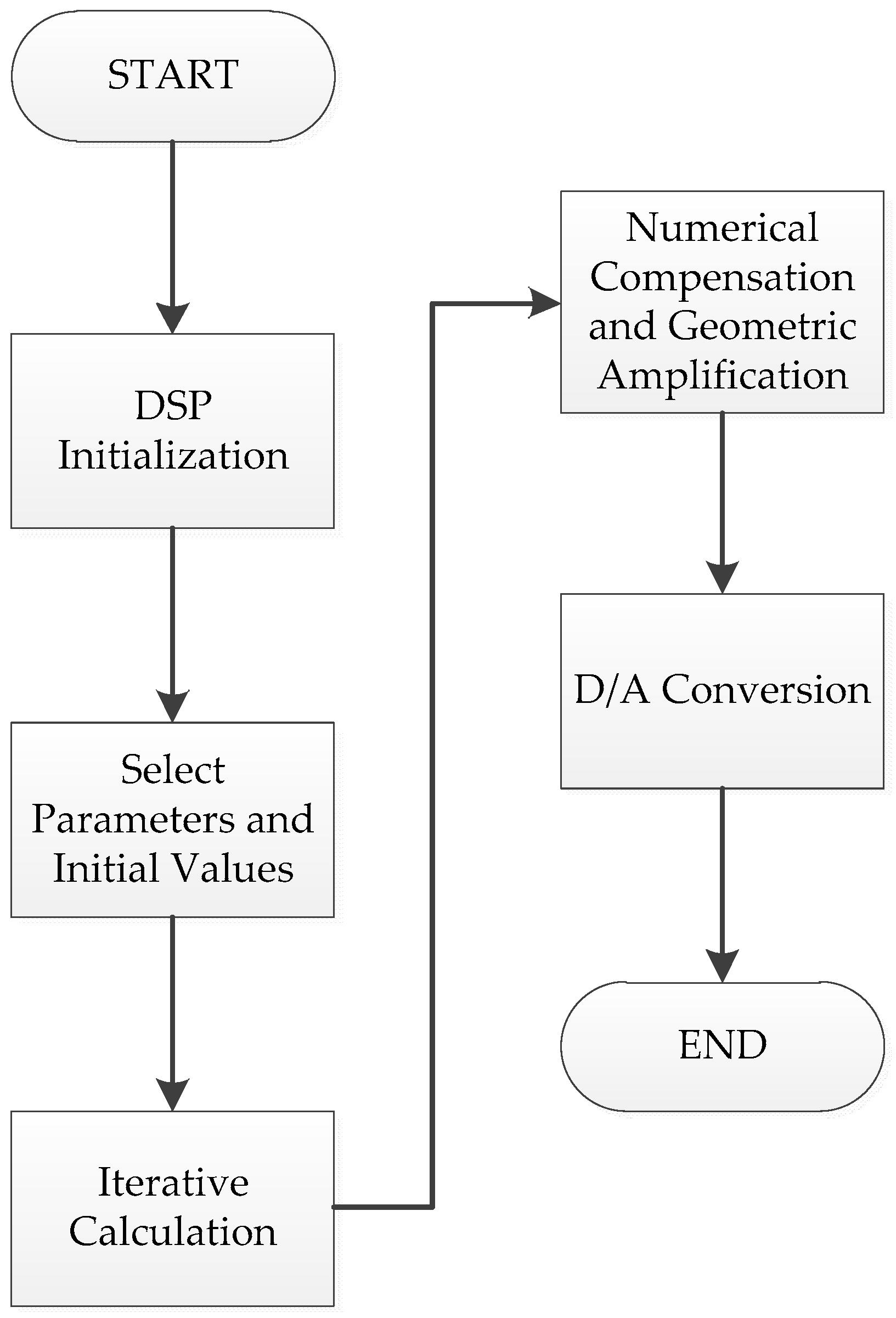
4. Experimental Verification
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Chua, L.O. Memristor-The missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Strachan, J.P.; Williams, R.S. Chaotics dynamics in namoscale NbO2 Mott memristors for analogue computing. Nature 2017, 548, 318–321. [Google Scholar] [CrossRef] [PubMed]
- Yuan, F.; Wang, G.Y.; Wang, X.Y. Dynamical characteristics of HP memristor based on equivalent circuit model in chaotic oscillator. Chin. Phys. B 2015, 24, 207–215. [Google Scholar] [CrossRef]
- Liu, G.Z.; Zheng, L.J.; Wang, G.Y. A carry lookahead adder based on hybrid CMOS-Memristor logic circuit. IEEE Access 2018, 7, 43691–43696. [Google Scholar] [CrossRef]
- Ma, D.; Wang, G.; Han, C.; Shen, Y.; Liang, Y. A memristive neural network model with associative memory for modeling affections. IEEE Access 2018, 6, 61614–61622. [Google Scholar] [CrossRef]
- Bertschinger, N.; Natschläger, T. Real-Time computation at the edge of chaos in recurrent neural networks. Neural Comput. 2004, 16, 1413–1436. [Google Scholar] [CrossRef] [PubMed]
- Buscarino, A.; Fortuna, L.; Frasca, M. A chaotic circuit based on Hewlett-Packard memristor. Chaos 2012, 22, 023136. [Google Scholar] [CrossRef]
- Itoh, M.; Chua, L.O. Memristor oscillators. Int. J. Bifurcat. Chaos 2008, 18, 3183–3206. [Google Scholar] [CrossRef]
- Wen, S.P.; Huang, T.; Zeng, Z. Adaptive synchronization of memristor-based Chua’s circuits. Phys. Lett. A 2012, 376, 2775–2780. [Google Scholar] [CrossRef]
- Li, Z.J.; Zeng, Y.C. A memristor oscillator based on a twin-T network. Chin. Phys. B 2013, 22, 040502. [Google Scholar] [CrossRef]
- Bao, B.C.; Xu, J.P.; Liu, Z. Initial state dependent dynamical behaviors in a memristor based chaotic circuit. Chin. Phys. Lett. 2010, 27, 51–53. [Google Scholar]
- Jin, P.P.; Wang, G.Y.; Iu, H.H.C. A locally-active memristor and its application in chaotic circuit. IEEE Trans. Circ. Syst. II Express Briefs 2017, 65, 246–250. [Google Scholar] [CrossRef]
- Chang, H.; Wang, Z.; Li, Y.X. Dynamic analysis of a bistable Bi-Local active memristor and its associated oscillator system. Int. J. Bifurcat. Chaos 2018, 28, 1850105. [Google Scholar] [CrossRef]
- Liu, C.X. Fractional-order Chaotic Circuit Theory and Applications; Xian Jiaotong University Press: Xi’an, China, 2011; pp. 61–65. [Google Scholar]
- Yu, Y.J.; Wang, Z.H. A fractional-order memristor model and the fingerprint of the simple series circuit including a fractional-order memrisotr. Acta Phys. Sin. 2015, 64, 238401. [Google Scholar]
- Ventra, M.D.; Pershin, Y.V.; Chua, L.O. Circuit elements with memory: Memristors, memcapacitors, and meminductors. Proc. IEEE 2009, 97, 1717–1724. [Google Scholar] [CrossRef]
- Petráš, I.; Chen, Y.Q. Fractional-Order Circuit Elements with Memory. In Proceedings of the 13th International Carpathian Control Conference, High Tatras, Slovakia, 28–31 May 2012; pp. 552–558. [Google Scholar]
- Fouda, M.E.; Ranwan, A.G. On the fractional-order memristor model. J. Fract. Calc. Appl. 2013, 4, 1–7. [Google Scholar]
- Fouda, M.E.; Ranwan, A.G. Fractional-order memristor response under DC and periodic signals. Circ. Syst. Singal Process. 2014, 34, 961–970. [Google Scholar] [CrossRef]
- Rashad, S.H.; Hamed, E.M.; Fouda, M.E. On the Analysis of Current-Controlled Fractional-Order Memristor Emulator. In Proceedings of the 6th International Conference on Modern Circuits and Systems Technologies, Thessaloniki, Greece, 4–6 May 2017. [Google Scholar]
- Hamed, E.M.; Fouda, M.E.; Radwan, A.G. Conditions and emulation of double pinch-off points in fractional-order memristor. In Proceedings of the IEEE International Symposium on Circuits and Systems, Florence, Italy, 27–30 May 2018. [Google Scholar]
- Elsafty, A.H.; Hamed, E.M.; Fouda, M.E.; Said, L.A.; Madian, A.H. Study of fractional flux-controlled memristor emulator connections. In Proceedings of the 7th International Conference on Modern Circuits and Systems Technologies, Thessaloniki, Greece, 7–9 May 2018. [Google Scholar]
- Yuan, F.; Li, Y.X.; Wang, G.Y.; Dou, G. Complex dynamics in a memcapacitor-based circuit. Entropy 2019, 21, 188. [Google Scholar] [CrossRef]
- Song, Y.X.; Yuan, F.; Li, Y.X. Coexisting attractors and multistability in a simple memristive wien-bridge chaotic circuit. Entropy 2019, 21, 678. [Google Scholar] [CrossRef]
- Pham, V.T.; Kingni, S.T.; Volos, C.; Jafari, S.; Kapitaniak, T. A simple three-dimensional fractional-order chaotic system without equilibrium: Dynamics, circuitry implementation, chaos control and synchronization. AEU-Int. J. Electron. Commun. 2017, 78, 220–227. [Google Scholar] [CrossRef]
- Petráš, I. Fractional-order memristor-based chua’s circuit. IEEE Trans. Circuits Syst. II Express Briefs 2011, 57, 975–979. [Google Scholar] [CrossRef]
- Cafagna, D.; Grassi, G. On the simplest fractional-order memristor-based chaotic system. Nonlinear Dyn. 2012, 70, 1185–1197. [Google Scholar] [CrossRef]
- Yu, Y.J.; Wang, Z.H. Initial state dependent nonsmooth bifurcations in a fractional-order memristive circuit. Int. J. Bifurcat. Chaos 2018, 28, 1850091. [Google Scholar] [CrossRef]
- Hajipour, A.; Tavakoli, H. Analysis and circuit simulation of a novel nonlinear fractional incommensurate order financial system. Optik 2016, 127, 10643–10652. [Google Scholar] [CrossRef]
- David, S.A.; Fischer, C.; Machado, J.T. Fractional electronic circuit simulation of a nonlinear macroeconomic model. AEU-Int. J. Electron. Commun. 2019, 84, 210–220. [Google Scholar] [CrossRef]
- Yang, N.N.; Xu, C.; Wu, C.J.; Jia, R. Modeling and analysis of a fractioanl-order generalized memristor-based chaotic system and circuit implementation. Int. J. Bifurcat. Chaos 2017, 27, 1750199. [Google Scholar] [CrossRef]
- Corinto, F.; Ascoli, A. A boundary condition-based approach to the modeling of memristor nanostructures. IEEE Trans. Circuits Syst. I Regul. Rap. 2012, 59, 2713–2726. [Google Scholar] [CrossRef]
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press: New York, NY, USA, 1974; pp. 396–400. [Google Scholar]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent. Ann. Geophys. 1966, 19, 529–539. [Google Scholar] [CrossRef]
- Hu, F.W.; Bao, B.C.; Wu, H.G. Equivalent circuit analysis model of charge-controlled memristor and its circuit characteristics. Acta Phys. Sin. 2013, 62, 218401. [Google Scholar]
- Chua, L.O. Five non-volatile memristor enigmas solved. Appl. Phys. A 2018, 124, 563. [Google Scholar] [CrossRef]
- Zouad, F.; Kemih, K.; Hamiche, H. A new secure communication scheme using fractional order delayed chaotic system: Design and electronics circuit simulation. Analog Integr. Circuits Signal Process. 2019, 99, 619–632. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific Publishing Co.: Munich, Germany, 2000; pp. 331–463. [Google Scholar]
- Westerlund, S. Dead matter has memory! Phys. Scr. 1991, 43, 174–179. [Google Scholar] [CrossRef]
- Chua, L.O. Loacl Activity is the origin of complexity. Int. J. Bifurcat. Chaos 2005, 15, 3435–3456. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Chen, L.P.; He, Y.G.; Lv, X.; Wu, R.C. Dynamic behaviours and control of fractional-order memristor-based system. Pramana 2015, 85, 91–104. [Google Scholar] [CrossRef]
- Marius-F, D.; Nikolay, K. Matlab code for lyapunov exponents of fractional-order systems. Inter. J. Bifurcat. Chaos 2018, 28, 1850067. [Google Scholar]
- Sun, K.H.; He, S.B.; He, Y.; Yin, L.Z. Complexity analysis of chaotic pseudo-random sequences based on spectral entropy algorithm. Acta Phys. Sin. 2013, 62, 010501. [Google Scholar]
- He, S.B.; Sun, K.H.; Wang, H.H. Solution of the fractional-order chaotic system based on adomian decomposition algorithm and its complexity analysis. Acta Phys. Sin. 2014, 63, 2965–2973. [Google Scholar]
- Gonzalo, A.; Li, S.J. Some basic cryptographic requirements for chaos-based cryptosystems. Int. J. Bifurcat. Chaos 2006, 16, 2129–2151. [Google Scholar]



| Dynamics | |||||
|---|---|---|---|---|---|
| 0 | 2.3207 | −1.0603 ± 2.3658i | 0 | 0.7318 | chaos |
| 0.1 | 2.1972 | −1.0480 ± 2.3250i | 0 | 0.7304 | chaos |
| 0.2 | 1.7968 | −0.9984 ± 2.1888i | 0 | 0.7275 | chaos |
| 0.3 | 0.9268 | −0.8134 ± 1.8831i | 0 | — | stable point |
| 0.4 | −1.4784 | 0.0393 ± 1.8748i | 1.5498 | — | stable point |
| 0.5 | −2.8613 | 0.2807 ± 2.4140i | 1.4550 | 0.9263 | chaos |
| 0.6 | −4.0000 | 0.3000 ± 2.7760i | 1.4632 | 0.9314 | chaos |
| 0.7 | −5.1933 | 0.2466 ± 3.0333i | 1.4897 | 0.9484 | limit cycle |
| 0.8 | −6.5296 | 0.1648 ± 3.2133i | 1.5195 | 0.9673 | limit cycle |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Wang, G.; Iu, H.H.-C.; Shen, Y.; Zhou, W. A Nonvolatile Fractional Order Memristor Model and Its Complex Dynamics. Entropy 2019, 21, 955. https://doi.org/10.3390/e21100955
Wu J, Wang G, Iu HH-C, Shen Y, Zhou W. A Nonvolatile Fractional Order Memristor Model and Its Complex Dynamics. Entropy. 2019; 21(10):955. https://doi.org/10.3390/e21100955
Chicago/Turabian StyleWu, Jian, Guangyi Wang, Herbert Ho-Ching Iu, Yiran Shen, and Wei Zhou. 2019. "A Nonvolatile Fractional Order Memristor Model and Its Complex Dynamics" Entropy 21, no. 10: 955. https://doi.org/10.3390/e21100955
APA StyleWu, J., Wang, G., Iu, H. H.-C., Shen, Y., & Zhou, W. (2019). A Nonvolatile Fractional Order Memristor Model and Its Complex Dynamics. Entropy, 21(10), 955. https://doi.org/10.3390/e21100955





