Complexity Synchronization of Energy Volatility Monotonous Persistence Duration Dynamics
Abstract
1. Introduction
2. Mathematical Concept Description of VMPD Series
- (i)
- If , the volatility sequence is thought to be locally falling at day t. Then we define the length of continuous growth at day t, namely
- (ii)
- If , the volatility sequence is thought to be locally rising at day t. Then we have define the length of sustained descent at day t, namely
- (iii)
- Specifically, when , we assume that = 0.
- (iv)
- Let denote the maximum fluctuation difference, in other words, it is also the largest growth or decline during the continuous variation length . Schematic diagrams of and are shown in Figure 1.
- (v)
- Then, the VMPD sequence is defined by:
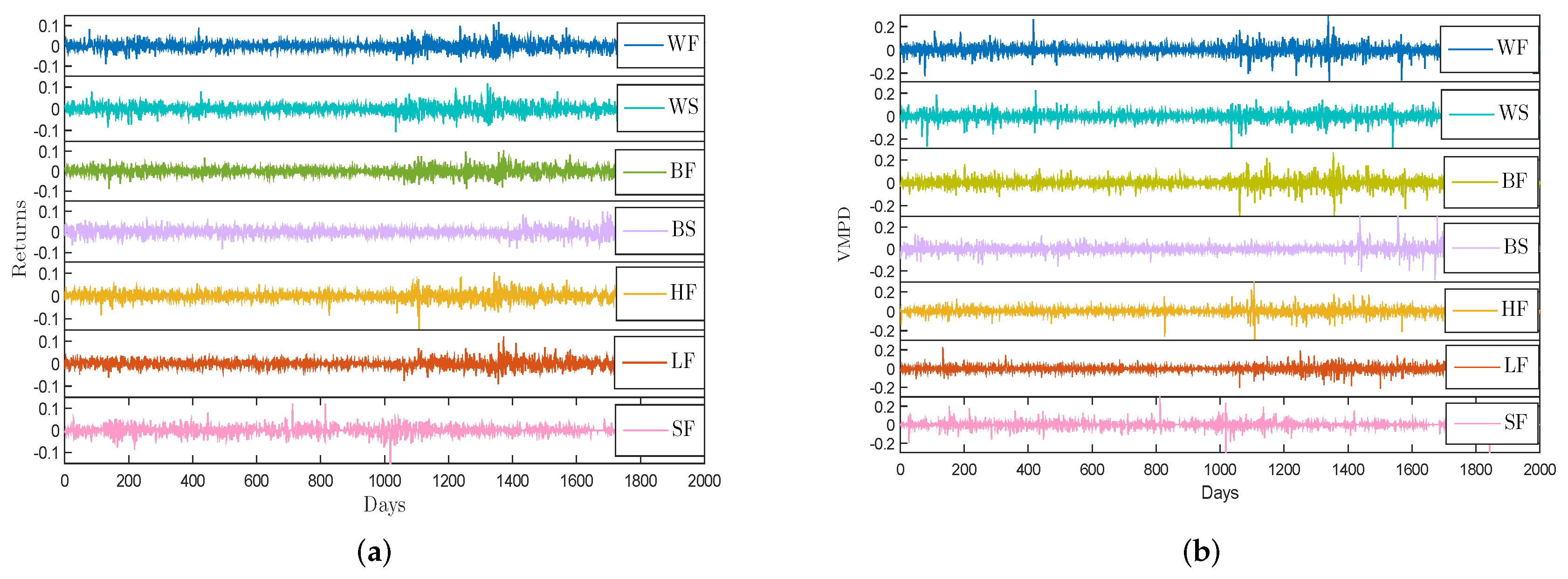
3. Basic Statistical Description of Data Sets
4. Statistical and Nonlinear Behaviors of Return Series and VMPD Series
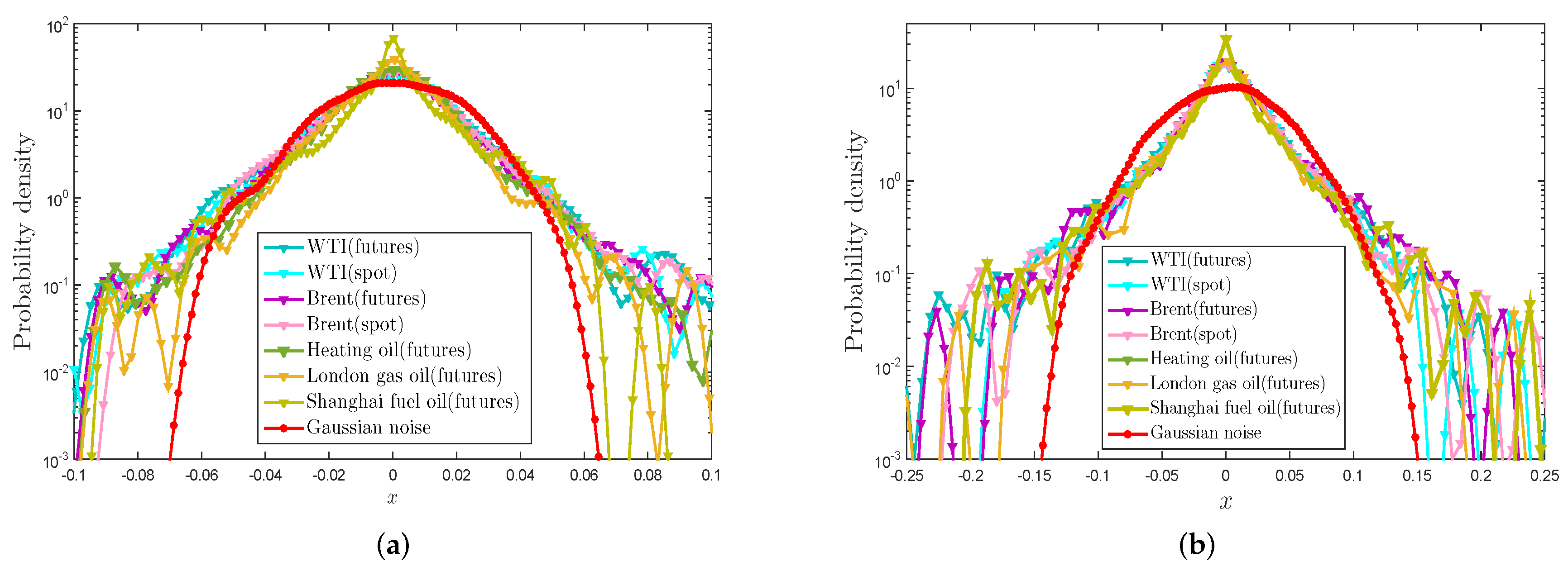
4.1. Probability Density Distribution
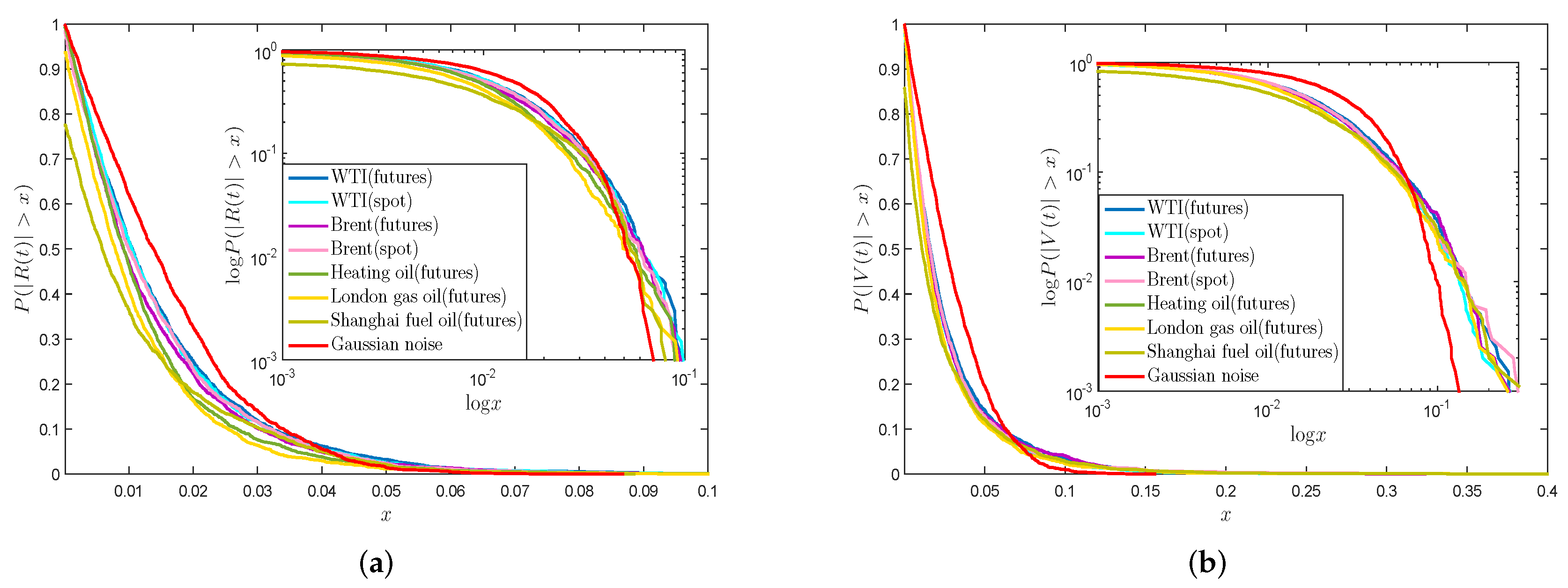
4.2. Power-law Behaviors
4.3. Autocorrelation Analysis
5. Complexity Synchronization of Return Series and VMPD Series
5.1. Mathematical Description of CCF Analysis
- (a)
- Given the embedding dimension m, we can define m-dimensional sequence vectors and as followswhere and denote the average of series segment, that is
- (b)
- represents the distance between vector and vector
- (c)
- The degree of synchrony can be defined by fuzzy function
- (d)
- For all , we work out the mean values of , given by
- (e)
- Finally, we can calculate the C-FuzzyEn of two time series and as
- (f)
- N is finite, then the C-FuzzyEn can be obtained asThe parameter m represents the embedding dimension, n is the gradient of boundary, and r is called as the width. In the following empirical analysis, m and n are set to be 2.
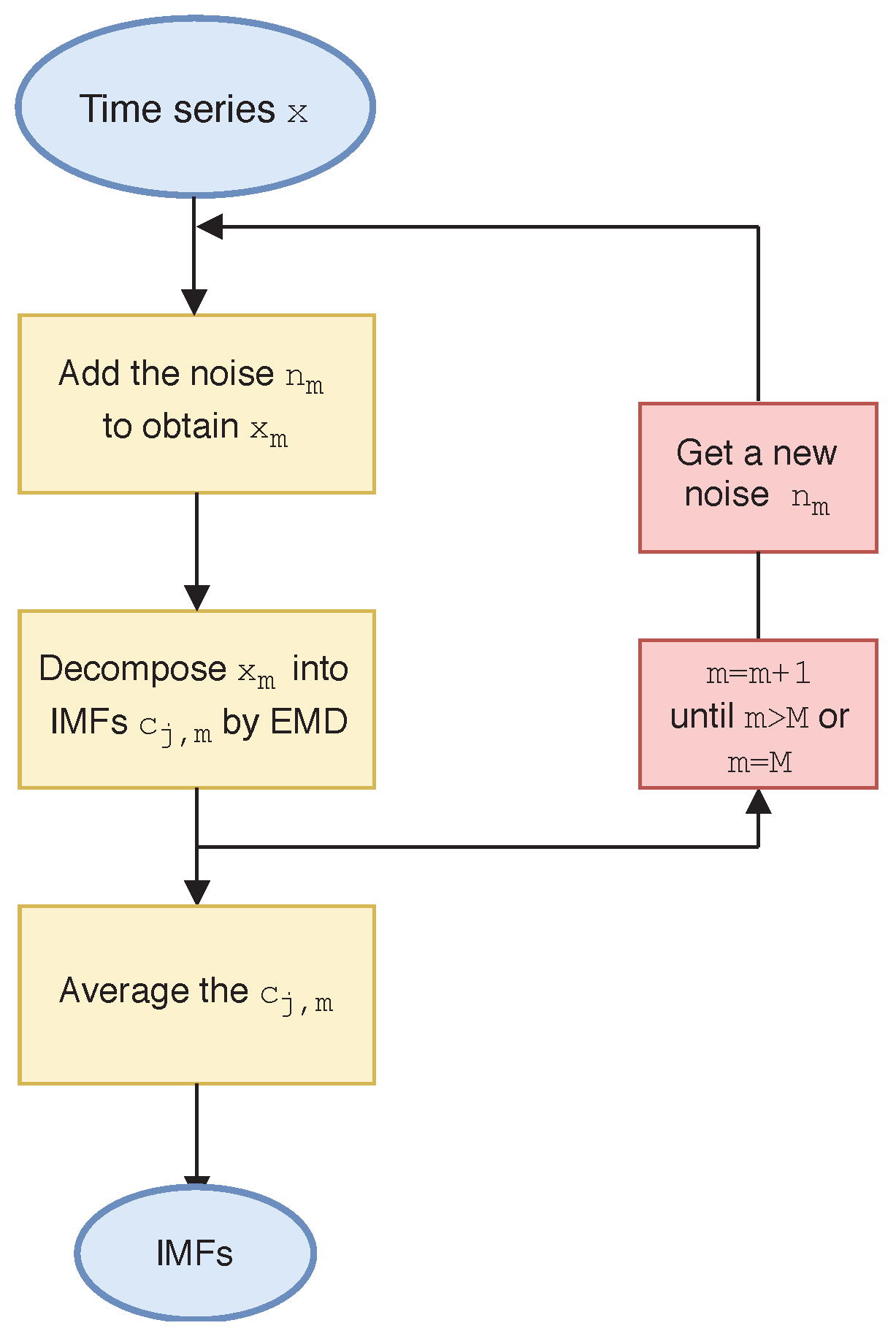
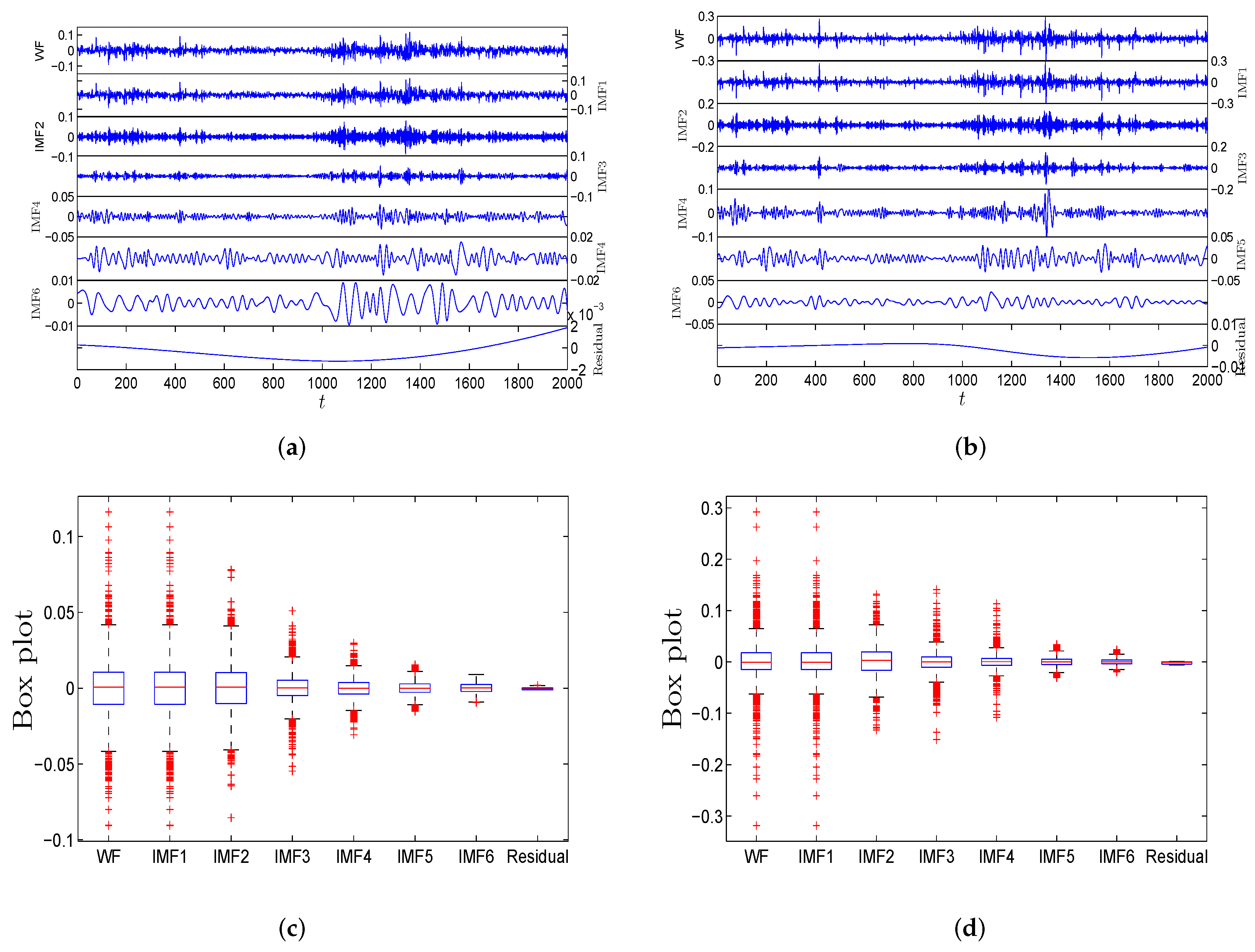
5.2. Mathematical Description of Ensemble Empirical Mode Decomposition
- (a)
- Add a white noise sequence to the time series x in the m-th test
- (b)
- (c)
- Repeat Procedure (a) and Procedure (b) for a pre-set value M of tests, and apply distinct white noise sequences which have the same amplitude every time.
- (d)
- Work out the mean value as the final IMFs, which is given by
5.3. Empirical Study for Complexity Synchronization
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| VMPD | Volatility monotonous persistence duration | WF | Crude oil WTI futures | |
| C-FuzzyEn | Cross-fuzzy entropy | WS | Crude oil WTI spot | |
| CID | Complexity invariant distance | HF | Heating oil futures | |
| CCF | Cross complexity invariant distance FuzzyEn | BF | Crude oil Brent futures | |
| IMF | Intrinsic mode function | BS | Crude oil Brent spot | |
| EMD | Eempirical mode decomposition | LF | London gas oil futures | |
| EEMD | Ensemble empirical mode decomposition | SF | Shanghai fuel oil futures |
References
- Veld, C.; Veld-Merkoulova, Y.V. The risk perceptions of individual investors. J. Econ. Psychol. 2008, 29, 226–252. [Google Scholar] [CrossRef]
- Mantegna, R.N.; Stanley, H.E. An Introduction to Econophysics: Correlations and Complexity in Finance; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Lux, T.; Marchesi, M. Scaling and criticality in a stochastic multi-agent model of a financial market. Volatility clustering in financial markets: A microsimulation of interacting agents. Nature 2000, 397, 498–500. [Google Scholar] [CrossRef]
- Bouri, E.; Shahzad, S.J.H.; Raza, N.; Roubaud, D. Oil volatility and sovereign risk of BRICS. Energy Econ. 2018, 70, 258–269. [Google Scholar] [CrossRef]
- Cunado, J.; Gracia, F.P.D. Oil prices, economic activity and inflation: evidence for some Asian countries. Q. Rev. Econ. Financ. 2005, 45, 65–83. [Google Scholar] [CrossRef]
- Martina, E.; Rodriguez, E.; Escarela-Perez, R.; Alvarez-Ramirez, J. Multiscale entropy analysis of crude oil price dynamics. Energy Econ. 2011, 33, 936–947. [Google Scholar] [CrossRef]
- Huang, L.; Wang, J. Global crude oil price prediction and synchronization based accuracy evaluation using random wavelet neural network. Energy 2018, 151, 875–888. [Google Scholar] [CrossRef]
- Anagnoste, S.; Caraiani, P. The Impact of Financial and Macroeconomic Shocks on the Entropy of Financial Markets. Entropy 2019, 21, 316. [Google Scholar] [CrossRef]
- Caraiani, P. Modeling the Comovement of Entropy between Financial Markets. Entropy 2018, 20, 417. [Google Scholar] [CrossRef]
- Pascoal, P.; Monteiro, A.M. Market Efficiency, Roughness and Long Memory in PSI20 Index Returns: Wavelet and Entropy Analysis. Entropy 2014, 16, 2768–2788. [Google Scholar] [CrossRef]
- Niu, H.; Zhang, L. Nonlinear Multiscale Entropy and Recurrence Quantification Analysis of Foreign Exchange Markets Efficiency. Entropy 2017, 20, 17. [Google Scholar] [CrossRef]
- Trivellato, B. Deformed Exponentials and Applications to Finance. Entropy 2013, 15, 3471–3489. [Google Scholar] [CrossRef]
- Wang, Y.D.; Zheng, S.Z.; Zhang, W.; Wang, J. Complex and Entropy of Fluctuations of Agent-Based Interacting Financial Dynamics with Random Jump. Entropy 2017, 19, 512. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, J. Nonlinear stochastic interacting dynamics and complexity of financial gasket fractal-like lattice percolation. Phys. Lett. A 2018, 18, 1218–1225. [Google Scholar] [CrossRef]
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Lopes, A.M.; Machado, J.A.T. Analysis of temperature time-series: Embedding dynamics into the MDS method. Commun. Nonlinear Sci. Numer. Simulat. 2014, 19, 851–871. [Google Scholar] [CrossRef]
- Machado, J.A.T.; Duarte, F.B.; Duarte, G.M. Analysis of stock market indices through multidimensional scaling. Commun. Nonlinear Sci. Numer. Simulat. 2016, 16, 4610–4618. [Google Scholar] [CrossRef]
- Stanley, H.E.; Gabaix, X.; Gopikrishnan, P.; Plerou, V. Economic fluctuations and statistica lphysics: The puzzle of large fluctuations. Nonlinear Dyn. 2006, 44, 329340. [Google Scholar] [CrossRef]
- Elliott, R.J.; Siu, T.K.; Fung, E.S. Filtering a nonlinear stochastic volatility model. Nonlinear Dyn. 2012, 67, 1295–1313. [Google Scholar] [CrossRef]
- French, K.R.; Schwert, G.W.; Stambaugh, R.F. Expected Stock Returns and Volatility. J. Financ. Econ. 1987, 19, 3–29. [Google Scholar] [CrossRef]
- Wang, T.; Wu, J.T.; Yang, J. Realized volatility and correlation in energy futures markets. J. Futures Mark. 2008, 28, 993–1011. [Google Scholar] [CrossRef]
- Wang, F.; Yamasaki, K.; Havlin, S.; Stanley, H.E. Scaling and memory of intraday volatility return intervals in stock markets. Phys. Rev. E 2016, 73, 026117. [Google Scholar] [CrossRef] [PubMed]
- Xie, W.J.; Jiang, Z.Q.; Zhou, W.X. Extreme value statistics and recurrence intervals of NYMEX energy futures volatility. Econ. Model. 2014, 36, 8–17. [Google Scholar] [CrossRef]
- Yang, G.; Wang, J.; Deng, W. Nonlinear analysis of volatility duration financial series model by stochastic interacting dynamic system. Nonlinear Dyn. 2015, 80, 701–713. [Google Scholar] [CrossRef]
- Niu, H.; Wang, J. Return volatility duration analysis of NYMEX energy futures and spot. Energy 2017, 140, 837–849. [Google Scholar] [CrossRef]
- Wang, G.C.; Wang, J. New approach of financial volatility duration dynamics by stochastic finite-range interacting voter system. Chaos 2017, 27, 013117. [Google Scholar] [CrossRef]
- Jia, L.L.; Ke, J.C.; Wang, J. Volatility aggregation intensity energy futures series on stochastic finite-range exclusion dynamics. Phys. A 2019, 514, 370–383. [Google Scholar] [CrossRef]
- Niu, H.; Wang, W.Q.; Zhang, J.H. Recurrence duration statistics and time-dependent instrinsic correlation analysis of trading volumes: A study of Chinese stock indices. Phys. A 2019, 514, 828–854. [Google Scholar] [CrossRef]
- Cont, R. Empirical properties of asset returns: Stylized facts and statistical issues. Quant. Financ. 2001, 1, 223–236. [Google Scholar] [CrossRef]
- Lux, T.; Marchesi, M. Volatility clustering in financial markets: A microsimulation of interacting agents. Int. J. Theor. Appl. Financ. 2000, 3, 675–702. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, J. Lattice-oriented percolation system applied to volatility behavior of stock market. J. Appl. Stat. 2012, 39, 785–797. [Google Scholar] [CrossRef]
- Alvarezramirez, J.; Alvarez, J.; Rodrguez, E. Asymmetric long-term autocorrelations in crude oil markets. Phys. A 2015, 424, 33–341. [Google Scholar]
- Wang, X.Y.; He, Y. Projective synchronization of fractional order chaotic system based on linear separation. Phys. Lett. A 2008, 372, 435–441. [Google Scholar] [CrossRef]
- Meng, J.; Wang, X.Y. Generalized synchronization via nonlinear control. Chaos 2018, 18, 023108. [Google Scholar]
- Wu, S.D.; Wu, C.W.; Lin, S.G.; Wang, C.C.; Lee, K.Y. Time series analysis using composite multiscale entropy. Entropy 2013, 15, 1069–1084. [Google Scholar] [CrossRef]
- Benettin, G.; Galgani, L.; Strelcyn, J.M. Kolmogorov entropy and numerical experiments. Phys. Rev. A 1976, 14, 2338–2345. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. 2000, 278, 2039–2049. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef]
- Chen, W.T.; Wang, Z.Z.; Xie, H.; Yu, W. Characterization of surface EMG signal based on fuzzy entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef]
- Chen, W.T.; Zhuang, J.; Yu, W.X.; Wang, Z.Z. Measuring complexity using FuzzyEn, ApEn, and SampEn. Med. Eng. Phys. 2009, 31, 61–68. [Google Scholar] [CrossRef]
- Wu, S.D.; Wu, P.H.; Wu, C.W.; Ding, J.J.; Wang, C.C. Bearing fault diagnosis based on multiscale permutation entropy and support vector machine. Entropy 2012, 14, 1343–1356. [Google Scholar] [CrossRef]
- Graff, B.; Graff, G.; Kaczkowska, A. Entropy measures of heart rate variability for short ECG datasets inpatients with congestive heart failure. Acta Phys. Pol. B Proc. Suppl. 2012, 5, 153–158. [Google Scholar] [CrossRef]
- Xie, H.B.; Zheng, Y.P.; Guo, J.Y.; Chen, X. Cross-fuzzy entropy: A new method to test pattern synchrony of bivariate time series. Inf. Sci. 2010, 180, 1715–1724. [Google Scholar] [CrossRef]
- Darbellay, G.A.; Wuertz, D. The entropy as a tool for analysing statistical dependences in financial time series. Phys. A 2000, 287, 429–439. [Google Scholar] [CrossRef]
- Risso, W.A. The informational efficiency and the financial crashes. Res. Int. Bus. Financ. 2008, 22, 396–408. [Google Scholar] [CrossRef]
- Batista, G.E.; Keogh, E.J.; Tataw, O.M.; de Souza, V.M. CID: An efficient complexity-invariant distance for time series. Data Min. Knowl. Discov. 2014, 28, 634–669. [Google Scholar] [CrossRef]
- Baumert, M.; Czippelova, B.; Porta, A.; Javorka, M. Decoupling of QT interval variability from heart rate variability with ageing. Physiol. Meas. 2013, 34, 1435–1448. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.H.; Huang, N.E. Ensemble empirical mode decomposition: a noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Sharma, G.K.; Kumar, A.; Jayakumar, T.; Rao, B.P.; Mariyappa, N. Ensemble empirical mode decomposition based methodology for ultrasonic testing of coarse grain austenitic stainless steels. Ultrasonics 2015, 57, 167–178. [Google Scholar] [CrossRef]
- Ilinski, K. Physics of Finance: Gauge Modelling in Non-Equilibrium Pricing; Wiley: New York, NJ, USA, 2001. [Google Scholar]
- Gabaix, X.; Gopikrishnan, P.; Plerou, V.; Stanley, H.E. A Theory of Power-Law Distributions in Financial Market Fluctuations. Nature 2003, 423, 267–270. [Google Scholar] [CrossRef]
- Lux, T. Financial Power Laws: Empirical Evidence, Models and Mechanisms; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Tsay, R.S. Analysis of Financial Time Series; Wiley: New York, NJ, USA, 2005. [Google Scholar]
- Yang, G.; Wang, J. Complexity and multifractal of volatility duration for agent-based financial dynamics and real markets. Fractals 2016, 23, 1650052. [Google Scholar] [CrossRef]
- Kyriazis, N.A. A survey on efficiency and profitable trading opportunities in cryptocurrency markets. J. Risk Financ. Manag. 2019, 12, 67. [Google Scholar] [CrossRef]
- Malkiel, B.G. The efficient market hypothesis and its critics. J. Econ. Perspect. 2003, 17, 59–82. [Google Scholar] [CrossRef]



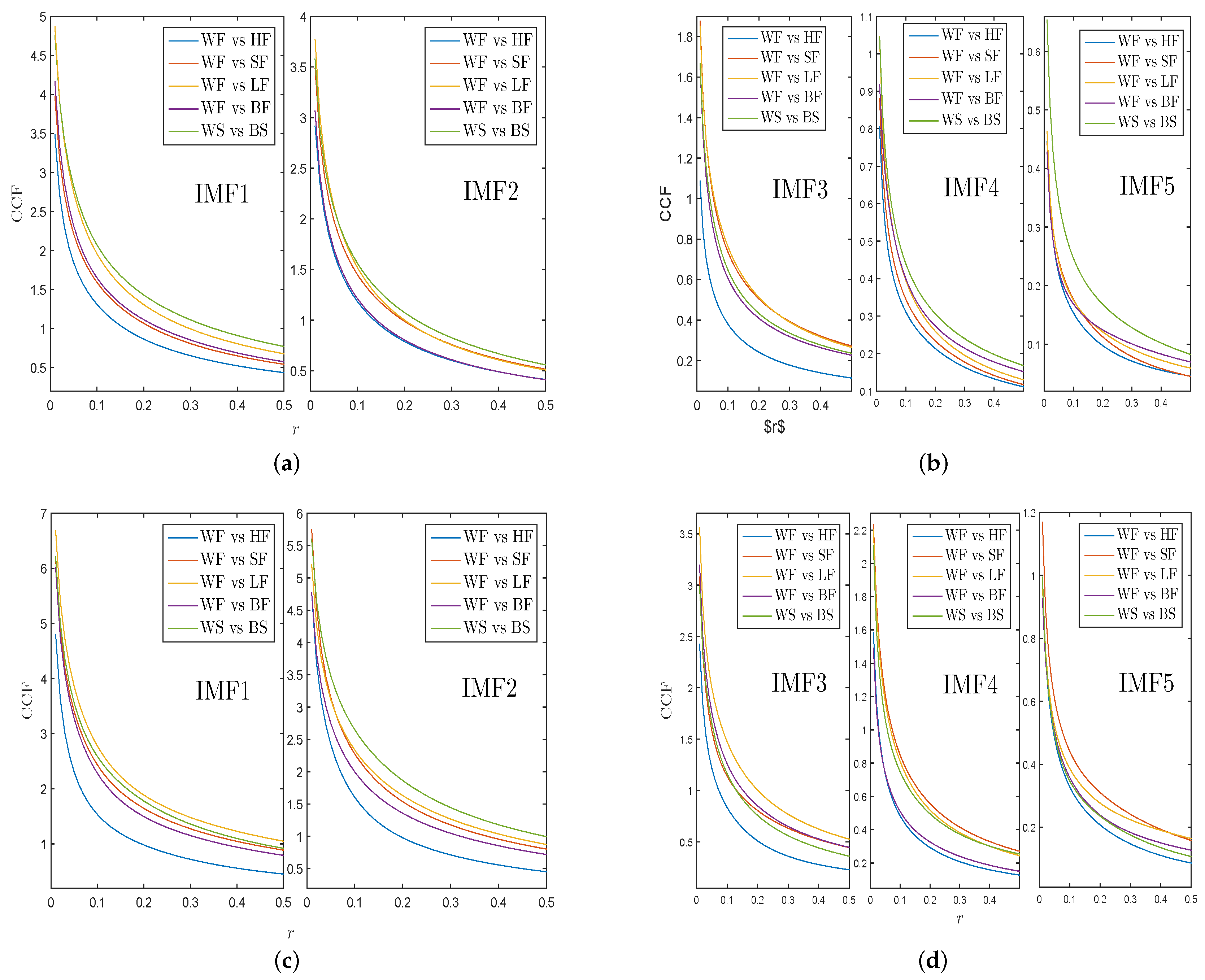
| Descriptive Statistics | K-S Test | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Returns | Mean | Std | Min | Max | Kurtosis | Skewness | stat | H | ||
| WF | −0.0001 | 0.0204 | −0.0907 | 0.1162 | 5.8938 | 0.1460 | 0.4715 | 1.0000 | ||
| WS | −0.0001 | 0.0198 | −0.1065 | 0.1172 | 6.0158 | 0.0262 | 0.4710 | 1.0000 | ||
| BF | −0.0001 | 0.0190 | −0.0896 | 0.1042 | 6.1393 | 0.1108 | 0.4711 | 1.0000 | ||
| BS | −0.0001 | 0.0195 | −0.0825 | 0.0990 | 5.4787 | 0.2114 | 0.4737 | 1.0000 | ||
| HF | 0.0000 | 0.0178 | −0.1973 | 0.1038 | 13.3248 | −0.6039 | 0.4729 | 1.0000 | ||
| LF | −0.0000 | 0.0161 | −0.0899 | 0.1209 | 7.8970 | 0.3297 | 0.4753 | 1.0000 | ||
| SF | 0.0004 | 0.0184 | −0.2480 | 0.1215 | 22.9517 | −1.1360 | 0.4742 | 1.0000 | ||
| VMPD | Mean | Std | Min | Max | Kurtosis | Skewness | stat | H | ||
| WF | 0.0002 | 0.0404 | −0.3188 | 0.2920 | 11.2956 | −0.3545 | 0.4462 | 1.0000 | ||
| WS | 0.0004 | 0.0374 | −0.3128 | 0.2250 | 12.1775 | −0.8374 | 0.4510 | 1.0000 | ||
| BF | 0.0017 | 0.0394 | −0.3240 | 0.2644 | 11.4187 | −0.2208 | 0.4446 | 1.0000 | ||
| BS | 0.0017 | 0.0400 | −0.2844 | 0.3496 | 15.6557 | 0.7868 | 0.4491 | 1.0000 | ||
| HF | 0.0007 | 0.0397 | −0.7714 | 0.3642 | 81.2650 | −3.3956 | 0.4513 | 1.0000 | ||
| LF | 0.0005 | 0.0327 | −0.2136 | 0.2296 | 10.3138 | −0.0179 | 0.4535 | 1.0000 | ||
| SF | −0.0003 | 0.0387 | −0.4821 | 0.3376 | 24.3661 | −0.8844 | 0.4473 | 1.0000 | ||
| Absolute Returns | |||||
| WF | −3.5225 | [−3.6036, −3.4415] | −14.1690 | [−14.4209, −13.9170] | 0.9742 |
| WS | −3.4647 | [−3.5343, −3.3950] | −14.1205 | [−14.3397, −13.9014] | 0.9802 |
| BF | −3.3820 | [−3.4449, −3.3191] | −13.9679 | [−14.1679, −13.7679] | 0.9830 |
| BS | −3.7610 | [−3.8267, −3.6953] | −15.0741 | [−15.2810, −14.8673] | 0.9852 |
| HF | −3.1425 | [−3.2046, −3.0804] | −13.5066 | [−13.7100, −13.3032] | 0.9807 |
| LF | −3.2734 | [−3.3305, −3.2164] | −14.2189 | [−14.4090, −14.0288] | 0.9861 |
| SF | −4.1244 | [−4.2191, −4.0296] | −16.2797 | [−16.5734, −15.9860] | 0.9809 |
| Absolute VMPD | |||||
| WF | −2.8520 | [−2.9075, −2.7966] | −10.0813 | [−10.2152, −9.9474] | 0.9814 |
| WS | −3.0446 | [−3.0999, −2.9894] | −10.7910 | [−10.9287, −10.6533] | 0.9838 |
| BF | −2.8119 | [−2.9011, −2.7227] | −9.9982 | [−10.2141, −9.7823] | 0.9517 |
| BS | −2.6108 | [−2.6395, −2.5820] | −9.6324 | [−9.7034, −9.5615] | 0.9940 |
| HF | −2.6961 | [−2.7462, −2.6460] | −10.0468 | [−10.1742, −9.9195] | 0.9829 |
| LF | −2.6410 | [−2.6972, −2.5847] | −10.1502 | [−10.2981, −10.0023] | 0.9780 |
| SF | −2.8223 | [−2.8821, −2.7624] | −10.1431 | [−10.2863, −9.9998] | 0.9819 |
| Rerurns | |||||
|---|---|---|---|---|---|
| BF vs. LF | 0.4143 | 0.5508 | 0.6289 | 0.6832 | 0.7234 |
| BF vs. SF | 0.2449 | 0.3919 | 0.4906 | 0.5620 | 0.6168 |
| BF vs. HF | 0.2445 | 0.3918 | 0.4897 | 0.5618 | 0.6175 |
| BF vs. WF | 0.1922 | 0.3280 | 0.4258 | 0.5022 | 0.5627 |
| BS vs. WS | 0.1261 | 0.2391 | 0.3289 | 0.4021 | 0.4628 |
| WF vs. HF | 0.2699 | 0.4209 | 0.5206 | 0.5923 | 0.6468 |
| WF vs. SF | 0.2036 | 0.3441 | 0.4457 | 0.5219 | 0.5812 |
| WF vs. LF | 0.1411 | 0.2706 | 0.3694 | 0.4465 | 0.5077 |
| WF vs. BF | 0.1922 | 0.3280 | 0.4258 | 0.5022 | 0.5627 |
| WS vs. BS | 0.1261 | 0.2391 | 0.3289 | 0.4021 | 0.4628 |
| VMPD | |||||
|---|---|---|---|---|---|
| BF vs. LF | 0.1685 | 0.2873 | 0.3719 | 0.4381 | 0.4924 |
| BF vs. SF | 0.1146 | 0.2371 | 0.3314 | 0.4072 | 0.4699 |
| BF vs. HF | 0.1606 | 0.3067 | 0.4128 | 0.4940 | 0.5583 |
| BF vs. WF | 0.1024 | 0.2242 | 0.3159 | 0.3901 | 0.4523 |
| BS vs. WS | 0.1024 | 0.2242 | 0.3159 | 0.3901 | 0.4523 |
| WF vs. HF | 0.2157 | 0.3750 | 0.4866 | 0.5710 | 0.6349 |
| WF vs. SF | 0.0879 | 0.1932 | 0.2793 | 0.3508 | 0.4114 |
| WF vs. LF | 0.0624 | 0.1515 | 0.2274 | 0.2924 | 0.3497 |
| WF vs. BF | 0.1024 | 0.2242 | 0.3159 | 0.3901 | 0.4523 |
| WS vs. BS | 0.0754 | 0.1690 | 0.2564 | 0.3329 | 0.3982 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, L.; Ke, J.; Wang, J. Complexity Synchronization of Energy Volatility Monotonous Persistence Duration Dynamics. Entropy 2019, 21, 1018. https://doi.org/10.3390/e21101018
Jia L, Ke J, Wang J. Complexity Synchronization of Energy Volatility Monotonous Persistence Duration Dynamics. Entropy. 2019; 21(10):1018. https://doi.org/10.3390/e21101018
Chicago/Turabian StyleJia, Linlu, Jinchuan Ke, and Jun Wang. 2019. "Complexity Synchronization of Energy Volatility Monotonous Persistence Duration Dynamics" Entropy 21, no. 10: 1018. https://doi.org/10.3390/e21101018
APA StyleJia, L., Ke, J., & Wang, J. (2019). Complexity Synchronization of Energy Volatility Monotonous Persistence Duration Dynamics. Entropy, 21(10), 1018. https://doi.org/10.3390/e21101018




