Optimized Dimensionality Reduction Methods for Interval-Valued Variables and Their Application to Facial Recognition
Abstract
1. The Center Method
2. The Best Point Method
- Case 1:
- Case 2:
- Case 3: Let and .For Case 1 applied toFor Case 2 applied to
2.1. Minimizing the Square of the Distance from the Hypercube Vertices to the Principal Axes of Z
| Algorithm 1 The computation of . |
| Require:Xan matrix of intervals, , s number of principal components. Ensure:
|
| Algorithm 2 Computation of the Best Matrix with respect to the distances of the vertices. |
| Require:Xa symbolic matrix of intervals of dimension , , s number of principal components, is the variation tolerance between iterations, and N is the maximum number of iterations. Ensure:.
|
2.2. Maximizing the Variance of the First Components
| Algorithm 3 The computation of . |
| Require:Xan symbolic matrix of intervals of dimension , s number of principal components. Ensure:.
|
| Algorithm 4 The computation of the Best Matrix with respect to inertia. |
| Require:Xan symbolic matrix of intervals of dimension, , s number of principal components. Ensure:.
|
3. Experimental Evaluation: The Application to Facial Recognition
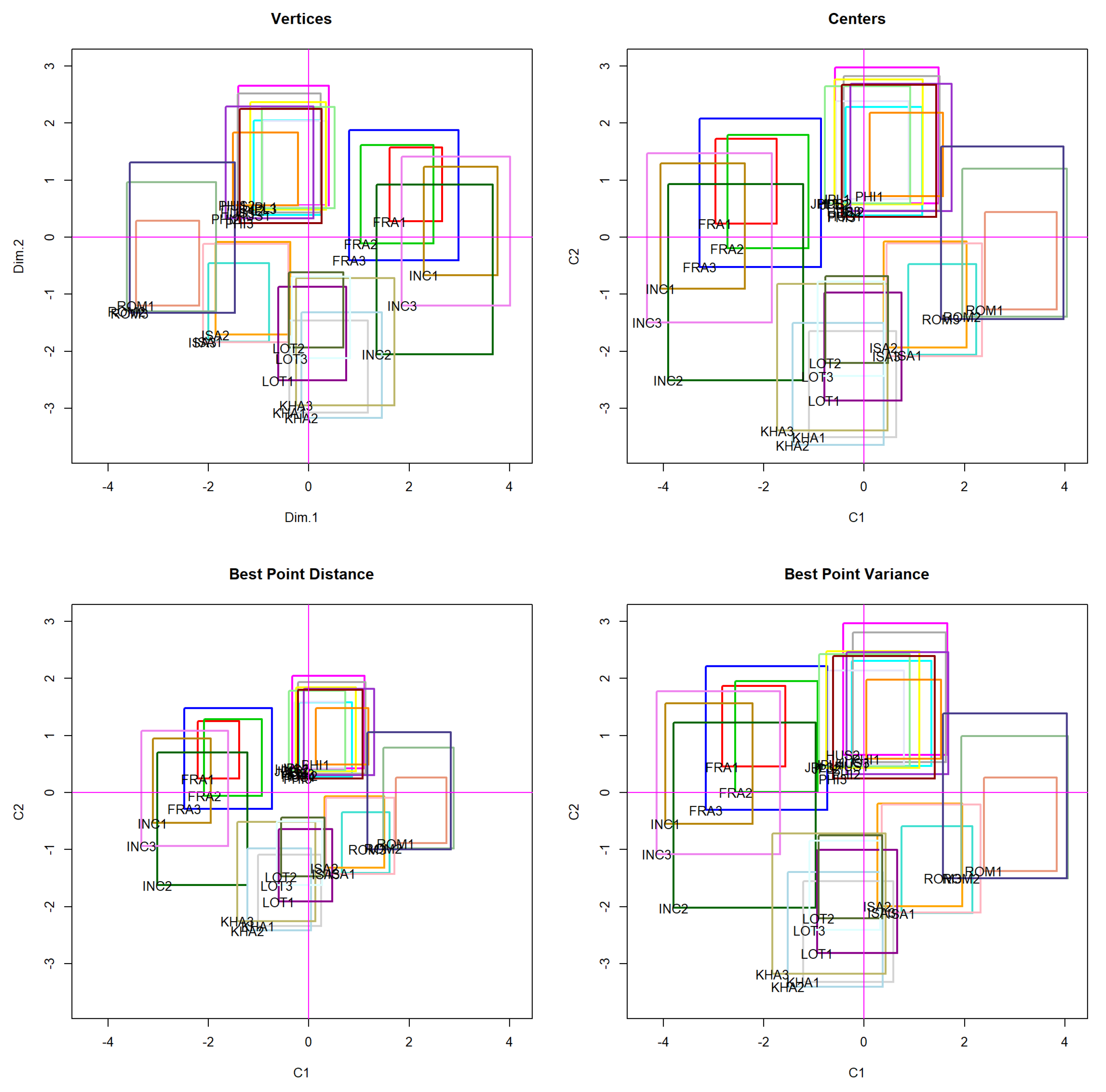
Comparison between the Center, Vertex, and Best Point Methods
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Diday, E. Introduction a lApproache Symbolique en Analyse des Données. RAIRO Oper. Res. 1989, 23, 193–236. [Google Scholar] [CrossRef]
- Billard, L.; Diday, E. Symbolic Data Analysis: Conceptual Statistics and Data Mining; John Wiley & Sons Ltd: Chichester, UK, 2006. [Google Scholar]
- Cazes, P.; Chouakria, A.; Diday, E.; Schektman, Y. Extension de l’analyse en com-posantes principales á des données de type intervalle. Rev. Stat. Appl. 1997, 3, 5–24. [Google Scholar]
- Douzal-Chouakria, A.; Billard, L.; Diday, E. Principal component analysis for interval-valued observations. Stat. Anal. Data Min. 2011, 4, 229–246. [Google Scholar] [CrossRef]
- Lauro, C.; Palumbo, F. Principal Component Analysis of Interval Data: A Symbolic Data Analysis Approach. Comput. Stat. 2000, 15, 73–87. [Google Scholar] [CrossRef]
- Le-Rademacher, J.; Billard, L. Symbolic Covariance Principal Component Analysis and Visualization for Interval-Valued Data. J. Comput. Gr. Stat. 2012, 21, 413–432. [Google Scholar] [CrossRef]
- Diday, E. Principal component analysis for bar charts and metabins tables. Stat. Anal. Data Min. 2013, 6, 403–430. [Google Scholar] [CrossRef]
- Diday, E.; Emilion, R.; Wang, C.; Wang, H.; Wang, S. Sampling Based Histogram PCA and its Mapreduce Parallel Implementation on Multicore. Symmetry 2018, 10, 5. [Google Scholar]
- Ichino, M. Symbolic PCA for histogram-valued data. In Proceedings of the IASC, Yokohama, Japan, 5–8 December 2008. [Google Scholar]
- Kallyth, S.M. Analyse en Composantes Principales de Variables Symboliques de Type Histogramme. Ph.D. Thesis, Université Paris-Dauphine, Paris, France, 2010. [Google Scholar]
- Rodrıguez, O.; Diday, E.; Winsberg, S. Generalization of the principal components analysis to histogram data. In Proceedings of the 4th European Conference on Principles of Data Mining and Knowledge Discovery, Lyon, France, 13–16 September 2000. [Google Scholar]
- Rodríguez, O. Classification et Modèles Linéaires en Analyse des Données Symboliques. PhD Thesis, Paris IX-Dauphine University, Paris, France, 2000. [Google Scholar]
- Arce, J. Dimensionality Reduction Methods for Symbolic Interval Variables. Master’s Thesis, University of Costa Rica, San José, Costa Rica, 2018. [Google Scholar]
- Leroy, B.; Chouakria, A.; Herlin, I.; Diday, E. Approche geometrique et classication pour la reconnaissance de visage. Reconnaissance des Forms et Intelligence Artificelle. In Proceedings of the Congrès de Reconnaissance des Formes et IntelligenceArtificielle, Rennes, France, January 1996; pp. 548–557. (In France). [Google Scholar]
- Rodríguez, O. RSDA—R to Symbolic Data Analysis. R Package Version 2.0.8. 2019. Available online: http://CRAN.R-project.org/package=RSDA (accessed on 16 October 2019).
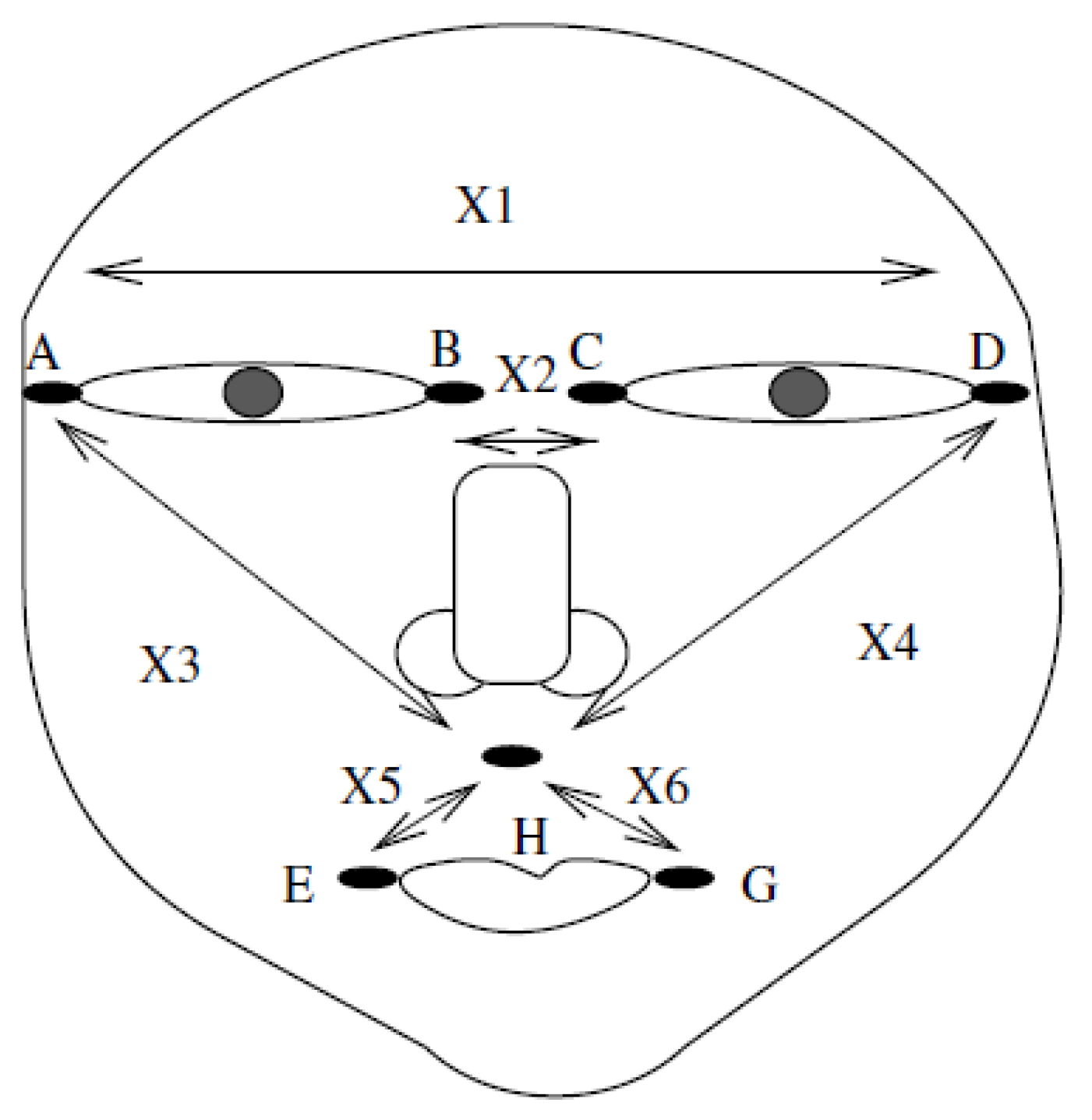
| Case | AD | BC | AH | DH | EH | GH |
|---|---|---|---|---|---|---|
| FRA1 | [155.00, 157.00] | [58.00, 61.01] | [100.45, 103.28] | [105.00, 107.30] | [61.40, 65.73] | [64.20, 67.80] |
| FRA2 | [154.00, 160.01] | [57.00, 64.00] | [101.98, 105.55] | [104.35, 107.30] | [60.88, 63.03] | [62.94, 66.47] |
| FRA3 | [154.01, 161.00] | [57.00, 63.00] | [99.36, 105.65] | [101.04, 109.04] | [60.95, 65.60] | [60.42, 66.40] |
| HUS1 | [168.9,172.84] | [58.55,63.39] | [102.83,106.53] | [122.38,124.52] | [56.73,61.07] | [60.44,64.54] |
| HUS2 | [169.8,175.03] | [60.21,64.38] | [102.94,108.71] | [120.24,124.52] | [56.73,62.37] | [60.44,66.84] |
| HUS3 | [168.8,175.15] | [61.4,63.51] | [104.35,107.45] | [120.93,125.18] | [57.2,61.72] | [58.14,67.08] |
| INC1 | [155.3,160.45] | [53.15,60.21] | [95.88,98.49] | [91.68,94.37] | [62.48,66.22] | [58.9,63.13] |
| INC2 | [156.3,161.31] | [51.09,60.07] | [95.77,99.36] | [91.21,96.83] | [54.92,64.2] | [54.41,61.55] |
| INC3 | [154.5,160.31] | [55.08,59.03] | [93.54,98.98] | [90.43,96.43] | [59.03,65.86] | [55.97,65.8] |
| ISA1 | [164,168] | [55.01,60.03] | [120.28,123.04] | [117.52,121.02] | [54.38,57.45] | [50.8,53.25] |
| ISA2 | [163,170] | [54.04,59] | [118.8,123.04] | [116.67,120.24] | [55.47,58.67] | [52.43,55.23] |
| ISA3 | [164,169.01] | [55,59.01] | [117.38,123.11] | [116.67,122.43] | [52.8,58.31] | [52.2,55.47] |
| JPL1 | [167.1,171.19] | [61.03,65.01] | [118.23,121.82] | [108.3,111.2] | [63.89,67.88] | [57.28,60.83] |
| JPL2 | [169.1,173.18] | [60.07,65.07] | [118.85,120.88] | [108.98,113.17] | [62.63,69.07] | [57.38,61.62] |
| JPL3 | [169,170.11] | [59.01,65.01] | [115.88,121.38] | [110.34,112.49] | [61.72,68.25] | [59.46,62.94] |
| KHA1 | [149.3,155.54] | [54.15,59.14] | [111.95,115.75] | [105.36,111.07] | [54.2,58.14] | [48.27,50.61] |
| KHA2 | [149.3,155.32] | [52.04,58.22] | [111.2,113.22] | [105.36,111.07] | [53.71,58.14] | [49.41,52.8] |
| KHA3 | [150.3,157.26] | [52.09,60.21] | [109.04,112.7] | [104.74,111.07] | [55.47,60.03] | [49.2,53.41] |
| LOT1 | [152.6,157.62] | [51.35,56.22] | [116.73,119.67] | [114.62,117.41] | [55.44,59.55] | [53.01,56.6] |
| LOT2 | [154.6,157.62] | [52.24,56.32] | [117.52,119.67] | [114.28,117.41] | [57.63,60.61] | [54.41,57.98] |
| LOT3 | [154.8,157.81] | [50.36,55.23] | [117.59,119.75] | [114.04,116.83] | [56.64,61.07] | [55.23,57.8] |
| PHI1 | [163.1,167.07] | [66.03,68.07] | [115.26,119.6] | [116.1,121.02] | [60.96,65.3] | [57.01,59.82] |
| PHI2 | [164,168.03] | [65.03,68.12] | [114.55,119.6] | [115.26,120.97] | [60.96,67.27] | [55.32,61.52] |
| PHI3 | [161,167] | [64.07,69.01] | [116.67,118.79] | [114.59,118.83] | [61.52,68.68] | [56.57,60.11] |
| ROM1 | [167.2,171.24] | [64.07,68.07] | [123.75,126.59] | [122.92,126.37] | [51.22,54.64] | [49.65,53.71] |
| ROM2 | [168.2,172.14] | [63.13,68.07] | [122.33,127.29] | [124.08,127.14] | [50.22,57.14] | [49.93,56.94] |
| ROM3 | [167.1,171.19] | [63.13,68.03] | [121.62,126.57] | [122.58,127.78] | [49.41,57.28] | [50.99,60.46] |
| Vertex | Center | Best Point Distance | Best Point Variance | |||||
|---|---|---|---|---|---|---|---|---|
| Cases | PC1 | PC2 | PC1 | PC2 | PC1 | PC2 | PC1 | PC2 |
| FRA1 | [1.61,2.66] | [0.27,1.57] | [-2.97,-1.75] | [0.24,1.72] | [,] | [0.24,1.25] | [,] | [0.45,1.87] |
| FRA2 | [1.03,2.49] | [,1.61] | [,] | [,1.79] | [,] | [,1.29] | [,] | [0.01,1.95] |
| FRA3 | [0.81,2.99] | [,1.88] | [,] | [,2.08] | [,] | [,1.48] | [,] | [,2.21] |
| HUS1 | [,0.24] | [0.39,2.05] | [,1.16] | [0.38,2.28] | [,0.86] | [0.28,1.58] | [,1.34] | [0.47,2.31] |
| HUS2 | [,0.4] | [0.56,2.65] | [,1.48] | [0.59,2.98] | [,1.11] | [0.42,2.04] | [,1.66] | [0.66,2.97] |
| HUS3 | [,0.24] | [0.43,2.52] | [,1.51] | [0.46,2.82] | [,1.13] | [0.33,1.94] | [,1.63] | [0.53,2.8] |
| INC1 | [2.29,3.77] | [,1.23] | [,] | [,1.29] | [,] | [,0.95] | [,] | [,1.56] |
| INC2 | [1.35,3.66] | [,0.92] | [,] | [,0.93] | [,] | [,0.7] | [,] | [,1.22] |
| INC3 | [1.86,4.02] | [,1.41] | [,] | [,1.47] | [,] | [,1.08] | [,] | [,1.77] |
| ISA1 | [,] | [,] | [0.88,2.24] | [,] | [0.66,1.61] | [,] | [0.75,2.15] | [,] |
| ISA2 | [,] | [,] | [0.39,2.04] | [,] | [0.32,1.51] | [,] | [0.26,1.95] | [,] |
| ISA3 | [,] | [,] | [0.44,2.36] | [,] | [0.34,1.7] | [,] | [0.35,2.32] | [,] |
| JPL1 | [,0.36] | [0.54,2.03] | [,0.89] | [0.67,2.38] | [,0.73] | [0.43,1.59] | [,0.79] | [0.49,2.14] |
| JPL2 | [,0.34] | [0.48,2.37] | [,1.17] | [0.58,2.76] | [,0.93] | [0.37,1.84] | [,1.1] | [0.43,2.47] |
| JPL3 | [,0.52] | [0.5,2.28] | [,0.92] | [0.59,2.64] | [,0.73] | [0.38,1.78] | [,0.91] | [0.45,2.43] |
| KHA1 | [,1.18] | [,] | [,0.64] | [,] | [,0.25] | [,] | [,0.58] | [,] |
| KHA2 | [,1.46] | [,] | [,0.39] | [,] | [,0.05] | [,] | [,0.37] | [,] |
| KHA3 | [,1.71] | [,] | [,0.47] | [,] | [,0.13] | [,] | [,0.43] | [,] |
| LOT1 | [,0.74] | [,] | [,0.74] | [,] | [,0.47] | [,] | [,0.66] | [,] |
| LOT2 | [,0.69] | [,] | [,0.47] | [,] | [,0.31] | [,] | [,0.36] | [,] |
| LOT3 | [,0.82] | [,] | [,0.41] | [,] | [,0.26] | [,] | [,0.33] | [,] |
| PHI1 | [,] | [0.56,1.84] | [0.11,1.57] | [0.72,2.18] | [0.14,1.19] | [0.49,1.47] | [0.05,1.53] | [0.59,1.97] |
| PHI2 | [,0.09] | [0.33,2.29] | [,1.74] | [0.45,2.69] | [,1.3] | [0.3,1.82] | [,1.67] | [0.32,2.46] |
| PHI3 | [,0.25] | [0.25,2.25] | [,1.44] | [0.36,2.67] | [,1.07] | [0.25,1.8] | [,1.4] | [0.24,2.39] |
| ROM1 | [,] | [,0.29] | [2.41,3.84] | [,0.44] | [1.74,2.74] | [,0.26] | [2.39,3.84] | [,0.26] |
| ROM2 | [,] | [,0.97] | [1.96,4.04] | [,1.2] | [1.49,2.89] | [,0.79] | [1.94,4.06] | [,0.99] |
| ROM3 | [,] | [,1.31] | [1.53,3.98] | [,1.58] | [1.17,2.83] | [,1.06] | [1.57,4.04] | [,1.39] |
| Vertex | Center | Best Point Distance | Best Point Variance | |
|---|---|---|---|---|
| PC1 | 42.67% | 46.47% | 45.49% | 56.01% |
| PC2 | 72.64% | 80.53% | 81.05% | 88.31% |
| PC3 | 83.35% | 89.65% | 91.25% | 99.72% |
| PC4 | 91.28% | 95.06% | 95.80% | 99.85% |
| PC5 | 96.86% | 98.96% | 99.28% | 99.97% |
| PC6 | 100.00% | 100.00% | 100.00% | 100.00% |
| Vertex | Center | Best Point Distance | Best Point Variance | |
|---|---|---|---|---|
| 10368.00 | 12719.64 | 6676.43 | 12457.09 |
| AD | BC | AH | DH | EH | GH | |
|---|---|---|---|---|---|---|
| Vertex-PC1 | 0.64 | 0.49 | 0.84 | 0.89 | −0.47 | −0.43 |
| Center-PC1 | 0.61 | 0.47 | 0.83 | 0.88 | −0.52 | −0.47 |
| BestPointDistance-PC1 | 0.65 | 0.48 | 0.84 | 0.90 | −0.46 | −0.43 |
| BestPointVariance-PC1 | 0.63 | 0.49 | 0.80 | 0.88 | −0.55 | −0.43 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arce Garro, J.; Rodríguez Rojas, O. Optimized Dimensionality Reduction Methods for Interval-Valued Variables and Their Application to Facial Recognition. Entropy 2019, 21, 1016. https://doi.org/10.3390/e21101016
Arce Garro J, Rodríguez Rojas O. Optimized Dimensionality Reduction Methods for Interval-Valued Variables and Their Application to Facial Recognition. Entropy. 2019; 21(10):1016. https://doi.org/10.3390/e21101016
Chicago/Turabian StyleArce Garro, Jorge, and Oldemar Rodríguez Rojas. 2019. "Optimized Dimensionality Reduction Methods for Interval-Valued Variables and Their Application to Facial Recognition" Entropy 21, no. 10: 1016. https://doi.org/10.3390/e21101016
APA StyleArce Garro, J., & Rodríguez Rojas, O. (2019). Optimized Dimensionality Reduction Methods for Interval-Valued Variables and Their Application to Facial Recognition. Entropy, 21(10), 1016. https://doi.org/10.3390/e21101016




