Using Multiscale Entropy to Assess the Efficacy of Local Cooling on Reactive Hyperemia in People with a Spinal Cord Injury
Abstract
1. Introduction
2. Methods
2.1. Participants
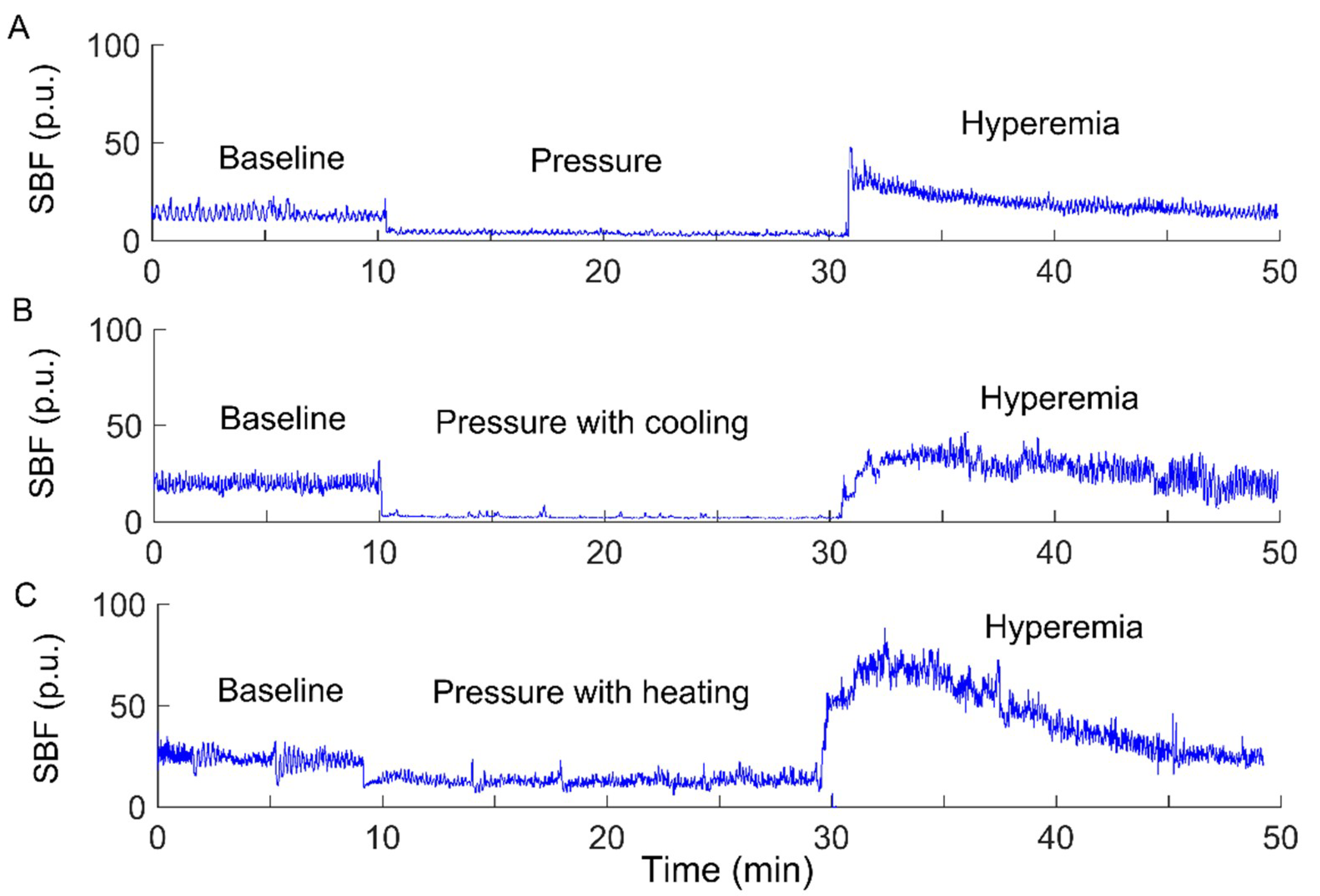
2.2. Data Collection
2.3. Data Analysis
2.3.1. Modified Sample Entropy
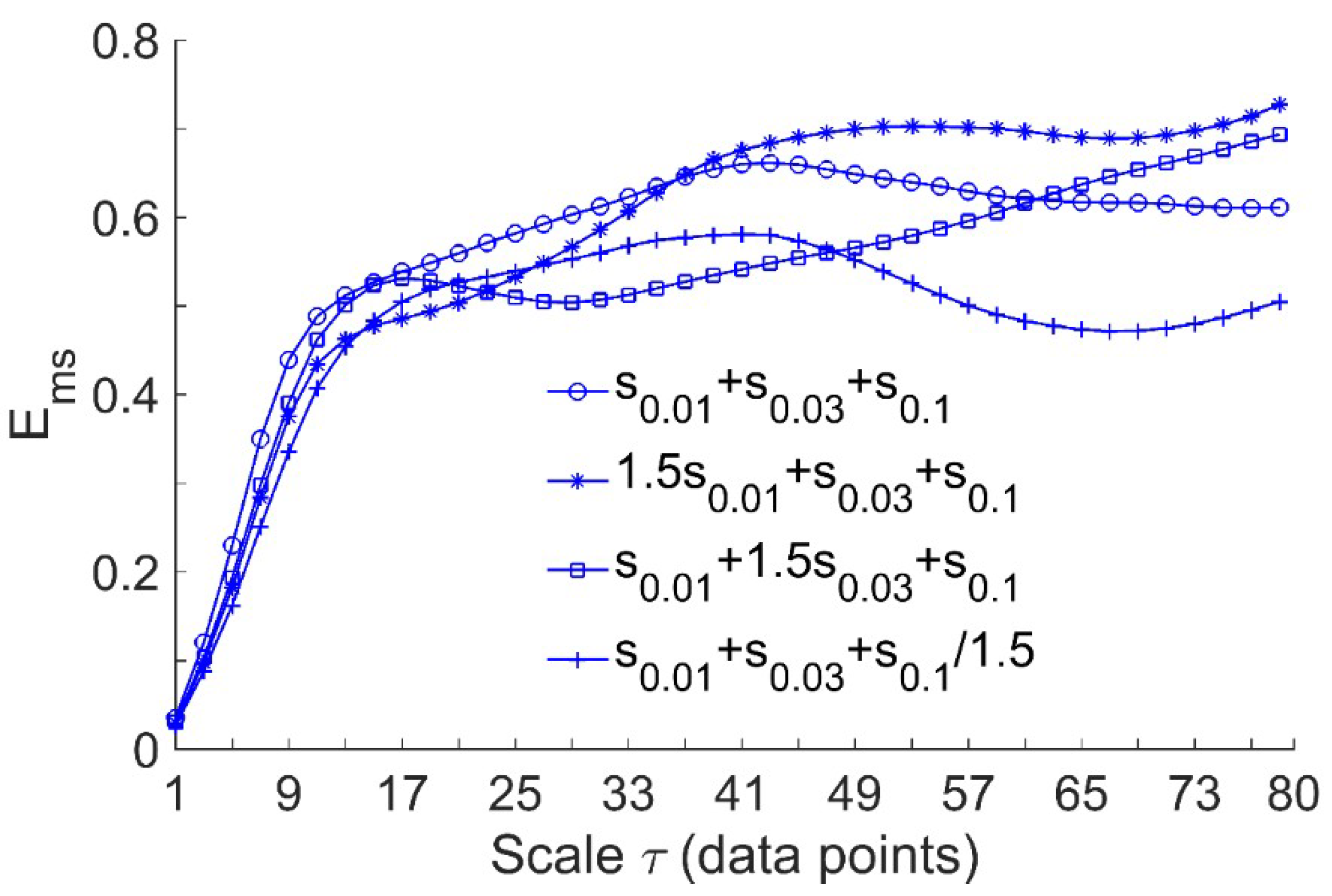
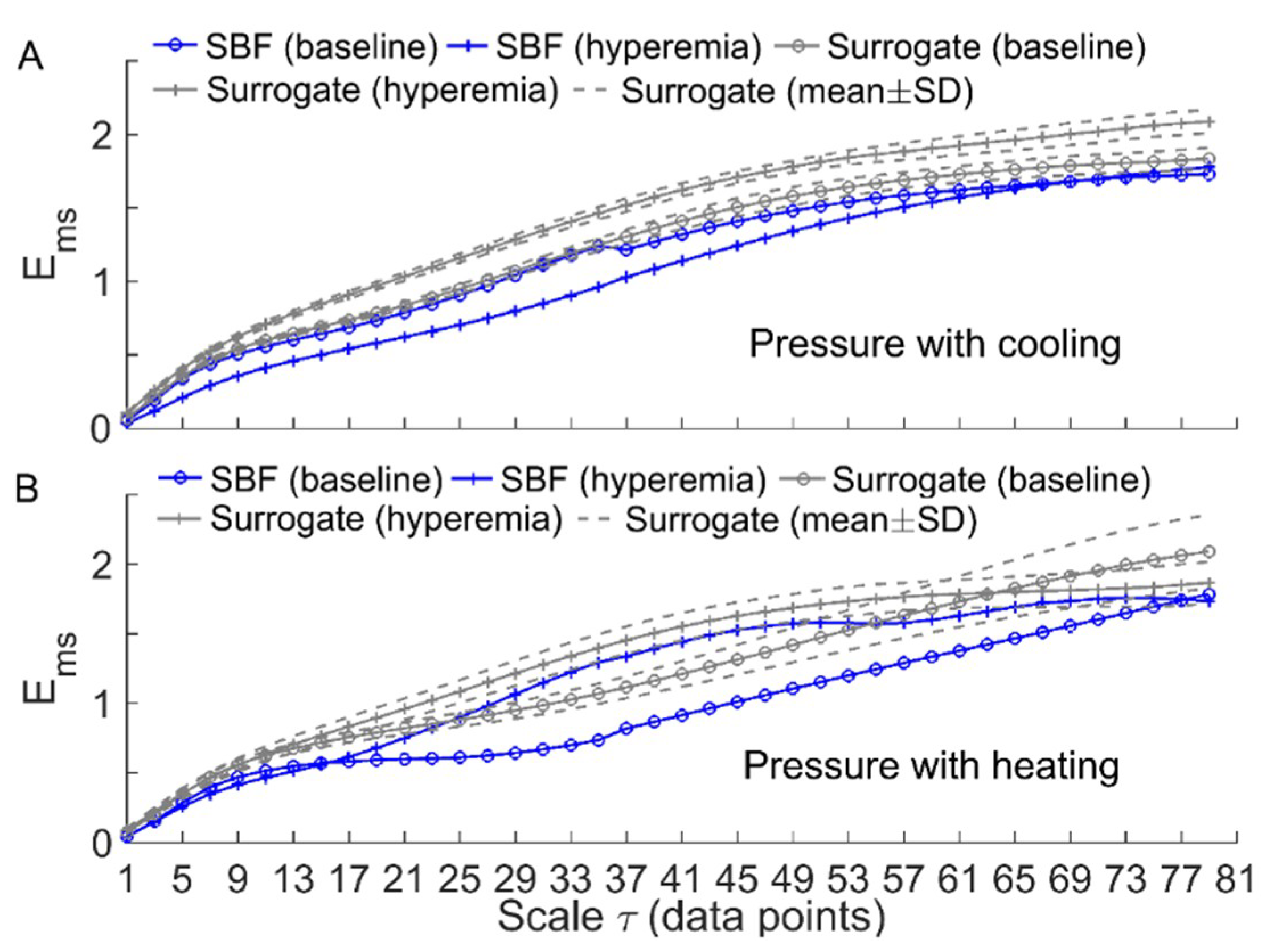
2.3.2. Multiscale Entropy Method
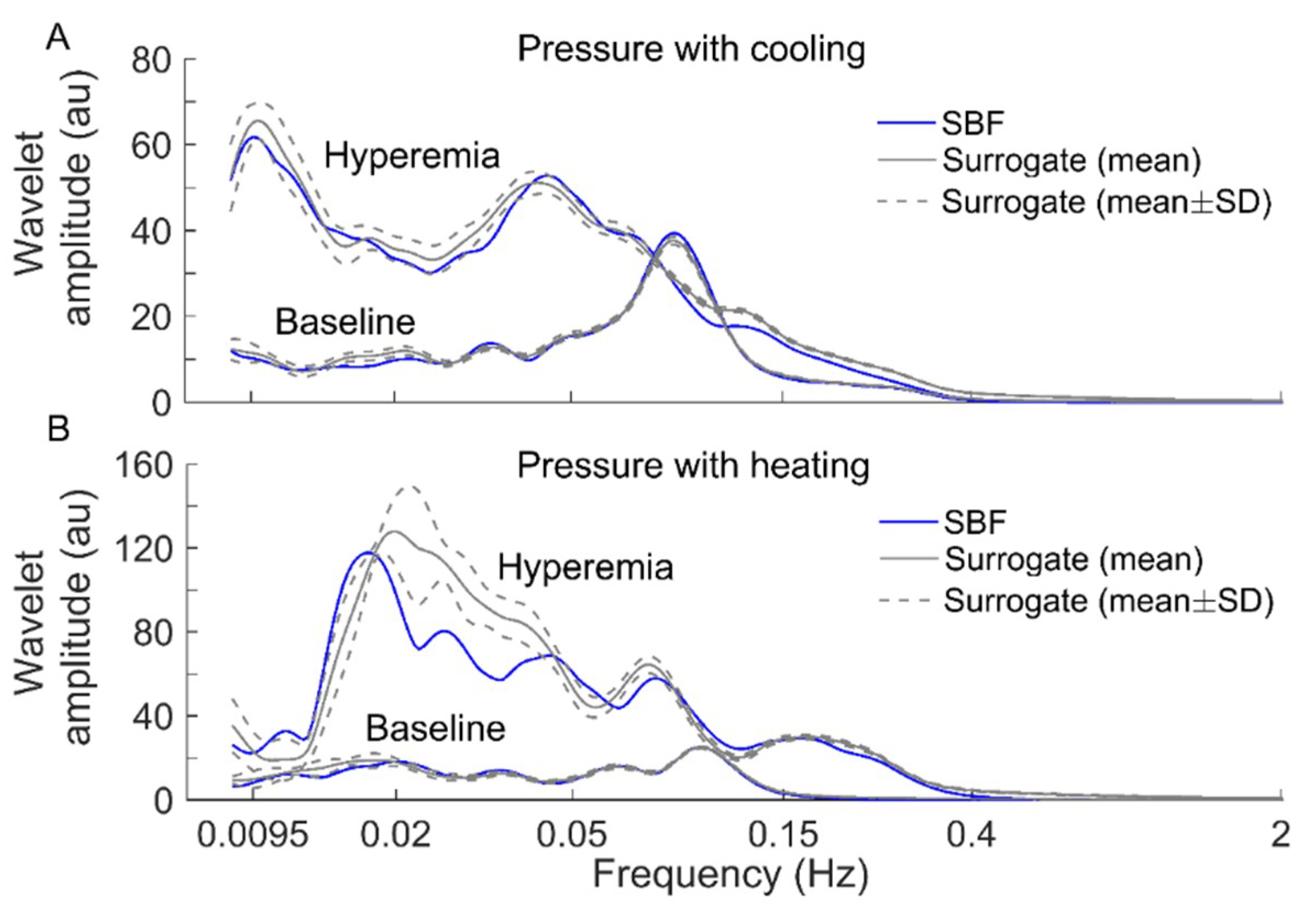
2.3.3. Multiscale Entropy of SBF Data
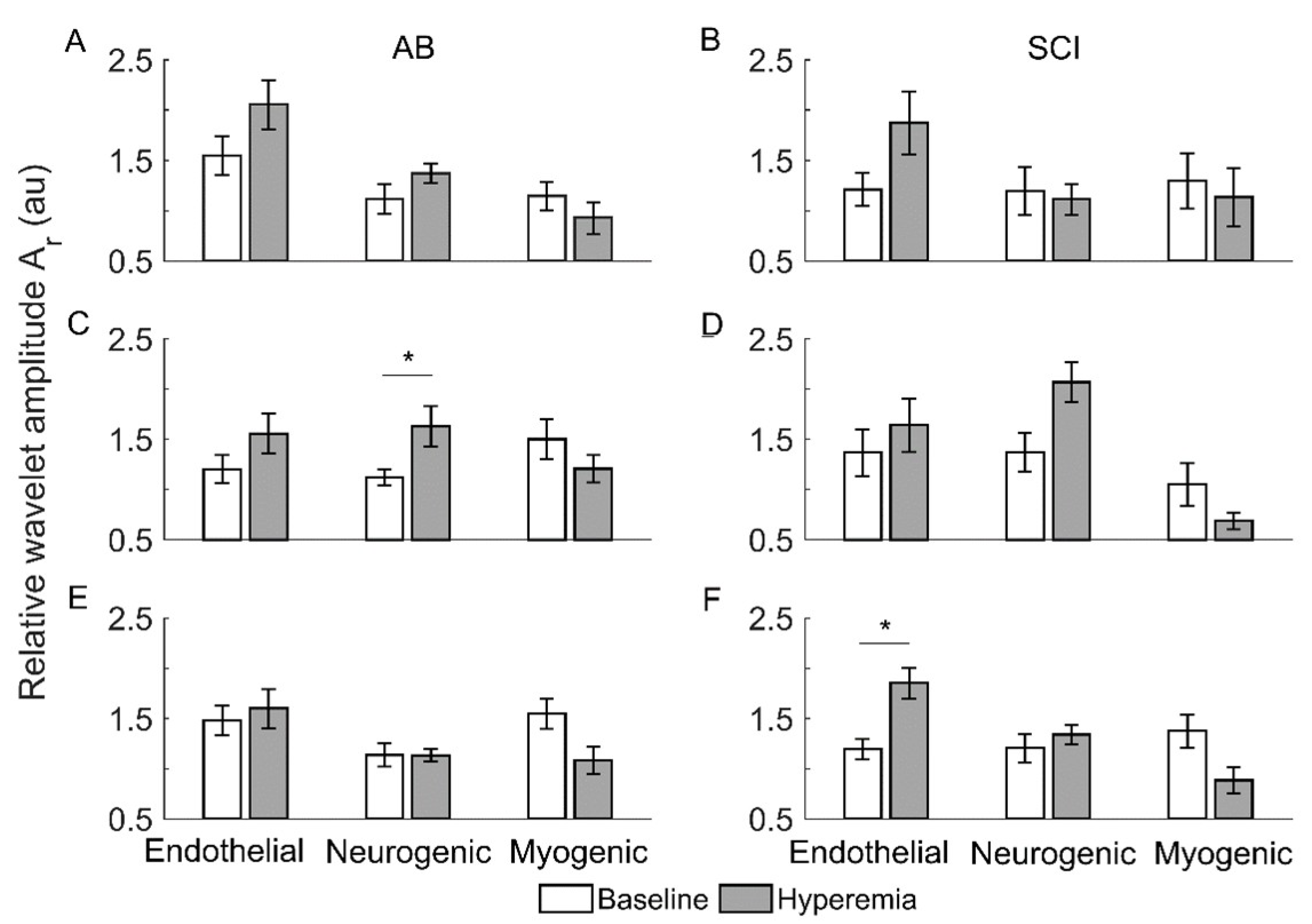
2.4. Relative Wavelet Amplitude of BFO
2.5. Statistical Analysis
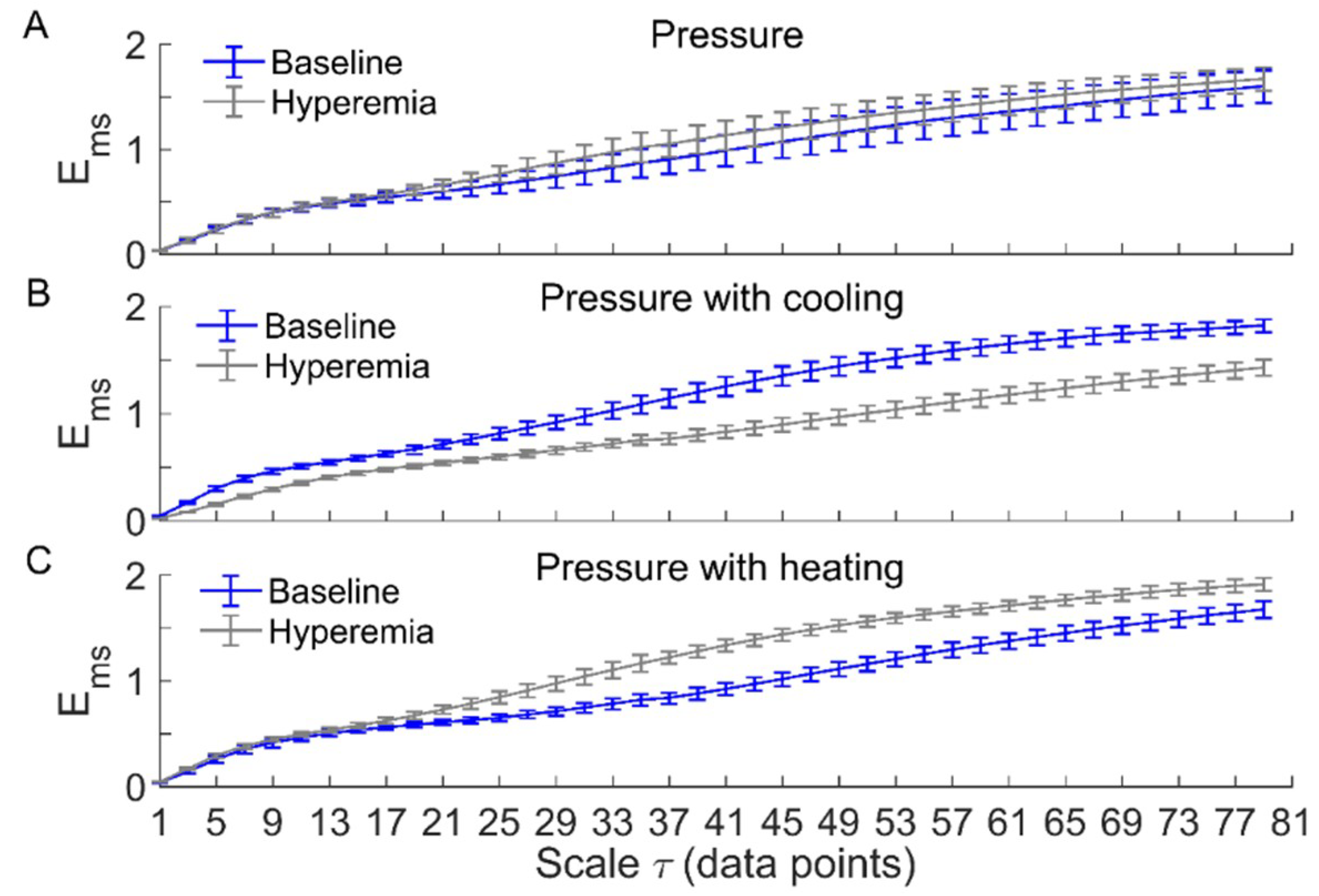
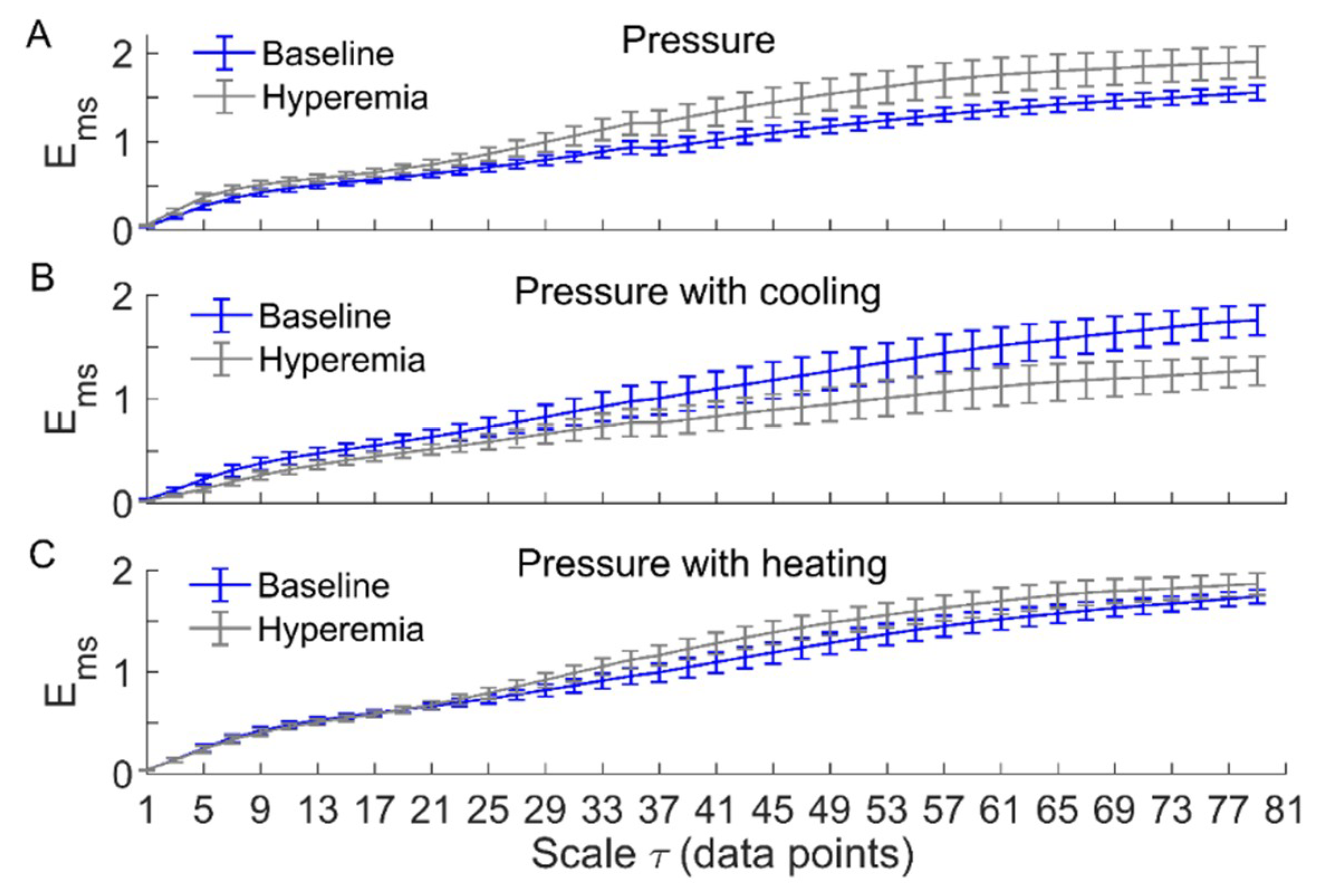
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Consortium for Spinal Cord Medicine Clinical Practice Guidelines. Pressure ulcer prevention and treatment following spinal cord injury: A clinical practice guideline for health-care professionals. J. Spinal Cord Med. 2001, 24, S40–S101. [Google Scholar] [CrossRef]
- Byrne, D.W.; Salzberg, C.A. Major risk factors for pressure ulcers in the spinal cord disabled: A literature review. Spinal Cord 1996, 34, 255–263. [Google Scholar] [CrossRef] [PubMed]
- Olesen, C.G.; de Zee, M.; Rasmussen, J. Missing links in pressure ulcer research—An interdisciplinary overview. J. Appl. Physiol. 2010, 108, 1458–1464. [Google Scholar] [CrossRef] [PubMed]
- Kokate, J.Y.; Leland, K.J.; Held, A.M.; Hansen, G.L.; Kveen, G.L.; Johnson, B.A.; Wilke, M.S.; Sparrow, E.M.; Iaizzo, P.A. Temperature-modulated pressure ulcers: A porcine model. Arch. Phys. Med. Rehabil. 1995, 76, 666–673. [Google Scholar] [CrossRef]
- Jan, Y.K.; Lee, B.; Liao, F.; Foreman, R.D. Local cooling reduces skin ischemia under surface pressure in rats: An assessment by wavelet analysis of laser Doppler blood flow oscillations. Physiol. Meas. 2012, 33, 1733–1745. [Google Scholar] [CrossRef] [PubMed]
- Iaizzo, P.A. Temperature modulation of pressure ulcer formation: Using a swine model. Wounds 2004, 16, 336–343. [Google Scholar]
- Jan, Y.K.; Liao, F.; Rice, L.A.; Woods, J.A. Using Reactive Hyperemia to Assess the Efficacy of Local Cooling on Reducing Sacral Skin Ischemia Under Surface Pressure in People with Spinal Cord Injury: A Preliminary Report. Arch. Phys. Med. Rehabil. 2013, 94, 1982–1989. [Google Scholar] [CrossRef]
- Tzen, Y.T.; Brienza, D.M.; Karg, P.; Loughlin, P. Effects of local cooling on sacral skin perfusion response to pressure: Implications for pressure ulcer prevention. J. Tissue Viability 2010, 19, 86–97. [Google Scholar] [CrossRef]
- Cracowski, J.L.; Minson, C.T.; Salvat-Melis, M.; Halliwill, J.R. Methodological issues in the assessment of skin microvascular endothelial function in humans. Trends Pharmacol. Sci. 2006, 27, 503–508. [Google Scholar] [CrossRef]
- Stefanovska, A.; Bracic, M. Physics of the human cardiovascular system. Contemp. Phys. 1999, 40, 31–55. [Google Scholar] [CrossRef]
- Kvandal, P.; Landsverk, S.A.; Bernjak, A.; Stefanovska, A.; Kvernmo, H.D.; Kirkebøen, K.A. Low-frequency oscillations of the laser Doppler perfusion signal in human skin. Microvasc. Res. 2006, 72, 120–127. [Google Scholar] [CrossRef] [PubMed]
- Jan, Y.K.; Shen, S.; Foreman, R.D.; Ennis, W.J. Skin blood flow response to locally applied mechanical and thermal stresses in the diabetic foot. Microvasc. Res. 2013, 89, 40–46. [Google Scholar] [CrossRef] [PubMed]
- Liao, F.Y.; Garrison, D.W.; Jan, Y.K. Relationship between nonlinear properties of sacral skin blood flow oscillations and vasodilatory function in people at risk for pressure ulcers. Microvasc. Res. 2010, 80, 44–53. [Google Scholar] [CrossRef] [PubMed]
- Liao, F.; Burns, S.; Jan, Y.K. Skin blood flow dynamics and its role in pressure ulcers. J. Tissue Viability 2013, 22, 25–36. [Google Scholar] [CrossRef] [PubMed]
- Liao, F.Y.; Jan, Y.K. Using Modified Sample Entropy to Characterize Aging-Associated Microvascular Dysfunction. Front. Physiol. 2016, 7, 126. [Google Scholar] [CrossRef] [PubMed]
- Liao, F.Y.; Jan, Y.K. Nonlinear dynamics of skin blood flow response to mechanical and thermal stresses in the plantar foot of diabetics with peripheral neuropathy. Clin. Hemorheol. Microcirc. 2017, 66, 197–210. [Google Scholar] [CrossRef] [PubMed]
- Liao, F.; Cheing, G.L.; Ren, W.; Jain, S.; Jan, Y.K. Application of Multiscale Entropy in Assessing Plantar Skin Blood Flow Dynamics in Diabetics with Peripheral Neuropathy. Entropy 2018, 20, 127. [Google Scholar] [CrossRef]
- Parthimos, D.; Schmiedel, O.; Harvey, J.N.; Griffith, T.M. Deterministic nonlinear features of cutaneous perfusion are lost in diabetic subjects with neuropathy. Microvasc. Res. 2011, 82, 42–51. [Google Scholar] [CrossRef]
- Roustit, M.; Cracowski, J.L. Assessment of endothelial and neurovascular function in human skin microcirculation. Trends Pharm. Sci. 2013, 34, 373–384. [Google Scholar] [CrossRef]
- Assous, S.; Humeau, A.; Tartas, M.; Abraham, P.; L’Huillier, J.P. S-transform applied to laser Doppler flowmetry reactive hyperemia signals. IEEE Trans. Biomed. Eng. 2006, 53, 1032–1037. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E Stat. Nonlin. Soft. Matter. Phys. 2005, 71, 021906. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [PubMed]
- Humeau-Heurtier, A. The Multiscale Entropy Algorithm and Its Variants: A Review. Entropy 2015, 17, 3110–3123. [Google Scholar] [CrossRef]
- Valencia, J.F.; Porta, A.; Vallverdu, M.; Claria, F.; Baranowski, R.; Orlowska-Baranowska, E.; Caminal, P. Refined multiscale entropy: Application to 24-h Holter recordings of heart period variability in healthy and aortic stenosis subjects. IEEE Trans. Biomed. Eng. 2009, 56, 2202–2213. [Google Scholar] [CrossRef]
- Zandiyeh, P.; von Tscharner, V. Reshape scale method: A novel multi scale entropic analysis approach. Phys. A Stat. Mech. Its Appl. 2013, 392, 6265–6272. [Google Scholar] [CrossRef]
- Chen, W.; Wang, Z.; Xie, H.; Yu, W. Characterization of surface EMG signal based on fuzzy entropy. IEEE Trans. Neural. Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef]
- Stefanovska, A.; Bracic, M.; Kvernmo, H.D. Wavelet analysis of oscillations in the peripheral blood circulation measured by laser Doppler technique. IEEE Trans. Biomed. Eng. 1999, 46, 1230–1239. [Google Scholar] [CrossRef]
- Bliss, M.R. Hyperaemia. J. Tissue Viability 1998, 8, 4–13. [Google Scholar] [CrossRef]
- Schreiber, T.; Schmitz, A. Improved surrogate data for nonlinearity tests. Phys. Rev. Lett. 1996, 77, 635–638. [Google Scholar] [CrossRef] [PubMed]
- Lorenzo, S.; Minson, C.T. Human cutaneous reactive hyperaemia: Role of BKCa channels and sensory nerves. J. Physiol. 2007, 585, 295–303. [Google Scholar] [CrossRef] [PubMed]
| Pressure with No Temperature Change | Pressure with Cooling | Pressure with Heating | ||||
|---|---|---|---|---|---|---|
| Baseline | Hyperemia | Baseline | Hyperemia | Baseline | Hyperemia | |
| AB | 84.4 ± 8.2 | 77.4 ± 18.7 | 77.5 ± 12.2 | 84.3 ± 9.5 | 80.5 ± 15.4 | 64.7 ± 10.3 |
| SCI | 78.9 ± 12.0 | 62.4 ± 17.3 | 67.3 ± 14.3 | 56.7 ± 25.5 | 79.8 ± 12.4 | 67.2 ± 12.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, F.; Yang, T.D.; Wu, F.-L.; Cao, C.; Mohamed, A.; Jan, Y.-K. Using Multiscale Entropy to Assess the Efficacy of Local Cooling on Reactive Hyperemia in People with a Spinal Cord Injury. Entropy 2019, 21, 90. https://doi.org/10.3390/e21010090
Liao F, Yang TD, Wu F-L, Cao C, Mohamed A, Jan Y-K. Using Multiscale Entropy to Assess the Efficacy of Local Cooling on Reactive Hyperemia in People with a Spinal Cord Injury. Entropy. 2019; 21(1):90. https://doi.org/10.3390/e21010090
Chicago/Turabian StyleLiao, Fuyuan, Tim D. Yang, Fu-Lien Wu, Chunmei Cao, Ayman Mohamed, and Yih-Kuen Jan. 2019. "Using Multiscale Entropy to Assess the Efficacy of Local Cooling on Reactive Hyperemia in People with a Spinal Cord Injury" Entropy 21, no. 1: 90. https://doi.org/10.3390/e21010090
APA StyleLiao, F., Yang, T. D., Wu, F.-L., Cao, C., Mohamed, A., & Jan, Y.-K. (2019). Using Multiscale Entropy to Assess the Efficacy of Local Cooling on Reactive Hyperemia in People with a Spinal Cord Injury. Entropy, 21(1), 90. https://doi.org/10.3390/e21010090






