Thermodynamic Analysis of Entropy Generation Minimization in Thermally Dissipating Flow Over a Thin Needle Moving in a Parallel Free Stream of Two Newtonian Fluids
Abstract
1. Introduction
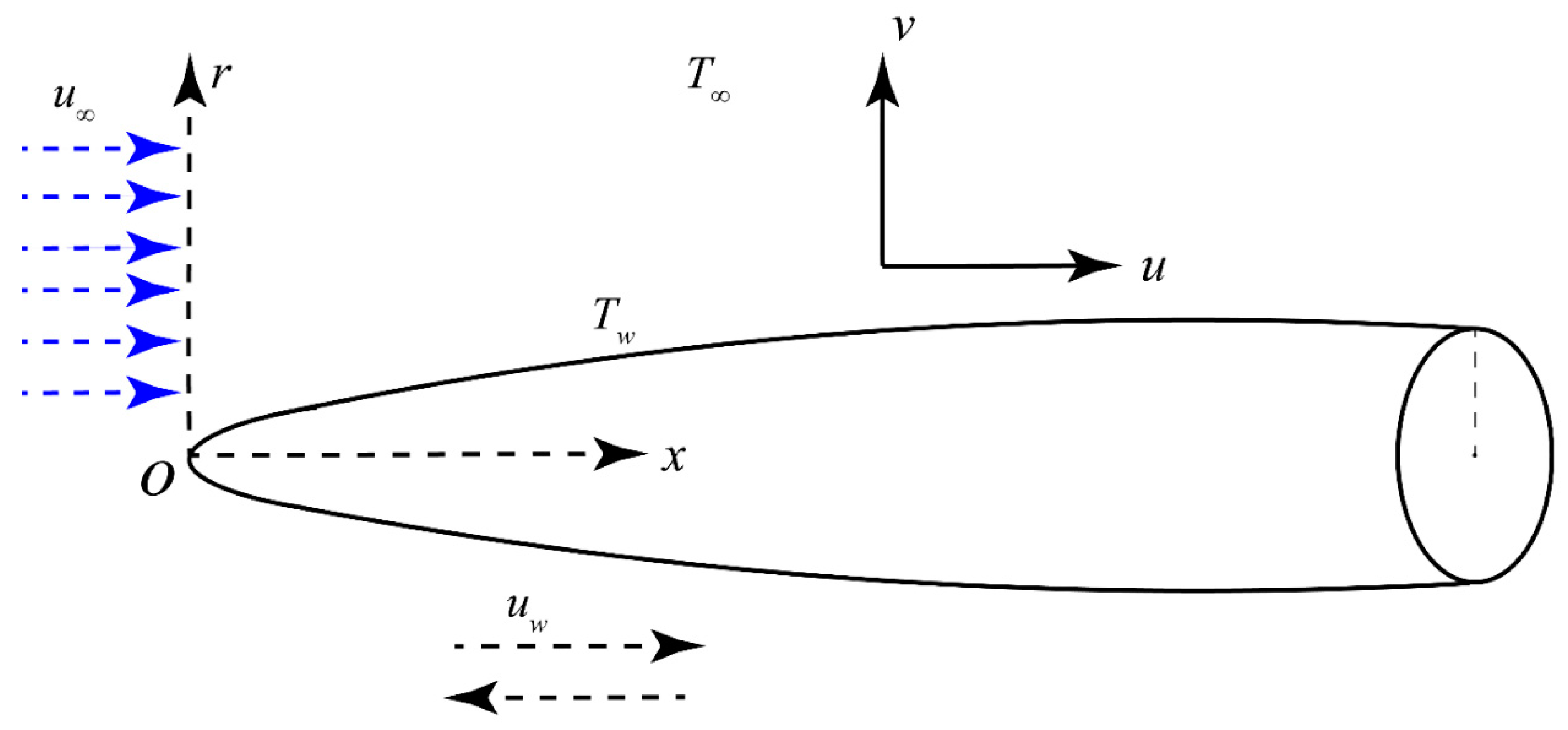
2. Flow Analysis
2.1. First Law Analysis
2.2. Second Law Analysis
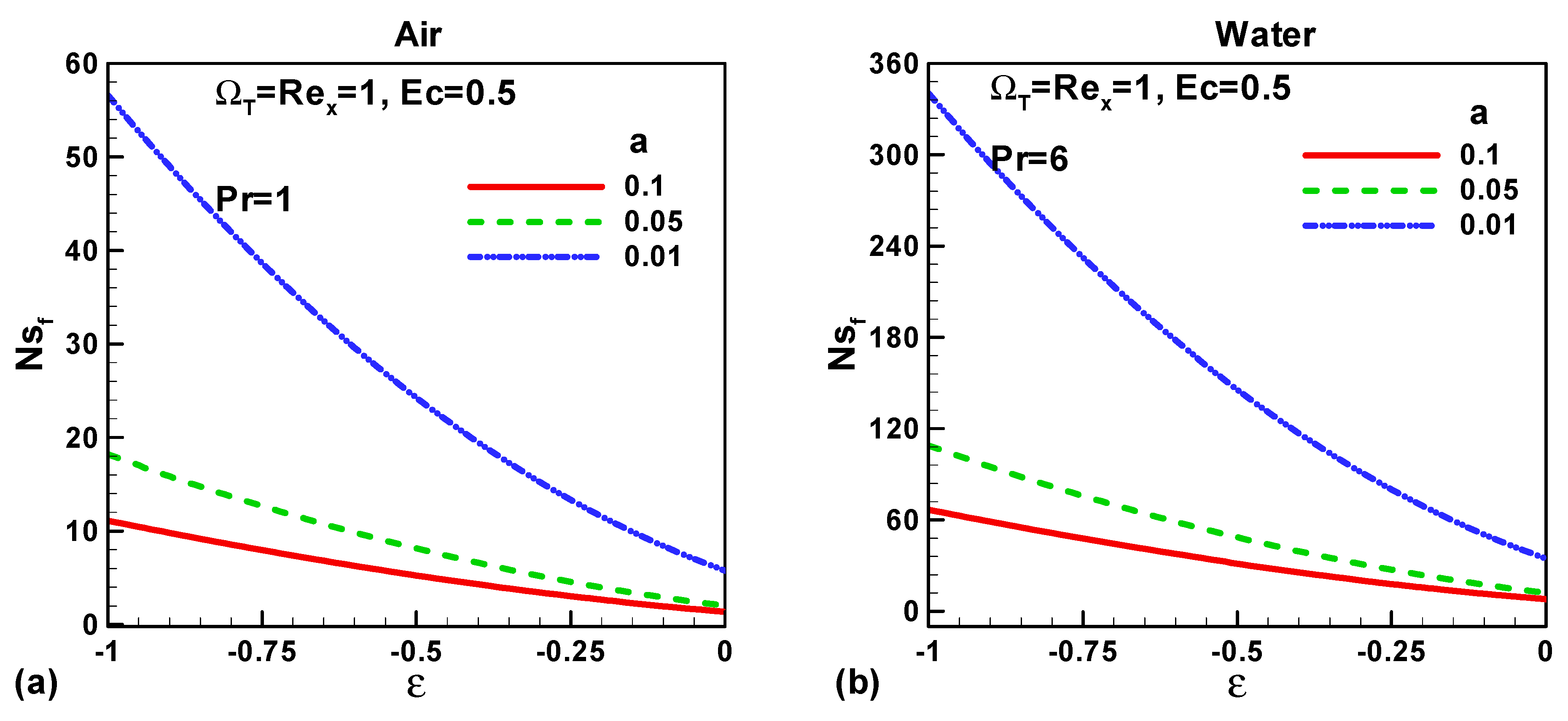
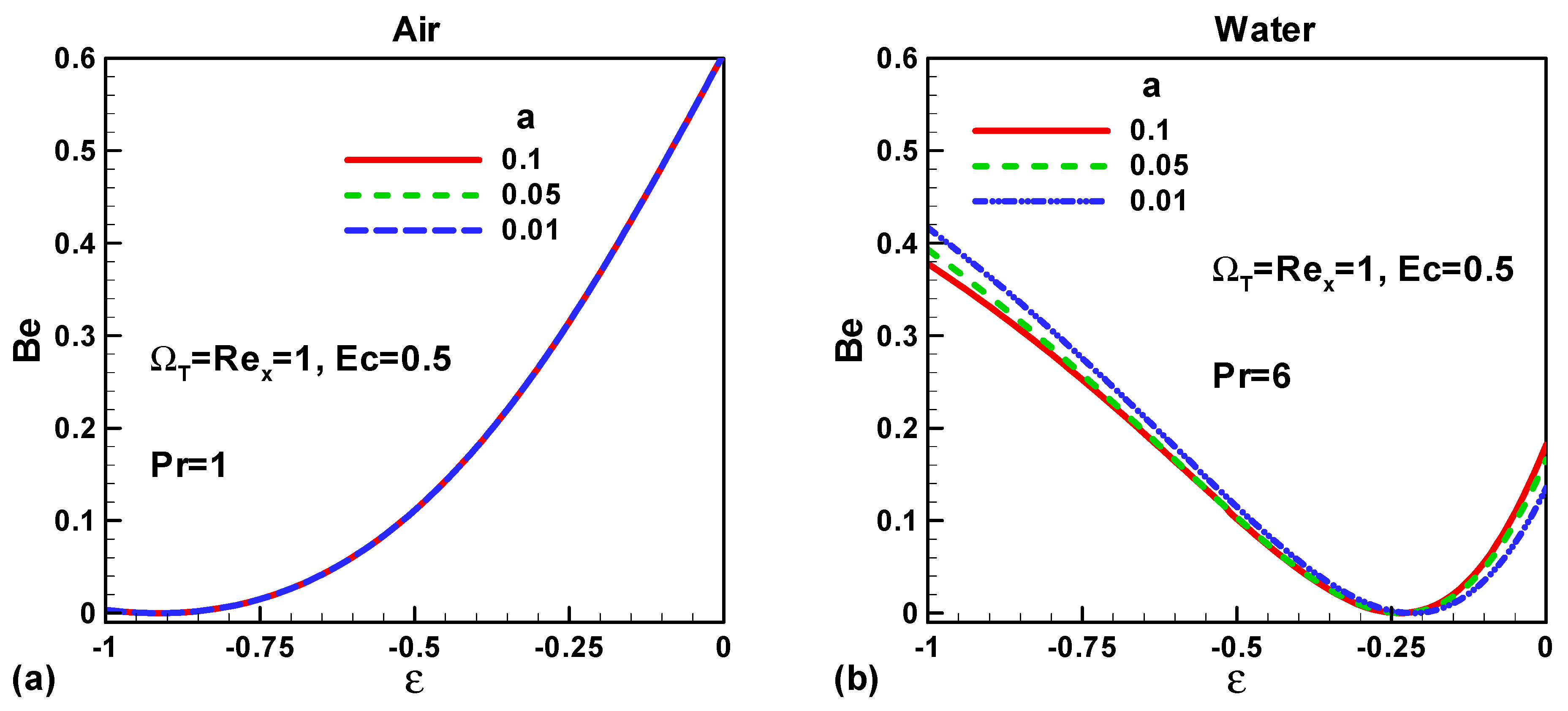
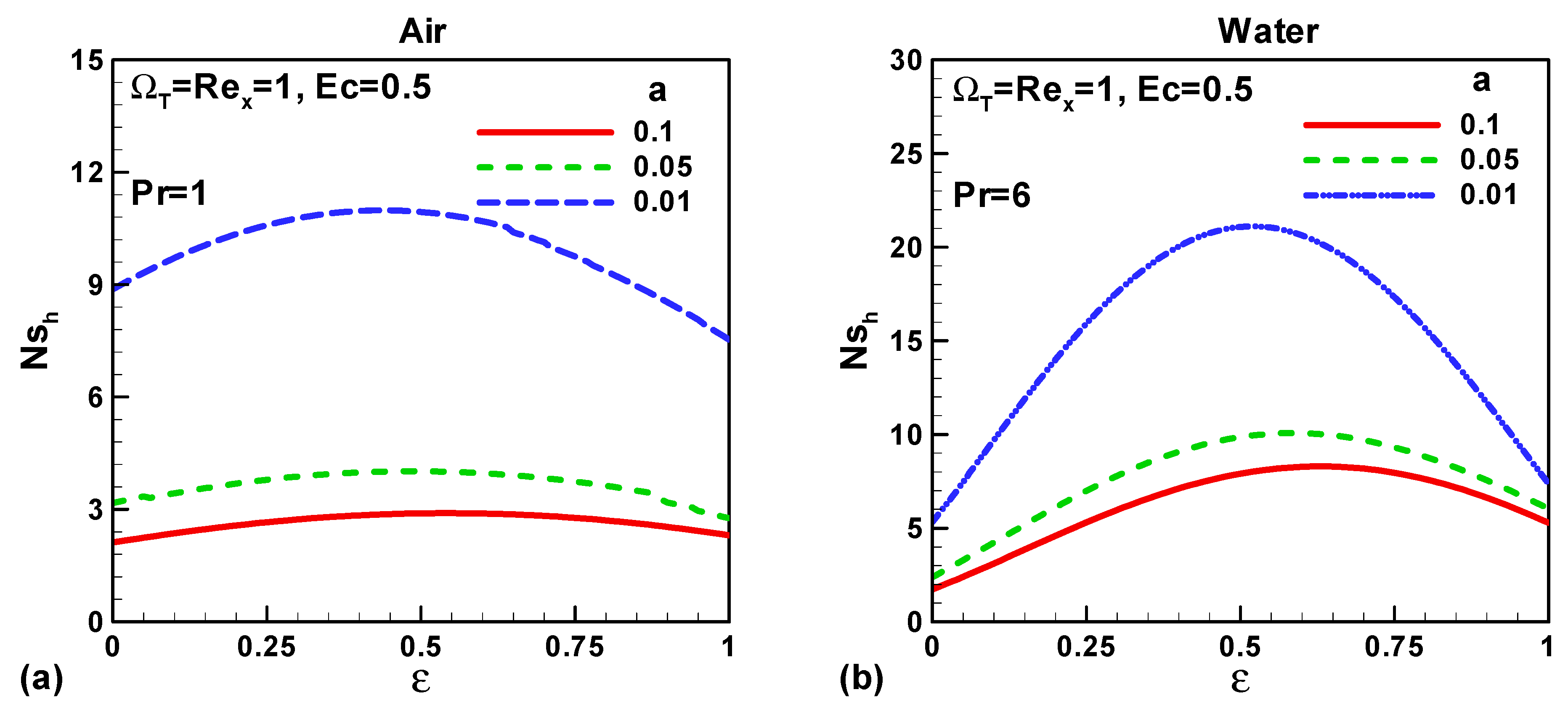
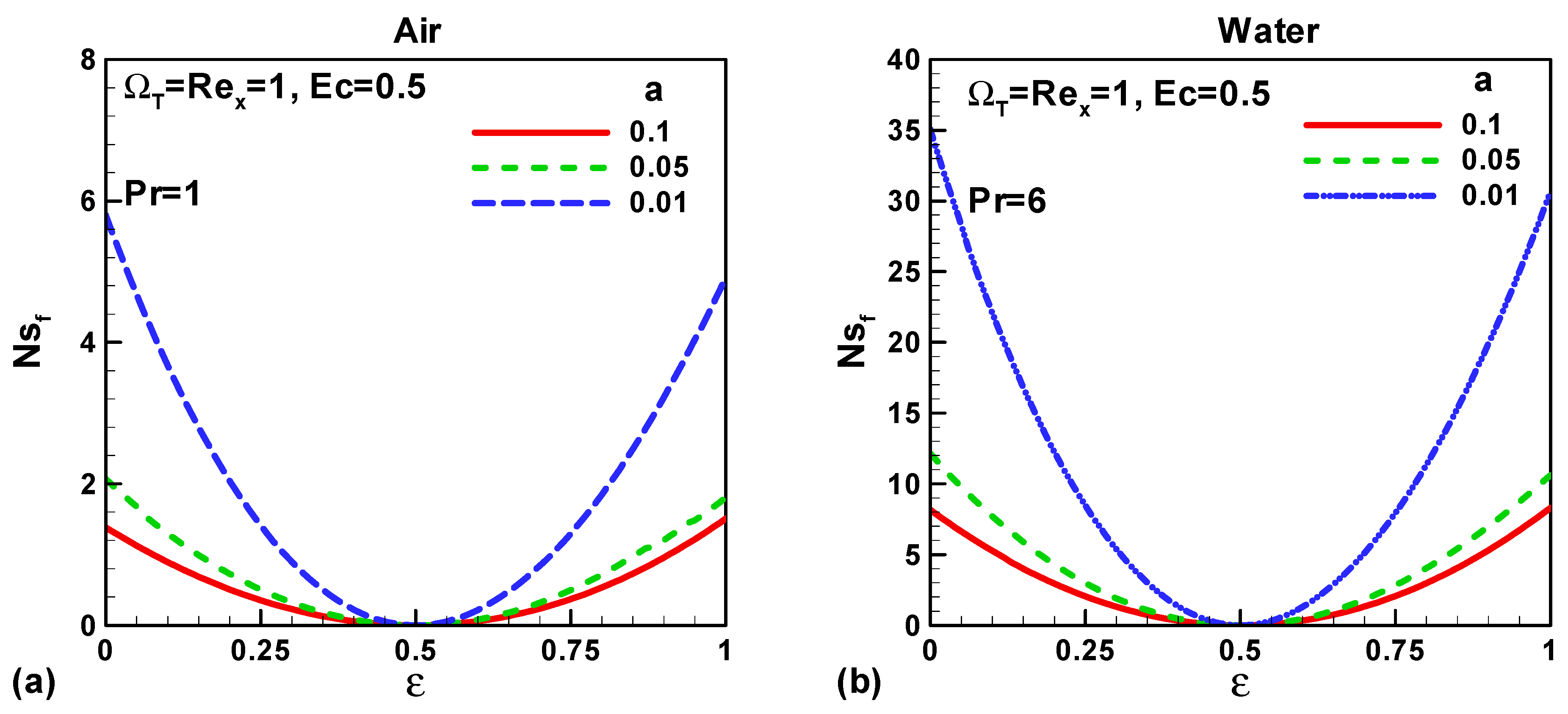
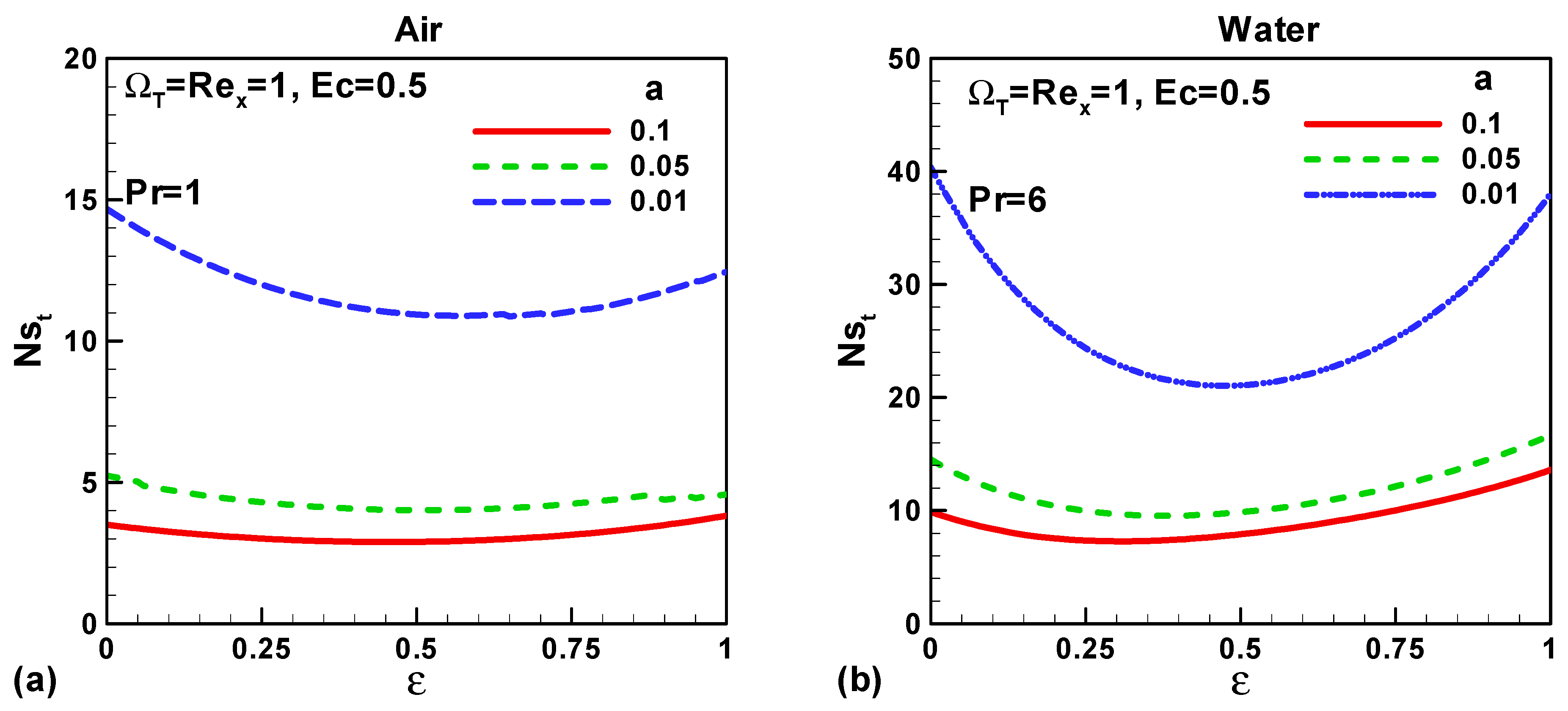
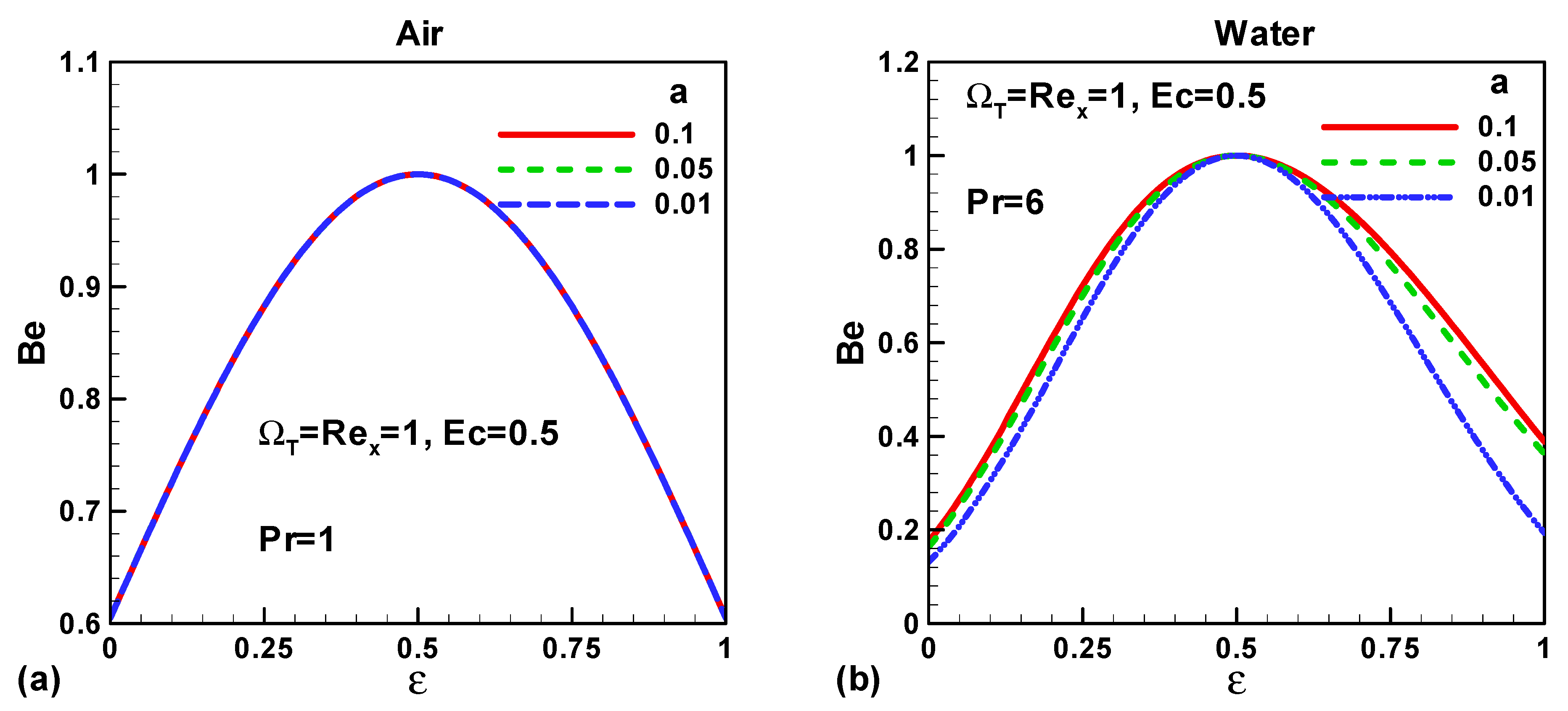
3. Results and Discussions
4. Closing Remarks
- Heat transfer and fluid friction irreversibility increases with the decreasing size of the thin needle for both type of fluids air and water.
- Total entropy enhances with the reduced size needle.
- Entropy generated due to heat transfer and fluid friction in water is more than in air.
- When ε < 0, entropy can be minimized either by increasing the free stream velocity or by decreasing the needle velocity.
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature
| Constant | |
| Bejan Number | |
| Brinkman number | |
| Specific heat | |
| Eckert number | |
| Dimensionless stream function | |
| Thermal conductivity | |
| Prandtl number | |
| Shape and size of the needle [m] | |
| Local Reynold number | |
| Temperature field [K] | |
| Composite velocity [] | |
| Velocity of needle and free stream, respectively [] | |
| Velocity components in axial and radial directions, respectively [m] | |
| Spatial coordinates measured in axial and radial directions, respectively [m] | |
| Non-dimensional temperature | |
| Density of fluid | |
| Dynamic viscosity | |
| Dimensional stream function | |
| Velocity ratio parameter |
References
- Bejan, A. A study of entropy generation in fundamental convective heat transfer. J. Heat Transf. 1979, 101, 718–725. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation through Heat and Fluid Flow; John Wiley and Sons: New York, NY, USA, 1982. [Google Scholar]
- Mahmud, S.; Fraser, R.A. Thermodynamics analysis of flow and heat transfer inside channel with two parallel plates. Exergy 2002, 2, 140–146. [Google Scholar] [CrossRef]
- Makinde, O.D. Irreversibility analysis for a gravity driven non-Newtonian liquid film along an inclined isothermal plate. Phys. Scr. 2006, 74, 642–645. [Google Scholar] [CrossRef]
- Makinde, O.D.; Maserumule, R.L. Thermal criticality and entropy analysis for a variable viscosity Couette flow. Phys. Scr. 2008, 78, 1–6. [Google Scholar] [CrossRef]
- Makinde, O.D. Second law analysis for variable viscosity hydromagnetic boundary layer flow with thermal radiation and Newtonian heating. Entropy 2011, 13, 1446–1464. [Google Scholar] [CrossRef]
- Aziz, A.; Khan, W.A. Entropy Generation in an Asymmetrically Cooled Slab with Temperature-Dependent Internal Heat Generation. Heat Transf.-Asian Res. 2012, 41, 260–271. [Google Scholar] [CrossRef]
- Mkwizu, M.; Makinde, O.D. Entropy generation in a variable viscosity channel flow of nanofluids with convective cooling. Compt. Rendus Mecanique 2015, 343, 38–56. [Google Scholar] [CrossRef]
- Makinde, O.D.; Khan, W.A.; Aziz, A. On inherent irreversibility in Sakiadis flow of nanofluids. Int. J. Exergy 2013, 13, 159–174. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Ali, M.; Freidoonimehr, N.; Nazari, F. Parametric analysis and optimization of entropy generation in unsteady MHD flow over a stretching rotating disk using artificial neural network and particle swarm optimization algorithm. Energy 2013, 55, 497–510. [Google Scholar] [CrossRef]
- Butt, A.S.; Ali, A. Investigation of entropy generation effects in magnetohydrodynamic three-dimensional flow and heat transfer of viscous fluid over a stretching surface. J. Braz. Soc. Mech. Sci. Eng. 2015, 37, 211–219. [Google Scholar] [CrossRef]
- Das, S.; Sarkar, B.C.; Jana, R.N. Entropy Generation in MHD free convection boundary layer flow past an inclined flat plat embedded in a porous medium with hall currents. Int. J. Comput. Appl. 2013, 8, 36–46. [Google Scholar]
- Govindaraju, M.; Saranya, S.; Hakeem, A.K.A.; Jayaprakash, R.; Ganga, B. Analysis of slip MHD nanofluid flow on entropy generation in a stretching sheet. Procedia Eng. 2015, 127, 501–507. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Mohammadi, F.; Abbasbandy, S.; Alhuthali, M.S. Entropy generation analysis for stagnation point flow in a porous medium over a permeable stretching surface. J. Appl. Fluid Mech. 2015, 8, 753–765. [Google Scholar] [CrossRef]
- Sheikholeslami, M. New computational approach for exergy and entropy analysis of nanofluid under the impact of Lorentz force through a porous media. Comput. Methods Appl. Mech. Eng. 2019, 344, 319–333. [Google Scholar] [CrossRef]
- Hakeem, A.K.A.; Govindaraju, M.; Ganga, B.; Kayalvizhi, M. Second law analysis for radiative MHD slip flow of a nanofluid over a stretching sheet with non-uniform heat source effect. Sci. Iran. 2016, 23, 1524–1538. [Google Scholar]
- Butt, A.S.; Ali, A.; Mehmood, A. Numerical investigation of magnetic field effects on entropy generation in viscous flow over a stretching cylinder embedded in a porous medium. Energy 2016, 99, 237–249. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M.; Khan, I.; Shafie, S.; Alshomrani, A.S. Entropy Generation in Magnetohydrodynamic Mixed Convection Flow over an Inclined Stretching Sheet. Entropy 2016, 19, 10. [Google Scholar] [CrossRef]
- Lee, L.L. Boundary Layer over a thin needle. Phys. Fluids 1967, 10, 820–822. [Google Scholar] [CrossRef]
- Chen, J.L.S.; Smith, T.N. Forced confection heat transfer from non-isothermal thin needles. J. Heat Transf. Trans. ASME 1978, 100, 1–5. [Google Scholar] [CrossRef]
- Ishaq, A.; Nazar, R.; Pop, I. Boundary layer flow over a continuously moving thin needle in a parallel free stream. Chin. Phys. Lett. 2007, 24, 2895. [Google Scholar] [CrossRef]
- Grosan, T.; Pop, I. Forced convection boundary layer flow past non isothermal thin needles in nanofluids. J. Heat Transf. 2011, 113, 054503-1. [Google Scholar] [CrossRef]
- Soid, S.K.; Ishak, A.; Pop, I. Boundary layer flow past a continuously moving thin needle. Appl. Therm. Eng. 2017, 114, 58–64. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M. Entropy generation and heat transfer in boundary layer flow over a thin needle moving in a parallel stream in the presence of nonlinear Rosseland radiation. Int. J. Ther. Sci. 2018, 123, 117–128. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, I.; Khan, W.A.; Qasim, M.; Afridi, I.; Alharbi, S.O. Thermodynamic Analysis of Entropy Generation Minimization in Thermally Dissipating Flow Over a Thin Needle Moving in a Parallel Free Stream of Two Newtonian Fluids. Entropy 2019, 21, 74. https://doi.org/10.3390/e21010074
Khan I, Khan WA, Qasim M, Afridi I, Alharbi SO. Thermodynamic Analysis of Entropy Generation Minimization in Thermally Dissipating Flow Over a Thin Needle Moving in a Parallel Free Stream of Two Newtonian Fluids. Entropy. 2019; 21(1):74. https://doi.org/10.3390/e21010074
Chicago/Turabian StyleKhan, Ilyas, Waqar A. Khan, Muhammad Qasim, Idrees Afridi, and Sayer O. Alharbi. 2019. "Thermodynamic Analysis of Entropy Generation Minimization in Thermally Dissipating Flow Over a Thin Needle Moving in a Parallel Free Stream of Two Newtonian Fluids" Entropy 21, no. 1: 74. https://doi.org/10.3390/e21010074
APA StyleKhan, I., Khan, W. A., Qasim, M., Afridi, I., & Alharbi, S. O. (2019). Thermodynamic Analysis of Entropy Generation Minimization in Thermally Dissipating Flow Over a Thin Needle Moving in a Parallel Free Stream of Two Newtonian Fluids. Entropy, 21(1), 74. https://doi.org/10.3390/e21010074




