1. Introduction
One of the main features of quantum mechanics in multipartite quantum systems is the presence of quantum correlation (QC). Though the entanglement is surely the most important among the QCs [
1,
2,
3,
4], the study and the characterization of QCs that go beyond the paradigm of entanglement have recently attracted more and more attention since non-entangled quantum correlations also play important roles in various quantum computing tasks and quantum communications [
5,
6,
7].
Quantifying QCs for continuous-variable systems was carried out in various ways. G.Adesso and A. Datta [
8] and P. Giorda and M. G. A. Paris [
9] independently proposed Gaussian quantum discord (GQD). In [
8], the authors analytically calculated the GQD for two-mode Gaussian states and claimed that almost all two-mode Gaussian states have quantum correlations. In [
9], for squeezed thermal states (STSs), an entanglement threshold in terms of GQD was given. It is in general difficult to compute GQD since it involves a minimization process over all possible local Gaussian positive operator-valued measurements (GPOVMs) in a bipartition. The authors in [
10] studied the computational complexity of quantum discord (QD) for finite-dimensional systems and found it increasing exponentially with the dimension of the Hilbert space. Many efforts have been made to find simpler methods to quantify these correlations. For example, in [
11], G. Adesso and D. Girolami gave Gaussian geometric discord (GGD) for Gaussian states and provided an explicit formula for two-mode STSs, and in addition, they discussed other approaches to quantify Gaussian quadrature correlations. In analogy with the GQD, in [
12], the measurement-induced disturbance (MID) of Gaussian states was studied by constraining the optimization to all bi-local GPOVMs, and an explicit formula for some families of states was given. In [
13], measurement-induced nonlocality (MIN) for Gaussian states was discussed, and analytic formulas for two-mode STSs, as well as mixed thermal states were provided. Gaussian discord of response (
) for two-mode Gaussian states can be found in [
14]. For other related results, see [
15,
16,
17,
18,
19,
20,
21,
22] and the references therein.
Despite some efforts, almost all known quantifications of various correlations for continuous-variable systems are difficult to evaluate and can only be calculated for -mode Gaussian states or some special states. Thus, it is natural and important to find more reliable and useful quantifications for QCs.
The purpose of this paper is to propose a correlation for continuous-variable systems in terms of local Gaussian unitary operations based on Uhlmann fidelity. We show that is a quantum correlation without the ancilla problem, is local Gaussian unitary invariant, is contained in any non-product state, is monotonically non-increasing under Gaussian quantum channels acting on the Subsystem B, and reduces to an entanglement measure for -mode pure Gaussian states. Furthermore, we give a concrete formula for any two-mode symmetric squeezed thermal states (SSTSs) and compare with some other QCs.
Uhlmann fidelity was firstly proposed as a measure of closeness between two arbitrary states
and
, defined as
[
23]. Uhlmann fidelity itself has many good properties, such as unitary invariance, monotonicity under quantum operations, and strong concavity [
23,
24,
25]; and so it has many applications; for example, see [
26,
27,
28,
29,
30,
31] and the references therein. Recently, Uhlmann fidelity for Gaussian states was studied and some useful results were obtained in [
32,
33]. Though Uhlmann fidelity itself is not a metric, one can define a metric based on it as
where
g is a monotonically-decreasing function of
F. Some well-known Uhlmann fidelity-induced metrics are the sine metric
, Bures metric
, and Bures angle
[
34].
Although we may use any metric to introduce the quantum correlation by local unitary operations, in the present paper, we accept as the metric for reasons of simplicity.
2. A Uhlmann Fidelity-Based Quantum Correlation and Its Properties
In this section, we define a QC by local unitary operations for -mode states using the sine metric based on Uhlmann fidelity and discuss its properties.
We first recall some notions and notations.
For convenience, we denote by
the set of all states of the quantum system described by the Hilbert space
H. Assume that
is any state of an
n-mode continuous-variable system with the state space
(
for each
). The characteristic function of
is defined as
, where
,
is the Weyl operator with
the Weyl operator of the
mode. Here,
and
are respectively the annihilation and creation operators in the
mode;
and
respectively stand for the position and momentum operators satisfying the canonical commutation relations (CCR)
and
,
.
is called a Gaussian state if
is of the form:
where
,
,
with
, and
. Here,
stands for the algebra of all
matrices over the real field
.
and
above are called respectively the covariance matrix (CM) and the mean of
. Note that
is real symmetric and satisfies
. In addition,
is pure if and only if
. If
is an
-mode Gaussian state of a bipartite continuous-variable system
, its CM
can be expressed as
, where
,
and
. Particularly, when
, up to a local Gaussian unitary operation (symplectic at the CM level),
has a standard form:
where
,
,
,
, and
. Note that a bipartite state
is a product state, i.e.,
, if and only if
C (
) in its CM (the standard form of its CM) is a zero matrix [
8].
For any unitary operator
U acting on
H, the unitary operation
is said to be Gaussian if it sends Gaussian states into Gaussian states, and such a
U is called a Gaussian unitary operator. It is well known that a unitary operator
U is Gaussian if and only if
for some vector
and some
, the symplectic group of all
real matrices. Thus, every Gaussian unitary operator
U is determined by some affine symplectic map
acting on the phase space and can be denoted by
[
35,
36].
Now, for any
-mode state
, denote by
the reduced state of
. Write:
where
stands for the set of all bounded linear operators acting on
H. It is obvious that the set
is nonempty for any state
; moreover, by [
15], for any Gaussian state
,
contains many nontrivial Gaussian unitary operators. Thus, we can define a quantum correlation
by local Gaussian unitary operations for any
-mode state.
Definition 1. For any -mode state , the quantity with respect to Subsystem A is defined as:where is the Uhlmann fidelity between the pre- and past-measured states, and the supremum is taken over all Gaussian unitary operators . Similarly, one can define with respect to Subsystem B. Since the properties of and are similar, we will focus on discussing the properties of . For the simplification, we will use by omitting the subsystem symbol A (B) unless otherwise specified.
Note that many quantum correlations have the ancilla problem, i.e., when an uncorrelated ancilla System C is appended, the quantities will change due to the local Subsystem C. For example, in [
15], a kind of quantum correlation
for
-mode continuous-variable systems was defined as:
where the supremum is taken over all unitary operators that maintain
invariant corresponding to Part A. If we append an uncorrelated ancilla System C, the state
can be regarded as a bipartite state with the partition A:BC. After some direct calculations, one has:
It is obvious that, as long as
is mixed, the quantity
differs arbitrarily due to local ancilla System C. There are other quantum correlations with a similar ancilla problem, such as the quantum correlations proposed in [
11,
16]. However, our quantity
keeps unchanged when appending an ancilla system; that is, we have the following result.
Theorem 1. is a quantum correlation without the ancilla problem.
Proof of Theorem 1. Suppose that
is any bipartite state and C is an uncorrelated ancilla system. Regarding the state
as a bipartite state with the partition A:BC, one has:
By Definition 1, we see that
, completing the proof. □
Theorem 2. is locally Gaussian unitary invariant, that is, for any -mode state of continuous-variable system , we have for all Gaussian unitary operators and .
In the rest of this paper, we mainly consider the case that is any Gaussian state.
Theorem 3. For any -mode Gaussian state and any Gaussian channel Φ performed on the Subsystem B, we have .
By Definition 1, it is easily checked that holds for any -mode product state ; but we do not know whether the converse is true. The following result reveals that the converse holds for any Gaussian states.
Theorem 4. For any -mode Gaussian state , if and only if is a product state.
Any
-mode pure Gaussian state can always be brought in the phase-space Schmidt form [
37]. The corresponding symplectic transformation
achieving the Schmidt decomposition is the direct sum of two diagonalizing matrices acting on the single-mode and
m-mode subsystems, respectively, i.e.,
. Suppose
is the CM of a
-mode pure Gaussian state; accordingly, the CM of its phase-space Schmidt form is:
with
the single-mode mixedness factor. We also call
the phase-space Schmidt form of
. It is clear that the phase-space Schmidt form of a
-mode pure Gaussian state is the tensor product of a two-mode squeezed state and an
-mode uncorrelated vacuum state [
38].
The following result gives a computation formula of for -mode pure Gaussian states.
Theorem 5. For any -mode pure Gaussian state with CM Γ
, we have:where is the single-mode mixedness factor in the phase-space Schmidt form of Γ
. Recall that a quantum state
is separable if it belongs to the closed convex hull of the set of all product states
under the trace norm topology. Note that a pure state
is separable if and only if it is a product state. The problem of how to quantify entanglement was studied extensively. Generally speaking, an entanglement measure
should meet the following conditions [
39]:
(i) vanishes on separable states;
(ii) does not increase under local operation and classic communications (LOCC);
(iii) is locally unitary invariant.
The reader can refer to [
1] for more details on entanglement measures.
In [
39], a kind of entanglement measure
for Gaussian states was proposed. It was shown that, for any
-mode pure Gaussian state
with CM
,
, where
F stands for the Uhlmann fidelity,
, and
is any traceless symplectic matrix performed on the single-mode. Furthermore,
with
the single-mode mixedness factor in the phase-space Schmidt form of
, which coincides with the quantity
by Theorem 5. This reveals that
is an entanglement measure when it is restricted to
-mode pure Gaussian states.
According to [
40,
41,
42,
43], a bona fide quantum correlation
for Gaussian states with respect to Subsystem A should satisfy:
(i) if and only if is a product state;
(ii) (Locally Gaussian unitary invariant) holds for any Gaussian unitary operators , and any Gaussian state ;
(iii) (Non-increasing under local Gaussian channels) holds for any Gaussian channel performed on Subsystem B and any Gaussian state ;
(iv) (Reducing to an entanglement measure for pure states) There exists an entanglement measure such that holds for any bipartite pure state .
By Theorems 2–4, satisfies (i)–(iii); Theorem 5 says that satisfies (iv) for any -mode Gaussian pure state. Therefore, at least for -mode Gaussian states, is a well-defined Gaussian quantum correlation.
In the rest of this section, let us discuss the question of how to calculate
. Note that, for any
-mode Gaussian states
and
with its characteristic function defined as in Equation (
1), together with the formula established in [
33], we have:
where
s
are the symplectic roots of the CM of
. In general, one can use the above fidelity formula to compute
for any
-mode Gaussian state
. Due to the theoretical and experimental importance of two-mode symmetric squeezed thermal states (SSTSs), as an example, we give an analytic computation formula for
-mode SSTSs here.
Recall that SSTSs are Gaussian states whose CMs as in Equation (
2) are parameterized by
and
such that
and
, where
is a mixing parameter with
and
is the mean photon number for each part [
44]. Thus, every SSTS can be parameterized as
, and the standard form of its CM is:
Theorem 6. For any -mode symmetric squeezed thermal state , we have:where:Moreover,holds for any . The proofs of Theorems 2–6 will be given in the
Appendix A.
Note that
holds for any Gaussian state
. However, unlike the Gaussian discord case, there is no threshold in terms of
for separable states; that is, there is no positive number
such that
holds for all separable states
. To see this, recall that a
-mode Gaussian state
is separable if and only if
, where
is the smallest symplectic eigenvalue of the CM of the partial transpose
[
45]. For any SSTS
with CM
, we have:
Thus,
if and only if either
or
. Given
,
for sufficiently large
, which guarantees the separability of
. However, by Theorem 6,
. Therefore,
is separable
.
3. Comparing with Other Quantum Correlations
As is seen,
describes the same correlation in Gaussian states as Gaussian quantum discord (GQD)
D, Gaussian geometric discord (GGD)
, the quantum correlation
Q proposed in [
16], and
proposed in [
46]. In this section, we will compare
with these QCs for two-mode SSTSs in scale. It is clear that, for any SSTS
, we have
. Hence, during the comparison process, we mainly focus our attention on the case
.
Recall that an
n-mode Gaussian positive operator-valued measurement (GPOVM) is a collection of positive operators
satisfying
, where
with
the Weyl operators and
an
n-mode Gaussian state, which is called the seed of the GPOVM
[
47]. Let
be an
-mode Gaussian state and
be a GPOVM of the Subsystem A. Denote by
the reduced state of the Subsystem B after the GPOVM
performed on the Subsystem A, where
. Then, the GQD of
is defined as:
where the infimum is taken over all GPOVMs
performed on Subsystem A and
is the von Neumann entropy [
8,
9]. It is known that, if the standard form of the CM of a
-mode Gaussian state
is as in Equation (
2), then:
where the infimum takes over all one-mode Gaussian states
,
,
and
are the symplectic eigenvalues of the CM of
, and
with
the CM of
. Denote by
,
,
and
; then, we have [
8]:
Particularly, if
is an SSTS, one can easily check that
always holds and
. In this case, we have:
where:
with
.
In the case
,
and hence,
. While,
therefore, when
,
D is much greater than
for large
. However, when
, a numerical method reveals that
, and by Theorem 6,
. This means that, for
and large
, we have
. Therefore, when we detect the correlation in SSTS,
is much better than
D for the case
and large
.
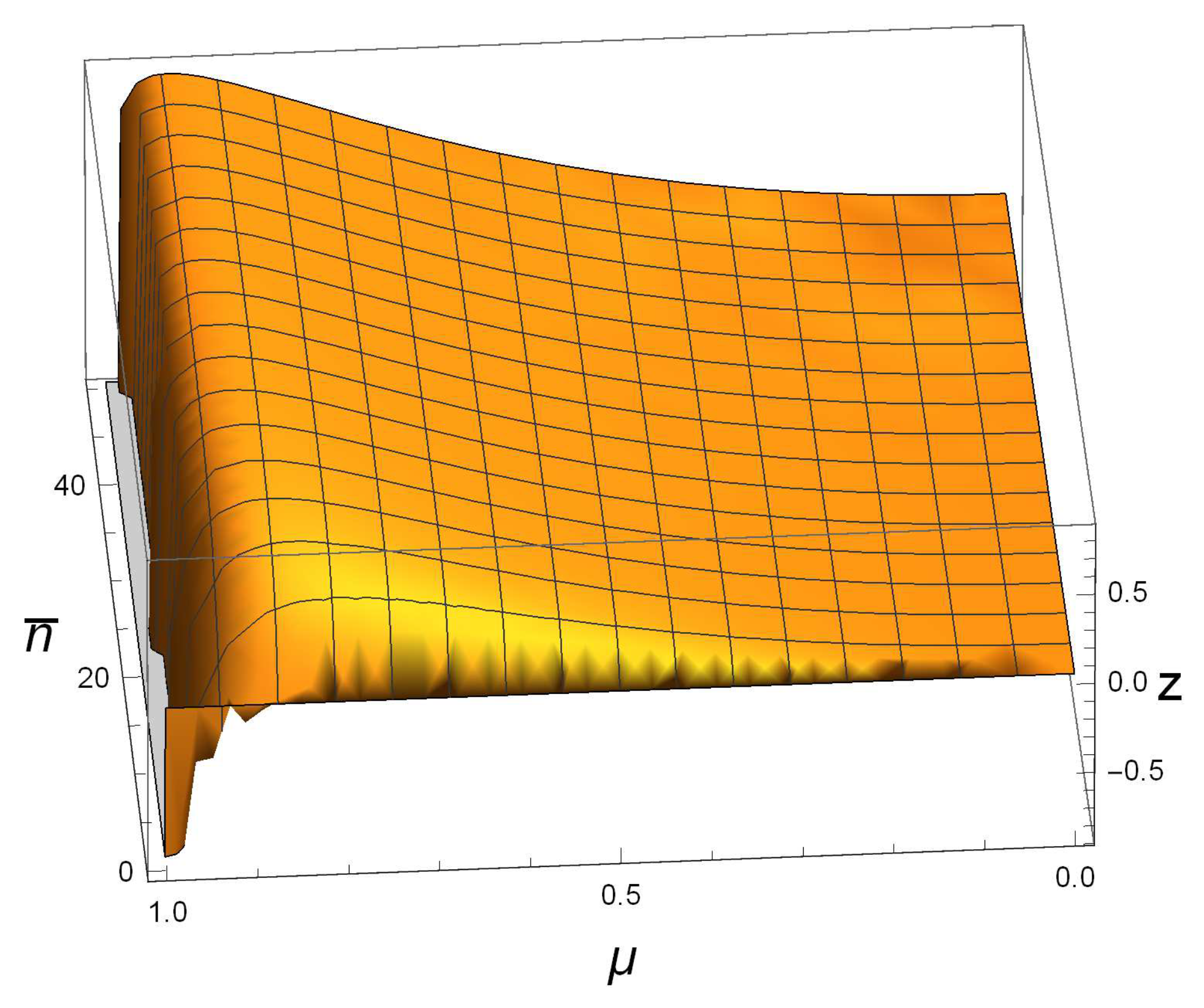
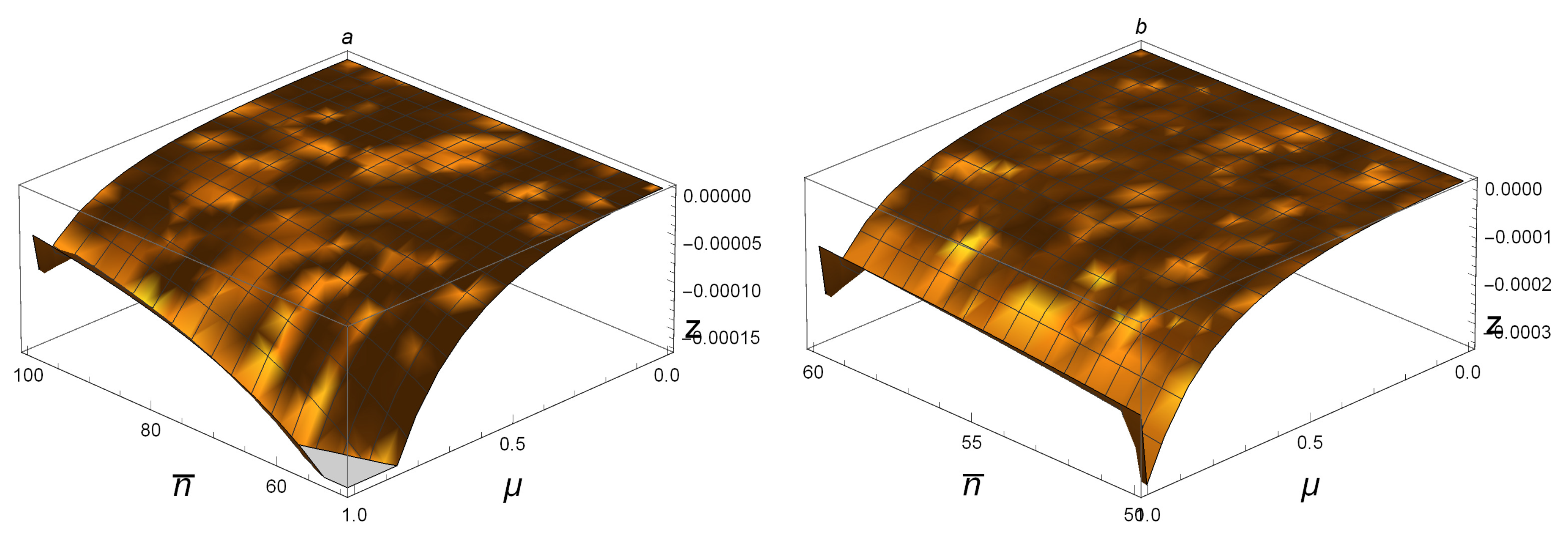
For small
, we display the image of
for SSTSs in
Figure 1 with
. It shows that
for most of the pairs
, and the inequality is invalid only when
is in a very small neighborhood of one. For example, by taking an SSTS
with
and
, we have
, which is too small and difficult to judge whether or not
is a product state. However,
is much bigger than zero, which guarantees that
is not a product state. In addition, since
is big enough, we conclude that, on the whole,
is better than
D in detecting the correlation in SSTSs, and it is a good choice if we take
as a quantification of this quantum correlation.
In [
11], the Gaussian geometric discord (GGD)
of any two-mode Gaussian state
is defined by:
where the infimum runs over all GPOVMs
of Subsystem
A and
. Moreover, it was shown that, for any SSTS
,
For
-mode continuous-variable systems, in [
16],
is a quantum correlation defined in terms of average distance between the reduced states under the LGPOVMs.
where the supremum is taken over all GPOVMs
on the subsystem
,
,
, and
.
For any SSTS
,
16] provided an analytical formula as:
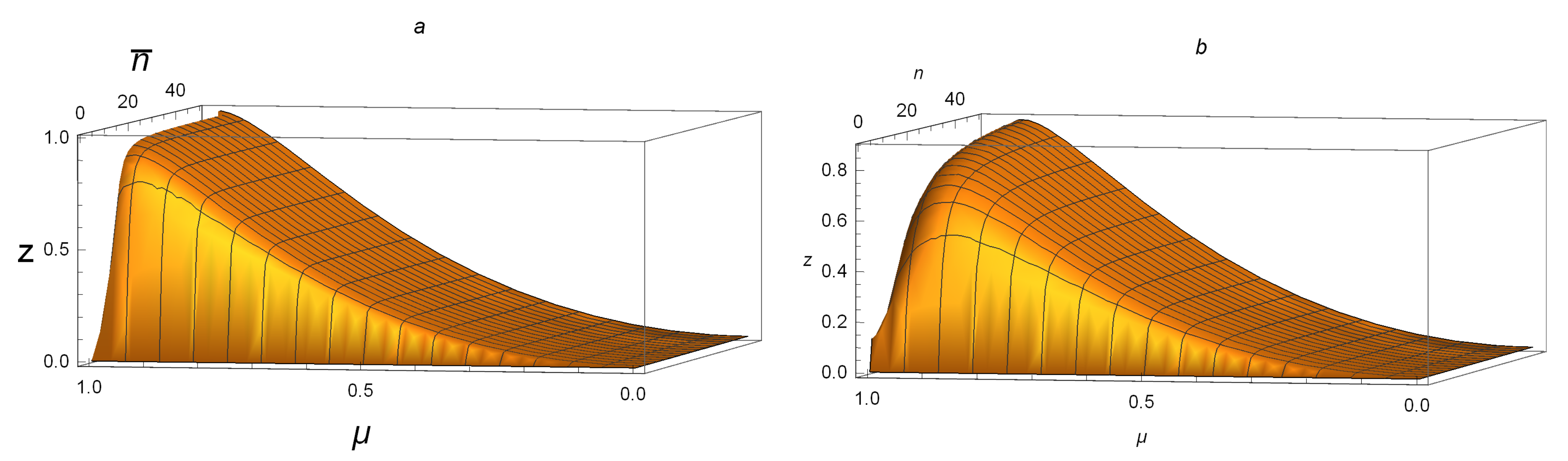
Figure 2a,b shows that
and
for all SSTSs with
and
. For example, taking
and
, one sees that
,
, while
. This suggests that
is better at detecting whether or not a state is a product state with small
.
When , it is clear that . Hence, is much greater than both and for those SSTSs with large mean photon number and . To be specific, let ; one has , while and are too small to ensure that such a state is not a product state.
Now, consider the case
. One has:
It is easy to verify that
, even though
.
The discussions above together with
Figure 2a,b suggest that
and
hold for all SSTSs. The numerical analysis supports these assertions.
In [
46], we proposed a quantum correlation
for
-mode Gaussian systems based on another form of fidelity
introduced in [
48], which is defined as:
The quantity
has several similar properties as
, but is easier to calculate. Particularly, for SSTS
, one has:
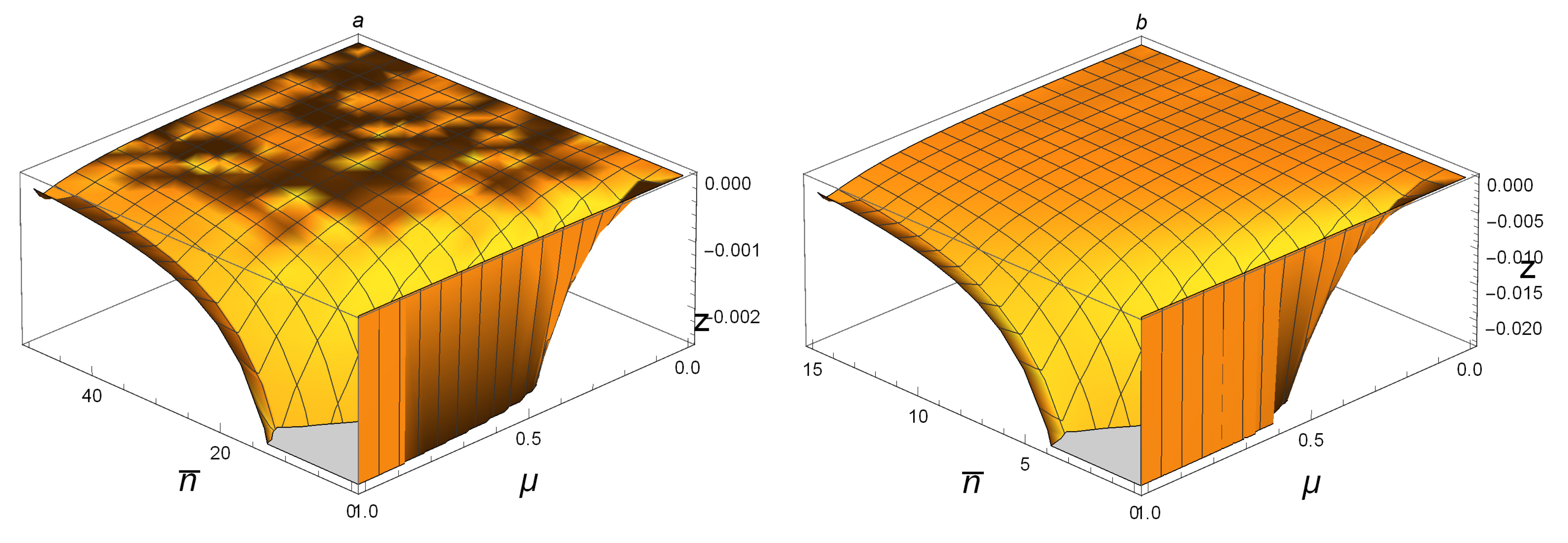
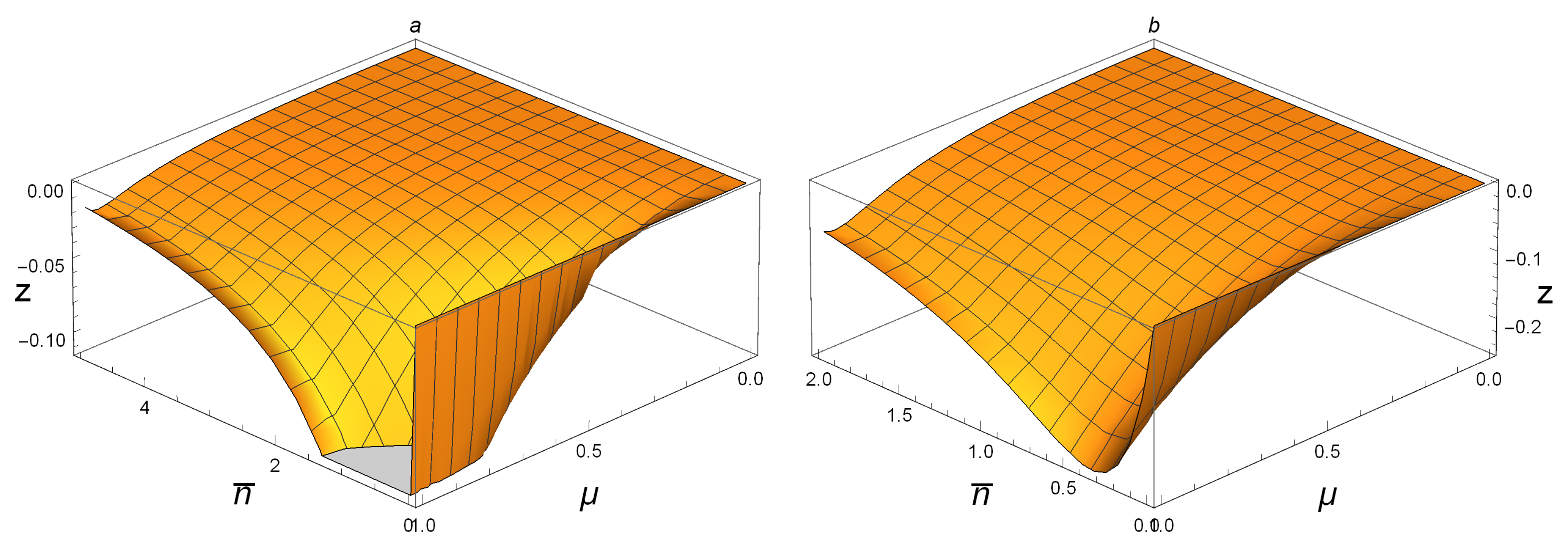
In order to get the full graph of
for SSTSs, we have to use six figures since there exist cutoffs caused by the drawing software. In
Figure 3a, we plot the function of
for SSTSs
with
and
. It is clear that, when
, one has
.
Figure 3b shows that
if
and
. The cases when
and
are shown in
Figure 4a and
Figure 4b, respectively. Accordingly, one can tell that
if
and
when
. Hence, for any Gaussian state
with
and
, one can conclude that
. When the average photon number gets bigger, as shown in
Figure 5a,b, one has
if
; when
, it holds that
. This means that, though
for small
, the difference between them is very small. For large
, as
, while
, we see that
for large
and
, and the difference between them may be very big. This can be seen by the fact
. For the special case
, we have:
It is clear that
is bigger than
for every
, but the difference between them is very small.
In summary, we can conclude that, if , on the whole, the behavior of is better than in detecting correlation contained in an SSTS.
From the above analysis, for Gaussian states, the quantity describes the same quantum correlation as D, , and Q. Furthermore, the quantity we proposed has no ancilla problem; for a fixed SSTS , is bigger than that of and Q in scale, which makes it better at detecting non-product Gaussian states; taking into consideration the physic resources consumed during the measurement process, consumes less and simpler resources compared with D, , and Q, since we use only part of unitary measurements, while the other three use all GPOVMs. Therefore, the quantity is a reasonable choice to quantify such Gaussian quantum correlations.
Also notice that, in [
14], for any two-mode Gaussian state
with CM
, the quantum correlation named Gaussian response of discord (
) is proposed, where the index
x stands for trace, Hellinger, or Bures distance. Precisely, with metrics
,
and
,
where the minimum is taken over all local unitaries of which the corresponding local symplectic transformations
are traceless, the normalization factors
and
, and
is the transformed state with CM
. Now, if the sine metric is applied, we can also get a kind of Gaussian response of discord:
One can verify that
is an alternative quantification of the quantum correlation for Gaussian states. Then, it is interesting to consider the relation between
and
. We claim that
even for the two-mode case. To see this, consider the two-mode Gaussian state
with CM
, where
,
and
satisfying
. Clearly,
and the set of all traceless symplectic matrices is:
Let:
and:
Then:
and:
Picking
, one has
with the maximum value achieved at
; while
with the minimum achieved at
. Therefore,
. However, for two-mode pure Gaussian states, we find that
because the extremal single-mode operation at the symplectic level coincides for the two quantities, i.e.,