Extracting Interactions between Flying Bat Pairs Using Model-Free Methods
Abstract
1. Introduction
2. Materials and Methods
2.1. Methods to Detect Directed Coupling
2.1.1. Transfer Entropy
2.1.2. Convergent Cross Map
2.1.3. Differences between TE and CCM
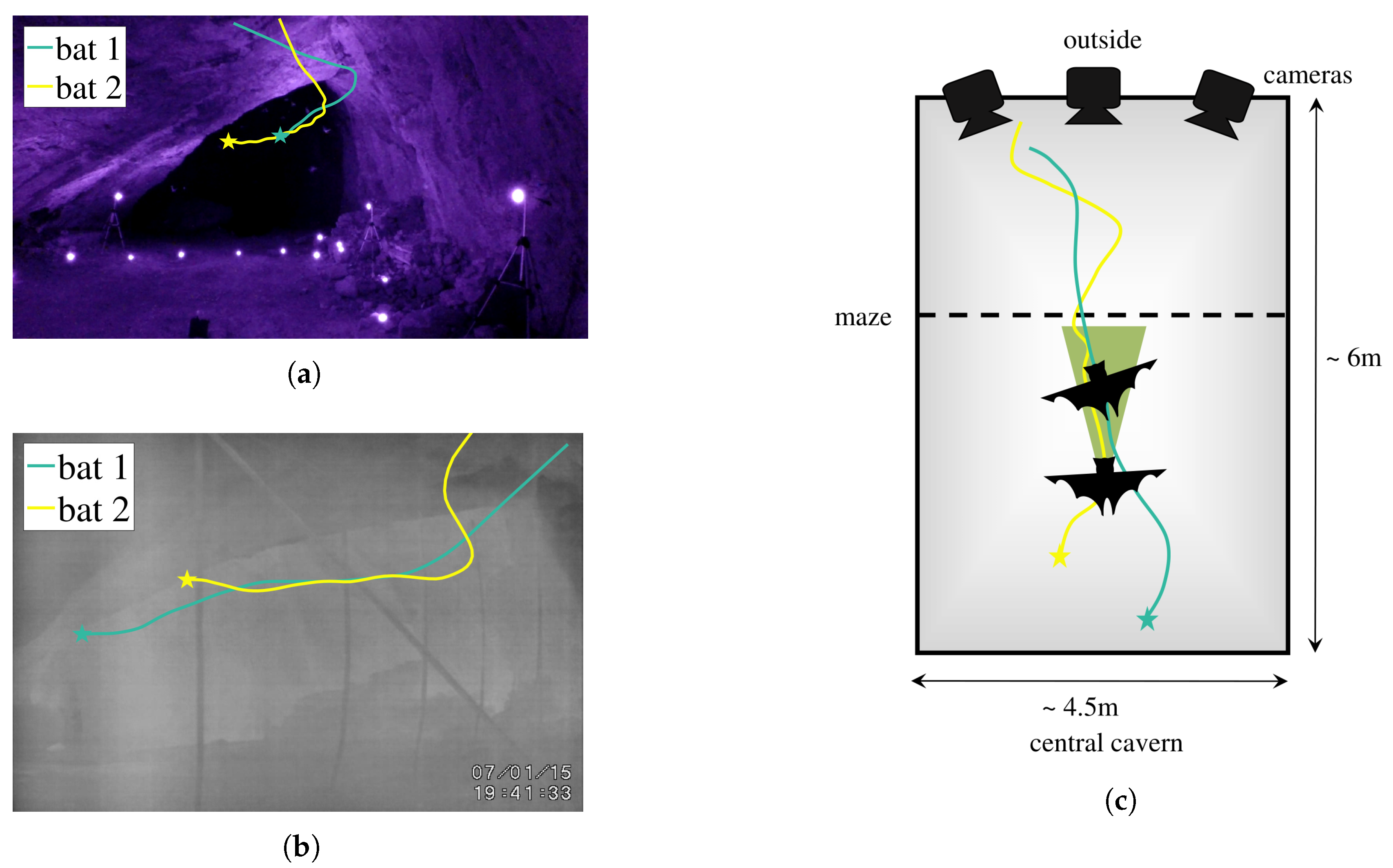
2.2. Experimental Setup and Data Collection
Data Availability
2.3. Data Analysis
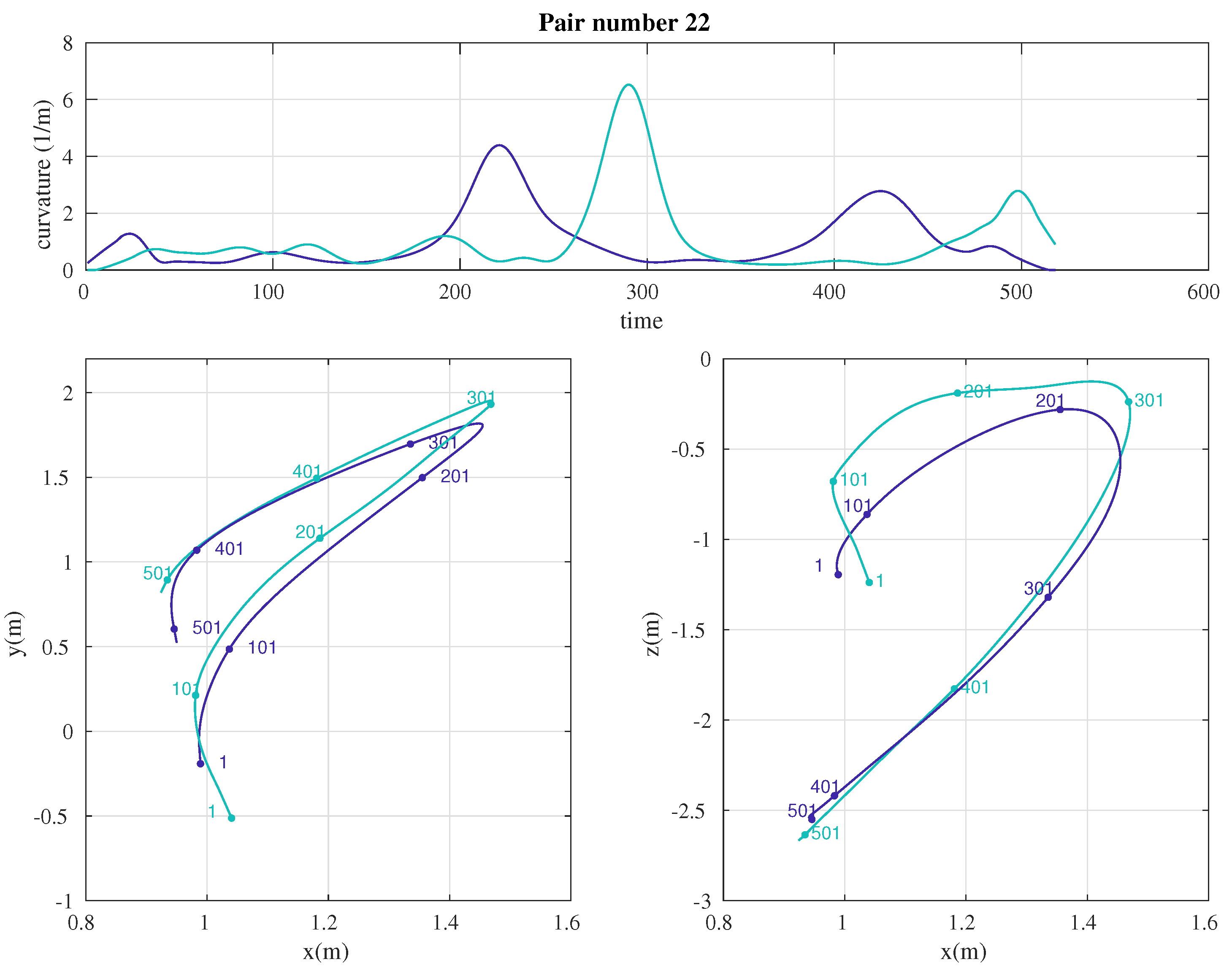
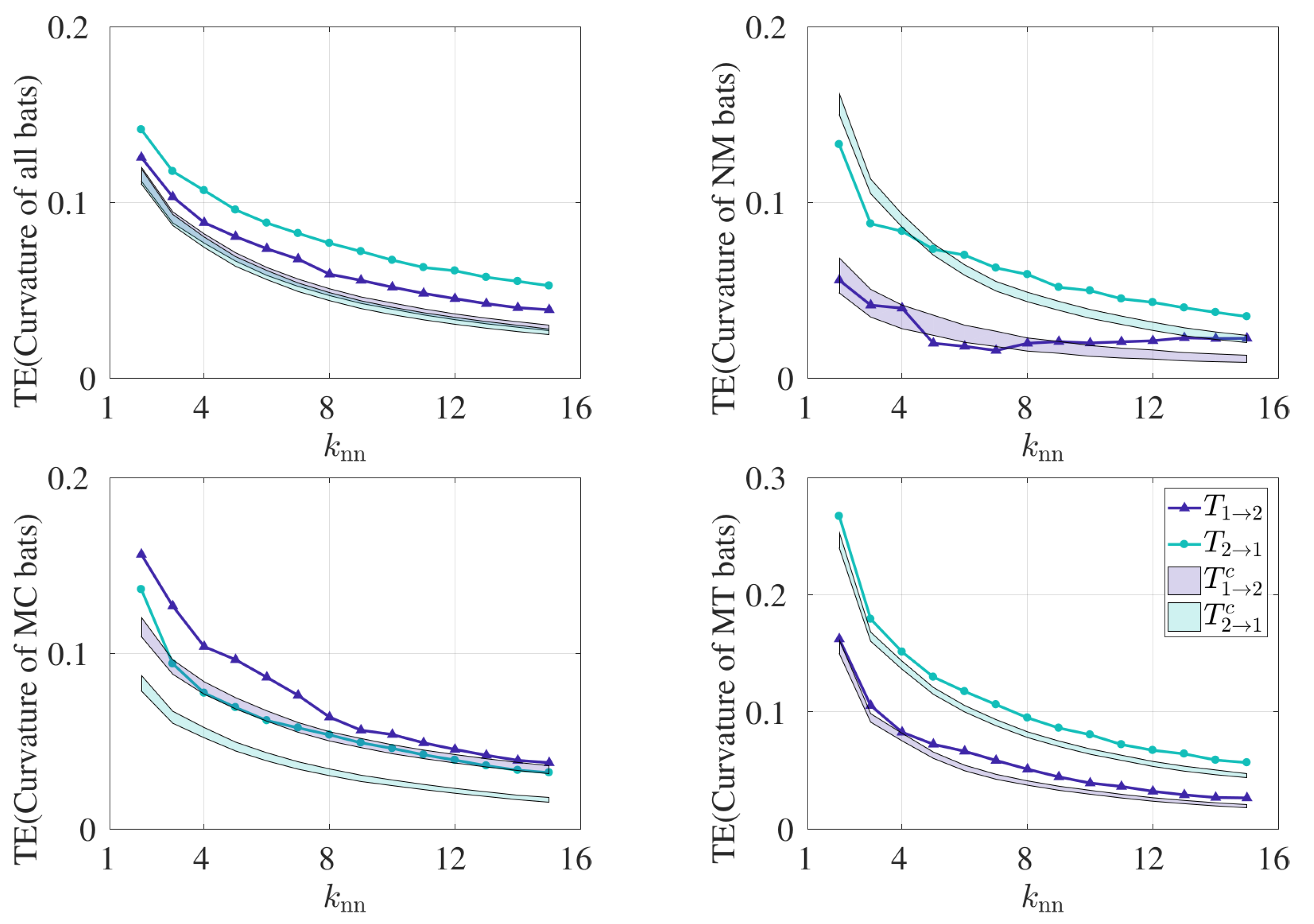
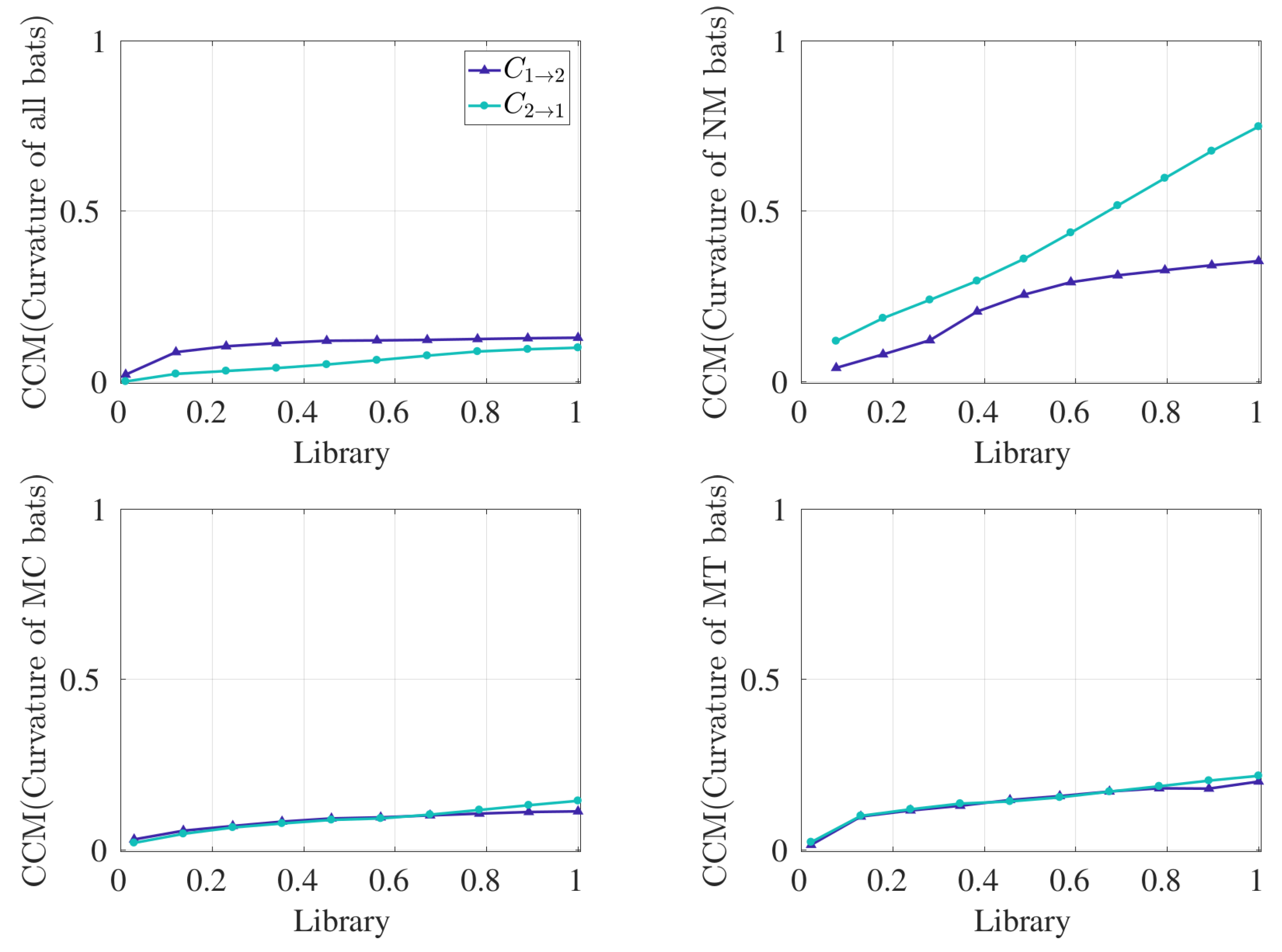
3. Results
4. Discussion
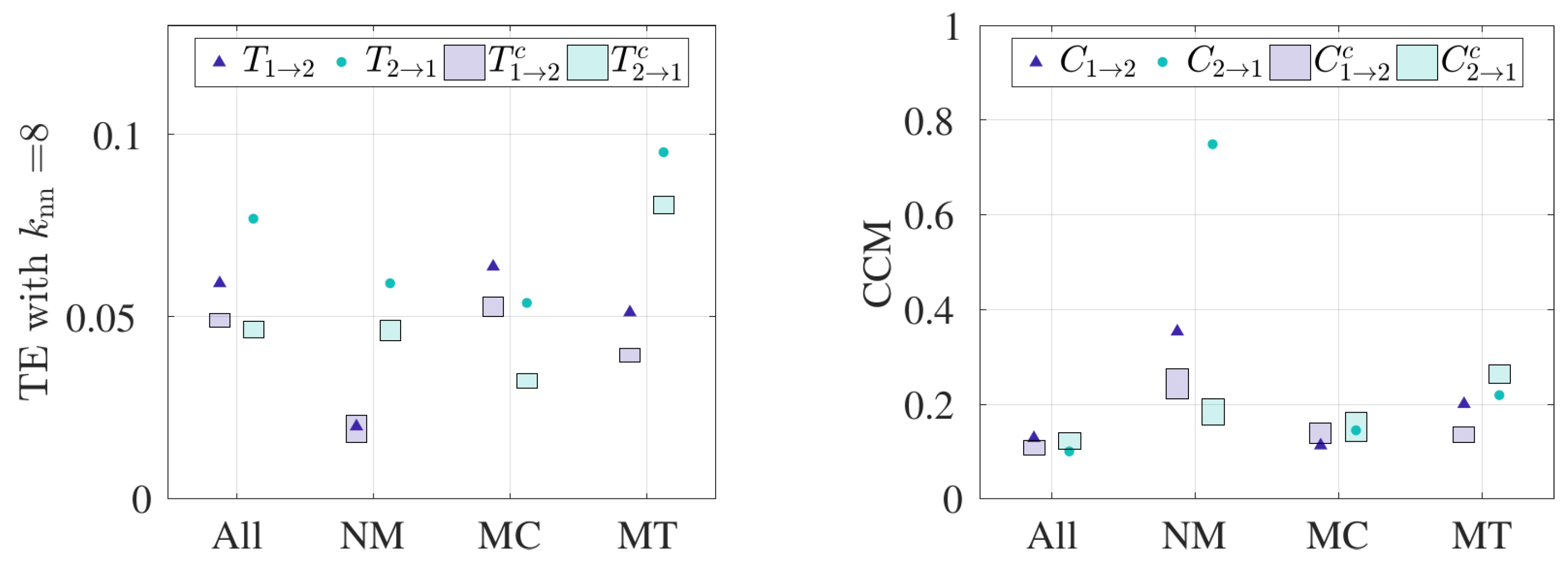
- Statistically significant coupling evidences pairwise interaction.TE and CCM results support the hypothesis that pairwise interactions involve additional coupling above control similarities in trajectories. TE captures significant bidirectional coupling between bats in all, MC, and MT pairs and significant unidirectional coupling from the rear to the front bat in NM pairs. On the other hand, CCM identifies leadership in the rear bat for NM pairs, and it gives no indication of leadership in the other pairs. Therefore, all unidirectional results are consistent, and bidirectional information flow (from TE) is equivalent to a lack of a directed causal relationship (from CCM). Since we selected the curvature time series as input for both analyses, these results evidence a relationship between how bats turn as they fly together. In this context, bidirectional coupling means that the two paired bats’ turning behaviors are mutually linked, while unidirectional coupling means that one bat drives the other to turn or not. In contrast, if we were to use velocity data for another TE analysis, then we would be able to test how the bats’ headings or speeds related.It is important to note that an alternative control condition can be used whereby the manufactured data can be shuffled in time. Shuffling in time refers to arbitrarily reordering the data between time steps for a given series, thus distorting its sequence. However, such a control is very liberal and leads to a zero mean and a standard deviation close to zero for virtually every case, resulting in statistical significance for all cases of TE and CCM. We chose a relatively conservative control condition in order to capture the information exchange above the effect of cave geometry and similarity in bat trajectories.
- TE and CCM identify directed coupling from rear to front bat flying in the absence of obstacles.This result may be counterintuitive, but it is certainly possible, given the bats’ orientation and sensing. These bats are effective users of active sensing, wherein the acoustic signal from the rear bat may discharge forward in space and hence to the front bat. It is also worth noting that a dominant coupling direction from the rear to the front individual previously has been identified in animal group motion in a study with meerkats [21]. However, to the best of our knowledge, our study is the first that indicates the possible presence of rear-to-front coupling in animals using active sensing.
- TE and CCM interpret coupling differently.As detailed in the Materials and Methods section, TE and CCM use fundamentally different approaches: TE measures information transfer, whereas CCM identifies the causal variable. The distinction between TE and causal effect was discussed in [38]. Particularly, TE with the assumption of a traditional first-order Markov process [23] means the current position of one bat is only affected by the values of one time step prior, which may be overcome by incorporating the idea of information storage [39]. On the contrary, CCM is a tool to detect the causal variable and is not an indicator of information transfer. In other words, TE picks up the traces of significant information transfer, whereas CCM inspects the dominant influence between a pair of time series variables (i.e., coupled turning behavior between bats in this study). As a result, it is not surprising that the results differ, as we used two different tools. However, we can interpret consistency between CCM and TE results by relating the concepts. For these data, CCM infers causality when TE suggests unidirectional information exchange, e.g., with NM pairs; CCM does not indicate causal coupling when TE suggests bidirectional information exchange, e.g., all, MC, and MT pairs. Therefore, these tools capture different features of the same phenomena.
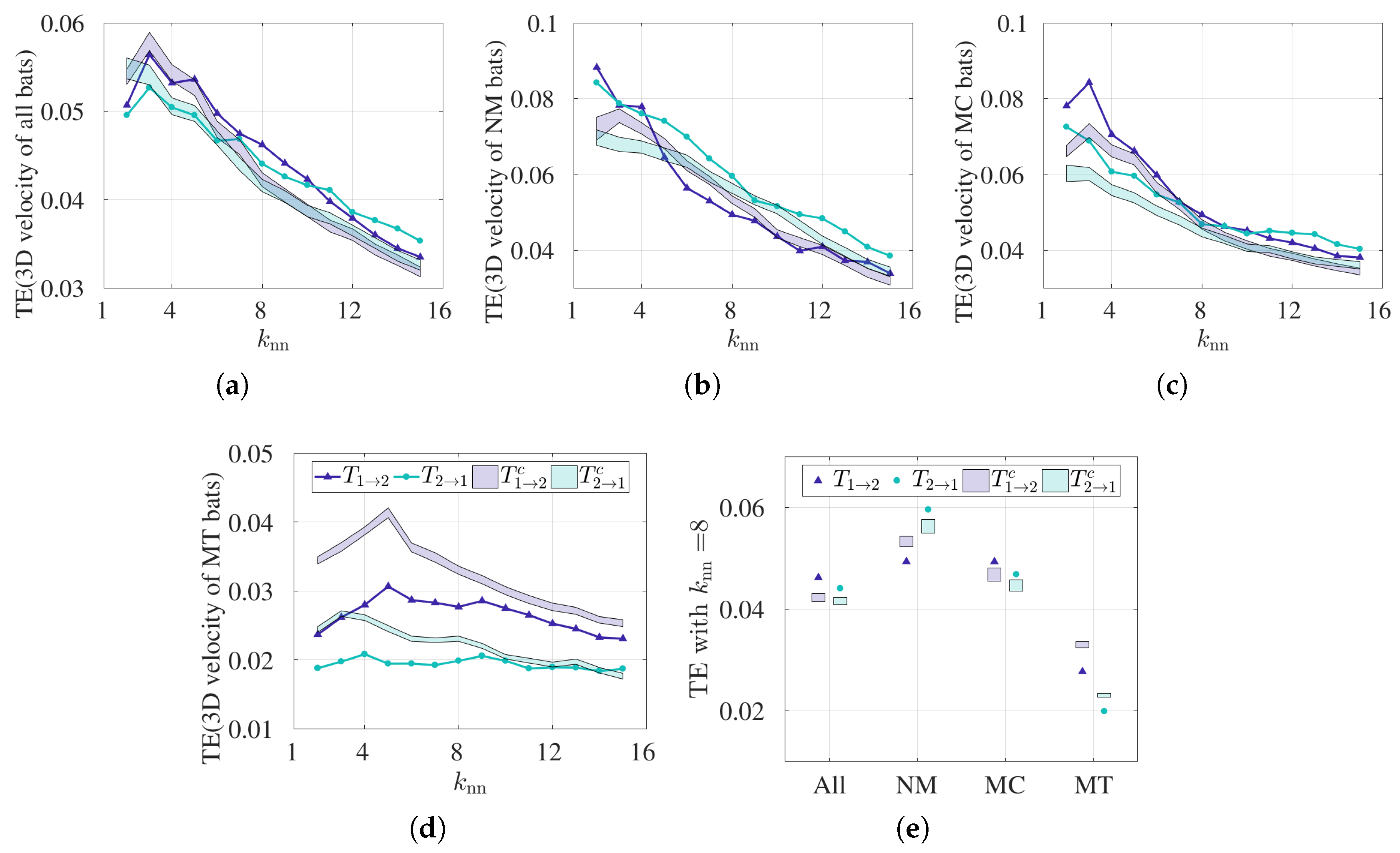
- TE is sensitive to the choice of independent variables used.To explore the sensitivity of TE results to the choice of independent variable, we adopted the multivariate functionality, whereby 3D velocity time series can be used to determine the coupling between two bats. Note that an analogous analysis was not performed for CCM since that algorithm only accepts univariate time series as input. The multivariate functionality in TE possesses a major limitation: namely, the method requires large datasets to build sufficiently dense 3D PDFs. Figure 6a–d show the sensitivity of the TE results to the choice of , and Figure 6e presents the summary of the result when we fix equal to 8. From Figure 6e, bidirectional coupling is noted when all 30 pairs and MC bats are considered, whereas unidirectional coupling is observed for NM bats. Specifically, TE recognizes bat 2 to bat 1 as the dominant coupling direction for NM pairs, which is consistent when curvature is used as an independent variable. However, the evidence of interaction is lost for MT pairs, as the TE results are not significant above the control condition, as observed in Figure 6e. We conclude that TE results are sensitive to the choice of independent variables, and this leads to inconsistent results for MT pairs. In general, each choice of independent variable requires a hypothesis to test, along with a control condition. In other words, using 3D velocity as the independent variable, the underlying hypothesis is that the pairwise interactions are manifested by changing speed and/or heading direction; when using curvature, the underlying hypothesis is that the pairwise interaction is manifested by turning. In fact, changing independent variable may change the mechanism of interaction and thus the coupling direction.
- Comparison with previous work.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Demonstration of TE and CCM
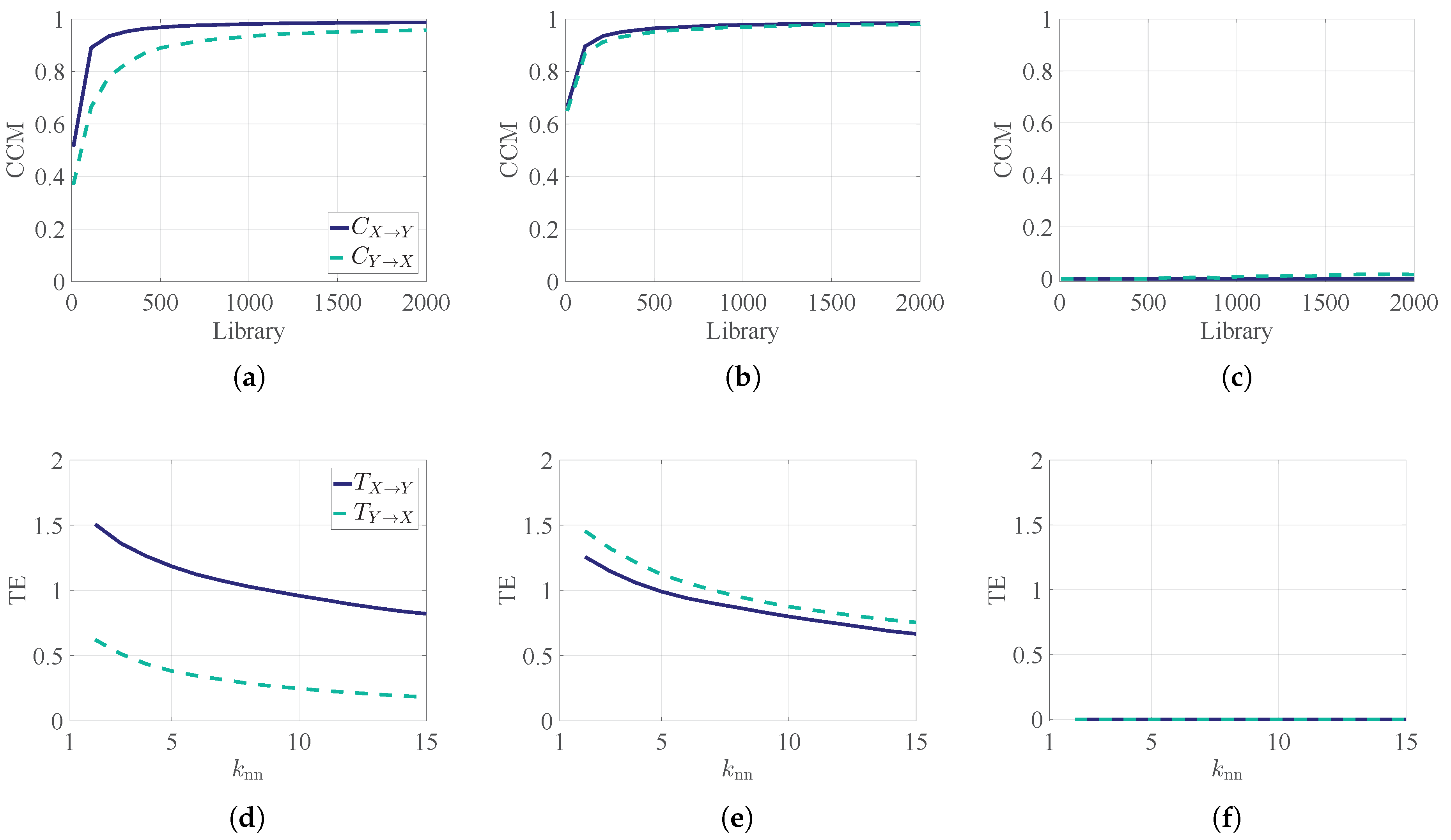
Appendix B. Experimental Details

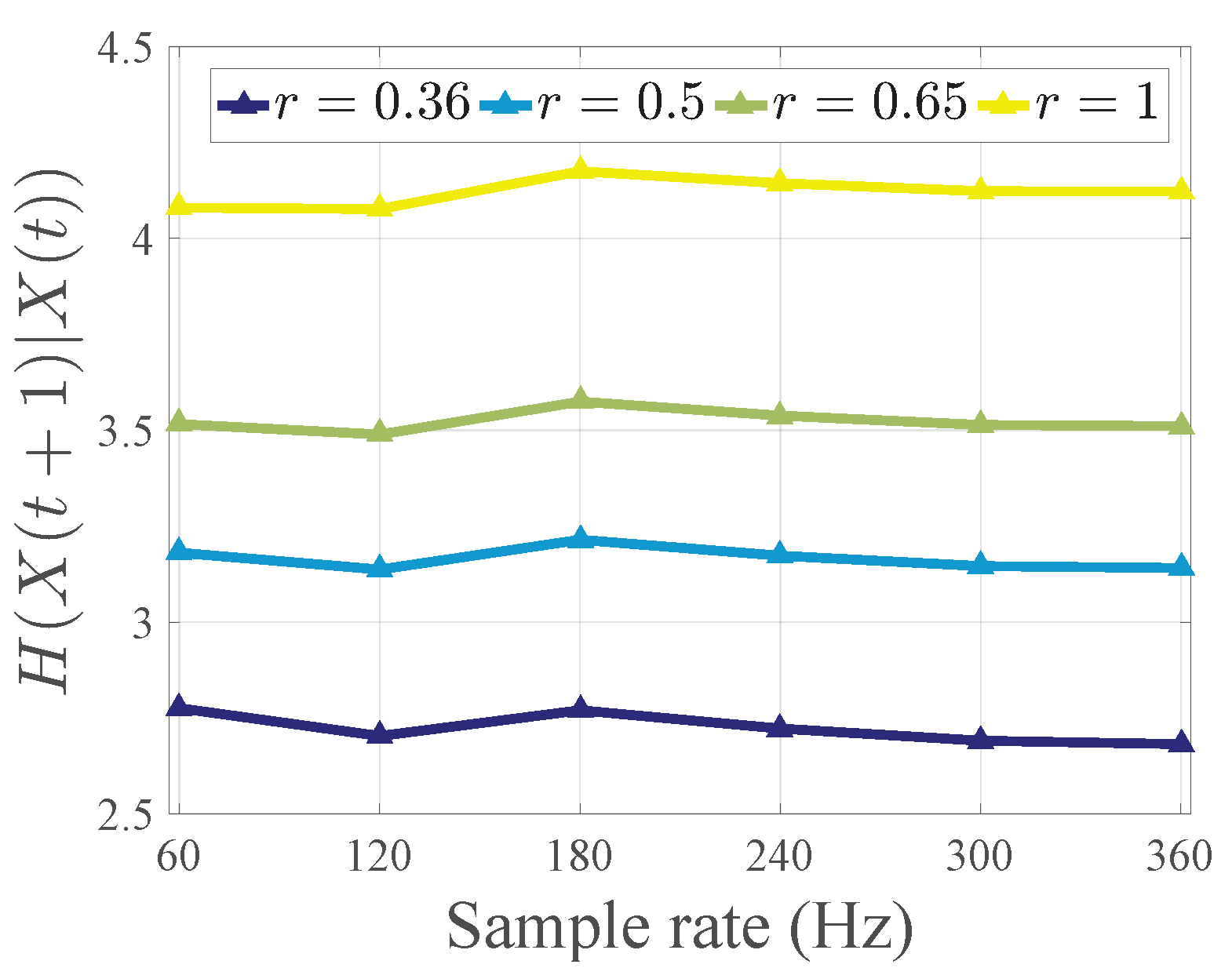
| Pair | Behavior | Bat 1 Path Length (m) | Bat 2 Path Length (m) | Duration (s) |
|---|---|---|---|---|
| 1 | NM | 3.03 | 2.28 | 0.42 |
| 2 | NM | 3.26 | 3.95 | 0.68 |
| 3 | NM | 4.54 | 3.87 | 1.32 |
| 4 | NM | 2.44 | 2.63 | 0.60 |
| 5 | NM | 3.91 | 3.54 | 0.64 |
| 6 | NM | 2.07 | 1.86 | 0.41 |
| 7 | NM | 3.61 | 2.61 | 0.62 |
| 8 | NM | 2.46 | 1.82 | 0.35 |
| 9 | NM | 5.35 | 7.28 | 1.20 |
| 10 | NM | 5.87 | 3.46 | 1.05 |
| 11 | MC | 3.48 | 2.29 | 1.67 |
| 12 | MT | 20.48 | 39.07 | 13.36 |
| 13 | MT | 15.82 | 8.88 | 3.28 |
| 14 | MC | 1.71 | 1.36 | 1.03 |
| 15 | MC | 3.89 | 0.97 | 1.80 |
| 16 | MC | 6.78 | 8.02 | 2.56 |
| 17 | MC | 3.25 | 0.55 | 0.52 |
| 18 | MC | 1.89 | 2.85 | 1.36 |
| 19 | MC | 6.75 | 2.57 | 1.12 |
| 20 | MC | 0.18 | 0.25 | 0.2 |
| 21 | MT | 4.43 | 2.18 | 2.08 |
| 22 | MT | 5.15 | 5.72 | 2.87 |
| 23 | MC | 2.65 | 2.36 | 2.68 |
| 24 | MC | 4.05 | 2.77 | 1.64 |
| 25 | MC | 5.27 | 1.89 | 1.36 |
| 26 | MT | 2.94 | 2.95 | 2.6 |
| 27 | MT | 3.17 | 5.07 | 2.16 |
| 28 | MC | 3.89 | 1.90 | 0.81 |
| 29 | MC | 2.10 | 1.87 | 1.08 |
| 30 | MC | 2.79 | 2.45 | 1.32 |
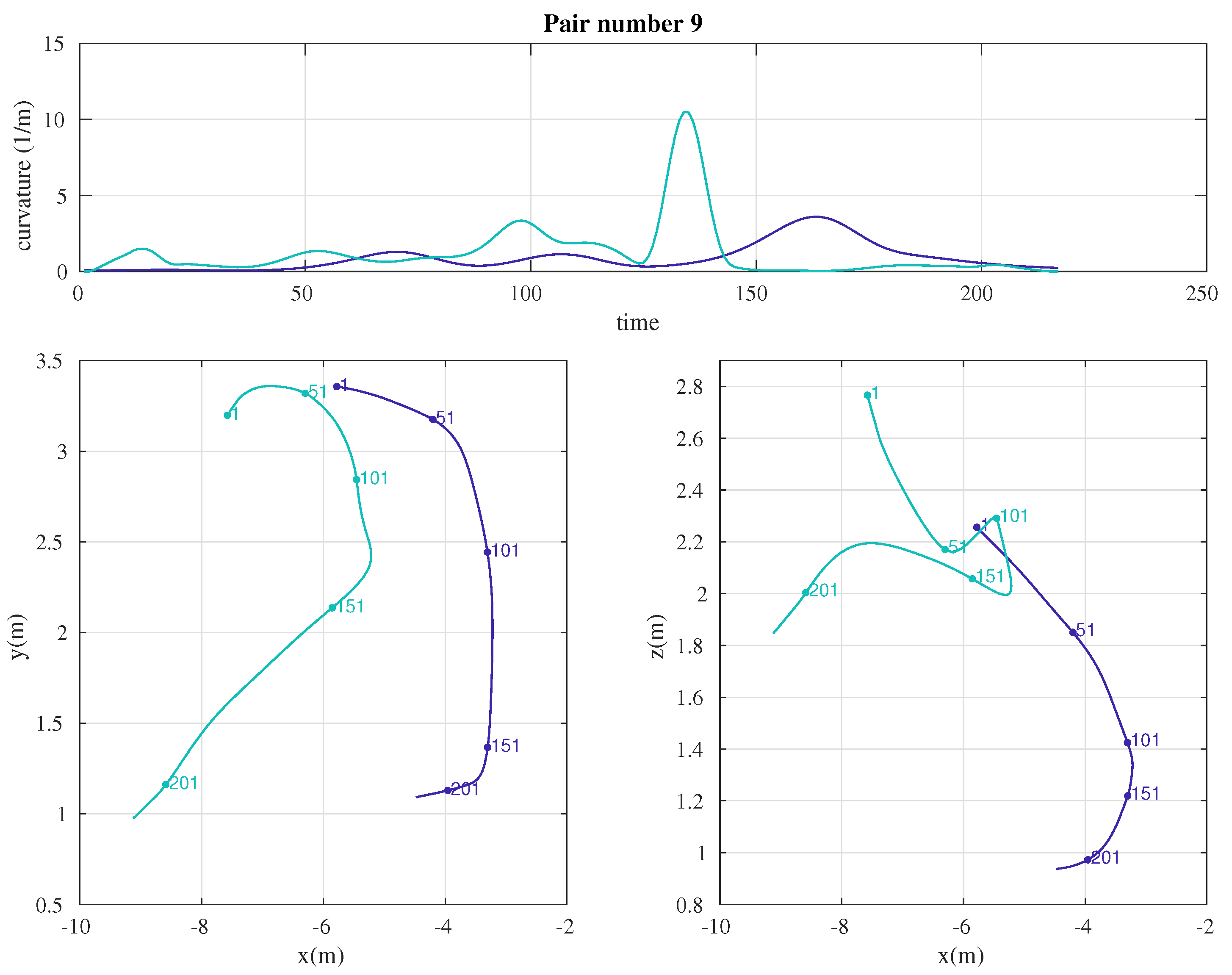
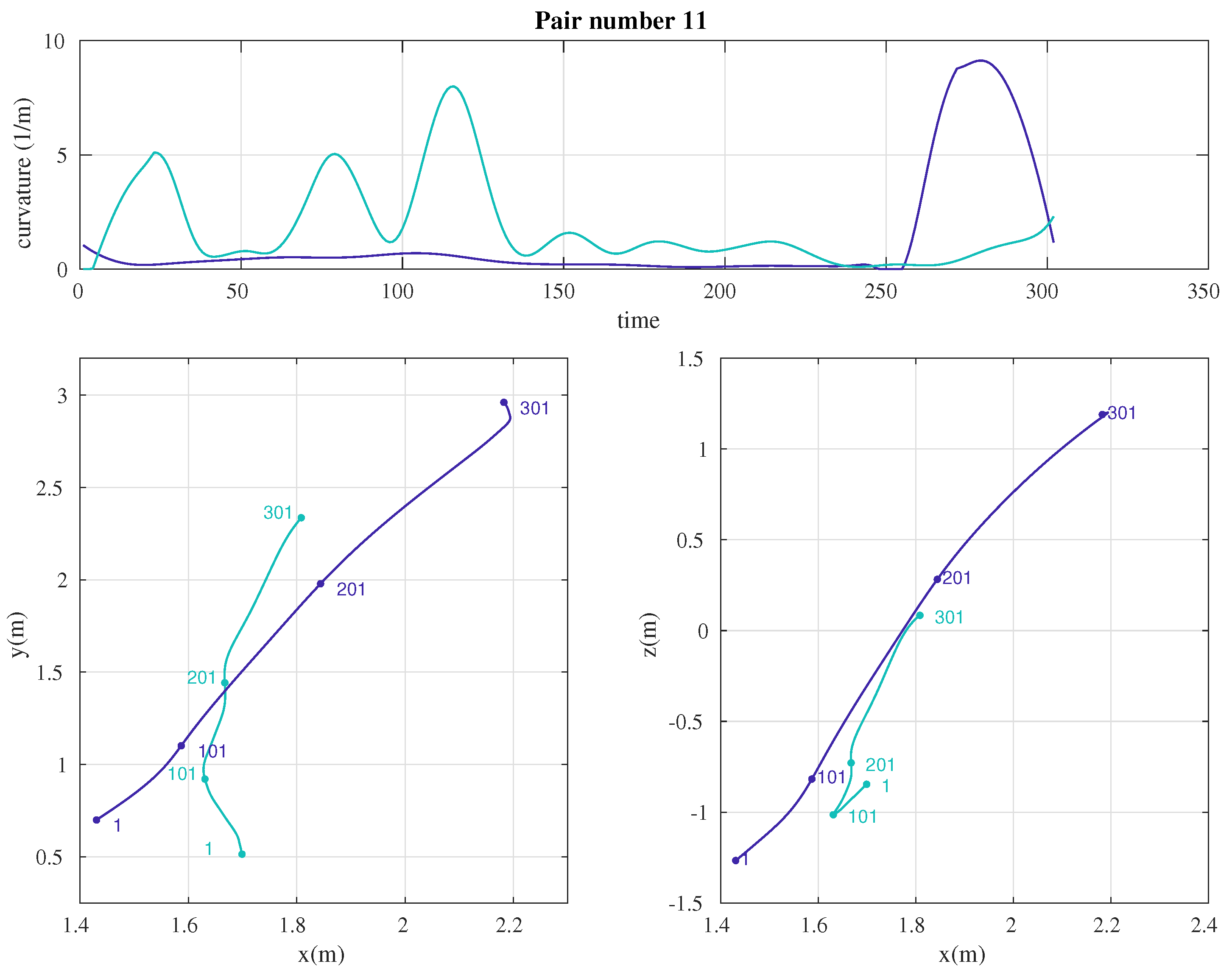
References and Note
- Krause, J.; Ruxton, G.D. Living in Groups; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Nelson, M.E.; MacIver, M.A. Sensory acquisition in active sensing systems. J. Comp. Physiol. A 2006, 192, 573–586. [Google Scholar] [CrossRef] [PubMed]
- Kong, Z.; Fuller, N.; Wang, S.; Ozcimder, K.; Gillam, E.; Theriault, D.; Betke, M.; Baillieul, J. Perceptual modalities guiding bat flight in a native habitat. Sci. Rep. 2016, 6, 27252. [Google Scholar] [CrossRef] [PubMed]
- Thomas, J.A.; Moss, C.F.; Vater, M. Echolocation in Bats and Dolphins; University of Chicago Press: Chicago, IL, USA, 2004. [Google Scholar]
- Ulanovsky, N.; Fenton, M.B.; Tsoar, A.; Korine, C. Dynamics of jamming avoidance in echolocating bats. Proc. R. Soc. Lond. Ser. B Biol. Sci. 2004, 271, 1467–1475. [Google Scholar] [CrossRef] [PubMed]
- Chiu, C.; Xian, W.; Moss, C.F. Flying in silence: Echolocating bats cease vocalizing to avoid sonar jamming. Proc. Natl. Acad. Sci. USA 2008, 105, 13116–13121. [Google Scholar] [CrossRef] [PubMed]
- Corcoran, A.J.; Conner, W.E. Bats jamming bats: Food competition through sonar interference. Science 2014, 346, 745–747. [Google Scholar] [CrossRef] [PubMed]
- Nagy, M.; Akos, Z.; Biro, D.; Vicsek, T. Hierarchical group dynamics in pigeon flocks. Nature 2010, 464, 890–893. [Google Scholar] [CrossRef]
- Razak, F.A.; Jensen, H.J. Quantifying ‘causality’ in complex systems: Understanding transfer entropy. PLoS ONE 2014, 9, e99462. [Google Scholar]
- Sugihara, G.; May, R.; Ye, H.; Hsieh, C.; Deyle, E.; Fogarty, M.; Munch, S. Detecting causality in complex ecosystems. Science 2012, 338, 496–500. [Google Scholar] [CrossRef]
- Vicente, R.; Wibral, M.; Lindner, M.; Pipa, G. Transfer entropy—A model-free measure of effective connectivity for the neurosciences. J. Comput. Neurosci. 2011, 30, 45–67. [Google Scholar] [CrossRef]
- Dimpfl, T.; Peter, F.J. Using transfer entropy to measure information flows between financial markets. Stud. Nonlinear Dyn. Econom. 2013, 17, 85–102. [Google Scholar] [CrossRef]
- Ver Steeg, G.; Galstyan, A. Information transfer in social media. In Proceedings of the 21st International Conference on World Wide Web, Lyon, France, 16–20 April 2012; pp. 509–518. [Google Scholar]
- Hlinka, J.; Hartman, D.; Vejmelka, M.; Runge, J.; Marwan, N.; Kurths, J.; Palus, M. Reliability of inference of directed climate networks using conditional mutual information. Entropy 2013, 15, 2023–2045. [Google Scholar] [CrossRef]
- McBride, J.C.; Zhao, X.; Munro, N.B.; Jicha, G.A.; Schmitt, F.A.; Kryscio, R.J.; Smith, C.D.; Jiang, Y. Sugihara causality analysis of scalp EEG for detection of early Alzheimer’s disease. NeuroImage Clin. 2015, 7, 258–265. [Google Scholar] [CrossRef]
- Dost, F. A non-linear causal network of marketing channel system structure. J. Retail. Consum. Serv. 2015, 23, 49–57. [Google Scholar] [CrossRef]
- Crosato, E.; Jiang, L.; Lecheval, V.; Lizier, J.T.; Wang, X.R.; Tichit, P.; Theraulaz, G.; Prokopenko, M. Informative and misinformative interactions in a school of fish. arXiv, 2017; arXiv:1705.01213. [Google Scholar]
- Butail, S.; Ladu, F.; Spinello, D.; Porfiri, M. Information flow in animal-robot interactions. Entropy 2014, 16, 1315–1330. [Google Scholar] [CrossRef]
- Butail, S.; Mwaffo, V.; Porfiri, M. Model-free information-theoretic approach to infer leadership in pairs of zebrafish. Phys. Rev. E 2016, 93, 042411. [Google Scholar] [CrossRef]
- Tomaru, T.; Murakami, H.; Niizato, T.; Nishiyama, Y.; Sonoda, K.; Moriyama, T.; Gunji, Y.P. Information transfer in a swarm of soldier crabs. Artif. Life Robot. 2016, 21, 177–180. [Google Scholar] [CrossRef]
- Richardson, T.O.; Perony, N.; Tessone, C.J.; Bousquet, C.A.; Manser, M.B.; Schweitzer, F. Dynamical coupling during collective animal motion. arXiv, 2013; arXiv:1311.1417. [Google Scholar]
- Lord, W.M.; Sun, J.; Ouellette, N.T.; Bollt, E.M. Inference of Causal Information Flow in Collective Animal Behavior. IEEE Trans. Mol. Biol. Multi-Scale Commun. 2016, 2, 107–116. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461. [Google Scholar] [CrossRef]
- Papana, A.; Kugiumtzis, D. Evaluation of mutual information estimators for time series. Int. J. Bifurc. Chaos 2009, 19, 4197–4215. [Google Scholar] [CrossRef]
- Lizier, J.T. JIDT: An information-theoretic toolkit for studying the dynamics of complex systems. arXiv, 2014; arXiv:1408.3270. [Google Scholar]
- Kraskov, A.; Stogbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef] [PubMed]
- McCracken, J.M.; Weigel, R.S. Convergent cross-mapping and pairwise asymmetric inference. Phys. Rev. E 2014, 90, 062903. [Google Scholar] [CrossRef] [PubMed]
- Sugihara, G.; Ye, H.; Clark, A.; Deyle, E.; Much, S.; Cai, J.; Cowles, J.; Edwards, A.; Keyes, O.; Stagge, J.; et al. Sugihara Lab Software Resources (rEDM). Available online: http://deepeco.ucsd.edu/resources/ (accessed on 1 November 2016).
- Deyle, E.R.; Fogarty, M.; Hsieh, C.H.; Kaufman, L.; MacCall, A.D.; Munch, S.B.; Perretti, C.T.; Ye, H.; Sugihara, G. Predicting climate effects on Pacific sardine. Proc. Natl. Acad. Sci. USA 2013, 110, 6430–6435. [Google Scholar] [CrossRef] [PubMed]
- Orange, N.; Abaid, N. A transfer entropy analysis of leader-follower interactions in flying bats. Eur. Phys. J. Spec. Top. 2015, 224, 3279–3293. [Google Scholar] [CrossRef]
- Sikes, R.S.; Gannon, W.L. Guidelines of the American Society of Mammalogists for the use of wild mammals in research. J. Mammal. 2011, 92, 235–253. [Google Scholar] [CrossRef]
- Svoboda, T.; Martinec, D.; Pajdla, T.; Bouguet, J.Y.; Werner, T.; Chum, O. Multi-Camera Self-Calibration; Czech Technical University: Prague, Czech Republic, 2003. [Google Scholar]
- Bouguet, J.Y. Camera Calibration Toolbox for Matlab. Available online: http://www.vision.caltech.edu/bouguetj/calib_doc/index.html (accessed on 16 November 2015).
- Puckett, J.G.; Kelley, D.H.; Ouellette, N.T. Searching for effective forces in laboratory insect swarms. Sci. Rep. 2014, 4, 4766. [Google Scholar] [CrossRef]
- Aziz, N.A. Transfer entropy as a tool for inferring causality from observational studies in epidemiology. bioRxiv 2017, 149625. [Google Scholar] [CrossRef]
- Montalto, A.; Faes, L.; Marinazzo, D. MuTE: A MATLAB toolbox to compare established and novel estimators of the multivariate transfer entropy. PLoS ONE 2014, 9, e109462. [Google Scholar] [CrossRef]
- Parker, R.E. Introductory Statistics for Biology; Cambridge University Press: Cambridge, UK, 1991; Volume 43. [Google Scholar]
- Lizier, J.T.; Prokopenko, M. Differentiating information transfer and causal effect. Eur. Phys. J. B 2010, 73, 605–615. [Google Scholar] [CrossRef]
- Wibral, M.; Lizier, J.T.; Vogler, S.; Priesemann, V.; Galuske, R. Local active information storage as a tool to understand distributed neural information processing. Front. Neuroinform. 2014, 8, 1. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Abaid, N. Modeling perspectives on echolocation strategies inspired by bats flying in groups. J. Theor. Biol. 2015, 387, 46–53. [Google Scholar] [CrossRef] [PubMed]
- Based on personal email conversation with Dr. Lizier, the author of JIDT toolkit, confirmed the use of kernel estimator to evaluate conditional entropy with the present version of JIDT.
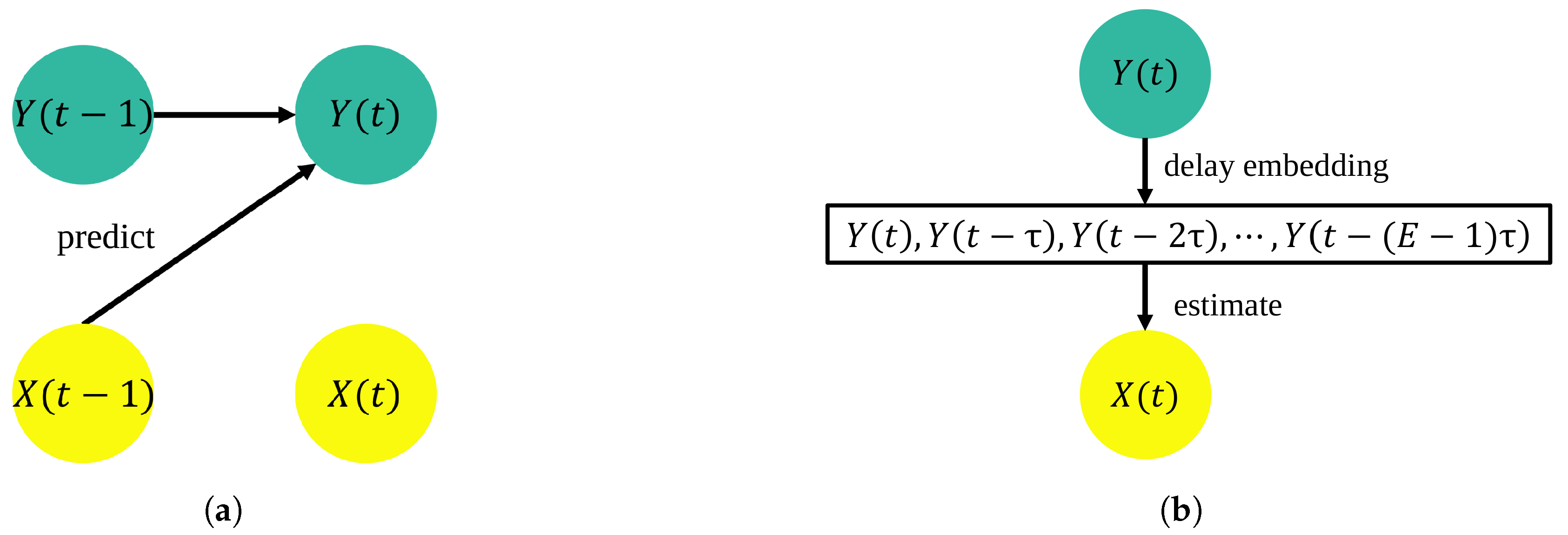
| Method | Input | Output |
|---|---|---|
| TE | ||
|
| |
| CCM | ||
|
|
| Cond | TE Using Curvature | CCM Using Curvature | TE Using 3D Velocity | Presence of Leadership |
|---|---|---|---|---|
| all | No | |||
|
| |||
| NM | Yes | |||
|
| (leadership by rear bat) | ||
| MC | No | |||
|
| |||
| MT | No | |||
|
|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roy, S.; Howes, K.; Müller, R.; Butail, S.; Abaid, N. Extracting Interactions between Flying Bat Pairs Using Model-Free Methods. Entropy 2019, 21, 42. https://doi.org/10.3390/e21010042
Roy S, Howes K, Müller R, Butail S, Abaid N. Extracting Interactions between Flying Bat Pairs Using Model-Free Methods. Entropy. 2019; 21(1):42. https://doi.org/10.3390/e21010042
Chicago/Turabian StyleRoy, Subhradeep, Kayla Howes, Rolf Müller, Sachit Butail, and Nicole Abaid. 2019. "Extracting Interactions between Flying Bat Pairs Using Model-Free Methods" Entropy 21, no. 1: 42. https://doi.org/10.3390/e21010042
APA StyleRoy, S., Howes, K., Müller, R., Butail, S., & Abaid, N. (2019). Extracting Interactions between Flying Bat Pairs Using Model-Free Methods. Entropy, 21(1), 42. https://doi.org/10.3390/e21010042






