d-Dimensional Classical Heisenberg Model with Arbitrarily-Ranged Interactions: Lyapunov Exponents and Distributions of Momenta and Energies
Abstract
1. Introduction
2. The Model
2.1. The and Limiting Cases
2.2. Equations of Motion
3. Results
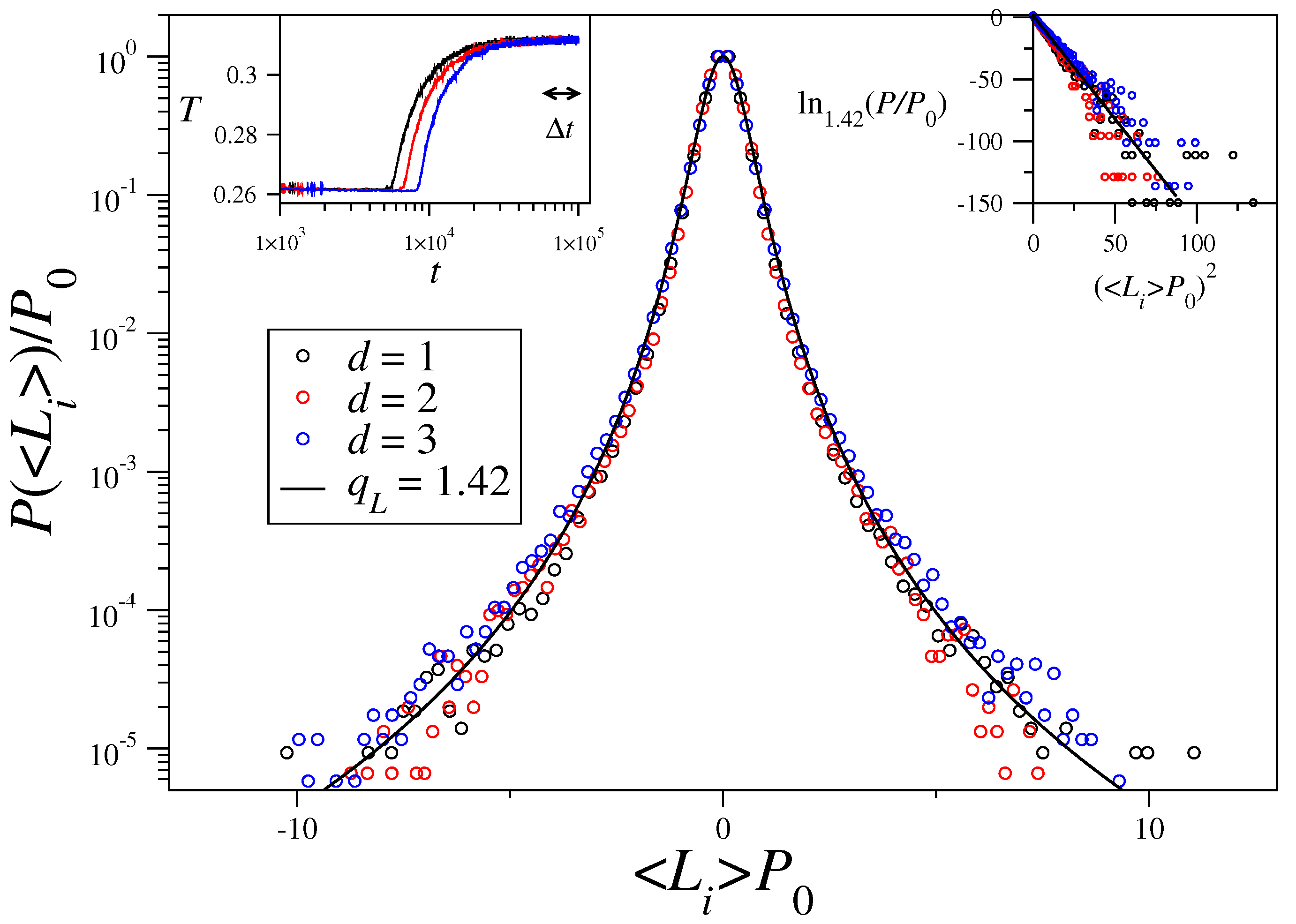
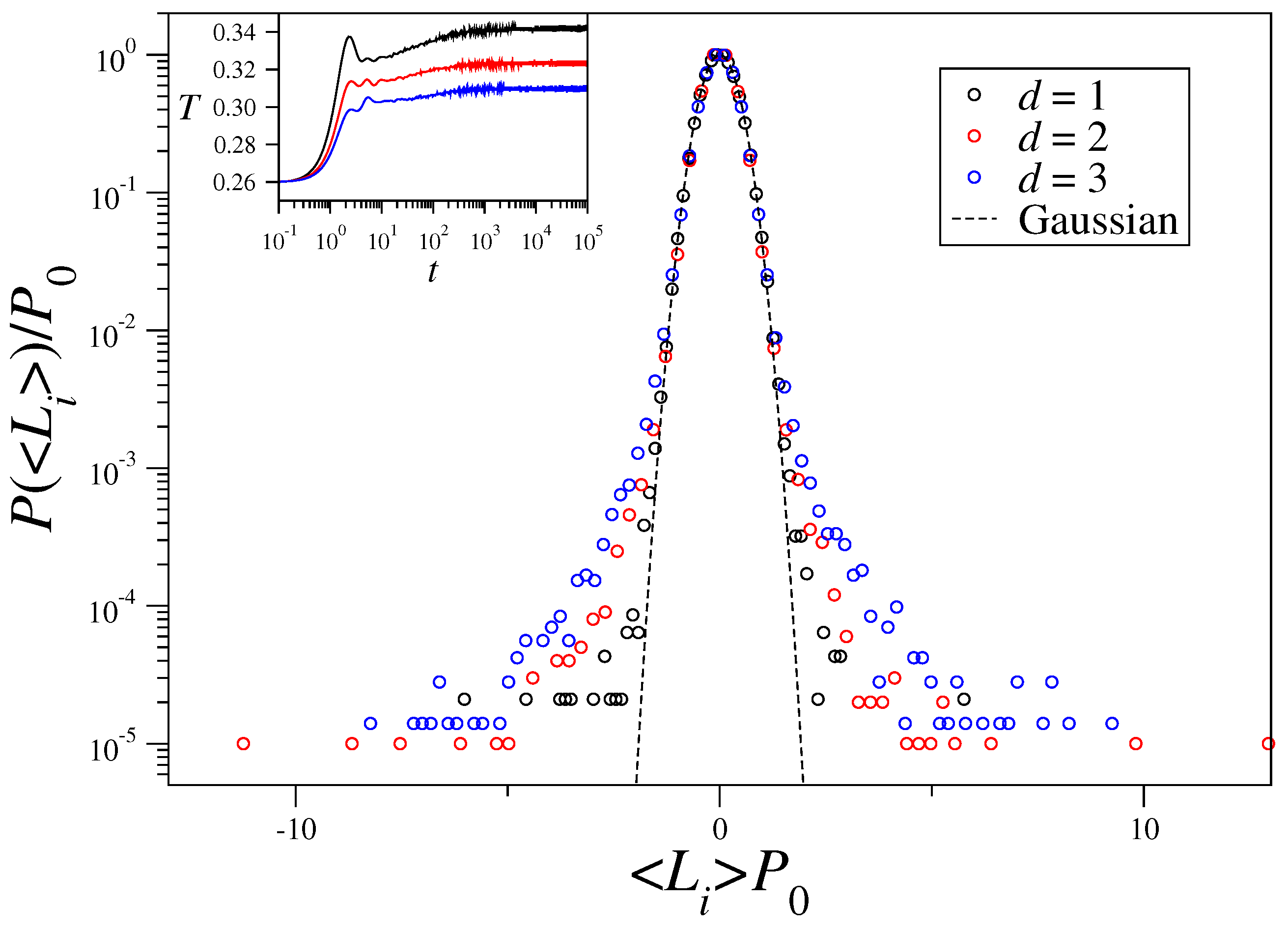
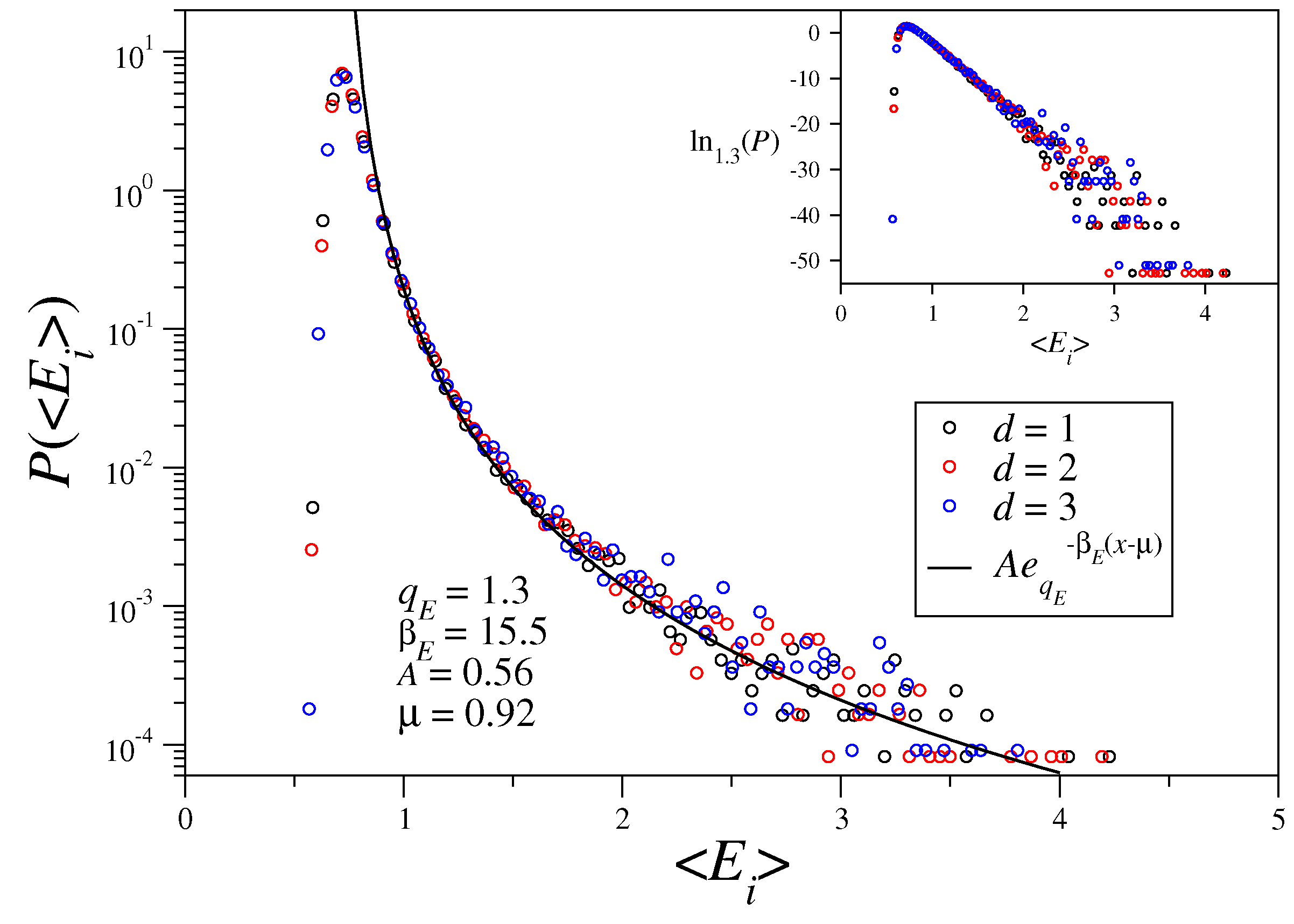
3.1. Time-Averaged Momenta and Energy One-Particle Distributions
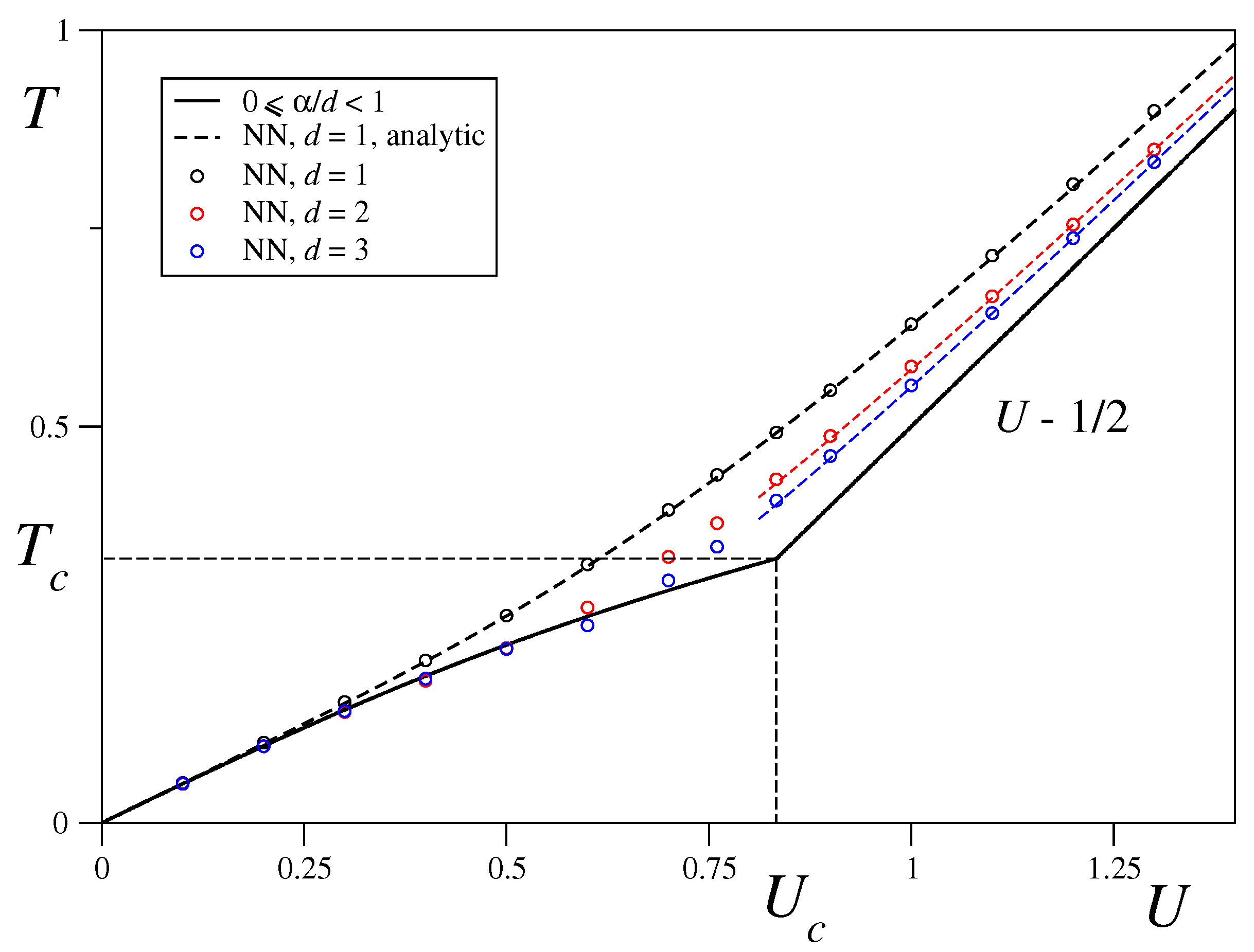
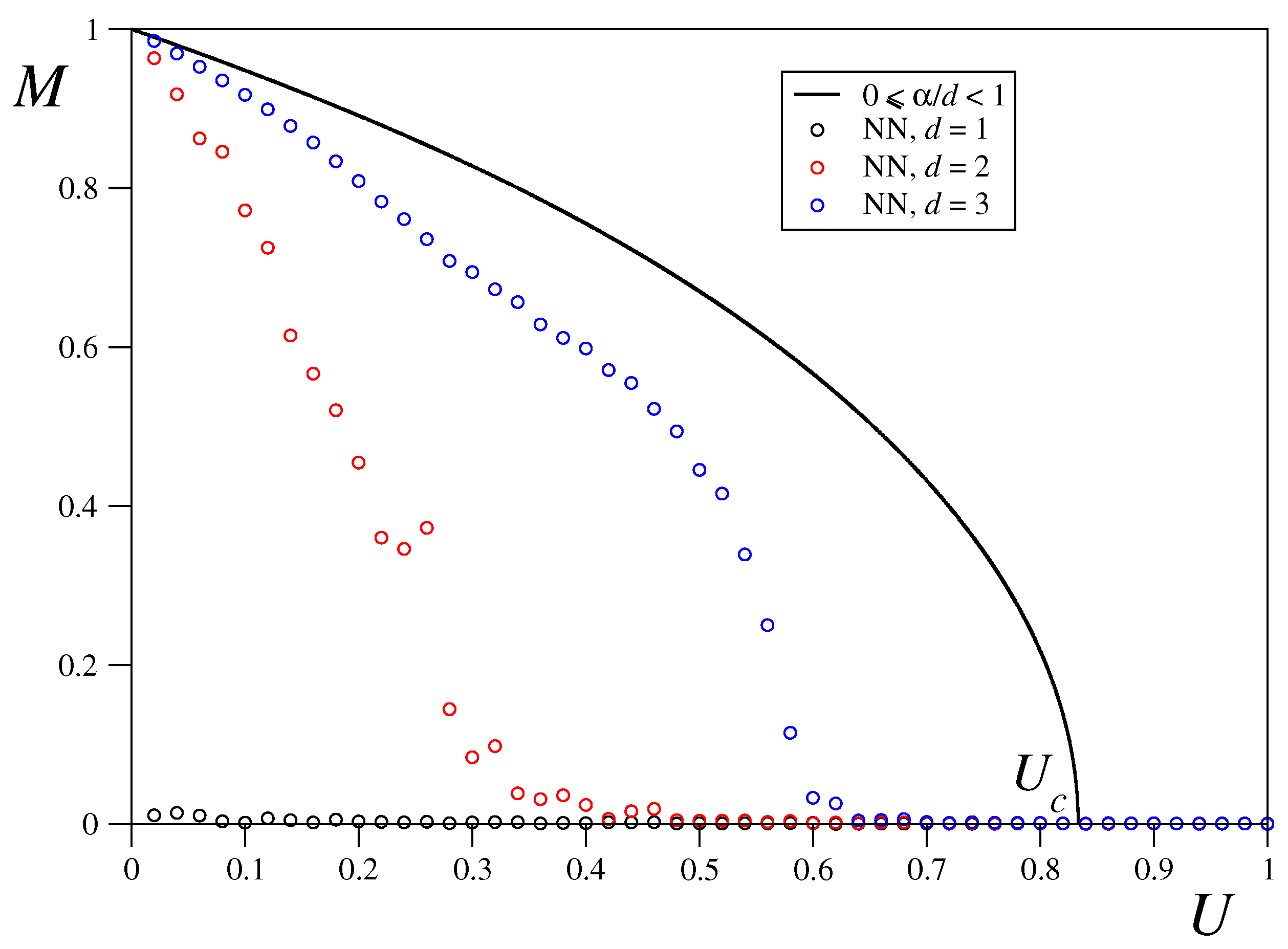
3.2. Nearest-Neighbour Limit
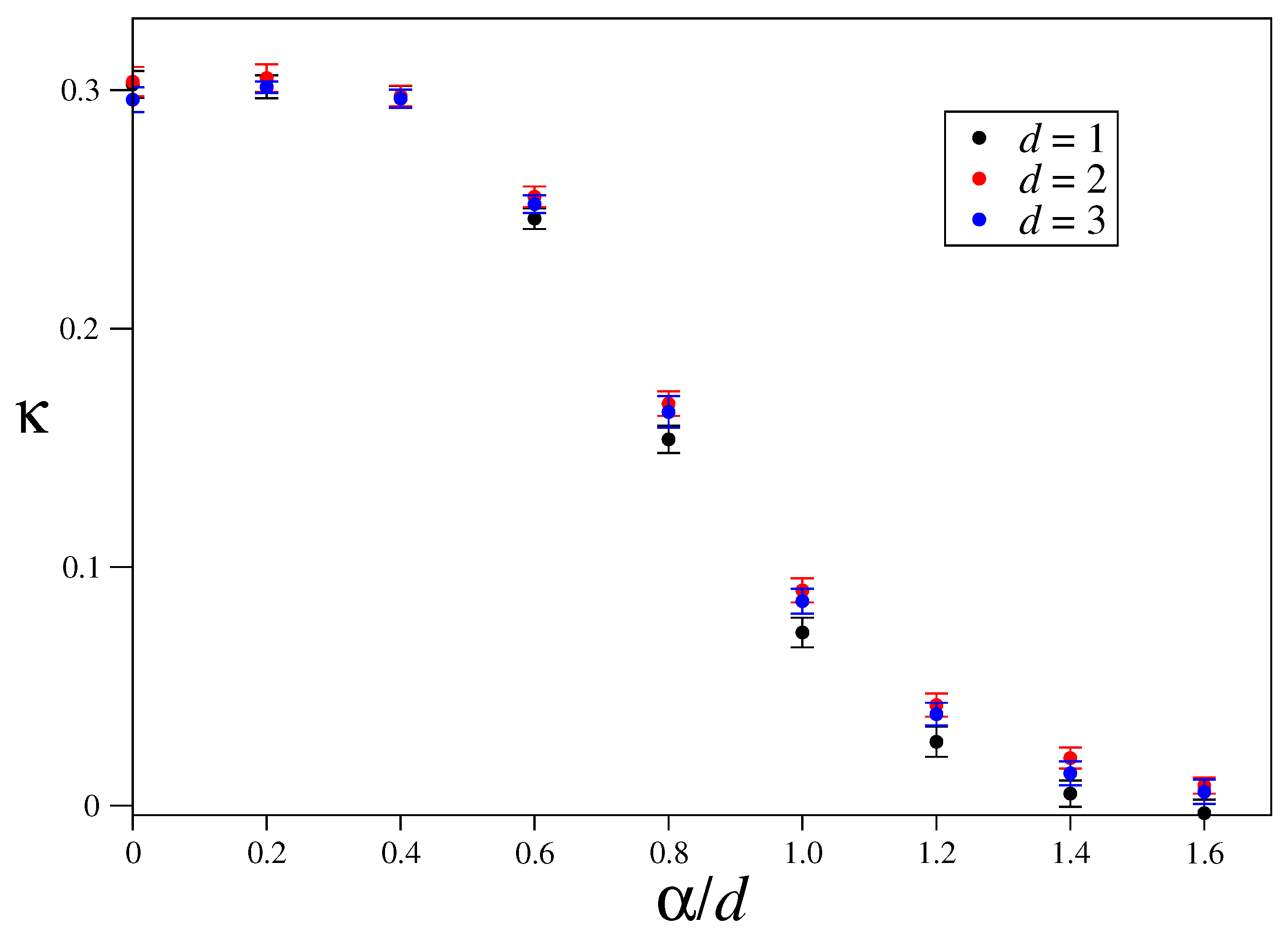
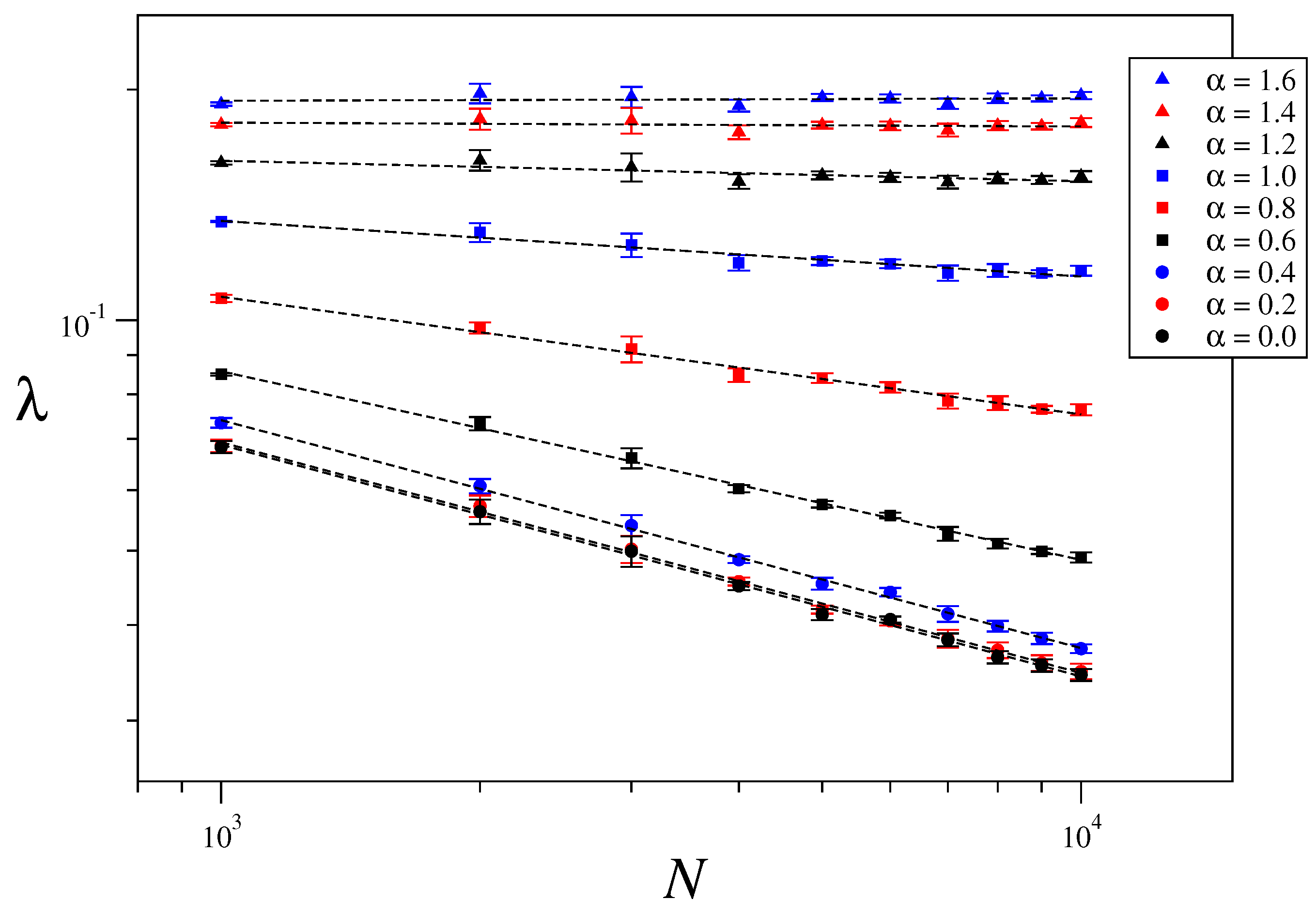
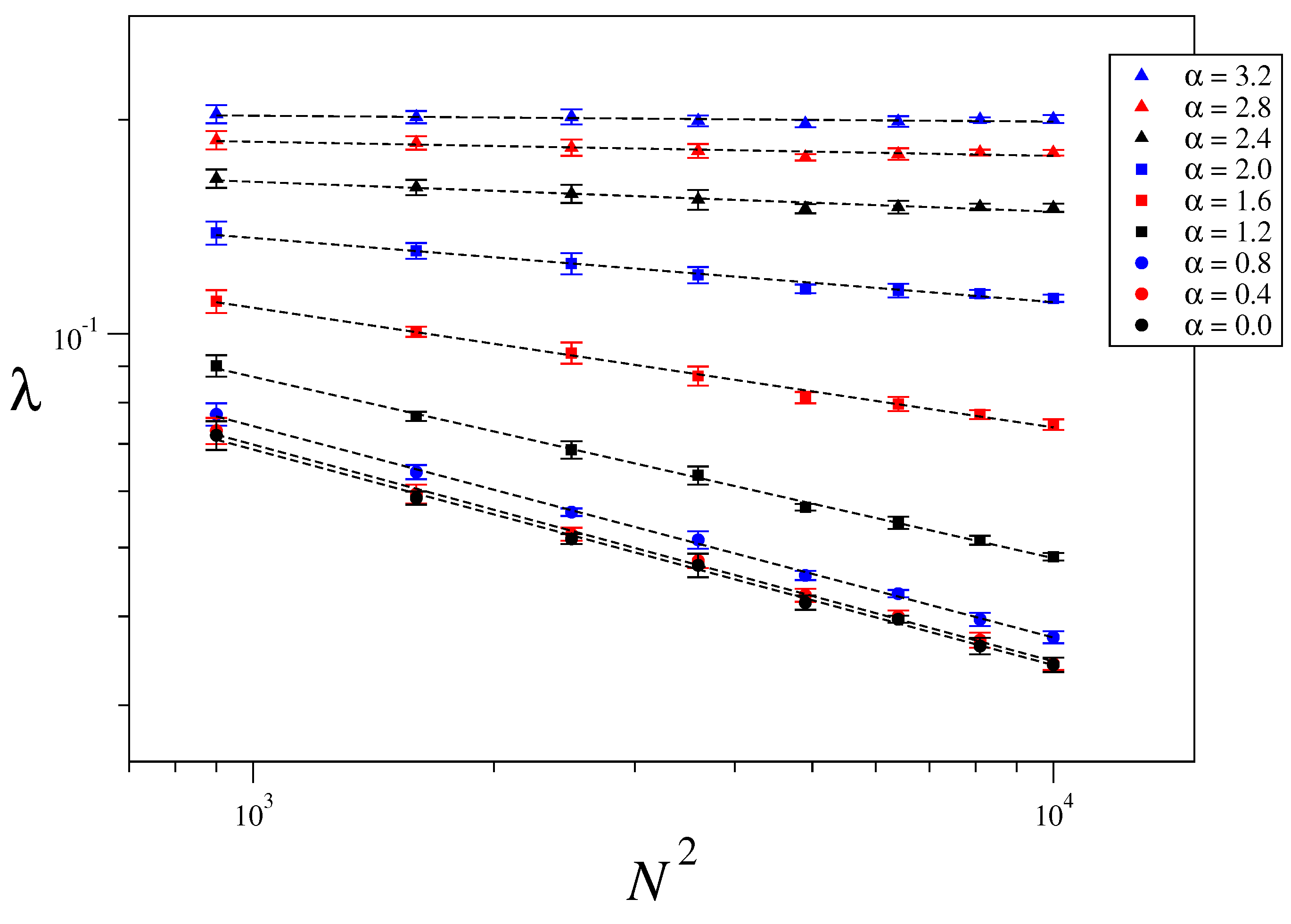
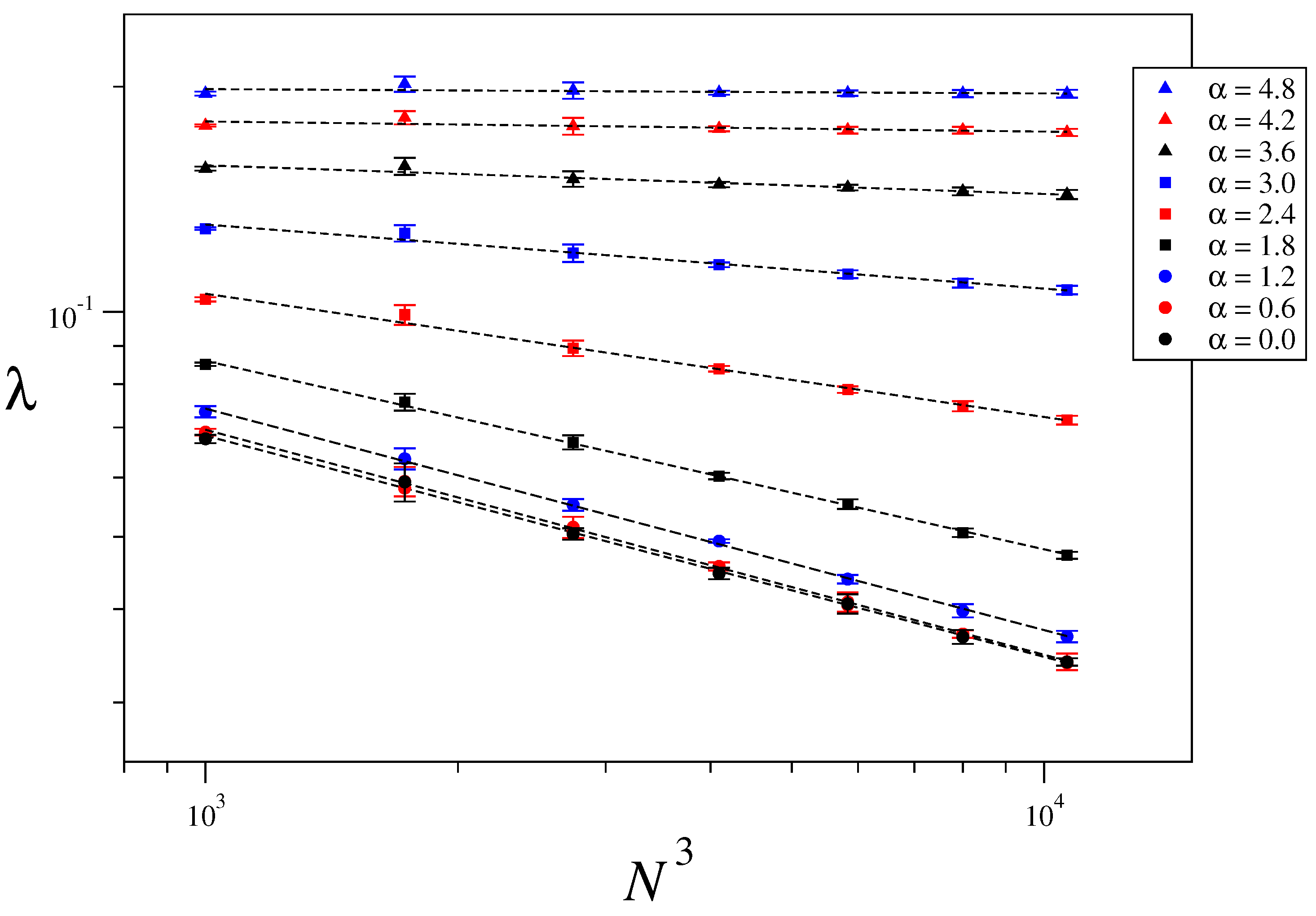
3.3. Size-Scaling of the Largest Lyapunov Exponent
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Stanley, H.E. Introduction to Phase Transitions and Critical Phenomena; Oxford University Press: Oxford, UK, 1971. [Google Scholar]
- Thompson, C.J. Classical Equilibrium Statistical Mechanics; Oxford University Press: Oxford, UK, 1988. [Google Scholar]
- Pathria, R.K.; Beale, P.D. Statistical Mechanics, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Fisher, M.E. Magnetism in One-Dimensional Systems-The Heisenberg Model for Infinite Spin. Am. J. Phys. 1963, 32, 343–346. [Google Scholar] [CrossRef]
- Joyce, G.S. Classical Heisenberg Model. Phys. Rev. 1967, 155, 478. [Google Scholar] [CrossRef]
- Stanley, H.E. Exact Solution for a Linear Chain in Isotropic Interacting Classical Spins of Arbitrary Dimensionality. Phys. Rev. 1969, 179, 570. [Google Scholar] [CrossRef]
- Tsallis, C. Classical Statistical Approach to Anisotropic Two-Dimensional XY-Model. Il Nuovo Cimento B 1976, 34, 411–435. [Google Scholar] [CrossRef]
- Mattis, D.C. Transfer matrix in plane-rotator model. Phys. Lett. 1984, 104A, 357–360. [Google Scholar] [CrossRef]
- Butera, P.; Caravati, G. Phase transitions and Lyapunov characteristic exponents. Phys. Rev. A 1987, 36, 962. [Google Scholar] [CrossRef]
- Escande, D.; Kantz, H.; Livi, R.; Ruffo, S. Self-Consistent Check of the Validity of Gibbs Calculus Using Dynamical Variables. J. Stat. Phys. 1994, 76, 605–626. [Google Scholar] [CrossRef]
- Leoncini, X.; Verga, A.D.; Ruffo, S. Hamiltonian dynamics and the phase transition of the XY model. Phys. Rev. E 1998, 57, 6377. [Google Scholar] [CrossRef]
- Antoni, M.; Ruffo, S. Clustering and relaxation in Hamiltonian long-range dynamics. Phys. Rev. E 1995, 52, 2361. [Google Scholar] [CrossRef]
- Firpo, M.-C. Analytic estimation of the Lyapunov exponent in a mean-field model undergoing a phase transition. Phys. Rev. E 1998, 57, 6599. [Google Scholar] [CrossRef]
- Latora, V.; Rapisarda, A.; Ruffo, S. Lyapunov Instability and Finite Size Effects in a System with Long-Range Forces. Phys. Rev. Lett. 1998, 80, 692. [Google Scholar] [CrossRef]
- Latora, V.; Rapisarda, A.; Ruffo, S. Superdiffusion and Out-of-Equilibrium Chaotic Dynamics with Many Degrees of Freedom. Phys. Rev. Lett. 1999, 83, 2104. [Google Scholar] [CrossRef]
- Latora, V.; Rapisarda, A.; Tsallis, C. Non-Gaussian equilibrium in a long-range Hamiltonian system. Phys. Rev. E 2001, 64, 056134. [Google Scholar] [CrossRef] [PubMed]
- Barré, J.; Bouchet, F.; Dauxois, T.; Ruffo, S. Out-of-Equilibrium States and Statistical Equilibria of an Effective Dynamics in a System with Long-Range Interactions. Phys. Rev. Lett. 2002, 89, 110601. [Google Scholar] [CrossRef] [PubMed]
- Pluchino, A.; Latora, V.; Rapisarda, A. Metastable states, anomalous distributions and correlations in the HMF model. Physica D 2004, 193, 315–328. [Google Scholar] [CrossRef]
- Pluchino, A.; Latora, V.; Rapisarda, A. Glassy phase in the Hamiltonian mean-field model. Phys. Rev. E 2004, 69, 056113. [Google Scholar] [CrossRef] [PubMed]
- Pluchino, A.; Latora, V.; Rapisarda, A. Dynamics and thermodynamics of a model with lon-range interactions. Contin. Mech. Thermodyn. 2004, 16, 245–255. [Google Scholar]
- Moyano, L.G.; Anteneodo, C. Diffusive anomalies in a long-range Hamiltonian system. Phys. Rev. E 2006, 74, 021118. [Google Scholar] [CrossRef]
- Pluchino, A.; Rapisarda, A.; Tsallis, C. Nonergodicity and central-limit behavior for long-range Hamiltonians. EPL 2007, 80, 26002. [Google Scholar] [CrossRef]
- Pluchino, A.; Rapisarda, A.; Tsallis, C. A closer look at the indications of q-generalized Central Limit Theorem behavior in quasi-stationary states of the HMF model. Physica A 2008, 387, 3121–3128. [Google Scholar] [CrossRef]
- Anteneodo, C.; Tsallis, C. Breakdown of Exponential Sensitivity to Initial Conditions: Role of the Range of Interactions. Phys. Rev. Lett. 1998, 24, 5313. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World; Springer: New York, NY, USA, 2009. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Campa, A.; Giansanti, A.; Moroni, D. Canonical solution of a system of long-range interacting rotators on a lattice. Phys. Rev. E 2000, 62, 303. [Google Scholar] [CrossRef]
- Tamarit, F.; Anteneodo, C. Rotators with Long-Range Interactions: Connection with the Mean-Field Approximation. Phys. Rev. Lett. 2000, 84, 208. [Google Scholar] [CrossRef] [PubMed]
- Campa, A.; Giansanti, A.; Moroni, D.; Tsallis, C. Classical spin systems with long-range interactions: Universal reduction of mixing. Phys. Lett. A 2001, 286, 251–256. [Google Scholar] [CrossRef]
- Firpo, M.-C.; Ruffo, S. Chaos suppression in the large size limit for long-range systems. J. Phys. A Math. Gen. 2001, 34, L511. [Google Scholar] [CrossRef]
- Anteneodo, C.; Vallejos, R.O. Scaling laws for the largest Lyapunov exponent in long-range systems: A random matrix approach. Phys. Rev. E 2001, 65, 016210. [Google Scholar] [CrossRef]
- Cabral, B.J.C.; Tsallis, C. Metastability and weak mixing in classical long-range many-rotator systems. Phys. Rev. E 2002, 66, 065101. [Google Scholar] [CrossRef]
- Cirto, L.J.L.; Assis, V.R.V.; Tsallis, C. Influence of the interaction range on the thermostatistics of a classical many-body system. Physica A 2014, 39, 286–296. [Google Scholar] [CrossRef]
- Cirto, L.J.L.; Rodríguez, A.; Nobre, F.D.; Tsallis, C. Validity and failure of the Boltzmann weight. EPL 2018, 123, 30003. [Google Scholar] [CrossRef]
- Antonopoulos, C.G.; Christodoulidi, H. Weak chaos detection in the Fermi-Pasta-Ulam-α system using q-Gaussian statistics. Int. J. Bifurc. Chaos 2011, 21, 2285–2296. [Google Scholar] [CrossRef]
- Christodoulidi, H.; Tsallis, C.; Bountis, T. Fermi-Pasta-Ulam model with long-range interactions: Dynamics and thermostatistics. EPL 2014, 108, 40006. [Google Scholar] [CrossRef]
- Christodoulidi, H.; Bountis, T.; Tsallis, C.; Drossos, L. Dynamics and Statistics of the Fermi-Pasta-Ulam β-model with different ranges of particle interactions. J. Stat. Mech. Theory Exp. 2016, 12, 123206. [Google Scholar] [CrossRef]
- Bagchi, D.; Tsallis, C. Sensitivity to initial conditions of a d-dimensional long-range interacting quartic Fermi-Pasta-Ulam model: Universal scaling. Phys. Rev. E 2016, 93, 062213. [Google Scholar] [CrossRef] [PubMed]
- Bagchi, D.; Tsallis, C. Fermi-Pasta-Ulam-Tsingou problems: Passage from Boltzmann to q-statistics. Physica A 2018, 491, 869–873. [Google Scholar] [CrossRef]
- Brito, S.; da Silva, L.R.; Tsallis, C. Role of dimensionality in complex networks. Sci. Rep. 2016, 6, 27992. [Google Scholar] [CrossRef] [PubMed]
- Nunes, T.C.; Brito, S.; da Silva, L.R.; Tsallis, C. Role of dimensionality in preferential attachment growth in the Bianconi-Barabási model. J. Stat. Mech. Theory Exp. 2017, 093402. [Google Scholar] [CrossRef]
- Moreira, A.A.; Vieira, C.M.; Carmona, H.A.; Andrade, J.S., Jr.; Tsallis, C. Overdamped dynamics of particles with repulsive power-law interactions. Phys. Rev. E 2018, 98, 032138. [Google Scholar] [CrossRef]
- Rapaport, D.C.; Landau, D.P. Critical dynamics of a dynamical version of the classical Heisenberg model. Phys. Rev. E 1996, 53, 4696. [Google Scholar] [CrossRef]
- Nobre, F.D.; Tsallis, C. Classical infinite-range-interaction Heisenberg ferromagnetic model: Metastability and sensitivity to initial conditions. Phys. Rev. E 2003, 68, 036115. [Google Scholar] [CrossRef]
- Nobre, F.D.; Tsallis, C. Metastable states of the classical inertial infinite-range-interaction Heisenberg ferromagnet: Role of initial conditions. Physica A 2004, 344, 587–594. [Google Scholar] [CrossRef]
- Gupta, S.; Mukamel, D. Quasistationarity in a model of long-range interacting particles moving on a sphere. Phys. Rev. E 2013, 88, 052137. [Google Scholar] [CrossRef] [PubMed]
- Cirto, L.J.L.; Lima, L.S.; Nobre, F.D. Controlling the range of interactions in the classical inertial ferromagnetic Heisenberg model: Analysis of metastable states. J. Stat. Mech. Theory Exp. 2015, 2015, P04012. [Google Scholar] [CrossRef]
- Hairer, E.; Lubich, C.; Wanner, G. Geometric Numerical Integration: Structure-Preserving Algorithms for Ordinary Differential Equations; Springer Science and Business Media: Dordrecht, The Netherlands, 2006; Volume 31. [Google Scholar]
- Butusov, D.N.; Karimov, A.I.; Pyko, N.S.; Pyko, S.A.; Bogachev, M.I. Discrete chaotic maps obtained by symmetric integration. Physica A 2018, 509, 955. [Google Scholar] [CrossRef]
- Pyko, N.S.; Pyko, S.A.; Markelov, O.A.; Karimov, A.I.; Butusov, D.N.; Zolotukhin, Y.V.; Bogachev, M.I. Assessment of cooperativity in complex systems with non-periodical dynamics: Comparison of five mutual information metrics. Physica A 2018, 503, 1054–1072. [Google Scholar] [CrossRef]
- Benettin, G.; Galgani, L.; Strelcyn, J.-M. Kolmogorov entropy and numerical experiments. Phys. Rev. A 1976, 14, 2338. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez, A.; Nobre, F.D.; Tsallis, C. d-Dimensional Classical Heisenberg Model with Arbitrarily-Ranged Interactions: Lyapunov Exponents and Distributions of Momenta and Energies. Entropy 2019, 21, 31. https://doi.org/10.3390/e21010031
Rodríguez A, Nobre FD, Tsallis C. d-Dimensional Classical Heisenberg Model with Arbitrarily-Ranged Interactions: Lyapunov Exponents and Distributions of Momenta and Energies. Entropy. 2019; 21(1):31. https://doi.org/10.3390/e21010031
Chicago/Turabian StyleRodríguez, Antonio, Fernando D. Nobre, and Constantino Tsallis. 2019. "d-Dimensional Classical Heisenberg Model with Arbitrarily-Ranged Interactions: Lyapunov Exponents and Distributions of Momenta and Energies" Entropy 21, no. 1: 31. https://doi.org/10.3390/e21010031
APA StyleRodríguez, A., Nobre, F. D., & Tsallis, C. (2019). d-Dimensional Classical Heisenberg Model with Arbitrarily-Ranged Interactions: Lyapunov Exponents and Distributions of Momenta and Energies. Entropy, 21(1), 31. https://doi.org/10.3390/e21010031