Rate Distortion Function of Gaussian Asymptotically WSS Vector Processes
Abstract
1. Introduction
2. Preliminaries
2.1. Notation
2.2. AWSS Vector Processes
2.3. MA and ARMA Vector Processes
2.4. RDF of Gaussian Vectors
3. Integral Formula for the RDF of Gaussian AWSS Vector Processes
4. Applications
4.1. Integral Formula for the RDF of Gaussian MA Vector Processes
- 1.
- is AWSS with APSD for all .
- 2.
- If is Gaussian, for all , and yieldswhere θ is the real number satisfying:
4.2. Integral Formula for the RDF of Gaussian ARMA AWSS Vector Processes
- 1.
- is AWSS with APSD for all .
- 2.
- If is Gaussian, for all , and yields:where θ is the real number satisfying:
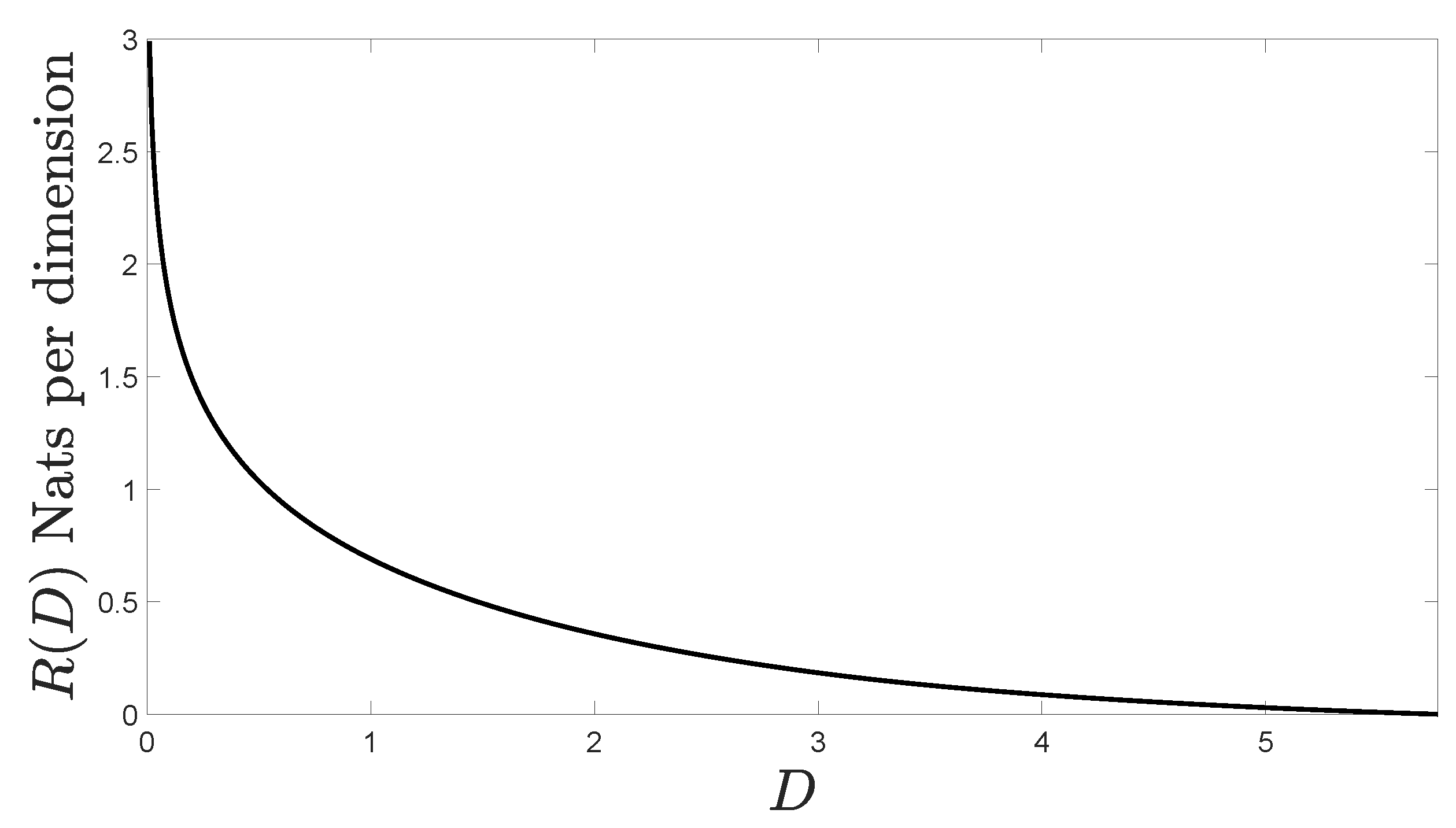
5. Numerical Example
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof of Theorem 1
Appendix B. Proof of Corollary 1
Appendix C. Proof of Theorem 2
Appendix D. Proof of Theorem 3
Appendix E. A Property of Asymptotically Equivalent Sequences of Invertible Matrices
References
- Hammerich, E. Waterfilling theorems for linear time-varying channels and related nonstationary sources. IEEE Trans. Inf. Theory 2016, 62, 6904–6916. [Google Scholar] [CrossRef]
- Kipnis, A.; Goldsmith, A.J.; Eldar, Y.C. The distortion rate function of cyclostationary Gaussian processes. IEEE Trans. Inf. Theory 2018, 64, 3810–3824. [Google Scholar] [CrossRef]
- Toms, W.; Berger, T. Information rates of stochastically driven dynamic systems. IEEE Trans. Inf. Theory 1971, 17, 113–114. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. On the Shannon theory of information transmission in the case of continuous signals. IRE Trans. Inf. Theory 1956, 2, 102–108. [Google Scholar] [CrossRef]
- Reinsel, G.C. Elements of Multivariate Time Series Analysis; Springer: Berlin, Germany, 1993. [Google Scholar]
- Gray, R.M. Toeplitz and circulant matrices: A review. Found. Trends Commun. Inf. Theory 2006, 2, 155–239. [Google Scholar] [CrossRef]
- Ephraim, Y.; Lev-Ari, H.; Gray, R.M. Asymptotic minimum discrimination information measure for asymptotically weakly stationary processes. IEEE Trans. Inf. Theory 1988, 34, 1033–1040. [Google Scholar] [CrossRef]
- Gray, R.M. On the asymptotic eigenvalue distribution of Toeplitz matrices. IEEE Trans. Inf. Theory 1972, 18, 725–730. [Google Scholar] [CrossRef]
- Gutiérrez-Gutiérrez, J.; Crespo, P.M. Asymptotically equivalent sequences of matrices and Hermitian block Toeplitz matrices with continuous symbols: Applications to MIMO systems. IEEE Trans. Inf. Theory 2008, 54, 5671–5680. [Google Scholar] [CrossRef]
- Gutiérrez-Gutiérrez, J.; Crespo, P.M. Asymptotically equivalent sequences of matrices and multivariate ARMA processes. IEEE Trans. Inf. Theory 2011, 57, 5444–5454. [Google Scholar] [CrossRef]
- Gutiérrez-Gutiérrez, J.; Crespo, P.M. Block Toeplitz matrices: Asymptotic results and applications. Found. Trends Commun. Inf. Theory 2011, 8, 179–257. [Google Scholar] [CrossRef]
- Gutiérrez-Gutiérrez, J.; Crespo, P.M.; Zárraga-Rodríguez, M.; Hogstad, B.O. Asymptotically equivalent sequences of matrices and capacity of a discrete-time Gaussian MIMO channel with memory. IEEE Trans. Inf. Theory 2017, 63, 6000–6003. [Google Scholar] [CrossRef]
- Kafedziski, V. Rate distortion of stationary and nonstationary vector Gaussian sources. In Proceedings of the IEEE/SP 13th Workshop on Statistical Signal Processing, Bordeaux, France, 17–20 July 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 1054–1059. [Google Scholar]
- Gazzah, H.; Regalia, P.A.; Delmas, J.P. Asymptotic eigenvalue distribution of block Toeplitz matrices and application to blind SIMO channel identification. IEEE Trans. Inf. Theory 2001, 47, 1243–1251. [Google Scholar] [CrossRef]
- Rudin, W. Principles of Mathematical Analysis; McGraw-Hill: New York, NY, USA, 1976. [Google Scholar]
- Gray, R.M. Information rates of autoregressive processes. IEEE Trans. Inf. Theory 1970, 16, 412–421. [Google Scholar] [CrossRef]
- Gallager, R.G. Information Theory and Reliable Communication; John Wiley & Sons: Hoboken, NJ, USA, 1968. [Google Scholar]
- Bhatia, R. Matrix Analysis; Springer: Berlin, Germany, 1997. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gutiérrez-Gutiérrez, J.; Zárraga-Rodríguez, M.; Crespo, P.M.; Insausti, X. Rate Distortion Function of Gaussian Asymptotically WSS Vector Processes. Entropy 2018, 20, 719. https://doi.org/10.3390/e20090719
Gutiérrez-Gutiérrez J, Zárraga-Rodríguez M, Crespo PM, Insausti X. Rate Distortion Function of Gaussian Asymptotically WSS Vector Processes. Entropy. 2018; 20(9):719. https://doi.org/10.3390/e20090719
Chicago/Turabian StyleGutiérrez-Gutiérrez, Jesús, Marta Zárraga-Rodríguez, Pedro M. Crespo, and Xabier Insausti. 2018. "Rate Distortion Function of Gaussian Asymptotically WSS Vector Processes" Entropy 20, no. 9: 719. https://doi.org/10.3390/e20090719
APA StyleGutiérrez-Gutiérrez, J., Zárraga-Rodríguez, M., Crespo, P. M., & Insausti, X. (2018). Rate Distortion Function of Gaussian Asymptotically WSS Vector Processes. Entropy, 20(9), 719. https://doi.org/10.3390/e20090719





