Entropy Contribution to the Line Tension: Insights from Polymer Physics, Water String Theory, and the Three-Phase Tension
Abstract
1. Introduction
2. “Water String Theory”, Insights from Polymer Physics and Entropy Contribution into Line Tension
3. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Origin of the Entropic Elastic Forces
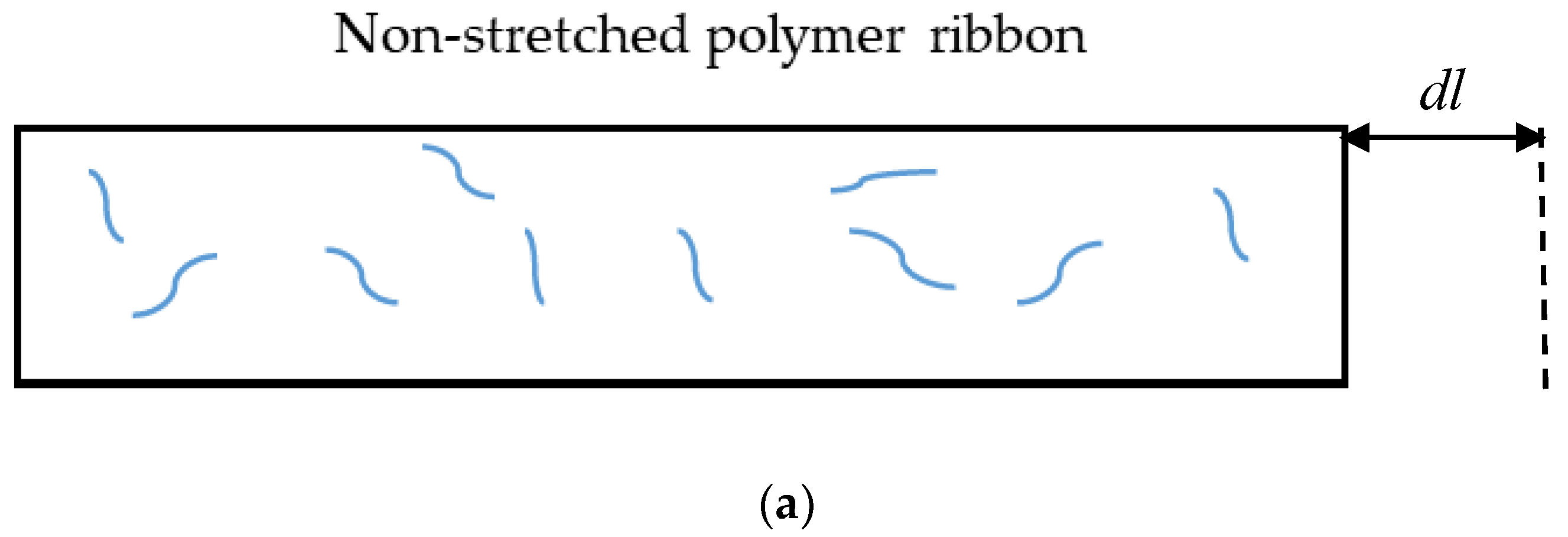
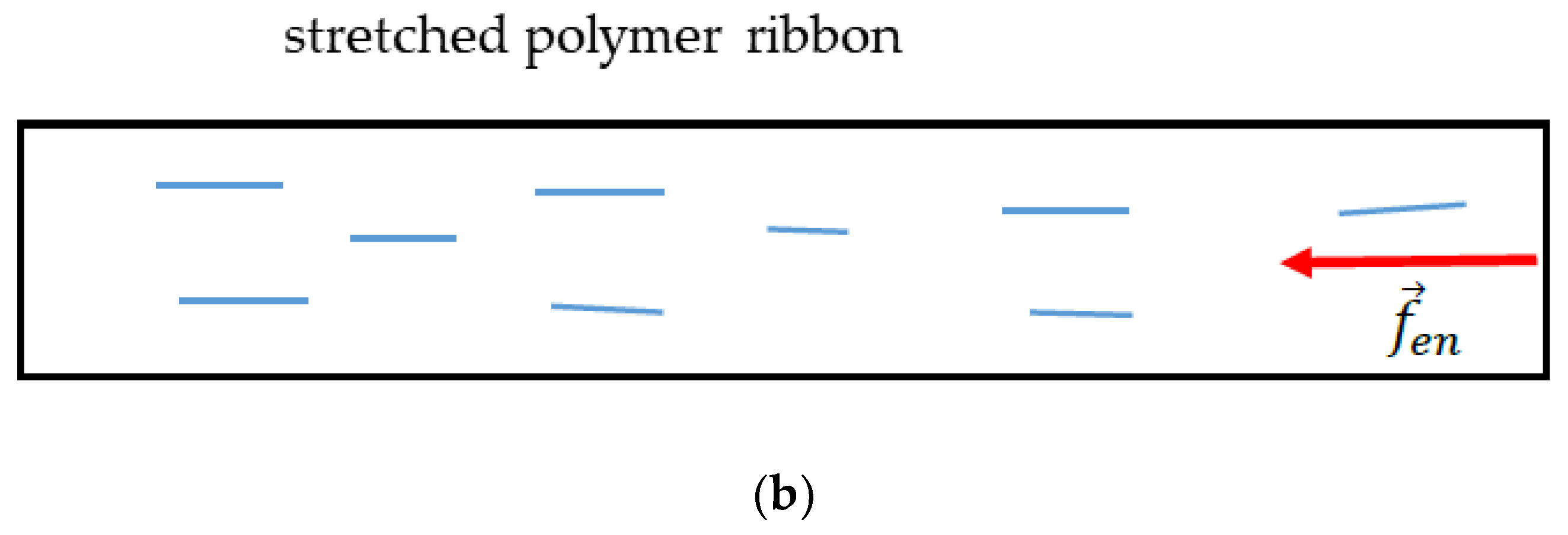
References
- Adamson, A.W.; Gast, A.P. Physical Chemistry of Surfaces, 6th ed.; Wiley Interscience Publishers: New York, NY, USA, 1990. [Google Scholar]
- Erbil, H.Y. Surface Chemistry of Solid and Liquid Interfaces. Wiley-Blackwell: Oxford, UK, 2006. [Google Scholar]
- De Gennes, P.G.; Brochard-Wyart, F.; Quéré, D. Capillarity and Wetting Phenomena: Drops Bubbles; Pearls, W., Ed.; Springer: New York, NY, USA, 2004. [Google Scholar]
- Bormashenko, Ed.Y. Wetting of Real Surfaces; Walter de Gruyter: Berlin, Germany, 2011. [Google Scholar]
- Gibbs, J.W. The Scientific Papers of J. W. Gibbs; Dover: New York, NY, USA, 1961; Volume 1, p. 288. [Google Scholar]
- Amirfazli, A.; Neumann, A.W. Status of the Three-Phase Line Tension. Adv. Colloid Interface Sci. 2004, 110, 121–141. [Google Scholar] [CrossRef] [PubMed]
- Drelich, J. The Significance and Magnitude of the Line Tension in Three-Phase (Solid-Liquid-Fluid) Systems. Colloids Surf. A 1996, 116, 43–54. [Google Scholar] [CrossRef]
- Das, S.K.; Egorov, S.A.; Virnau, P.; Winter, D.; Binde, R. Do the Contact Angle and Line Tension of Surface-Attached Droplets Depend on the Radius of Curvature? J. Phys. Condens. Matter 2018, 30, 255001. [Google Scholar] [CrossRef] [PubMed]
- Zhelev, D.V.; Needham, D. Tension-stabilized Pores in Giant Vesicles: Determination of Pore Size and Pore Line Tension. Biochim. Biophys. Acta 1993, 1147, 89–104. [Google Scholar] [CrossRef]
- De Feijter, J.A.; Vrij, I. Transition Regions, Line tensions and Contact Angles in Soap Films. J. Electroanal. Chem. Interfacial Electrochem. 1972, 37, 9–22. [Google Scholar] [CrossRef]
- Law, B.M.; McBride, S.P.; Wang, J.Y.; Wi, H.S.; Paneru, G.; Betelu, S.; Ushijima, B.; Takata, Y.; Flanders, B.; Bresme, F.; et al. Line Tension and its Influence on Droplets and Particles at Surfaces. Prog. Surface Sci. 2017, 92, 1–39. [Google Scholar] [CrossRef]
- Alexandrov, A.D.; Toshev, B.V.; Scheludko, A.D. Nucleation from Supersaturated Water Vapors on n-Hexadecane: Temperature Dependence of Critical Supersaturation and Line Tension. Langmuir 1991, 7, 3211–3215. [Google Scholar] [CrossRef]
- Checco, A.; Guenoun, P. Nonlinear Dependence of the Contact Angle of Nanodroplets on Contact Line Curvature. Phys. Rev. Lett. 2003, 91, 186101. [Google Scholar] [CrossRef] [PubMed]
- Pompe, T.; Fery, A.; Herminghaus, S. Measurement of Contact Line Tension by Analysis of the Three-Phase Boundary with Nanometer Resolution. In Apparent and Microscopic Contact Angles; Drelich, J., Laskowski, J.S., Mittal, K.L., Eds.; VSP: Utrecht, The Netherlands, 2000; pp. 3–12. [Google Scholar]
- Marmur, A. Line Tension and the Intrinsic Contact Angle in Solid-Liquid-Fluid Systems. J. Colloid Interface Sci. 1997, 186, 462–466. [Google Scholar] [CrossRef] [PubMed]
- Marmur, A. Line Tension Effect on Contact Angles: Axisymmetric and Cylindrical Systems with Rough or Heterogeneous Solid surfaces. Colloids Surf. A 1998, 136, 81–88. [Google Scholar] [CrossRef]
- Bormashenko, E.; Whyman, G. On the Role of the Line Tension in the Stability of Cassie Wetting. Langmuir 2013, 29, 5515–5519. [Google Scholar] [CrossRef] [PubMed]
- Schimmele, L.; Napiórkowski, M.; Dietrich, S. Conceptual Aspects of Line Tensions. J. Chem. Phys. 2007, 127, 164715. [Google Scholar] [CrossRef] [PubMed]
- Weijs, J.H.; Marchand, A.; Andreotti, B.; Lohse, D.; Snoeije, J.H. Origin of Line Tension for a Lennard-Jones Nanodroplet. Phys. Fluids 2011, 23, 022001. [Google Scholar] [CrossRef]
- Khalkhali, M.; Kazemi, N.; Zhang, H.; Liu, Q. Wetting at the Nanoscale: A Molecular Dynamics Study. J. Chem. Phys. 2017, 146, 114704. [Google Scholar] [CrossRef] [PubMed]
- Nosonovsky, M.; Ramachandran, R. Geometric Interpretation of Surface Tension Equilibrium in Superhydrophobic Systems. Entropy 2015, 17, 4684–4700. [Google Scholar] [CrossRef]
- Wernet, P.; Nordlund, D.; Bergmann, U.; Cavalleri, M.; Odelius, M.; Ogasawara, H.; Näslund, L.Å.; Hirsch, T.K.; Ojamäe, L.; Glatzel, P.; et al. The Structure of the First Coordination Shell in Liquid Water. Science 2004, 304, 995–999. [Google Scholar] [CrossRef] [PubMed]
- Head-Gordon, T.; Johnson, M.E. Tetrahedral Structure or Chains for Liquid Water. PNAS 2006, 103, 7973–7977. [Google Scholar] [CrossRef] [PubMed]
- Ball, P. Water: Water—An Enduring Mystery. Nature 2008, 452, 291–292. [Google Scholar] [CrossRef] [PubMed]
- Scatena, L.F.; Brown, M.G.; Richmond, G.L. Water at Hydrophobic Surfaces: Weak Hydrogen Bonding and Strong Orientation Effects. Science 2001, 292, 908–912. [Google Scholar] [CrossRef] [PubMed]
- Strazdaite, S.; Versluis, J.; Backus, E.H.G.; Bakker, H.J. Enhanced Ordering of Water at Hydrophobic Surfaces. J. Chem. Phys. 2014, 140, 054711. [Google Scholar] [CrossRef] [PubMed]
- Strazdaite, S.; Versluis, J.; Bakker, H.J. Water Orientation at Hydrophobic Interfaces. J. Chem. Phys. 2015, 143, 084708. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, M.; Colby, R.H. Polymer Physics; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Rowlinson, J.S.; Widom, B. Molecular Theory of Capillarity; Clarendon: Oxford, UK, 1982. [Google Scholar]
- Pohl, R.W. Mechanic, Akystik und Wärmlehre; Springer: Berlin, Germany, 1964. [Google Scholar]
- Wang, J.Y.; Betelu, S.; Law, B.M. Line Tension Approaching a First-Order Wetting Transition: Experimental Results from Contact Angle Measurements. Phys. Rev. E 2001, 63, 031601. [Google Scholar] [CrossRef] [PubMed]
- Tadmor, R. Line Energy and the Relation between Advancing, Receding, and Young Contact Angles. Langmuir 2004, 20, 7659–7664. [Google Scholar] [CrossRef] [PubMed]
- Tadmor, R. Line Energy, Line Tension and Drop Size. Surf. Sci. 2008, 602, L108–L111. [Google Scholar] [CrossRef]
- Schmitt, M.; Groß, K.; Grub, J.; Heib, F. Detailed Statistical Contact Angle Analyses; “Slow Moving” Drops on Inclining Silicon-Oxide Surfaces. J. Colloid Interface Sci. 2015, 447, 229–239. [Google Scholar] [CrossRef] [PubMed]
- Schmitt, M.; Heib, F. High-Precision Drop Shape Analysis on Inclining Flat Surfaces: Introduction and Comparison of This Special Method with Commercial Contact Angle Analysis. J. Chem. Phys. 2013, 139, 134201. [Google Scholar] [CrossRef] [PubMed]
- Bar-Ziv, R.; Frisch, T. Moses, Entropic Expulsion in Vesicles. Phys. Rev. Lett. 1995, 75, 3481–3484. [Google Scholar] [CrossRef] [PubMed]
- Evans, E.; Rawicz, W. Entropy-Driven Tension and Bending Elasticity in Condensed-Fluid Membranes. Phys. Rev. Lett. 1990, 64, 2094–2097. [Google Scholar] [CrossRef] [PubMed]
- Linde, M.; Sens, P.; Phillips, R. Entropic Tension in Crowded Membranes. PLoS Comput. Biol. 2012, 8, e100243. [Google Scholar]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bormashenko, E. Entropy Contribution to the Line Tension: Insights from Polymer Physics, Water String Theory, and the Three-Phase Tension. Entropy 2018, 20, 712. https://doi.org/10.3390/e20090712
Bormashenko E. Entropy Contribution to the Line Tension: Insights from Polymer Physics, Water String Theory, and the Three-Phase Tension. Entropy. 2018; 20(9):712. https://doi.org/10.3390/e20090712
Chicago/Turabian StyleBormashenko, Edward. 2018. "Entropy Contribution to the Line Tension: Insights from Polymer Physics, Water String Theory, and the Three-Phase Tension" Entropy 20, no. 9: 712. https://doi.org/10.3390/e20090712
APA StyleBormashenko, E. (2018). Entropy Contribution to the Line Tension: Insights from Polymer Physics, Water String Theory, and the Three-Phase Tension. Entropy, 20(9), 712. https://doi.org/10.3390/e20090712




