1. Introduction
Network virtualization (NV) allows multiple heterogeneous virtual networks (VNs) to be embedded onto the shared substrate network (SN), providing users with a variety of network services which has become one of the most promising technologies for future Internet [
1,
2,
3]. It can decouple the network infrastructure and network services, and allow multiple heterogeneous VNs to share the SN resources through abstraction, distribution and isolation mechanism. In recent years, NV has been widely used in various fields, such as fog-supported software defined network (SDN) [
4] and virtualized networked data centers [
5]. One of the most challenging problems raised in NV is the virtual network embedding (VNE) problem, which has been known as the non-deterministic polynomial hard (NP-hard) problem [
6].
In recent years, the SN failure events occur frequently. SN failures degrade the service performance and reliability of VNs [
7]. SN failures include node failure and link failure. In network virtualization, multiple VNs are embedded onto the same SN and share the common substrate resources. Hence, substrate node failure causes virtual node and its adjacent virtual link failure. Substrate link failure causes virtual link failure. Also, there are single node/link failures and multiple node/link failures in SN which will cause complex and multiple virtual network (VN) failures [
8]. Therefore, adopting suitable survivability strategies to against the increasingly complex network failures has become one of the main challenges in VN survivability.
A number of mechanisms have been proposed to improve the VN survivability [
9]. These mechanisms can be broadly classified into two categories: backup mechanism [
10] and reconfiguration mechanism [
11]. The backup mechanism can also be classified into dedicated backup [
12] and shared backup [
13]. In shared backup mechanism, the backup resources can be shared with different VNs. In the dedicated case, the backup resources only can be used for dedicated VN. However, preallocating a backup resource is extremely expensive.
Instead, the reconfiguration mechanism can re-embed the faulty part of a VN without huge backup resource consumption. In reconfiguration mechanisms, backup resources are not preallocated, and the faulty parts of VNs are re-embedded after SN failures [
14]. For instance, a topology awareness VN reconfiguration algorithm is proposed in [
15]. The virtual node to be migrated is mapped onto the nearest mapped substrate node which is the neighbor mapping node of the migration virtual node. This algorithm takes topology indicator into consideration and improves the resource utilization. However, resource indicator is not considered in its node re-embedding strategy. To survive link failures, a novel recovery approach to restore VN without reserving backup resources prior to embedding is proposed in [
16]. It not only considers the end-delay and delay variation requirements, but also takes actions to find a constrained shortest path between the nodes utilized by the failed VNs. The resource utilization is improved. However, this algorithm cannot deal with the problem of recovering VNs from node failures. As can be seen from above two algorithms, they cannot deal with the hybrid failures which include node failures and link failures.
To survive hybrid failures in SN, a heuristic survivable VNE based on node migration and link remapping is proposed in [
17]. In VNE, the artificial bee colony algorithm is proposed to achieve an optimal solution. If the substrate node fails, the failed node is migrated to a normal node based on the greed rules, and the affected links are remapped based on the shortest path algorithm. Then, the shortest path is used to provide the best bandwidth principle to remap the affected links that connect with the failed node. This algorithm can deal with hybrid failures. However, the greed rules only take resource indicator into consideration and their re-embedding performance is limited. Also, they do not consider the hybrid failures in multiple faulty VNs.
To solve the problem of recovering a batch of VNs affected by a substrate node failure, a recovery approach for maximizing recovery and minimizing the cost of recovery is designed in [
18]. An integer linear programming (ILP) formulation of this recovery scheme is provided, and a fast and scalable heuristic algorithm is also proposed to tackle the computational complexity of the ILP solution. It can recover a batch of VNs affected by a substrate node failure efficiently. However, it sorts the faulty VNs and virtual nodes based on the adjacent bandwidth resource, and it ignores the topology indicators. A generalized recovery approach that can achieve customized objectives is designed, and the corresponding ILP formulation is provided in [
19]. Then, a fast and scalable heuristic algorithm to tackle the computational complexity of the ILP solution is proposed, and it is demonstrated that this heuristic algorithm has good recovery performance. However, it focuses on the problem of recovering from a node failure in VNE and ranks faulty VNs based on service level agreements. It cannot deal with the problem of recovering a batch of VNs affected by hybrid failures which include node and link failures. Also, in different recovery objects, recovering the faulty VNs based on service level agreements is not suitable.
As can be seen from the current research, the VN reconfiguration mechanisms focus on taking effective measures for network recovery after failures without preallocating resources. Although numerous efforts have been devoted, there are four obvious defects in existing VN reconfiguration algorithms. At first, VN reconfiguration for different types of failures in one VN and VN reconfiguration for single type of failures in multiple VNs are both studied. However, the VN reconfiguration for multiple types of failures in multiple VNs is not studied. Secondly, in reconfiguration of multiple faulty VNs, a single indicator is selected in most faulty VN ranking strategies. In different recovery objects, these strategies are not always suitable. Thirdly, a single resource indicator or topology indicator is taken into consideration in VN re-embedding, and the performance is limited. At last, the failures are not classified into certain types, and the recovery order of different types of failures is not researched.
In this paper, an ILP formulation of VN reconfiguration is provided, firstly. Then, the heuristic algorithm, called dynamic virtual network reconfiguration method for hybrid multiple failures based on weighted relative entropy (DVNRM-HMF-WRE), is proposed to solve the ILP formulation. In DVNRM-HMF-WRE, the faulty VN reconfiguration ranking method based on weighted relative entropy (FVNRRM-WRE), hybrid multiple failures ranking algorithm (HMFRA), and virtual node migration method based on weighted relative entropy (VNMM-WRE), are proposed. At last, five comparative experiments are set to demonstrate the performance of DVNRM-HMF-WRE.
The main contributions of this paper can be summarized as follows:
- (1)
We provide an ILP formulation of VN reconfiguration and propose the DVNRM-HMF-WRE to solve it. VNE is already intractable, and the combinatorial number of sequences of VNs in batch re-embedding further increases the complexity. Therefore, we only re-embed the faulty nodes and links without disrupting their unaffected parts in VN.
- (2)
We introduce a weighted relative entropy (WRE) method into FVNRRM-WRE and VNMM-WRE. In FVNRRM-WRE, we rank the faulty VNs with the help of multiple indicators, and combine them based on WRE. In VNMM-WRE, we use the WRE method to change the coefficients of node resource, and topology indicator to select the suitable candidate substrate node to reduce the resource consumption.
- (3)
We propose the HMFRA to handle the hybrid multiple failures. In HMFRA, faulty virtual node and its connective virtual links are handled first, which are the hardest the recover. HMFRA can make full use of the limited resources and improve the recovery performance.
- (4)
Five different simulation scenarios are conducted to validate the performance of DVNRM-HMF-WRE. The performance of DVNRM-HMF-WRE is compared with other algorithms in the first simulation experiment. Next, we simulate the impact of FVNRRM-WRE, HMFRA, and VNMM-WRE on the performance of DVNRM-HMF-WRE. At last, two factors are set to evaluate their influences on DVNRM-HMF-WRE.
The rest of this paper is organized as follows.
Section 2 presents the models and evaluation indicators. In
Section 3, we propose the ILP of VN reconfiguration. The DVNRM-HMF-WRE is given, and its details are shown in
Section 4. In
Section 5, we evaluate the proposed algorithm through extensive simulations and experiments. We conclude this paper with a summary and areas for future exploration in
Section 6.
4. DVNRM-HMF-WRE
4.1. Problem Statement
The VN reconfiguration is a complex and dynamic process. There are many event statements at the same time. We analyze the possible event statements and provide the dynamic process of VN reconfiguration first. Then, three algorithms in DVNRM-HMF-WRE are proposed.
VN embeds and leaves dynamically. Many types of failures occur randomly in SN. At time t, there are four possible event statements:
When the lifetime of VN ends, the corresponding SN resources are released.
When the faulty component in SN is repaired, its resources also return to normal.
When SN failure occurs, the resources of faulty component are set to zero and the VN embedded on it needs to be re-embedded. If multiple failures occur at the same time, the faulty VNs will be re-embedded one by one. When all faulty virtual components in one VN are re-embedded successfully, the VN reconfiguration is successful.
When VN request arriving, VN begins to embed. If succeed, the corresponding resources are used.
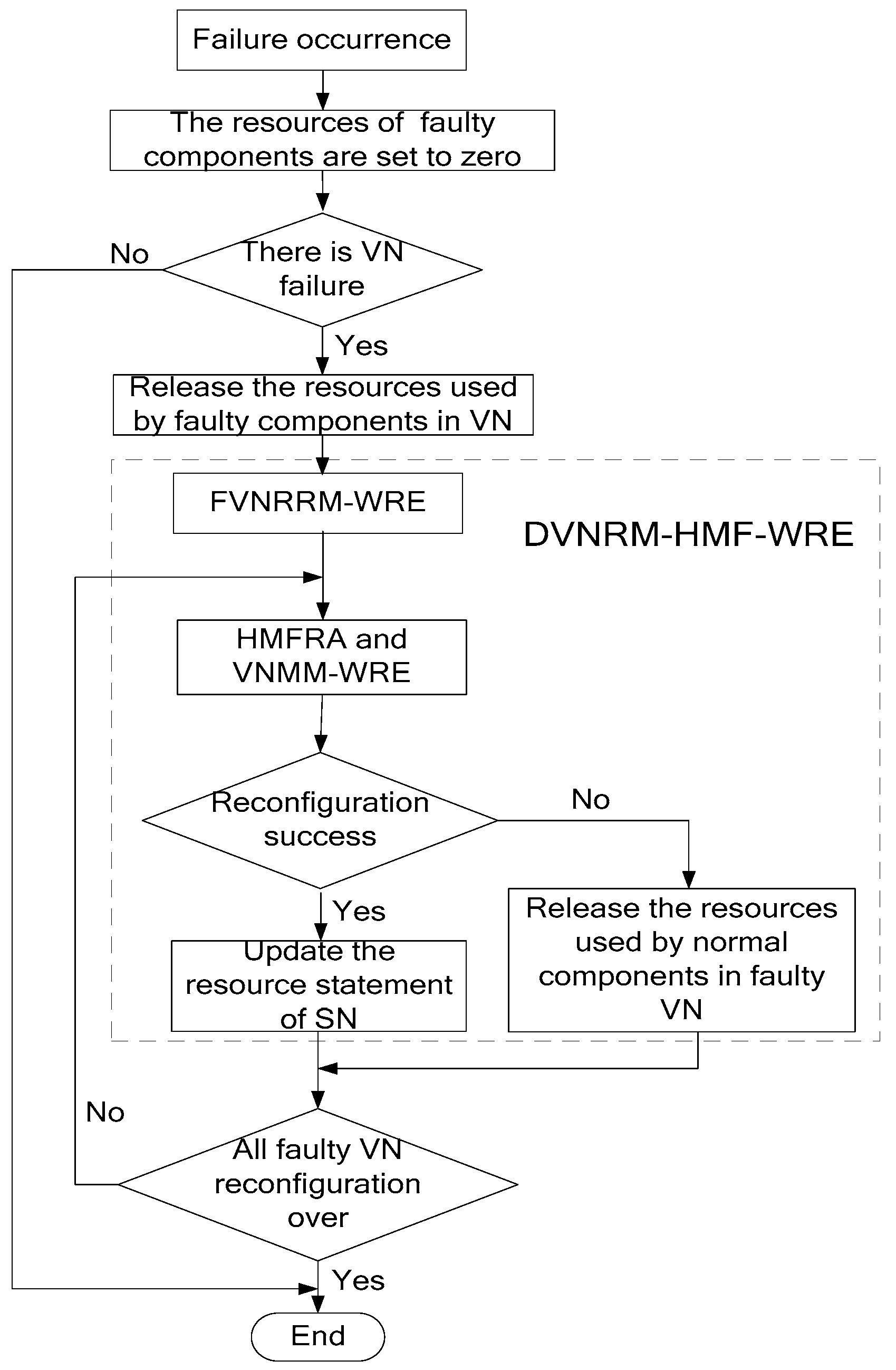
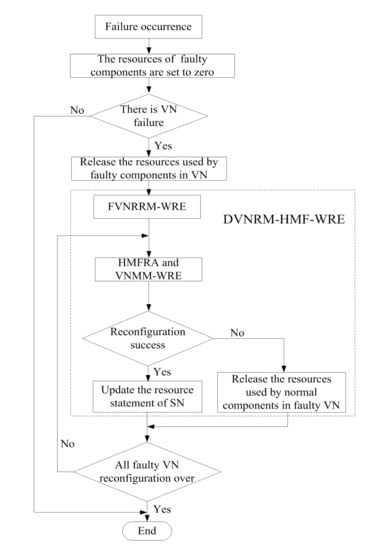
When multiple SN failures occur, the process of DVNRM-HMF-WRE is shown in
Figure 2.
As can be seen that, from
Figure 2, when failure occurs, the resources of faulty components are set to zero. If there are some VNs embedded onto the faulty components, the resources used by faulty components in VNs are released. Then, the DVNRM-HMF-WRE is used to re-embed the faulty VNs. In DVNRM-HMF-WRE, the FVNRRM-WRE is used to rank multiple faulty VNs to decide which faulty VN should be re-embedded first. The HMFRA and VNMM-WRE are used together to recover the hybrid multiple failures in one VN. The HMFRA is proposed to rank hybrid multiple faulty nodes/links in one VN, and the VNMM-WRE is provided to improve the efficiency of virtual node migration. If the VN reconfiguration is successful, the resource statement of SN I updated, otherwise, the resources used by normal components in faulty VN are released. If all VN reconfigurations are over, the DVNRM-HMF-WRE is stopped.
4.2. FVNRRM-WRE
When multiple failures occur at the same time, and substrate resources are limited, the reconfiguration sequence of faulty VNs is especially important. In faulty VN ranking strategies, ranking indicators and ranking method are very important. Among them, faulty component number, VN revenue, and remaining lifetime of the faulty VN all have obvious impact on the reconfiguration performance. They are selected to rank the faulty VNs. When ranking faulty VNs, a fixed formula is usually used, and it cannot adapt to the changing environment. Therefore, the WRE method is introduced in this paper.
The WRE method is a classical ranking method which can adjust the indicator coefficients to adapt the changing environment. It is improved by the classical technique for order preference by similarity to an ideal solution (TOPSIS) [
20]. In TOPSIS, the generalized distance is unable to distinguish the point in perpendicular bisector between positive and negative ideal solution [
21]. Therefore, the relative entropy is used, instead, to the generalized distance.
For system A and B in state
Ai and
Bi (
i = 1, 2,…,
N), their relative entropy,
C, can be defined by
There are N faulty VNs, and each faulty VN has M evaluation indicators. The
j-th indicator coefficient of the
i-th node is denoted as
Xij (
i = 1, 2, …,
N;
j = 1, 2, …,
M), and all coefficients of faulty VNs constitute a decision matrix
X which is denoted as
Also, the coefficient is normalized to make a fair comparison between different indicators.
In different environments, each indicator has a different importance. The weighting coefficient of the
j-th indicator is expressed as
(
,
), and the weighted normalized decision matrix is denoted by
The positive and negative ideal solutions
A+ and
A− are determined as
The relative entropies of each solution to positive and negative ideal solution are calculated as
The similarity between each solution and the ideal one is calculated as
The details of FVNRRM-WRE method are described in Algorithm 1.
| Algorithm 1. The FVNRRM-WRE |
| Input: X, weighting coefficients |
| Output: Zi |
| 1. Bring X and the weighting coefficient of each indicator into Formula (25) to construct the weighted normalized matrix Y. |
| 2. Calculate the positive and negative ideal scheme A+ and A−. |
| 3. Calculate the positive and negative ideal solution C+ and C−. |
| 4. Calculate Zi and get the importance degrees of faulty VNs. |
In Algorithm 1, X is the multiple indicators decision matrix which includes three indicators, called faulty components number, VN revenue, and remaining lifetime of the faulty VN. To calculate Zi, which is the importance degree of faulty VNi, the WRE method is widely used based on Formulas (26)–(30). After getting the importance degrees of faulty VNs, rank the faulty VNs in order of importance degree, from large to small, which can re-embed the important VN first.
4.3. HMFRA
In a faulty VN, there are multiple failures which include node failures and link failures. Recovery sequence is important in VN reconfiguration, and the HMFRA is proposed to recover different types of failures in a suitable manner. The details of HMFRA are shown in Algorithm 2.
| Algorithm 2. The HMFRA |
| Input: GS, GV, the set of faulty node, the set of VN link failure I, the set of VN link failure II, the set of VN link failure III |
| Output: GS, GV |
| 1. if the faulty node set is not empty |
| 2. Migrate the virtual nodes using VNMM-WRE and re-embed all their connective links (VN |
| link failures I) using k-shortest path algorithm. |
| 3. if all virtual nodes are migrated and all their adjacent links are re-embedded successfully |
| 4. Update GS and GV |
| 5. if the set of VN link failure II is not empty |
| 6. Re-embed all VN link failures II |
| 7. if all VN link failures II are re-embedded successfully |
| 8. Update GS and GV |
| 9. if the set of VN link failure III is not empty |
| 10. Re-embed all of them |
| 11. if all VN link failures III are re-embedded successfully |
| 12. Update GS and GV |
| 13. Return VN_RE-EMBED_SUCCESS |
| 14. else release the resources in GS which are used by the normal parts |
| 15. Update GS |
| 16. Return VN_RE-EMBED_FAILURE |
| 17. end if |
| 18. else update GS and GV |
| 19. Return VN_RE-EMBED_SUCCESS |
| 20. end if |
| 21. else release the resources in GS which are used by the normal parts |
| 22. Update GS |
| 23. Return VN_RE-EMBED_ FAILURE |
| 24. end if |
| 25. else update GS and GV |
| 26. Return VN_RE-EMBED_SUCCESS |
| 27. end if |
| 28. else release the resources in GS which are used by the normal parts |
| 29. Update GS |
| 30. Return VN_RE-EMBED_ FAILURE |
| 31. end if |
| 32. else |
| 33. if the set of VN link failure III is not empty |
| 34. Re-embed all of them |
| 35. if all VN link failures III are re-embedded successfully |
| 36. Update GS and GV |
| 37. Return VN_RE-EMBED_SUCCESS |
| 38. else release the resources in GS which are caused by the normal parts |
| 39. Update GS |
| 40. Return VN_RE-EMBED_ FAILURE |
| 41. end if |
| 42. end if |
| 43. end if |
As can be seen from Algorithm 2:
Faulty virtual node and its connective links (VN link failures I) are recovered first. If substrate node is faulty, virtual node and its connective virtual links both need to be re-embedded. They will consume huge substrate node and link resources. They are the hardest to re-embed. If this succeeds, go on re-embedding virtual links in the set of VN link failure II. Otherwise, VN reconfiguration has failed.
If the VN link failures II are re-embedded successfully, then judge if there are VN link failures III. If there are VN link failures III, re-embed them. If this succeeds, VN reconfiguration is successful.
If there is no VN link failure III after re-embedding the VN link failure II successfully, the faulty VN returns to normal. If the VN link failure II fails to re-embed, the faulty VN reconfiguration has failed.
If there is only VN link failure III, re-embed these faulty virtual links. If this succeeds, VN reconfiguration is successful.
4.4. VNMM-WRE
In HMFRA, the method of faulty virtual node migration is called VNMM-WRE, which is proposed in this section and the method of virtual link re-embedding is
k-shortest path algorithm [
22].
Similar to FVNRRM-WRE, the WRE method is also introduced into VNMM-WRE. In virtual node ranking, the importance degree of each virtual node
Z(
nv) is calculated using WRE method, which selects node CPU resource and node adjacent link bandwidth resource as the indicators. In substrate node ranking, the importance degree of each substrate node
Z(
ns) is calculated using WRE method which selects node CPU resource, node adjacent link bandwidth resource and the reciprocal of hop counts between candidate substrate node and substrate node which is embedded by the neighboring virtual node of the migrated virtual node as the indicators [
23].
The details of VNMM-WRE are shown in Algorithm 3
| Algorithm 3. The VNMM-WRE |
| Input: Faulty virtual nodes which need to migrate |
| Output: NodeMigraingList |
| 1. for each virtual node nv∈NV |
| 2. Calculate the Z(nv) |
| 3. end for |
| 4. Rank virtual nodes in order of Z(nv) from large to small |
| 5. Save virtual node ranking order into VirtualNodeList |
| 6. for each virtual node in VirtualNodeList |
| 7. Select the candidate substrate node set Can(nvi) which satisfies the resource constraints |
| 8. Remove the embedded substrate nodes from Can(nvi) |
| 9. if Can(nvi) is empty |
| 10. Return NODE_ MIGRATE_FAILURE |
| 11. else |
| 12. for each candidate node ns in Can(nvi) |
| 13. Calculate the Z(ns) of each substrate node in Can(nvi) |
| 14. end for |
| 15. for each virtual node in Can(nvi) |
| 16. Re-embed nv to ns which has the largest Z(ns) value |
| 17. Re-embed the virtual links which connect the virtual node |
| 18. if all virtual links are re-embedded successfully |
| 19. Save the substrate node ns into NodeMigratingList |
| 20. break |
| 21. else |
| 22. Remove the virtual node nv from Can(nvi) |
| 23. end if |
| 24. end for |
| 25. Update GS and GV |
| 26. Return NODE_MIGRATE_SUCCESS |
| 27. end if |
| 28. end for |
In Algorithm 3:
Lines 1–5: calculate the Z(nv) of each faulty virtual node and rank them based on Z(nv). Then save the ranking results into VirtualNodeList.
Lines 6–14: select the candidate substrate nodes and calculate their Z(ns).
Lines 15–28: re-embed the virtual node and its adjacent virtual links.
In summary, with the help of FVNRRM-WRE, HMFRA, and VNMM-WRE, the faulty VNs caused by hybrid multiple failures can be recovered.
4.5. COMPLEXITY ANALYSIS
The DVNRM-HMF-WRE includes FVNRRM-WRE, HMFRA, and VNMM-WRE. In FVNRRM-WRE, all faulty VNs are ranked based on the WRE method. Its complexity is , in which is the total number of faulty VNs. The HMFRA and VNMM-WRE are used, together, to recover the hybrid multiple failures in VNs. In the recovery of faulty VNs, the complexity of virtual node re-embedding is . is the total number of faulty virtual nodes in all faulty VNs and is the total number of substrate nodes. The virtual link re-embedding algorithm is k-shortest path algorithm and its complexity is . represents the total number of faulty virtual links in all faulty VNs and represents the total number of substrate links. Therefore, the total complexity of DVNRM-HMF-WRE is .
6. Conclusions and Future Work
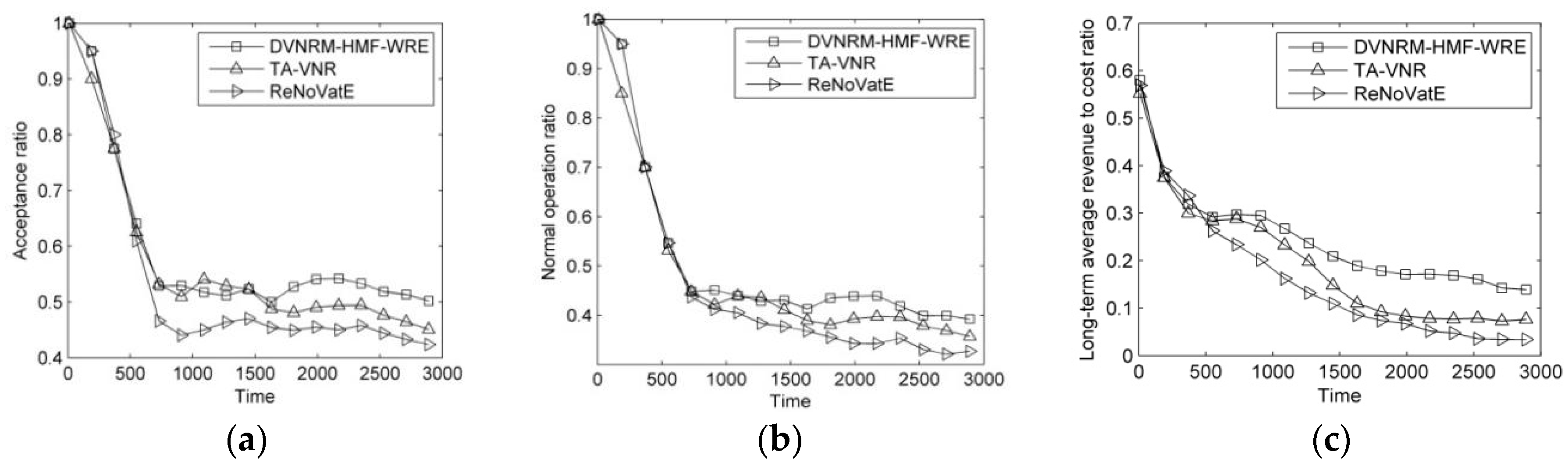
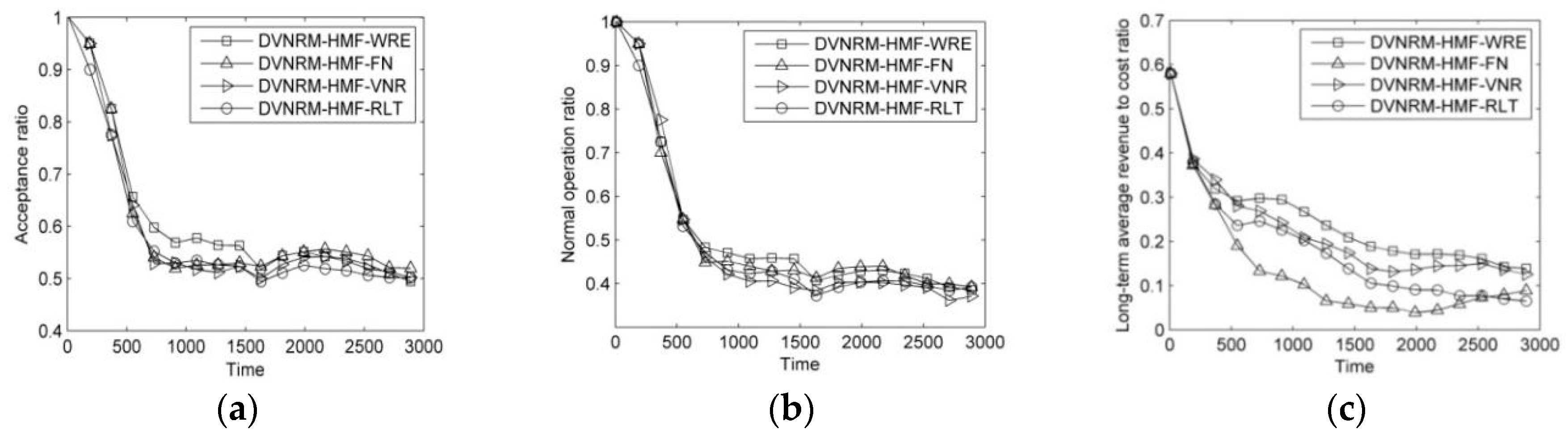
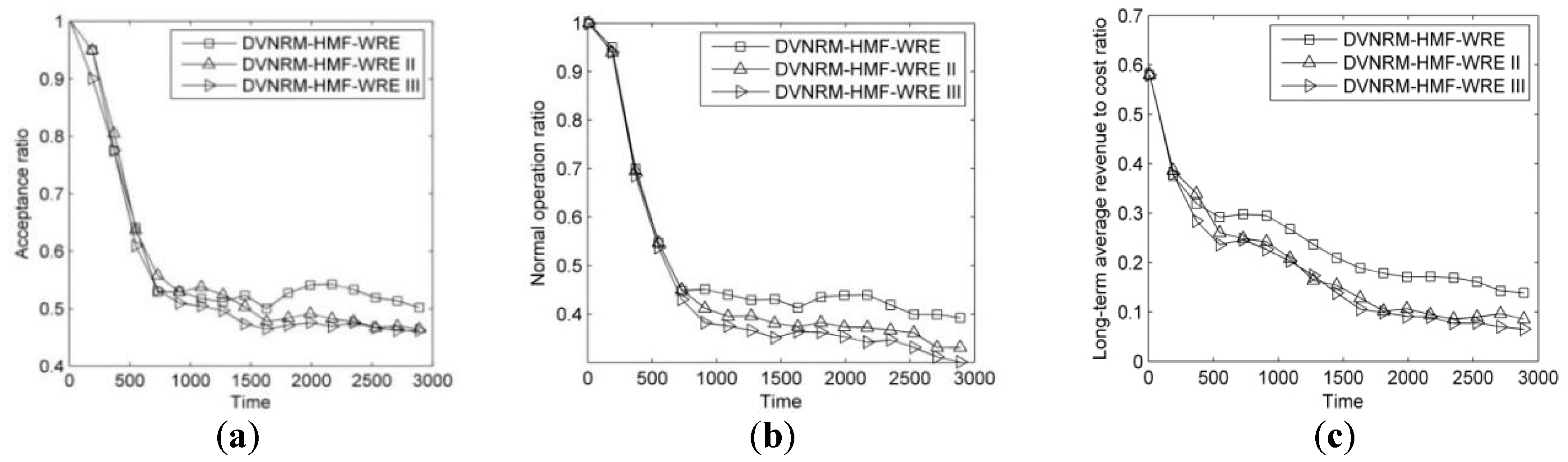
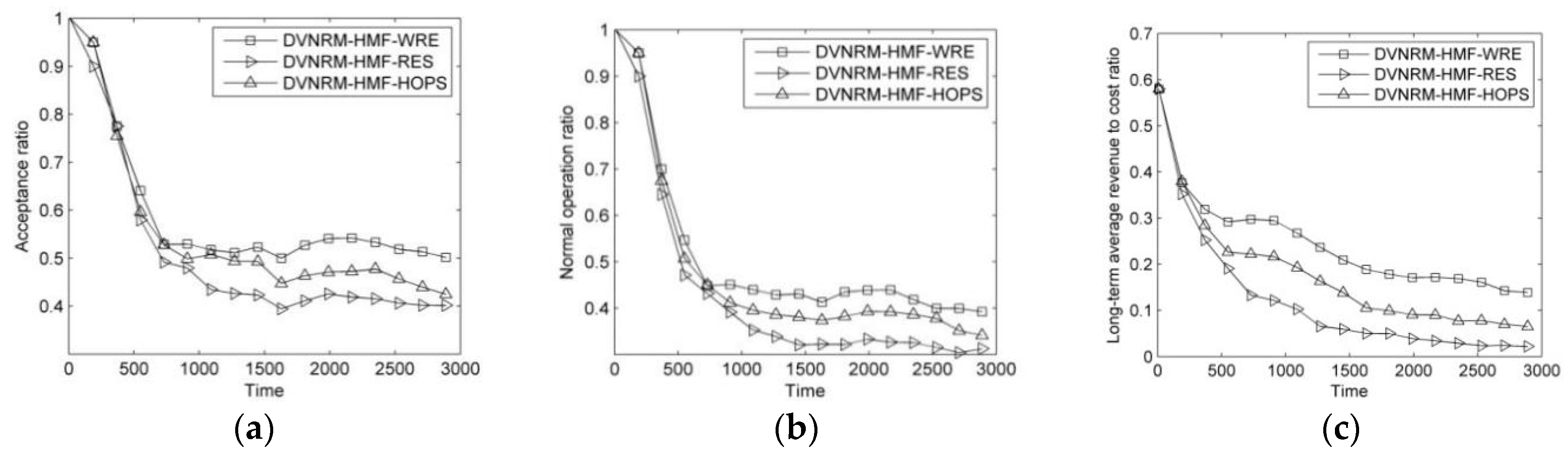
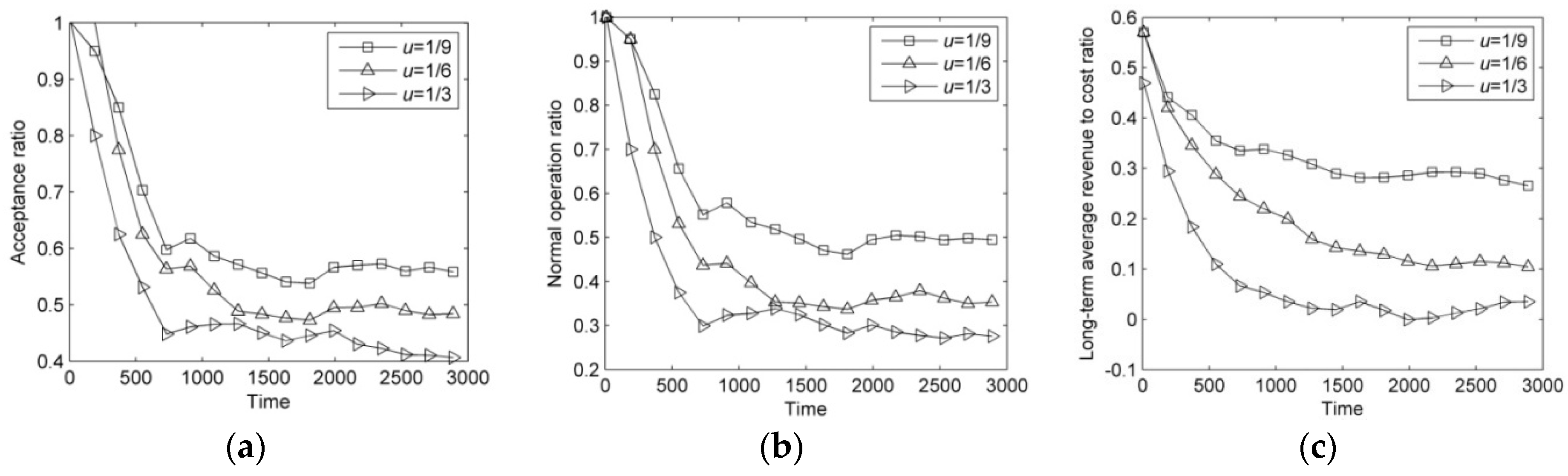
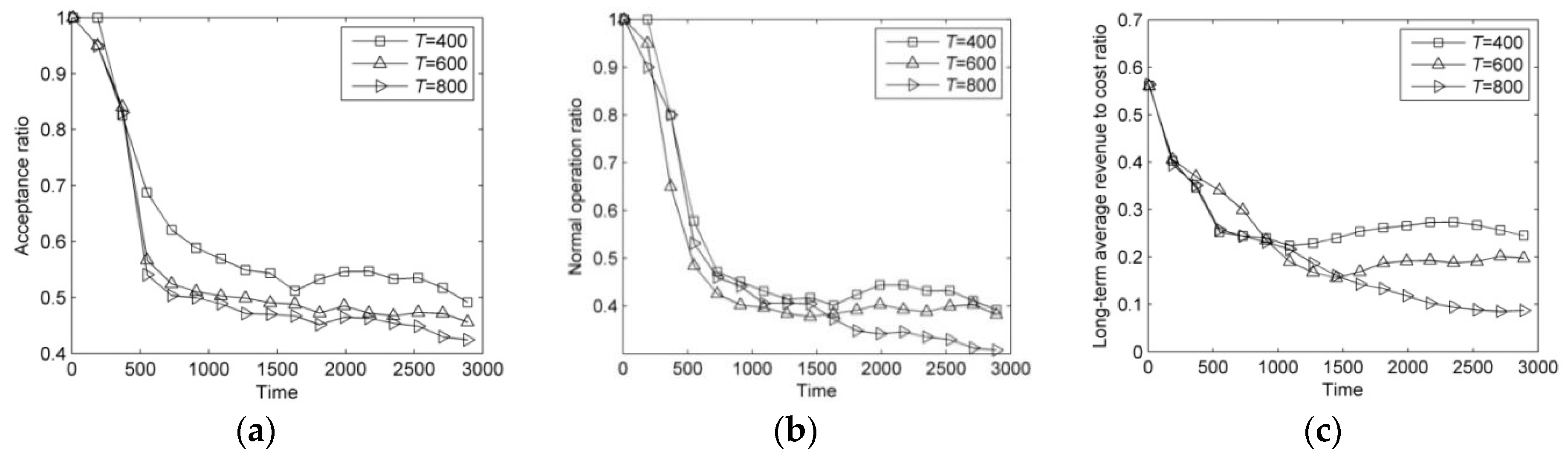
In this paper, we have addressed the problem of recovering faulty VNs affected by hybrid multiple failures in SN. In this regard, we have formulated the VN reconfiguration to an ILP model to maximize the LAR/CR. We have proposed an efficient heuristic policy called DVNRM-HMF-WRE to solve this ILP model. In DVNRM-HMF-WRE, the WRE method is introduced into FVNRRM-WRE and VNMM-WRE. In FVNRRM-WRE, the WRE method is used to rank the multiple faulty VNs. In VNMM-WRE, candidate substrate node are selected based on WRE method which takes resource and topology indicators into consideration. Also, a failure handling method called HMFRA is proposed, which handles virtual node failure and VN link failure I first. At last, five experiments are designed. The first experiment verifies that the proposed DVNRM-HMF-WRE has excellent performance than other typical VN reconfiguration methods. The next three experiments assess that our proposed faulty VN ranking method, failure handling method, and VN node migration method perform better than other corresponding methods. The last experiment sets two different scenarios to evaluate the performance of DVNRM-HMF-WRE in different arrival rates and lifetimes of failures. Evaluation results show that decreasing the arrival rate and the lifetime of failure can improve the performance of VN reconfiguration.
In future research, we will introduce the privacy and energy consumption into VN reconfiguration. Without adequate protection, users from a VN might be able to gain unauthorized access to data being transmitted through other VNs, violating the privacy of the entities that own those networks. Hence, privacy-oriented VNE and preserving privacy with VN stacks gradually get more and more attention. Also, energy consumption has become another hot topic in NV. With the increase of communication traffic every year, some energy models have been proposed to minimize the energy consumption in NV, such as the load-dependent power consumption model in VNE, the energy-efficient resource management for real-time service function chain in fog-supported SDN and network-aware energy optimization model for VN. Therefore, the ILP formulation and the heuristic algorithm could be extended to consider the privacy and energy consumption in future work.