1. Introduction
Since the entropy is a popular randomness measure, many studies are devoted to the efficient estimation of the Shannon or Rényi entropy for given random samples. In particular, one of the important applications for entropy estimator is random number generators (RNGs). RNG is one of the fundamental cryptographic primitives and a good RNG can be modelled as an ergodic random source. For block ciphers and public key cryptography, an RNG also can be used as a key-stream generator. In addition, the digital signature algorithm (DSA) requires a random number for its computation [
1]. Since a statistical bias in random numbers can be exploited to reduce the computational complexity of the exhaustive search by an attacker, the entire security of the crypto-systems usually depends on the statistically quality of RNG output.
In order to obtain the unpredictability of random output, many crypto-systems require a true (physical) random number generator (TRNG) [
2,
3,
4] as well as pseudo-random number generators (PRNG). However, a TRNG output can be easily influenced by environments such as temperature, electro-magnetic wave, and so on. Therefore, an on-the-fly statistical test scheme, as known as online test, is requested to guarantee the statistical quality of RNG output in cryptographic standards [
5]. In particular for the applications with stringent resource constraints such as sensor nodes, smart cards, etc., an online test scheme for RNG should both have compact size in hardware/software and detect a various range of statistical bias to ensure the security of the systems [
6]. That is, we need a good and efficient test scheme of the statistical quality of random sources. Therefore, it is highly desirable to construct low-cost and reliable entropy estimation methods of the random output of TRNG.
When it comes to the randomness measure, the Shannon entropy is one of the widely used measures. Let
be the finite field with two elements. Let
X be a random variable for
L-bit random symbols in
from the random source
S and the probability of occurring random symbol
b from the random source
S is denoted by
. Then, the Shannon entropy of
L-bit blocks from the random source
S is defined as
In various literature, there have been developed efficient estimators of the Shannon entropy [
7,
8,
9,
10,
11]. In addition, the complexity of estimating the Shannon entropy of a distribution on
k elements from independent samples also has been developed [
10,
12,
13].
In 1961, another generalized entropy measure is defined by Rényi [
14]. The Rényi entropy is popularly used in a number of signal processing and pattern recognition applications [
15,
16,
17]. For example, Rényi entropy has been used in cryptography, in the study of bio-informatics, and in the bio-medical applications [
18]. Sometimes, the Rényi entropy can provide more strict randomness measure for the cryptographic applications such as the privacy amplification [
19]. Rényi entropy of order
for
L-bit blocks from the random source
S is defined as
where
and
. Note that Rényi entropy is defined as the log base 2 of the expectation of
normalized by
.
Generally, a random source used in a cryptographic protocol should have a maximum entropy. As a result, Shannon entropy (or Rényi entropy) is recognized as one important measure of randomness. For example, standards such as NIST STS (Statistical Test Suits) [
20] or AIS.31 [
5], a widely used standard for evaluating TRNGs, include Entropy Estimation items. The proposed method estimates the actual Rényi entropy value very accurately, as can be confirmed from the simulation results. Therefore, if the estimation result shows a lower value (from the maximum), it can be interpreted as a signal that the random sources are generating a significant deviated output from the perfect.
The Rényi entropy is a generalization of the Shannon entropy since it contains the definition of the Shannon entropy when
approaches to one [
21]. In particular, notice that it is easy to prove the Rényi entropy is always less than or equal to Shannon entropy by using Jensen’s inequality [
22] for
, i.e.,
Here, the equality holds for the equiprobable random source. Therefore, Rényi entropy can be used as the lower bound of the Shannon entropy for a random source S.
There are some studies for the estimation of Rényi entropy [
15,
23,
24]. In particular, many applications such as machine learning [
16], blind deconvolution of linear channels [
25], information flows in financial data [
26] and cryptography [
19] have paid attention to the Rényi entropy of order 2, also called the
quadratic entropy or
collision entropy [
15]. The most straightforward approach for entropy estimation is the direct calculation of entropy based on the probability mass function (pmf) or the probability density function (pdf) of empirical data. For example, Erdogmus and Principe proposed the Rényi entropy or order estimator by using the non-parametic estimation of the pdf of a random variable [
16]. In order to estimate the pdf of a given sample distribution, they used the Parzen windowing method, in which the pdf is approximated by the sum of kernels such as the Gaussian function. In addition, there are many non-parametric approaches to estimate entropies, which are usually based on the data compression [
27] or the nearest neighbor distance [
7,
8,
28,
29]. There are results on the estimation of Rényi entropy rate of Markov chains [
30]. This can be also considered for randomness measure for RNG because a skewed RNG can be modelled as Markov chain with vaying transition probability. However, many of them are not suitable in constrained devices with stringent resource restriction due to the computational complexity.
In this paper, we propose a low complexity estimation method of the Rényi entropy of order
, where
is a real number. This method does not require any initialization phase contrary to the previous Maurer’s universal statistical test [
8] and Coron’s refined test [
7] which are widely used for estimating Shannon entropy especially in cryptographic applications [
5,
20]. In the proposed scheme, we can estimate the Rényi entropy of order
without introducing complicated computations such as logarithms or divisions. We show that the expected value of the proposed test function is equivalent with the Rényi entropy of order
. That is, the output of the proposed estimation method almost surely converges to the Rényi entropy of order
values with large samples. Because the requirement of a large sample size for accurate estimation can be a drawback of the proposed scheme in some applications, we also propose an iterative algorithm for the Rényi entropy of order 2, which requires a relatively short sample size and shows accurate test results. Using the simple counting method, we can efficiently implement test module of RNGs based on the Rényi entropy of order 2. Therefore, it can be used as a statistical tester of RNGs for many embedded security systems such as smart cards. This is an extended version of the conference paper [
31]. In this paper, we generalized the order from integer to real number. Also, iterative estimation method is included for more constrained environments.
The remainder of this paper is organized as follows: in
Section 2, previous entropy estimation schemes are reviewed. In particular, for the comparison, Maurer’s universal statistical test and Coron’s refined scheme are presented in detail since they are the popular nearest neighbor distance based schemes, which are exploited by the proposed scheme. In
Section 3, the proposed estimation scheme for the Rényi entropy of order
is presented. Firstly, we describe the estimation method and show that the expected value of the proposed test function is equivalent with the Rényi entropy of order
. We suggest the iterative estimation algorithm, which requires a relatively small sample size. Then, numerical results are given in
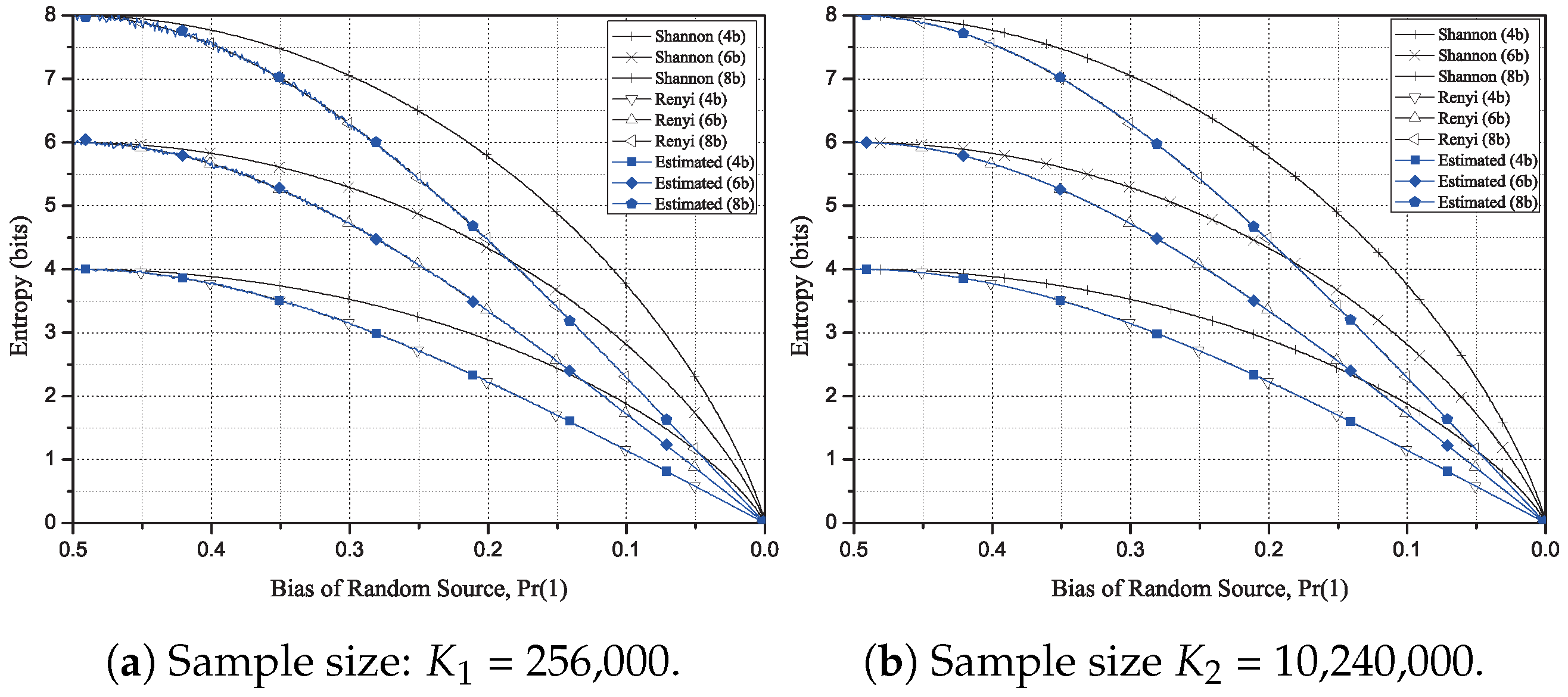
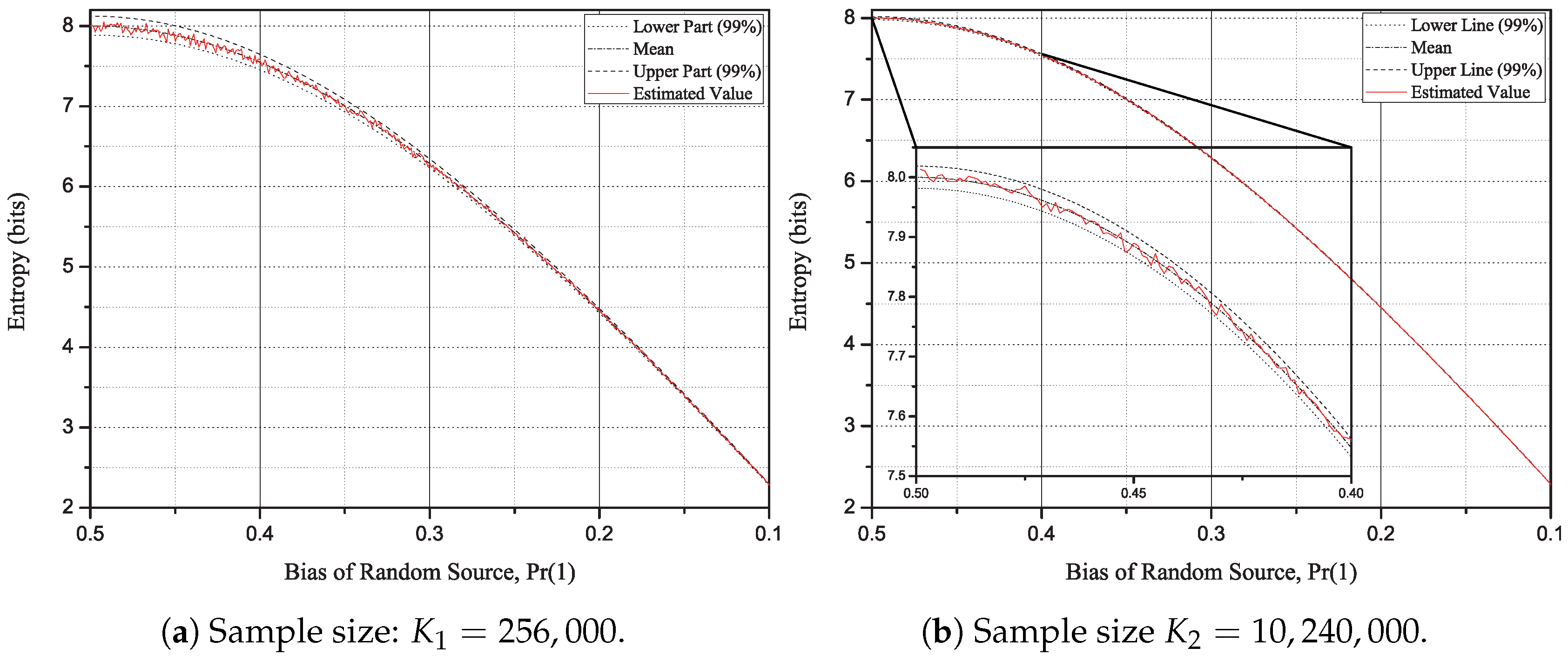
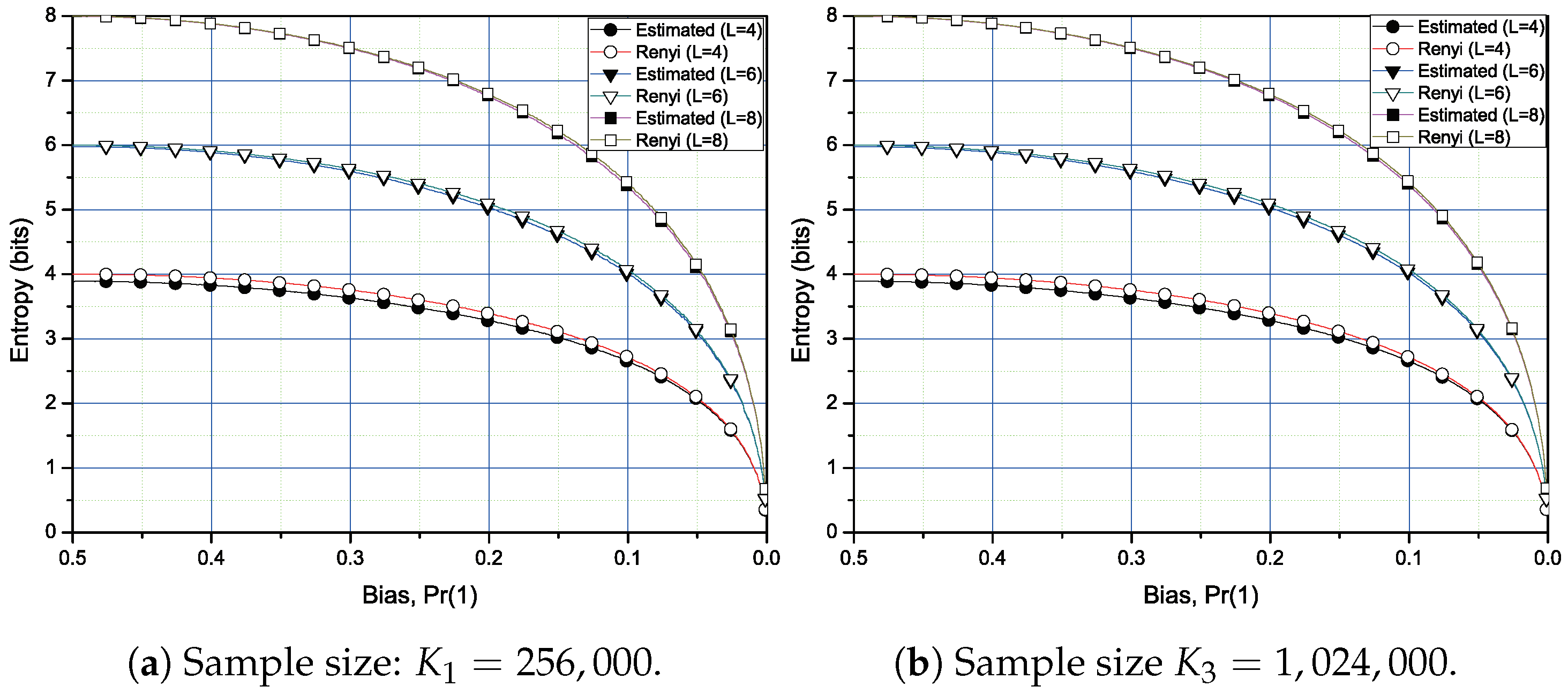
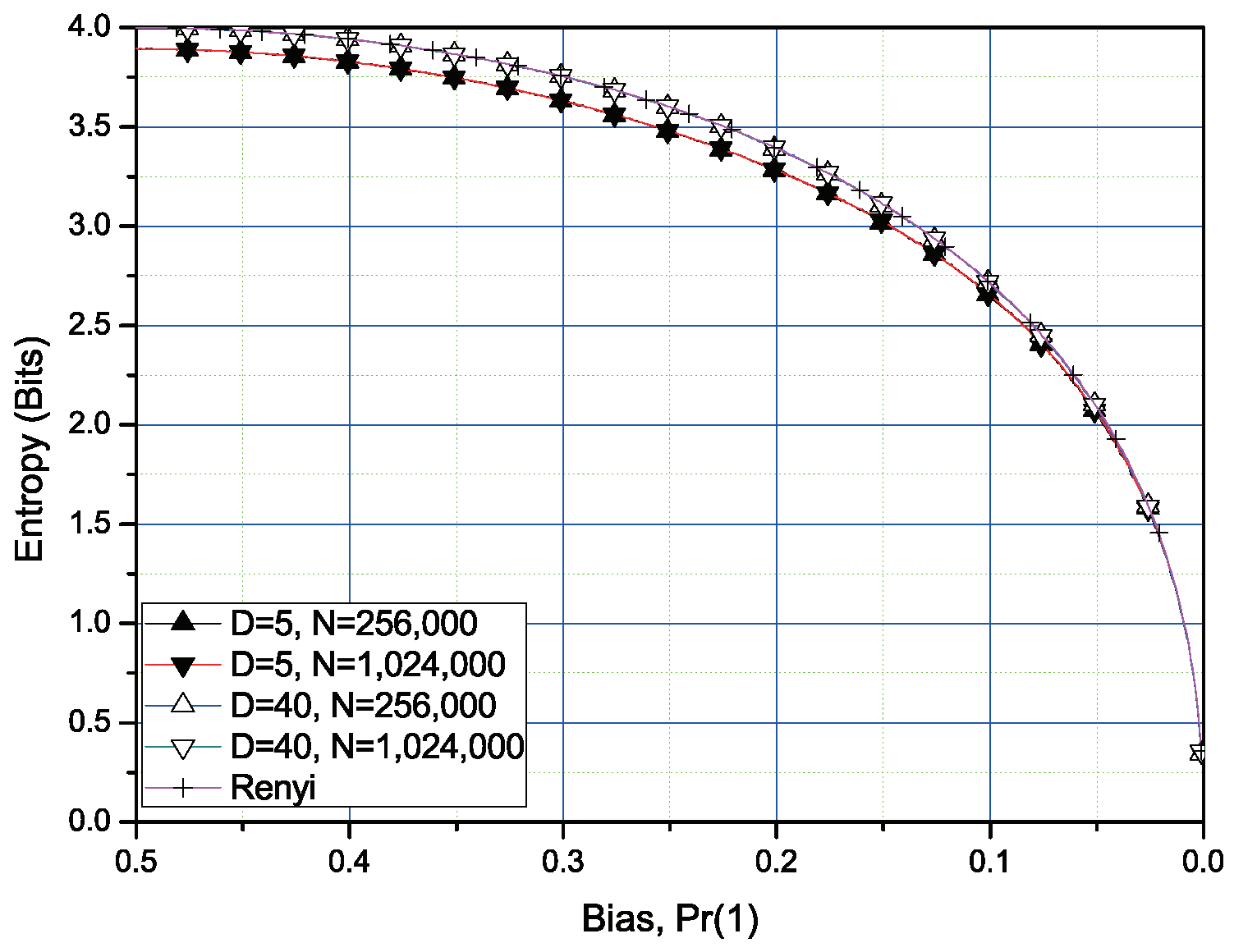
Section 4. For the three block sizes and two sample sizes, the estimated values are compared with the Rényi entropy of order 2 or order 1/2. For the iterative algorithm, we can check that the proposed algorithm is more stable with less sample size. Finally, we conclude this paper in
Section 5.
3. New Estimation Method of the Rényi Entropy of Order
In this section, we derive the parameters for the estimation of the Rényi entropy of order
, for a real number
. In this derivation, we assume that an ergodic random source
S and random sequences from the source
S are over
and consecutive and distinct
L symbols are treated as a basic element of test function. Thus, the maximum value of Rényi entropy (and also Shannon entropy) will be
L-bit. For the estimation of Rényi entropy, we firstly focus on the estimation of inner summation in (
2). Then, to obtain exact value of Rényi entropy, the logarithm and division by
will be applied to the result of the estimation. The test function is given as
where
is the index distance defined in (
4). Now, for given real number
and the index distance
, we are going to find the values of
for each
which is closely related to the inner summation (
2) for the estimation of Rényi entropy of order
. The following theorem gives us the general representation of
for given
.
Main Result: Proposed Test Function of Rényi Entropy of Order
For the estimation of Rényi entropy of order α, the parameters of estimator for given index distance k in (10) are given aswhere The derivation of the proposed test function can be justifed as in the following proof.
Proof. We start from the the expectation of the test function
given as
where
is a vector of random variables for random sequence
of
L-bit symbols and
is the
k-th parameter for the estimation. Then, the probability
can be represented as
If the random variable is stationary, we have
From (
13) and (
14), the expectation can be represented as
where
is defined as
Here, we are going to find the representation of
that satisfies the expected value of
. Then, we have
By removing
x at both sides, the equation is simplified as
By substituting
, we have
From (
15), for
, we have
. That is,
, otherwise
. For
, the Tayler series at
of the right hand side of (
15),
, is given as
where
and
. Note that the combination in (
16) is a generalized binomial expansion for the real number
and a positive integer
k [
33]. Thus, we have
Finally, the parameter
of the estimator for the exact Rényi entropy of order
for a real number
is given as
☐
Table 1 shows examples of parameters of the proposed estimator for some cases of
. For the integer
, we can see the negative values of
. This means that the test function in (
10) may be negative after accumulation of parameters for given random samples. Therefore, in this case, we need to take absolute value of test result before applying logarithm to calculate actual Rényi entropy of order
.
Now we are going to derive representation of for some particular orders, , , and in the next subsections. First, let us start from the case of approaching to 1, where Rényi entropy converges to Shannon entropy.
3.1. Convergence of Rényi Entropy and Shannon Entropy
The proposed estimation method converges to the same estimator of Shannon entropy by Coron [
7] as in the following theorem.
Theorem 1. The proposed test function of Rényi entropy converges to the test function of Shannon entropy by Coron when goes to 1.
Proof. If
, from (
11), the parameter converges
This means that every case will be counted and the test function
in (
10) will always converge to 1. To obtain actual value of Rényi entropy, the test function
should be applied by the logarithm of base 2 and divided by
. To obtain the converged value for
, we can use L’Hospital’s theorem to
. Then, we have
From (
11), we can obtain the derivative of
with respect to
as
From (
17), we also have
when
goes 1. Therefore, from (
18) and (
19), we have
where
for
. It is exactly the same result by Coron given in (
6) and (
7) [
32]. ☐
That is, the proposed estimator includes the previous result as a special case and it can be considered as evidence that the proposed approach is valid for the entropy estimation.
3.2. Proposed Test Function for Rényi Entropy of Order
In this subsection, we will derive a simplified test function for Rényi entropy of order 1/2. This order of Rényi entropy is closely related to the exponent of the average growth rate of average guesswork [
34,
35]. From the main result, for
and
, we have
However, the calculation of the factorial is a complicated task and takes a long time even for the moderate size of integer. Therefore, we need to simplify (
20) for the practical implementation. First, we can use the Stirling’s approximation given as
Note that, for large enough
k, the right-most factor in the last equality converges to the natural number
e as follows:
Thus, we have for large
kWhen it comes to a big enough size of
k, if
, the error rate of the original value of
and its approximation in (
21) is less than 1.31%. In
Section 4, we use only the first five
for Rényi entropy of order 1/2 such as
,
,
,
, and
. The remainder terms are estimated as
for
:
where
(
) is the number of symbol
k of random samples with length
N. In
Section 4, we will see the small block size such as
or
, the number of uses of exact values of
should be large to obtain more exact estimation results. However, for
, only the first five exact values of
is enough to obtain good results.
3.3. Estimation of Collision Entropy
In this section, we discuss the estimation method of the Rényi entropy of for L-bit blocks. This case is both one of the widely used Rényi entropy orders and we can very efficiently implement the estimator for this case. We will see that this case is based on a simple counting of consecutive occurrence of the same L-bit random samples. The test value eventually converges to the Rényi entropy of order 2 with increasing sample size.
Assume an ergodic random source
S. Then, from (
12), the test function for ‘collision entropy’ is given as
where
The proposed scheme can be classified as the entropy estimator based on the nearest neighbor distance, which is also used in the Maurer’s and Coron’s tests.
From the main result, it can be readily proved that the expected value of the proposed test function in (
22) is equivalent to the Rényi entropy of order 2 as in the following proposition.
Proposition 1. The expected value of the test function in (22) is equivalent with the Rényi entropy of order 2 (collision entropy) of L-bit sample from an ergodic random source S. Notice that the test function in (
22) can be efficiently implemented as in the following description. Let
be the threshold to accept a given sample as random. The threshold
can be determined according to applications and a relevant statistical significant level. For implementation, the division and log base 2 in (
22) are not essential for the decision and it is enough to only count the number of occurrences such that
. For example, in order to accept the given sample as random, the test function in (
22) should be greater than the specified threshold of estimated entropy value as follows:
Then, (
24) can be converted into the following relation:
Since the right-hand side (RHS) is fixed in (
25) when the sample size
K is also fixed, it is enough to check the number of times that the specified event on the left-hand side (LHS) is less than the pre-determined value in the RHS. This testing function will be referred to as the
basic test of the iterative estimation algorithm presented in the following subsection.
Now, let us compare the computational complexity required by the proposed Rényi entropy estimation method with the complexity required by another entropy estimation methods based on the neareast neighbor distance. The required number of operations for three entropy estimation methods based on the nearest neighbor distance is listed in
Table 2.
As you can seed in
Table 2, the proposed method can minimize the number of logarithms and divisions for estimation. Note that the logarithm or division is much more complicated than summation. Therefore, the proposed method has the lowest computational complexity when it is compared with the other nearest neighbor distance based estimations, Maurer’s method in NIST STS [
20] and Coron’s method in AIS.31 [
5].
3.4. Iterative Estimation Algorithm for Collision Entropy
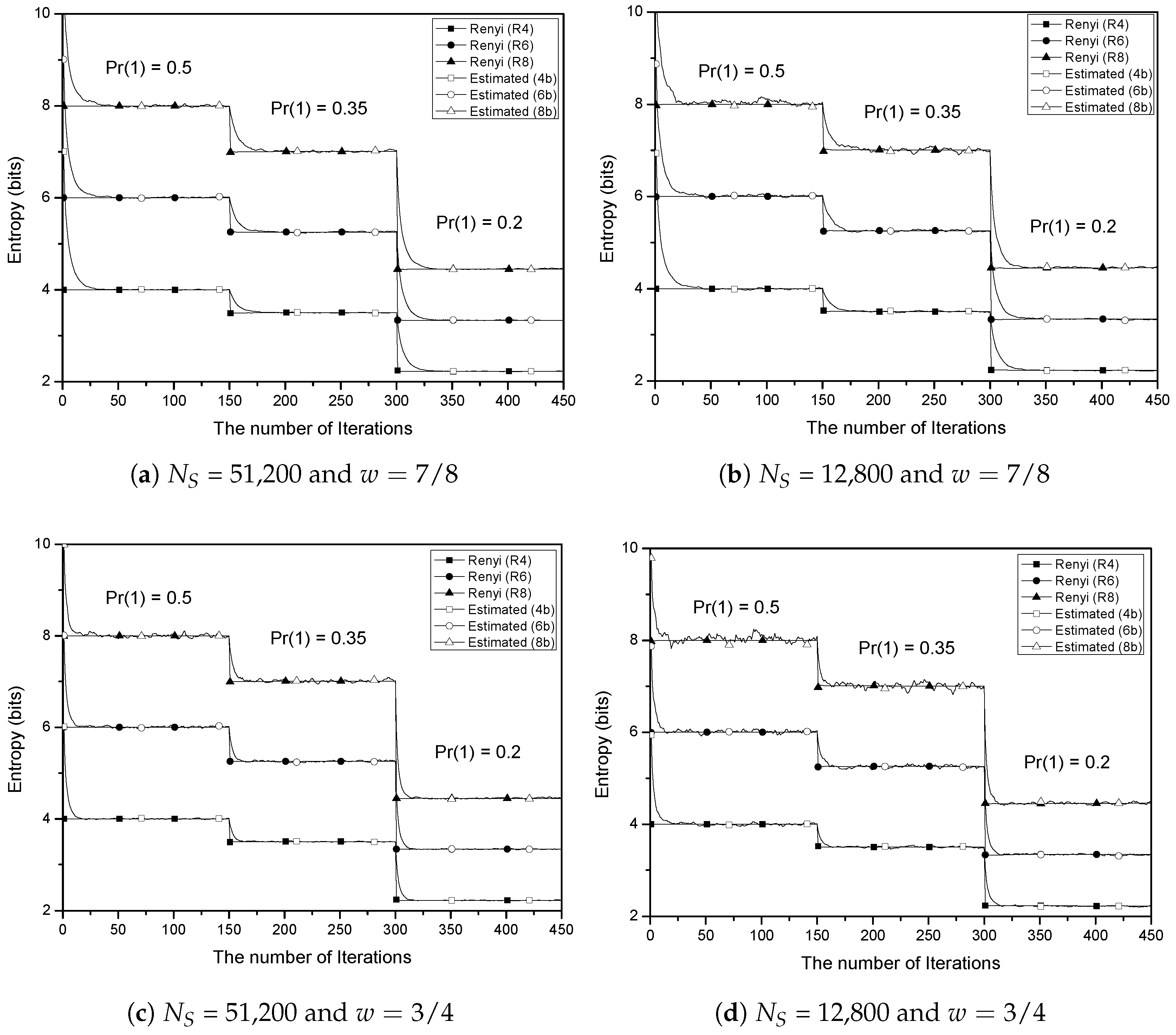
For the accurate estimation, the proposed test scheme requires a large sample size, which can be a drawback of the proposed scheme in some applications since it takes much time to collect enough samples for a single estimation. In order to mitigate this drawback, we propose an iterative testing scheme, which will always watch the generated random samples on-the-fly and continuously update the test value with a new counting result for a shorter sample size. The proposed iteration algorithm is presented in Algorithm 1.
In Algorithm 1,
is the sample size for the basic test and
w (
) is the weight of the previously accumulated value. Algorithm 1 consists of basic tests, which are continuously carried out when the test is running. The inside statements of for-loop in Algorithm 1 correspond to the basic test that is explained in
Section 3.3. Let
be the number of iterations. Algorithm 1 can be justified as in the following proposition.
| Algorithm 1: Iterative Estimation Algorithm for Rényi Entropy of Order 2 (Collision Entropy) |
![Entropy 20 00657 i001 Entropy 20 00657 i001]() |
Proposition 2. For the stationary random source, after sufficiently large number of iterations, the test value in Algorithm 1 will converge to the Rényi entropy of order 2 (collision entropy).
Proof. For convenience, let us introduce indices to the counted value
C and the accumulated value
S in Algorithm 1 such as
and
where
. Then, the final accumulated value in Algorithm 1 is given as
Suppose that the bias of random sample is stationary. That is, the bias level which can be represented as
in the binary representation is fixed for several consecutive iterations, namely
iterations. Then, we can substitute the counted values
with the average of them,
where
Then, the
can be represented as
For a large integer
, we have
. That is,
in Algorithm 1 can be rewritten as
That is, the output
of Algorithm 1 is the average of counted values from the basic tests over the sample size
. Due to the time average in (
26), the proposed algorithm can give us more stable estimated entropy values of the given random samples. ☐
The weight w will determine a trade-off between converging speed and reducing fluctuation, which will be shown in the next section. If w is close to 1, the estimated value shows less fluctuation at the cost of the sensitivity to the bias changes. In addition, if we choose , then the multiplication in the final step corresponds to m-bit left shift. Moreover, in Algorithm 1 can be implemented using m-bit left shift, -bit subtraction, and m-bit right shift.