A Simple Chaotic Map-Based Image Encryption System Using Both Plaintext Related Permutation and Diffusion
Abstract
1. Introduction
- (1)
- The proposed encryption system can be used to encrypt color images or gray images of any size. Some algorithms [5,8,9,10,15,29,31,33,35] mentioned above are developed to encrypt gray images. If these algorithms are used to encrypt R, G and B channels of original color image and then transform three encrypted gray imges into encrypted color image, the encryption system has less plaintext sensitivity because three channels of original color image are encrypted separately and do not have interaction in the encryption process. Furthermore, some other algorithms [7,10,11] are suitable for encrypting the original square image.
- (2)
- As mentioned above, most plaintext related image encryption schemes used only plaintext related confusion operation [28,29,30,31,32] or only plaintext related diffusion operation [33,34,35,36,37] related to plaintext inadequately. For security purposes, in our scheme, both permutation operation and diffusion operation are related to plain images, which can achieve high plaintext sensitivity to chosen/known plaintext attack efficiently.
- (3)
- Different from most chaotic based image cryptosystems in [4,5,6,7,9,10,12,16,19,28,29,31,36], in which the permutation–diffusion operation is performed several times to obtain the desired security level, the plaintext related permutation and diffusion in our scheme is only performed a single time in the entire encryption process.
- (4)
- Complete simulations are given and the simulation results prove an excellent performance in security and efficiency.
2. Related Work
2.1. Extended Arnold Map
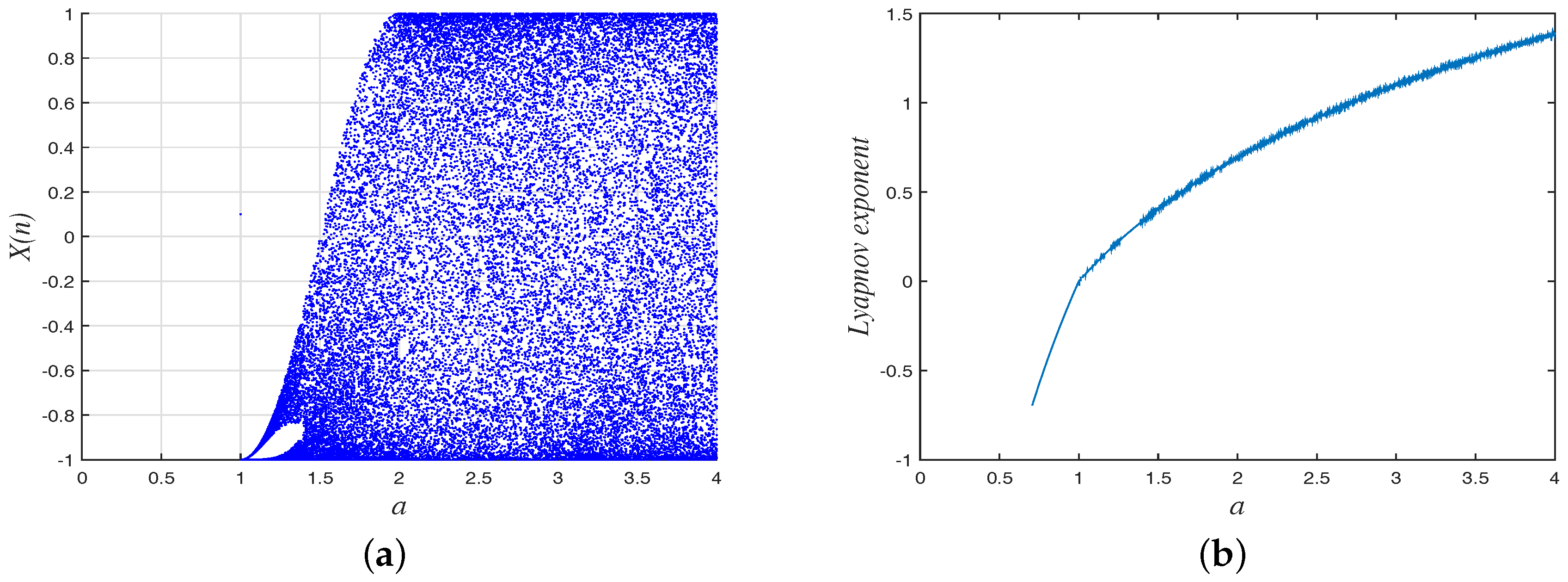
2.2. Chebyshev Map
3. Algorithm of Image Encryption
3.1. Secret Key Formulation
3.2. Encryption Process
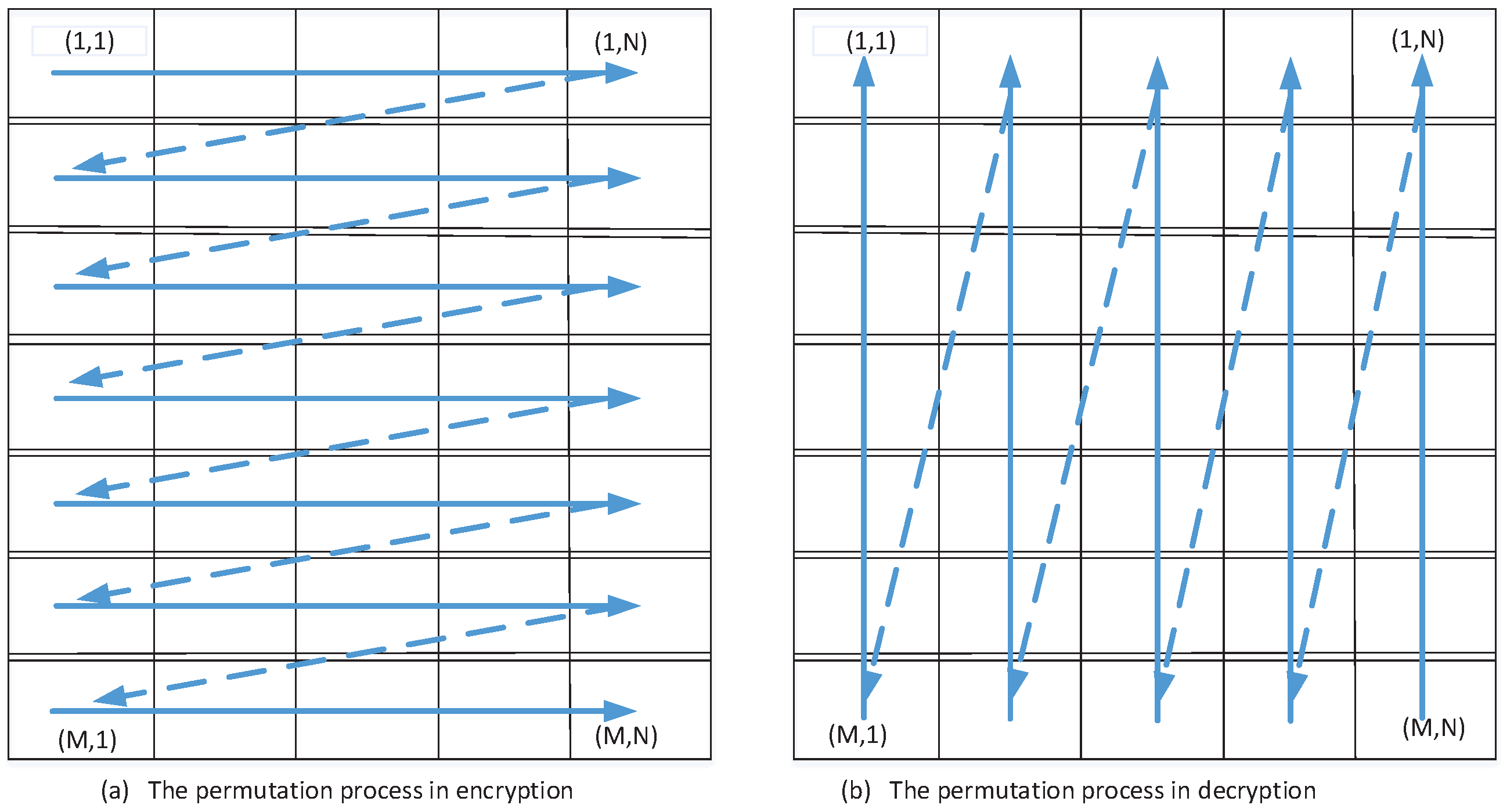
3.2.1. Permutation Stage
3.2.2. Diffusion Stage
3.3. Decryption Process
4. Experimental Results and Security Analysis
4.1. Security Key Space
4.2. Histogram Analysis
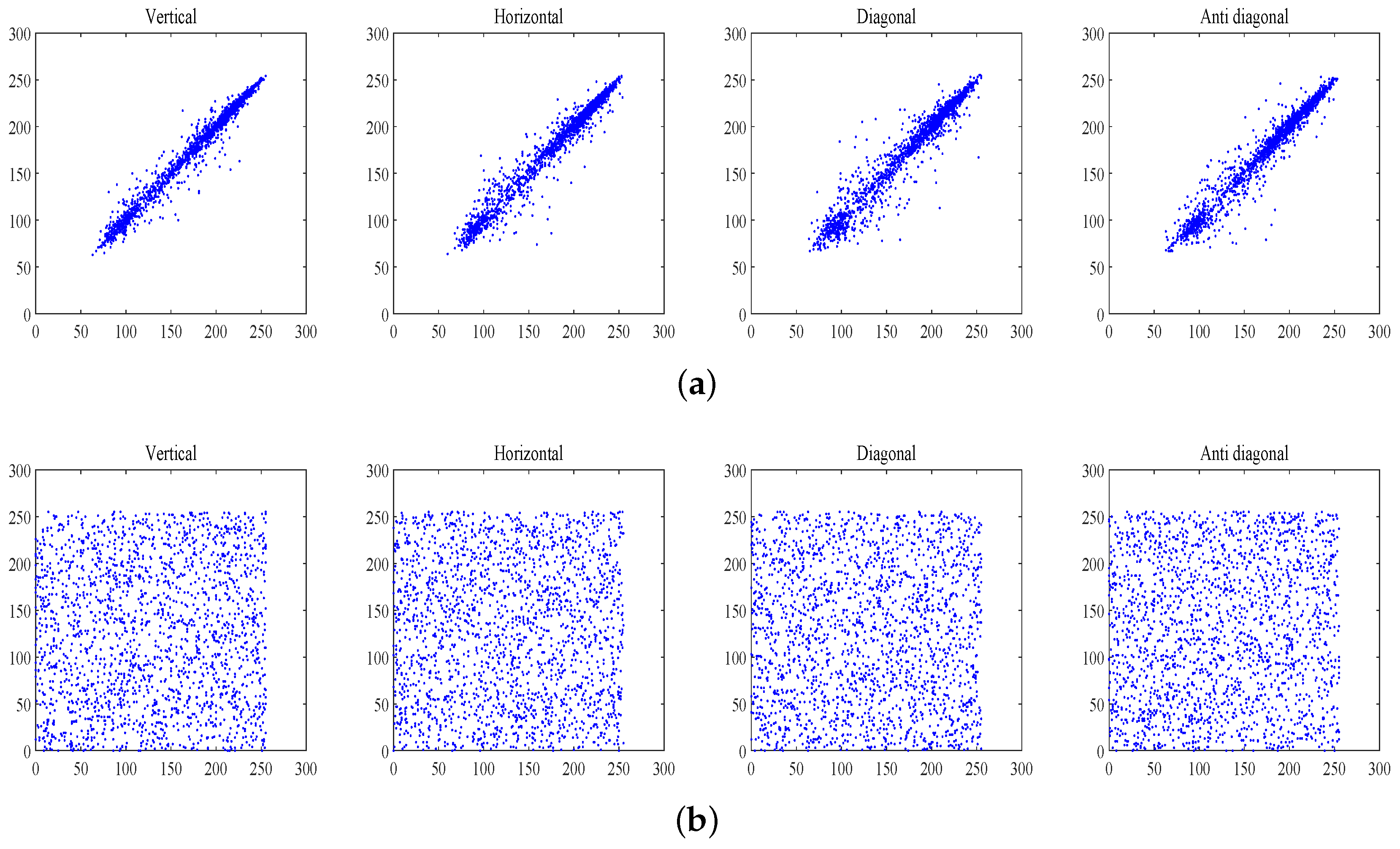
4.3. Correlation Analysis
4.4. Sensitivity Analysis
4.5. Known and Chosen Plaintext Analysis
4.6. Robustness against Noise and Occlusion Attacks
4.7. Information Entropy
4.8. Encryption Speed Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ye, G. Image scrambling encryption algorithm of pixel bit based on chaos map. Pattern Recognit. Lett. 2010, 31, 347–354. [Google Scholar] [CrossRef]
- Fu, C.; Lin, B.; Miao, Y.; Liu, X.; Chen, J. A novel chaos-based bit-level permutation scheme for digital image encryption. Opt. Commun. 2011, 284, 5415–5423. [Google Scholar] [CrossRef]
- Fridrich, J. Symmetric ciphers based on two-dimensional chaotic maps. Int. J. Bifurc. Chaos 1998, 8, 1259–1284. [Google Scholar] [CrossRef]
- Zhang, W.; Wong, K.W.; Yu, H.; Zhu, Z.L. A symmetric color image encryption algorithm using the intrinsic features of bit distributions. Commun. Nonlinear Sci. Numer Simul. 2013, 18, 584–600. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Wang, X.Y. A new image encryption algorithm based on non-adjacent coupled map lattices. Appl. Soft Comput. 2015, 26, 10–20. [Google Scholar] [CrossRef]
- Zhou, G.; Zhang, D.; Liu, Y.; Yuan, Y.; Liu, Q. A novel image encryption algorithm based on chaos and Line map. Neurocomputing 2015, 169, 150–157. [Google Scholar] [CrossRef]
- Zhang, W.; Yu, H.; Zhao, Y.L.; Zhu, Z.L. Image encryption based on three-dimensional bit matrix permutation. Signal Process. 2016, 118, 36–50. [Google Scholar] [CrossRef]
- Chai, X. An image encryption algorithm based on bit level Brownian motion and new chaotic systems. Multimed. Tools Appl. 2017, 76, 1159–1175. [Google Scholar] [CrossRef]
- Huang, X. Image encryption algorithm using chaotic Chebyshev generator. Nonlinear Dyn. 2012, 67, 2411–2417. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, Z.; Fu, C.; Zhang, L.; Zhang, Y. An efficient image encryption scheme using lookup table-based confusion and diffusion. Signal Process. 2015, 81, 1151–1166. [Google Scholar] [CrossRef]
- Tong, X.J.; Zhang, M.; Wang, Z.; Liu, Y.; Xu, H.; Ma, J. A fast encryption algorithm of color image based on four-dimensional chaotic system. J. Vis. Commun. Image Represent. 2015, 33, 219–234. [Google Scholar] [CrossRef]
- Stoyanov, B.; Kordov, K. Image Encryption Using Chebyshev Map and Rotation Equation. Entropy 2015, 17, 2117–2139. [Google Scholar] [CrossRef]
- Stoyanov, B.; Kordov, K. Novel Image Encryption Scheme Based on Chebyshev Polynomial and Duffing Map. Sci. World J. 2014, 2014, 283639. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Tong, X.; Ma, J. Image encryption algorithm based on hyper-chaotic system and dynamic S-box. Multimed. Tools Appl. 2016, 75, 7739–7759. [Google Scholar] [CrossRef]
- Abundiz-Pérez, F.; Cruz-Hernández, C.; Murillo-Escobar, M.A.; López-Gutiérrez, R.M.; Arellano-Delgado, A. A Fingerprint Image Encryption Scheme Based on Hyperchaotic Rössler Map. Math. Probl. Eng. 2016, 2016, 2670494. [Google Scholar] [CrossRef]
- Liu, L.; Miao, S. A new image encryption algorithm based on logistic chaotic map with varying parameter. Springerplus 2016, 5, 289. [Google Scholar] [CrossRef] [PubMed]
- Zahmoul, R.; Ejbali, R.; Zaied, M. Image encryption based on new Beta chaotic maps. Opt. Lasers Eng. 2017, 96, 39–49. [Google Scholar] [CrossRef]
- Pak, C.; Huang, L. A new color image encryption using combination of the 1d chaotic map. Signal Process. 2017, 138, 129–137. [Google Scholar] [CrossRef]
- Enayatifar, R.; Abdullah, A.H.; Isnin, I.F.; Altameem, A.; Lee, M. Image encryption using a synchronous permutation–diffusion technique. Opt. Lasers Eng. 2017, 90, 146–154. [Google Scholar] [CrossRef]
- Li, C.; Lin, D.; Lü, J. Cryptanalyzing an Image-Scrambling Encryption Algorithm of Pixel Bits. IEEE MultiMedia 2017, 24, 64–71. [Google Scholar] [CrossRef]
- Hoang, T.M.; Thanh, H.X. Cryptanalysis and security improvement for a symmetric color image encryption algorithm. Optik 2018, 155, 366–383. [Google Scholar] [CrossRef]
- Chen, L.; Ma, B.; Zhao, X.; Wang, S. Differential cryptanalysis of a novel image encryption algorithm based on chaos and Line map. Nonlinear Dyn. 2016, 84, 1–11. [Google Scholar] [CrossRef]
- Wu, J.; Liao, X.; Yang, B. Cryptanalysis and Enhancements of Image Encryption Based on Three-dimensional Bit Matrix Permutation. Signal Process. 2018, 142, 292–300. [Google Scholar] [CrossRef]
- Wang, X.; Luan, D.; Bao, X. Cryptanalysis of an image encryption algorithm using Chebyshev generator. Digit. Signal Process. 2014, 25, 244–247. [Google Scholar] [CrossRef]
- Hu, G.; Xiao, D.; Wang, Y.; Li, X. Cryptanalysis of a chaotic image cipher using Latin square-based confusion and diffusion. Nonlinear Dyn. 2017, 88, 1305–1316. [Google Scholar] [CrossRef]
- Zhang, X.; Nie, W.; Ma, Y.; Tian, Q. Cryptanalysis and improvement of an image encryption algorithm based on hyper-chaotic system and dynamic S-box. Multimed. Tools Appl. 2017, 76, 1–19. [Google Scholar] [CrossRef]
- Wang, H.; Xiao, D.; Chen, X.; Huang, H. Cryptanalysis and Enhancements of Image Encryption Using Combination of the 1D Chaotic Map. Signal Process. 2018, 144, 444–452. [Google Scholar] [CrossRef]
- Mollaeefar, M.; Sharif, A.; Nazari, M. A novel encryption scheme for colored image based on high level chaotic maps. Multimedia Tools Appl. 2017, 1, 607–629. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, Y. A plaintext-related image encryption algorithm based on chaos. Multimed. Tools Appl. 2018, 77, 1–23. [Google Scholar] [CrossRef]
- Liu, L.; Chen, Y.; Ye, R. A Plain Image Dependent Image Encryption Scheme Using Half Pixel Level Interchange Permutation Operation. Int. J. Netw. Secur. Appl. 2017, 9, 57–75. [Google Scholar] [CrossRef]
- Ye, G.; Huang, X. An efficient symmetric image encryption algorithm based on an intertwining logistic map. Neurocomputing 2017, 251, 45–53. [Google Scholar] [CrossRef]
- Cai, S.; Huang, L.; Chen, X.; Xiong, X. A Symmetric Plaintext-Related Color Image Encryption System Based on Bit Permutation. Entropy 2018, 20, 282. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, S.; Chang, Y.; Li, X. A novel image encryption scheme based on an improper fractional-order chaotic system. Nonlinear Dyn. 2015, 80, 1721–1729. [Google Scholar] [CrossRef]
- Murillo-Escobar, M.A.; Cruz-Hernández, C.; Abundiz-Pérez, F.; López-Gutiérrez, R.M.; Campo, O.R.A.D. A rgb image encryption algorithm based on total plain image characteristics and chaos. Signal Process. 2015, 109, 119–131. [Google Scholar] [CrossRef]
- Parvin, Z.; Seyedarabi, H.; Shamsi, M. A new secure and sensitive image encryption scheme based on new substitution with chaotic function. Multimed. Tools Appl. 2016, 75, 10631–10648. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, B.; Hu, Y.; Ran, Y. A novel color image encryption scheme using rectangular transform-enhanced chaotic tent maps. IEEE Access 2017, 5, 6429–6436. [Google Scholar] [CrossRef]
- Li, L.; Yao, Y.; Chang, X. Plaintext-dependent selective image encryption scheme based on chaotic maps and DNA coding. In Proceedings of the 2017 International Conference on Dependable Systems and Their Applications (DSA), Beijing, China, 31 October–2 November 2017; pp. 57–65. [Google Scholar] [CrossRef]
- Luo, Y.; Zhou, R.; Liu, J.; Qiu, S.; Cao, Y. An efficient and self-adapting colour-image encryption algorithm based on chaos and interactions among multiple layers. Multimed. Tools Appl. 2018, 1–27. [Google Scholar] [CrossRef]
- Norouzi, B.; Mirzakuchaki, S. Breaking a novel image encryption scheme based on an improper fractional order chaotic system. Multimed. Tools Appl. 2017, 76, 1817–1826. [Google Scholar] [CrossRef]
- Fan, H.; Li, M.; Liu, D.; An, K. Cryptanalysis of a plaintext-related chaotic RGB image encryption scheme using total plain image characteristics. Multimed. Tools Appl. 2017, 4, 1–25. [Google Scholar] [CrossRef]
- Norouzi, B.; Mirzakuchaki, S. Breaking an image encryption algorithm based on the new substitution stage with chaotic functions. Optik 2016, 127, 5695–5701. [Google Scholar] [CrossRef]
- Yue, W.; Noonan, J.P.; Agaian, S. NPCR and UACI Randomness Tests for Image Encryption. Cyber J. J. Sel. Areas Telecommun. 2011, 2, 31–38. [Google Scholar]
- Huynh-The, T.; Banos, O.; Lee, S.; Yoon, Y.; Le-Tien, T. Improving digital image watermarking by means of optimal channel selection. Expert Syst. Appl. 2016, 62, 177–189. [Google Scholar] [CrossRef]
- Huynh-The, T.; Hua, C.H.; Tu, N.A.; Hur, T.; Bang, J.; Kim, D.; Amin, M.B.; Kang, B.H.; Seung, H.; Lee, S. Selective Bit Embedding Scheme For Robust Blind Color Image Watermarking. Inf. Sci. 2018, 426, 1–18. [Google Scholar] [CrossRef]






| Cryptosystems | Attacked by | Attack Approaches |
|---|---|---|
| Zhang et al. (2013) [4] | Hoang et al. (2018) [21] | chosen ciphertext |
| Zhou et al. (2015) [6] | Chen et al. (2017) [22] | Differential |
| Zhang et al. (2016) [7] | Wu et al. (2018) [23] | chosen plaintext |
| Huang et al. (2012) [9] | Wang et al. (2014) [24] | chosen plaintext |
| Chen et al. (2015) [10] | Hu et al. (2017) [25] | chosen plaintext and ciphertext |
| Liu et al. (2016) [14] | Zhang et al. (2017) [26] | chosen plaintext |
| Pak et al. (2017) [18] | Wang et al. (2018) [27] | chosen plaintext |
| Image | Lena | Baboon | Flower | Fruits | Yacht | Girl | Flowers |
|---|---|---|---|---|---|---|---|
| Variance | 898.25 | 1017.29 | 1095.71 | 899.87 | 917.07 | 1413.86 | 783.00 |
| Image | Original-Image | Encrypted-Image | |||||||
|---|---|---|---|---|---|---|---|---|---|
| V | H | D | A | V | H | D | A | ||
| Lena | R | 0.9798 | 0.9893 | 0.9777 | 0.9697 | 0.0003 | 0.0040 | 0.0013 | 0.0021 |
| G | 0.9689 | 0.9824 | 0.9653 | 0.9554 | −0.0018 | 0.0005 | 0.0002 | 0.0009 | |
| B | 0.9325 | 0.9574 | 0.9253 | 0.9181 | 0.0019 | −0.0093 | 0.0002 | 0.0005 | |
| baboon | R | 0.9231 | 0.8660 | 0.8519 | 0.8543 | 0.0002 | 0.0019 | −0.0005 | 0.0022 |
| G | 0.8654 | 0.7650 | 0.7249 | 0.7348 | −0.0019 | −0.0046 | 0.0040 | 0.0010 | |
| B | 0.9072 | 0.8808 | 0.8424 | 0.8398 | −0.0039 | −0.0062 | 0.0013 | 0.0020 | |
| fruits | R | 0.9936 | 0.9928 | 0.9897 | 0.9868 | −0.0022 | −0.0021 | −0.0027 | 0.0010 |
| G | 0.9855 | 0.9848 | 0.9783 | 0.9694 | 0.0069 | 0.0073 | 0.0021 | −0.0016 | |
| B | 0.9265 | 0.9192 | 0.8809 | 0.8531 | 0.0007 | 0.0088 | −0.0003 | −0.0010 | |
| flowers | R | 0.9718 | 0.9719 | 0.9504 | 0.9551 | 0.0045 | −0.0002 | −0.0005 | 0.0007 |
| G | 0.9510 | 0.9497 | 0.9123 | 0.9218 | 0.0047 | −0.0015 | 0.0026 | 0.0022 | |
| B | 0.9527 | 0.9527 | 0.9178 | 0.9256 | 0.0004 | −0.0032 | 0.0019 | −0.0008 | |
| Direction | Original Image | Our Scheme | Ref. [11] | Ref. [18] | Ref. [28] | Ref. [32] | Ref. [36] |
|---|---|---|---|---|---|---|---|
| Horizontal | 0.9853 | 0.0003 | 0.0013 | −0.0038 | −0.0031 | 0.0046 | 0.0005 |
| Vertical | 0.9753 | 0.0040 | 0.0034 | −0.0026 | 0.0025 | −0.0028 | −0.0070 |
| Diagonal | 0.9734 | 0.0013 | 0.0072 | 0.0017 | −0.0001 | 0.0014 | 0.0006 |
| Image | NPCR (99.6094) | UACI (33.4635) | |||||
|---|---|---|---|---|---|---|---|
| R | G | B | R | G | B | ||
| Lena | 99.6089 | 99.6089 | 99.6085 | 33.4589 | 33.4598 | 33.4624 | |
| 99.6092 | 99.6075 | 99.6095 | 33.4615 | 33.4676 | 33.4624 | ||
| 99.6082 | 99.6101 | 99.6087 | 33.4626 | 33.4670 | 33.4686 | ||
| 99.6087 | 99.6094 | 99.6098 | 33.4609 | 33.4623 | 33.4628 | ||
| 99.6090 | 99.6091 | 99.6090 | 33.4662 | 33.4619 | 33.4684 | ||
| baboon | 99.6086 | 99.6096 | 99.6106 | 33.4639 | 33.4621 | 33.4641 | |
| 99.6107 | 99.6089 | 99.6093 | 33.4641 | 33.4651 | 33.4696 | ||
| 99.6083 | 99.6103 | 99.6093 | 33.4685 | 33.4653 | 33.4620 | ||
| 99.6087 | 99.6112 | 99.6087 | 33.4616 | 33.4636 | 33.4593 | ||
| 99.6096 | 99.6090 | 99.6087 | 33.4686 | 33.4645 | 33.4662 | ||
| Image | NPCR (99.6094) | UACI (33.4635) | ||||
|---|---|---|---|---|---|---|
| R | G | B | R | G | B | |
| Lena | 99.6091 | 99.6099 | 99.6090 | 33.4678 | 33.4577 | 33.4608 |
| baboon | 99.6111 | 99.6097 | 99.6094 | 33.4617 | 33.4680 | 33.4617 |
| fruits | 99.6091 | 99.6081 | 99.6091 | 33.4631 | 33.4663 | 33.4593 |
| Girl | 99.6090 | 99.6100 | 99.6095 | 33.4627 | 33.4597 | 33.4588 |
| Flower | 99.6113 | 99.6098 | 99.6100 | 33.4603 | 33.4666 | 33.4588 |
| Yacht | 99.6092 | 99.6095 | 99.6099 | 33.4613 | 33.4666 | 33.4651 |
| Lena in Ref. [11] | 99.6892 | 99.6943 | 99.6922 | 33.3256 | 33.3324 | 33.3313 |
| Lena in Ref. [18] | 99.6552 | 99.6277 | 99.5882 | 33.4846 | 33.4132 | 33.3441 |
| Lena in Ref. [28] | 99.6917 | 99.6887 | 99.6704 | 33.5418 | 33.5327 | 33.5164 |
| Lena in Ref. [32] | 99.6086 | 99.6083 | 99.6104 | 33.4709 | 33.4683 | 33.4682 |
| Theoretically NPCR Critical Value [42] | |||
| Tested Image Size | NPCR Test Results | ||
| 0.05-level | 0.01-level | 0.001-level | |
| 512 by 512 | 4/4 | 4/4 | 4/4 |
| 256 by 256 | 4/4 | 4/4 | 4/4 |
| Theoretically UACI Critical Value [42] | |||
| Tested Image Size | UACI Test Results | ||
| 0.05-level | c0.01-level | 0.001-level | |
| 512 by 512 | 4/4 | 4/4 | 4/4 |
| 256 by 256 | 4/4 | 4/4 | 4/4 |
| Original Image | NPCR (99.6094) | UACI (33.4635) | ||||
|---|---|---|---|---|---|---|
| R | G | B | R | G | B | |
| All-black | 99.6121 | 99.6102 | 99.6105 | 33.5744 | 33.5200 | 33.3917 |
| All-white | 99.6075 | 99.6100 | 99.6100 | 33.4578 | 33.4683 | 33.4555 |
| 99.5284 | 99.4976 | 99.4469 | 33.4466 | 33.6076 | 33.3642 | |
| 99.6104 | 99.6089 | 99.6113 | 33.4254 | 33.5033 | 33.4453 | |
| Noise Attacks or Date Loss | MSE (Proposed) | PSNR (Proposed) | MSE (Ref. [35]) | PSNR (Ref. [35]) |
|---|---|---|---|---|
| Salt & peppers noise (density 0.05) | 734.3922 | 19.4715 | 869.8890 | 18.7362 |
| Salt & pepper noise (density 0.1) | 1465.4644 | 16.4711 | 1829.6416 | 15.5071 |
| (100:220,110:230)=0 | 1729.6835 | 15.7511 | 2894.6596 | 13.5148 |
| (90:110,:)=0 | 658.2202 | 19.9471 | 1073.0810 | 17.8245 |
| (100:240,:)=0 | 4335.8104 | 11.7601 | 6813.5770 | 9.7971 |
| (:,100:120)=0 | 632.5614 | 20.1198 | 946.0235 | 18.3718 |
| Image | Plain-Image | Encrypted Image | ||||
|---|---|---|---|---|---|---|
| R | G | B | R | G | B | |
| Lena | 7.2531 | 7.5952 | 6.9686 | 7.9993 | 7.9994 | 7.9994 |
| baboon | 7.7067 | 7.4753 | 7.7522 | 7.9993 | 7.9993 | 7.9993 |
| fruits | 7.5172 | 7.3230 | 6.7785 | 7.9991 | 7.9993 | 7.9991 |
| flower | 7.4428 | 7.4062 | 7.3371 | 7.9993 | 7.9994 | 7.9994 |
| Girl | 7.4346 | 7.2354 | 7.0578 | 7.9996 | 7.9995 | 7.9995 |
| Yacht | 7.6071 | 7.4062 | 7.3371 | 7.9993 | 7.9993 | 7.9991 |
| Lena in Ref. [11] | 7.2531 | 7.5952 | 6.9686 | 7.9996 | 7.9997 | 7.9997 |
| Lena in Ref. [28] | 7.2531 | 7.5952 | 6.9686 | 7.9972 | 7.9972 | 7.9976 |
| Lena in Ref. [32] | 7.2531 | 7.5952 | 6.9686 | 7.9992 | 7.9993 | 7.9994 |
| Image Size | Proposed Method | Ref. [28] (2015) | Ref. [32] (2018) | Ref. [36] (2017) | Ref. [38] (2017) |
|---|---|---|---|---|---|
| 4.4113 | 3.0080 | 4.6058 | 14.8119 | 21.1786 | |
| 1.0896 | 0.6650 | 1.1347 | 3.6175 | 4.7795 |
| Scheme | ET in MBps | Number of Cycles Per Byte |
|---|---|---|
| Proposed | 0.170 | 19634.47 |
| Mollaeefar et al. (2015) Ref. [28] | 0.249 | 13405.06 |
| Cai et al. (2018) Ref. [32] | 0.165 | 20229.45 |
| Wu et al. (2018) Ref. [36] | 0.050 | 66757.20 |
| Luo et al. (2017) Ref. [38] | 0.035 | 95367.43 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, L.; Cai, S.; Xiao, M.; Xiong, X. A Simple Chaotic Map-Based Image Encryption System Using Both Plaintext Related Permutation and Diffusion. Entropy 2018, 20, 535. https://doi.org/10.3390/e20070535
Huang L, Cai S, Xiao M, Xiong X. A Simple Chaotic Map-Based Image Encryption System Using Both Plaintext Related Permutation and Diffusion. Entropy. 2018; 20(7):535. https://doi.org/10.3390/e20070535
Chicago/Turabian StyleHuang, Linqing, Shuting Cai, Mingqing Xiao, and Xiaoming Xiong. 2018. "A Simple Chaotic Map-Based Image Encryption System Using Both Plaintext Related Permutation and Diffusion" Entropy 20, no. 7: 535. https://doi.org/10.3390/e20070535
APA StyleHuang, L., Cai, S., Xiao, M., & Xiong, X. (2018). A Simple Chaotic Map-Based Image Encryption System Using Both Plaintext Related Permutation and Diffusion. Entropy, 20(7), 535. https://doi.org/10.3390/e20070535





