On Chaos in the Fractional-Order Discrete-Time Unified System and Its Control Synchronization
Abstract
1. Introduction
2. Results
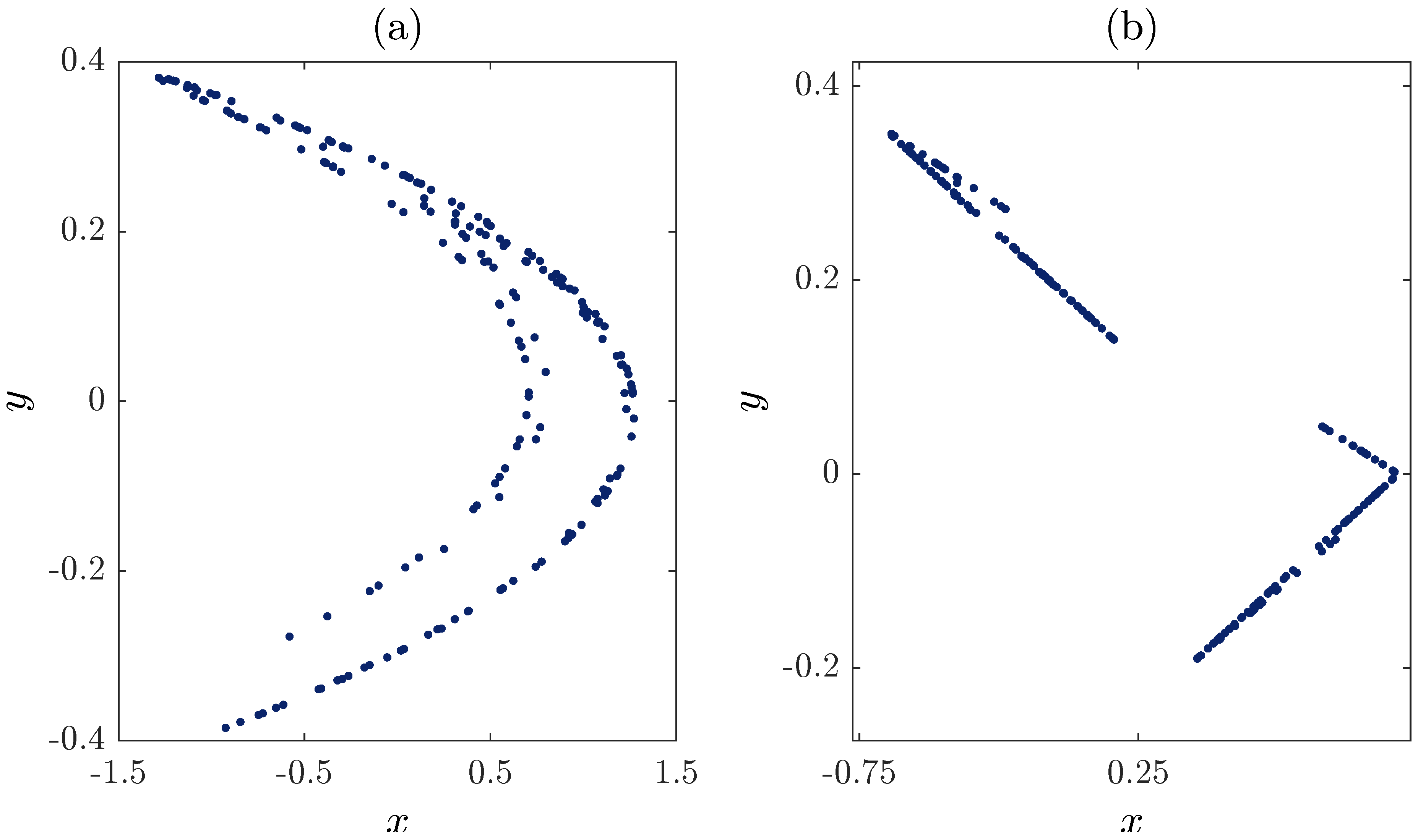
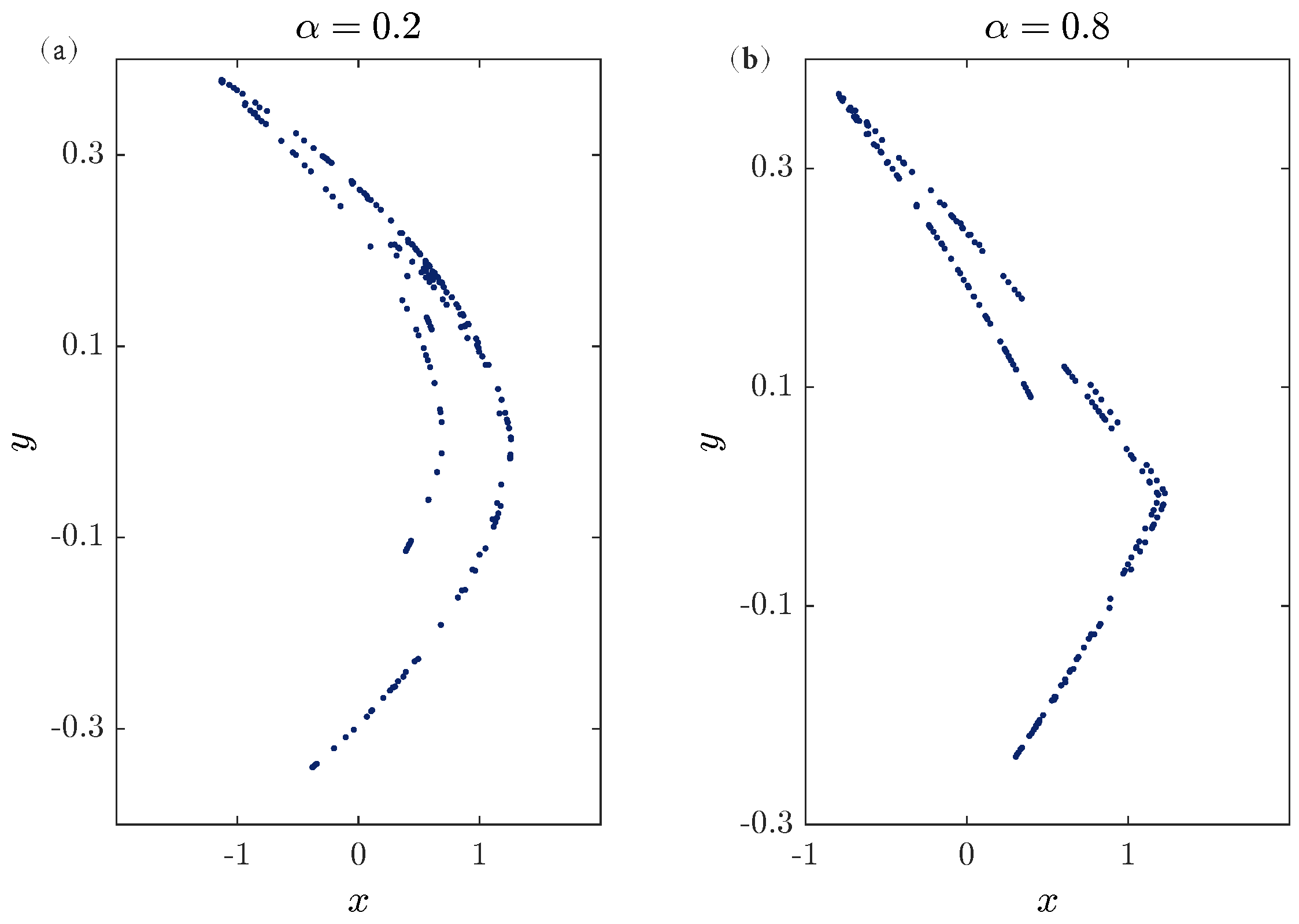
2.1. Chaos in the Fractional-Order Unified Map
2.2. Control of the Fractional-Order Unified Map
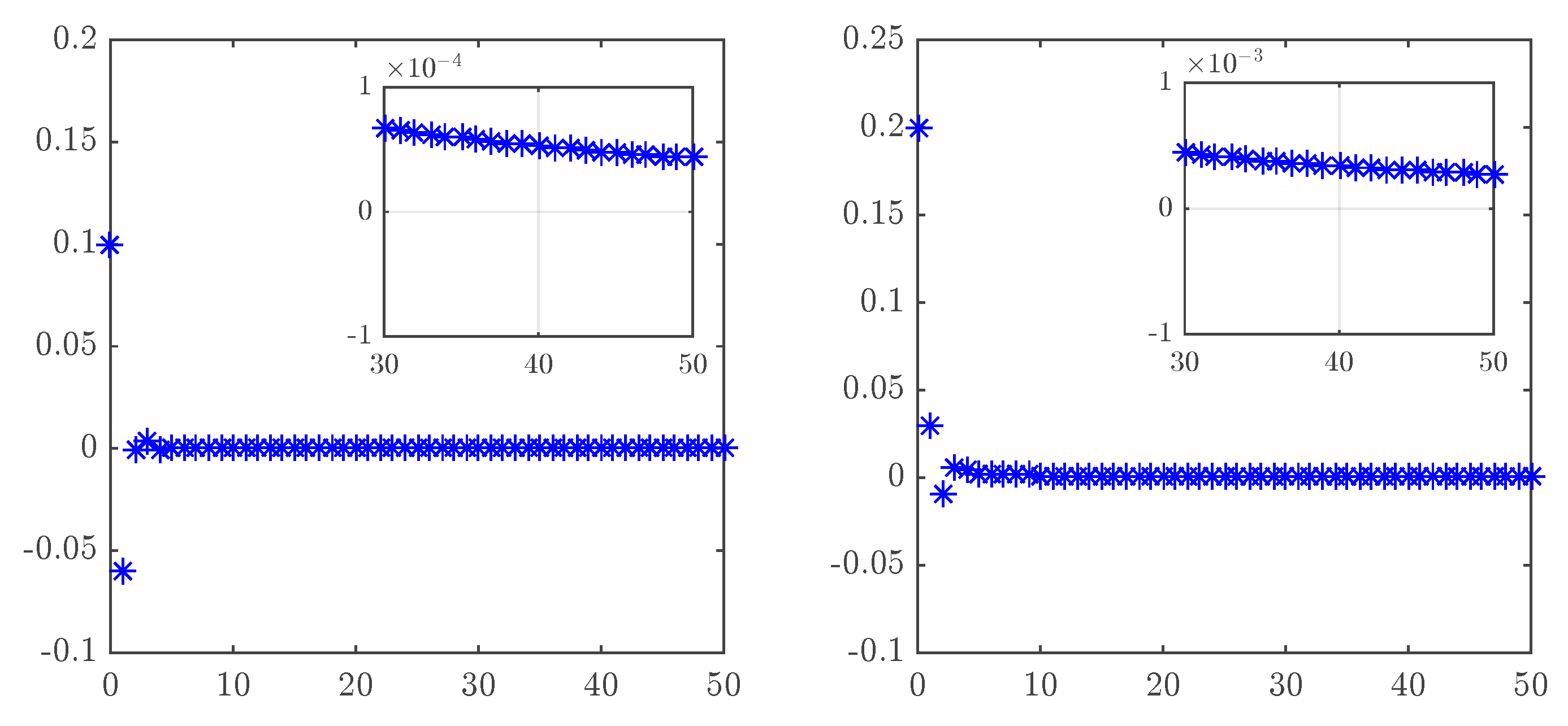
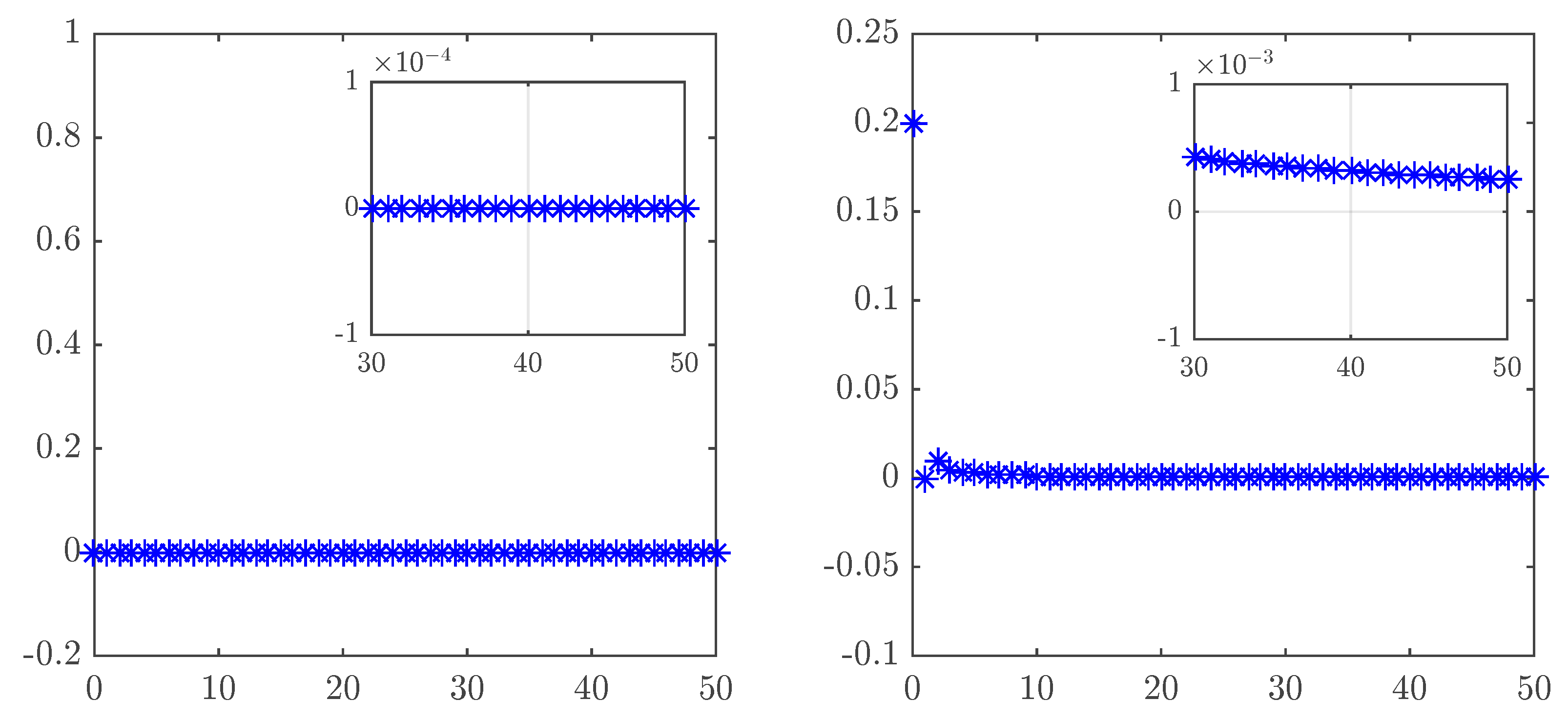
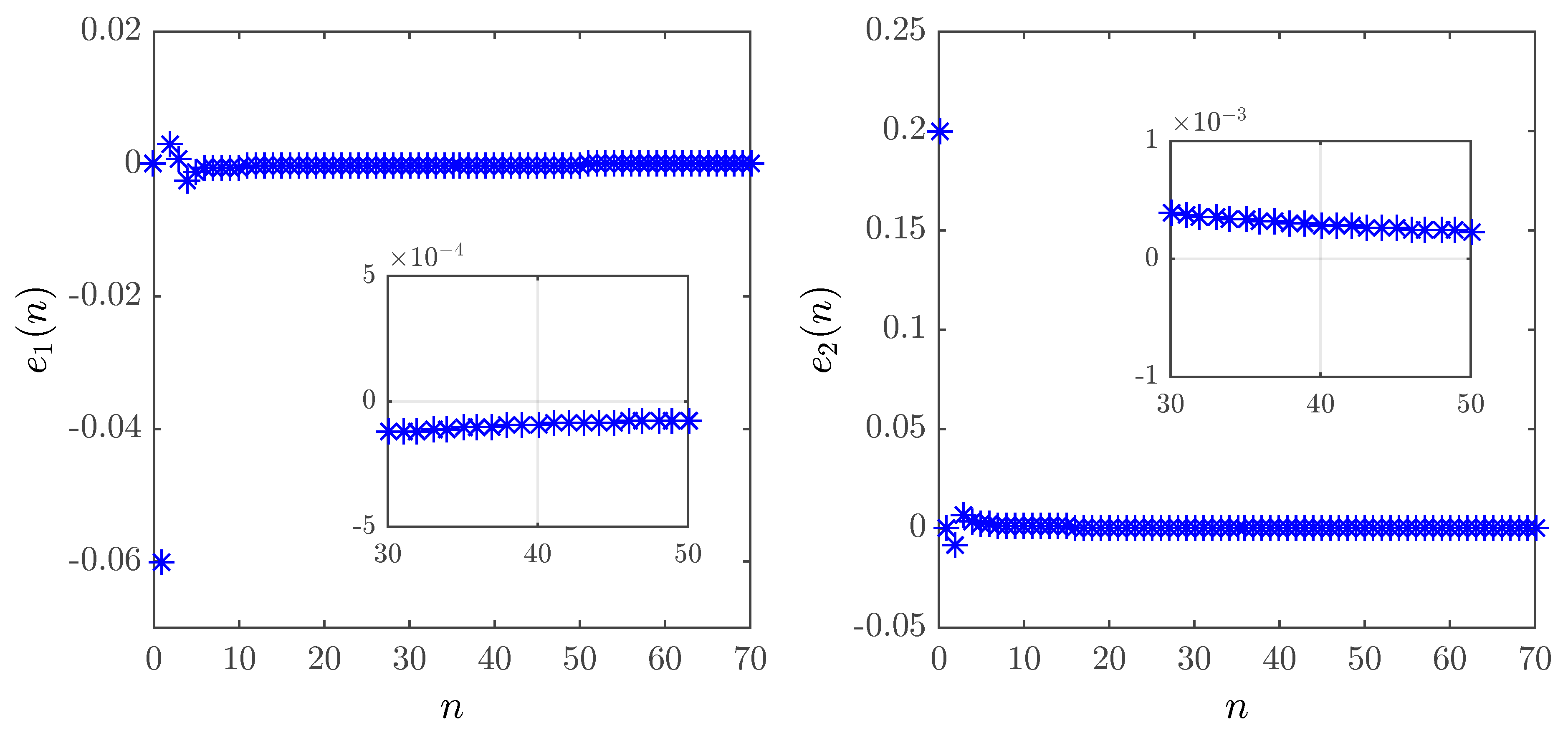
2.3. Synchronization
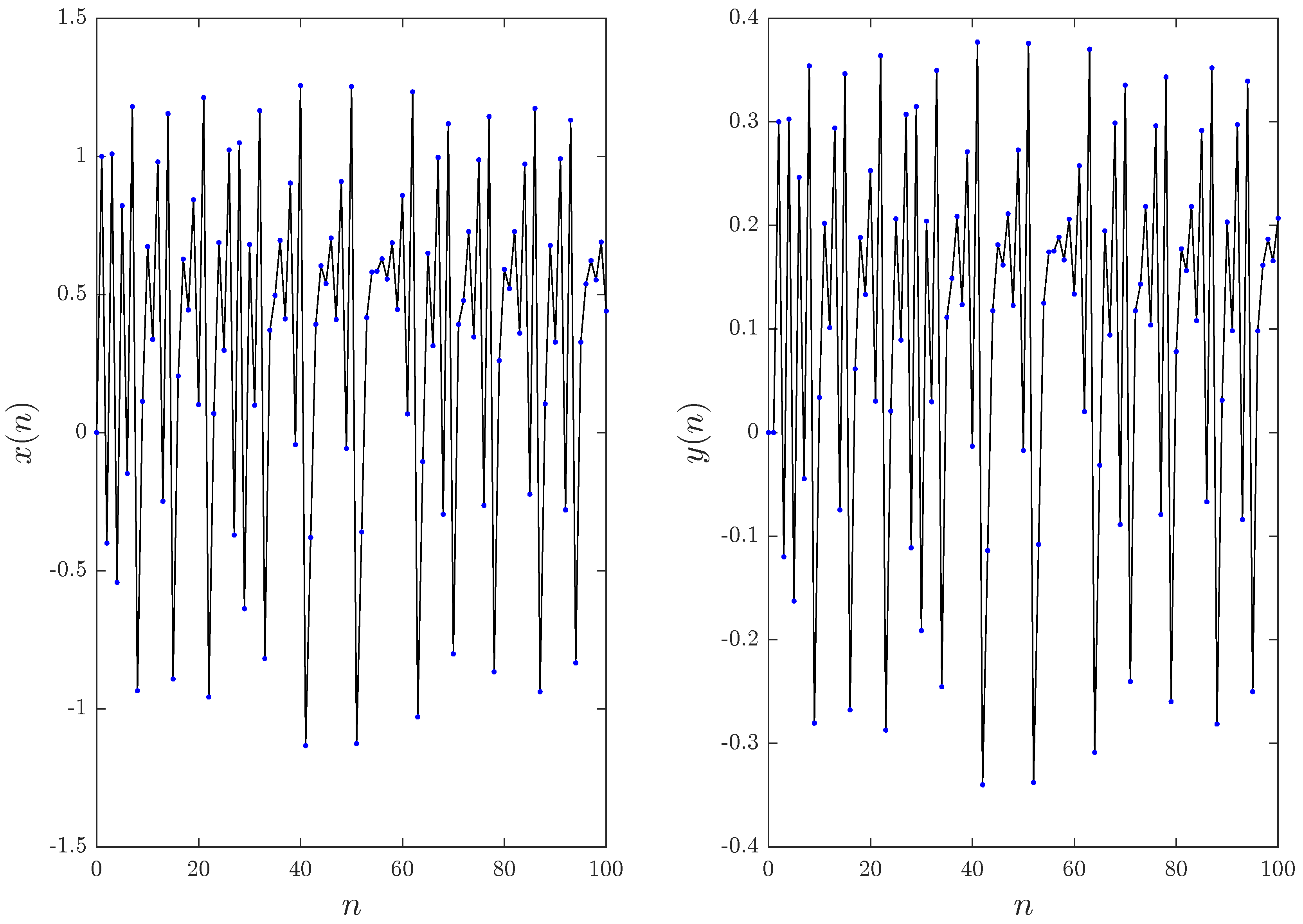
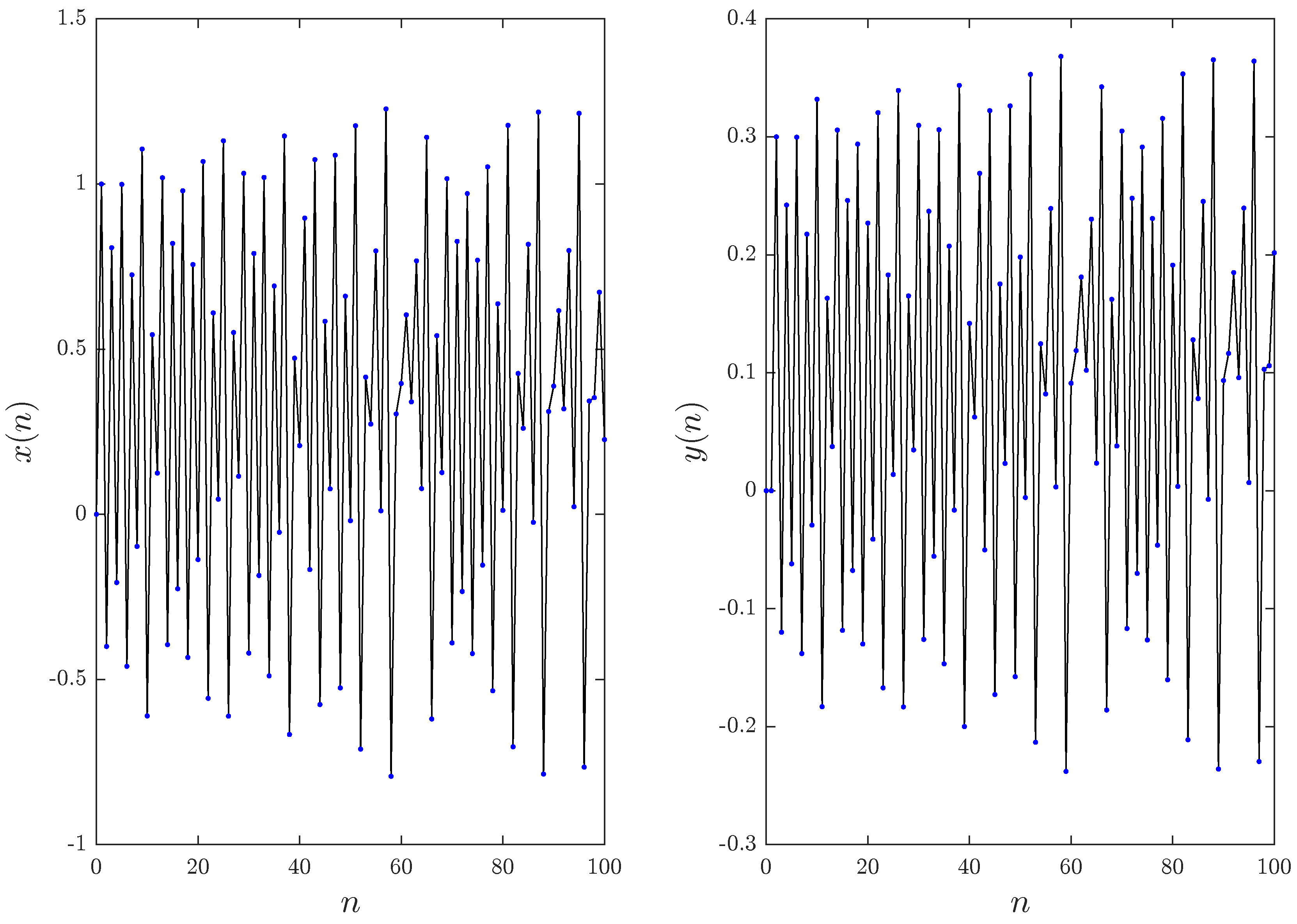
2.3.1. Synchronization of Identical Fractional Unified Maps
2.3.2. Synchronization of Different Fractional Unified Maps
3. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Hénon, M. A two-dimensional mapping with a strange attractor. Comms. Math. Phys. 1976, 50, 69–77. [Google Scholar] [CrossRef]
- Lozi, R. Un atracteur étrange du type attracteur de Hénon. J. Phys. 1978, 39, 9–10. [Google Scholar]
- Hitzl, D.L.; Zele, F. An exploration of the Hénon quadratic map. Phys. D Nonlinear Phenom. 1985, 14, 305–326. [Google Scholar] [CrossRef]
- Baier, G.G.; Sahle, S. Design of hyperchaotic flows. Phys. Rev. E 1995, 51, 2712–2714. [Google Scholar] [CrossRef]
- Stefanski, K. Modelling chaos and hyperchaos with 3D maps. Chaos Solitons Fractals 1998, 9, 83–93. [Google Scholar] [CrossRef]
- Itoh, M.; Yang, T.; Chua, L.O. Conditions for impulsive synchronization of chaotic and hyperchaotic systems. Int. J. Bifurcation Chaos Appl. Sci. Eng. 2001, 11, 551–558. [Google Scholar] [CrossRef]
- Wang, X.Y. Chaos in Complex Nonlinear Systems; Publishing House of Electronics Industry: Beijing, China, 2003. [Google Scholar]
- Zeraoulia, E.; Sprott, J.C. A unified piecewise smooth chaotic mapping that contains the Hénon and the Lozi systems. Ann. Rev. Chaos Theory Bifurcations Dyn. Syst. 2012, 1, 50–60. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Associated Press: New York, NY, USA, 1999. [Google Scholar]
- Diaz, J.B.; Olser, T.J. Differences of fractional order. Math. Comput. 1974, 28, 185–202. [Google Scholar] [CrossRef]
- Atici, F.M.; Eloe, P.W. Discrete fractional calculus with the nabla operator. Electron. J. Qual. Theory Differ. Equ. Spec. Ed. I 2009, 3, 1–12. [Google Scholar] [CrossRef]
- Abdeljawad, T. On Riemann and Caputo fractional differences. Comput. Math. Appl. 2011, 62, 1602–1611. [Google Scholar]
- Abdeljawad, T.; Baleanu, D.; Jarad, F.; Agarwal, R.P. Fractional sums and differences with binomial coefficients. Discret. Dyn. Nat. Soc. 2013, 2013, 104173. [Google Scholar] [CrossRef]
- Baleanu, D.; Wu, G.; Bai, Y.; Chen, F. Stability analysis of Caputo—Like discrete fractional systems. Commun. Nonlinear Sci. Numer. Simul. 2017, 48, 520–530. [Google Scholar] [CrossRef]
- Goodrich, C.; Peterson, A.C. Discrete Fractional Calculus; Springer: New York, NY, USA, 2015. [Google Scholar]
- Wu, G.C.; Baleanu, D. Discrete fractional logistic map and its chaos. Nonlinear Dyn. 2013, 75, 283–287. [Google Scholar] [CrossRef]
- Hu, T. Discrete Chaos in Fractional Henon Map. Appl. Math. 2014, 5, 2243–2248. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D. Discrete chaos in fractional delayed logistic maps. Nonlinear Dyn. 2014, 80, 1697–1703. [Google Scholar] [CrossRef]
- Shukla, M.K.; Sharma, B.B. Investigation of chaos in fractional order generalized hyperchaotic Henon map. Int. J. Electron. Comm. 2017, 78, 265–273. [Google Scholar] [CrossRef]
- Boccaletti, S.; Grebogi, C.; Lai, Y.C.; Mancini, H.; Maza, D. The control of chaos: theory and applications. Phys. Rep. 2000, 329, 103–197. [Google Scholar] [CrossRef]
- Fradkov, A.L.; Evans, R.J.; Andrievsky, B.R. Control of chaos: Methods and applications in mechanics. Philos. Trans. A Math. Phys. Eng. Sci. 2006, 364, 2279–2307. [Google Scholar] [CrossRef] [PubMed]
- Ouannas, A.; Azar, A.T.; Abu-Saris, R. A new type of hybrid synchronization between arbitrary hyperchaotic maps. R. Int. J. Mach. Learn. Cyber. 2017, 8, 1887–1894. [Google Scholar] [CrossRef]
- Ouannas, A.; Grassi, G. A new approach to study co-existence of some synchronization types between chaotic maps with different dimensions. Nonlinear Dyn. 2016, 86, 1319–1328. [Google Scholar] [CrossRef]
- Ouannas, A.; Odibat, Z. Generalized synchronization of different dimensional chaotic dynamical systems in discrete-time. Nonlinear Dyn. 2015, 81, 765–771. [Google Scholar] [CrossRef]
- Ouannas, A. A new generalized-type of synchronization for discrete chaotic dynamical systems. J. Comp. Nonlinear Dyn. 2015, 10, 061019-5. [Google Scholar] [CrossRef]
- Ouannas, A.; Grassi, G. Inverse full state hybrid projective synchronization for chaotic maps with different dimensions. Chin. Phys. B 2016, 25, 090503-6. [Google Scholar] [CrossRef]
- Ouannas, A.; Grassi, G.; Karouma, A.; Ziar, T.; Wang, X.; Pham, V.T. New type of chaos synchronization in discrete-time systems: The F-M synchronization. Open Phys. 2018, 16, 174–182. [Google Scholar] [CrossRef]
- Ouannas, A.; Obidat, Z.; Shawagfeh, N. Universal chaos synchronization control laws for general quadratic discrete-time systems. Appl. Theor. Model. 2017, 45, 636–641. [Google Scholar] [CrossRef]
- Ouannas, A.; Odibat, Z.; Shawagfeh, N. A new Q–S synchronization results for discrete chaotic systems. Differ. Equ. Dyn. Syst. 2016. [Google Scholar] [CrossRef]
- Ouannas, A.; Al-Sawalha, M.M. A new approach to synchronize different dimensional chaotic maps using two scaling matrices. Nonlinear Dyn. Syst. Theory 2015, 15, 400–408. [Google Scholar]
- Ouannas, A.; Al-Sawalha, M.M. Synchronization of chaotic dynamical systems in discrete-time. In Advances in Chaos Theory and Intelligent Control: Studies in Fuziness and Soft Computing; Azar, A., Vaydiyanathan, S., Eds.; Springer: New York, NY, USA, 2017. [Google Scholar]
- Grassi, G.; Ouannas, A.; Pham, V.T. A general unified approach to chaos synchronization in continuous-time systems (with or without equilibrium points) as well as in discrete-time systems. Arch. Control Sci. 2018, 28, 135–154. [Google Scholar]
- Wu, G.; Baleanu, D. Chaos synchronization of the discrete fractional logistic map. Signal Process. 2014, 102, 96–99. [Google Scholar] [CrossRef]
- Wu, G.; Baleanu, D.; Xie, H.; Chen, F. Chaos synchronization of fractional chaotic maps based on the stability condition. Phys. A Stat. Mech. Its Appl. 2016, 460, 374–383. [Google Scholar] [CrossRef]
- Xin, B.; Liu, L.; Hou, G.; Ma, Y. Chaos synchronization of nonlinear fractional discrete dynamical systems via linear control. Entropy 2017, 19, 351. [Google Scholar] [CrossRef]
- Anastassiou, G.A. Principles of delta fractional calculus on time scales and inequalities. Math. Comput. Model. 2010, 52, 556–566. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Pincus, S. Approximate entropy (ApEn) as a complexity measure. Chaos Interdiscipl. J. Nonlinear Sci. 1995, 5, 110–117. [Google Scholar] [CrossRef] [PubMed]
- Xu, G.H.; Shekofteh, Y.; Akgül, A.; Li, C.B.; Panahi, S. A New Chaotic System with a Self-Excited Attractor: Entropy Measurement, Signal Encryption, and Parameter Estimation. Entropy 2018, 20, 86. [Google Scholar] [CrossRef]
- Wang, C.; Ding, Q. A new two-dimensional map with hidden attractors. Entropy 2018, 20, 322. [Google Scholar] [CrossRef]

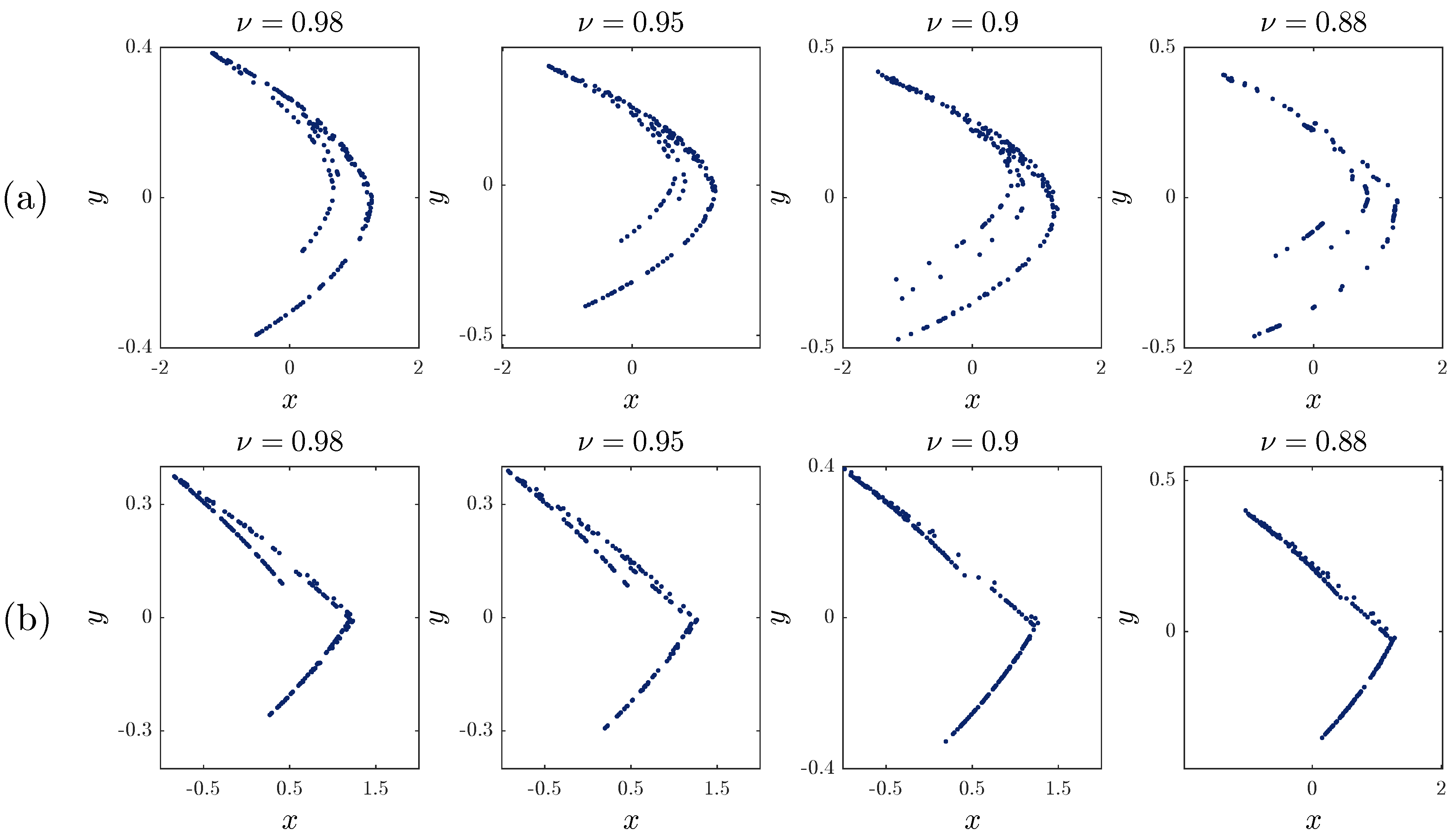
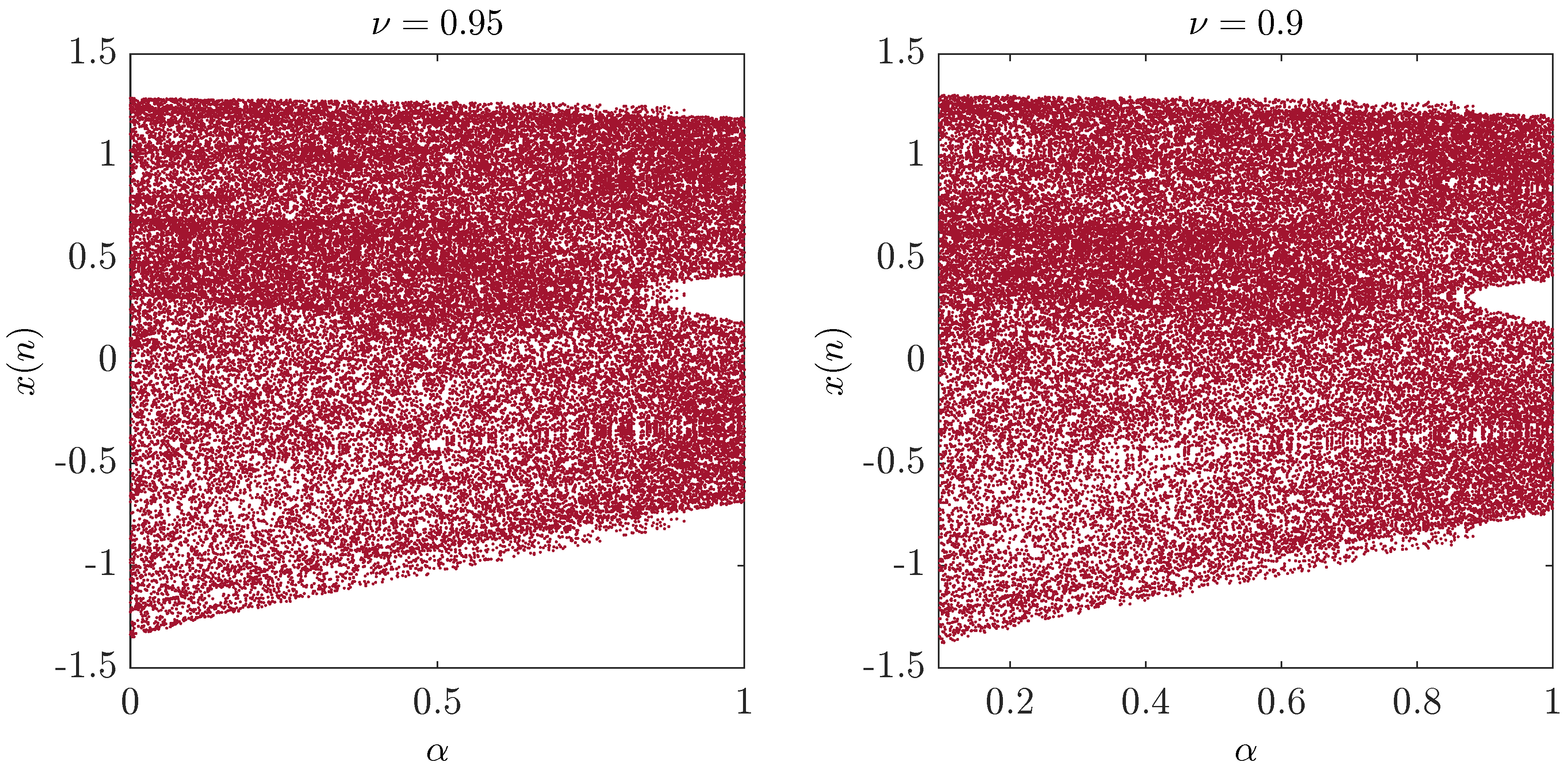
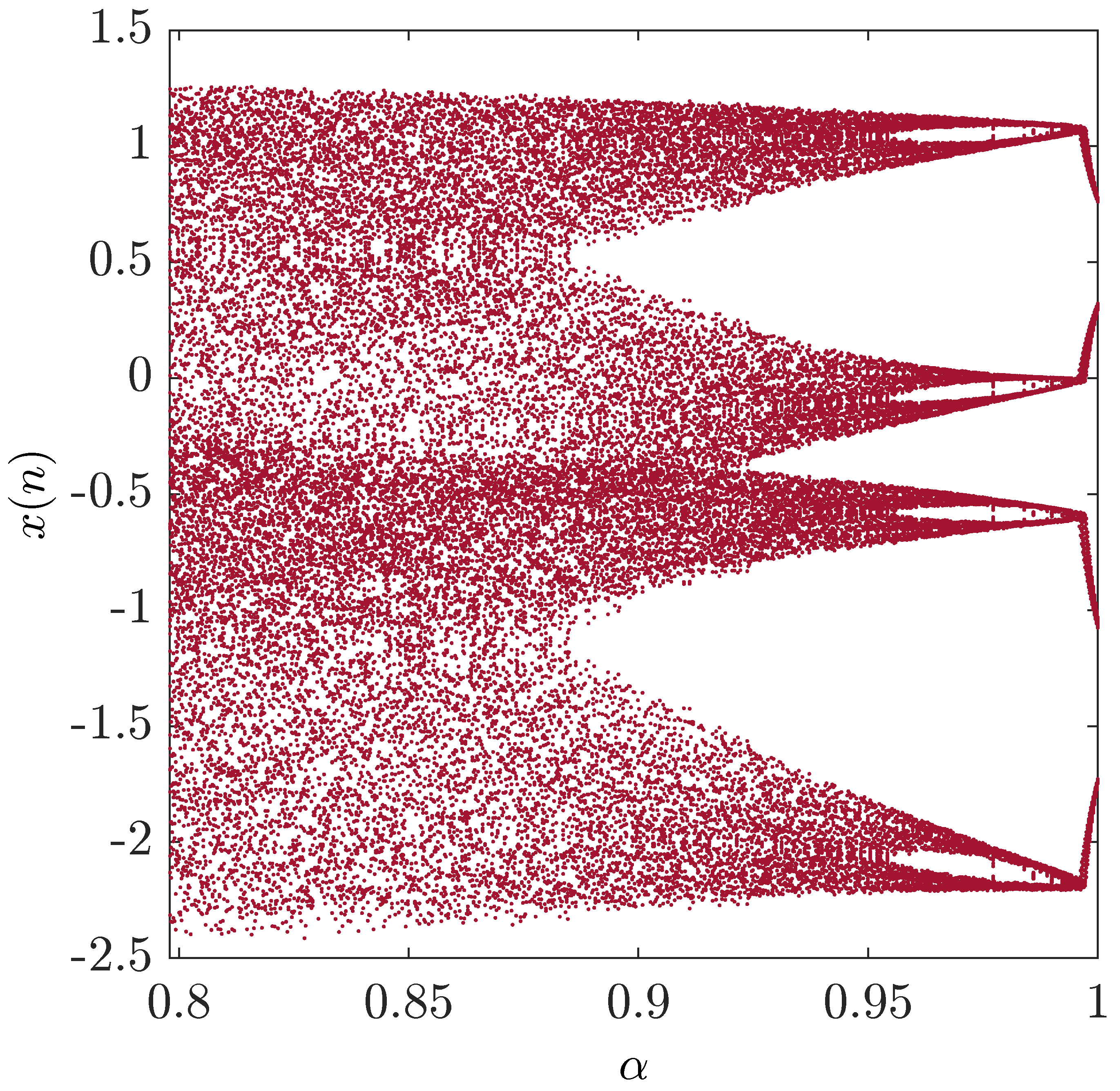
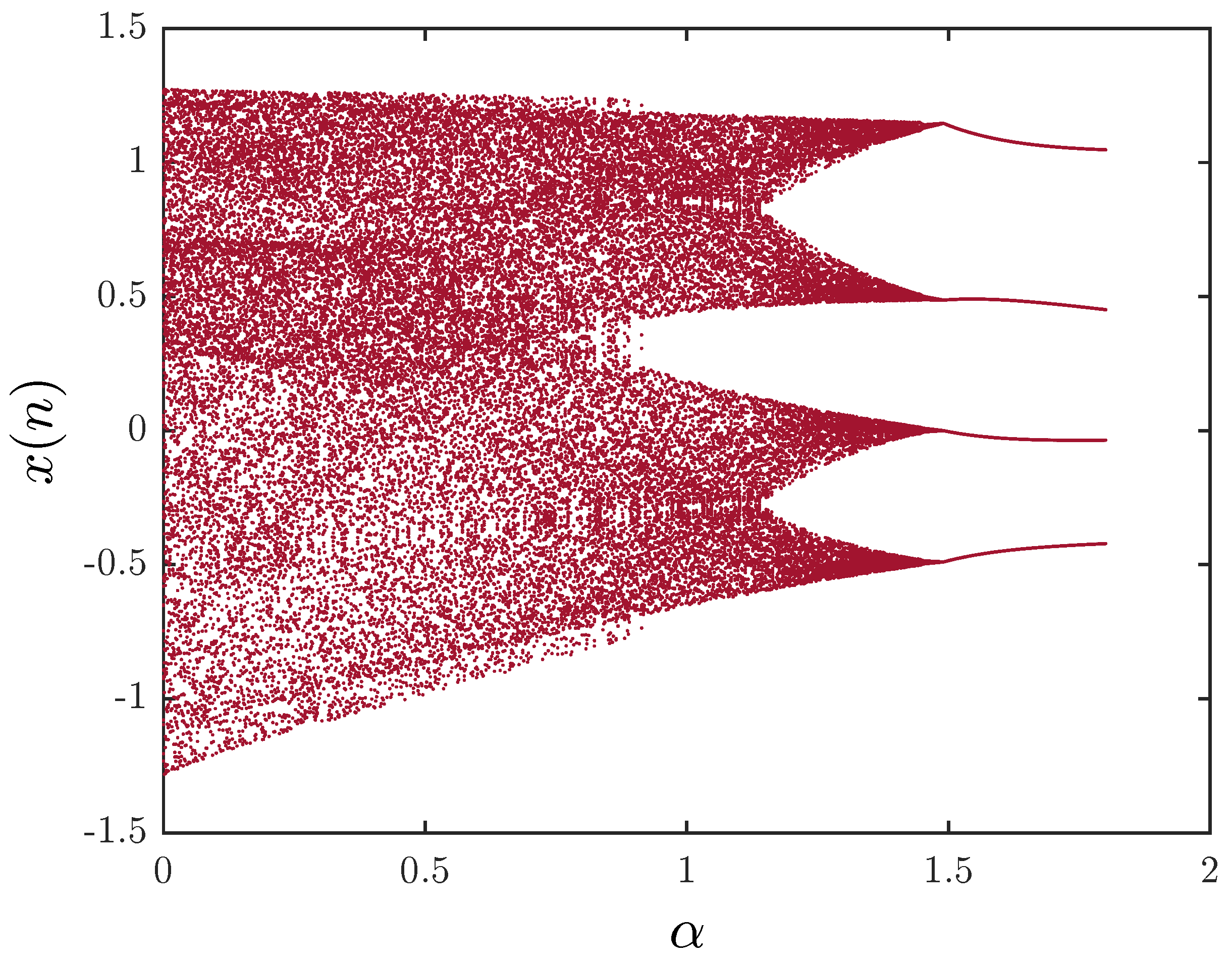
| ApEn | ApEn | ||||
| 0.2 | 0.98 | 0.4037 | 0.8 | 0.98 | 0.2451 |
| 0.2 | 0.95 | 0.4511 | 0.8 | 0.95 | 0.2571 |
| 0.2 | 0.90 | 0.4407 | 0.8 | 0.90 | 0.2304 |
| 0.2 | 0.88 | 0.0981 | 0.8 | 0.88 | 0.2530 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khennaoui, A.-A.; Ouannas, A.; Bendoukha, S.; Wang, X.; Pham, V.-T. On Chaos in the Fractional-Order Discrete-Time Unified System and Its Control Synchronization. Entropy 2018, 20, 530. https://doi.org/10.3390/e20070530
Khennaoui A-A, Ouannas A, Bendoukha S, Wang X, Pham V-T. On Chaos in the Fractional-Order Discrete-Time Unified System and Its Control Synchronization. Entropy. 2018; 20(7):530. https://doi.org/10.3390/e20070530
Chicago/Turabian StyleKhennaoui, Amina-Aicha, Adel Ouannas, Samir Bendoukha, Xiong Wang, and Viet-Thanh Pham. 2018. "On Chaos in the Fractional-Order Discrete-Time Unified System and Its Control Synchronization" Entropy 20, no. 7: 530. https://doi.org/10.3390/e20070530
APA StyleKhennaoui, A.-A., Ouannas, A., Bendoukha, S., Wang, X., & Pham, V.-T. (2018). On Chaos in the Fractional-Order Discrete-Time Unified System and Its Control Synchronization. Entropy, 20(7), 530. https://doi.org/10.3390/e20070530





