Analysis of Cell Signal Transduction Based on Kullback–Leibler Divergence: Channel Capacity and Conservation of Its Production Rate during Cascade
Abstract
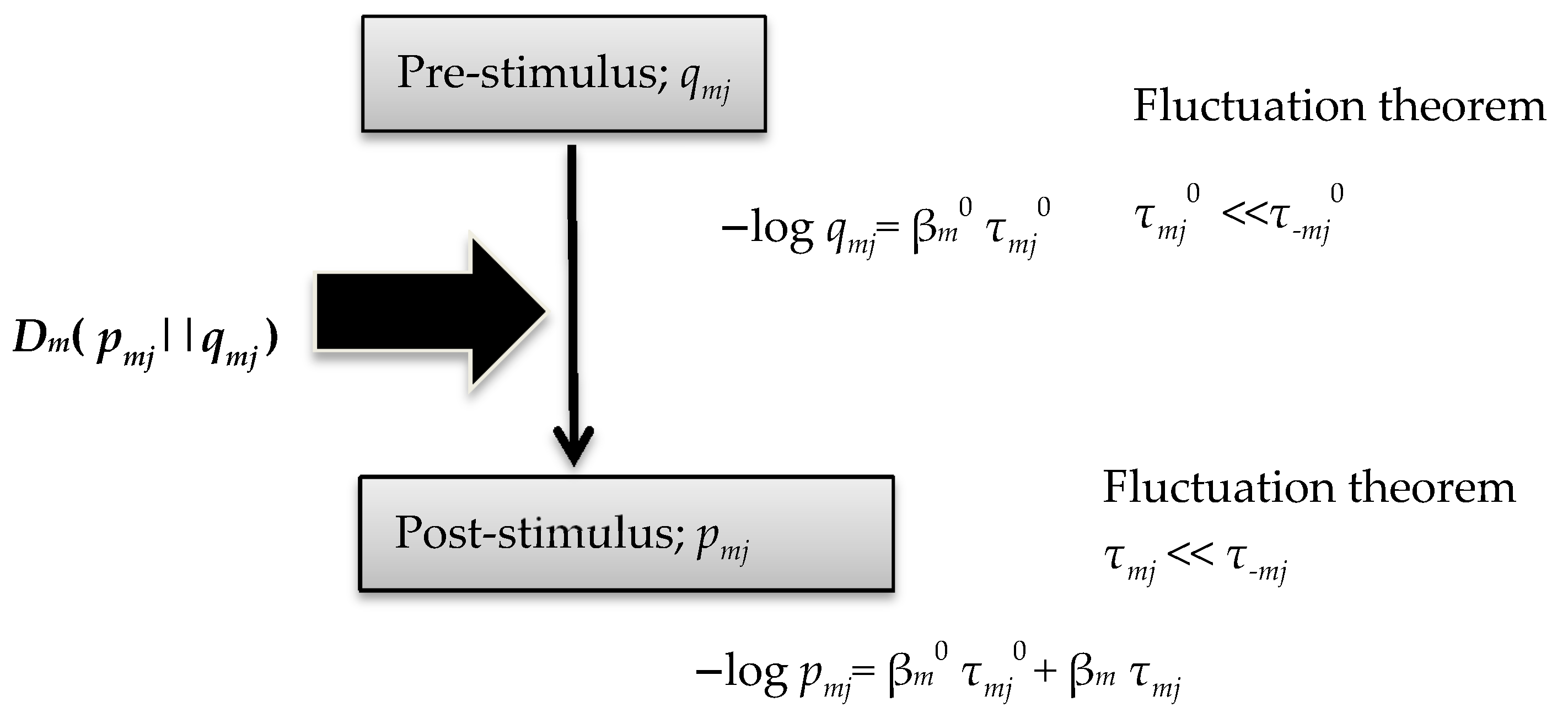
1. Introduction
Signal Cascade Model
2. Results
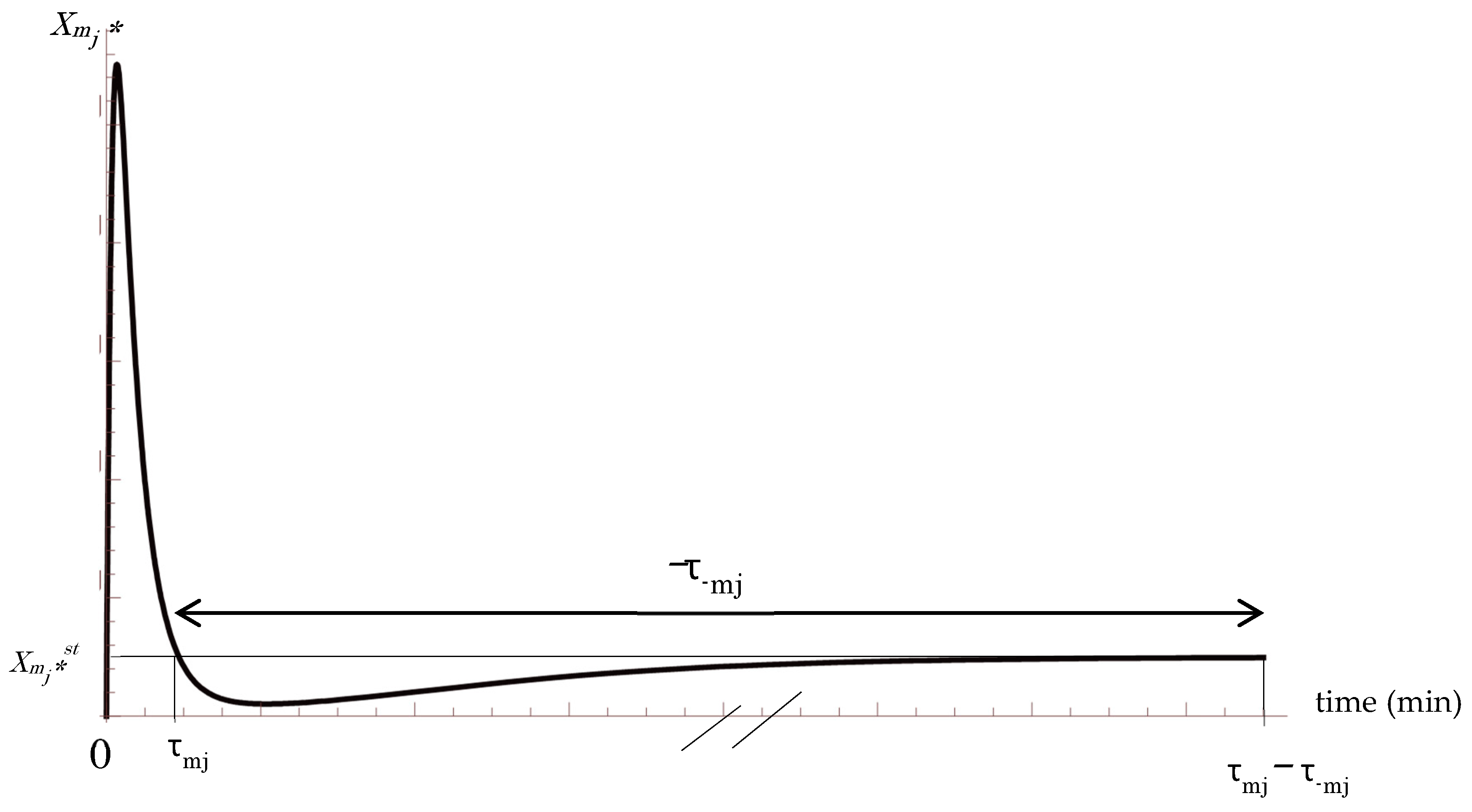
2.1. A Prior Probability Distribution of Signaling Molecules
2.2. Average Entropy Production Rate in a Signal Cascade
2.3. Multinomial Distribution with Population Distribution
3. Conclusions
Funding
Conflicts of Interest
References
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Liang, S.; Yang, F.; Wen, T.; Yao, Z.; Huang, Q.; Ye, C. Nonlocal total variation based on symmetric kullback-leibler divergence for the ultrasound image despeckling. BMC Med. Imaging 2017, 17, 57. [Google Scholar] [CrossRef] [PubMed]
- Maddux, N.R.; Daniels, A.L.; Randolph, T.W. Microflow imaging analyses reflect mechanisms of aggregate formation: Comparing protein particle data sets using the kullback-leibler divergence. J. Pharm. Sci. 2017, 106, 1239–1248. [Google Scholar] [CrossRef] [PubMed]
- Granero-Belinchon, C.; Roux, S.G.; Garnier, N.B. Kullback-leibler divergence measure of intermittency: Application to turbulence. Phys. Rev. E 2018, 97, 013107. [Google Scholar] [CrossRef] [PubMed]
- Edward Jero, S.; Ramu, P.; Ramakrishnan, S. Discrete wavelet transform and singular value decomposition based ecg steganography for secured patient information transmission. J. Med. Syst. 2014, 38, 132. [Google Scholar] [CrossRef] [PubMed]
- Mager, D.E.; Merritt, M.M.; Kasturi, J.; Witkin, L.R.; Urdiqui-Macdonald, M.; Sollers, J.J., 3rd; Evans, M.K.; Zonderman, A.B.; Abernethy, D.R.; Thayer, J.F. Kullback-leibler clustering of continuous wavelet transform measures of heart rate variability. Biomed. Sci. Instrum. 2004, 40, 337–342. [Google Scholar] [PubMed]
- Arribas, J.I.; Calhoun, V.D.; Adali, T. Automatic bayesian classification of healthy controls, bipolar disorder, and schizophrenia using intrinsic connectivity maps from fmri data. IEEE Trans. Biomed. Eng. 2010, 57, 2850–2860. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Ji, S.; Ye, J. Adaptive diffusion kernel learning from biological networks for protein function prediction. BMC Bioinform. 2008, 9, 162. [Google Scholar] [CrossRef] [PubMed]
- Hsiao, C.; Liu, M.; Stanton, R.; McGee, M.; Qian, Y.; Scheuermann, R.H. Mapping cell populations in flow cytometry data for cross-sample comparison using the friedman-rafsky test statistic as a distance measure. Cytometry A 2016, 89, 71–88. [Google Scholar] [CrossRef] [PubMed]
- Wedagedera, J.R.; Burroughs, N.J. T-cell activation: A queuing theory analysis at low agonist density. Biophys. J. 2006, 91, 1604–1618. [Google Scholar] [CrossRef] [PubMed]
- Dragalin, V.; Fedorov, V.; Patterson, S.; Jones, B. Kullback–leibler divergence for evaluating bioequivalence. Stat. Med. 2003, 22, 913–930. [Google Scholar] [CrossRef] [PubMed]
- Cannon, L.; Garcia, C.A.V.; Piovoso, M.J.; Zurakowski, R. Prospective hiv clinical trial comparison by expected kullback-leibler divergence. In Proceedings of the American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 1295–1300. [Google Scholar]
- Vogt, M.; Bajorath, J. Bayesian similarity searching in high-dimensional descriptor spaces combined with kullback-leibler descriptor divergence analysis. J. Chem. Inf. Model. 2008, 48, 247–255. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.P.; Ghosh, M. A kullback-leibler divergence for bayesian model diagnostics. Open J. Stat. 2011, 1, 172–184. [Google Scholar] [CrossRef] [PubMed]
- Crofts, A.R. Life, information, entropy, and time: Vehicles for semantic inheritance. Complexity 2007, 13, 14–50. [Google Scholar] [CrossRef] [PubMed]
- Luo, L.-F. Entropy production in a cell and reversal of entropy flow as an anticancer therapy. Front. Phys. China 2009, 4, 122–136. [Google Scholar] [CrossRef]
- Edwards, D.; Wang, L.; Sorensen, P. Network-enabled gene expression analysis. BMC Bioinform. 2012, 13, 167. [Google Scholar] [CrossRef] [PubMed]
- Teschendorff, A.E.; Sollich, P.; Kuehn, R. Signalling entropy: A novel network-theoretical framework for systems analysis and interpretation of functional omic data. Methods 2014, 67, 282–293. [Google Scholar] [CrossRef] [PubMed]
- Sato, M.; Kawana, K.; Adachi, K.; Fujimoto, A.; Yoshida, M.; Nakamura, H.; Nishida, H.; Inoue, T.; Taguchi, A.; Ogishima, J.; et al. Intracellular signaling entropy can be a biomarker for predicting the development of cervical intraepithelial neoplasia. PLoS ONE 2017, 12, e0176353. [Google Scholar] [CrossRef] [PubMed]
- Teschendorff, A.E.; Banerji, C.R.; Severini, S.; Kuehn, R.; Sollich, P. Increased signaling entropy in cancer requires the scale-free property of protein interaction networks. Sci. Rep 2015, 5, 9646. [Google Scholar] [CrossRef] [PubMed]
- Teschendorff, A.E.; Breeze, C.E.; Zheng, S.C.; Beck, S. A comparison of reference-based algorithms for correcting cell-type heterogeneity in epigenome-wide association studies. BMC Bioinform. 2017, 18, 105. [Google Scholar] [CrossRef] [PubMed]
- White, D.R.; Kejzar, N.; Tsallis, C.; Farmer, D.; White, S. Generative model for feedback networks. Phys. Rev. E 2006, 73, 016119. [Google Scholar] [CrossRef] [PubMed]
- Levchenko, A.; Nemenman, I. Cellular noise and information transmission. Curr. Opin. Biotechnol. 2014, 28, 156–164. [Google Scholar] [CrossRef] [PubMed]
- Ellison, D.; Mugler, A.; Brennan, M.D.; Lee, S.H.; Huebner, R.J.; Shamir, E.R.; Woo, L.A.; Kim, J.; Amar, P.; Nemenman, I.; et al. Cell-cell communication enhances the capacity of cell ensembles to sense shallow gradients during morphogenesis. Proc. Natl. Acad. Sci. USA 2016, 113, E679–E688. [Google Scholar] [CrossRef] [PubMed]
- Maire, T.; Youk, H. Molecular-level tuning of cellular autonomy controls the collective behaviors of cell populations. Cell Syst. 2015, 1, 349–360. [Google Scholar] [CrossRef] [PubMed]
- Guo, M.; Bao, E.L.; Wagner, M.; Whitsett, J.A.; Xu, Y. Slice: Determining cell differentiation and lineage based on single cell entropy. Nucleic Acids Res. 2017, 45, e54. [Google Scholar] [CrossRef] [PubMed]
- Becker, N.B.; Mugler, A.; Ten Wolde, P.R. Optimal prediction by cellular signaling networks. Phys. Rev. Lett. 2015, 115, 258103. [Google Scholar] [CrossRef] [PubMed]
- Brillouin, L. Science and Information Theory, 2nd ed.; Dover Publication Inc.: Mineola, NY, USA, 2013; p. 42. [Google Scholar]
- Tsuruyama, T. Channel capacity of coding system on tsallis entropy and q-statistics. Entropy 2017, 19, 682. [Google Scholar] [CrossRef]
- Uda, S.; Kuroda, S. Analysis of cellular signal transduction from an information theoretic approach. Semin. Cell Dev. Biol. 2016, 51, 24–31. [Google Scholar] [CrossRef] [PubMed]
- Sagawa, T.; Kikuchi, Y.; Inoue, Y.; Takahashi, H.; Muraoka, T.; Kinbara, K.; Ishijima, A.; Fukuoka, H. Single-cell E. Coli response to an instantaneously applied chemotactic signal. Biophys. J. 2014, 107, 730–739. [Google Scholar] [CrossRef] [PubMed]
- Ito, S.; Sagawa, T. Maxwell’s demon in biochemical signal transduction with feedback loop. Nat. Commun. 2015, 6, 7498. [Google Scholar] [CrossRef] [PubMed]
- Ito, S.; Sagawa, T. Information thermodynamics on causal networks. Phys. Rev. Lett. 2013, 111, 18063. [Google Scholar] [CrossRef] [PubMed]
- Tsuruyama, T. Information thermodynamics derives the entropy current of cell signal transduction as a model of a binary coding system. Entropy 2018, 20, 145. [Google Scholar] [CrossRef]
- Tsuruyama, T. The conservation of average entropy production rate in a model of signal transduction: Information thermodynamics based on the fluctuation theorem. Entropy 2018, 20, 303. [Google Scholar] [CrossRef]
- Kim, D.S.; Hwang, E.S.; Lee, J.E.; Kim, S.Y.; Kwon, S.B.; Park, K.C. Sphingosine-1-phosphate decreases melanin synthesis via sustained erk activation and subsequent mitf degradation. J. Cell Sci. 2003, 116, 1699–1706. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.S.; Park, M.; Han, J.; Lee, J.H.; Bae, I.H.; Choi, H.; Son, E.D.; Park, Y.H.; Lim, K.M. Liver x receptor activation inhibits melanogenesis through the acceleration of erk-mediated mitf degradation. J. Investig. Dermatol. 2013, 133, 1063–1071. [Google Scholar] [CrossRef] [PubMed]
- Mackeigan, J.P.; Murphy, L.O.; Dimitri, C.A.; Blenis, J. Graded mitogen-activated protein kinase activity precedes switch-like c-fos induction in mammalian cells. Mol. Cell Biol. 2005, 25, 4676–4682. [Google Scholar] [CrossRef] [PubMed]
- Newman, D.R.; Li, C.M.; Simmons, R.; Khosla, J.; Sannes, P.L. Heparin affects signaling pathways stimulated by fibroblast growth factor-1 and-2 in type ii cells. Am. J. Physiol. Lung Cell. Mol. Physiol. 2004, 287, L191–L200. [Google Scholar] [CrossRef] [PubMed]
- Petropavlovskaia, M.; Daoud, J.; Zhu, J.; Moosavi, M.; Ding, J.; Makhlin, J.; Assouline-Thomas, B.; Rosenberg, L. Mechanisms of action of islet neogenesis-associated protein: Comparison of the full-length recombinant protein and a bioactive peptide. Am. J. Physiol. Endocrinol. Metab. 2012, 303, E917–E927. [Google Scholar] [CrossRef] [PubMed]
- Tao, R.; Hoover, H.E.; Honbo, N.; Kalinowski, M.; Alano, C.C.; Karliner, J.S.; Raffai, R. High-density lipoprotein determines adult mouse cardiomyocyte fate after hypoxia-reoxygenation through lipoprotein-associated sphingosine 1-phosphate. Am. J. Physiol. Heart Circ. Physiol. 2010, 298, H1022–E1028. [Google Scholar] [CrossRef] [PubMed]
- Mina, M.; Magi, S.; Jurman, G.; Itoh, M.; Kawaji, H.; Lassmann, T.; Arner, E.; Forrest, A.R.; Carninci, P.; Hayashizaki, Y.; et al. Promoter-level expression clustering identifies time development of transcriptional regulatory cascades initiated by erbb receptors in breast cancer cells. Sci. Rep. 2015, 5, 11999. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Ubl, J.J.; Stricker, R.; Reiser, G. Thrombin (par-1)-induced proliferation in astrocytes via mapk involves multiple signaling pathways. Am. J. Physiol. Cell Physiol. 2002, 283, C1351–C1364. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.Y.; Liu, Y.; Ni, X.Y.; Bai, Z.H.; Chen, Q.Y.; Zhang, Y.; Gao, F.G. Nicotine promotes cell proliferation and induces resistance to cisplatin by alpha7 nicotinic acetylcholine receptor-mediated activation in raw264.7 and el4 cells. Oncol. Rep. 2014, 31, 1480–1488. [Google Scholar] [CrossRef] [PubMed]
- Yeung, K.; Seitz, T.; Li, S.; Janosch, P.; McFerran, B.; Kaiser, C.; Fee, F.; Katsanakis, K.D.; Rose, D.W.; Mischak, H.; et al. Suppression of raf-1 kinase activity and map kinase signalling by rkip. Nature 1999, 401, 173–177. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.Z.; Yano, N.; Deng, M.Z.; Mao, Q.F.; Shaw, S.K.; Tseng, Y.T. Beta-adrenergic receptor-pi3k signaling crosstalk in mouse heart: Elucidation of immediate downstream signaling cascades. PLoS ONE 2011, 6, e26581. [Google Scholar]
- Cheong, R.; Rhee, A.; Wang, C.J.; Nemenman, I.; Levchenko, A. Information transduction capacity of noisy biochemical signaling networks. Science 2011, 334, 354–358. [Google Scholar] [CrossRef] [PubMed]
- Roldan, E.; Parrondo, J.M. Entropy production and kullback-leibler divergence between stationary trajectories of discrete systems. Phys. Rev. E 2012, 85, 031129. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsuruyama, T. Analysis of Cell Signal Transduction Based on Kullback–Leibler Divergence: Channel Capacity and Conservation of Its Production Rate during Cascade. Entropy 2018, 20, 438. https://doi.org/10.3390/e20060438
Tsuruyama T. Analysis of Cell Signal Transduction Based on Kullback–Leibler Divergence: Channel Capacity and Conservation of Its Production Rate during Cascade. Entropy. 2018; 20(6):438. https://doi.org/10.3390/e20060438
Chicago/Turabian StyleTsuruyama, Tatsuaki. 2018. "Analysis of Cell Signal Transduction Based on Kullback–Leibler Divergence: Channel Capacity and Conservation of Its Production Rate during Cascade" Entropy 20, no. 6: 438. https://doi.org/10.3390/e20060438
APA StyleTsuruyama, T. (2018). Analysis of Cell Signal Transduction Based on Kullback–Leibler Divergence: Channel Capacity and Conservation of Its Production Rate during Cascade. Entropy, 20(6), 438. https://doi.org/10.3390/e20060438



