Complexity Analysis of Global Temperature Time Series
Abstract
1. Introduction
2. Mathematical Fundamentals
2.1. Lempel–Ziv Complexity
- Initialize:
- (a)
- The parsed sequence, ;
- (b)
- An auxiliary sequence, ;
- (c)
- A pointer, , such that, points to the symbol, , of S;
- (d)
- .
- At the iteration p:
- (a)
- Advance from to and extend the auxiliary sequence, Q, by appending the symbol ;
- (b)
- Check whether the current auxiliary sequence Q matches any subsequence of . If no match is found, then append, as a new word, the auxiliary sequence, Q, to the parsed sequence, , and reset to ;
- Increment p;
- (a)
- If , then go to step 2;
- (b)
- If , then append Q to to yield the final parsed sequence;
- Count the number of different words, , in .
2.2. Sample Entropy
- Generate a set of m-dimensional vectors, ,representing m consecutive values of , starting at point p;
- Determine the similarity, , between and (i.e., the vector representing m consecutive values of , starting at point q), by calculatingwhere is a distance, and r is a tolerance value;
- Compute the correlation sum, , under the constraint , to exclude self-matches,
- Find the probability, , of template matching for all vectors by
- Calculate the as
2.3. Fourier Analysis
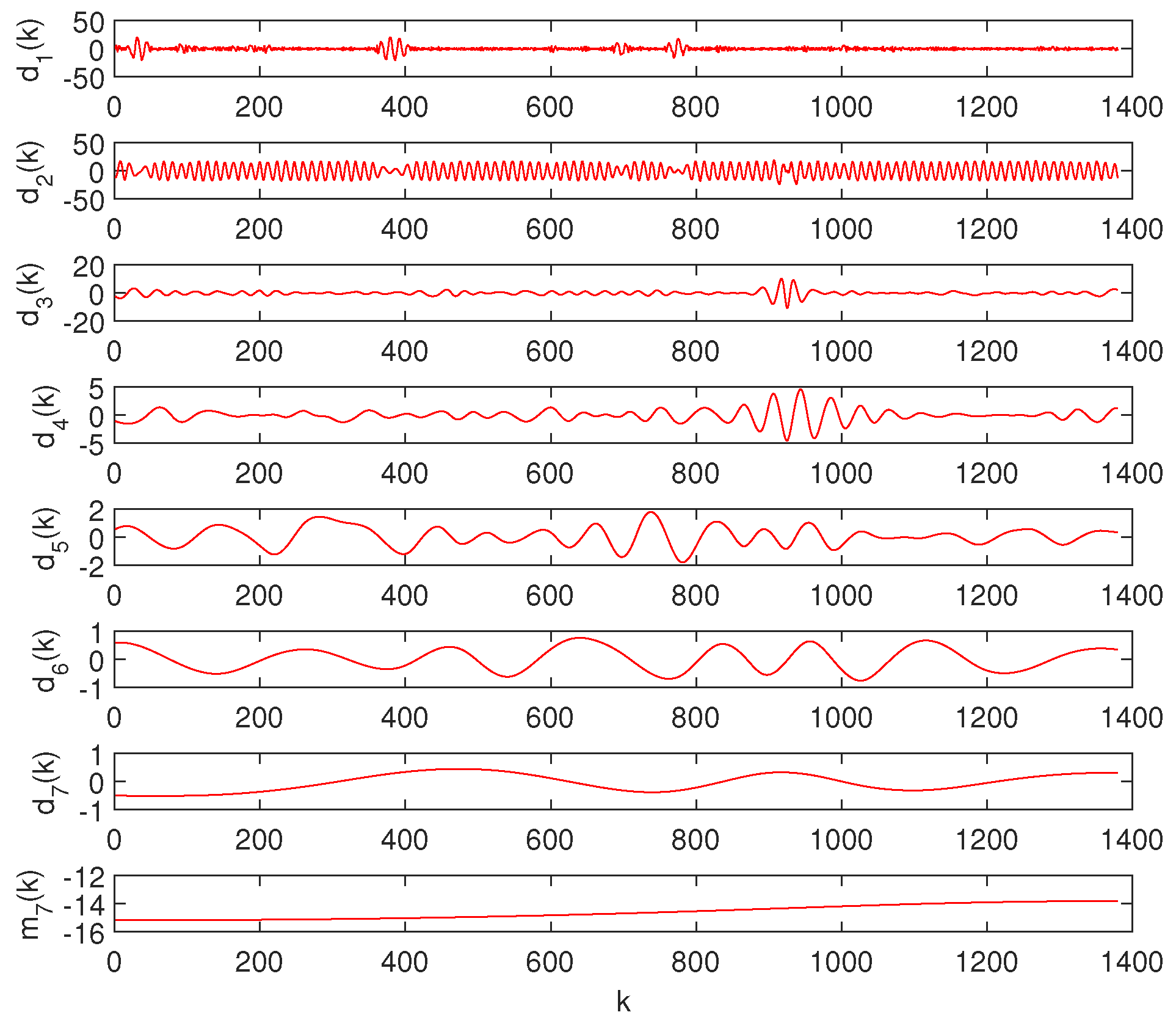
2.4. Empirical Mode Decomposition
- Identify all extrema of ;
- Interpolate between minima and maxima, and find the lower and upper envelopes, and , respectively;
- Calculate the mean using ;
- Extract the details using ;
- Iterate on the residual, .
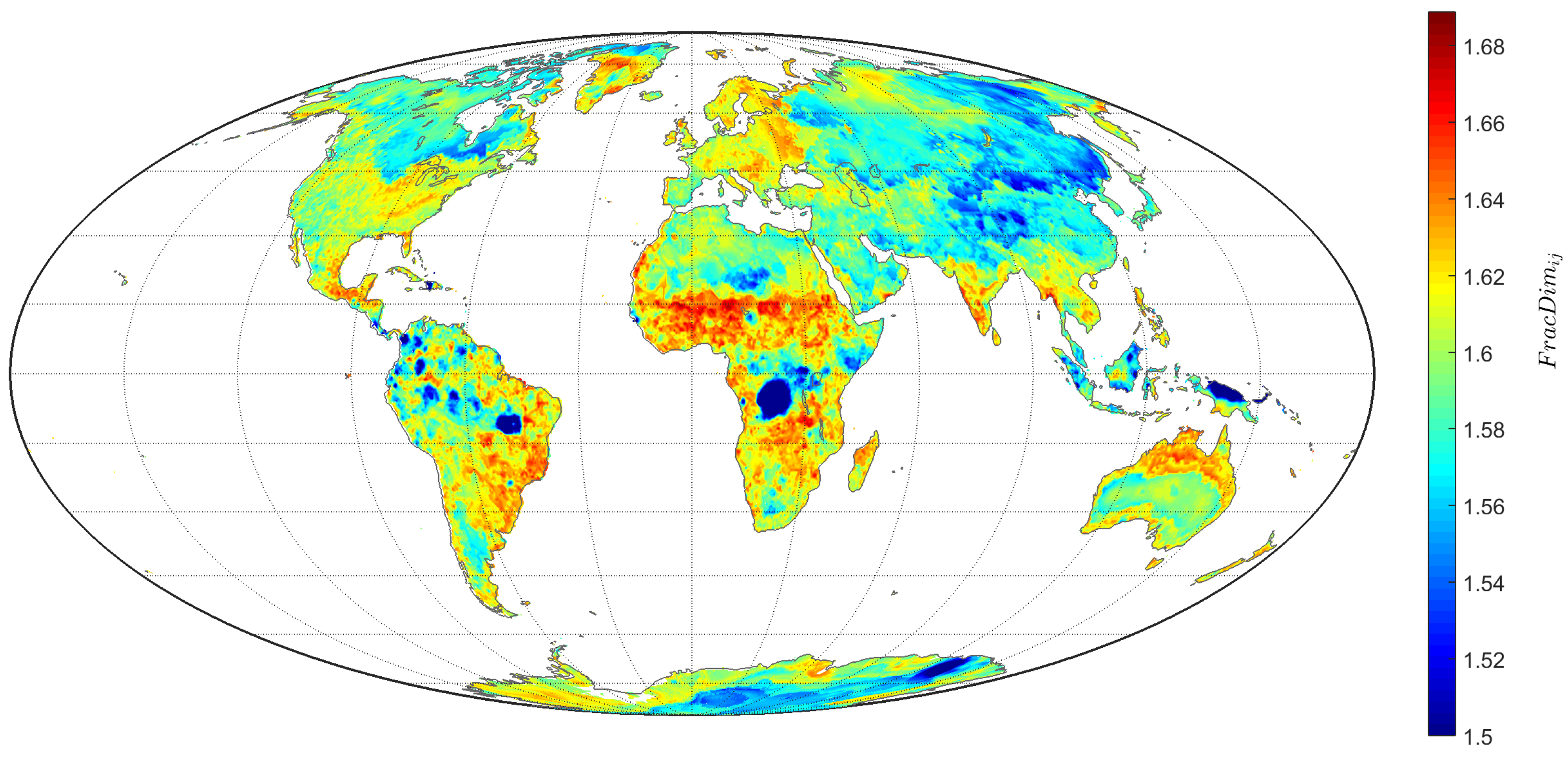
2.5. Fractal Dimension
- Pad the image with background pixels so that its dimensions are at a power of 2;
- Cover the fractal object with a grid of squares with size (in the first iteration, there is just one square of equal size to the size of the image);
- Count the number of boxes (i.e., squares), , needed to cover the object;
- If , then make and repeat step 2.
- Estimate the as the slope of the log-log plot, versus , calculated by means of the least squares method.
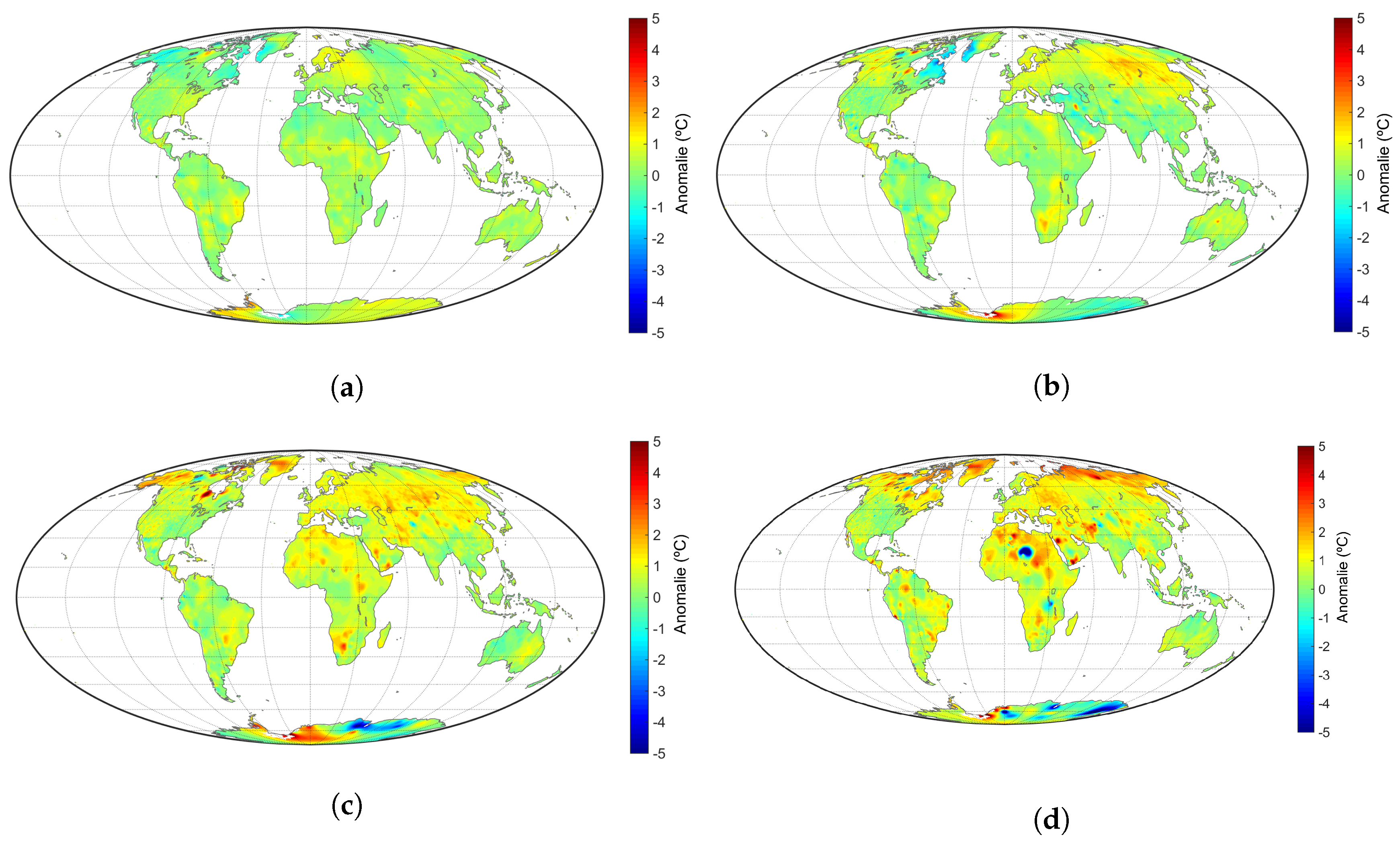
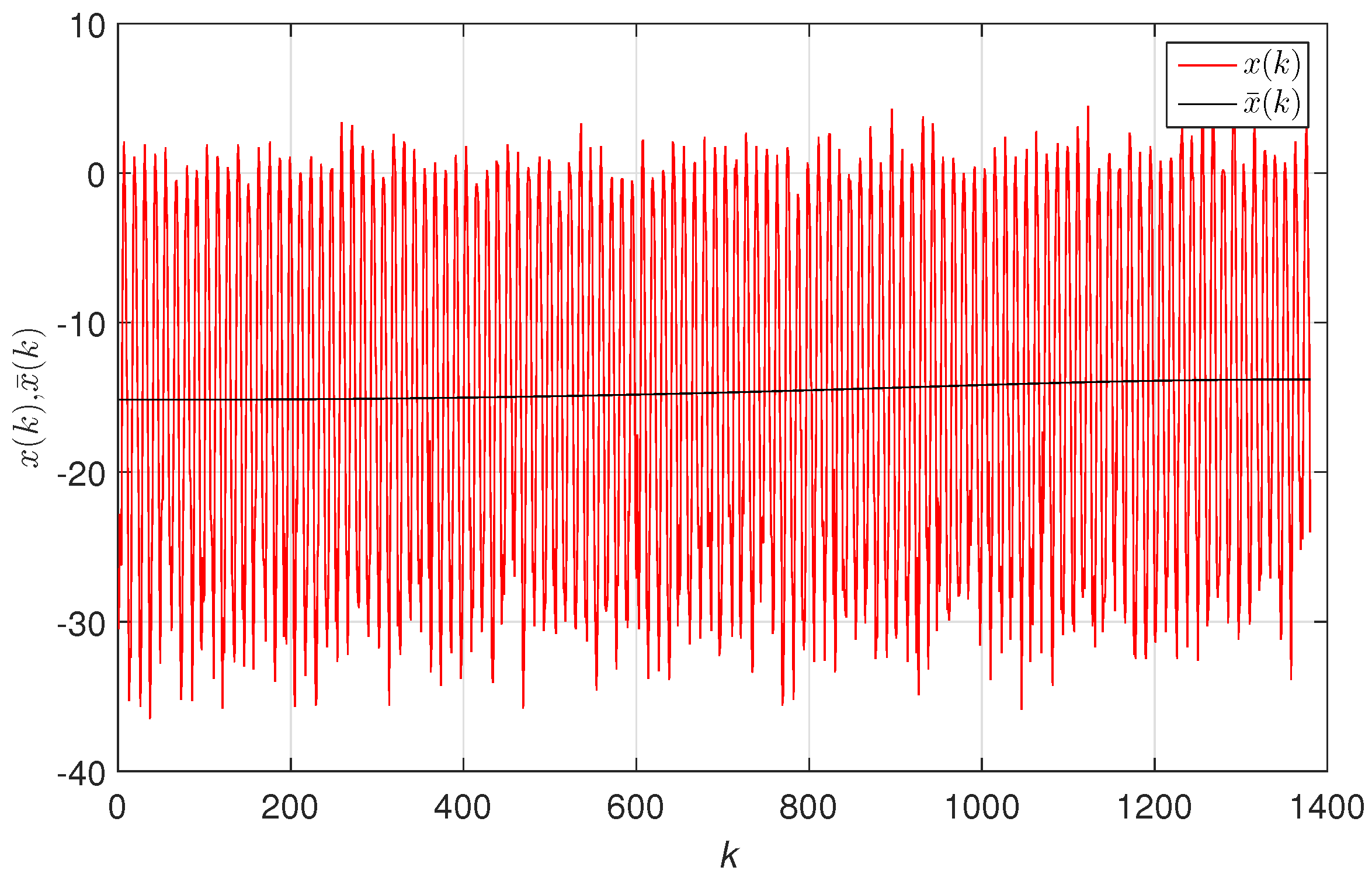
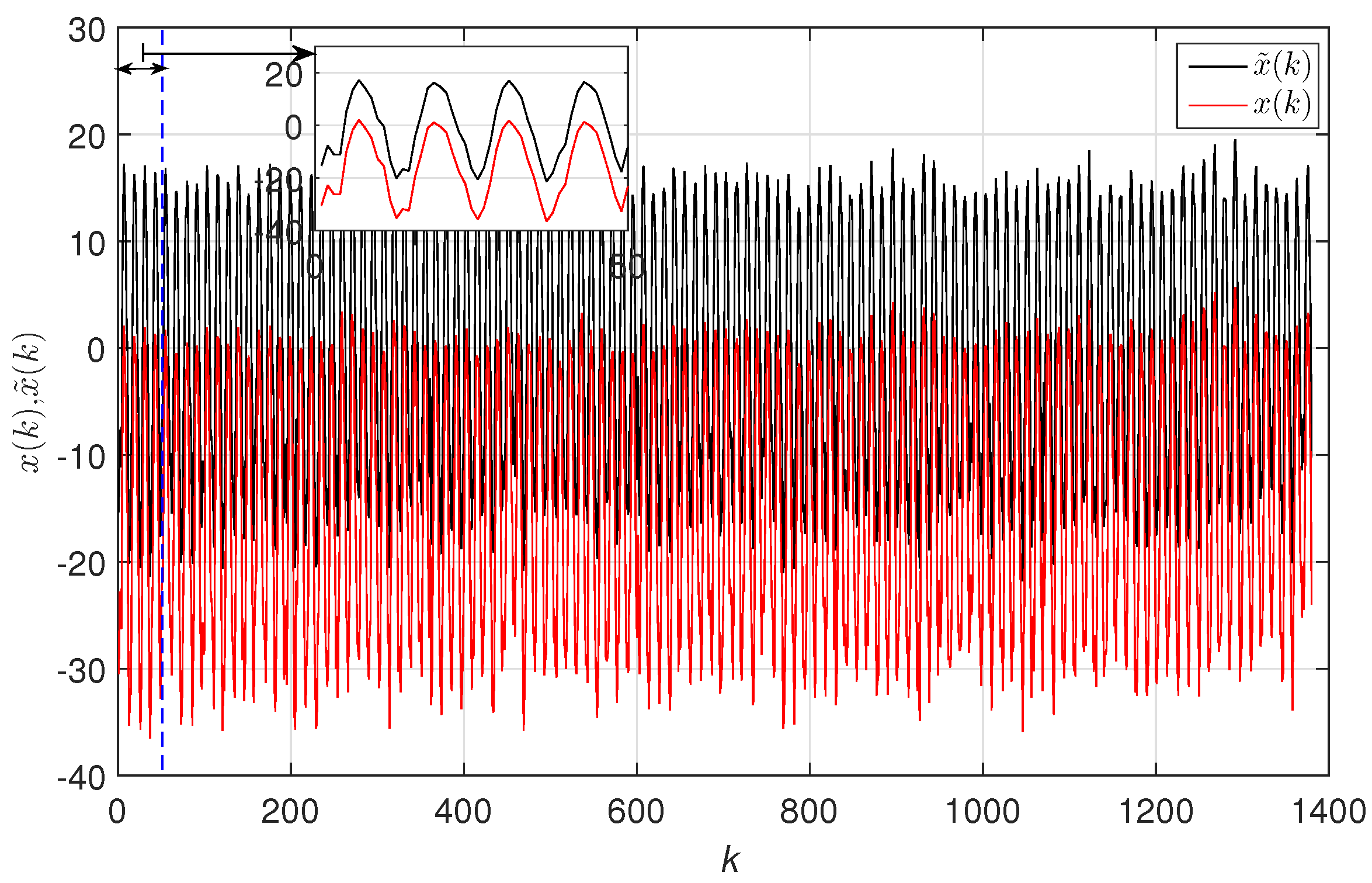
3. Dataset
4. On the Complexity of TTS
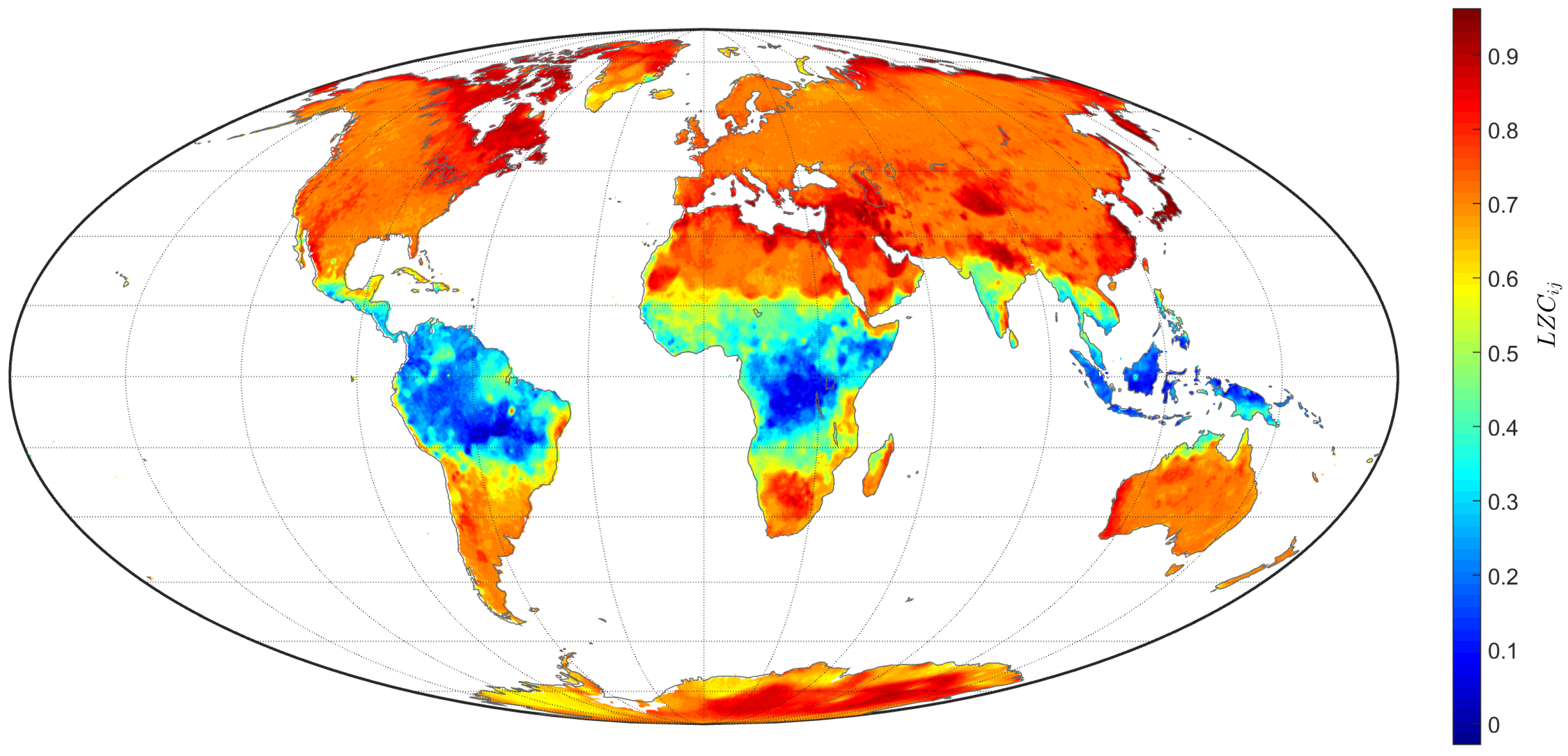
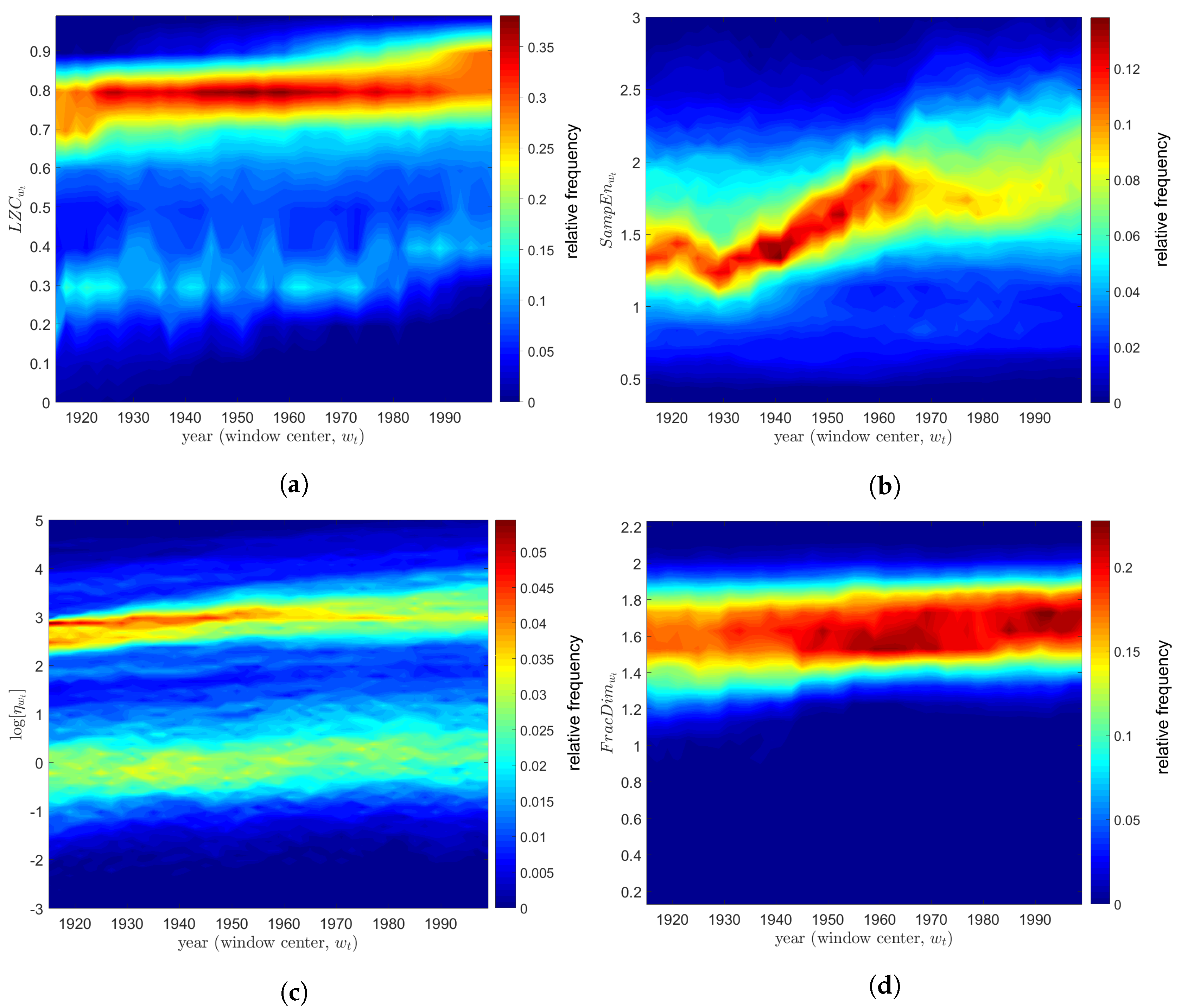
4.1. Lempel–Ziv Complexity of the TTS
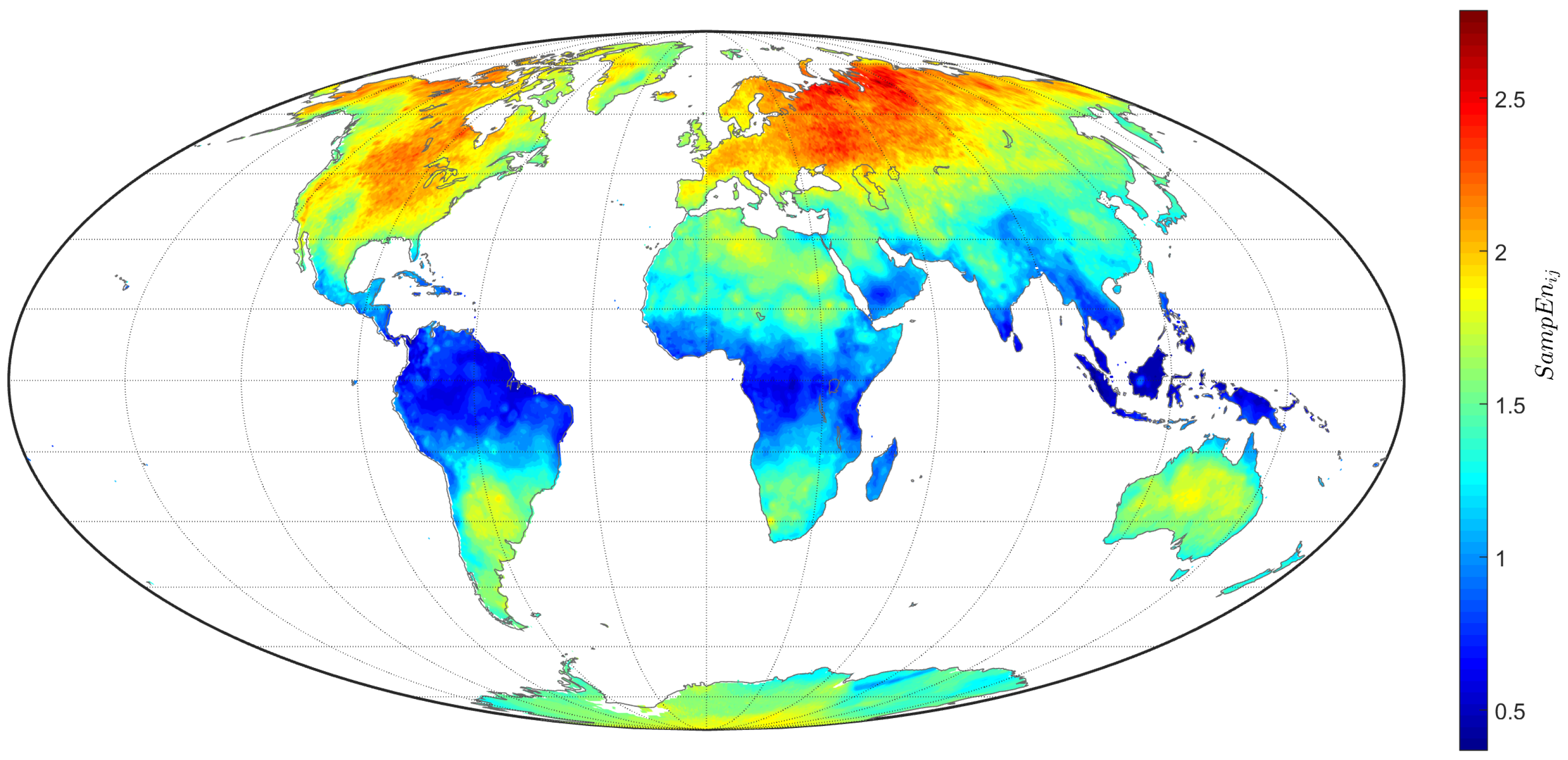
4.2. Sample Entropy of the TTS
4.3. Harmonic Content of the TTS
4.4. Fractal Dimension of the TTS
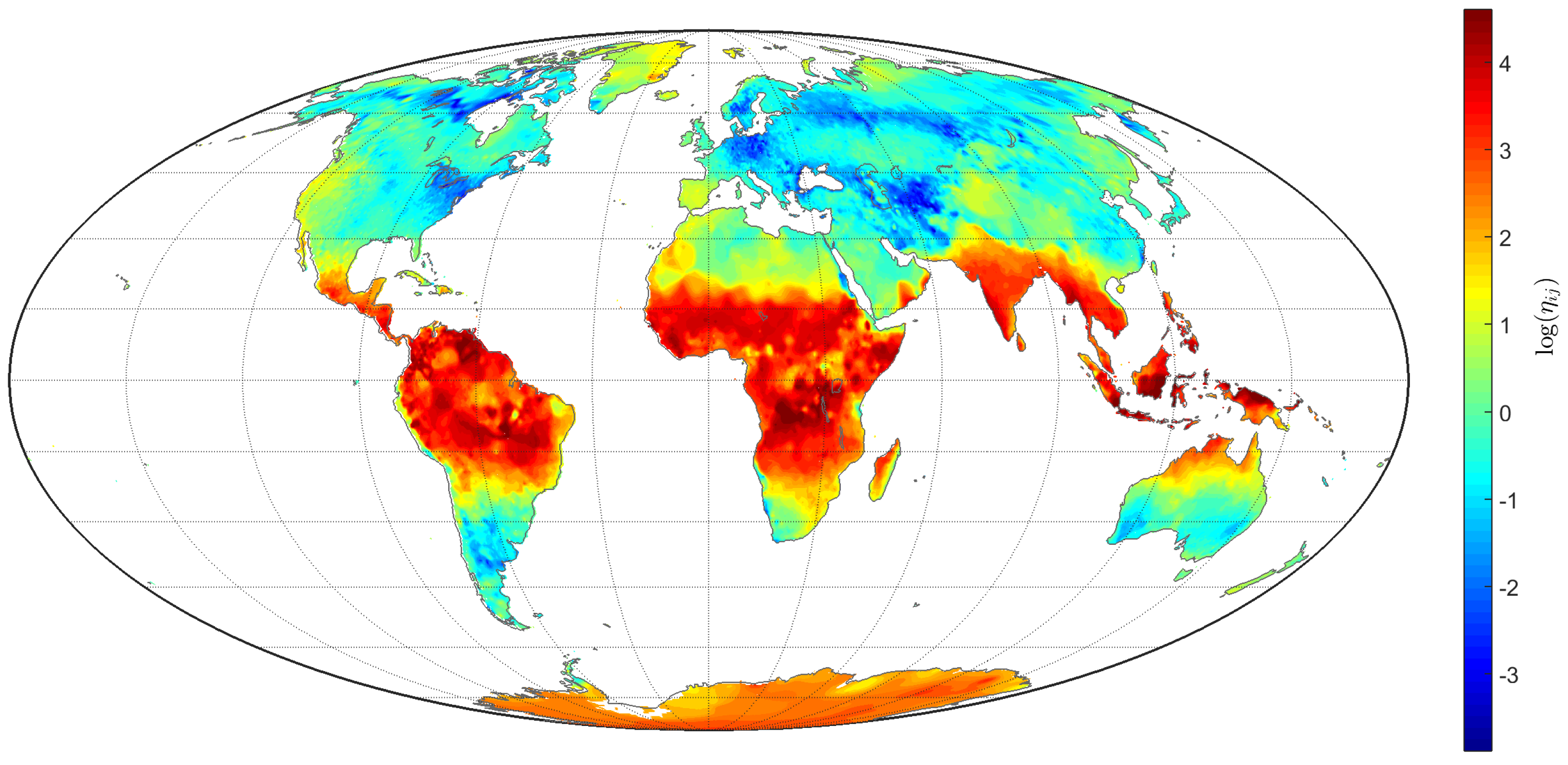
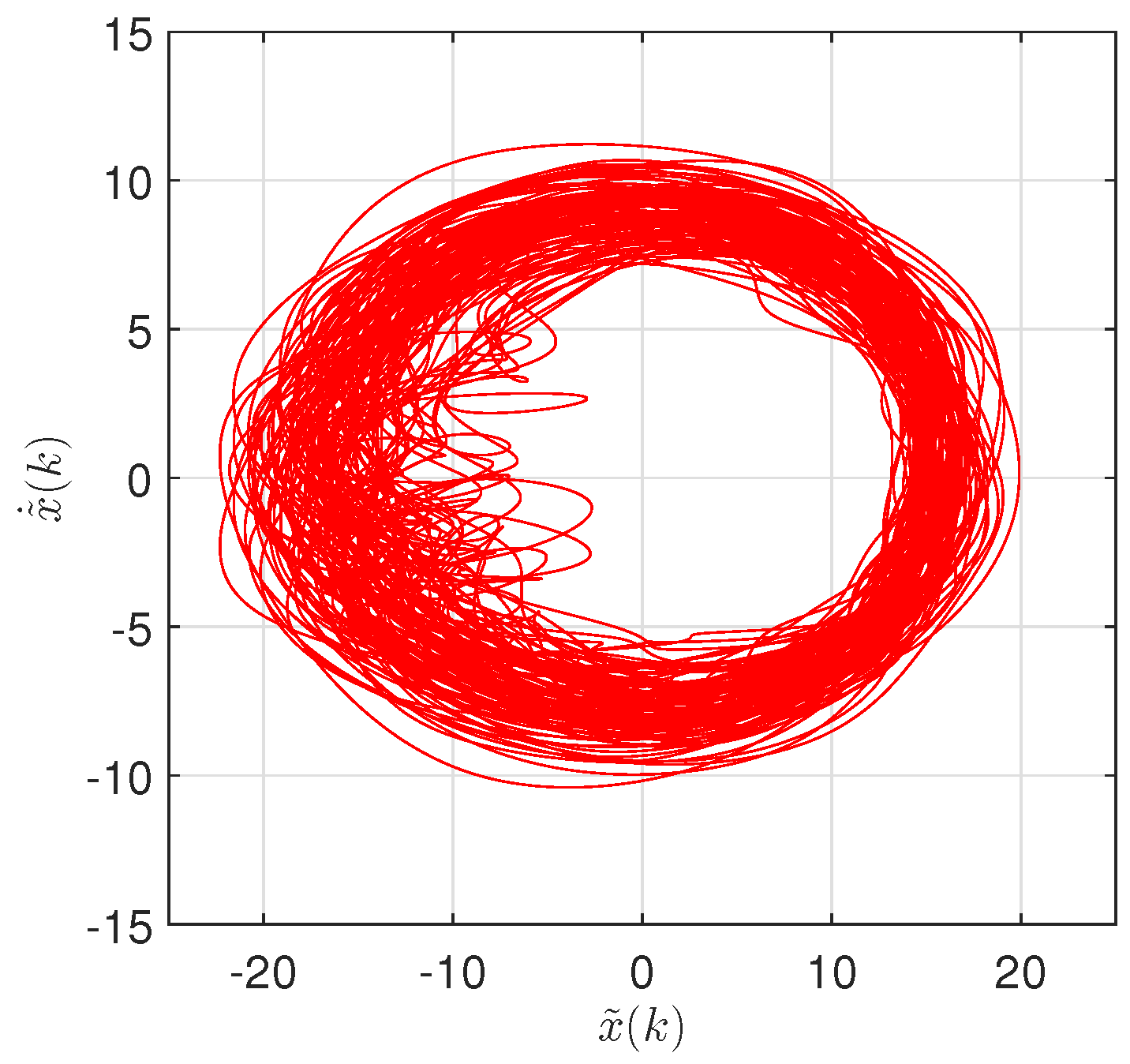
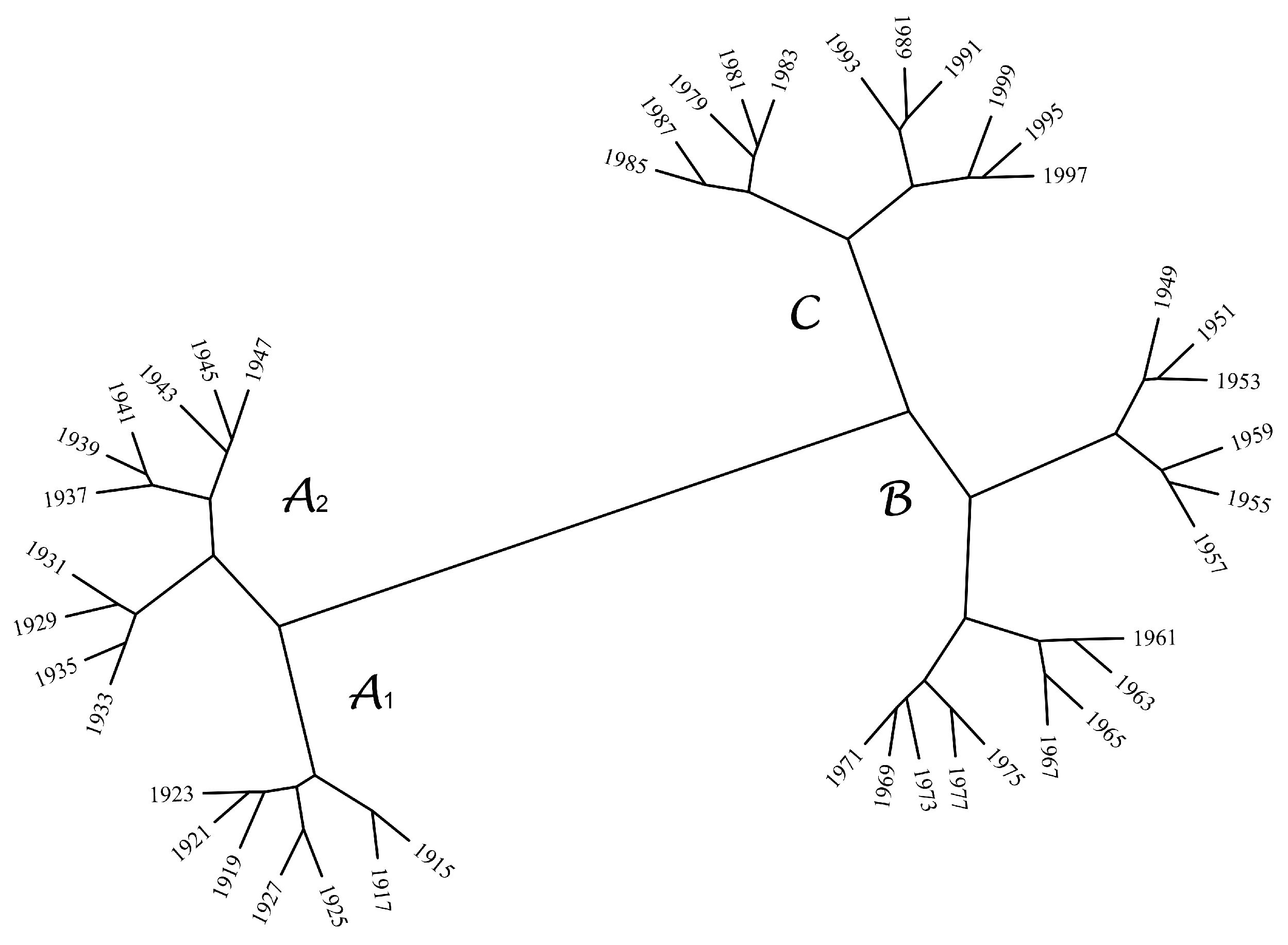
5. Temporal Dynamics of Global Warming
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Solomon, S.; Qin, D.; Manning, M.; Chen, Z.; Marquis, M.; Averyt, K.B.; Tignor, M.; Miller, H.L. Contribution of Working Group I to the Fourth Assessment Report Of the Intergovernamental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007. [Google Scholar]
- Root, T.L.; Price, J.T.; Hall, K.R.; Schneider, S.H.; Rosenzweig, C.; Pounds, J.A. Fingerprints of global warming on wild animals and plants. Nature 2003, 421, 57–60. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Yu, H.; Dai, A.; Wei, Y.; Kang, L. Drylands face potential threat under 2 ∘C global warming target. Nat. Clim. Chang. 2017, 7, 417–422. [Google Scholar] [CrossRef]
- Desch, S.J.; Smith, N.; Groppi, C.; Vargas, P.; Jackson, R.; Kalyaan, A.; Nguyen, P.; Probst, L.; Rubin, M.E.; Singleton, H.; et al. Arctic ice management. Earth’s Future 2017, 5, 107–127. [Google Scholar] [CrossRef]
- Lopes, A.M.; Machado, J.A.T. Analysis of temperature time-series: Embedding dynamics into the MDS method. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 851–871. [Google Scholar] [CrossRef]
- Alexiadis, A. Global warming and human activity: A model for studying the potential instability of the carbon dioxide/temperature feedback mechanism. Ecol. Model. 2007, 203, 243–256. [Google Scholar] [CrossRef]
- Working Group, I. The Scientific Basis. Climate Change; Third Assessment Report of the Intergovernamental Panel on Climate Change; IPCC: Geneva, Switzerland, 2001. [Google Scholar]
- Dai, A. Drought under global warming: A review. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 45–65. [Google Scholar] [CrossRef]
- You, Q.; Kang, S.; Pepin, N.; Flügel, W.A.; Sanchez-Lorenzo, A.; Yan, Y.; Zhang, Y. Climate warming and associated changes in atmospheric circulation in the eastern and central Tibetan Plateau from a homogenized dataset. Glob. Planet. Chang. 2010, 72, 11–24. [Google Scholar] [CrossRef]
- Jevrejeva, S.; Moore, J.C.; Grinsted, A. Sea level projections to AD2500 with a new generation of climate change scenarios. Glob. Planet. Chang. 2012, 80, 14–20. [Google Scholar] [CrossRef]
- Giannakopoulos, C.; le Sager, P.; Bindi, M.; Moriondo, M.; Kostopoulou, E.; Goodess, C. Climatic changes and associated impacts in the Mediterranean resulting from a 2 ∘C global warming. Glob. Planet. Chang. 2009, 68, 209–224. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, H.; Zhou, W.; Ma, J. Recent changes in the summer precipitation pattern in East China and the background circulation. Clim. Dyn. 2011, 36, 1463–1473. [Google Scholar] [CrossRef]
- Hansen, J.; Ruedy, R.; Sato, M.; Lo, K. Global surface temperature change. Rev. Geophys. 2010, 48, RG4004. [Google Scholar] [CrossRef]
- Brohan, P.; Kennedy, J.J.; Harris, I.; Tett, S.F.; Jones, P.D. Uncertainty estimates in regional and global observed temperature changes: A new data set from 1850. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Menne, M.J.; Williams, C.N., Jr. Homogenization of temperature series via pairwise comparisons. J. Clim. 2009, 22, 1700–1717. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E.; Wallace, J.M.; Smoliak, B.V.; Chen, X. On the time-varying trend in global-mean surface temperature. Clim. Dyn. 2011, 37, 759–773. [Google Scholar] [CrossRef]
- Rohde, R.; Muller, R.; Jacobsen, R.; Perlmutter, S.; Rosenfeld, A.; Wurtele, J.; Curry, J.; Wickhams, C.; Mosher, S. Berkeley Earth temperature averaging process. Geoinf. Geostat. Overv. 2013, 1, 1–13. [Google Scholar] [CrossRef]
- Lawrimore, J.H.; Menne, M.J.; Gleason, B.E.; Williams, C.N.; Wuertz, D.B.; Vose, R.S.; Rennie, J. An overview of the Global Historical Climatology Network monthly mean temperature data set, version 3. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Jones, P.; Lister, D.; Osborn, T.; Harpham, C.; Salmon, M.; Morice, C. Hemispheric and large-scale land-surface air temperature variations: An extensive revision and an update to 2010. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Capilla, C. Time series analysis and identification of trends in a Mediterranean urban area. Glob. Planet. Chang. 2008, 63, 275–281. [Google Scholar] [CrossRef]
- Grieser, J.; Trömel, S.; Schönwiese, C.D. Statistical time series decomposition into significant components and application to European temperature. Theor. Appl. Climatol. 2002, 71, 171–183. [Google Scholar] [CrossRef]
- Hughes, G.L.; Rao, S.S.; Rao, T.S. Statistical analysis and time-series models for minimum/maximum temperatures in the Antarctic Peninsula. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2007, 463, 241–259. [Google Scholar] [CrossRef]
- Viola, F.M.; Paiva, S.L.; Savi, M.A. Analysis of the global warming dynamics from temperature time series. Ecol. Model. 2010, 221, 1964–1978. [Google Scholar] [CrossRef]
- Founda, D.; Papadopoulos, K.; Petrakis, M.; Giannakopoulos, C.; Good, P. Analysis of mean, maximum, and minimum temperature in Athens from 1897 to 2001 with emphasis on the last decade: Trends, warm events, and cold events. Glob. Planet. Chang. 2004, 44, 27–38. [Google Scholar] [CrossRef]
- Ge, Q.S.; Zheng, J.Y.; Hao, Z.X.; Shao, X.M.; Wang, W.C.; Luterbacher, J. Temperature variation through 2000 years in China: An uncertainty analysis of reconstruction and regional difference. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Deser, C.; Phillips, A.S.; Alexander, M.A. Twentieth century tropical sea surface temperature trends revisited. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Oñate, J.J.; Pou, A. Temperature variations in Spain since 1901: A preliminary analysis. Int. J. Climatol. 1996, 16, 805–815. [Google Scholar] [CrossRef]
- Stephenson, D.B.; Doblas-Reyes, F.J. Statistical methods for interpreting Monte Carlo ensemble forecasts. Tellus A 2000, 52, 300–322. [Google Scholar] [CrossRef]
- Machado, J.A.T.; Lopes, A.M.; Galhano, A.M. Multidimensional scaling visualization using parametric similarity indices. Entropy 2015, 17, 1775–1794. [Google Scholar] [CrossRef]
- Lempel, A.; Ziv, J. On the complexity of finite sequences. IEEE Trans. Inf. Theory 1976, 22, 75–81. [Google Scholar] [CrossRef]
- Shao, Z.G. Contrasting the complexity of the climate of the past 122,000 years and recent 2000 years. Sci. Rep. 2017, 7, 4143. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wei, S.; di Maria, C.; Liu, C. Using Lempel–Ziv complexity to assess ECG signal quality. J. Med. Biol. Eng. 2016, 36, 625–634. [Google Scholar] [CrossRef] [PubMed]
- Abásolo, D.; Simons, S.; da Silva, R.M.; Tononi, G.; Vyazovskiy, V.V. Lempel-Ziv complexity of cortical activity during sleep and waking in rats. J. Neurophysiol. 2015, 113, 2742–2752. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Xu, J. Complexity and brain function. Acta Biophy. Sin. 1991, 7, 103–106. [Google Scholar]
- Radhakrishnan, N.; Gangadhar, B. Estimating regularity in epileptic seizure time-series data. IEEE Eng. Med. Biol. Mag. 1998, 17, 89–94. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Li, Z.; Zheng, X.; Ma, H.; Yu, X. A generalization of Lempel-Ziv complexity and its application to the comparison of protein sequences. J. Math. Chem. 2010, 48, 330–338. [Google Scholar] [CrossRef]
- Nagarajan, R. Quantifying physiological data with Lempel-Ziv complexity-certain issues. IEEE Trans. Biomed. Eng. 2002, 49, 1371–1373. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Gao, J.; Principe, J.C. Analysis of biomedical signals by the Lempel-Ziv complexity: The effect of finite data size. IEEE Trans. Biomed. Eng. 2006, 53, 2606–2609. [Google Scholar] [PubMed]
- Zhang, X.S.; Zhu, Y.S.; Thakor, N.V.; Wang, Z.Z. Detecting ventricular tachycardia and fibrillation by complexity measure. IEEE Trans. Biomed. Eng. 1999, 46, 548–555. [Google Scholar] [CrossRef] [PubMed]
- Aboy, M.; Hornero, R.; Abásolo, D.; Álvarez, D. Interpretation of the Lempel-Ziv complexity measure in the context of biomedical signal analysis. IEEE Trans. Biomed. Eng. 2006, 53, 2282–2288. [Google Scholar] [CrossRef] [PubMed]
- Melchert, O.; Hartmann, A. Analysis of the phase transition in the two-dimensional Ising ferromagnet using a Lempel-Ziv string-parsing scheme and black-box data-compression utilities. Phys. Rev. E 2015, 91, 023306. [Google Scholar] [CrossRef] [PubMed]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Pincus, S. Approximate entropy (ApEn) as a complexity measure. Chaos Interdiscip. J. Nonlinear Sci. 1995, 5, 110–117. [Google Scholar] [CrossRef] [PubMed]
- Tang, L.; Lv, H.; Yang, F.; Yu, L. Complexity testing techniques for time series data: A comprehensive literature review. Chaos Solitons Fractals 2015, 81, 117–135. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Alcaraz, R.; Rieta, J. A novel application of sample entropy to the electrocardiogram of atrial fibrillation. Nonlinear Anal. Real World Appl. 2010, 11, 1026–1035. [Google Scholar] [CrossRef]
- Eduardo Virgilio Silva, L.; Otavio Murta, L., Jr. Evaluation of physiologic complexity in time series using generalized sample entropy and surrogate data analysis. Chaos Interdiscip. J. Nonlinear Sci. 2012, 22, 043105. [Google Scholar] [CrossRef] [PubMed]
- Mihailović, D.; Nikolić-Đorić, E.; Drešković, N.; Mimić, G. Complexity analysis of the turbulent environmental fluid flow time series. Phys. Stat. Mech. Its Appl. 2014, 395, 96–104. [Google Scholar] [CrossRef]
- Stein, E.M.; Shakarchi, R. Fourier Analysis: An Introduction; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Dym, H.; McKean, H. Fourier Series and Integrals; Academic Press: San Diego, CA, USA, 1972. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Pachori, R.B. Discrimination between ictal and seizure-free EEG signals using empirical mode decomposition. Res. Lett. Signal Process. 2008, 2008, 14. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E.; Long, S.R.; Peng, C.K. On the trend, detrending, and variability of nonlinear and nonstationary time series. Proc. Natl. Acad. Sci. USA 2007, 104, 14889–14894. [Google Scholar] [CrossRef] [PubMed]
- Berry, M.V. Diffractals. J. Phys. Math. Gen. 1979, 12, 781–797. [Google Scholar] [CrossRef]
- Fleckinger-Pelle, J.; Lapidus, M. Tambour fractal: Vers une résolution de la conjecture de Weyl-Berry pour les valeurs propres du laplacien. C. R. Acad. Sci. Sér. Math. 1988, 306, 171–175. [Google Scholar]
- Valério, D.; Lopes, A.M.; Tenreiro Machado, J.A.T. Entropy Analysis of a Railway Network’s Complexity. Entropy 2016, 18, 388. [Google Scholar] [CrossRef]
- Menne, M.J.; Durre, I.; Vose, R.S.; Gleason, B.E.; Houston, T.G. An overview of the global historical climatology network-daily database. J. Atmos. Ocean. Technol. 2012, 29, 897–910. [Google Scholar] [CrossRef]
- Steffen, K.; Box, J.; Abdalati, W. Greenland Climate Network: GC-Net; US Army Cold Regions Reattach and Engineering (CRREL), CRREL Special Report; CRREL: Hanover, NH, USA, 1996; pp. 98–103. [Google Scholar]
- Willmott, C.J.; Matsuura, K. Terrestrial Air Temperature and Precipitation: Monthly and Annual Time Series (1950–1996). 2000. Available online: http://climate.geog.udel.edu/~climate/html_pages/Global2014/README.GlobalTsT2014.html (accessed on 20 February 2018).
- Huang, N.E.; Wu, M.L.C.; Long, S.R.; Shen, S.S.; Qu, W.; Gloersen, P.; Fan, K.L. A confidence limit for the empirical mode decomposition and Hilbert spectral analysis. Proc. R. Soc. Math. Phys. Eng. Sci. 2003, 459, 2317–2345. [Google Scholar] [CrossRef]
- Polderman, J.W.; Willems, J.C. Introduction to Mathematical Systems Theory: A Behavioral Approach; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Lopes, A.M.; Machado, J.A.T. State space analysis of forest fires. J. Vib. Control 2016, 22, 2153–2164. [Google Scholar] [CrossRef]
- Machado, J.A.T.; Lopes, A.M. Analysis and visualization of seismic data using mutual information. Entropy 2013, 15, 3892–3909. [Google Scholar] [CrossRef]
- Murtagh, F. A survey of recent advances in hierarchical clustering algorithms. Comput. J. 1983, 26, 354–359. [Google Scholar] [CrossRef]
- Cha, S.H. Comprehensive survey on distance/similarity measures between probability density functions. Int. J. Math. Models Methods Appl. Sci. 2007, 4, 300–307. [Google Scholar]
- Ellenburg, W.; McNider, R.; Cruise, J.; Christy, J.R. Towards an understanding of the twentieth-century cooling trend in the southeastern United States: Biogeophysical impacts of land-use change. Earth Interact. 2016, 20, 1–31. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lopes, A.M.; Tenreiro Machado, J.A. Complexity Analysis of Global Temperature Time Series. Entropy 2018, 20, 437. https://doi.org/10.3390/e20060437
Lopes AM, Tenreiro Machado JA. Complexity Analysis of Global Temperature Time Series. Entropy. 2018; 20(6):437. https://doi.org/10.3390/e20060437
Chicago/Turabian StyleLopes, António M., and J. A. Tenreiro Machado. 2018. "Complexity Analysis of Global Temperature Time Series" Entropy 20, no. 6: 437. https://doi.org/10.3390/e20060437
APA StyleLopes, A. M., & Tenreiro Machado, J. A. (2018). Complexity Analysis of Global Temperature Time Series. Entropy, 20(6), 437. https://doi.org/10.3390/e20060437





