Entropy Generation Minimization for Reverse Water Gas Shift (RWGS) Reactors
Abstract
:1. Introduction
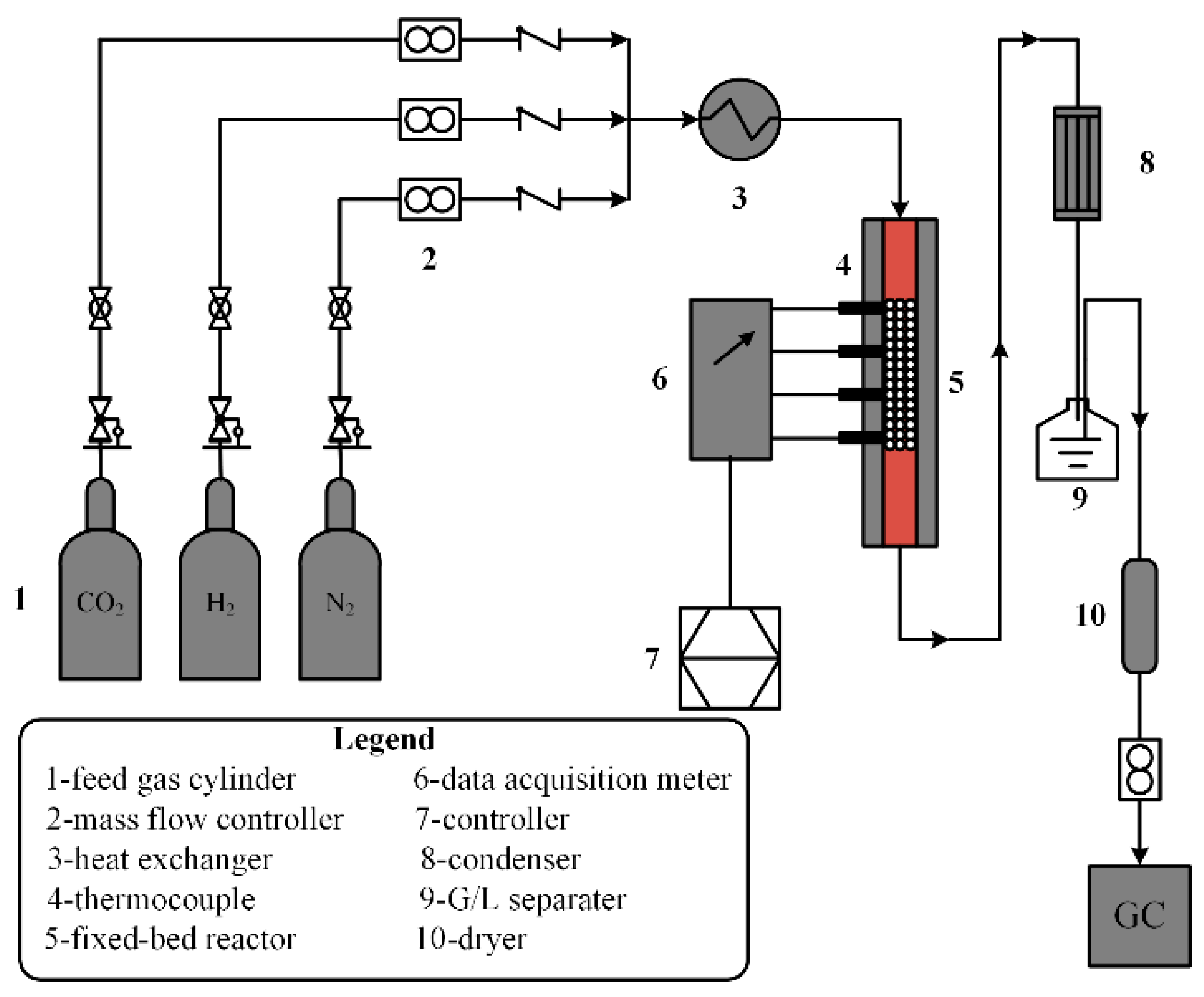
2. The RWGS Reactor System
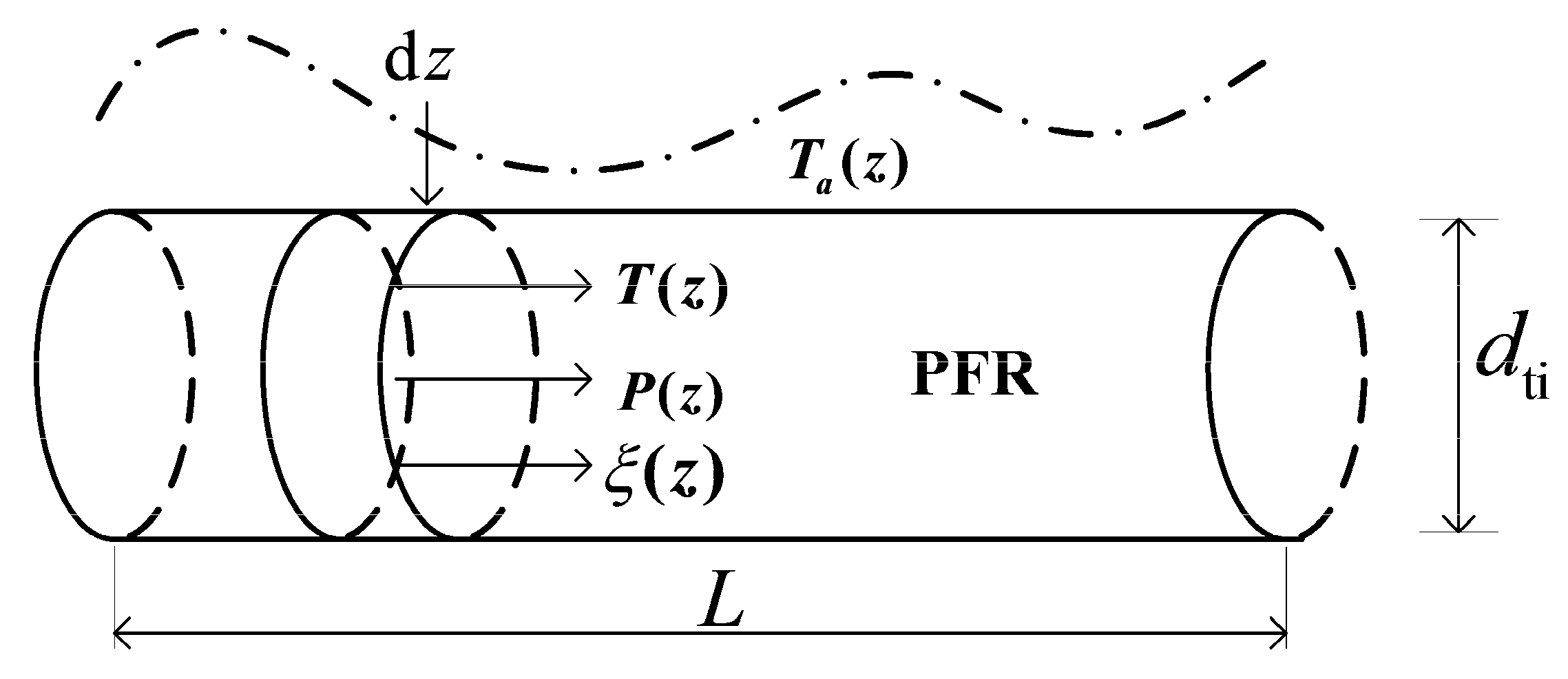
2.1. The Technical Reactor Model
2.2. Conservation Equations
2.3. Chemical Reaction Rate
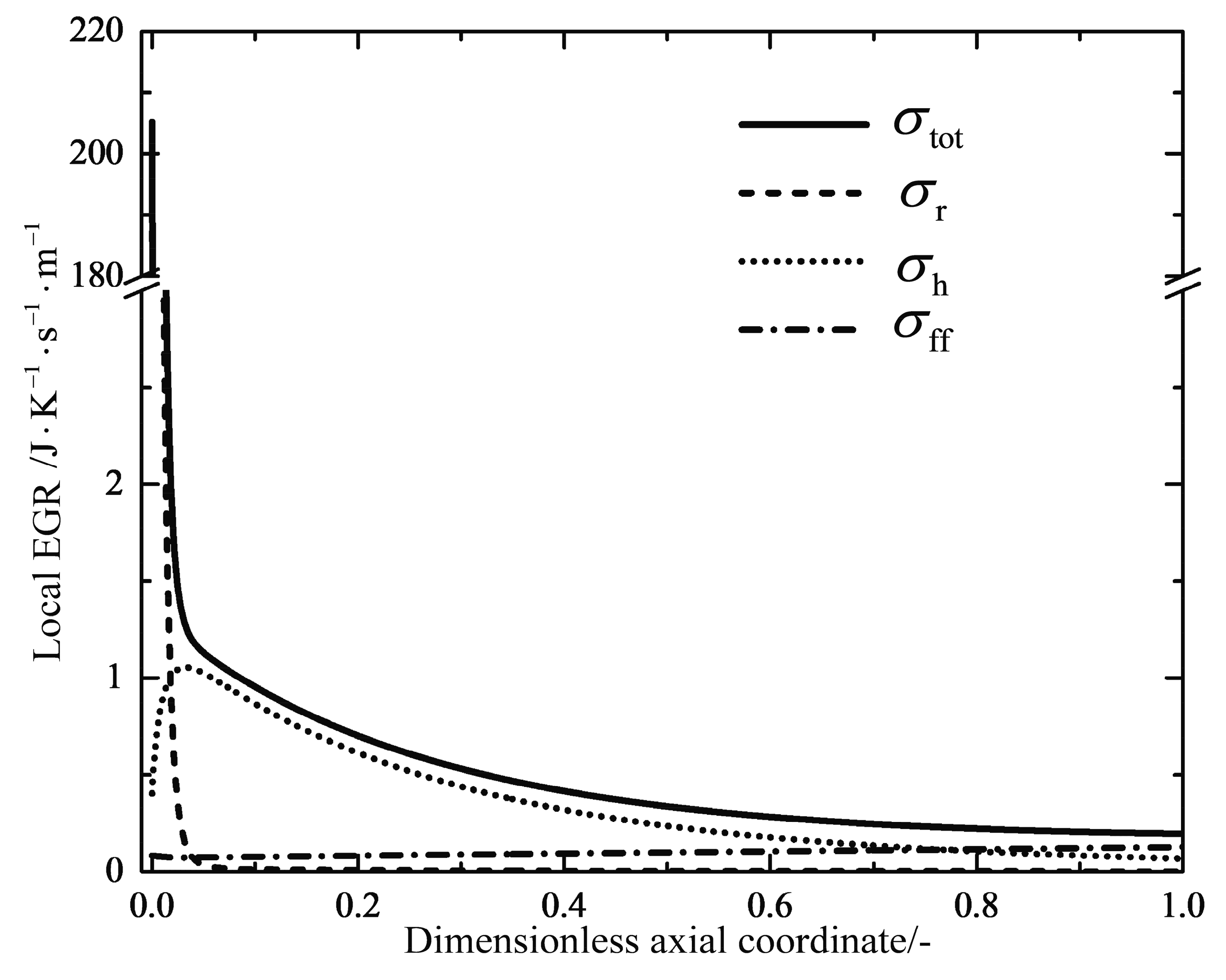
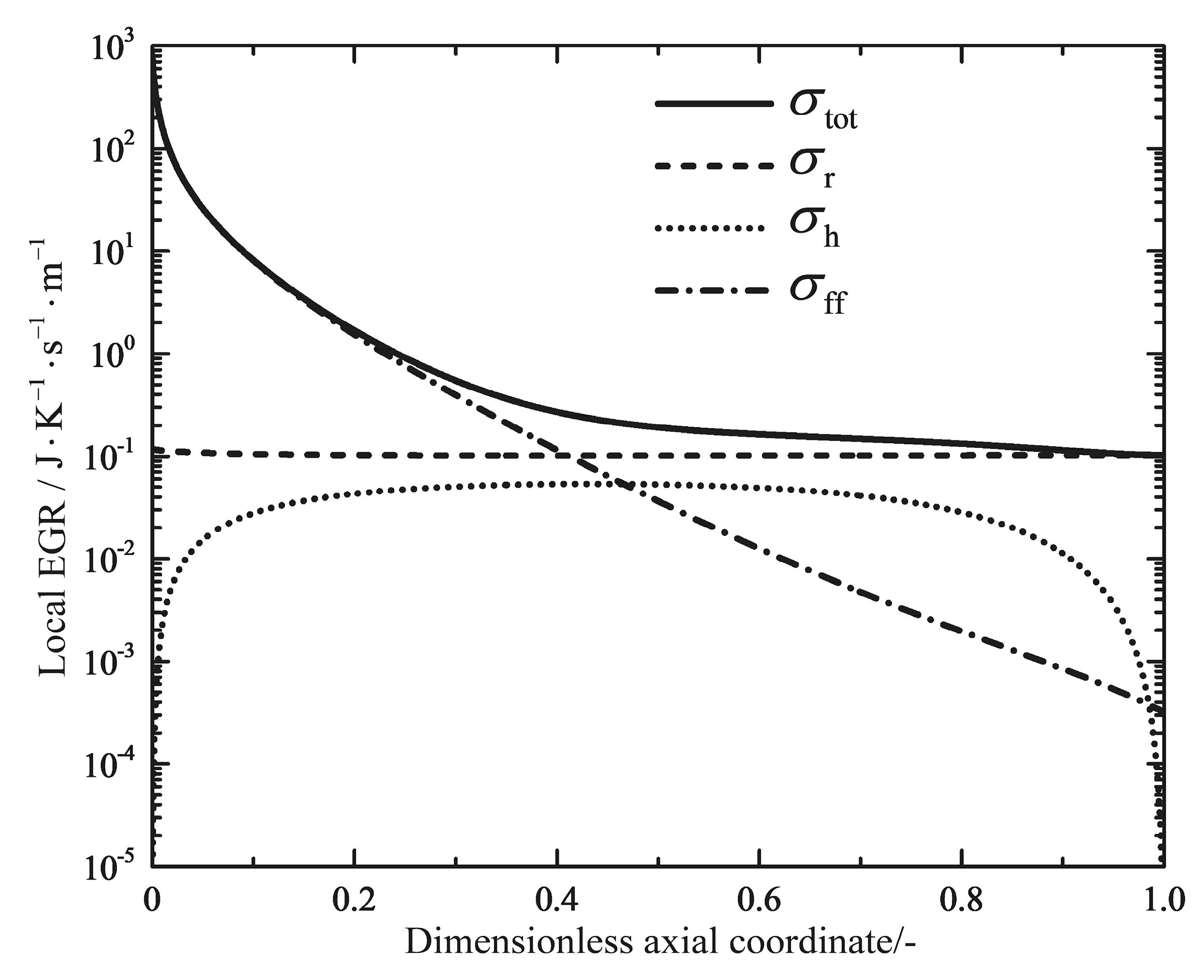
2.4. Entropy Generation Rate
3. Optimal Configurations of the RWGS Reactor
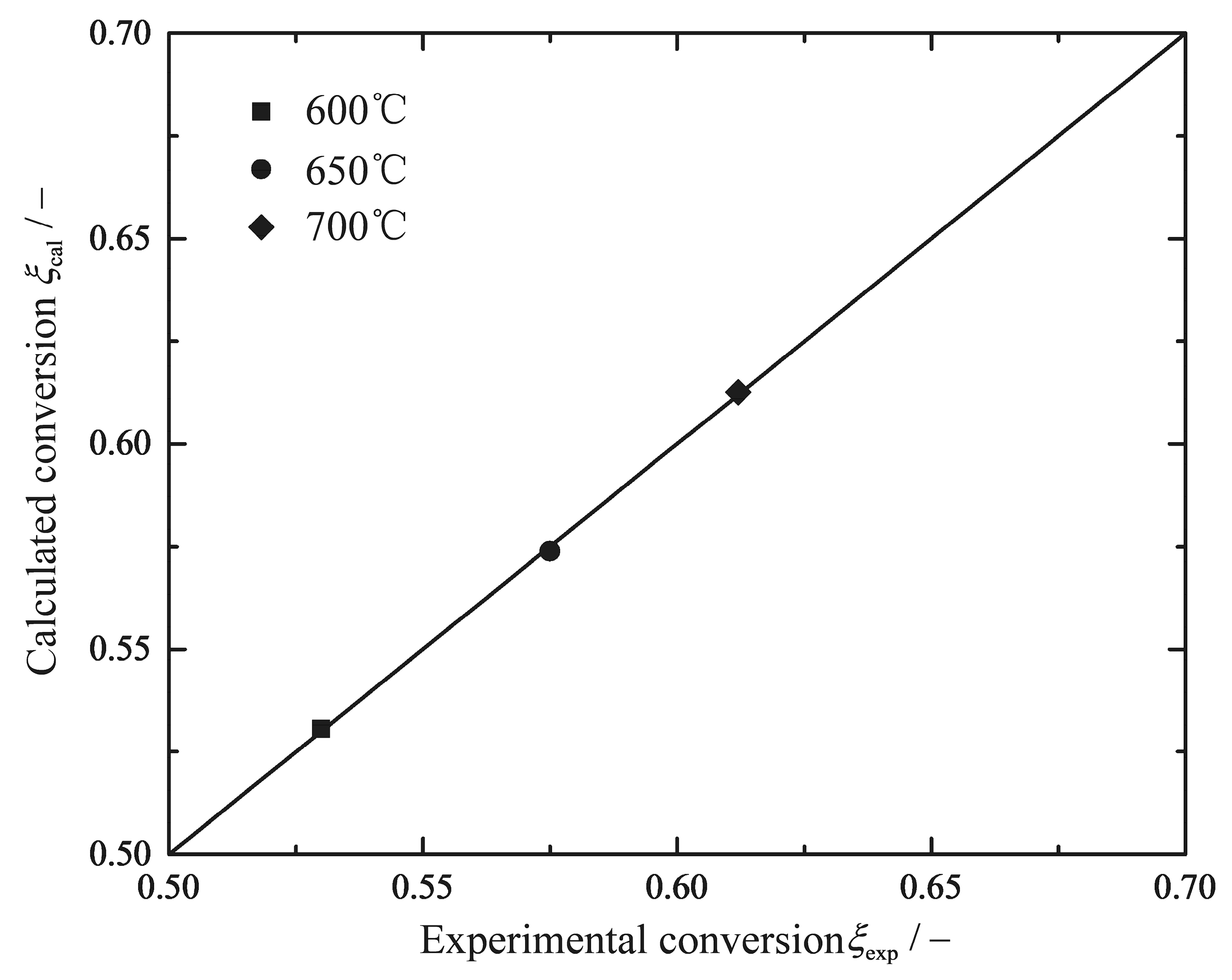
3.1. Parameter Settings of Reference Reactors
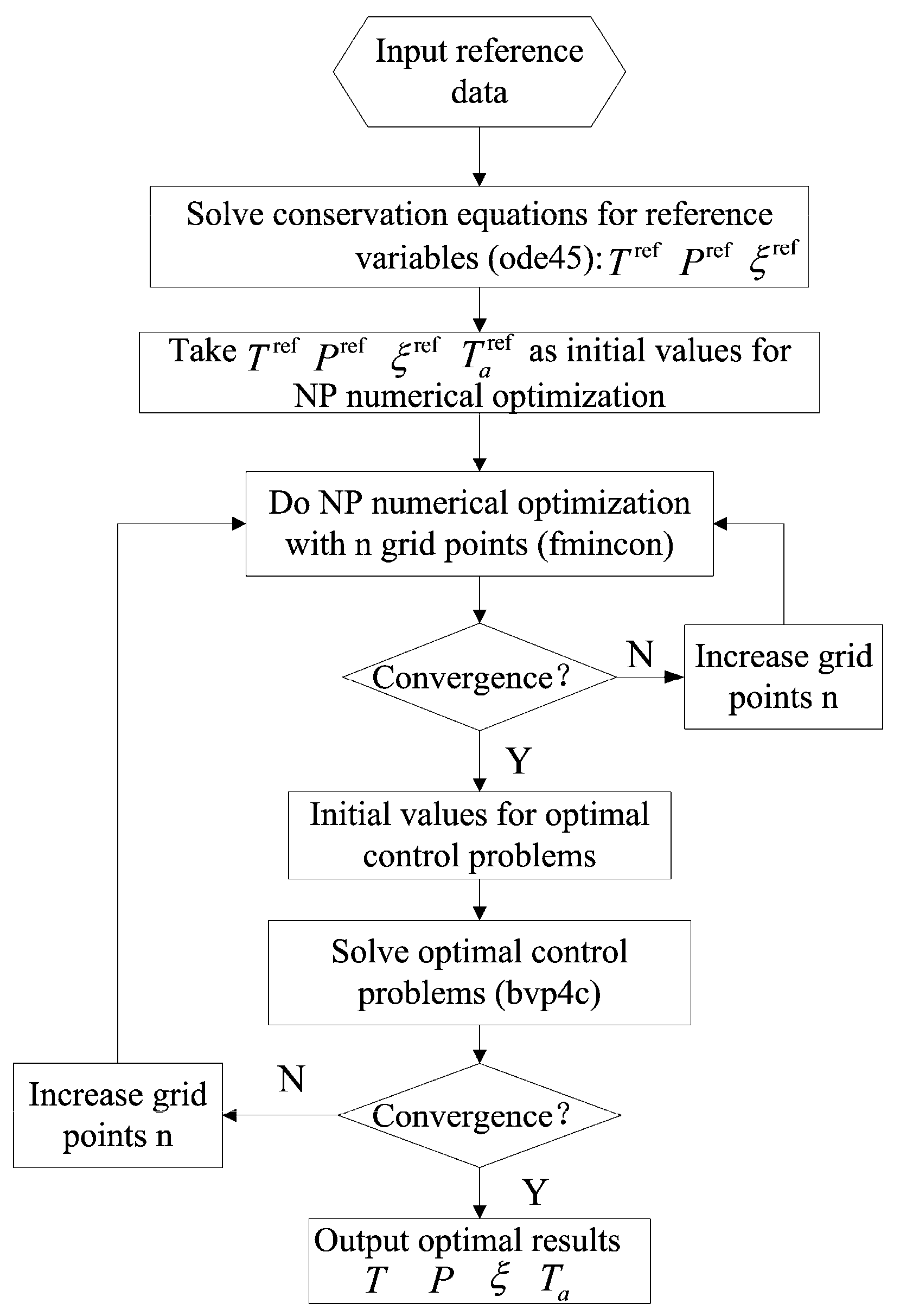
3.2. Optimal Control Theory
- (1)
- Solve the reference reactor models to provide the boundary conditions for the following optimizations.
- (2)
- The reactor model is optimized using as the control variable with a fixed inlet temperature of the feed gas , the optimal result is called “Case 1”.
- (3)
- Take the reactor length as an additional variable, the same optimization in step 2 is done between the range . The optimal solution corresponding to the optimal reactor length is called “Case 2”.
- (4)
- The following optimization is completed with as the control variable, but with a free inlet temperature of the feed gas, the optimal result is called “Case 3”.
- (5)
- Finally, the reactor length is taken as an additional variable again with a free inlet temperature of the feed gas, the optimization work is performed repeatedly between the range . The optimal solution corresponding to the optimal reactor length is called “Case 4”.
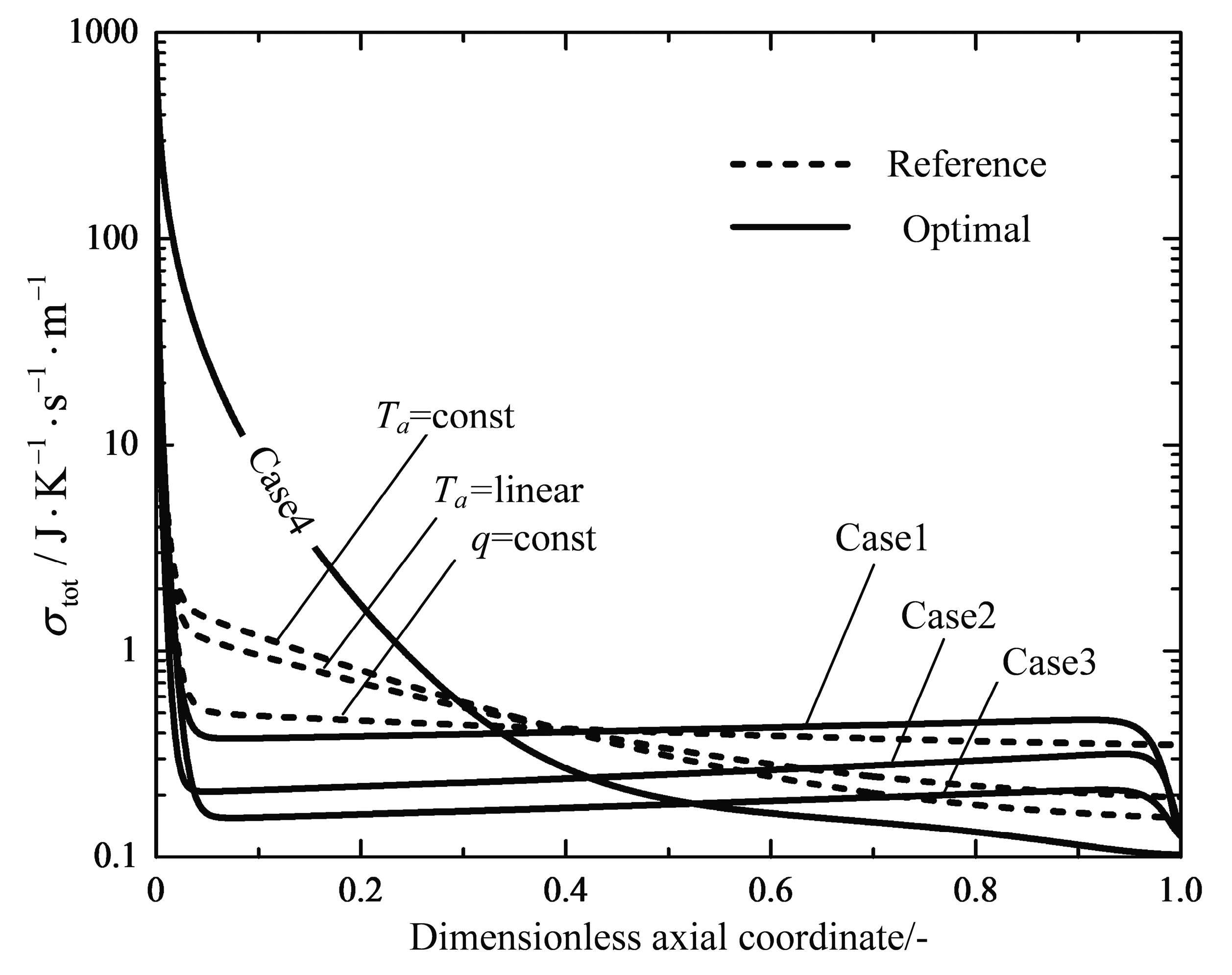
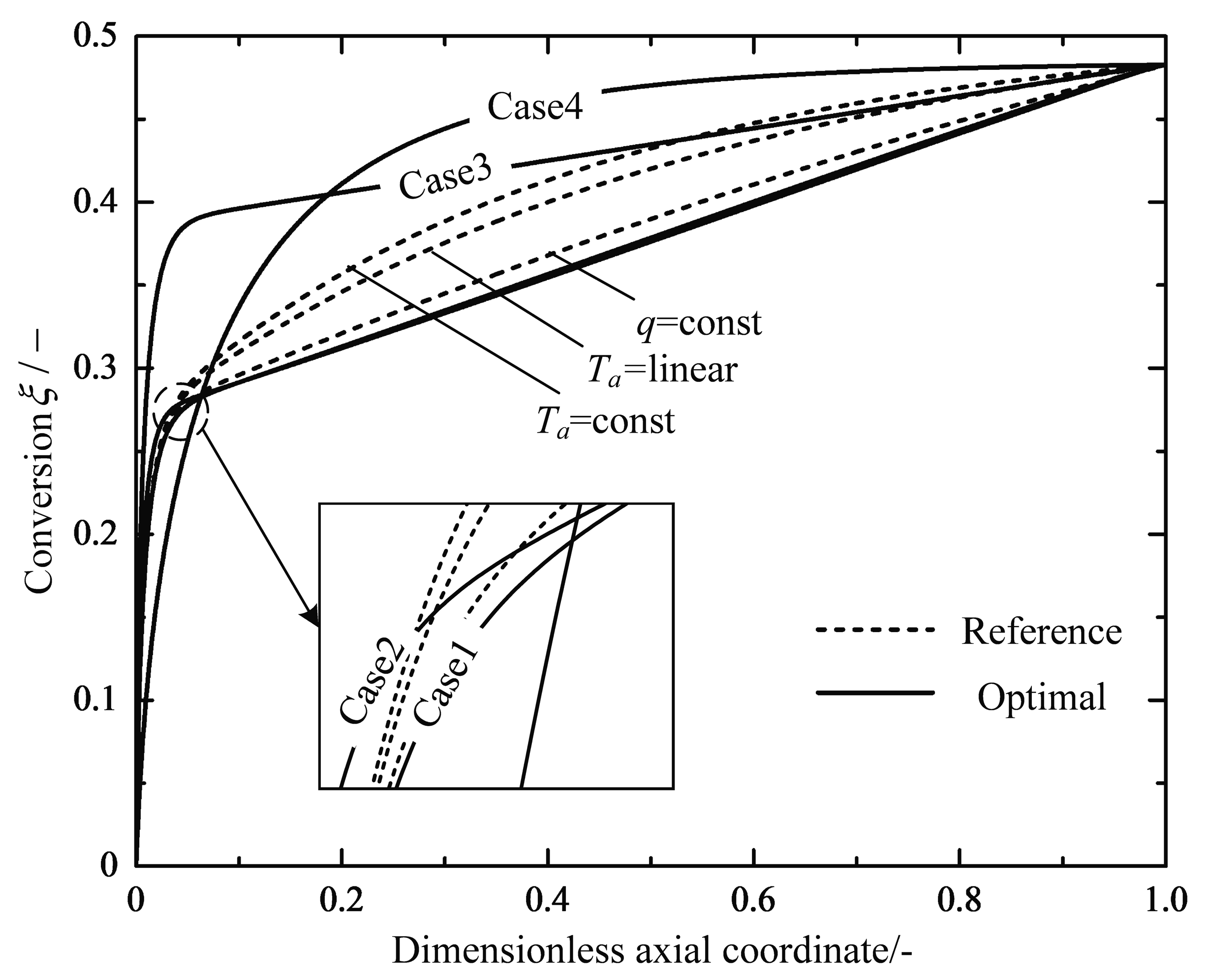
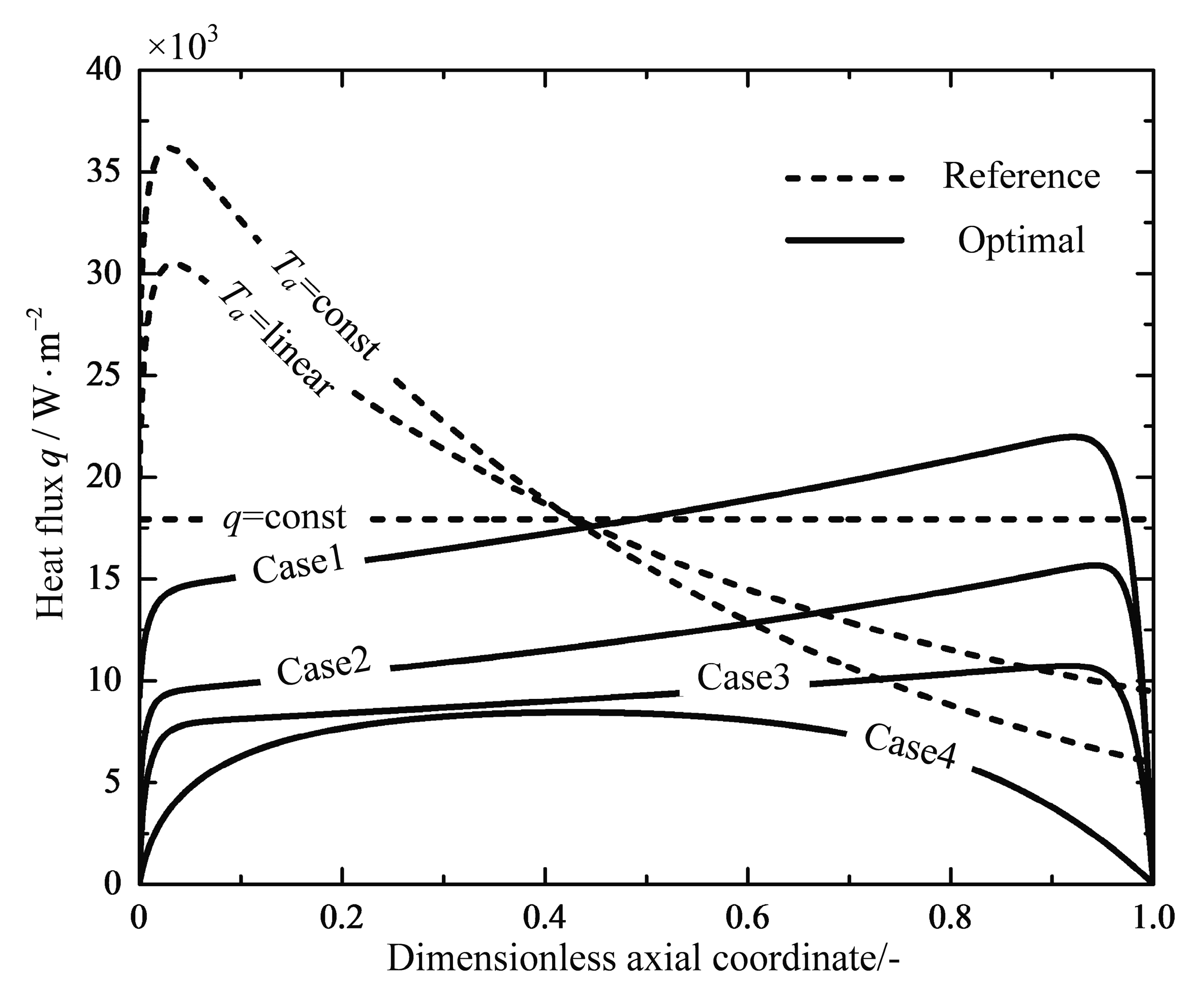
4. Numerical Examples and Discussions
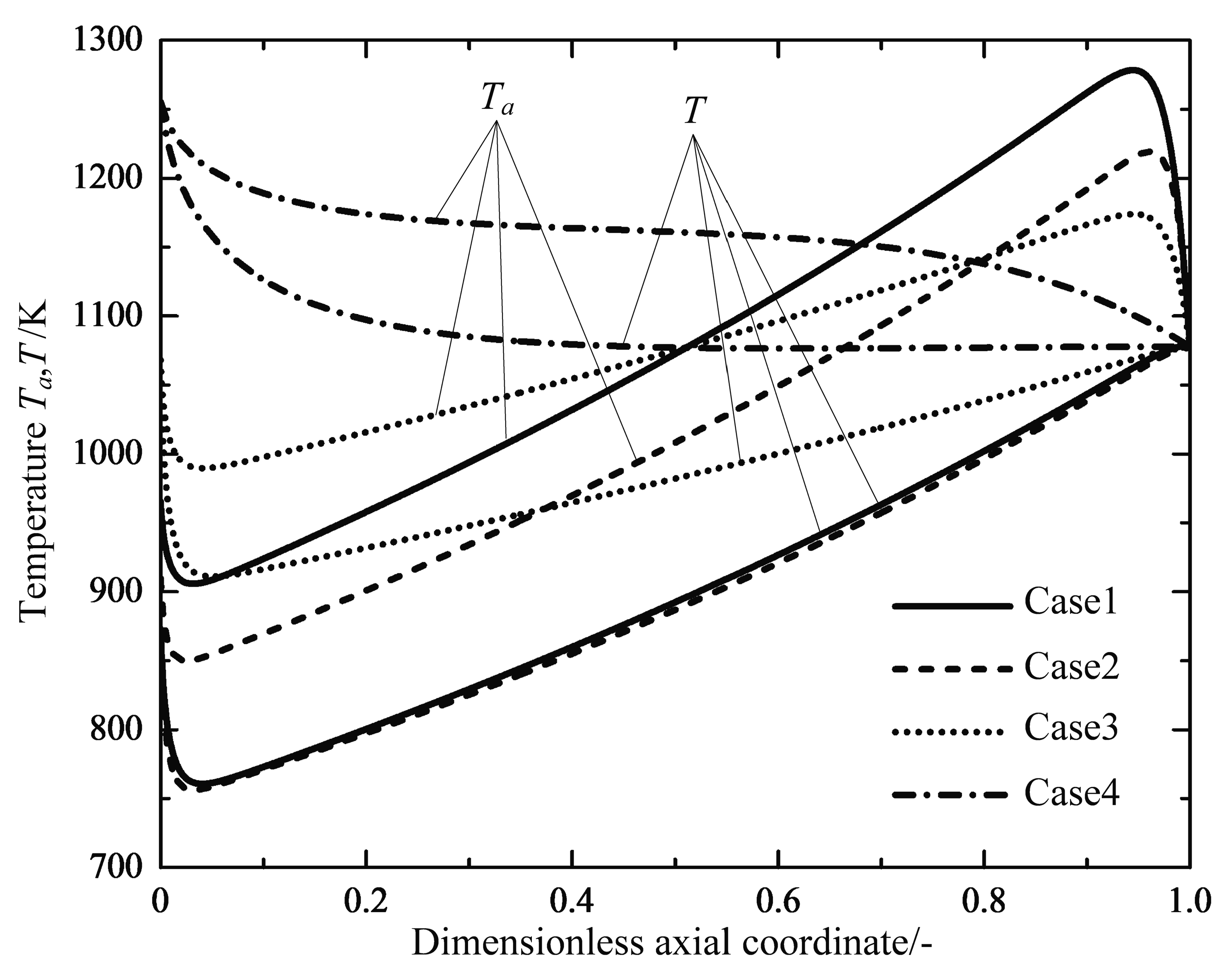
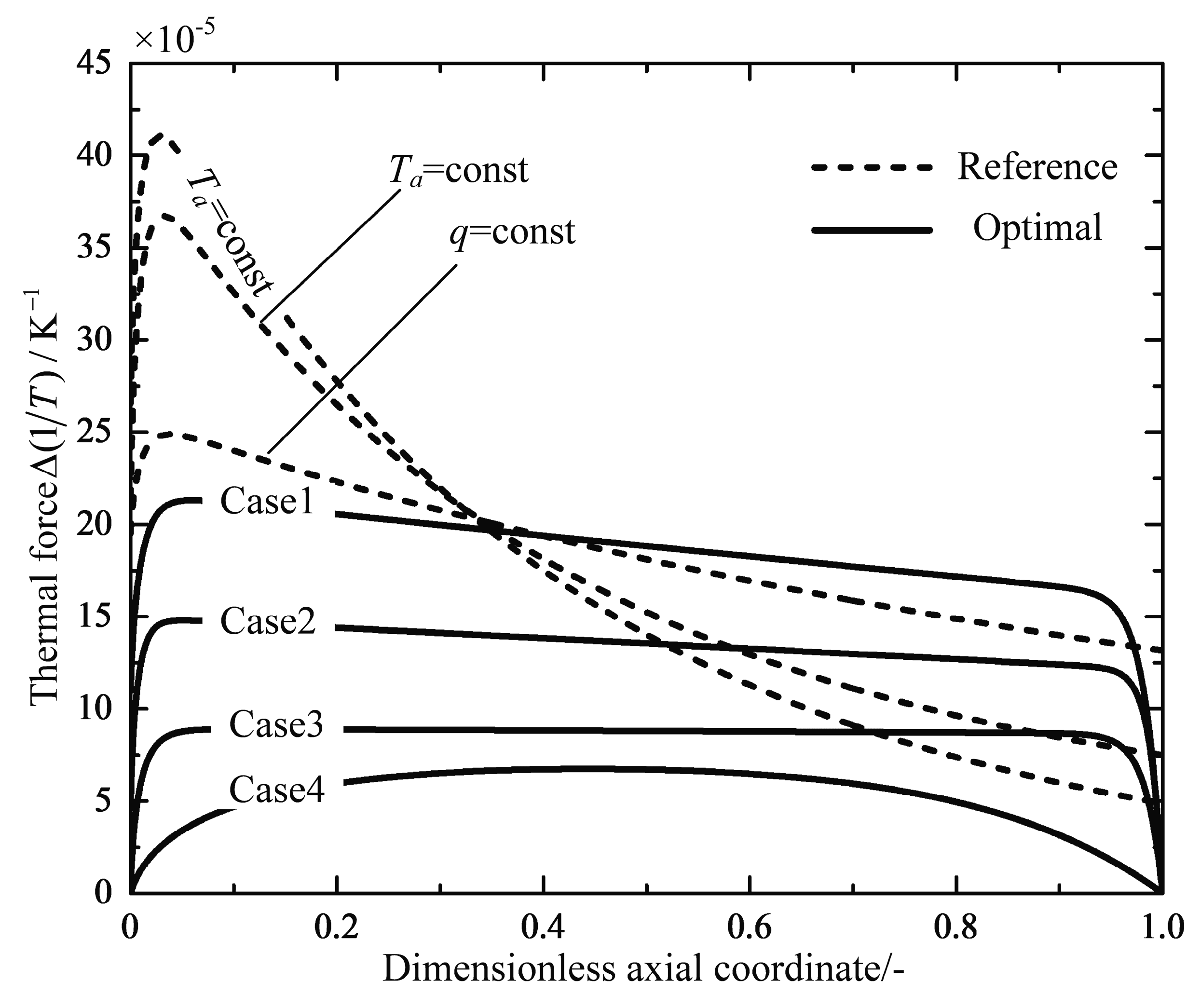
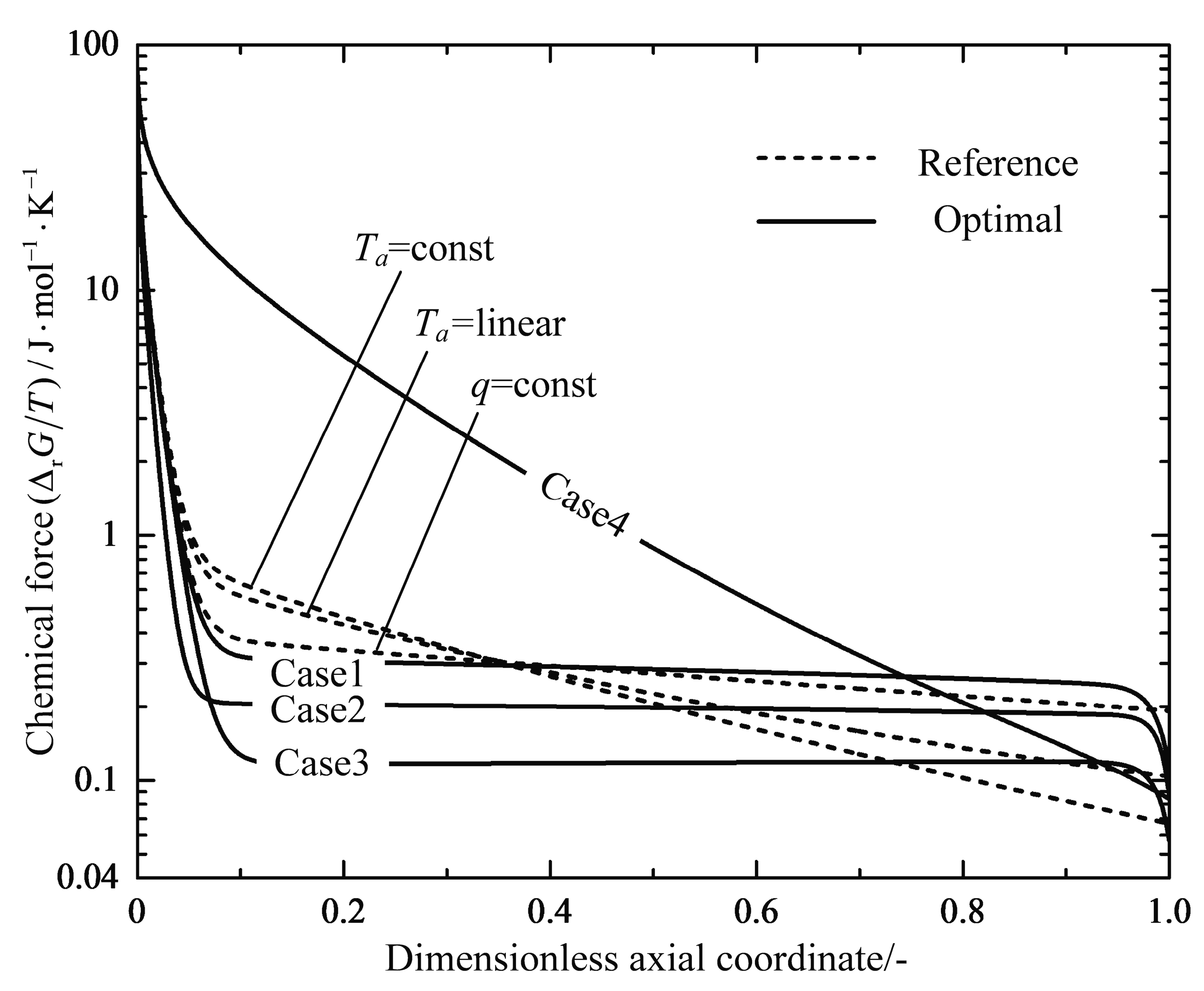
4.1. Analyses of Numerical Results
4.2. Engineering Applications
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Saeidi, S.; Najari, S.; Fazlollahi, F.; Nikoo, M.K.; Sefidkon, F.; Klemeš, J.J. Mechanisms and kinetics of CO2 hydrogenation to value-added products: A detailed review on current status and future trends. Renew. Sustain. Energy Rev. 2017, 80, 1292–1311. [Google Scholar] [CrossRef]
- Centi, G.; Perathoner, S. Opportunities and prospects in the chemical recycling of carbon dioxide to fuels. Catal. Today 2009, 148, 191–205. [Google Scholar] [CrossRef]
- Wei, J.; Ge, Q.J.; Yao, R.W.; Wen, Z.Y.; Fang, C.Y.; Guo, L.S. Directly converting CO2 into a gasoline fuel. Nat. Commun. 2017, 8, 15174. [Google Scholar] [CrossRef] [PubMed]
- Abanades, J.C.; Rubin, E.S.; Mazzotti, M.; Herzog, H.J. On the climate change mitigation potential of CO2 conversion to fuels. Energy Environ. Sci. 2017, 10, 2491–2499. [Google Scholar] [CrossRef]
- Saeidi, S.; Amin, N.A.S.; Rahimpour, M.R. Hydrogenation of CO2 to value-added products–A review and potential future developments. J. CO2 Util. 2014, 5, 66–81. [Google Scholar] [CrossRef]
- Dorner, R.W.; Hardy, D.R.; Williams, F.W.; Willauer, H.D. Heterogeneous catalytic CO2 conversion to value-added hydrocarbons. Energy Environ. Sci. 2010, 3, 884–890. [Google Scholar] [CrossRef]
- Willauer, H.D.; Hardy, D.R.; Baldwin, J.W.; DiMascio, F.; Williams, F.W.; Bradley, M.J. Economic comparisons of littoral production of low carbon fuel from non-fossil energy sources and seawater. J. Clean. Prod. 2018, 170, 1473–1483. [Google Scholar] [CrossRef]
- Porosoff, M.D.; Yan, B.H.; Chen, J.G. Catalytic reduction of CO2 by H2 for synthesis of CO, methanol and hydrocarbons: Challenges and opportunities. Energy Environ. Sci. 2016, 9, 62–73. [Google Scholar] [CrossRef]
- Willauer, H.D.; Hardy, D.R.; Moyer, S.A.; DiMascio, F.; Williams, F.W.; Drab, D.M. An economic basis for littoral land-based production of low carbon fuel from nuclear electricity and seawater for naval or commercial use. Energy Policy 2015, 81, 67–75. [Google Scholar] [CrossRef]
- Kaiser, P.; Unde, R.B.; Kern, C.; Jess, A. Production of light hydrocarbons with CO2 as carbon source based on reverse water-gas shift and Fischer-Tropsch synthesis. Chem. Ing. Tech. 2013, 85, 489–499. [Google Scholar] [CrossRef]
- Porosoff, M.D.; Baldwin, J.W.; Peng, X.; Mpourmpakis, G.; Willauer, H.D. Potassium-promoted molybdenum carbide as a highly active and selective catalyst for CO2 conversion to CO. ChemSusChem 2017, 10, 2408–2415. [Google Scholar] [CrossRef] [PubMed]
- Gao, P.; Li, S.G.; Bu, X.N.; Dang, S.S.; Liu, Z.Y.; Wang, H. Direct conversion of CO2 into liquid fuels with high selectivity over a bifunctional catalyst. Nat. Chem. 2017, 9, 1019–1024. [Google Scholar] [CrossRef] [PubMed]
- Bradley, M.J.; Ananth, R.; Willauer, H.D.; Baldwin, J.W. The role of catalyst environment on CO2 hydrogenation in a fixed-bed reactor. J. CO2 Util. 2017, 17, 1–9. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, L.G.; Xia, S.J.; Wang, C.; Sun, F.R. Thermodynamics analyses of hydrogenation of carbon dioxide to light olefins. J. Eng. Thermophys. 2017, 38, 1135–1143. (In Chinese) [Google Scholar]
- Daza, Y.A.; Kuhn, J.N. CO2 conversion by reverse water gas shift catalysis: comparison of catalysts, mechanisms and their consequences for CO2 conversion to liquid fuels. RSC Adv. 2016, 6, 49675–49691. [Google Scholar] [CrossRef]
- Kharaji, A.G.; Shariati, A.; Takassi, M.A. A novel γ-alumina supported Fe-Mo bimetallic catalyst for reverse water gas shift reaction. Chin. J. Chem. Eng. 2013, 21, 1007–1014. [Google Scholar] [CrossRef]
- Ghodoosi, F.; Khosravi-Nikou, M.R.; Shariati, A. Mathematical modeling of reverse water-gas shift reaction over Fe-Mo/Al2O3 catalyst in a fixed bed reactor. Chem. Eng. Technol. 2017, 40, 598–607. [Google Scholar] [CrossRef]
- Andresen, B.; Berry, R.S.; Ondrechen, M.J.; Salamon, P. Thermodynamics of processes in finite time. Acc. Chem. Res. 1984, 17, 266–271. [Google Scholar] [CrossRef]
- Andresen, B.; Salamon, P.; Berry, R.S. Thermodynamics in finite time. Phys. Today 1984, 37, 62. [Google Scholar] [CrossRef]
- Sieniutycz, S.; Shiner, J.S. Thermodynamics of irreversible processes and its relation to chemical engineering: Second law analyses and finite time thermodynamics. J. Non-Equil. Thermodyn. 1994, 19, 303–348. [Google Scholar]
- Chen, L.G.; Wu, C.; Sun, F.R. Finite time thermodynamic optimization or entropy generation minimization of energy systems. J. Non-Equil. Thermodyn. 1999, 22, 327–359. [Google Scholar] [CrossRef]
- Chen, L.G. Finite-Time Thermodynamic Analysis of Irreversible Processes and Cycles; Higher Education Press: Beijing, China, 2005. (In Chinese) [Google Scholar]
- Schön, J.C. Finite-time thermodynamics and the optimal control of chemical syntheses. Z. Anorg. Allg. Chem. 2009, 635, 1794–1806. [Google Scholar] [CrossRef]
- Ge, Y.L.; Chen, L.G.; Sun, F.R. Progress in finite time thermodynamic studies for internal combustion engine cycles. Entropy 2016, 18, 139. [Google Scholar] [CrossRef]
- Chen, L.G.; Feng, H.J.; Xie, Z.H. Generalized thermodynamic optimization for iron and steel production processes: Theoretical exploration and application cases. Entropy 2016, 18, 353. [Google Scholar] [CrossRef]
- Kosloff, R.; Rezek, Y. The quantum harmonic Otto cycle. Entropy 2017, 19, 136. [Google Scholar] [CrossRef]
- Chen, L.G.; Xia, S.J. Generalized Thermodynamic Dynamic-Optimization for Irreversible Processes; Science Press: Beijing, China, 2017. (In Chinese) [Google Scholar]
- Chen, L.G.; Xia, S.J. Generalized Thermodynamic Dynamic-Optimization for Irreversible Cycles–Thermodynamic and Chemical Theoretical Cycles; Science Press: Beijing, China, 2017. (In Chinese) [Google Scholar]
- Chen, L.G.; Xia, S.J. Generalized Thermodynamic Dynamic-Optimization for Irreversible Cycles–Engineering Thermodynamic Plants and Generalized Engine Cycles; Science Press: Beijing, China, 2017. (In Chinese) [Google Scholar]
- Feidt, M. The history and perspectives of efficiency at maximum power of the Carnot engine. Entropy 2017, 19, 369. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Minimization: The Method of Thermodynamic Optimization of Finite-Size Systems and Finite-Time Processes; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Bejan, A. Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes. J. Appl. Phys. 1996, 79, 1191–1218. [Google Scholar] [CrossRef]
- Bejan, A. Notes on the history of the method of entropy generation minimization (finite time thermodynamics). J. Non-Equil. Thermodyn. 1996, 21, 239–242. [Google Scholar]
- Bejan, A. Entropy generation minimization, exergy analysis, and the constructal law. Arab. J. Sci. Eng. 2013, 38, 329–340. [Google Scholar] [CrossRef]
- Sciacovelli, A.; Verda, V.; Sciubba, E. Entropy generation analysis as a design tool—A review. Renew. Sustain. Energy Rev. 2015, 43, 1167–1181. [Google Scholar] [CrossRef]
- Månson, B.; Andresen, B. Optimal temperature profile for an ammonia reactor. Ind. Eng. Chem. Process Des. Dev. 1986, 25, 59–65. [Google Scholar] [CrossRef]
- Bak, T.A.; Salamon, P.; Andresen, B. Optimal behavior of consecutive chemical reaction . J. Phys. Chem. A 2002, 106, 10961–10964. [Google Scholar] [CrossRef]
- Chen, L.G.; Song, H.J.; Sun, F.R. Optimal path of consecutive chemical reactions . Phys. Scr. 2009, 79, 55802. [Google Scholar]
- Wang, C.; Chen, L.G.; Xia, S.J.; Sun, F.R. Optimal concentration configuration of consecutive chemical reaction for minimum entropy generation. J. Non-Equil. Thermodyn. 2016, 41, 313–326. [Google Scholar] [CrossRef]
- Chen, L.G.; Xia, S.J.; Sun, F.R. Performance limits for a class of irreversible internal combustion engines. Energy Fuel. 2010, 24, 295–301. [Google Scholar] [CrossRef]
- Wagner, K.; Hoffmann, K.H. Chemical reactions in endoreversible thermodynamics. Eur. J. Phys. 2016, 37, 15101. [Google Scholar] [CrossRef]
- Wagner, K.; Hoffmann, K.H. Endoreversible modeling of a PEM fuel cell. J. Non-Equil. Thermodyn. 2015, 40, 283–294. [Google Scholar] [CrossRef]
- Johannessen, E.; Kjelstrup, S. Minimum entropy production rate in plug flow reactors: An optimal control problem solved for SO2 oxidation. Energy 2004, 29, 2403–2423. [Google Scholar] [CrossRef]
- Nummedal, L.; Røsjorde, A.; Johannessen, E.; Kjelstrup, S. Second law optimization of a tubular steam reformer. Chem. Eng. Proc. 2005, 44, 429–440. [Google Scholar] [CrossRef]
- Wilhelmsen, Ø.; Johannessen, E.; Kjelstrup, S. Energy efficient reactor design simplified by second law analysis. Int. J. Hydrog. Energy 2010, 35, 13219–13231. [Google Scholar] [CrossRef]
- Van der Ham, L.V.; Gross, J.; Verkooijen, A.; Kjelstrup, S. Efficient conversion of thermal energy into hydrogen: comparing two methods to reduce exergy losses in a sulfuric acid decomposition reactor. Ind. Eng. Chem. Res. 2009, 48, 8500–8507. [Google Scholar] [CrossRef]
- Ao, C.Y.; Xia, S.J.; Song, H.J.; Chen, L.G. Entropy generation minimization of steam methane reforming reactor with linear phenomenological heat transfer law. Sci. Sin. Tech. 2018, 48, 25–38. (In Chinese) [Google Scholar] [CrossRef]
- Kigston, D.; Razzitte, A.C. Entropy production in chemical reactors. J. Non-Equil. Thermodyn. 2017, 42, 265–275. [Google Scholar]
- Kingston, D.; Razzitte, A.C. Entropy generation minimization in dimethyl ether synthesis: A case study. J. Non-Equil. Thermodyn. 2018, 43, 111–120. [Google Scholar] [CrossRef]
- Wang, C.; Chen, L.G.; Xia, S.J.; Sun, F.R. Maximum production rate optimization for sulphuric acid decomposition process in tubular plug-flow reactor. Energy 2016, 99, 152–158. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, L.G.; Sun, F.R. Power optimization chemically driven heat engine based on first and second order reaction kinetic theory and probability theory. Physica A 2016, 445, 221–230. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, L.G.; Sun, F.R. Finite-time thermodynamic analysis for a chemically driven heat engine based on probability theory. Sci. Sin. Tech. 2016, 46, 535–546. (In Chinese) [Google Scholar]
- Chen, L.G.; Wang, C.; Xia, S.J.; Sun, F.R. Thermodynamic analyses and optimizations of extraction process of CO2 from acid seawater by using hollow fiber membrane contactor. Int. J. Heat Mass Trans. 2018, 124, 1310–1320. [Google Scholar] [CrossRef]
- Chen, L.G.; Zhang, L.; Xia, S.J.; Sun, F.R. Entropy generation minimization for CO2 hydrogenation to light olefins. Energy 2018, 147, 187–196. [Google Scholar] [CrossRef]
- Watowich, S.J.; Berry, R.S. Optimal current path for model electrochemical systems. J. Phys. Chem. 1986, 90, 4624–4631. [Google Scholar] [CrossRef]
- Szwast, Z.; Sieniutycz, S. Optimal temperature profiles for parallel-consecutive reactions with deactivating catalyst. Catal. Today 2001, 66, 461–466. [Google Scholar] [CrossRef]
- Forment, G.F.; Bischoff, K.B. Chemical Reactor Analysis and Design, 2nd ed.; Wiley: New York, NY, USA, 1990. [Google Scholar]
- Wilhelmsen, Ø. The State of Minimum Entropy Production in Reactor Design. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, January 2010. [Google Scholar]
- Willauer, H.D.; Ananth, R.; Olsen, M.T.; Drab, D.M.; Hardy, D.R.; Williams, F.W. Modeling and kinetic analysis of CO2 hydrogenation using a Mn and K-promoted Fe catalyst in a fixed-bed reactor. J. CO2 Util. 2013, 3–4, 56–64. [Google Scholar] [CrossRef]
- Riedel, T.; Schaub, G.; Jun, K.W.; Lee, K.W. Kinetics of CO2 hydrogenation on a K-promoted Fe catalyst. Ind. Eng. Chem. Res. 2001, 40, 1355–1363. [Google Scholar] [CrossRef]
- Chen, L.G.; Shen, X.; Xia, S.J.; Sun, F.R. Thermodynamic analyses for recovering residual heat of high-temperature basic oxygen gas (BOG) by the methane reforming with carbon dioxide reaction. Energy 2017, 118, 906–913. [Google Scholar] [CrossRef]
- Yaws, C.L. Chemical Properties Handbook; McGraw-Hill: New York, NY, USA, 1999. [Google Scholar]
- Bryson, A.; Ho, Y. Applied Optimal Control: Optimization, Estimation and Control; Hemisphere Publishing Corporation: Washington, NY, USA, 1975. [Google Scholar]
- Kjelstrup, S.; Bedeaux, D.; Johannessen, E.; Gross, J. Non-Equilibrium Thermodynamics for Engineers; World Scientific Publishing: Singapore, 2010. [Google Scholar]
- Frost, L.; Elangovan, E.; Hartvigsen, J. Production of synthetic fuels by high-temperature co-electrolysis of carbon dioxide and steam with Fischer-Tropsch synthesis. Can. J. Chem. Eng. 2016, 94, 636–641. [Google Scholar] [CrossRef]
- Johannessen, E.; Kjelstrup, S. A highway in state space for reactors with minimum entropy production. Chem. Eng. Sci. 2005, 60, 3347–3361. [Google Scholar] [CrossRef]
- Spirkl, W.; Ries, H. Optimal finite-time endoreversible processes. Phys. Rev. E 1995, 52, 3485. [Google Scholar] [CrossRef]
- Sauar, E.; Kjelstrup, S.; Lien, K.M. Equipartition of forces: A new principle for process design and optimization. Ind. Eng. Chem. Res. 1996, 35, 4147–4153. [Google Scholar] [CrossRef]

| (600 °C) | (650 °C) | (700 °C) | - | - | ||
|---|---|---|---|---|---|---|
| 0.0429 | 0.0547 | 0.0646 | 65 | 7.4 | 2.324 | 28.91 |
| Parameter | Symbol | Value |
|---|---|---|
| Overall heat transfer coefficient | 100 J∙m−2∙K−1∙s−1 | |
| Reaction mixture viscosity | 3.137 × 10−5 kg∙m−1∙s−1 | |
| Catalyst bed void fraction | 0.65 | |
| Catalyst pellet diameter | 0.006 m | |
| Inlet total molar flow | 0.5 mol∙s−1 | |
| Catalyst bed density | 1603 kg∙m−3 | |
| Reactor inner diameter | 0.03 m | |
| Reactor length | 5 m | |
| Inlet temperature of feed gas | 873 K | |
| Inlet total pressure | 1 MPa | |
| Inlet CO2 molar fraction | 0.495 | |
| Inlet H2 molar fraction | 0.495 | |
| Inlet CO molar fraction | 0.005 | |
| Inlet H2O molar fraction | 0.005 | |
| Inlet reservoir temperature | 1073 K | |
| Outlet reservoir temperature | 1173 K |
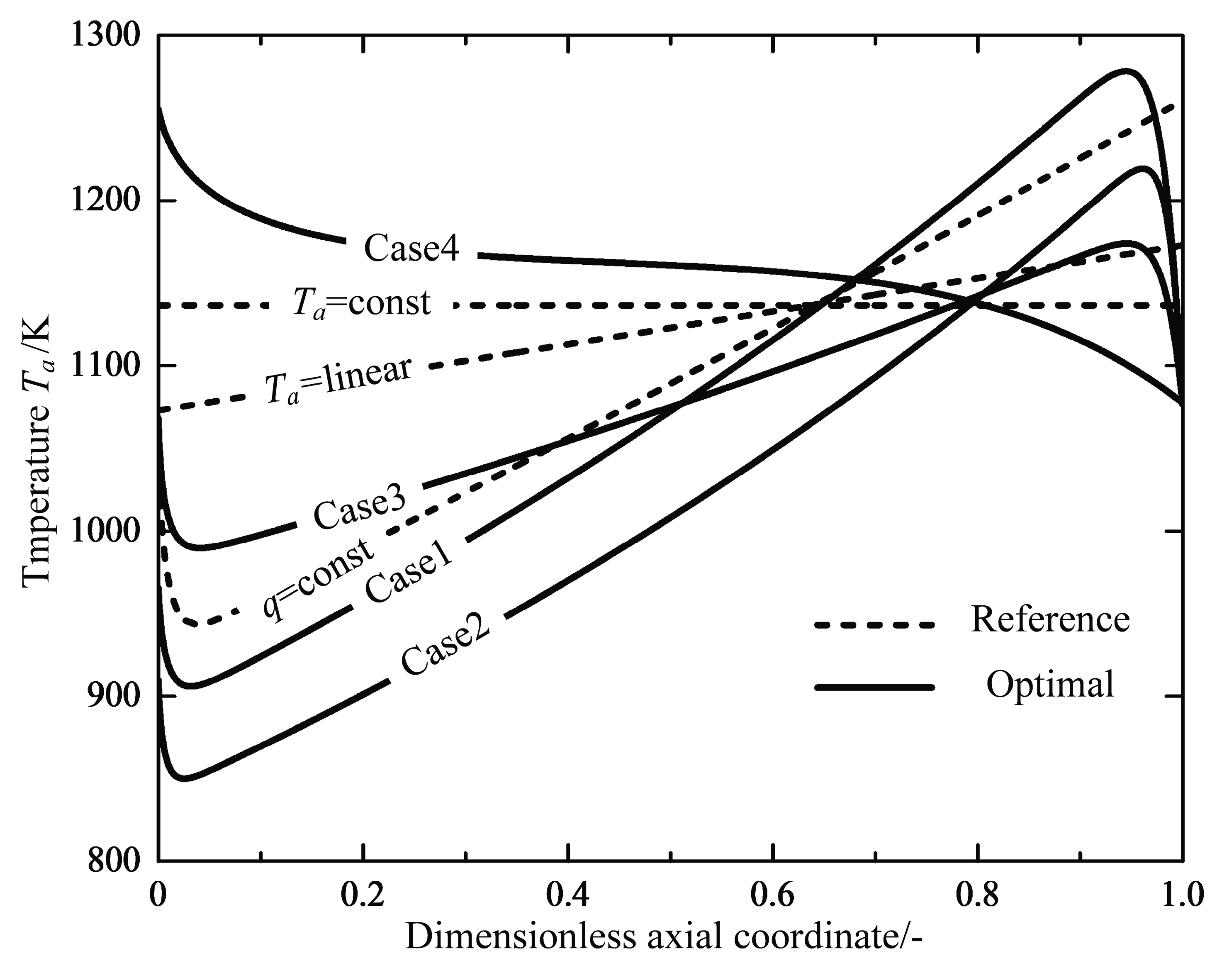
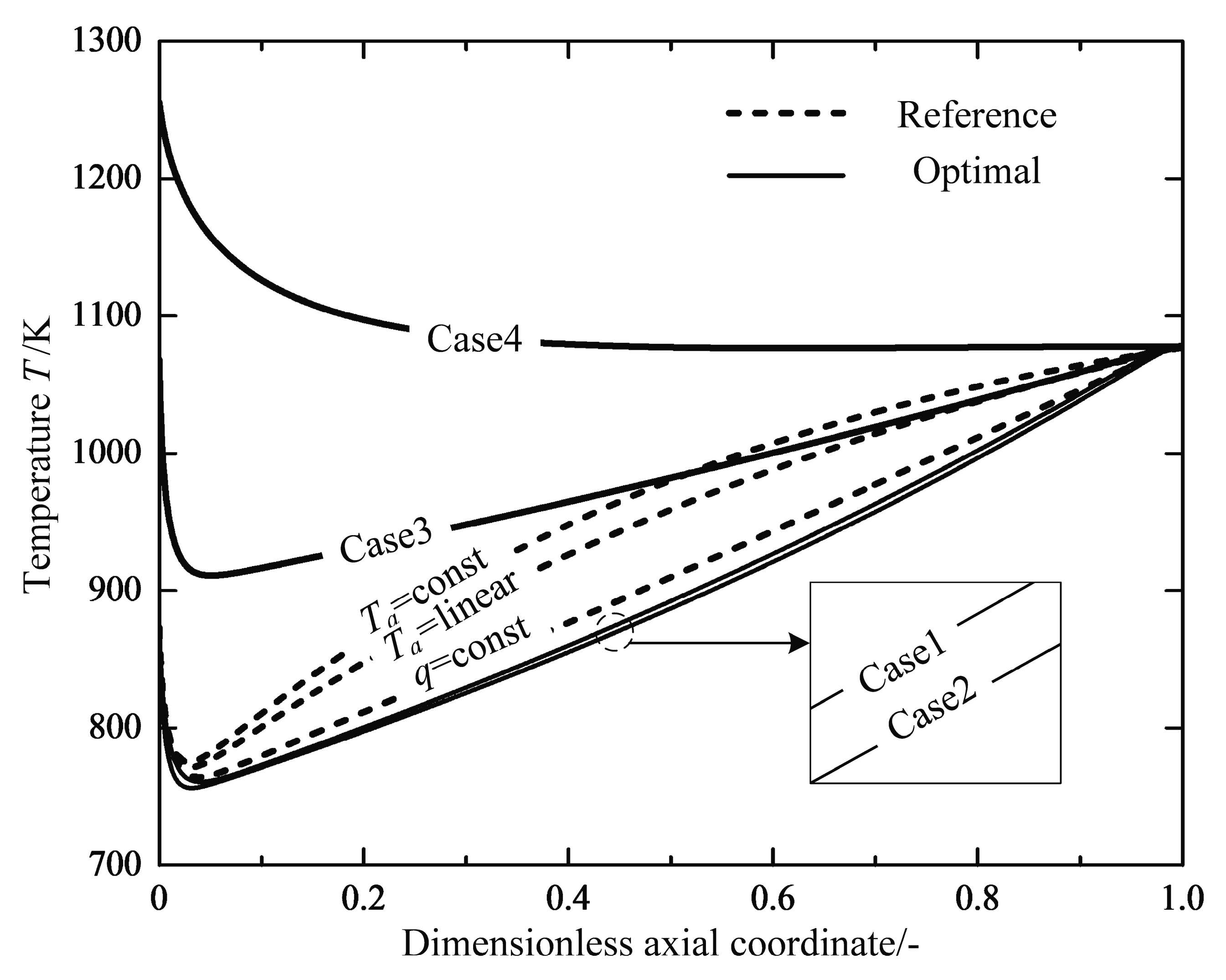
| Optimal Reactor Case | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|
| Inlet temperature | - | - | ||
| Inlet pressure | ||||
| Inlet conversion | 0 | 0 | 0 | 0 |
| Outlet temperature | - | - | - | - |
| Outlet pressure | - | - | - | - |
| Outlet conversion | ||||
| Reactor length |
| Case | Case 1 | Case 2 | Case 3 | Case 4 | |||
|---|---|---|---|---|---|---|---|
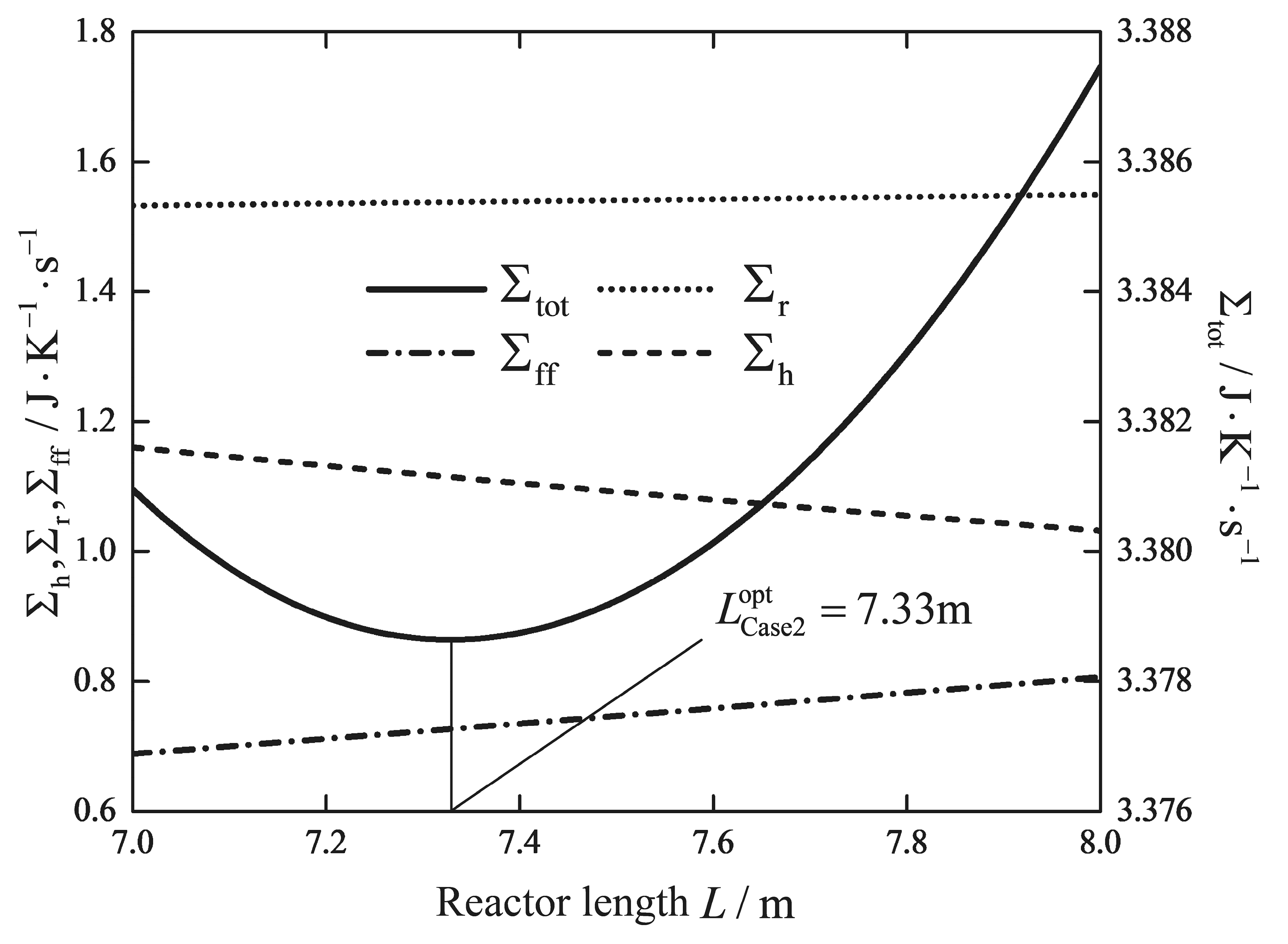
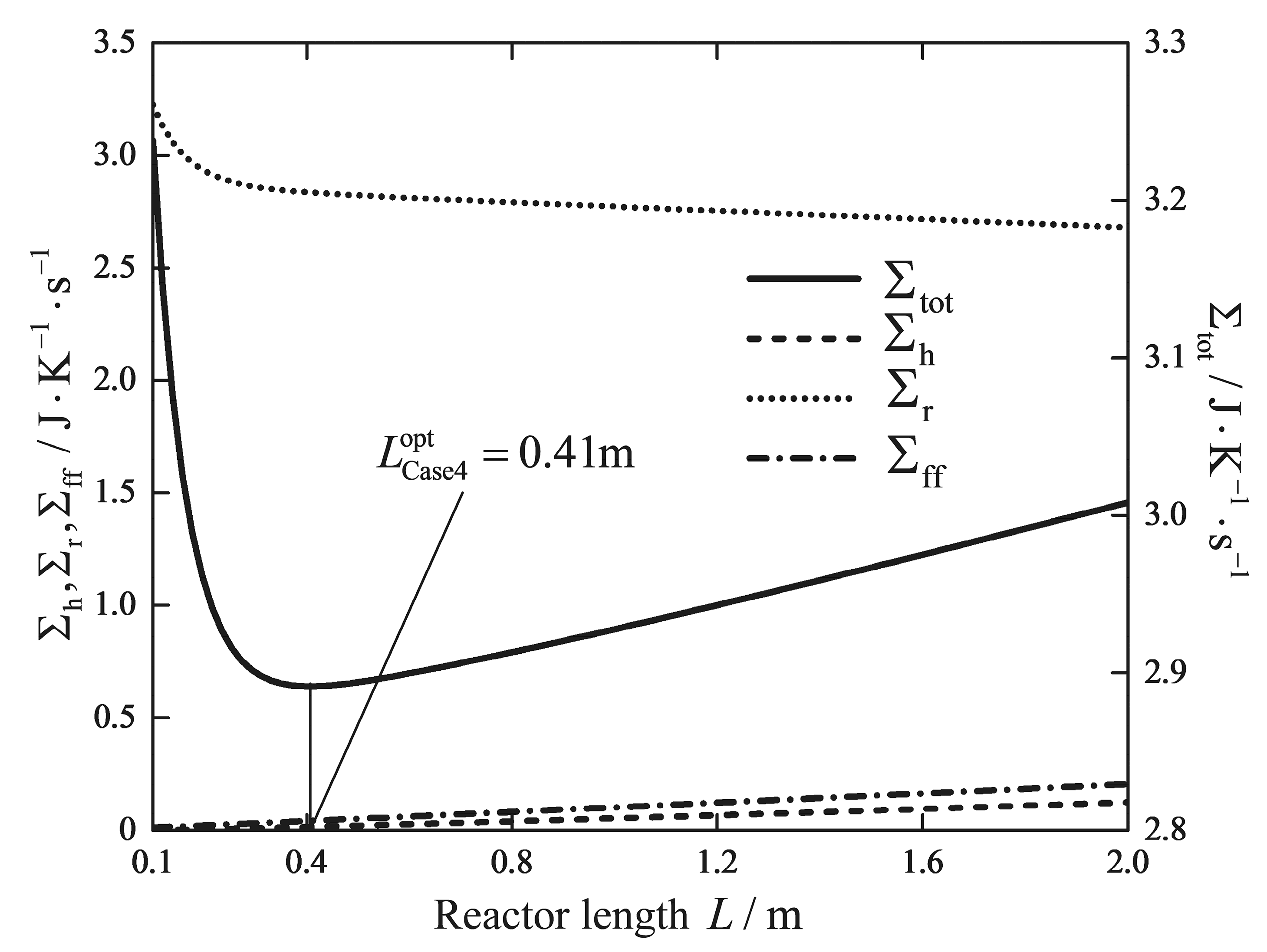
| Reactor length/m | 5 | 5 | 5 | 5 | 7.33 | 5 | 0.41 |
| /(W/K) | 1.5231 | 1.5308 | 1.5120 | 1.5068 | 1.5377 | 2.3475 | 2.8344 |
| /(W/K) | 0.4952 | 0.5037 | 0.4762 | 0.4698 | 0.7267 | 0.5200 | 0.0422 |
| /(W/K) | 1.7501 | 1.9029 | 1.5634 | 1.5497 | 1.1143 | 0.3716 | 0.0148 |
| /(W/K) | 3.7684 | 3.9374 | 3.5516 | 3.5263 | 3.3787 | 3.2391 | 2.8913 |
| Reduction/% | - | - | - | 6.42 | 10.34 | 14.05 | 23.28 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Chen, L.; Xia, S.; Wang, C.; Sun, F. Entropy Generation Minimization for Reverse Water Gas Shift (RWGS) Reactors. Entropy 2018, 20, 415. https://doi.org/10.3390/e20060415
Zhang L, Chen L, Xia S, Wang C, Sun F. Entropy Generation Minimization for Reverse Water Gas Shift (RWGS) Reactors. Entropy. 2018; 20(6):415. https://doi.org/10.3390/e20060415
Chicago/Turabian StyleZhang, Lei, Lingen Chen, Shaojun Xia, Chao Wang, and Fengrui Sun. 2018. "Entropy Generation Minimization for Reverse Water Gas Shift (RWGS) Reactors" Entropy 20, no. 6: 415. https://doi.org/10.3390/e20060415
APA StyleZhang, L., Chen, L., Xia, S., Wang, C., & Sun, F. (2018). Entropy Generation Minimization for Reverse Water Gas Shift (RWGS) Reactors. Entropy, 20(6), 415. https://doi.org/10.3390/e20060415





