Vague Entropy Measure for Complex Vague Soft Sets
Abstract
:1. Introduction
2. Preliminaries
- (i)
- A ⊆ B if tA(x) ≤ tB(x) and 1 − fA(x) ≤ 1 − fB(x) for all x.
- (ii)
- Complement: AC = {<x, [fA(x), 1 − tA(x)]>: x ∈ U}.
- (iii)
- Union: A∪B = {<x, [max(tA(x), tB(x)),max(1 − fA(x),1 − fB(x))]>: x ∈ U}
- (iv)
- Intersection: A∩B = {<x, [min(tA(x), tB(x)), min(1 − fA(x),1 − fB(x))]>: x ∈ U}
- (i)
- if and only if the following conditions are satisfied for all
- (a)
- and;
- (b)
- and.
- (ii)
- Null CVSS:ifandfor all.
- (iii)
- Absolute CVSS:ifandfor all
3. Axiomatic Definition of Distance Measure and Vague Entropy
- (D1)
- (D2)
- (D3)
- bothandare crisp sets in i.e.,
- and,
- orand,
- orand,
- orand
- (D4)
- Ifthen
- (M1)
- .
- (M2)
- is a crisp set onfor allandi.e.,andorandorandorand
- (M3)
- and is completely vaguei.e.,and
- (M4)
- (M5)
- If the following two cases holds for alland
4. Relations between the Proposed Distance Measure and Vague Entropy
- (i)
- (ii)
- (iii)
5. Illustrative Example
- (i)
- = 1 − 0.1708 = 0.8292.
- (ii)
- = 0.2167.
- (iii)
- = 1 − 0.1708 = 0.8292.
- (iv)
- = .
- (v)
- .
- (vi)
- .
- (vii)
- .
- (viii)
- (ix)
- (x)
- (xi)
5.1. The Scenario
5.2. Formation of CVSS and Calculation of Entropies
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Deluca, A.; Termini, S. A definition of non-probabilistic entropy in setting of fuzzy set theory. Inf. Control 1971, 20, 301–312. [Google Scholar] [CrossRef]
- Liu, X. Entropy, distance measure and similarity measure of fuzzy sets and their relations. Fuzzy Sets Syst. 1992, 52, 305–318. [Google Scholar]
- Fan, J.; Xie, W. Distance measures and induced fuzzy entropy. Fuzzy Sets Syst. 1999, 104, 305–314. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Gau, W.L.; Buehrer, D.J. Vague sets. IEEE Trans. Syst. Man Cybern. 1993, 23, 610–613. [Google Scholar] [CrossRef]
- Atanassov, K.; Gargov, G. Interval-valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Szmidt, E.; Kacprzyk, J. Entropy for intuitionistic fuzzy sets. Fuzzy Sets Syst. 2001, 118, 467–477. [Google Scholar] [CrossRef]
- Vlachos, I.K.; Sergiadis, G.D. Intuitionistic fuzzy information—Application to pattern recognition. Pattern Recognit. Lett. 2007, 28, 197–206. [Google Scholar] [CrossRef]
- Burillo, P.; Bustince, H. Entropy on intuitionistic fuzzy sets and on interval-valued fuzzy sets. Fuzzy Sets Syst. 1996, 78, 305–316. [Google Scholar] [CrossRef]
- Garg, H.; Agarwal, N.; Tripathi, A. Generalized intuitionistic fuzzy entropy measure of order α and degree β and its applications to multi-criteria decision making problem. Int. J. Fuzzy Syst. Appl. 2017, 6, 86–107. [Google Scholar] [CrossRef]
- Liao, H.; Xu, Z.; Zeng, X. Distance and similarity measures for hesitant fuzzy linguistic term sets and their application in multi-criteria decision making. Inf. Sci. 2014, 271, 125–142. [Google Scholar] [CrossRef]
- Garg, H.; Agarwal, N.; Tripathi, A. A novel generalized parametric directed divergence measure of intuitionistic fuzzy sets with its application. Ann. Fuzzy Math. Inform. 2017, 13, 703–727. [Google Scholar]
- Gou, X.; Xu, Z.; Liao, H. Hesitant fuzzy linguistic entropy and cross-entropy measures and alternative queuing method for multiple criteria decision making. Inf. Sci. 2017, 388–389, 225–246. [Google Scholar] [CrossRef]
- Liu, W.; Liao, H. A bibliometric analysis of fuzzy decision research during 1970–2015. Int. J. Fuzzy Syst. 2017, 19, 1–14. [Google Scholar] [CrossRef]
- Garg, H. Hesitant pythagorean fuzzy sets and their aggregation operators in multiple attribute decision making. Int. J. Uncertain. Quantif. 2018, 8, 267–289. [Google Scholar] [CrossRef]
- Garg, H. Distance and similarity measure for intuitionistic multiplicative preference relation and its application. Int. J. Uncertain. Quantif. 2017, 7, 117–133. [Google Scholar] [CrossRef]
- Dimuro, G.P.; Bedregal, B.; Bustince, H.; Jurio, A.; Baczynski, M.; Mis, K. QL-operations and QL-implication functions constructed from tuples (O, G, N) and the generation of fuzzy subsethood and entropy measures. Int. J. Approx. Reason. 2017, 82, 170–192. [Google Scholar] [CrossRef]
- Liao, H.; Xu, Z.; Viedma, E.H.; Herrera, F. Hesitant fuzzy linguistic term set and its application in decision making: A state-of-the art survey. Int. J. Fuzzy Syst. 2017, 1–27. [Google Scholar] [CrossRef]
- Garg, H.; Agarwal, N.; Tripathi, A. Choquet integral-based information aggregation operators under the interval-valued intuitionistic fuzzy set and its applications to decision-making process. Int. J. Uncertain. Quantif. 2017, 7, 249–269. [Google Scholar] [CrossRef]
- Garg, H. Linguistic Pythagorean fuzzy sets and its applications in multiattribute decision-making process. Int. J. Intell. Syst. 2018, 33, 1234–1263. [Google Scholar] [CrossRef]
- Garg, H. A robust ranking method for intuitionistic multiplicative sets under crisp, interval environments and its applications. IEEE Trans. Emerg. Top. Comput. Intell. 2017, 1, 366–374. [Google Scholar] [CrossRef]
- Yu, D.; Liao, H. Visualization and quantitative research on intuitionistic fuzzy studies. J. Intell. Fuzzy Syst. 2016, 30, 3653–3663. [Google Scholar] [CrossRef]
- Garg, H. Generalized intuitionistic fuzzy entropy-based approach for solving multi-attribute decision-making problems with unknown attribute weights. Proc. Natl. Acad. Sci. India Sect. A Phys. Sci. 2017, 1–11. [Google Scholar] [CrossRef]
- Garg, H. A new generalized improved score function of interval-valued intuitionistic fuzzy sets and applications in expert systems. Appl. Soft Comput. 2016, 38, 988–999. [Google Scholar] [CrossRef]
- Molodtsov, D. Soft set theory—First results. Comput. Math. Appl. 1999, 27, 19–31. [Google Scholar] [CrossRef]
- Maji, P.K.; Biswas, R.; Roy, A. Intuitionistic fuzzy soft sets. J. Fuzzy Math. 2001, 9, 677–692. [Google Scholar]
- Maji, P.K.; Biswas, R.; Roy, A.R. Fuzzy soft sets. J. Fuzzy Math. 2001, 9, 589–602. [Google Scholar]
- Yang, H.L. Notes on generalized fuzzy soft sets. J. Math. Res. Expos. 2011, 31, 567–570. [Google Scholar]
- Majumdar, P.; Samanta, S.K. Generalized fuzzy soft sets. Comput. Math. Appl. 2010, 59, 1425–1432. [Google Scholar] [CrossRef]
- Agarwal, M.; Biswas, K.K.; Hanmandlu, M. Generalized intuitionistic fuzzy soft sets with applications in decision-making. Appl. Soft Comput. 2013, 13, 3552–3566. [Google Scholar] [CrossRef]
- Garg, H.; Arora, R. Generalized and group-based generalized intuitionistic fuzzy soft sets with applications in decision-making. Appl. Intell. 2018, 48, 343–356. [Google Scholar] [CrossRef]
- Majumdar, P.; Samanta, S. Similarity measure of soft sets. New Math. Nat. Comput. 2008, 4, 1–12. [Google Scholar] [CrossRef]
- Garg, H.; Arora, R. Distance and similarity measures for dual hesitant fuzzy soft sets and their applications in multi criteria decision-making problem. Int. J. Uncertain. Quantif. 2017, 7, 229–248. [Google Scholar] [CrossRef]
- Kharal, A. Distance and similarity measures for soft sets. New Math. Nat. Comput. 2010, 6, 321–334. [Google Scholar] [CrossRef]
- Jiang, Y.; Tang, Y.; Liu, H.; Chen, Z. Entropy on intuitionistic fuzzy soft sets and on interval-valued fuzzy soft sets. Inf. Sci. 2013, 240, 95–114. [Google Scholar] [CrossRef]
- Garg, H.; Agarwal, N.; Tripathi, A. Fuzzy number intuitionistic fuzzy soft sets and its properties. J. Fuzzy Set Valued Anal. 2016, 2016, 196–213. [Google Scholar] [CrossRef]
- Arora, R.; Garg, H. Prioritized averaging/geometric aggregation operators under the intuitionistic fuzzy soft set environment. Sci. Iran. E 2018, 25, 466–482. [Google Scholar] [CrossRef]
- Arora, R.; Garg, H. Robust aggregation operators for multi-criteria decision making with intuitionistic fuzzy soft set environment. Sci. Iran. E 2018, 25, 931–942. [Google Scholar] [CrossRef]
- Garg, H.; Arora, R. A nonlinear-programming methodology for multi-attribute decision-making problem with interval-valued intuitionistic fuzzy soft sets information. Appl. Intell. 2017, 1–16. [Google Scholar] [CrossRef]
- Garg, H.; Arora, R. Bonferroni mean aggregation operators under intuitionistic fuzzy soft set environment and their applications to decision-making. J. Oper. Res. Soc. 2018, 1–14. [Google Scholar] [CrossRef]
- Xu, W.; Ma, J.; Wang, S.; Hao, G. Vague soft sets and their properties. Comput. Math. Appl. 2010, 59, 787–794. [Google Scholar] [CrossRef]
- Chen, S.M. Measures of similarity between vague sets. Fuzzy Sets Syst. 1995, 74, 217–223. [Google Scholar] [CrossRef]
- Wang, C.; Qu, A. Entropy, similarity measure and distance measure of vague soft sets and their relations. Inf. Sci. 2013, 244, 92–106. [Google Scholar] [CrossRef]
- Selvachandran, G.; Maji, P.; Faisal, R.Q.; Salleh, A.R. Distance and distance induced intuitionistic entropy of generalized intuitionistic fuzzy soft sets. Appl. Intell. 2017, 1–16. [Google Scholar] [CrossRef]
- Ramot, D.; Milo, R.; Fiedman, M.; Kandel, A. Complex fuzzy sets. IEEE Trans. Fuzzy Syst. 2002, 10, 171–186. [Google Scholar] [CrossRef]
- Ramot, D.; Friedman, M.; Langholz, G.; Kandel, A. Complex fuzzy logic. IEEE Trans. Fuzzy Syst. 2003, 11, 450–461. [Google Scholar] [CrossRef]
- Greenfield, S.; Chiclana, F.; Dick, S. Interval-Valued Complex Fuzzy Logic. In Proceedings of the IEEE International Conference on Fuzzy Systems (FUZZ), Vancouver, BC, Canada, 24–29 July 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Yazdanbakhsh, O.; Dick, S. A systematic review of complex fuzzy sets and logic. Fuzzy Sets Syst. 2018, 338, 1–22. [Google Scholar] [CrossRef]
- Alkouri, A.; Salleh, A. Complex Intuitionistic Fuzzy Sets. In Proceedings of the 2nd International Conference on Fundamental and Applied Sciences, Kuala Lumpur, Malaysia, 12–14 June 2012; Volume 1482, pp. 464–470. [Google Scholar]
- Alkouri, A.U.M.; Salleh, A.R. Complex Atanassov’s intuitionistic fuzzy relation. Abstr. Appl. Anal. 2013, 2013, 287382. [Google Scholar] [CrossRef]
- Rani, D.; Garg, H. Distance measures between the complex intuitionistic fuzzy sets and its applications to the decision-making process. Int. J. Uncertain. Quantif. 2017, 7, 423–439. [Google Scholar] [CrossRef]
- Kumar, T.; Bajaj, R.K. On complex intuitionistic fuzzy soft sets with distance measures and entropies. J. Math. 2014, 2014, 972198. [Google Scholar] [CrossRef]
- Selvachandran, G.; Majib, P.; Abed, I.E.; Salleh, A.R. Complex vague soft sets and its distance measures. J. Intell. Fuzzy Syst. 2016, 31, 55–68. [Google Scholar] [CrossRef]
- Selvachandran, G.; Maji, P.K.; Abed, I.E.; Salleh, A.R. Relations between complex vague soft sets. Appl. Soft Comput. 2016, 47, 438–448. [Google Scholar] [CrossRef]
- Selvachandran, G.; Garg, H.; Alaroud, M.H.S.; Salleh, A.R. Similarity measure of complex vague soft sets and its application to pattern recognition. Int. J. Fuzzy Syst. 2018, 1–14. [Google Scholar] [CrossRef]
- Singh, P.K. Complex vague set based concept lattice. Chaos Solitons Fractals 2017, 96, 145–153. [Google Scholar] [CrossRef]
- Hu, D.; Hong, Z.; Wang, Y. A new approach to entropy and similarity measure of vague soft sets. Sci. World J. 2014, 2014, 610125. [Google Scholar] [CrossRef] [PubMed]
- Arora, R.; Garg, H. A robust correlation coefficient measure of dual hesitant fuzzy soft sets and their application in decision making. Eng. Appl. Artif. Intell. 2018, 72, 80–92. [Google Scholar] [CrossRef]
- Qiu, D.; Lu, C.; Zhang, W.; Lan, Y. Algebraic properties and topological properties of the quotient space of fuzzy numbers based on mares equivalence relation. Fuzzy Sets Syst. 2014, 245, 63–82. [Google Scholar] [CrossRef]
- Garg, H. Generalised Pythagorean fuzzy geometric interactive aggregation operators using Einstein operations and their application to decision making. J. Exp. Theor. Artif. Intell. 2018. [Google Scholar] [CrossRef]
- Garg, H.; Arora, R. Novel scaled prioritized intuitionistic fuzzy soft interaction averaging aggregation operators and their application to multi criteria decision making. Eng. Appl. Artif. Intell. 2018, 71, 100–112. [Google Scholar] [CrossRef]
- Qiu, D.; Zhang, W. Symmetric fuzzy numbers and additive equivalence of fuzzy numbers. Soft Comput. 2013, 17, 1471–1477. [Google Scholar] [CrossRef]
- Garg, H.; Kumar, K. Distance measures for connection number sets based on set pair analysis and its applications to decision making process. Appl. Intell. 2018, 1–14. [Google Scholar] [CrossRef]
- Qiu, D.; Zhang, W.; Lu, C. On fuzzy differential equations in the quotient space of fuzzy numbers. Fuzzy Sets Syst. 2016, 295, 72–98. [Google Scholar] [CrossRef]
- Garg, H.; Kumar, K. An advanced study on the similarity measures of intuitionistic fuzzy sets based on the set pair analysis theory and their application in decision making. Soft Comput. 2018. [Google Scholar] [CrossRef]
- Garg, H.; Nancy. Linguistic single-valued neutrosophic prioritized aggregation operators and their applications to multiple-attribute group decision-making. J. Ambient Intell. Hum. Comput. 2018, 1–23. [Google Scholar] [CrossRef]
- Garg, H.; Kumar, K. Some aggregation operators for Linguistic intuitionistic fuzzy set and its application to group decision-making process using the set pair analysis. Arab. J. Sci. Eng. 2018, 43, 3213–3227. [Google Scholar] [CrossRef]

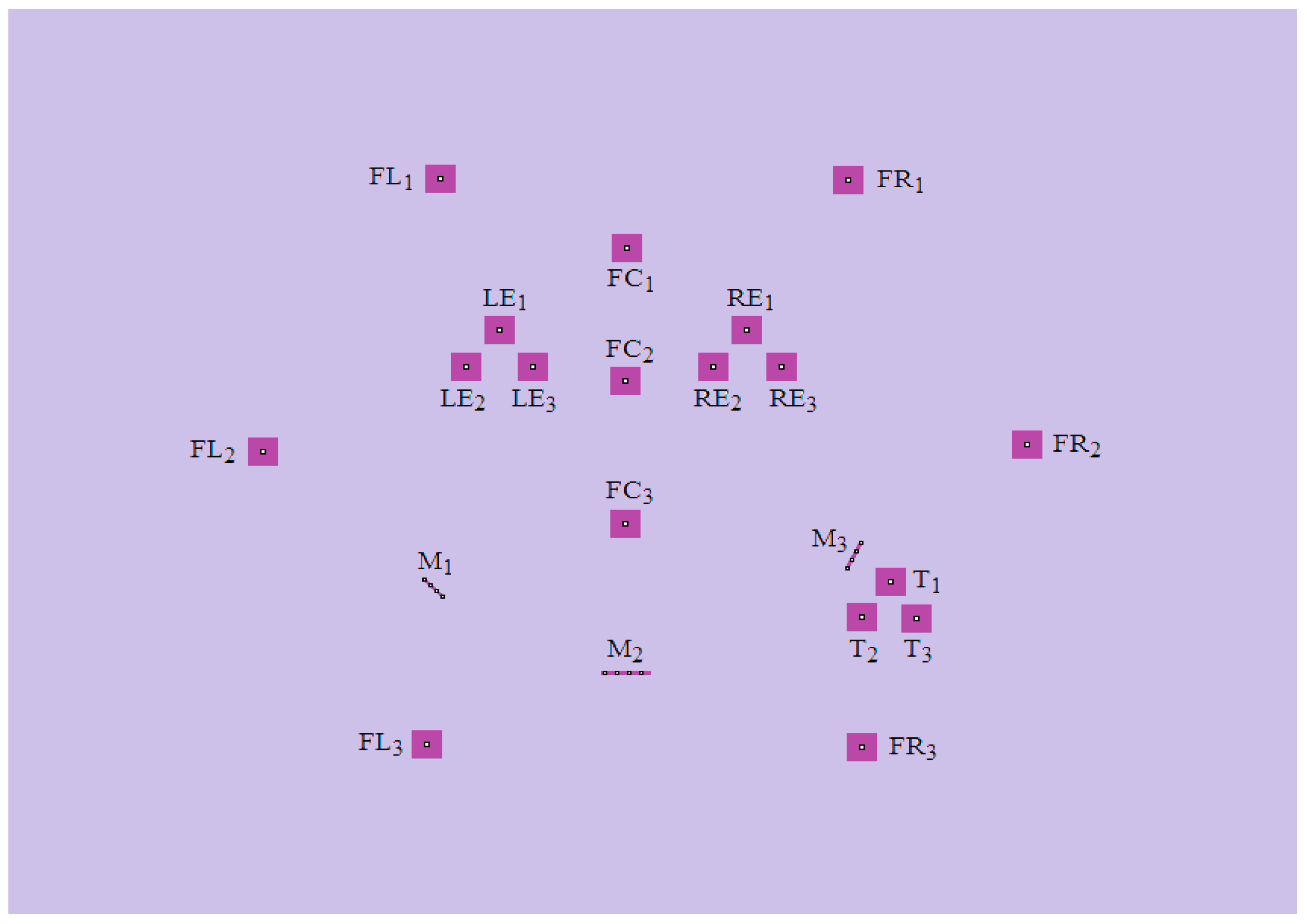



| 1st Position (n = 1) | 2nd Position (n = 2) | 3rd Position (n = 3) | |
|---|---|---|---|
| “Left Eye” (LEn) | (323, 226), (324, 226), (323, 227), (324, 227), | (301, 252), (302, 252), (301, 253), (302, 253), | (345, 252), (346, 252), (345, 253), (346, 253), |
| “Right Eye” (REn) | (486, 226), (487, 226), (486, 227), (487, 227), | (464, 252), (465, 252), (464, 253), (465, 253), | (509, 252), (510, 252), (509, 253), (510, 253), |
| “Left side of Face” (LFn) | (284, 119), (285, 119), (284, 120), (285, 120), | (167, 312), (168, 312), (167, 313), (168, 313), | (275, 519), (276, 519), (275, 520), (276, 520), |
| “Centre of Face” (CFn) | (407, 168), (408, 168), (407, 169), (408, 169), | (406, 262), (407, 262), (406, 263), (407, 263), | (406, 363), (407, 363), (406, 364), (407, 364), |
| “Right side of Face” (RFn) | (553, 120), (554, 120), (553, 121), (554, 121), | (671, 307), (672, 307), (671, 308), (672, 308), | (562, 521), (563, 521), (562, 522), (563, 522), |
| “Tongue” (Tn) | (581, 404), (582, 404), (581, 405), (582, 405), | (562, 429), (563, 429), (562, 430), (563, 430), | (598, 430), (599, 430), (598, 431), (599, 431), |
| “Mouth” (Mn) | (274, 403), (278, 407), (282, 411), (286, 415), | (393, 469), (401, 469), (409, 469), (417, 469), | (553, 395), (556, 389), (559, 383), (562, 377), |
| pic001.bmp (Memory) | Image A | Image B | Image C | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n = 1 | n = 2 | n = 3 | n = 1 | n = 2 | n = 3 | n = 1 | n = 2 | n = 3 | n = 1 | n = 2 | n = 3 | |
| LE |  |  |  |  | ||||||||
| RE | ||||||||||||
| LF | ||||||||||||
| CF | ||||||||||||
| RF | ||||||||||||
| T | ||||||||||||
| M | ||||||||||||
| pic001.bmp (Memory), m = 0 | Image A m = 1 | Image B m = 2 | Image C m = 3 | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n = 1 | n = 2 | n = 3 | n = 1 | n = 2 | n = 3 | n = 1 | n = 2 | n = 3 | n = 1 | n = 2 | n = 3 | |||||||||||||
| LE | 23 | 23 | 23 | 24 | 24 | 23 | 24 | 27 | 34 | 33 | 32 | 32 | 5 | 6 | 97 | 96 | 74 | 72 | 27 | 128 | 57 | 54 | 180 | 2 |
| 24 | 24 | 24 | 24 | 24 | 25 | 25 | 28 | 38 | 39 | 31 | 31 | 6 | 6 | 116 | 110 | 81 | 80 | 25 | 82 | 78 | 107 | 120 | 26 | |
| RE | 24 | 23 | 21 | 24 | 23 | 24 | 43 | 44 | 41 | 42 | 47 | 46 | 7 | 7 | 8 | 7 | 8 | 7 | 28 | 112 | 48 | 0 | 2 | 120 |
| 23 | 24 | 22 | 21 | 24 | 22 | 45 | 46 | 41 | 43 | 48 | 48 | 6 | 6 | 8 | 8 | 7 | 7 | 120 | 64 | 0 | 67 | 0 | 97 | |
| LF | 101 | 99 | 104 | 105 | 90 | 90 | 78 | 79 | 55 | 57 | 96 | 96 | 3 | 3 | 162 | 163 | 122 | 120 | 58 | 63 | 24 | 31 | 62 | 24 |
| 96 | 100 | 106 | 106 | 91 | 88 | 78 | 78 | 55 | 56 | 95 | 95 | 3 | 3 | 163 | 163 | 125 | 122 | 65 | 67 | 14 | 61 | 40 | 96 | |
| CF | 85 | 88 | 80 | 83 | 78 | 79 | 97 | 102 | 103 | 104 | 102 | 101 | 6 | 5 | 79 | 77 | 24 | 24 | 49 | 28 | 0 | 22 | 109 | 56 |
| 88 | 89 | 81 | 82 | 78 | 78 | 97 | 98 | 103 | 104 | 99 | 100 | 5 | 5 | 81 | 81 | 33 | 32 | 60 | 81 | 3 | 139 | 27 | 96 | |
| RF | 83 | 82 | 64 | 64 | 60 | 59 | 119 | 119 | 136 | 136 | 139 | 141 | 6 | 6 | 16 | 15 | 62 | 63 | 98 | 40 | 93 | 94 | 56 | 16 |
| 84 | 84 | 65 | 63 | 59 | 59 | 120 | 119 | 135 | 134 | 138 | 139 | 6 | 6 | 16 | 14 | 61 | 64 | 64 | 0 | 20 | 30 | 45 | 44 | |
| T | 60 | 60 | 59 | 59 | 58 | 59 | 142 | 143 | 144 | 144 | 152 | 151 | 116 | 117 | 27 | 27 | 127 | 127 | 74 | 28 | 0 | 75 | 81 | 198 |
| 59 | 61 | 61 | 62 | 60 | 59 | 144 | 144 | 145 | 144 | 150 | 148 | 120 | 119 | 25 | 24 | 125 | 125 | 120 | 25 | 104 | 3 | 0 | 75 | |
| M | 26 | 23 | 15 | 14 | 9 | 9 | 19 | 21 | 34 | 40 | 33 | 35 | 81 | 87 | 175 | 191 | 36 | 42 | 77 | 22 | 112 | 15 | 14 | 24 |
| 25 | 26 | 13 | 13 | 8 | 8 | 19 | 20 | 43 | 40 | 36 | 36 | 86 | 93 | 181 | 145 | 79 | 66 | 113 | 84 | 121 | 115 | 31 | 33 | |
| pic001.bmp (Memory), m = 0 | Image A m = 1 | Image B m = 2 | Image C m = 3 | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n = 1 | n = 2 | n = 3 | n = 1 | n = 2 | n = 3 | n = 1 | n = 2 | n = 3 | n = 1 | n = 2 | n = 3 | |||||||||||||
| LE | 12 | 12 | 10 | 10 | 12 | 12 | 17 | 17 | 15 | 15 | 18 | 16 | 187 | 160 | 8 | 8 | 6 | 7 | 55 | 80 | 23 | 160 | 226 | 27 |
| 13 | 12 | 9 | 10 | 13 | 12 | 17 | 17 | 15 | 15 | 18 | 16 | 160 | 160 | 8 | 8 | 6 | 7 | 214 | 173 | 127 | 70 | 168 | 66 | |
| RE | 13 | 13 | 13 | 13 | 12 | 11 | 19 | 19 | 18 | 18 | 20 | 20 | 160 | 160 | 160 | 160 | 160 | 160 | 112 | 64 | 227 | 160 | 220 | 119 |
| 13 | 13 | 13 | 12 | 12 | 11 | 19 | 19 | 18 | 18 | 19 | 20 | 160 | 160 | 160 | 160 | 160 | 160 | 152 | 150 | 160 | 177 | 160 | 77 | |
| LF | 31 | 31 | 31 | 31 | 31 | 30 | 28 | 28 | 27 | 27 | 31 | 31 | 187 | 187 | 173 | 167 | 7 | 7 | 12 | 167 | 169 | 67 | 57 | 211 |
| 31 | 30 | 31 | 31 | 31 | 30 | 29 | 28 | 27 | 27 | 31 | 30 | 187 | 187 | 171 | 167 | 9 | 7 | 23 | 237 | 18 | 76 | 186 | 199 | |
| CF | 29 | 29 | 29 | 28 | 29 | 29 | 30 | 29 | 30 | 30 | 31 | 30 | 160 | 160 | 8 | 8 | 224 | 230 | 155 | 86 | 160 | 214 | 177 | 0 |
| 29 | 29 | 29 | 29 | 29 | 29 | 30 | 29 | 30 | 30 | 30 | 30 | 180 | 180 | 8 | 8 | 213 | 220 | 42 | 51 | 200 | 107 | 97 | 165 | |
| RF | 29 | 30 | 29 | 29 | 31 | 31 | 30 | 30 | 32 | 32 | 33 | 33 | 160 | 160 | 160 | 160 | 139 | 139 | 154 | 5 | 238 | 68 | 94 | 36 |
| 30 | 30 | 29 | 29 | 31 | 31 | 30 | 30 | 32 | 32 | 32 | 33 | 160 | 160 | 160 | 153 | 137 | 141 | 68 | 160 | 192 | 76 | 131 | 158 | |
| T | 11 | 11 | 11 | 12 | 10 | 10 | 12 | 12 | 12 | 12 | 13 | 12 | 13 | 9 | 168 | 165 | 7 | 7 | 119 | 212 | 160 | 45 | 160 | 130 |
| 11 | 11 | 9 | 9 | 9 | 10 | 12 | 12 | 11 | 12 | 13 | 12 | 9 | 13 | 164 | 160 | 8 | 10 | 29 | 205 | 31 | 67 | 160 | 200 | |
| M | 11 | 10 | 13 | 13 | 18 | 14 | 16 | 15 | 18 | 20 | 17 | 16 | 10 | 14 | 19 | 18 | 208 | 183 | 145 | 118 | 195 | 26 | 124 | 160 |
| 11 | 12 | 13 | 13 | 14 | 18 | 15 | 16 | 21 | 19 | 16 | 17 | 13 | 14 | 17 | 15 | 184 | 5 | 42 | 29 | 49 | 181 | 115 | 220 | |
| n | ||||
| 1 | 2 | 3 | ||
| k | LE | [0.996, 1.000]e2πi[0.996, 0.997] | [0.960, 0.987]e2πi[0.994, 0.996] | [0.987, 0.994]e2πi[0.994, 0.998] |
| RE | [0.920, 0.945]e2πi[0.994, 0.994] | [0.927, 0.955]e2πi[0.994, 0.996] | [0.899, 0.927]e2πi[0.987, 0.992] | |
| LF | [0.920, 0.955]e2πi[0.998, 0.999] | [0.666, 0.708]e2πi[0.997, 0.997] | [0.990, 0.997]e2πi[0.999, 1.000] | |
| CF | [0.955, 0.990]e2πi[0.999, 1.000] | [0.913, 0.939]e2πi[0.999, 0.999] | [0.913, 0.939]e2πi[0.999, 0.999] | |
| RF | [0.798, 0.825]e2πi[0.999, 1.000] | [0.434, 0.475]e2πi[0.998, 0.998] | [0.349, 0.386]e2πi[0.999, 0.999] | |
| T | [0.323, 0.358]e2πi[0.999, 0.999] | [0.314, 0.349]e2πi[0.998, 1.000] | [0.251, 0.298]e2πi[0.997, 0.999] | |
| M | [0.992, 0.999]e2πi[0.994, 0.998] | [0.868, 0.945]e2πi[0.990, 0.996] | [0.884, 0.913]e2πi[0.998, 0.999] | |
| N | ||||
| 1 | 2 | 3 | ||
| k | LE | [0.945, 0.955]e2πi[0.008, 0.034] | [0.258, 0.444]e2πi[0.999, 0.999] | [0.591, 0.708]e2πi[0.992, 0.996] |
| RE | [0.950, 0.960]e2πi[0.034, 0.034] | [0.955, 0.973]e2πi[0.032, 0.034] | [0.955, 0.969]e2πi[0.031, 0.032] | |
| LF | [0.222, 0.258]e2πi[0.021, 0.022] | [0.580, 0.612]e2πi[0.042, 0.055] | [0.807, 0.876]e2πi[0.913, 0.933] | |
| CF | [0.332, 0.377]e2πi[0.028, 0.068] | [0.994, 1.000]e2πi[0.933, 0.939] | [0.623, 0.728]e2πi[0.001, 0.005] | |
| RF | [0.386, 0.405]e2πi[0.068, 0.071] | [0.666, 0.708]e2πi[0.068, 0.090] | [0.996, 0.999]e2πi[0.150, 0.172] | |
| T | [0.559, 0.623]e2πi[0.999, 0.999] | [0.798, 0.852]e2πi[0.019, 0.032] | [0.475, 0.516]e2πi[0.998, 1.000] | |
| M | [0.465, 0.623]e2πi[0.997, 1.000] | [0.007, 0.071]e2πi[0.994, 0.999] | [0.454, 0.892]e2πi[0.002, 0.987] | |
| N | ||||
| 1 | 2 | 3 | ||
| k | LE | [0.178, 0.999]e2πi[0.001, 0.759] | [0.332, 0.868]e2πi[0.028, 0.973] | [0.021, 0.999]e2πi[0.000, 0.969] |
| RE | [0.229, 0.997]e2πi[0.048, 0.666] | [0.718, 0.933]e2πi[0.000, 0.034] | [0.222, 0.939]e2πi[0.001, 0.516] | |
| LF | [0.749, 0.876]e2πi[0.001, 0.992] | [0.266, 0.749]e2πi[0.051, 0.973] | [0.495, 0.996]e2πi[0.005, 0.899] | |
| CF | [0.559, 0.997]e2πi[0.083, 0.973] | [0.340, 0.612]e2πi[0.004, 0.386] | [0.655, 0.955]e2πi[0.032, 0.876] | |
| RF | [0.332, 0.969]e2πi[0.068, 0.913] | [0.728, 0.884]e2πi[0.001, 0.788] | [0.738, 0.998]e2πi[0.080, 0.996] | |
| T | [0.559, 0.973]e2πi[0.001, 0.950] | [0.548, 0.973]e2πi[0.028, 0.945] | [0.046, 0.965]e2πi[0.003, 0.105] | |
| M | [0.282, 0.999]e2πi[0.057, 0.955] | [0.161, 1.000]e2πi[0.005, 0.973] | [0.906, 0.996]e2πi[0.001, 0.229] | |
| Entropy Measure | Image A | Image B | Image C |
|---|---|---|---|
| 0.571 | 0.647 | 0.847 | |
| 0.039 | 0.089 | 0.328 | |
| 0.571 | 0.647 | 0.847 | |
| 0.084 | 0.202 | 0.682 | |
| 0.084 | 0.202 | 0.682 | |
| 0.084 | 0.202 | 0.682 | |
| 0.084 | 0.202 | 0.682 | |
| 0.571 | 0.647 | 0.847 | |
| 0.571 | 0.647 | 0.847 | |
| 0.571 | 0.647 | 0.847 | |
| 0.571 | 0.647 | 0.847 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Selvachandran, G.; Garg, H.; Quek, S.G. Vague Entropy Measure for Complex Vague Soft Sets. Entropy 2018, 20, 403. https://doi.org/10.3390/e20060403
Selvachandran G, Garg H, Quek SG. Vague Entropy Measure for Complex Vague Soft Sets. Entropy. 2018; 20(6):403. https://doi.org/10.3390/e20060403
Chicago/Turabian StyleSelvachandran, Ganeshsree, Harish Garg, and Shio Gai Quek. 2018. "Vague Entropy Measure for Complex Vague Soft Sets" Entropy 20, no. 6: 403. https://doi.org/10.3390/e20060403
APA StyleSelvachandran, G., Garg, H., & Quek, S. G. (2018). Vague Entropy Measure for Complex Vague Soft Sets. Entropy, 20(6), 403. https://doi.org/10.3390/e20060403






