Effective Boundary Slip Induced by Surface Roughness and Their Coupled Effect on Convective Heat Transfer of Liquid Flow
Abstract
:1. Introduction
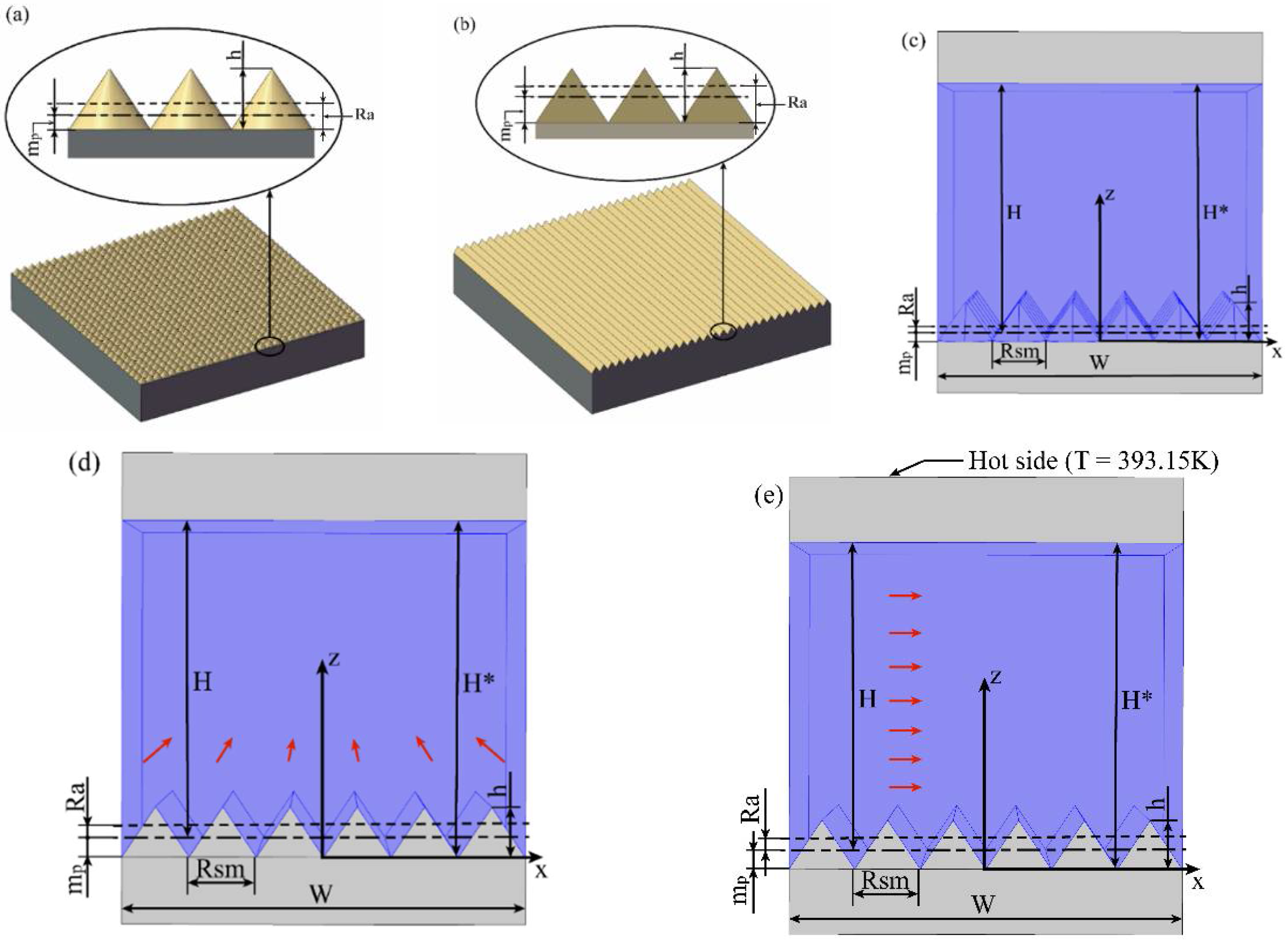
2. Simulation Model
3. Results and Discussion
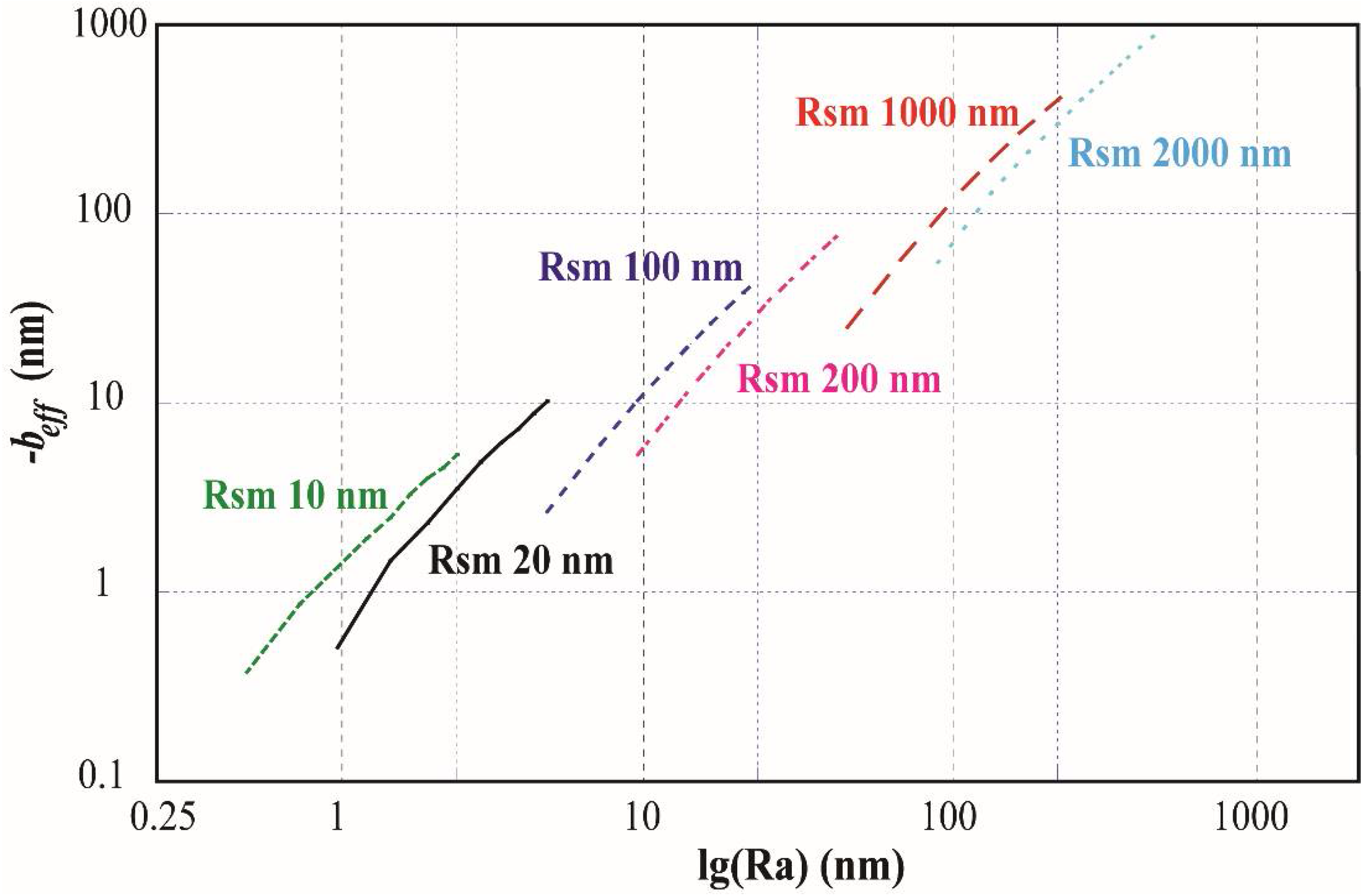
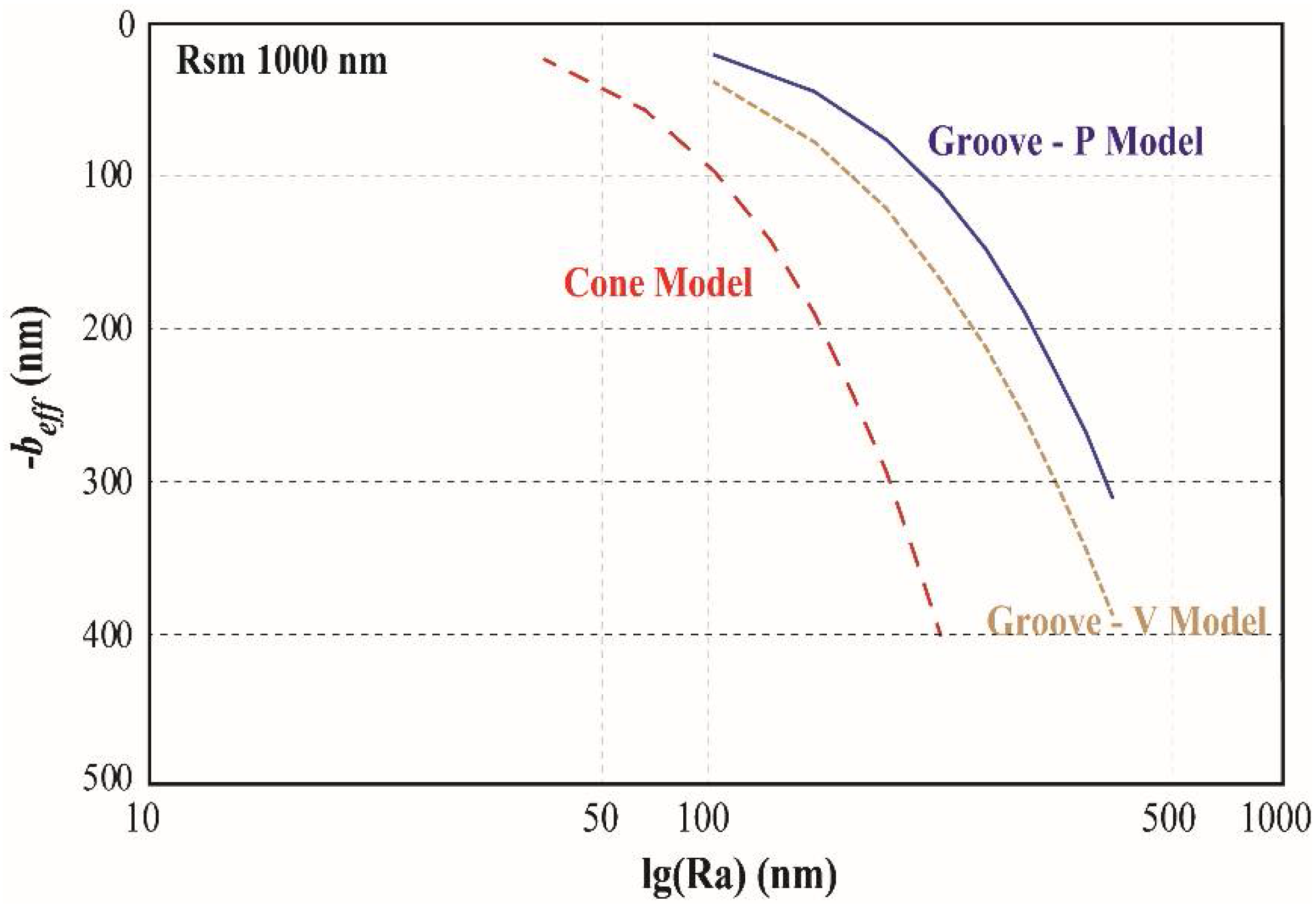
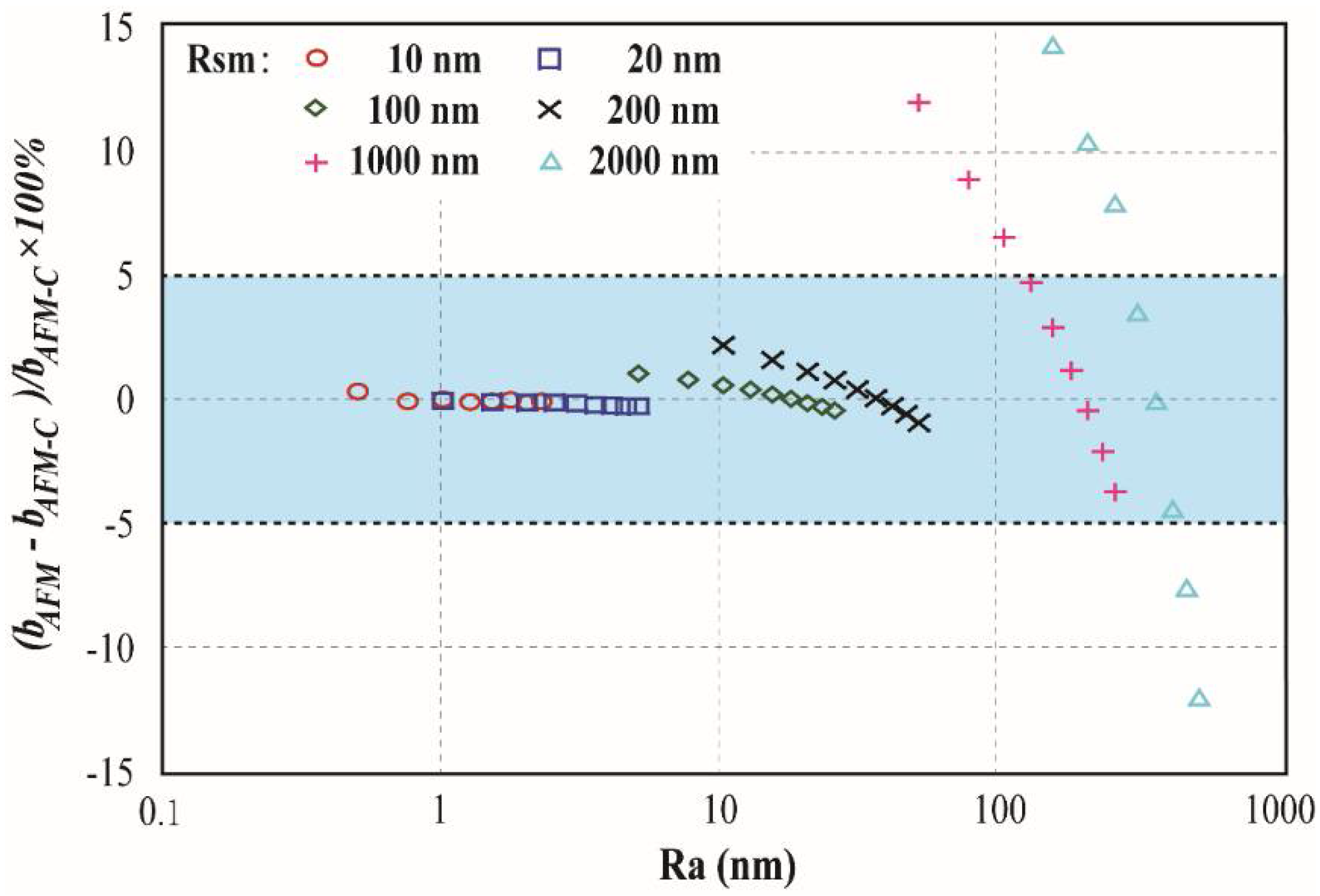
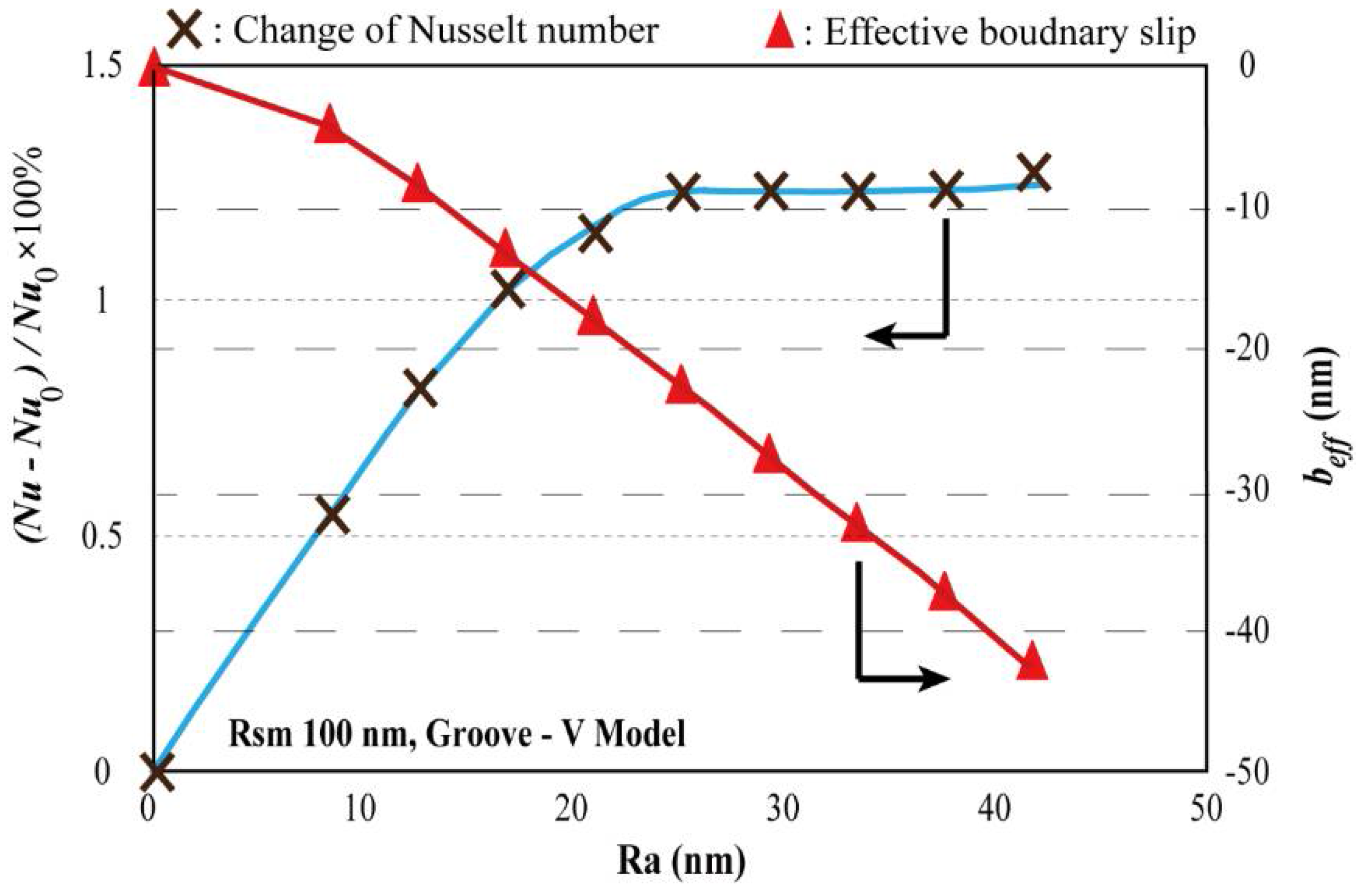
3.1. Effective Boundary Slip
3.2. Convective Heat Transfer
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Stokes, V.K. Couple stresses in fluids. Phys. Fluids 1996, 9, 1709–1715. [Google Scholar] [CrossRef]
- Vinogradova, O.I. Drainage of a Thin Liquid-Film Confined between Hydrophobic Surfaces. Langmuir 1995, 11, 2213–2220. [Google Scholar] [CrossRef]
- Ou, J.; Perot, B.; Rothstein, J.P. Laminar drag reduction in microchannels using ultrahydrophobic surfaces. Phys. Fluids 2004, 16, 4635–4643. [Google Scholar] [CrossRef]
- Choi, C.-H.; Kim, C.-J. Large Slip of Aqueous Liquid Flow over a Nanoengineered Superhydrophobic Surface. Phys. Rev. Lett. 2006, 96, 066001. [Google Scholar] [CrossRef] [PubMed]
- Steinberger, A.; Cottin-Bizonne, C.; Kleimann, P.; Charlaix, E. High friction on a bubble mattress. Nat. Mater. 2007, 6, 665–668. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Kim, C.J. Maximizing the Giant Liquid Slip on Superhydrophobic Microstructures by Nanostructuring Their Sidewalls. Langmuir 2009, 25, 12812–12818. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Bhushan, B. Boundary slip and nanobubble study in micro/nanofluidics using atomic force microscopy. Soft Matter 2010, 6, 29–66. [Google Scholar] [CrossRef]
- Pan, Y.; Bhushan, B.; Zhao, X. The study of surface wetting, nanobubbles and boundary slip with an applied voltage: A review. Beilstein J. Nanotech. 2014, 5, 1042–1065. [Google Scholar] [CrossRef] [PubMed]
- Di Federicao, V.; Longo, S.; King, S.E.; Chiapponi, L.; Petrolo, D.; Ciriello, V. Gravity-driven flow of Herschel–Bulkley fluid in a fracture and in a 2D porous medium. J. Fluid Mech. 2017, 821, 59–84. [Google Scholar] [CrossRef]
- Longo, S.; Chiapponi, L.; Di Federicao, V. On the propagation of viscous gravity currents of non-Newtonian fluids in channels with varying cross section and inclination. J. Non-Newton Fluid 2016, 235, 95–108. [Google Scholar] [CrossRef]
- Choi, W.; Tuteja, A.; Chhatre, S.; Mabry, J.M.; Cohen, R.E.; McKinley, G.H. Fabrics with tunable oleophobicity. Adv. Mater. 2009, 21, 2190–2195. [Google Scholar] [CrossRef]
- Brown, P.S.; Bhushan, B. Bioinspired, roughness-induced, water and oil super-philic and super-phobic coatings prepared by adaptable layer-by-layer technique. Sci. Rep. 2015, 5, 14030. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Wang, Z.; Huang, S.; Pan, Y.; Zhao, X. Flexible, Durable, and Unconditioned Superoleophobic/Superhydrophilic Surfaces for Controllable Transport and Oil–Water Separation. Adv. Func. Mater. 2018, 28. [Google Scholar] [CrossRef]
- Bakli, C.; Chakraborty, S. Slippery to Sticky Transition of Hydrophobic Nanochannels. Nano Lett. 2015, 15, 7497–7502. [Google Scholar] [CrossRef] [PubMed]
- Vo, T.Q.; Park, B.; Park, C.; Kim, B. Nano-scale liquid film sheared between strong wetting surfaces: Effects of interface region on the flow. J. Mech. Sci. Technol. 2015, 29, 1681–1688. [Google Scholar] [CrossRef]
- Bao, L.; Priezjev, N.V.; Hu, H.; Luo, K. Effects of viscous heating and wall-fluid interaction energy on rate-dependent slip behavior of simple fluids. Phys. Rev. E 2017, 96. [Google Scholar] [CrossRef] [PubMed]
- Ghorbanian, J.; Beskok, A. Scale effects in Nano-channel liquid flows. Microfluid Nanofluid 2016, 20, 121. [Google Scholar] [CrossRef]
- Jeong, M.; Kim, Y.; Zhou, W.; Tao, W.; Ha, M.Y. Effects of surface wettability, roughness and moving wall velocity on the Couette flow in nano-channel using multi-scale hybrid method. Comput. Fluid. 2017, 147, 1–11. [Google Scholar] [CrossRef]
- Noorian, H.; Toghraie, D.; Azimian, A.R. Molecular dynamics simulation of Poiseuille flow in a rough nano channel with checker surface roughnesses geometry. Heat Mass Transf. 2014, 50, 105–113. [Google Scholar] [CrossRef]
- Cao, B.; Chen, M.; Guo, Z. Effect of surface roughness on gas flow in microchannels by molecular dynamics simulation. Int. J. Eng. Sci. 2006, 44, 927–937. [Google Scholar] [CrossRef]
- Nosonovsky, M.; Bhushan, B. Multiscale Dissipative Mechanisms and Hierarchical Surfaces: Friction, Superhydrophobicity, and Biomimetics; Springer: Heidelberg, Germany, 2008. [Google Scholar]
- Baldoni, F. On slippage induced by surface diffusion. J. Eng. Math. 1996, 30, 647–659. [Google Scholar] [CrossRef]
- Jabbarzadeh, A.; Atkinson, J.D.; Tanner, R.I. Effect of the wall roughness on slip and rheological properties of hexadecane in molecular dynamics simulation of Couette shear flow between two sinusoidal walls. Phys. Rev. E 2000, 61, 690–699. [Google Scholar] [CrossRef]
- Pit, R.; Hervet, H.; Leger, L. Direct experimental evidence of slip in hexadecane: Solid interfaces. Phys. Rev. Lett. 2000, 85, 980–983. [Google Scholar] [CrossRef] [PubMed]
- Ponomarev, I.V.; Meyerovich, A.E. Surface roughness and effective stick-slip motion. Phys. Rev. E 2003, 67, 026302. [Google Scholar] [CrossRef] [PubMed]
- Bonaccurso, E.; Butt, H.-J.; Craig, V.S.J. Surface Roughness and Hydrodynamic Boundary Slip of a Newtonian Fluid in a Completely Wetting System. Phys. Rev. E 2003, 90, 144501. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Granick, S. Limits of the Hydrodynamic No-Slip Boundary Condition. Phys. Rev. Lett. 2002, 88, 106102. [Google Scholar] [CrossRef] [PubMed]
- Schmatko, T.; Hervet, H.; Léger, L. Effect of nanometric-scale roughness on slip at the wall of simple fluids. Langmuir 2006, 22, 6843–6850. [Google Scholar] [CrossRef] [PubMed]
- Guriyanova, S.; Semin, B.; Rodrigues, T.S.; Butt, H.-J.; Bonaccurso, E. Hydrodynamic drainage force in a highly confined geometry: Role of surface roughness on different length scales. Microfluid Nanofluid 2010, 8, 653–663. [Google Scholar] [CrossRef]
- Pan, Y.; Jing, D.; Zhao, X. Effect of Surface Roughness on the Measurement of Boundary Slip Based on Atomic Force Microscope. Sci. Adv. Mater. 2017, 9, 122–127. [Google Scholar] [CrossRef]
- Vinogradova, O.I.; Yakubov, G.E. Surface roughness and hydrodynamic boundary conditions. Phys. Rev. E 2006, 73, 045302(R). [Google Scholar] [CrossRef] [PubMed]
- Cottin-Bizonne, C.; Cross, B.; Steinberger, A.; Charlaix, E. Boundary slip on smooth hydrophobic surfaces: Intrinsic effects and possible artifacts. Phys. Rev. Lett. 2005, 94, 056102. [Google Scholar] [CrossRef] [PubMed]
- Bhushan, B.; Wang, Y.; Maali, A. Boundary Slip Study on Hydrophilic, Hydrophobic, and Superhydrophobic Surfaces with Dynamic Atomic Force Microscopy. Langmuir 2009, 25, 8117–8121. [Google Scholar] [CrossRef] [PubMed]
- Jing, D.; Bhushan, B. The coupling of surface charge and boundary slip at the solid–liquid interface and their combined effect on fluid drag: A review. J. Colloid Interface Sci. 2015, 454, 152–179. [Google Scholar] [CrossRef] [PubMed]
- Kandlikar, S.G.; Garimella, S.; Li, D.Q.; Colin, S.; King, M.R. Heat Transfer and Fluid Flow in Minichannels and Microchannels; Elsevier: Oxford, UK, 2006. [Google Scholar]
- Li, D. Encyclopedia of Microfluidics and Nanofluidics; Springer Science & Business Media: Berlin, Germany, 2008. [Google Scholar]
- Lin, B. Microfluidics: Technologies and Applications; Springer: Berlin, Germany, 2011. [Google Scholar]
- Ngoma, G.D.; Erchiqui, F. Heat flux and slip effects on liquid flow in a microchannel. Int. J. Therm. Sci. 2007, 46, 1076–1083. [Google Scholar] [CrossRef]
- Yavari, H.; Sadeghi, A.; Saidi, M.H.; Chakraborty, S. Combined influences of viscous dissipation, non-uniform Joule heating and variable thermophysical properties on convective heat transfer in microtubes. Int. J. Heat Mass Transf. 2012, 55, 762–772. [Google Scholar] [CrossRef]
- Tan, D.K.; Liu, Y. Combined effects of streaming potential and wall slip on flow and heat transfer in microchannels. Int. Commun. Heat Mass 2014, 53, 39–42. [Google Scholar] [CrossRef]
- Keramati, H.; Sadeghi, A.; Saidi, M.H.; Chakraborty, S. Analytical solutions for thermo-fluidic transport in electroosmotic flow through rough microtubes. Int. J. Heat Mass Transf. 2016, 92, 244–251. [Google Scholar] [CrossRef]
- Jing, D.; Pan, Y. Electroviscous effect and convective heat transfer of pressure-driven flow through microtubes with surface charge-dependent slip. Int. J. Heat Mass Transf. 2016, 101, 648–655. [Google Scholar] [CrossRef]
- Jing, D.; Pan, Y.; Wang, X. Joule heating, viscous dissipation and convective heat transfer of pressure-driven flow in a microchannel with surface charge-dependent slip. Int. J. Heat Mass Transf. 2017, 108, 1305–1313. [Google Scholar] [CrossRef]
- Anonymous. Geometrical Product Specifications—Surface Texture: Profile Method-Nominal Characteristics of Contact (Stylus) Instruments. ISO3274. International Standardization Organization: Geneva, Switzerland, 1 December 1996. [Google Scholar]
- Anonymous. Surface Texture (Surface Roughness, Waviness, and Lay). ANSI/ASME B46.1-2009. ASME: New York, NY, USA, 20 August 2010. [Google Scholar]
- Haynes, W.M. Handbook of Chemistry and Physics, 96th ed.; Academic Press: New York, NY, USA, 2015. [Google Scholar]
- Huang, Y.; Zhao, X.; Pan, Y.; Ahmad, K. Simulation of effective slip and drag in pressure-driven flow on superhydrophobic surfaces. J. Nanomater. 2016, 2016. [Google Scholar] [CrossRef]
- Li, Z.; He, Y.L.; Tang, G.H.; Tao, W.Q. Experimental and numerical studies of liquid flow and heat transfer in microtubes. Int. J. Heat. Mass Transf. 2007, 50, 3447–3460. [Google Scholar] [CrossRef]
- Wu, H.Y.; Cheng, P. An experimental study of convective heat transfer in silicon microchannels with different surface conditions. Int. J. Heat. Mass Transf. 2003, 46, 2547–2556. [Google Scholar] [CrossRef]
- Guo, L.; Xu, H.; Gong, L. Influence of wall roughness models on fluid flow and heat transfer in microchannels. Appl. Therm. Eng. 2015, 84, 399–408. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, Y.; Jing, D.; Zhang, H.; Zhao, X. Effective Boundary Slip Induced by Surface Roughness and Their Coupled Effect on Convective Heat Transfer of Liquid Flow. Entropy 2018, 20, 334. https://doi.org/10.3390/e20050334
Pan Y, Jing D, Zhang H, Zhao X. Effective Boundary Slip Induced by Surface Roughness and Their Coupled Effect on Convective Heat Transfer of Liquid Flow. Entropy. 2018; 20(5):334. https://doi.org/10.3390/e20050334
Chicago/Turabian StylePan, Yunlu, Dalei Jing, He Zhang, and Xuezeng Zhao. 2018. "Effective Boundary Slip Induced by Surface Roughness and Their Coupled Effect on Convective Heat Transfer of Liquid Flow" Entropy 20, no. 5: 334. https://doi.org/10.3390/e20050334
APA StylePan, Y., Jing, D., Zhang, H., & Zhao, X. (2018). Effective Boundary Slip Induced by Surface Roughness and Their Coupled Effect on Convective Heat Transfer of Liquid Flow. Entropy, 20(5), 334. https://doi.org/10.3390/e20050334




