Quantifying Configuration-Sampling Error in Langevin Simulations of Complex Molecular Systems
Abstract
:1. Introduction
KL Divergence as a Natural Measure of Sampling Bias
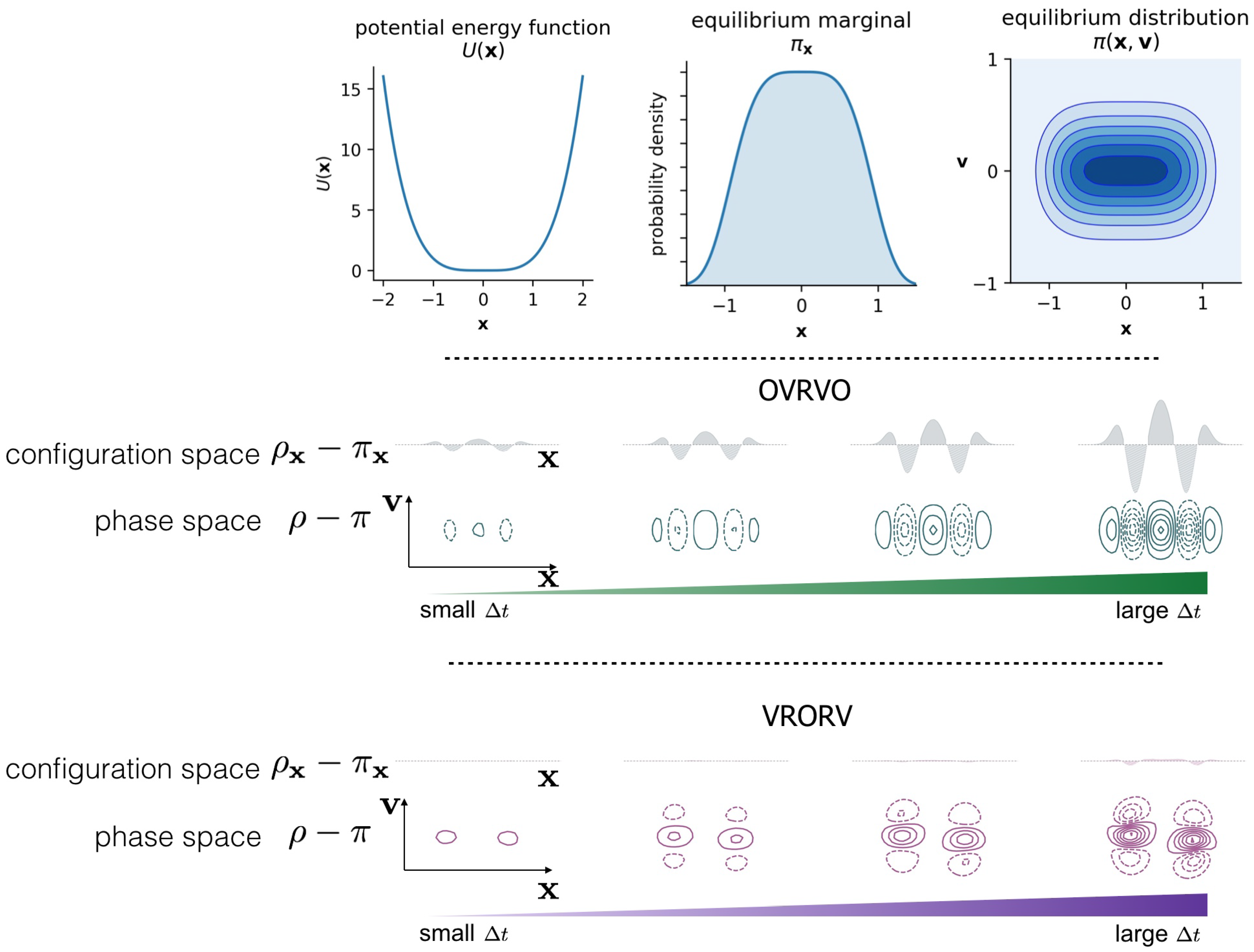
2. Numerical Discretization Methods and Timestep-Dependent Bias
Langevin Integrators Introduce Sampling Bias That Grows with the Size of the Timestep
3. Estimators for KL Divergence and the Configurational KL Divergence
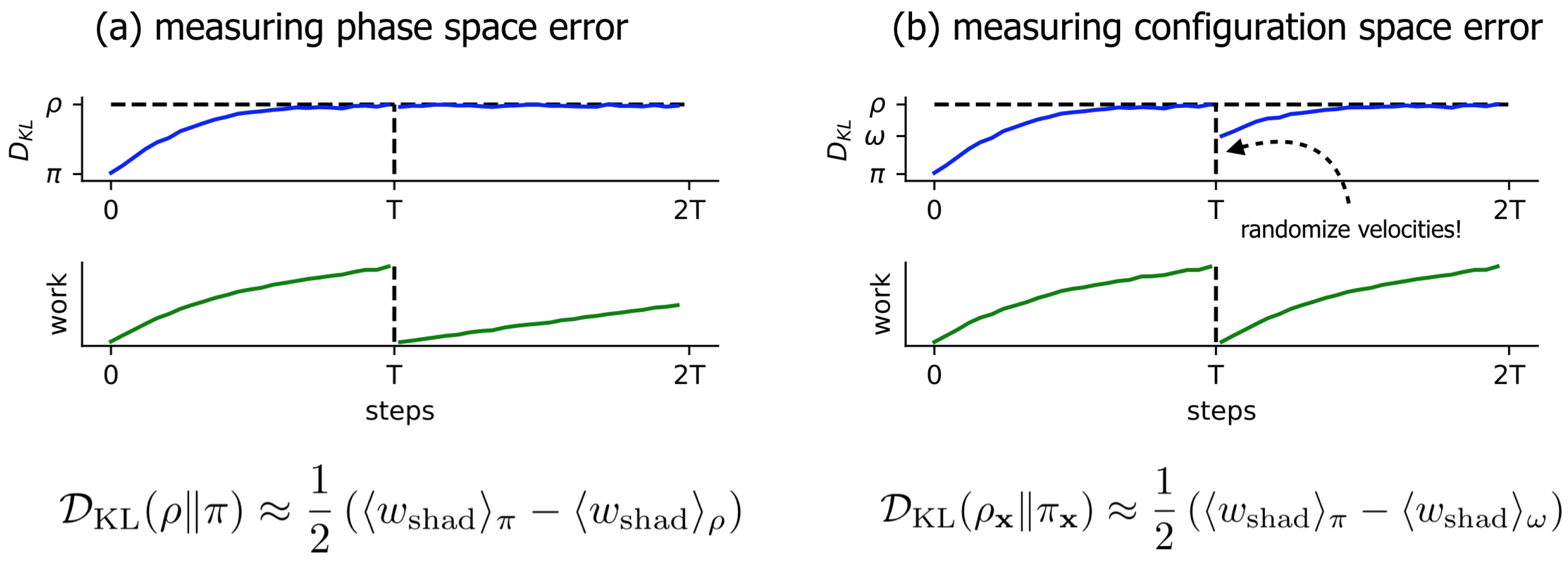
3.1. Near-Equilibrium Estimators for KL Divergence
3.2. A Simple Modification to the Near-Equilibrium Estimator Can Compute KL Divergence in Configuration Space
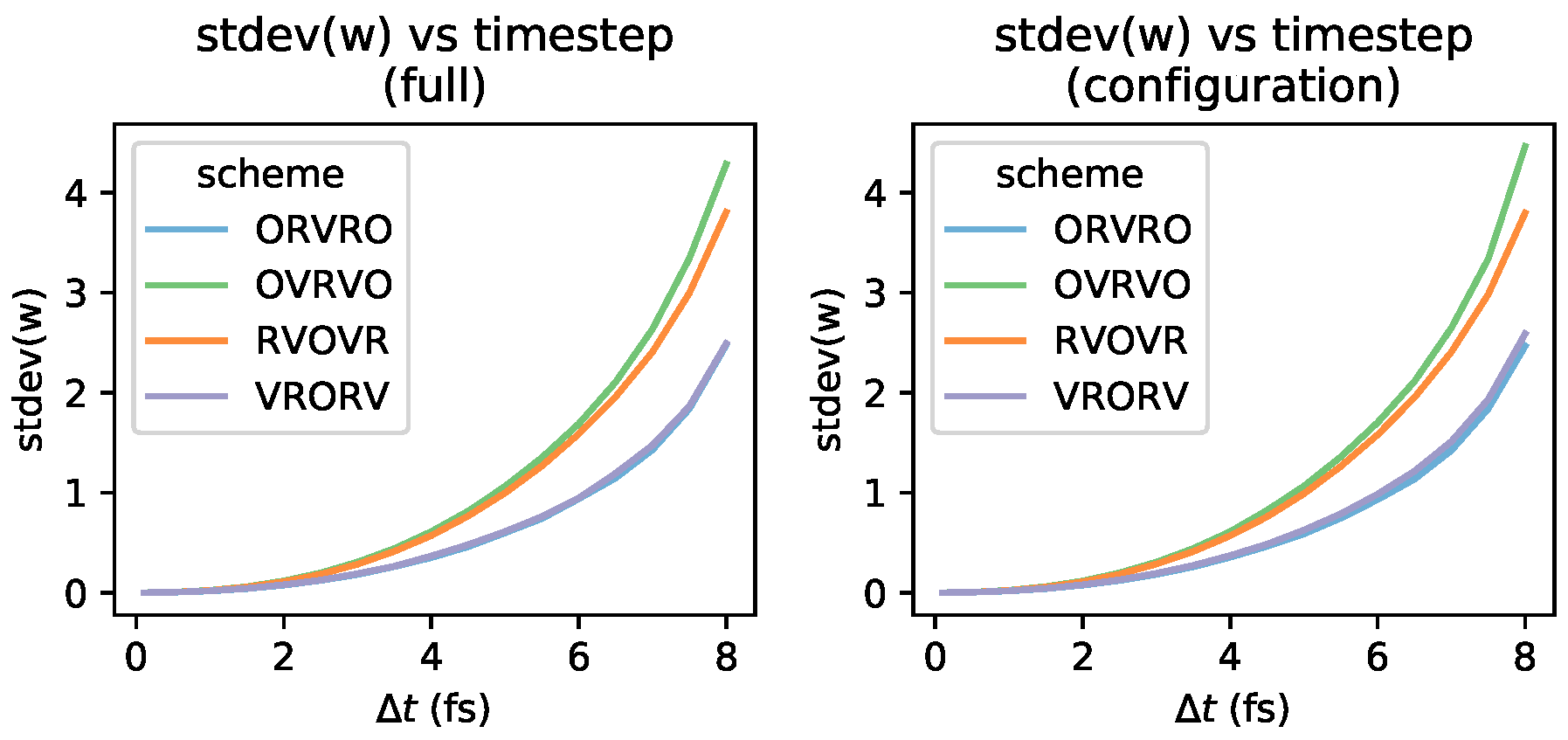
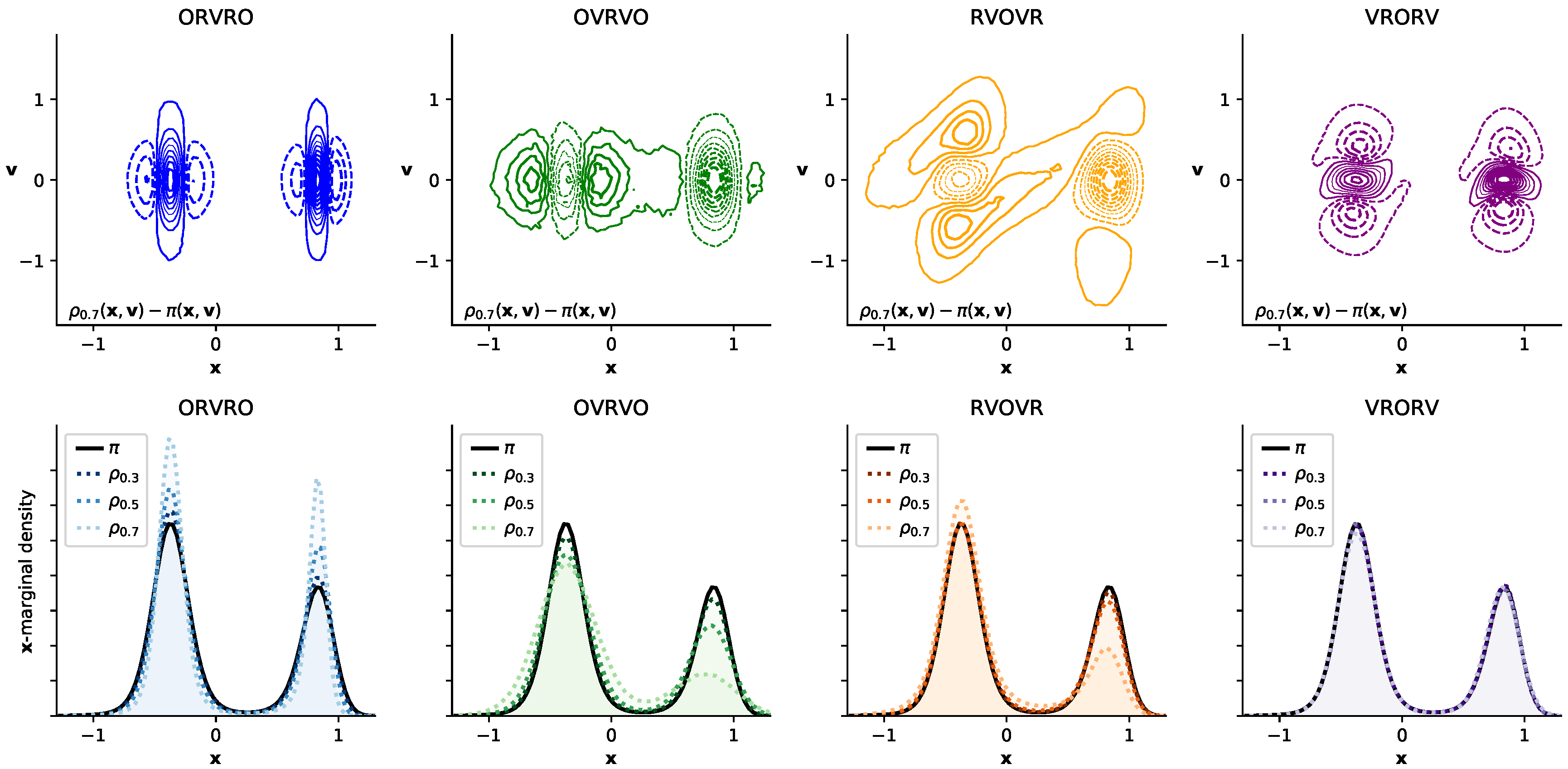
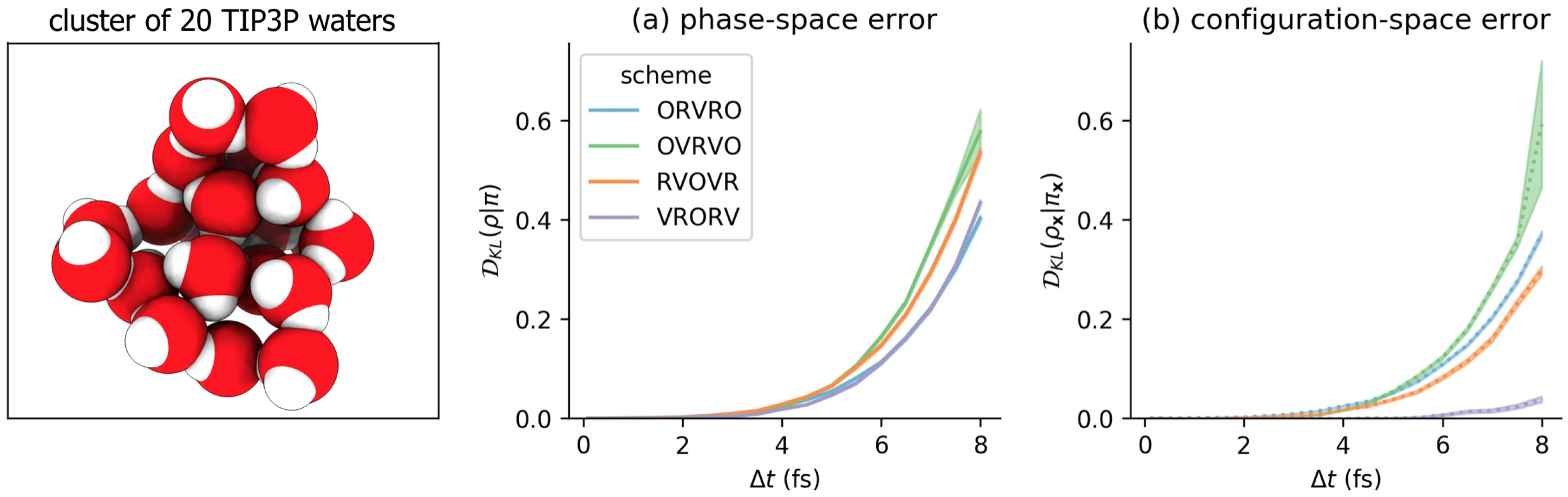
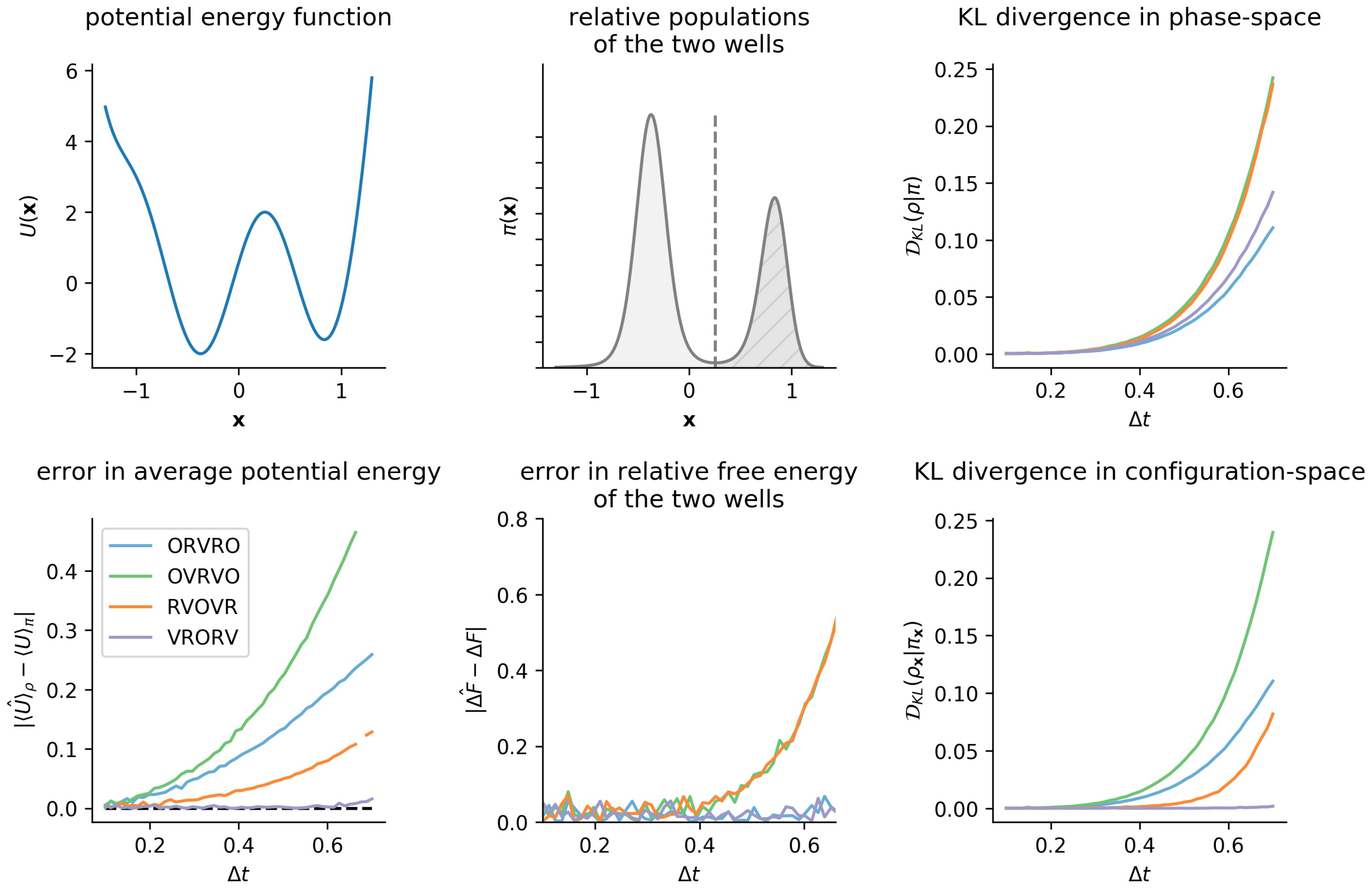
3.3. Comparison of Phase-Space Error for Different Integrators
3.4. Comparison of Configurational KL Divergence for Different Integrators
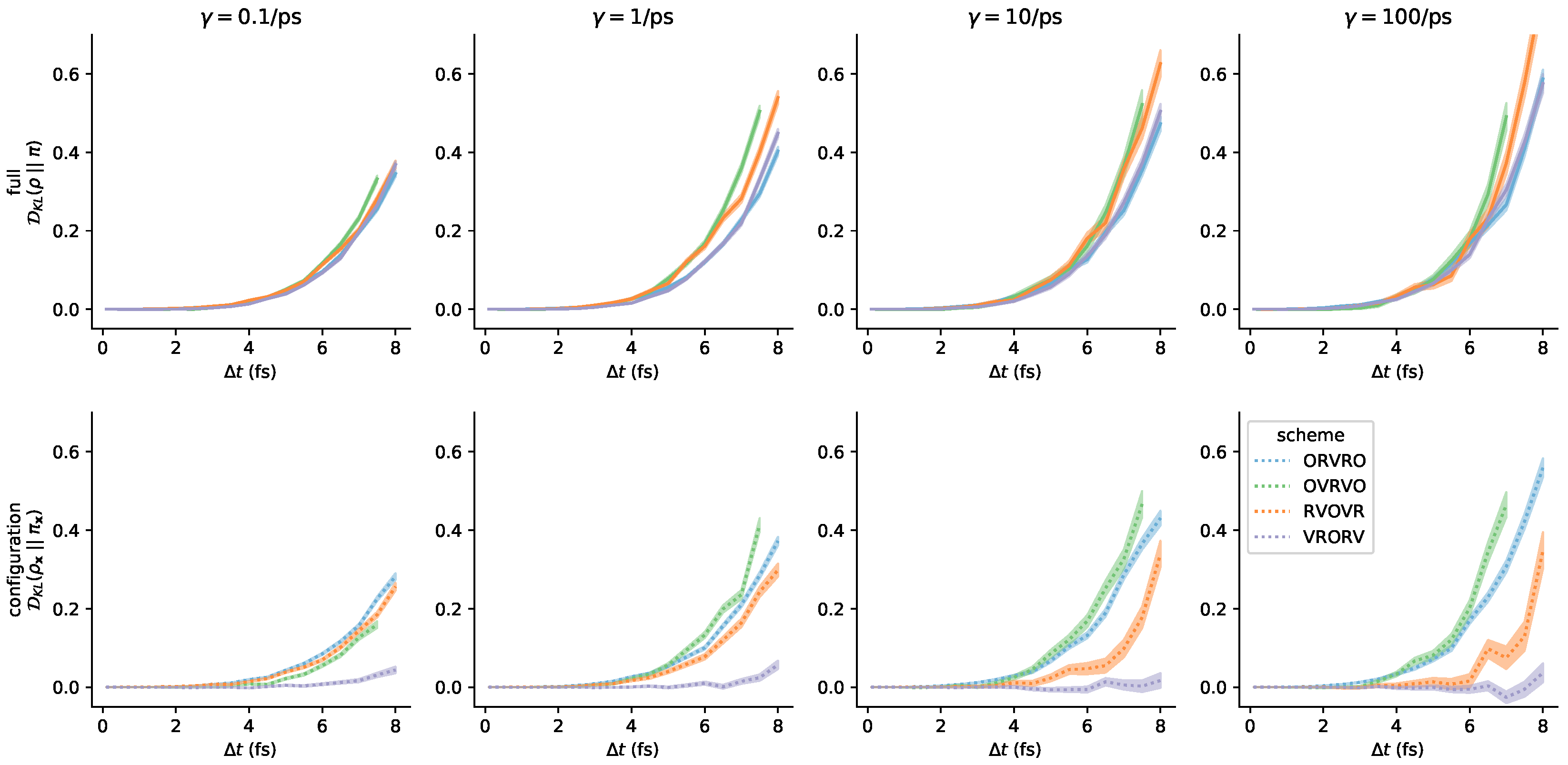
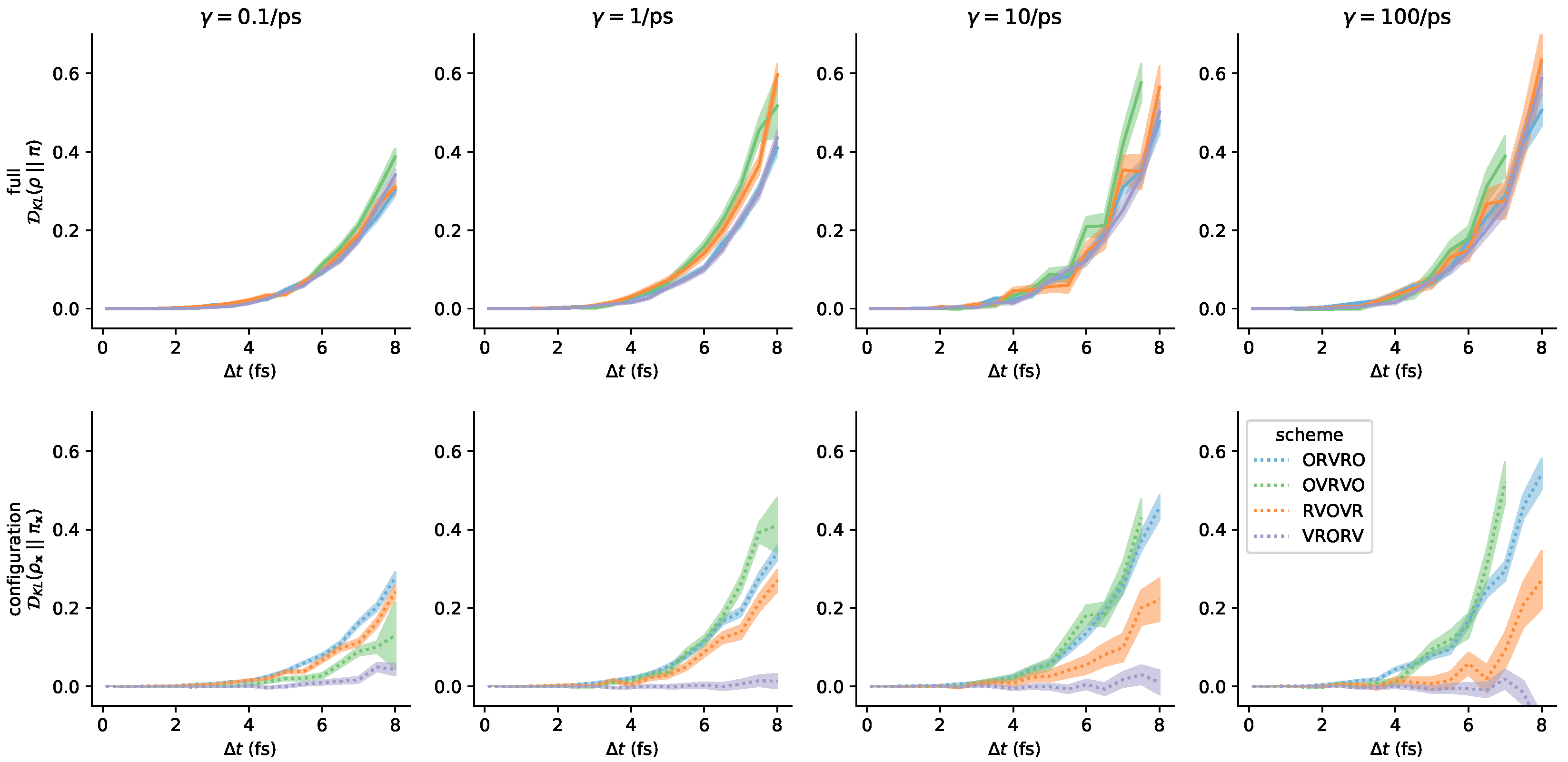
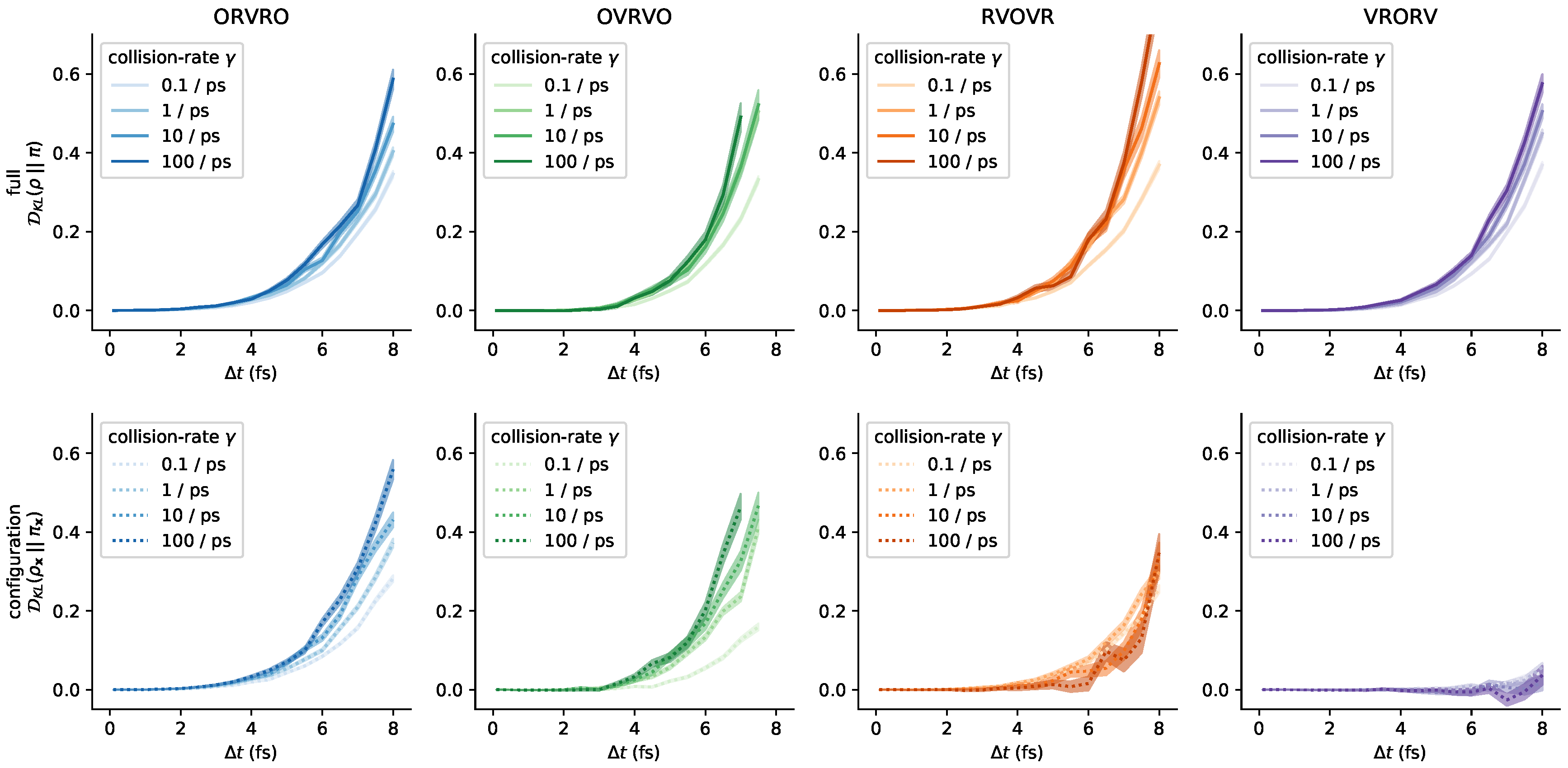
3.5. Influence of the Collision Rate
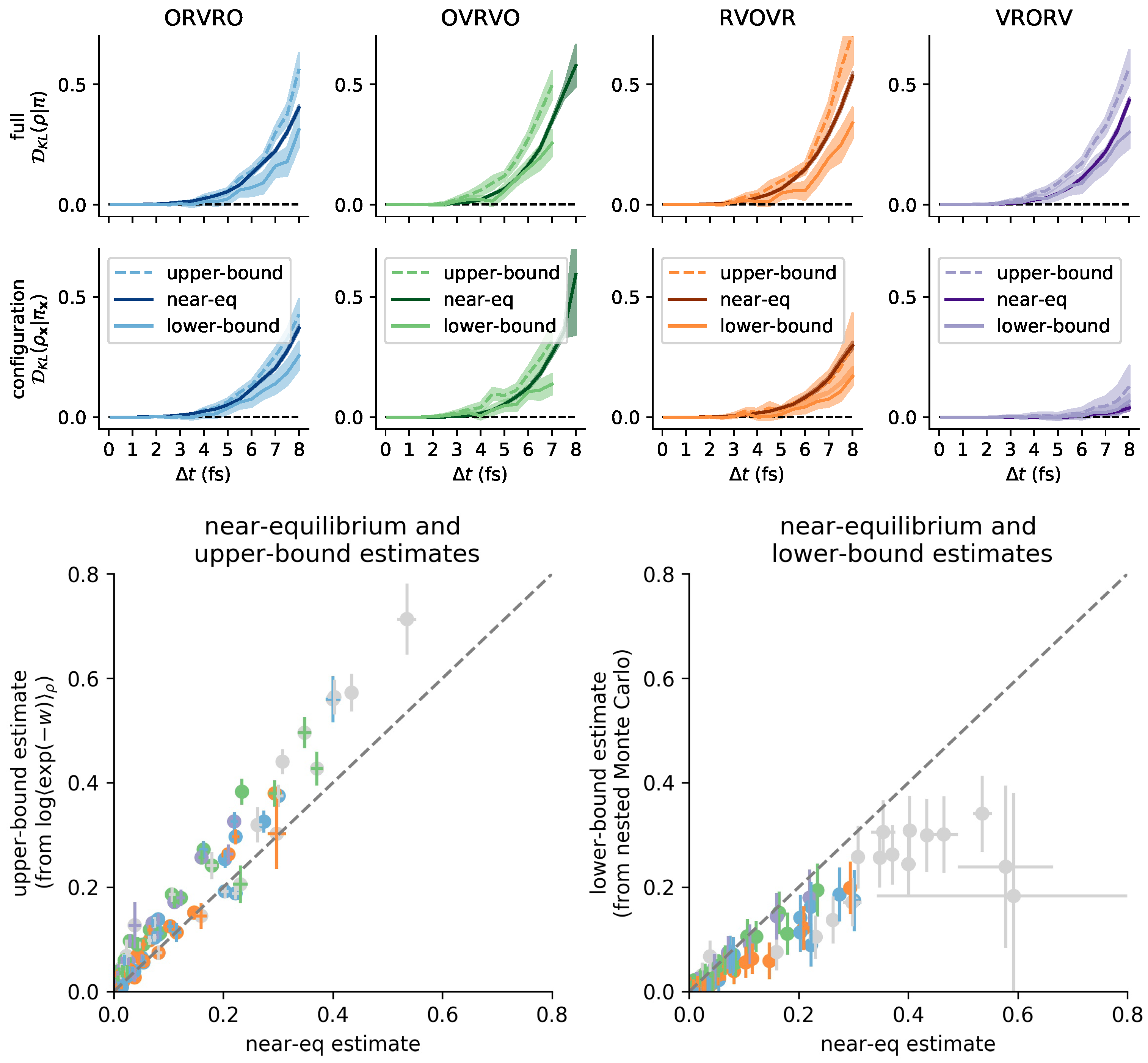
3.6. Comparison with Reference Methods Validates the Near-Equilibrium Estimate
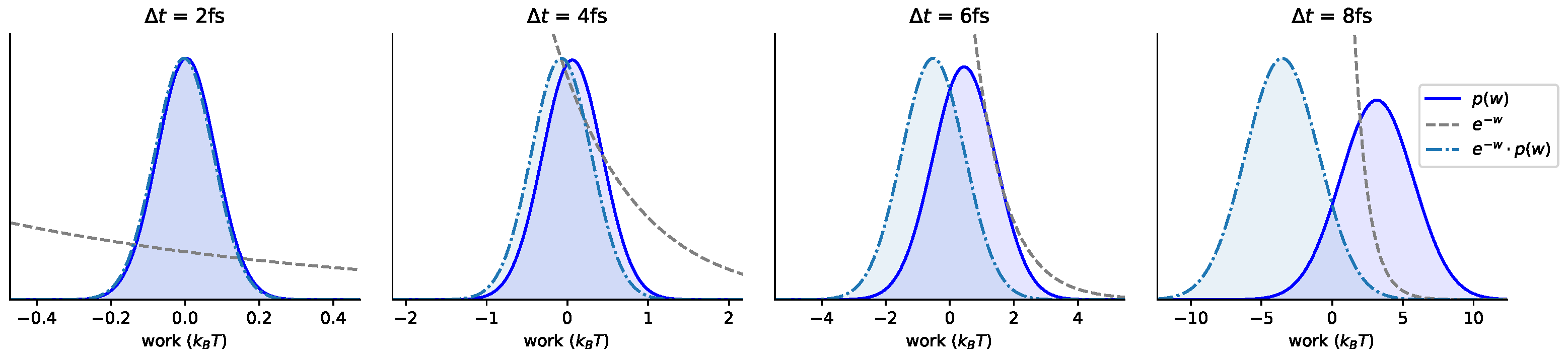
3.6.1. Practical Lower Bound from Nested Monte Carlo
3.6.2. Practical Upper Bound from Jensen’s Inequality
3.6.3. Sandwiching the KL Divergence to Validate the Near-Equilibrium Estimate
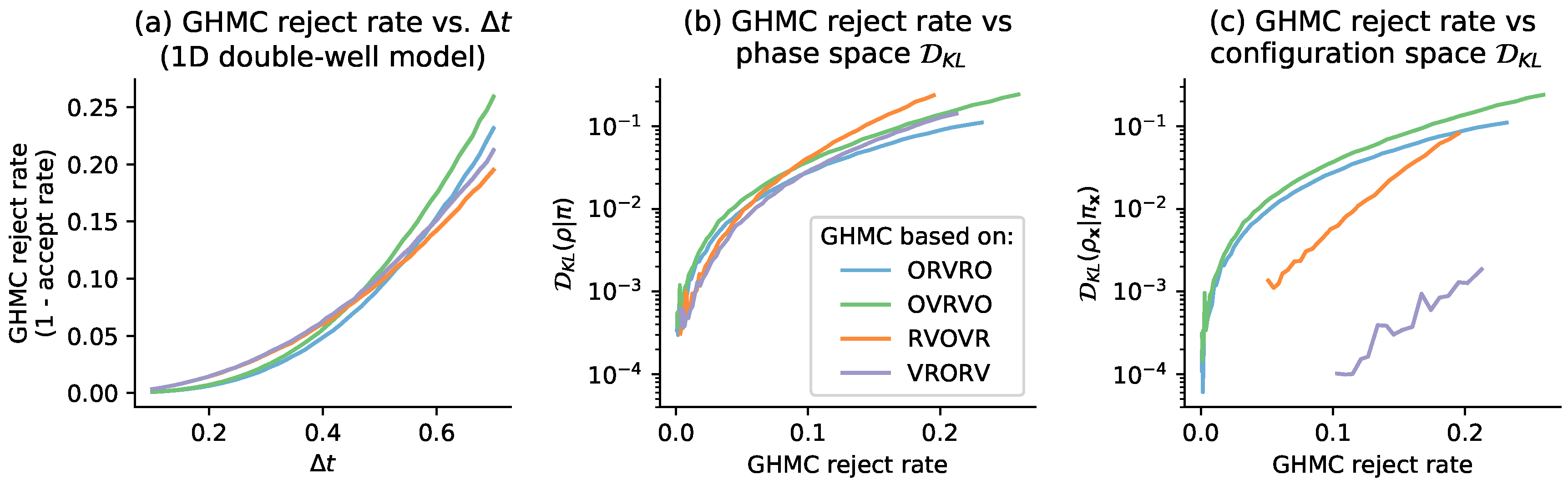
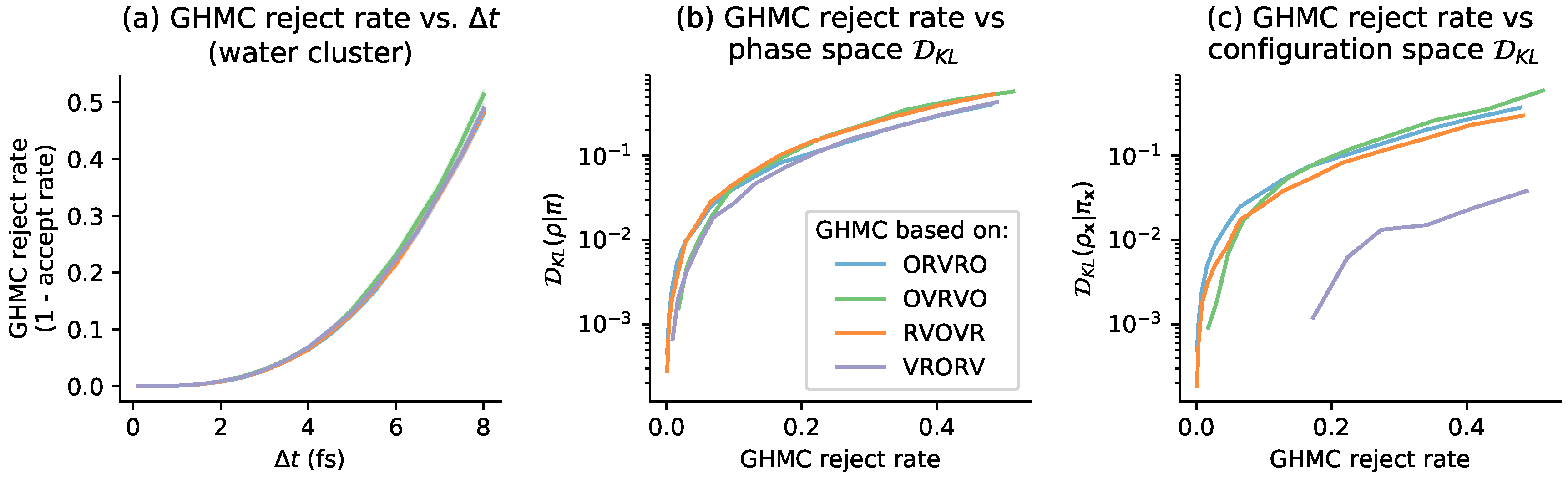
4. Relation to GHMC Acceptance Rates
5. Discussion
Future Directions
6. Detailed Methods
6.1. One-Dimensional Model System: Double Well
6.2. Model Molecular Mechanics System: A Harmonically Restrained Water Cluster
- The test system must have interactions typical of solvated molecular mechanics models, so that we would have some justification for generalizing from the results. This rules out 1D systems, for example, and prompted us to search for systems that were not alanine dipeptide in vacuum.
- The test system must have sufficiently few degrees of freedom that the nested Monte Carlo estimator remains feasible. Because the nested estimator requires converging many exponential averages, the cost of achieving a fixed level of precision grows dramatically with the standard deviation of the steady-state shadow work distribution. The width of this distribution is extensive in system size. Empirically, this ruled out using the first water box we had tried (with approximately 500 rigid TIP3P waters [21], with 3000 degrees of freedom). Practically, there was also a limit to how small it is possible to make a water system with periodic boundary conditions in OpenMM (about 100 waters, or 600 degrees of freedom), which was also infeasible.
- The test system must have enough disordered degrees of freedom that the behavior of work averages is typical of larger systems. This was motivated by our observation that it was paradoxically much easier to converge estimates for large disordered systems than it was to converge estimates for the 1D toy system.
6.3. Caching Equilibrium Samples
6.4. Computing Shadow Work for Symmetric Strang Splittings
6.5. Computation of Shadow Work for OVRVO
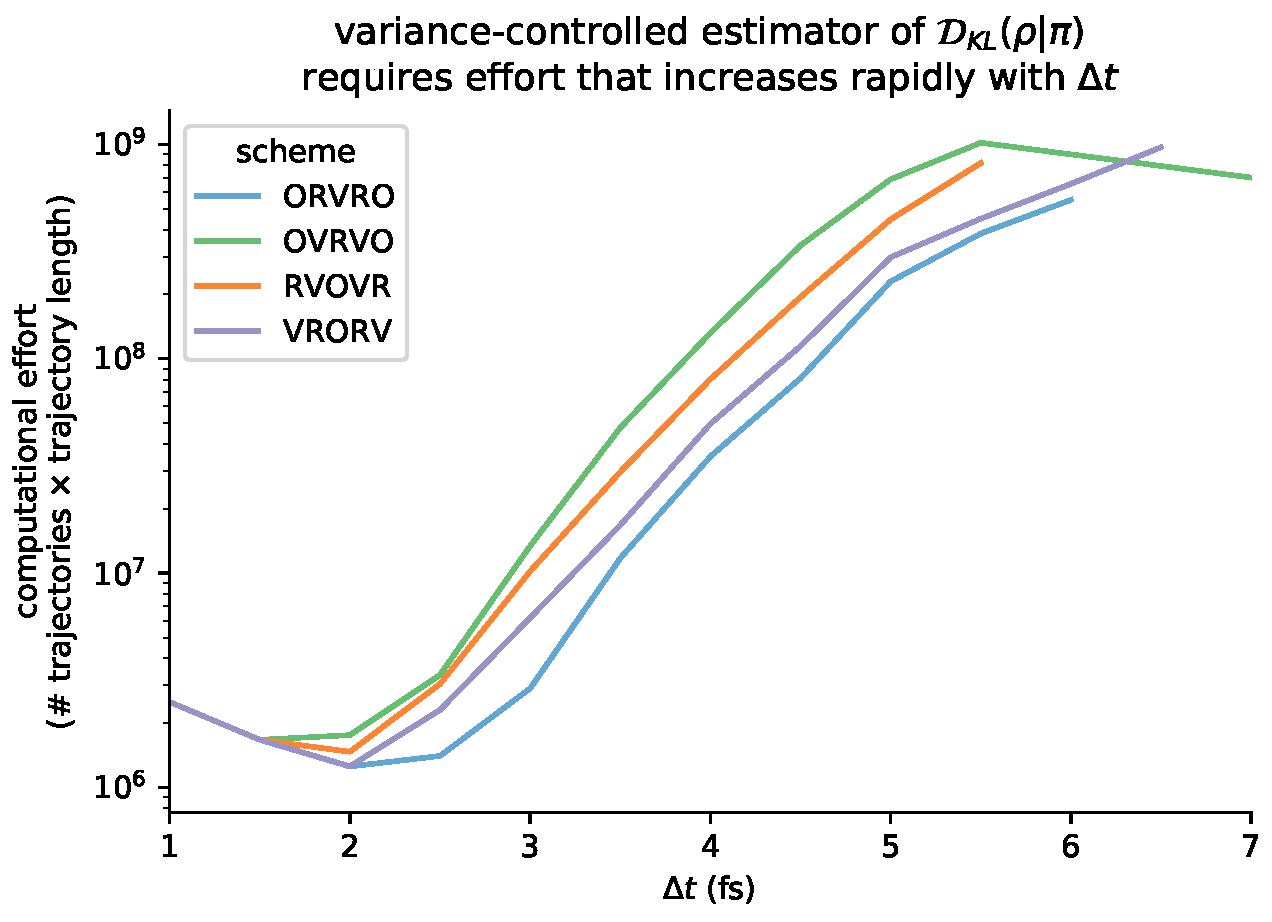
6.6. Variance-Controlled Adaptive Estimator for KL Divergence
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A. Statistics of Shadow Work Distributions
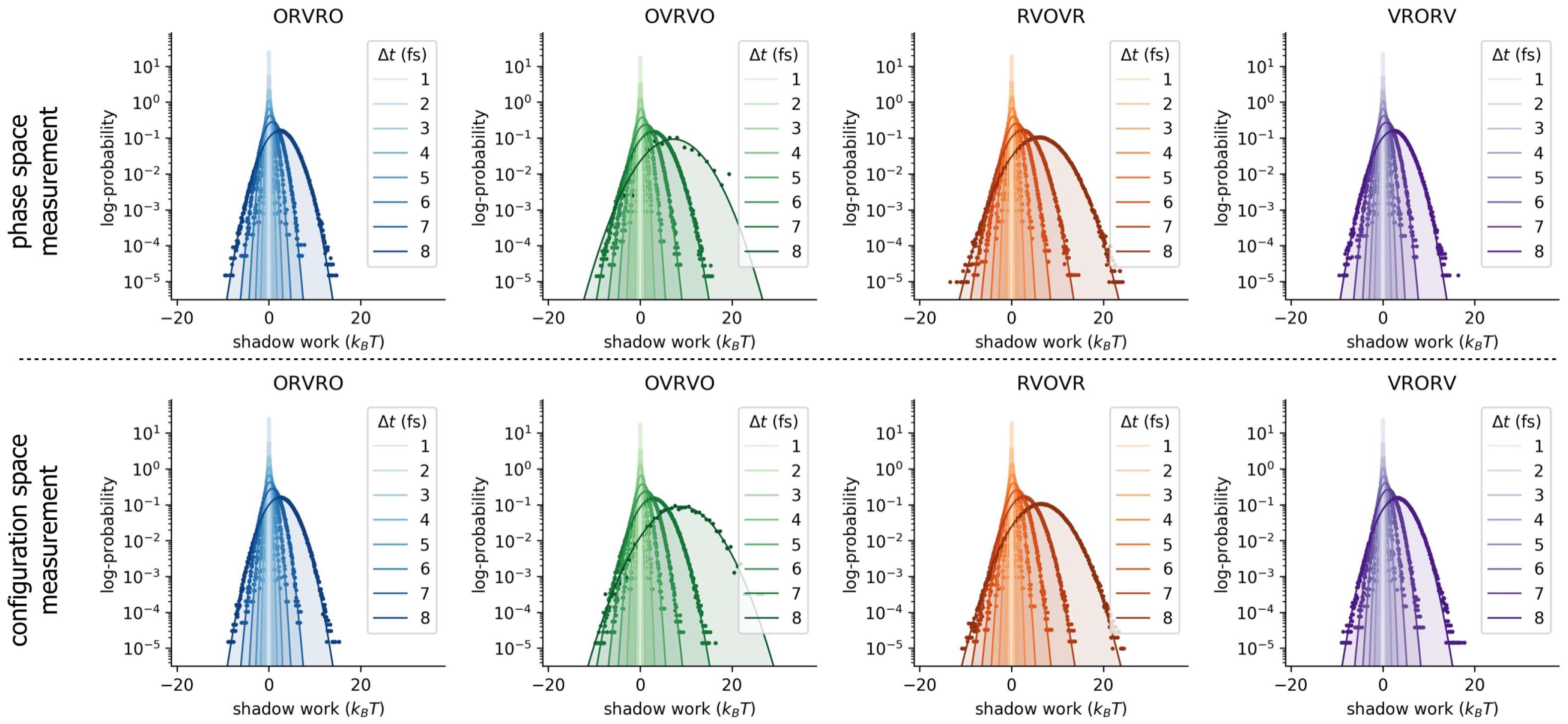
Appendix B. Log-Scale Plots
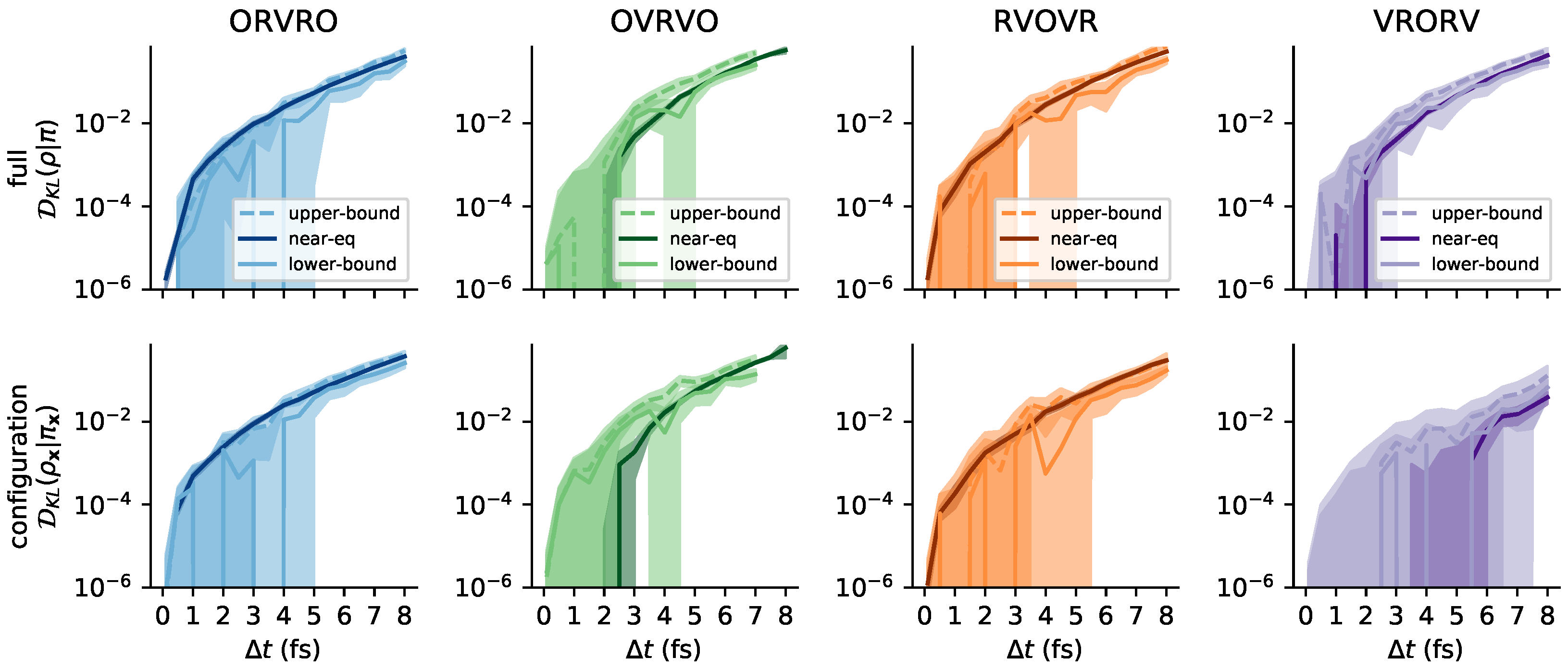
Appendix C. Further Comments on the Collision Rate
References
- Lemons, D.S.; Gythiel, A. Paul Langevin’s 1908 paper “On the Theory of Brownian Motion” [“Sur la théorie du mouvement brownien,” C. R. Acad. Sci. (Paris) 146, 530–533 (1908)]. Am. J. Phys. 1997, 65, 1079–1081. [Google Scholar] [CrossRef]
- Lelièvre, T.; Stoltz, G.; Rousset, M. Free Energy Computations: A Mathematical Perspective; Imperial College Press: London, UK; Hackensack, NJ, USA, 2010. [Google Scholar]
- Leimkuhler, B.; Matthews, C. Molecular Dynamics: With Deterministic and Stochastic Numerical Methods; Springer: Cham, Germany, 2015. [Google Scholar]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation, 2nd ed.; Academic Press, Inc.: Orlando, FL, USA, 2001. [Google Scholar]
- Maruyama, G. Continuous Markov Processes and Stochastic Equations. Rend. Circolo Mat. Palermo 1955, 4, 48–90. [Google Scholar] [CrossRef]
- Ermak, D.L.; Yeh, Y. Equilibrium Electrostatic Effects on the Behavior of Polyions in Solution: Polyion-Mobile Ion Interaction. Chem. Phys. Lett. 1974, 24, 243–248. [Google Scholar] [CrossRef]
- Brünger, A.; Brooks, C.L.; Karplus, M. Stochastic Boundary Conditions for Molecular Dynamics Simulations of ST2 Water. Chem. Phys. Lett. 1984, 105, 495–500. [Google Scholar] [CrossRef]
- Pastor, R.W.; Brooks, B.R.; Szabo, A. An Analysis of the Accuracy of Langevin and Molecular Dynamics Algorithms. Mol. Phys. 1988, 65, 1409–1419. [Google Scholar] [CrossRef]
- Athénes, M. A Path-Sampling Scheme for Computing Thermodynamic Properties of a Many-Body System in a Generalized Ensemble. Eur. Phys. J. B Condens. Matter Complex Syst. 2004, 38, 651–663. [Google Scholar] [CrossRef]
- Adjanor, G.; Athènes, M.; Calvo, F. Free Energy Landscape from Path-Sampling: Application to the Structural Transition in LJ38. Eur. Phys. J. B Condens. Matter Complex Syst. 2006, 53, 47–60. [Google Scholar] [CrossRef]
- Bussi, G.; Parrinello, M. Accurate Sampling Using Langevin Dynamics. Phys. Rev. E 2007, 75, 056707. [Google Scholar] [CrossRef] [PubMed]
- Izaguirre, J.A.; Sweet, C.R.; Pande, V.S. Multiscale Dynamics of Macromolecules Using Normal Mode Langevin. In Biocomputing 2010; World Scientific: Singapore, 2009; pp. 240–251. [Google Scholar] [CrossRef]
- Leimkuhler, B.; Matthews, C. Robust and Efficient Configurational Molecular Sampling via Langevin Dynamics. J. Chem. Phys. 2013, 138, 174102. [Google Scholar] [CrossRef] [PubMed]
- Leimkuhler, B.; Matthews, C. Efficient Molecular Dynamics Using Geodesic Integration and Solvent–solute Splitting. Proc. R. Soc. A 2016, 472, 20160138. [Google Scholar] [CrossRef] [PubMed]
- Grubmüller, H.; Tavan, P. Multiple Time Step Algorithms for Molecular Dynamics Simulations of Proteins: How Good Are They? J. Comput. Chem. 1998, 19, 1534–1552. [Google Scholar] [CrossRef]
- Hopkins, C.W.; Le Grand, S.; Walker, R.C.; Roitberg, A.E. Long-Time-Step Molecular Dynamics through Hydrogen Mass Repartitioning. J. Chem. Theory Comput. 2015, 11, 1864–1874. [Google Scholar] [CrossRef] [PubMed]
- Butler, B.D.; Ayton, G.; Jepps, O.G.; Evans, D.J. Configurational Temperature: Verification of Monte Carlo Simulations. J. Chem. Phys. 1998, 109, 6519–6522. [Google Scholar] [CrossRef]
- Leimkuhler, B.; Matthews, C. Rational Construction of Stochastic Numerical Methods for Molecular Sampling. Appl. Math. Res. eXpress 2013, 2013, 34–56. [Google Scholar] [CrossRef]
- Sweet, C.R.; Hampton, S.S.; Skeel, R.D.; Izaguirre, J.A. A Separable Shadow Hamiltonian Hybrid Monte Carlo Method. J. Chem. Phys. 2009, 131, 174106. [Google Scholar] [CrossRef] [PubMed]
- Sivak, D.A.; Chodera, J.D.; Crooks, G.E. Using nonequilibrium fluctuation theorems to understand and correct errors in equilibrium and nonequilibrium simulations of discrete Langevin dynamics. Phys. Rev. X 2013, 3, 011007. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Sivak, D.A.; Chodera, J.D.; Crooks, G.E. Time Step Rescaling Recovers Continuous-Time Dynamical Properties for Discrete-Time Langevin Integration of Nonequilibrium Systems. J. Phys. Chem. B 2014, 118, 6466–6474. [Google Scholar] [CrossRef] [PubMed]
- Melchionna, S. Design of quasisymplectic propagators for Langevin dynamics. J. Chem. Phys. 2007, 127, 044108. [Google Scholar] [CrossRef] [PubMed]
- Skeel, R.D.; Izaguirre, J.A. An impulse integrator for Langevin dynamics. Mol. Phys. 2002, 100, 3885–3891. [Google Scholar] [CrossRef]
- Serrano, M.; De Fabritiis, G.; Espanol, P.; Coveney, P. A stochastic Trotter integration scheme for dissipative particle dynamics. J. Math. Comput. Simul. 2006, 72, 190–194. [Google Scholar] [CrossRef]
- Thalmann, F.; Farago, J. Trotter derivation of algorithms for Brownian and dissipative particle dynamics. J. Chem. Phys. 2007, 127, 124109. [Google Scholar] [CrossRef] [PubMed]
- Leimkuhler, B.; Matthews, C.; Stoltz, G. The Computation of Averages from Equilibrium and Nonequilibrium Langevin Molecular Dynamics. IMA J. Numer. Anal. 2016, 36, 13–79. [Google Scholar] [CrossRef]
- Swope, W.C.; Andersen, H.C.; Berens, P.H.; Wilson, K.R. A Computer Simulation Method for the Calculation of Equilibrium Constants for the Formation of Physical Clusters of Molecules: Application to Small Water Clusters. J. Chem. Phys. 1982, 76, 637–649. [Google Scholar] [CrossRef]
- Bennett, C.H. Mass Tensor Molecular Dynamics. J. Comput. Phys. 1975, 19, 267–279. [Google Scholar] [CrossRef]
- Pomès, R.; McCammon, J.A. Mass and Step Length Optimization for the Calculation of Equilibrium Properties by Molecular Dynamics Simulation. Chem. Phys. Lett. 1990, 166, 425–428. [Google Scholar] [CrossRef]
- Plecháč, P.; Rousset, M. Implicit Mass-Matrix Penalization of Hamiltonian Dynamics with Application to Exact Sampling of Stiff Systems. Multiscale Model. Simul. 2010, 8, 498–539. [Google Scholar] [CrossRef]
- Sivak, D.A.; Crooks, G.E. Near-Equilibrium Measurements of Nonequilibrium Free Energy. Phys. Rev. Lett. 2012, 108. [Google Scholar] [CrossRef] [PubMed]
- Perez-Cruz, F. Kullback-Leibler Divergence Estimation of Continuous Distributions. In Proceedings of the 2008 IEEE International Symposium on Information Theory, New Orleans, LA, USA, 30 November–4 December 2008; pp. 1666–1670. [Google Scholar] [CrossRef]
- Dhabal, D.; Nguyen, A.H.; Singh, M.; Khatua, P.; Molinero, V.; Bandyopadhyay, S.; Chakravarty, C. Excess Entropy and Crystallization in Stillinger-Weber and Lennard-Jones Fluids. J. Chem. Phys. 2015, 143, 164512. [Google Scholar] [CrossRef] [PubMed]
- Athènes, M.; Adjanor, G. Measurement of Nonequilibrium Entropy from Space-Time Thermodynamic Integration. J. Chem. Phys. 2008, 129, 024116. [Google Scholar] [CrossRef] [PubMed]
- Shirts, M.R.; Pande, V.S. Comparison of Efficiency and Bias of Free Energies Computed by Exponential Averaging, the Bennett Acceptance Ratio, and Thermodynamic Integration. J. Chem. Phys. 2005, 122, 144107. [Google Scholar] [CrossRef] [PubMed]
- Campos, C.M.; Sanz-Serna, J.M. Extra Chance Generalized Hybrid Monte Carlo. J. Comput. Phys. 2015, 281, 365–374. [Google Scholar] [CrossRef]
- Athènes, M.; Marinica, M.C. Free Energy Reconstruction from Steered Dynamics without Post-Processing. J. Comput. Phys. 2010, 229, 7129–7146. [Google Scholar] [CrossRef]
- Wagoner, J.A.; Pande, V.S. Reducing the Effect of Metropolization on Mixing Times in Molecular Dynamics Simulations. J. Chem. Phys. 2012, 137, 214105. [Google Scholar] [CrossRef] [PubMed]
- Nilmeier, J.P.; Crooks, G.E.; Minh, D.D.L.; Chodera, J.D. Nonequilibrium Candidate Monte Carlo Is an Efficient Tool for Equilibrium Simulation. Proc. Natl. Aacd. Sci. USA 2011, 108, E1009–E1018. [Google Scholar] [CrossRef] [PubMed]
- Eastman, P.; Swails, J.; Chodera, J.D.; McGibbon, R.T.; Zhao, Y.; Beauchamp, K.A.; Wang, L.P.; Simmonett, A.C.; Harrigan, M.P.; Stern, C.D.; et al. OpenMM 7: Rapid Development of High Performance Algorithms for Molecular Dynamics. PLOS Comput. Biol. 2017, 13, e1005659. [Google Scholar] [CrossRef] [PubMed]
- Lam, S.K.; Pitrou, A.; Seibert, S. Numba: A LLVM-Based Python JIT Compiler. In Proceedings of the Second Workshop on the LLVM Compiler Infrastructure in HPC, Austin, TX, USA, 15 November 2015; ACM: New York, NY, USA, 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Chodera, J.; Rizzi, A.; Naden, L.; Beauchamp, K.; Grinaway, P.; Fass, J.; Rustenburg, B.; Ross, G.A.; Simmonett, A.; Swenson, D.W. Openmmtools: 0.14.0—Exact Treatment of Alchemical PME Electrostatics, Water Cluster Test System, Optimizations; GitHub: San Francisco, CA, USA, 2018. [Google Scholar] [CrossRef]
- Akhmatskaya, E.; Bou-Rabee, N.; Reich, S. Erratum to “A Comparison of Generalized Hybrid Monte Carlo Methods with and without Momentum Flip” [J. Comput. Phys. 228 (2009) 2256–2265]. J. Computat. Phys. 2009, 228, 7492–7496. [Google Scholar] [CrossRef]
- Adjanor, G.; Athènes, M. Gibbs Free-Energy Estimates from Direct Path-Sampling Computations. J. Chem. Phys. 2005, 123, 234104. [Google Scholar] [CrossRef] [PubMed]
- Adib, A.B. Comment on “On the Crooks fluctuation theorem and the Jarzynski equality” [J. Chem. Phys. 129, 091101 (2008)]. J. Chem. Phys. 2009, 130, 247101. [Google Scholar] [CrossRef] [PubMed]
- Shirts, M.R.; Chodera, J.D. Statistically Optimal Analysis of Samples from Multiple Equilibrium States. J. Chem. Phys. 2008, 129, 124105. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fass, J.; Sivak, D.A.; Crooks, G.E.; Beauchamp, K.A.; Leimkuhler, B.; Chodera, J.D. Quantifying Configuration-Sampling Error in Langevin Simulations of Complex Molecular Systems. Entropy 2018, 20, 318. https://doi.org/10.3390/e20050318
Fass J, Sivak DA, Crooks GE, Beauchamp KA, Leimkuhler B, Chodera JD. Quantifying Configuration-Sampling Error in Langevin Simulations of Complex Molecular Systems. Entropy. 2018; 20(5):318. https://doi.org/10.3390/e20050318
Chicago/Turabian StyleFass, Josh, David A. Sivak, Gavin E. Crooks, Kyle A. Beauchamp, Benedict Leimkuhler, and John D. Chodera. 2018. "Quantifying Configuration-Sampling Error in Langevin Simulations of Complex Molecular Systems" Entropy 20, no. 5: 318. https://doi.org/10.3390/e20050318
APA StyleFass, J., Sivak, D. A., Crooks, G. E., Beauchamp, K. A., Leimkuhler, B., & Chodera, J. D. (2018). Quantifying Configuration-Sampling Error in Langevin Simulations of Complex Molecular Systems. Entropy, 20(5), 318. https://doi.org/10.3390/e20050318





