On the Reduction of Computational Complexity of Deep Convolutional Neural Networks †
Abstract
:1. Introduction
2. Related Work
3. Optimization of Deep Convolutional Neural Networks—An Information-Theoretic Approach
4. Methodology
4.1. Separable Filters
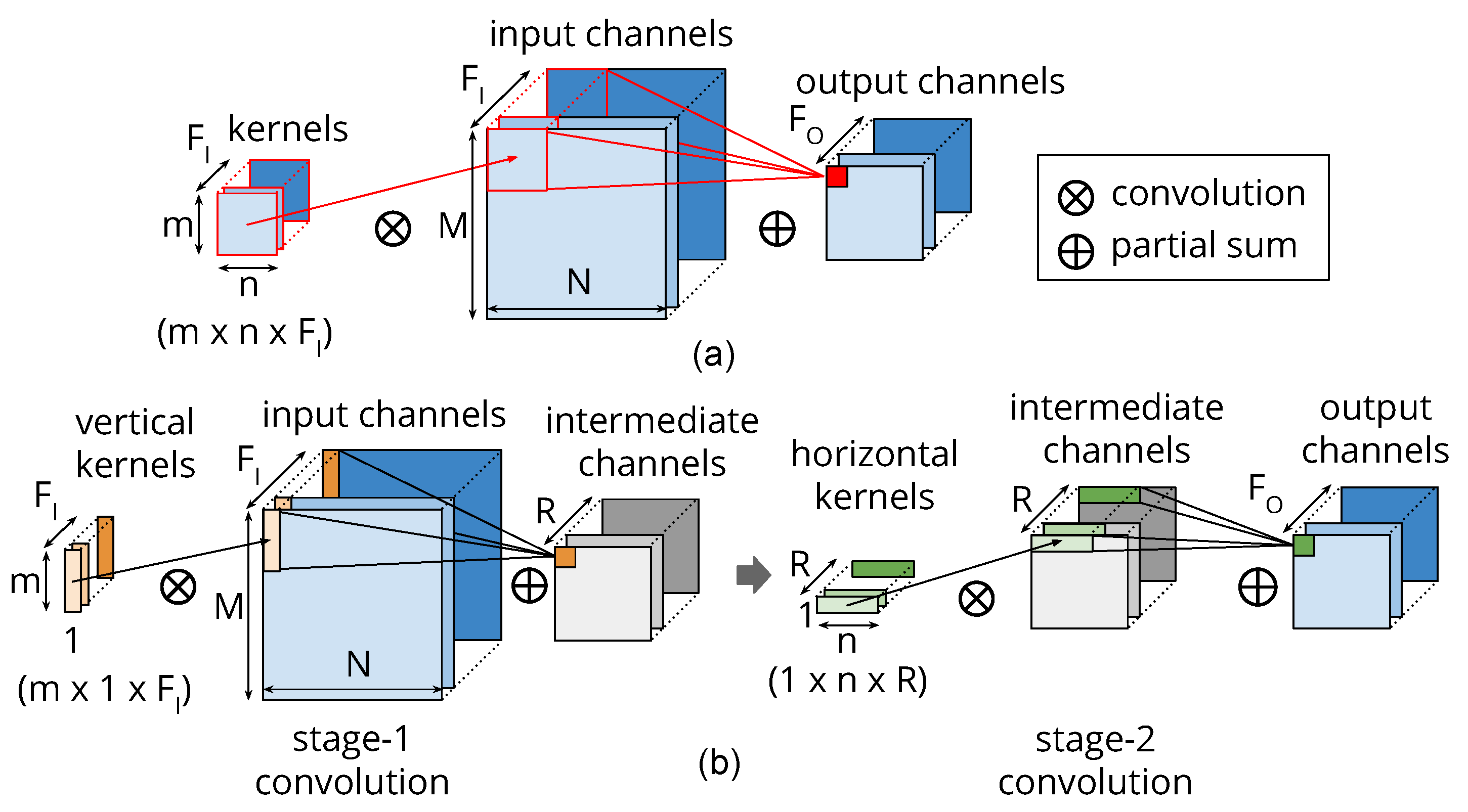
4.2. Layerwise Approximation and Convolution by Separability
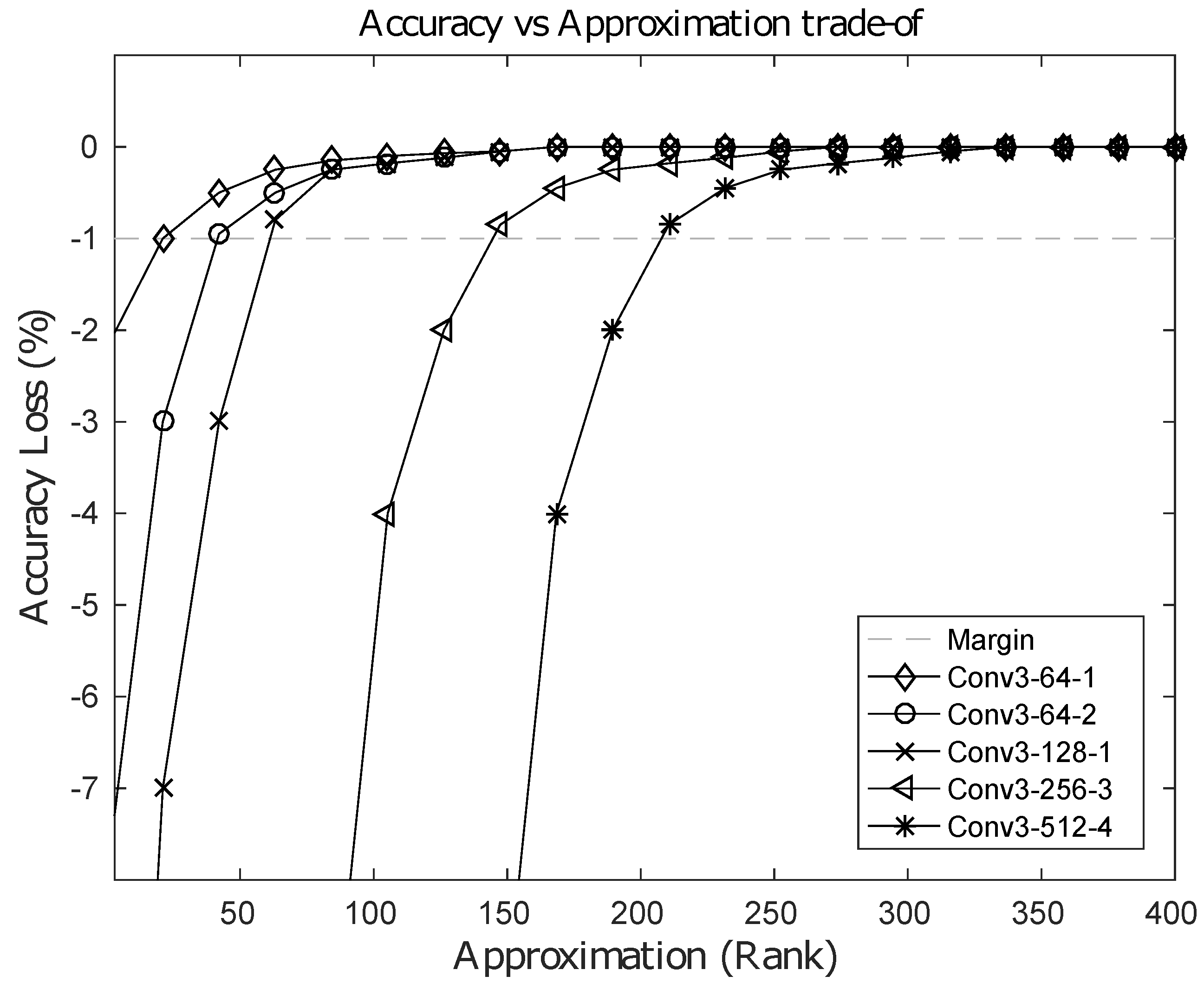
4.3. Rank Search and Layer Restructuring Algorithm
| Algorithm 1: Rank approximation and the layer restructuring algorithm |
 |
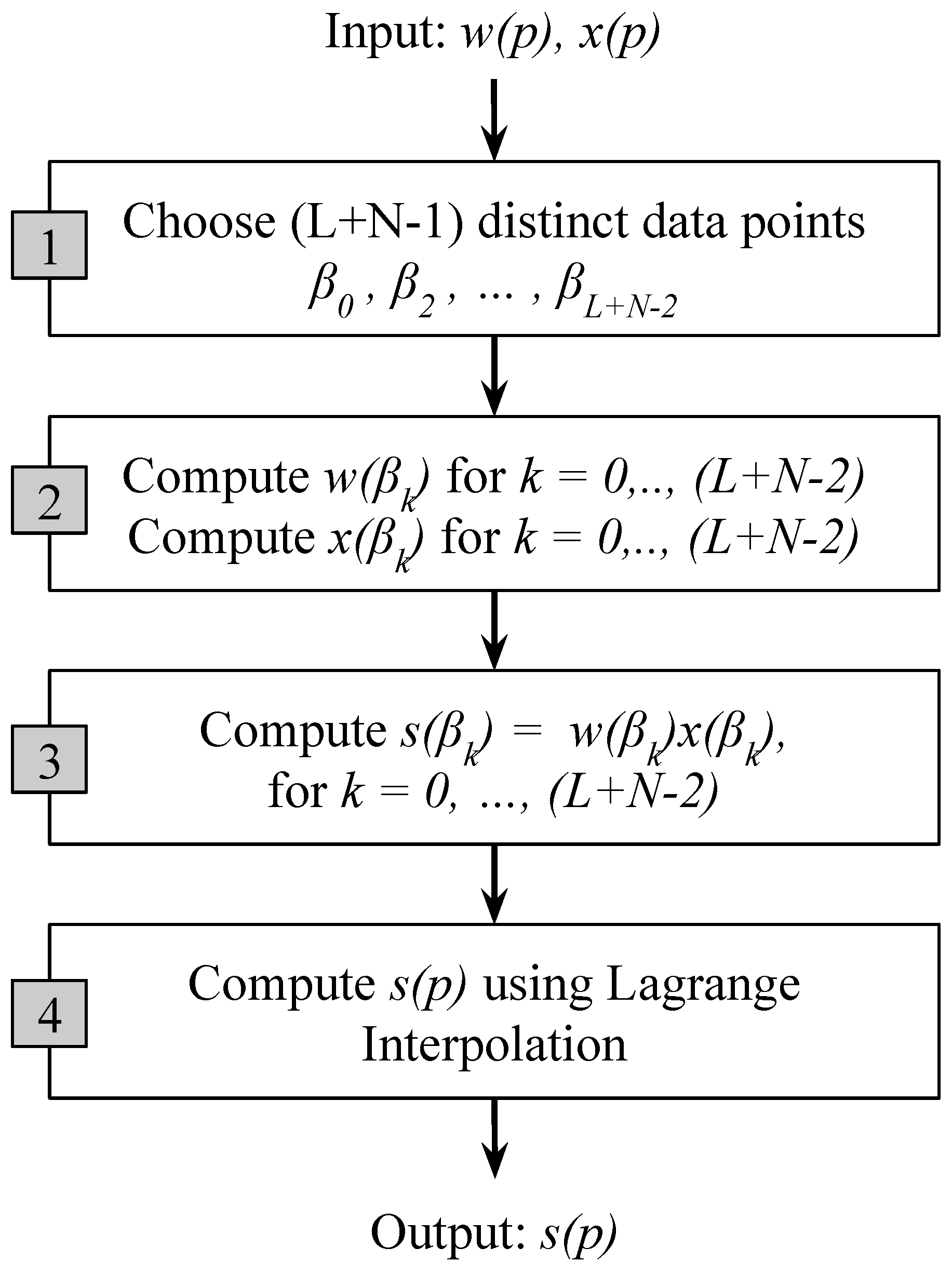
4.4. The Modified Toom–Cook’s Fast 1D Convolution
- Choose distinct data points , ,…,.
- Evaluate and for all the data points.
- Compute .
- Finally, compute by Lagrange interpolation as follows:
4.5. A Fast Convolution Algorithm for Filtering of Dimension Three Using the Modified Toom–Cook Scheme
5. Results and Discussion
- MULs: Total number of strong operations (i.e., multiplications) in the convolutional layers
- Speedup: Total speedup achieved as compared to baseline 2D convolution
- Fine-Tuning Time: Average fine-tuning time in number of epochs. The fine-tuning is the process of re-training a CNN after having trained it once and then having reduced its complexity. An epoch is a complete pass through the training set.
5.1. Speedup from the Low-Rank Approximation Stage:
5.2. Speedup from the Fast Convolution Stage
5.3. Efficient Use of Memory Bandwidth and Improved Local Reuse
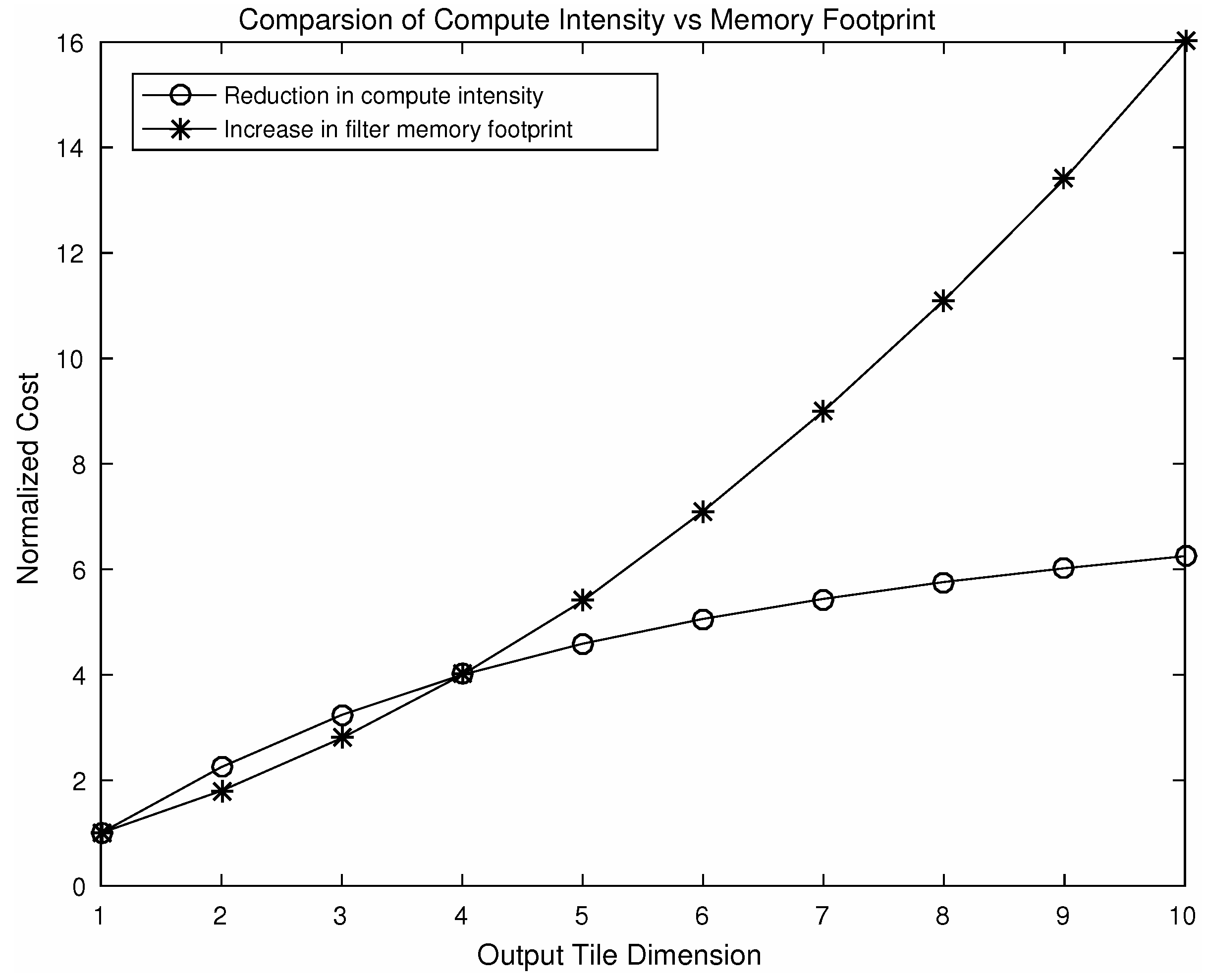
5.4. Extension of the 1D Algorithm to a 2D Variant and Its Limitations
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ConvNet | Convolutional Neural Network |
| ILSVRC | The ImageNet Large Scale Visual Recognition Challenge |
| 1D-FALCON | One-Dimensional Fast Approximate Low-rank Convolution |
Appendix A. Algorithm F(2×1, 3×1, {4×1})
Appendix B. Algorithm F(3×1, 3×1, {5×1})
Appendix C. Additional Results from Other Widely Used CNNs
Appendix D. Algorithm F(6×1, 3×1, {8×1})
References
- Abdel-Hamid, O.; Mohamed, A.; Jiang, H.; Deng, L.; Penn, G.; Yu, D. Convolutional Neural Networks for Speech Recognition. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 22, 1533–1545. [Google Scholar] [CrossRef]
- Gehring, J.; Auli, M.; Grangier, D.; Yarats, D.; Dauphin, Y.N. Convolutional Sequence to Sequence Learning. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Caesars Palace, NV, USA, 26 June–1 July 2016; pp. 779–788. [Google Scholar]
- Sun, Y.; Wang, X.; Tang, X. Deep Learning Face Representation from Predicting 10,000 Classes. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1891–1898. [Google Scholar]
- Masoumi, M.; Hamza, A.B. Spectral shape classification: A deep learning approach. J. Vis. Commun. Image Represent. 2017, 43, 198–211. [Google Scholar] [CrossRef]
- Cong, J.; Xiao, B. Minimizing Computation in Convolutional Neural Networks. In Artificial Neural Networks and Machine Learning—ICANN 2014; Wermter, S., Weber, C., Duch, W., Honkela, T., Koprinkova-Hristova, P., Magg, S., Palm, G., Villa, A.E.P., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 281–290. [Google Scholar]
- Han, S.; Pool, J.; Tran, J.; Dally, W.J. Learning Both Weights and Connections for Efficient Neural Networks. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2015; pp. 1135–1143. [Google Scholar]
- Sze, V.; Chen, Y.H.; Einer, J.; Suleiman, A.; Zhang, Z. Hardware for machine learning: Challenges and opportunities. In Proceedings of the 2017 IEEE Custom Integrated Circuits Conference (CICC), Austin, TX, USA, 30 April–3 May 2017; pp. 1–8. [Google Scholar]
- Forecast: The Internet of Things, Worldwide. 2013. Available online: https://www.gartner.com/doc/2625419/forecast-internet-things-worldwide- (accessed on 24 December 2017).
- Tishby, N.; Zaslavsky, N. Deep Learning and the Information Bottleneck Principle. In Proceedings of the 2015 IEEE Information Theory Workshop (ITW), Jerusalem, Israel, 26 April–1 May 2015. [Google Scholar]
- Cun, Y.L.; Denker, J.S.; Solla, S.A. Advances in Neural Information Processing Systems 2; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1990; pp. 598–605. [Google Scholar]
- Hassibi, B.; Stork, D.G.; Wolff, G.J. Optimal Brain Surgeon and general network pruning. In Proceedings of the IEEE International Conference on Neural Networks, San Francisco, CA, USA, 28 March–1 April 1993; pp. 293–299. [Google Scholar]
- Han, S.; Mao, H.; Dally, W.J. Deep Compression: Compressing Deep Neural Network with Pruning, Trained Quantization and Huffman Coding. arXiv, 2015; arXiv:1510.00149. [Google Scholar]
- Liu, B.; Wang, M.; Foroosh, H.; Tappen, M.; Penksy, M. Sparse Convolutional Neural Networks. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 806–814. [Google Scholar]
- Denton, E.; Zaremba, W.; Bruna, J.; LeCun, Y.; Fergus, R. Exploiting Linear Structure Within Convolutional Networks for Efficient Evaluation. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2014; pp. 1269–1277. [Google Scholar]
- Jaderberg, M.; Vedaldi, A.; Zisserman, A. Speeding up Convolutional Neural Networks with Low Rank Expansions. arXiv, 2014; arXiv:1405.3866. [Google Scholar]
- Mamalet, F.; Garcia, C. Simplifying ConvNets for Fast Learning. In Artificial Neural Networks and Machine Learning—ICANN 2012; Villa, A.E.P., Duch, W., Érdi, P., Masulli, F., Palm, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 58–65. [Google Scholar]
- Rigamonti, R.; Sironi, A.; Lepetit, V.; Fua, P. Learning Separable Filters. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 2754–2761. [Google Scholar]
- Gupta, S.; Agrawal, A.; Gopalakrishnan, K.; Narayanan, P. Deep Learning with Limited Numerical Precision. In Proceedings of the 32nd International Conference on International Conference on Machine Learning, Lille, France, 6–11 July 2015; Volume 37, pp. 1737–1746. [Google Scholar]
- Hubara, I.; Courbariaux, M.; Soudry, D.; El-Yaniv, R.; Bengio, Y. Binarized Neural Networks. In Advances in Neural Information Processing Systems 29; Lee, D.D., Sugiyama, M., Luxburg, U.V., Guyon, I., Garnett, R., Eds.; Curran Associates, Inc.: New York, NY, USA, 2016; pp. 4107–4115. [Google Scholar]
- Gysel, P.; Motamedi, M.; Ghiasi, S. Hardware-oriented Approximation of Convolutional Neural Networks. arXiv, 2016; arXiv:1604.03168. [Google Scholar]
- Vasilache, N.; Johnson, J.; Mathieu, M.; Chintala, S.; Piantino, S.; LeCun, Y. Fast Convolutional Nets With fbfft: A GPU Performance Evaluation. arXiv, 2014; arXiv:1412.7580. [Google Scholar]
- Lavin, A.; Gray, S. Fast Algorithms for Convolutional Neural Networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Caesars Palace, NV, USA, 26 June–1 July 2016; pp. 4013–4021. [Google Scholar]
- Li, S.R.; Park, J.; Tang, P.T.P. Enabling Sparse Winograd Convolution by Native Pruning. arXiv, 2017; arXiv:1702.08597. [Google Scholar]
- Shwartz-Ziv, R.; Tishby, N. Opening the Black Box of Deep Neural Networks via Information. arXiv, 2017; arXiv:1703.00810. [Google Scholar]
- Hummel, R.L.; Lowe, D.G. Computing Large-Kernel Convolutions of Images; New York University: New York, NY, USA, 1987. [Google Scholar]
- Eckart, C.; Young, G. The approximation of one matrix by another of lower rank. Psychometrika 1936, 1, 211–218. [Google Scholar] [CrossRef]
- Wang, Y.; Parhi, K. Explicit Cook-Toom algorithm for linear convolution. In Proceedings of the 2000 IEEE International Conference on Acoustics, Speech, and Signal Processing, Istanbul, Turkey, 5–9 June 2000; Volume 6, pp. 3279–3282. [Google Scholar]
- Maji, P.; Mullins, R. 1D-FALCON: Accelerating Deep Convolutional Neural Network Inference by Co-optimization ofModels and Underlying Arithmetic Implementation. In Artificial Neural Networks and Machine Learning—ICANN 2017; Lintas, A., Rovetta, S., Verschure, P.F., Villa, A.E., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 21–29. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv, 2014; arXiv:1409.1556. [Google Scholar]
- Kim, Y.; Park, E.; Yoo, S.; Choi, T.; Yang, L.; Shin, D. Compression of Deep Convolutional Neural Networks for Fast and Low Power Mobile Applications. arXiv, 2015; arXiv:1511.06530. [Google Scholar]
- Molchanov, P.; Tyree, S.; Karras, T.; Aila, T.; Kautz, J. Pruning Convolutional Neural Networks for Resource Efficient Transfer Learning. arXiv, 2016; arXiv:1611.06440. [Google Scholar]
- Lebedev, V.; Lempitsky, V. Fast ConvNets Using Group-Wise Brain Damage. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Caesars Palace, NV, USA, 26 June–1 July 2016; pp. 2554–2564. [Google Scholar]
- Dally, B. Power, Programmability, and Granularity: The Challenges of ExaScale Computing. In Proceedings of the 2011 IEEE International Parallel Distributed Processing Symposium, Anchorage, AK, USA, 16–20 May 2011; p. 878. [Google Scholar]
- Horowitz, M. 1.1 Computing’s energy problem (and what we can do about it). In Proceedings of the 2014 IEEE International Solid-State Circuits Conference Digest of Technical Papers (ISSCC), San Francisco, CA, USA, 9–13 February 2014; pp. 10–14. [Google Scholar]
- Chen, Y.H.; Emer, J.; Sze, V. Eyeriss: A Spatial Architecture for Energy-Efficient Dataflow for Convolutional Neural Networks. In Proceedings of the 2016 ACM/IEEE 43rd Annual International Symposium on Computer Architecture (ISCA), Seoul, Korea, 18–22 June 2016; pp. 367–379. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Advances in Neural Information Processing Systems 25; Pereira, F., Burges, C.J.C., Bottou, L., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2012; pp. 1097–1105. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.E.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. arXiv, 2014; arXiv:1409.4842. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv, 2015; arXiv:1512.03385. [Google Scholar]


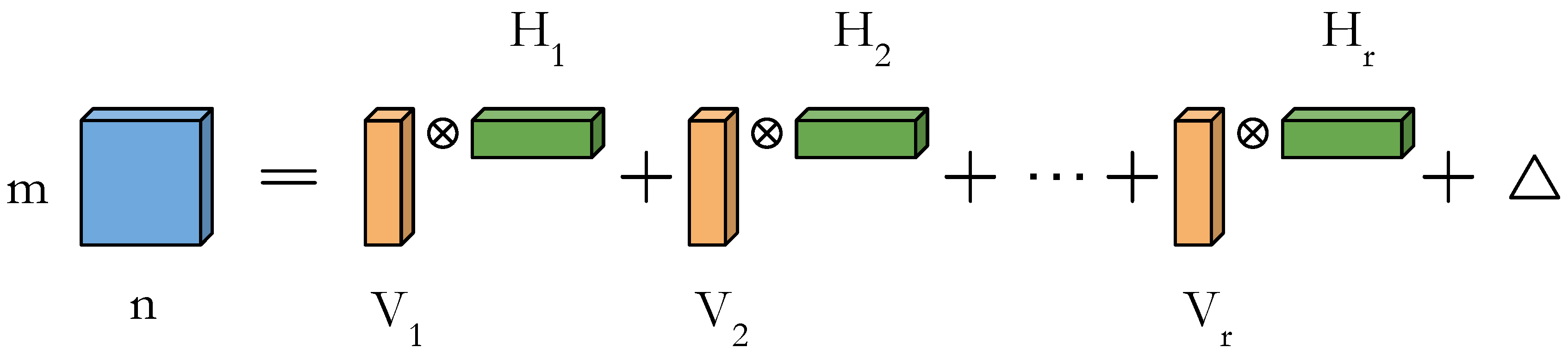

| Optimization Scheme | #MULs | Speedup | Top-5 Error (%) | Fine-Tuning Time |
|---|---|---|---|---|
| 2D Convolution [30] | 15.3G | 1.0× | 9.4 | None |
| Group-Wise Sparsification [33] | 7.6G | 2.0× | 10.1 | >10 epochs |
| Iterative Pruning [32] | 4.5G | 3.4× | 13.0 | 60 epochs |
| Winograd’s Filtering [23] | 3.8G | 4.0× | 9.4 | None |
| Pruning+Retraining [7] | 3.0G | 5.0× | 10.88 | 20–40 epochs |
| Tucker Decomposition [31] | 3.0G | 5.0× | 11.60 | 5–10 epochs |
| 1D FALCON [Our scheme] | 1.3G | 11.4× | 9.5 | 1–2 epochs |
| Layer | Original (ms) | Compressed (ms) | Speedup |
|---|---|---|---|
| conv3-64-1.1 | 28.5 | 15.0 | 1.9× |
| conv3-64-1.2 | 168.1 | 32.3 | 5.2× |
| conv3-128-2.1 | 74.1 | 25.6 | 2.9× |
| conv3-128-2.2 | 147.3 | 42.1 | 3.5× |
| conv3-256-3.1 | 67.3 | 15.7 | 4.3× |
| conv3-256-3.2 | 134.2 | 25.8 | 5.2× |
| conv3-256-3.3 | 134.5 | 27.4 | 4.9× |
| conv3-512-4.1 | 65.2 | 12.8 | 5.1× |
| conv3-512-4.2 | 129.9 | 22.0 | 5.9× |
| conv3-512-4.3 | 130.1 | 21.3 | 6.1× |
| conv3-512-5.1 | 33.4 | 4.3 | 7.8× |
| conv3-512-5.2 | 33.5 | 4.2 | 7.9× |
| conv3-512-5.3 | 33.4 | 4.2 | 7.9× |
| Total | 1432.3 | 252.8 | 5.7× |
| Layer | No. of Parameters | Compressed Column | Compressed Row | Reduction in Layer Size |
|---|---|---|---|---|
| conv3x3-64-1.1 | 2K | 2.1× | ||
| conv3x3-64-1.2 | 37K | 8.0× | ||
| conv3x3-128-2.1 | 74K | 3.2× | ||
| conv3x3-128-2.2 | 148K | 4.8× | ||
| conv3x3-256-3.1 | 295K | 5.1× | ||
| conv3x3-256-3.2 | 590K | 6.4× | ||
| conv3x3-256-3.3 | 590K | 5.5× | ||
| conv3x3-512-4.1 | 1M | 6.4× | ||
| conv3x3-512-4.2 | 2M | 7.7× | ||
| conv3x3-512-4.3 | 2M | 7.0× | ||
| conv3x3-512-5.1 | 2M | 9.6× | ||
| conv3x3-512-5.2 | 2M | 9.8× | ||
| conv3x3-512-5.3 | 2M | 9.8× |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maji, P.; Mullins, R. On the Reduction of Computational Complexity of Deep Convolutional Neural Networks. Entropy 2018, 20, 305. https://doi.org/10.3390/e20040305
Maji P, Mullins R. On the Reduction of Computational Complexity of Deep Convolutional Neural Networks. Entropy. 2018; 20(4):305. https://doi.org/10.3390/e20040305
Chicago/Turabian StyleMaji, Partha, and Robert Mullins. 2018. "On the Reduction of Computational Complexity of Deep Convolutional Neural Networks" Entropy 20, no. 4: 305. https://doi.org/10.3390/e20040305
APA StyleMaji, P., & Mullins, R. (2018). On the Reduction of Computational Complexity of Deep Convolutional Neural Networks. Entropy, 20(4), 305. https://doi.org/10.3390/e20040305





