BROJA-2PID: A Robust Estimator for Bivariate Partial Information Decomposition
Abstract
:1. Introduction
Notation and Background
An asterisk stands for “sum over everything that can be plugged in instead of the ∗”, e.g., if ,We do not use the symbol ∗ in any other context.
2. Cone Programming Model for Bivariate PID
2.1. Background on Cone Programming
- 1.
- A vector (respectively, ) is said to be a feasible solution of (2) (respectively, (3)) if and (respectively, and ), i.e., none of the constraints in (2) (respectively, (3)) are violated by w (respectively, ).
- 2.
- We say that (2) and (3) satisfy weak duality if for all w and all feasible solutions of (2) and (3), respectively,
- 3.
- If w is a feasible solution of (2) and is a feasible solution of (3), then the duality gap d is
- 4.
- We say that (2) and (3) satisfy strong duality when the feasible solutions w and are optimal in (2) and (3), respectively, if and only if d is zero.
- is a feasible solution of (P).
- There exists such that for any , we have whenever
- 1.
- Weak duality always hold for (P) and (D).
- 2.
- If is finite and (P) has an interior point , then strong duality holds for (P) and (D).
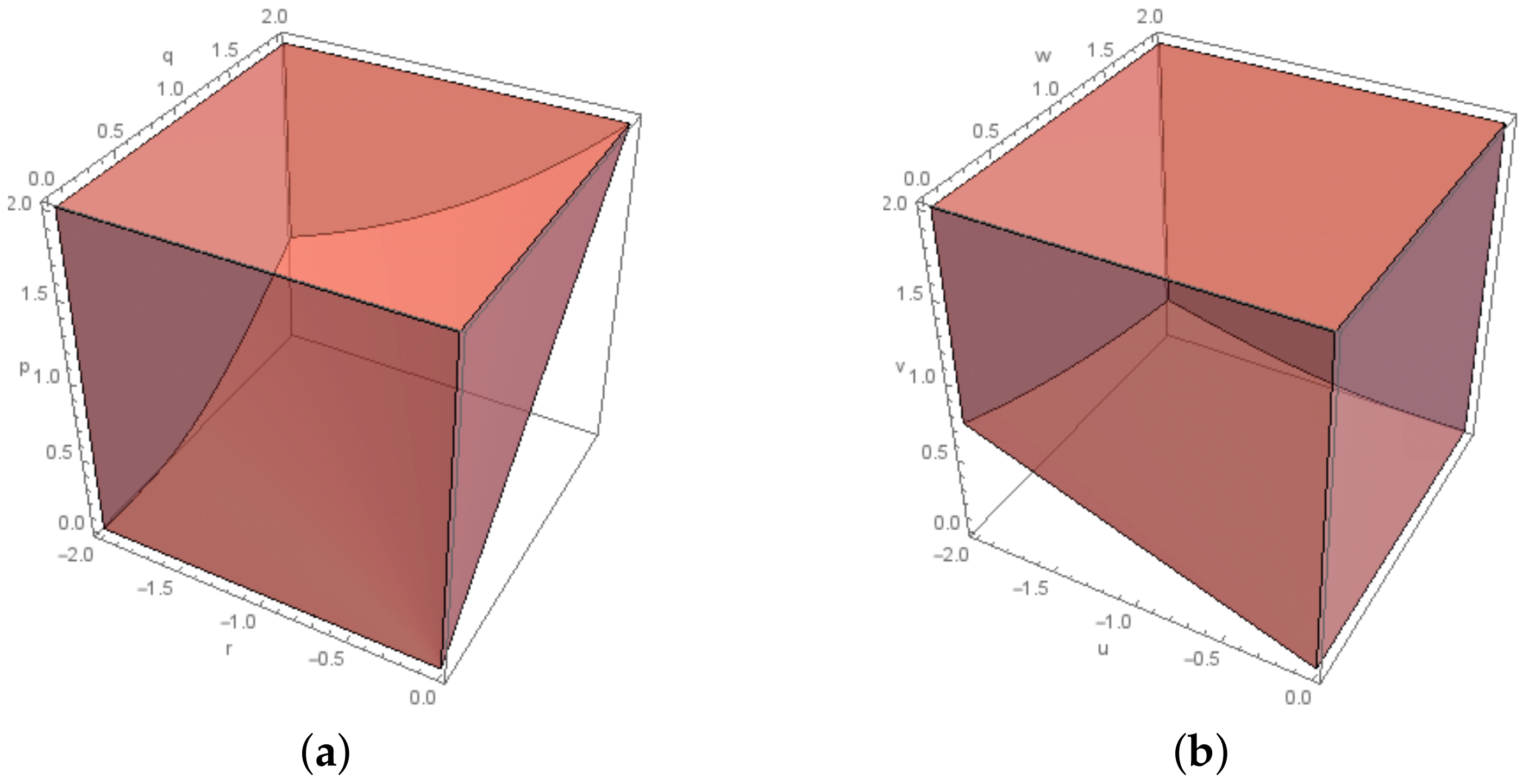
2.2. The Exponential Cone Programming Model
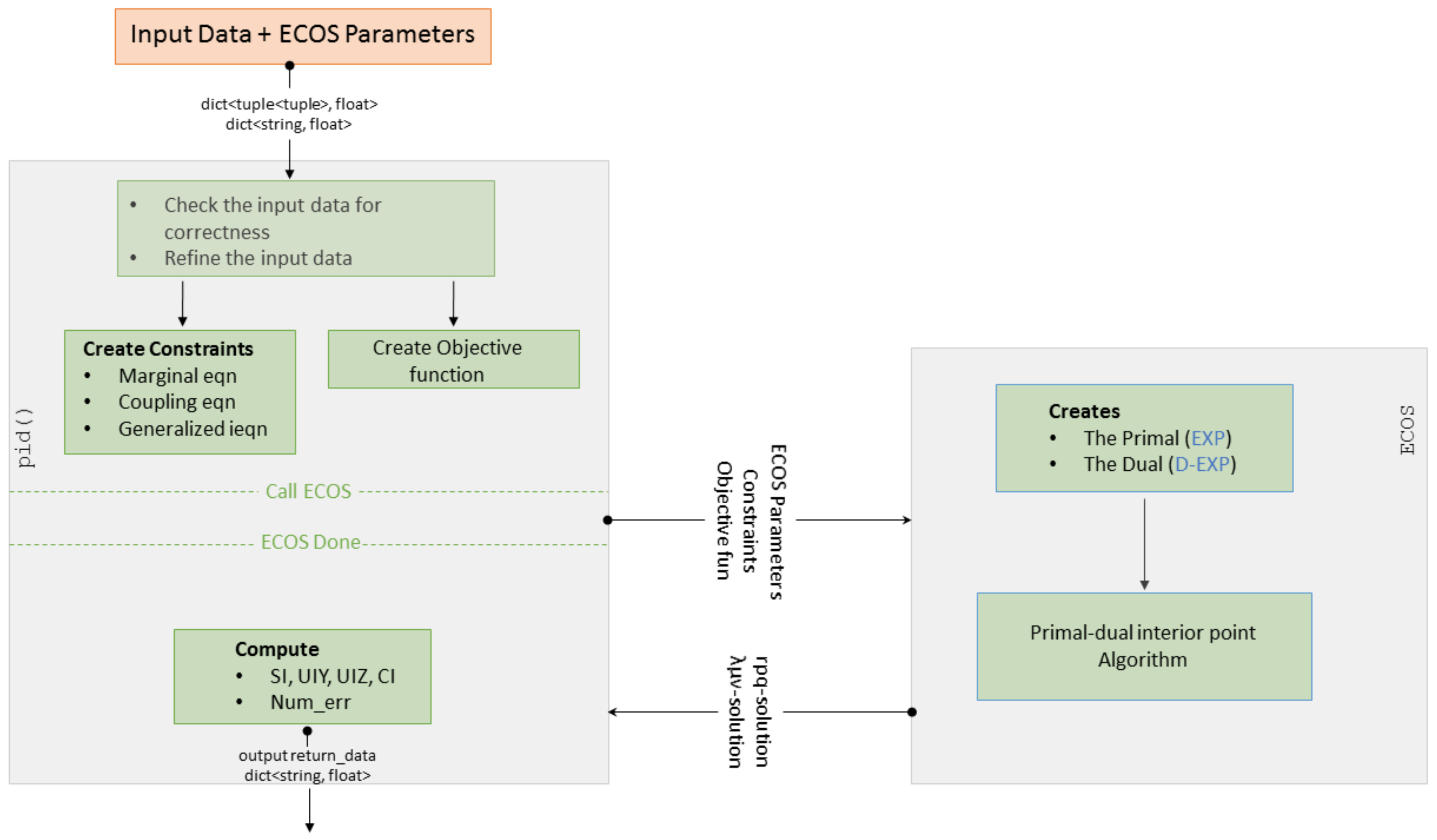
3. The BROJA_2PID Estimator
3.1. Installation
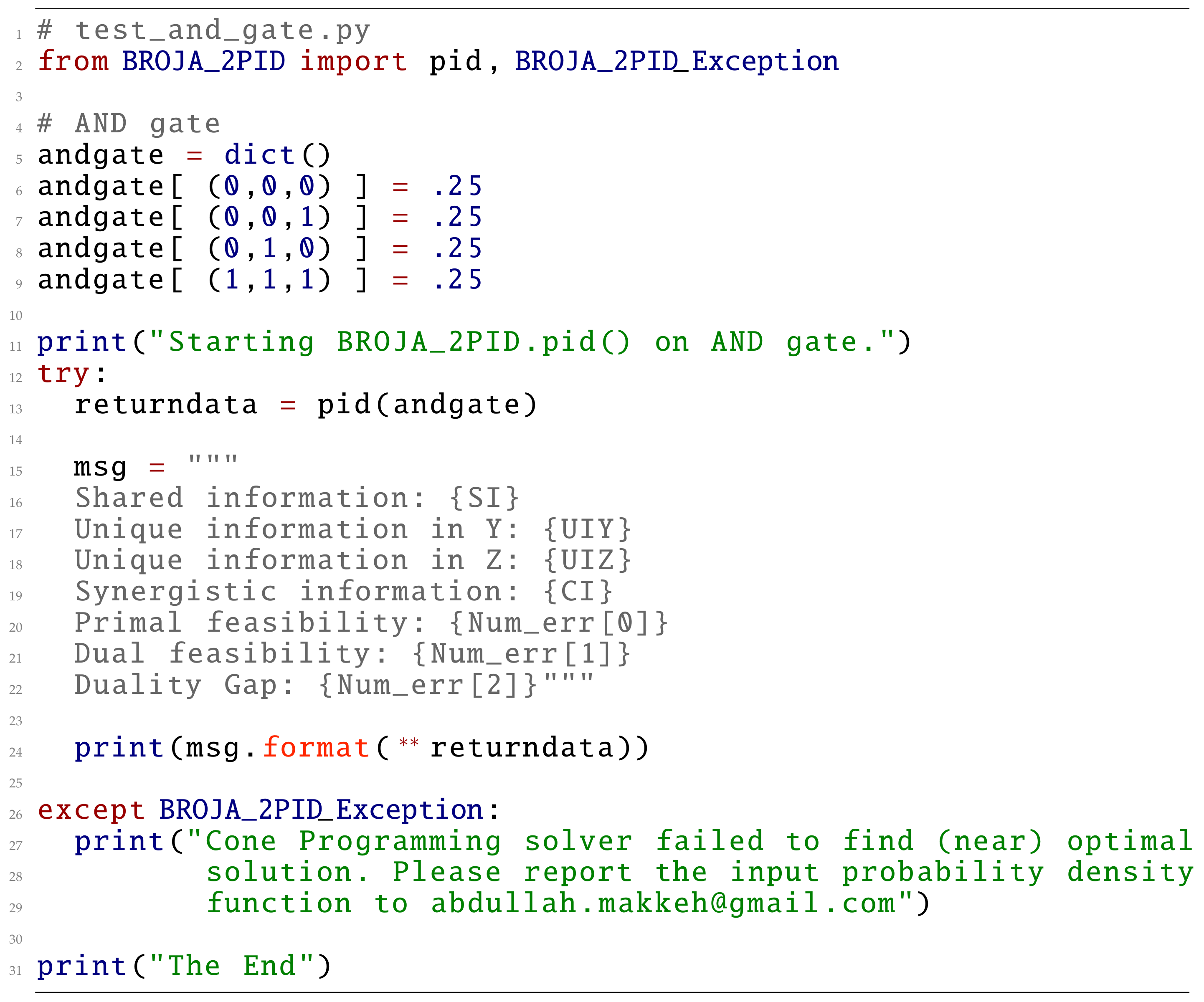
3.2. Computing Bivariate PID
3.3. Input and Parameters
3.4. Returned Data
4. Tests
4.1. Paradigmatic Gates
4.1.1. Data
4.1.2. Testing
4.1.3. Comparison with Other Estimators
4.2. Copy Gate
4.2.1. Data
4.2.2. Testing
4.2.3. Comparison with Other Estimators
4.3. Random Probability Distributions
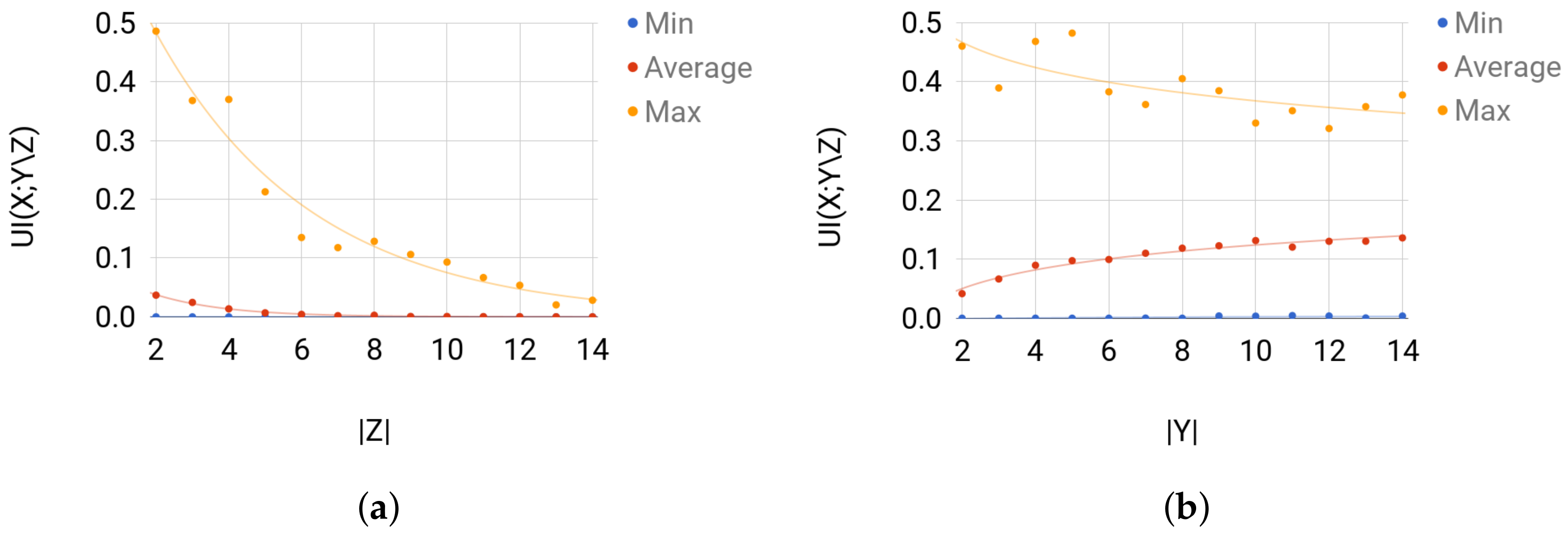
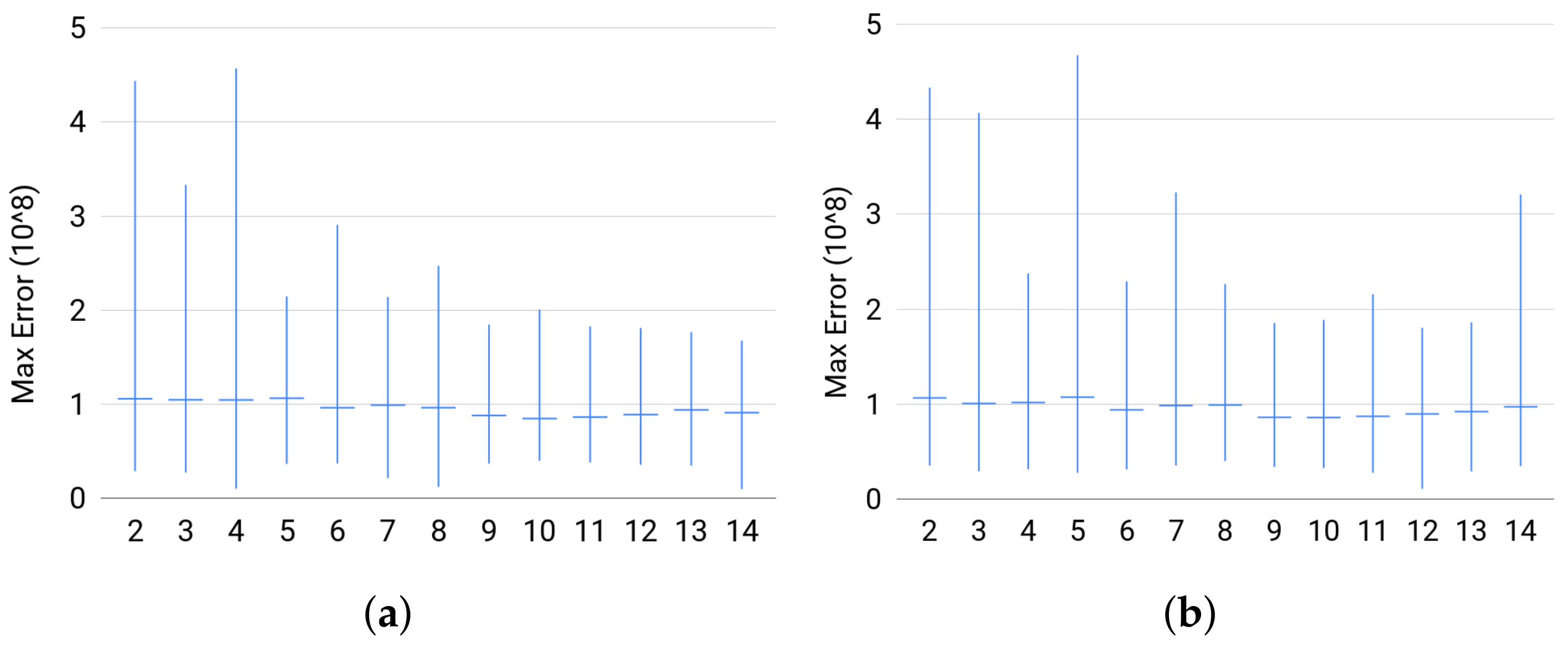
4.3.1. Data
- (a)
- For Set 1, we fix and vary in . Then, for each size of Z, we sample uniformly at random 500 joint distribution of over the probability simplex.
- (b)
- For Set 2, we fix and vary in . Then, for each value of , we sample uniformly at random 500 joint distribution of over the probability simplex.
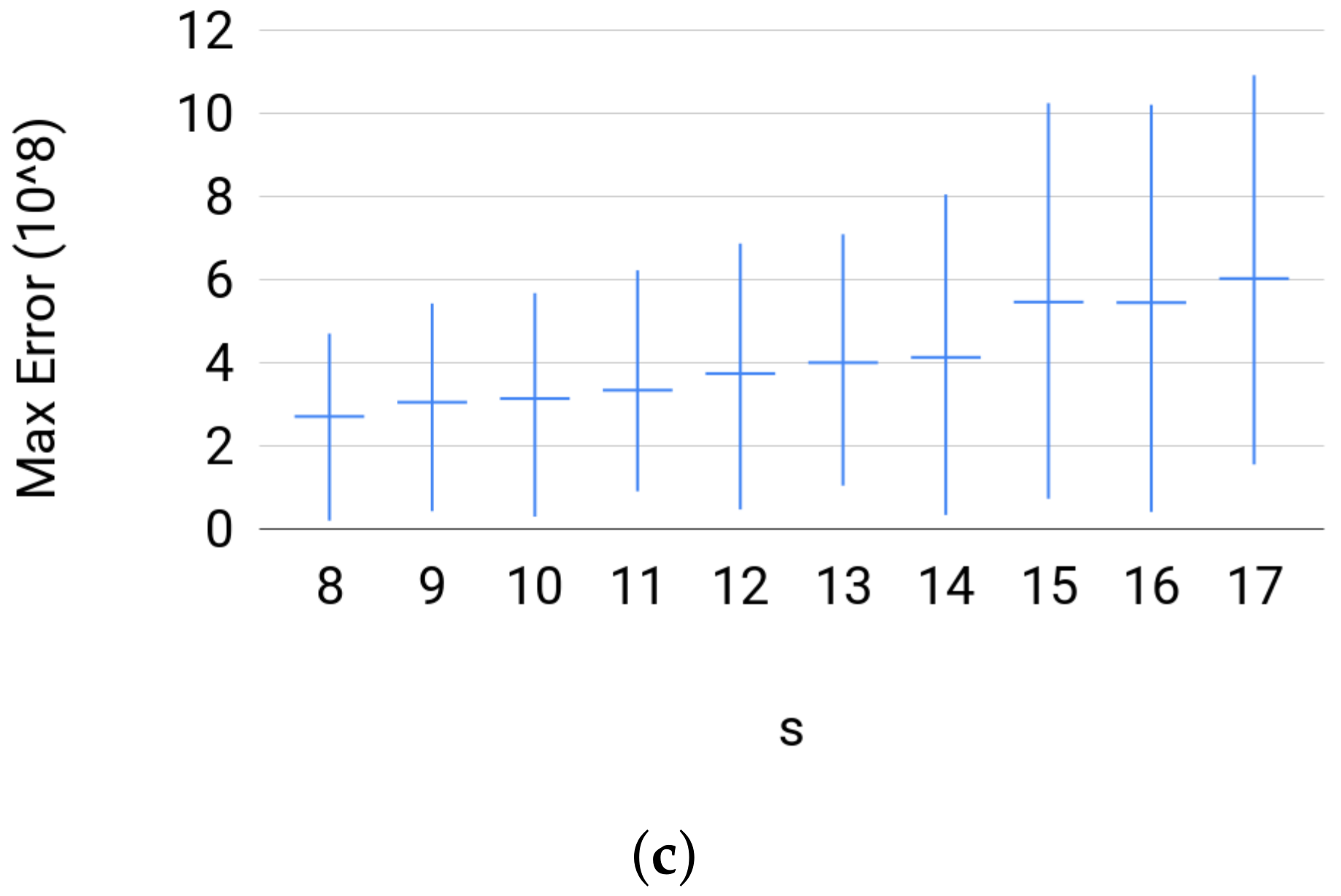
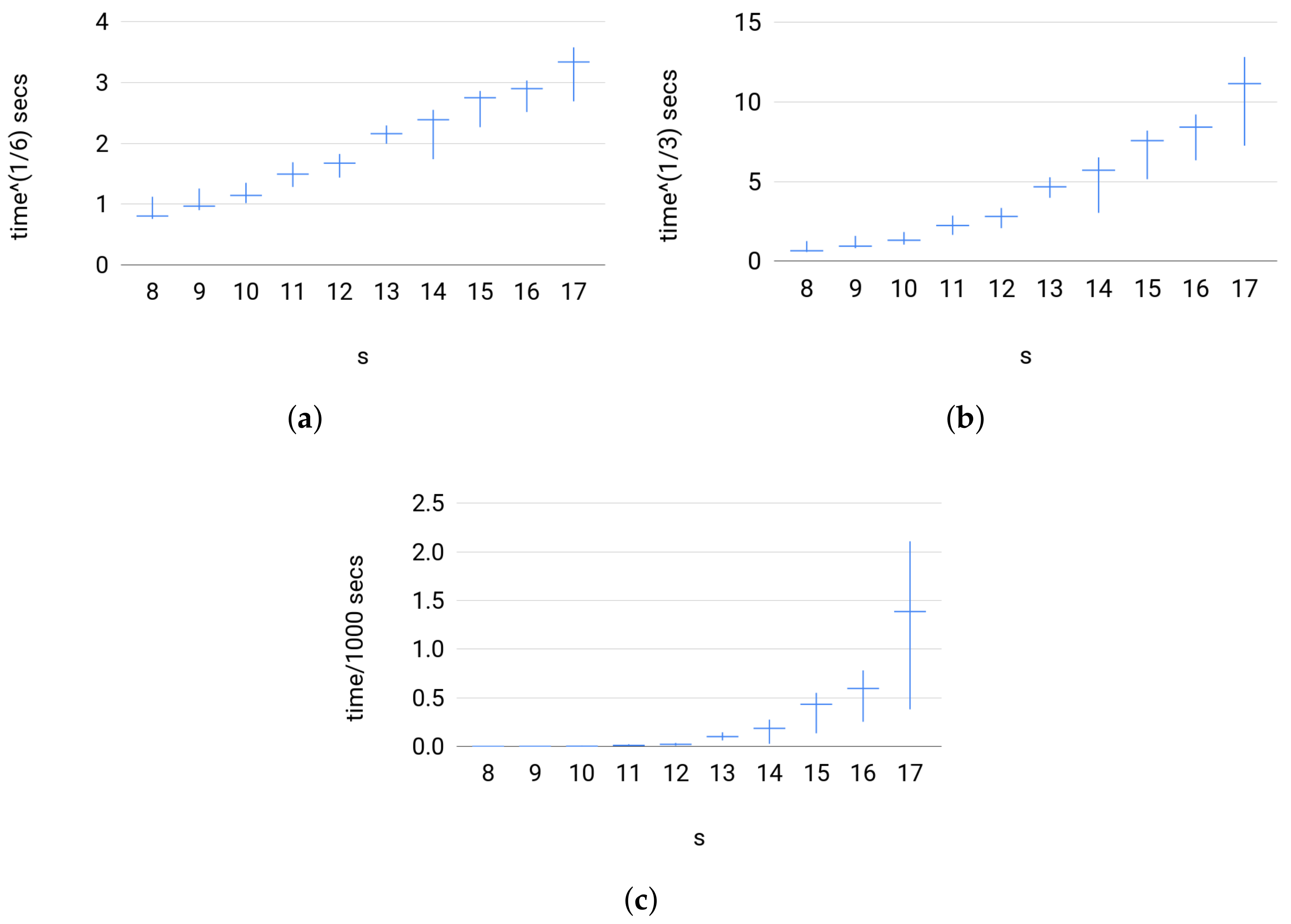
- (c)
- For Set 3, we fix where . Then, for each s, we sample uniformly at random 500 joint distribution of over the probability simplex.
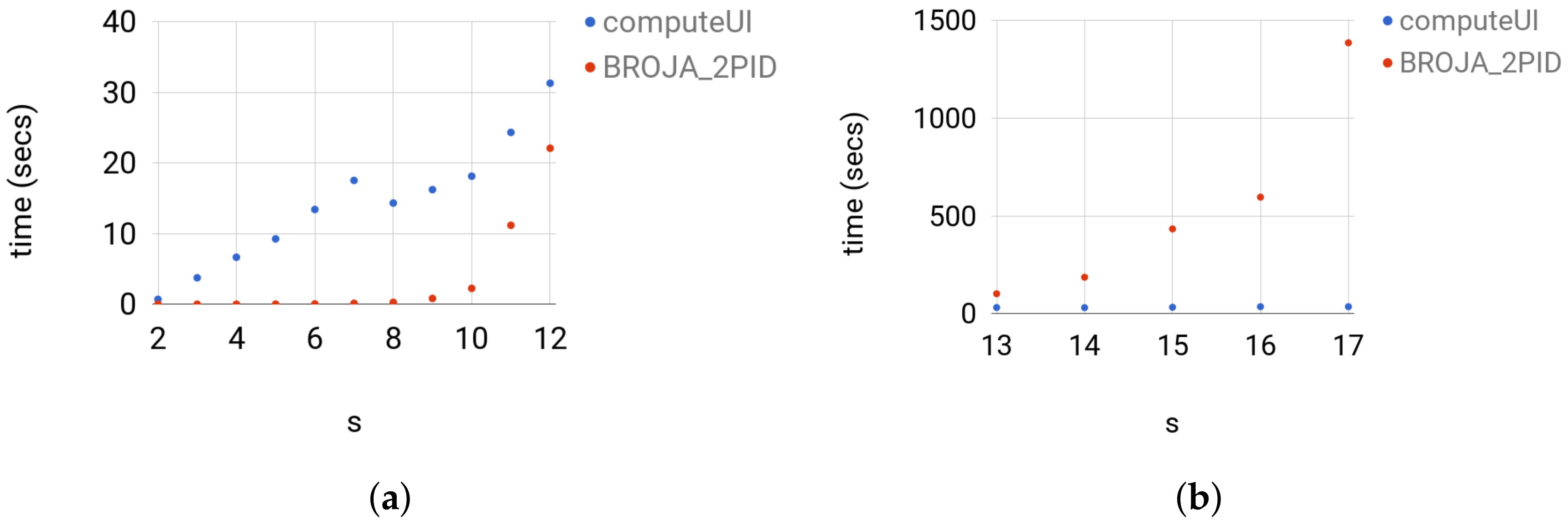
4.3.2. Testing
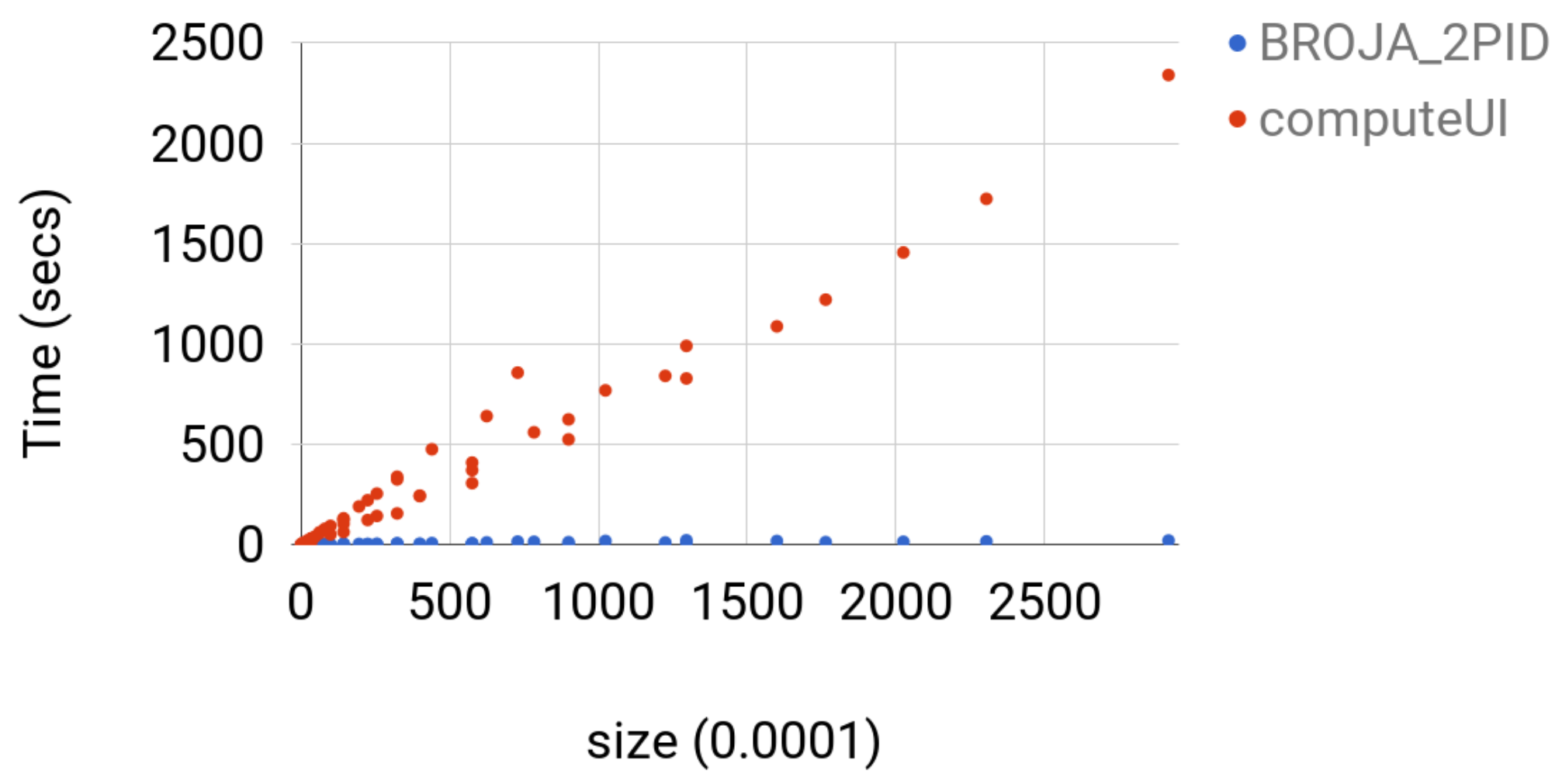
4.3.3. Comparison with Other Estimators
5. Cone Programming Model for Multivariate PID
6. Outlook
Thanks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J.; Ay, N. Quantifying unique information. Entropy 2014, 16, 2161–2183. [Google Scholar] [CrossRef]
- Griffith, V.; Koch, C. Quantifying synergistic mutual information. In Guided Self-Organization: Inception; Springer: Berlin, Germany, 2014; pp. 159–190. [Google Scholar]
- Harder, M.; Salge, C.; Polani, D. Bivariate measure of redundant information. Phys. Rev. E 2013, 87, 012130. [Google Scholar] [CrossRef] [PubMed]
- Williams, P.L.; Beer, R.D. Nonnegative decomposition of multivariate information. arXiv, 2010; arXiv:1004.2515. [Google Scholar]
- Makkeh, A.; Theis, D.O.; Vicente, R. Bivariate Partial Information Decomposition: The Optimization Perspective. Entropy 2017, 19, 530. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Banerjee, P.K.; Rauh, J.; Montúfar, G. Computing the Unique Information. arXiv, 2017; arXiv:1709.07487. [Google Scholar]
- Chicharro, D. Quantifying multivariate redundancy with maximum entropy decompositions of mutual information. arXiv, 2017; arXiv:1708.03845. [Google Scholar]
- Domahidi, A.; Chu, E.; Boyd, S. ECOS: An SOCP solver for embedded systems. In Proceedings of the European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 3071–3076. [Google Scholar]
- O’Donoghue, B.; Chu, E.; Parikh, N.; Boyd, S. SCS: Splitting Conic Solver, Version 1.2.7, 2016. Available online: https://github.com/cvxgrp/scs (accessed on 26 November 2017).
- Luenberger, D.G.; Ye, Y. Linear and Nonlinear Programming; Springer: Berlin, Germany, 1984; Volume 2. [Google Scholar]
- Gärtner, B.; Matousek, J. Approximation Algorithms and Semidefinite Programming; Springer: Berlin, Germany, 2012. [Google Scholar]
- Chares, R. Cones and Interior-Point Algorithms for Structured Convex Optimization Involving Powers Andexponentials. Ph.D. Thesis, UCL-Université Catholique de Louvain, Louvain-la-Neuve, Belgium, 2009. [Google Scholar]
- Makkeh, A. Applications of Optimization in Some Complex Systems. Ph.D. Thesis, University of Tartu, Tartu, Estonia, 2018. forthcoming. [Google Scholar]

| Parameter | Description | Recommended Value |
|---|---|---|
| feastol | primal/dual feasibility tolerance | |
| abstol | absolute tolerance on duality gap | |
| reltol | relative tolerance on duality gap | |
| feastol_inacc | primal/dual infeasibility relaxed tolerance | |
| abstol_inacc | absolute relaxed tolerance on duality gap | |
| reltol_inacc | relaxed relative duality gap | |
| max_iter | maximum number of iterations that “ECOS” does | 100 |
| Output | Description |
|---|---|
| 0 (default) | pid() prints its output (python dictionary, see Section 3.4). |
| 1 | In addition to output=0, pid() prints a flags when it starts preparing (EXP). |
| 2 | and another flag when it calls the conic optimization solver. |
| In addition to output=1, pid() prints the conic optimization solver’s output. | |
| (The conic optimization solver usually prints out the problem statistics and the status of optimization.) |
| Key | Value |
|---|---|
| ’SI’ | Shared information, . |
| (All information quantities are returned in bits.) | |
| ’UIY’ | Unique information of Y, . |
| ’UIZ’ | Unique information of Z, . |
| ’CI’ | Synergistic information, . |
| ’Num_err’ | information about the quality of the solution. |
| ’Solver’ | name of the solver used to optimize (CP). |
| (In this version, we only use ECOS, but other solvers might be added in the future.) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makkeh, A.; Theis, D.O.; Vicente, R. BROJA-2PID: A Robust Estimator for Bivariate Partial Information Decomposition. Entropy 2018, 20, 271. https://doi.org/10.3390/e20040271
Makkeh A, Theis DO, Vicente R. BROJA-2PID: A Robust Estimator for Bivariate Partial Information Decomposition. Entropy. 2018; 20(4):271. https://doi.org/10.3390/e20040271
Chicago/Turabian StyleMakkeh, Abdullah, Dirk Oliver Theis, and Raul Vicente. 2018. "BROJA-2PID: A Robust Estimator for Bivariate Partial Information Decomposition" Entropy 20, no. 4: 271. https://doi.org/10.3390/e20040271
APA StyleMakkeh, A., Theis, D. O., & Vicente, R. (2018). BROJA-2PID: A Robust Estimator for Bivariate Partial Information Decomposition. Entropy, 20(4), 271. https://doi.org/10.3390/e20040271





