A Decentralized Receiver in Gaussian Interference
Abstract
:1. Introduction
1.1. Results
- Upper and lower bounds on the system’s achievable communication rate in correlated Gaussian noise and regimes where these bounds are tight (Section 3). The strongest lower bound is given in Theorem 7.
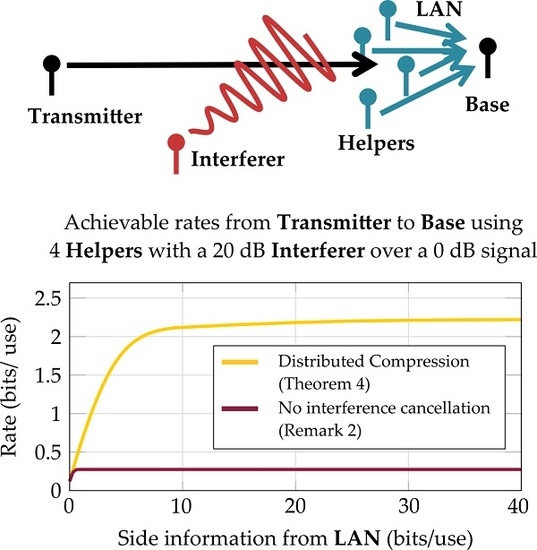
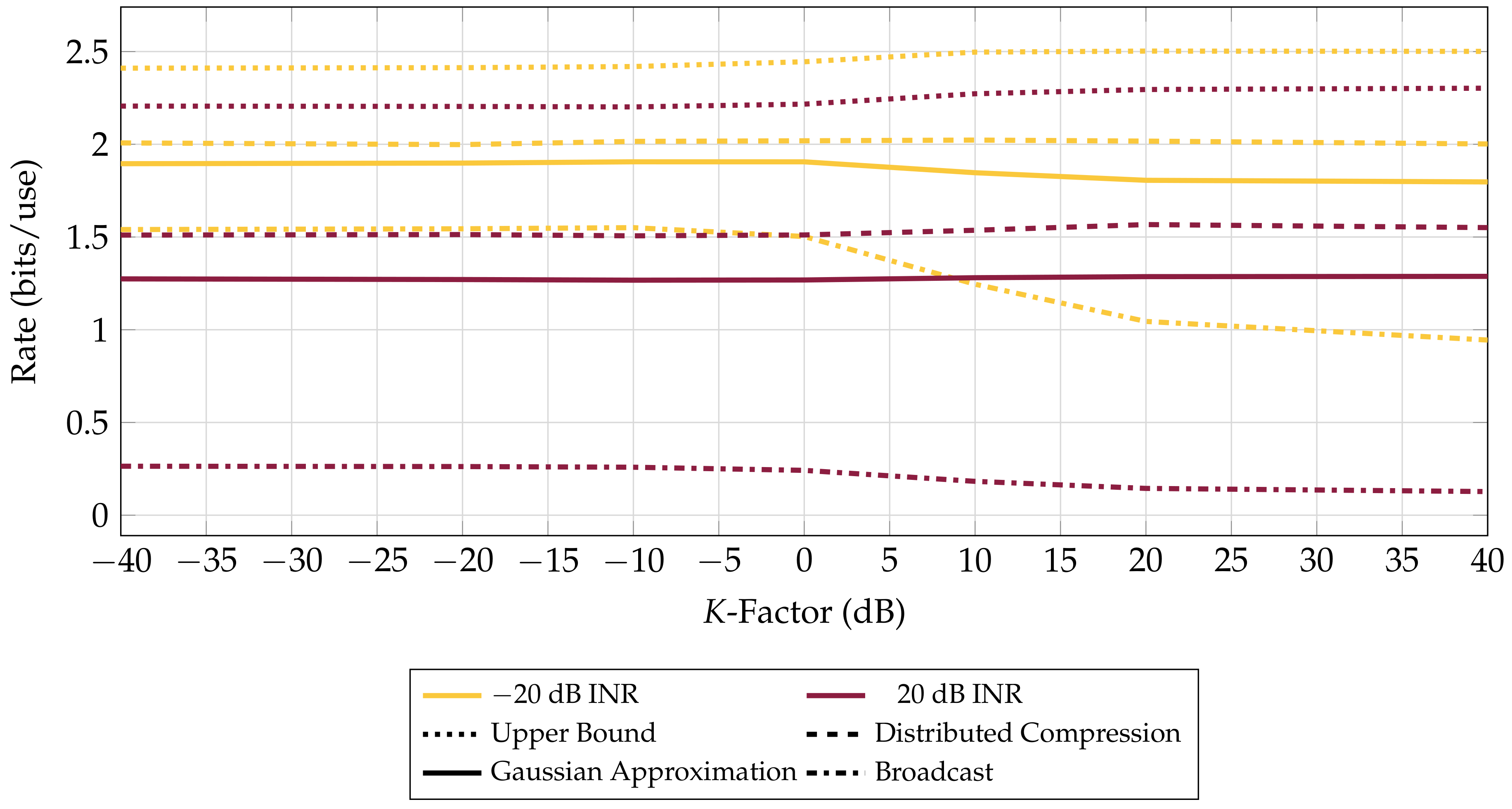
- Performance characteristics of these rates in the presence of an interferer (Section 4.1).
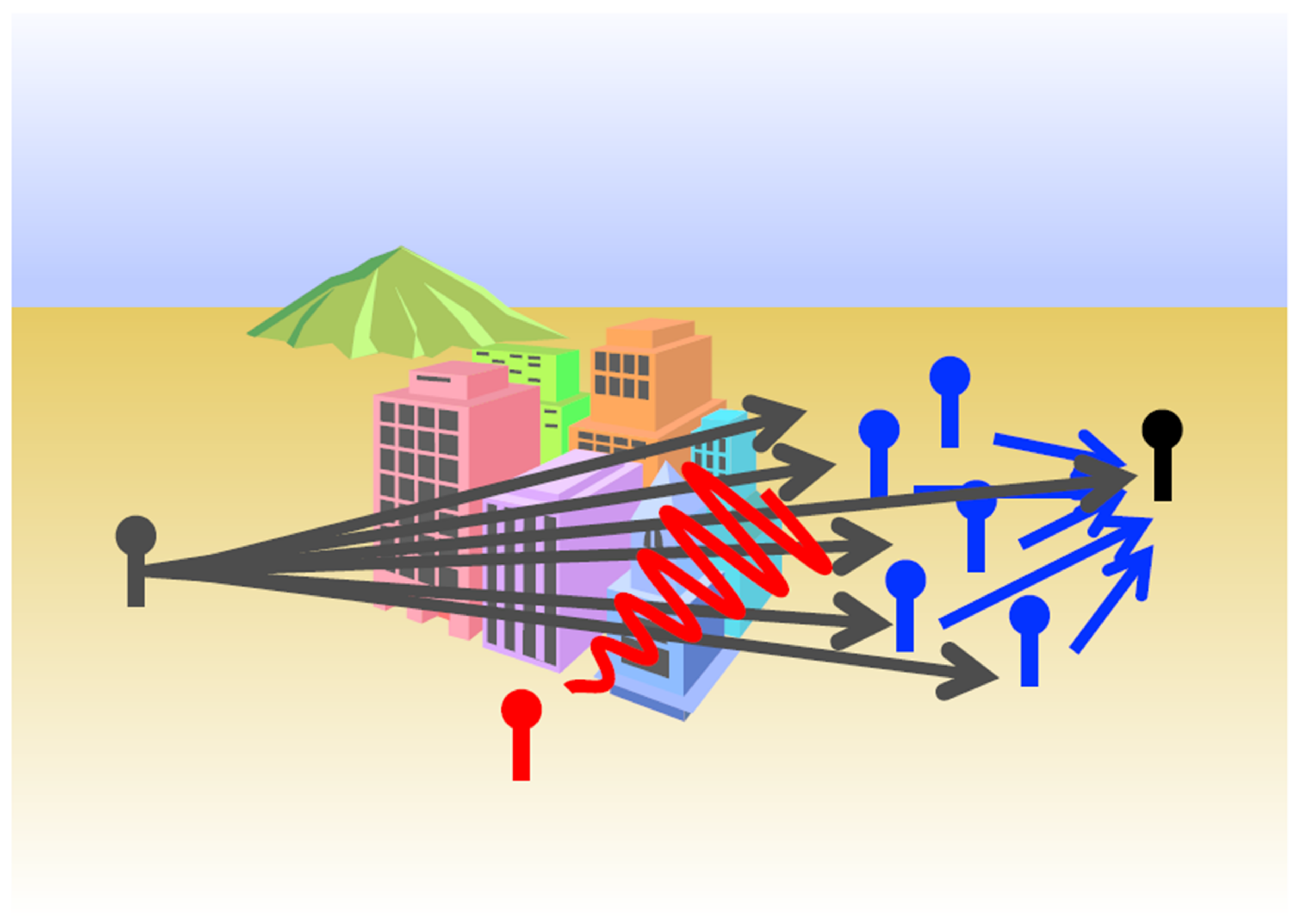
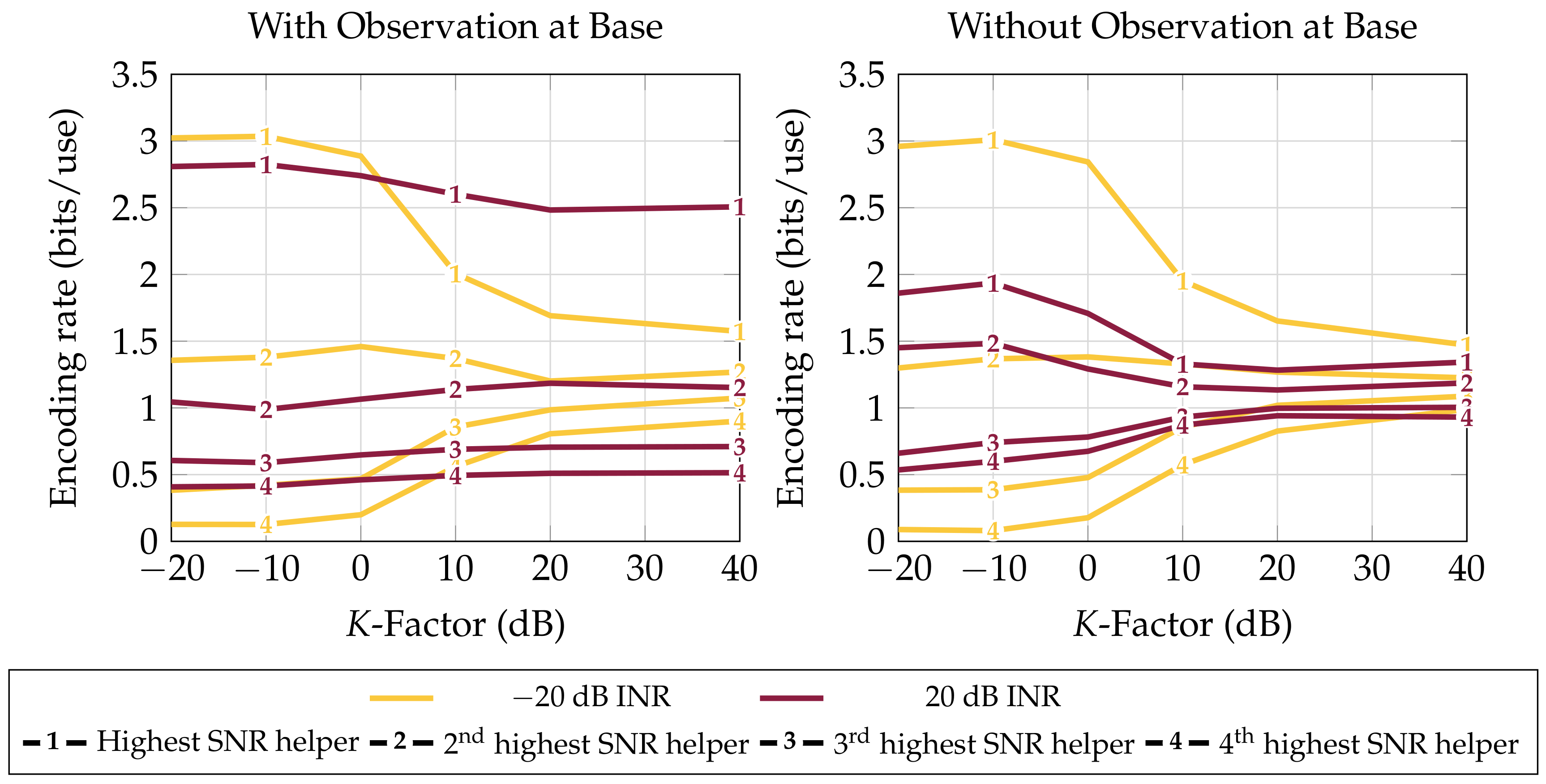
- Behavior of the strategies in various scattering environments (Section 4.2). The scattering environment is seen to not affect average performance if LAN resource sharing adapts to the channel.
- A strengthening of an existing achievability proof for the system, where the same rate is achieved using less cooperation between nodes (Remark 7).
1.2. Background
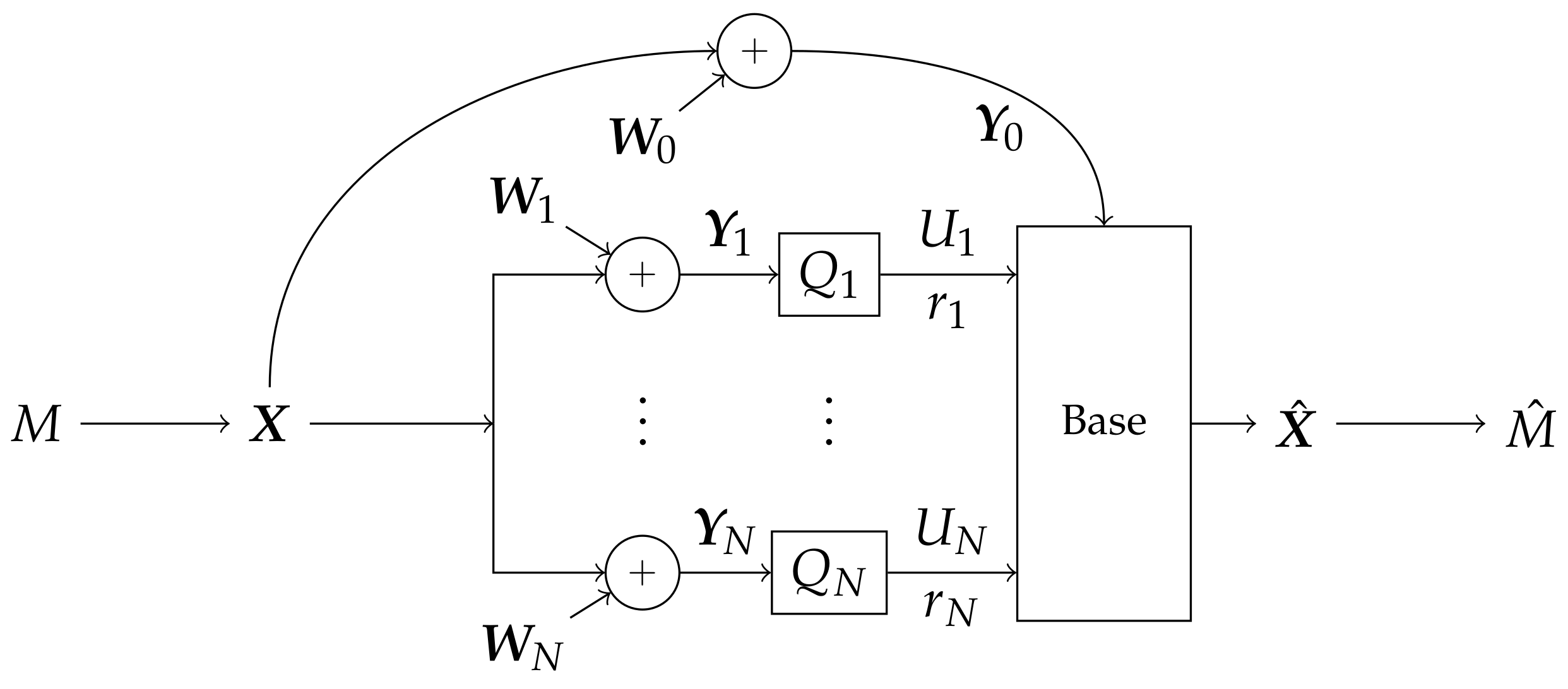
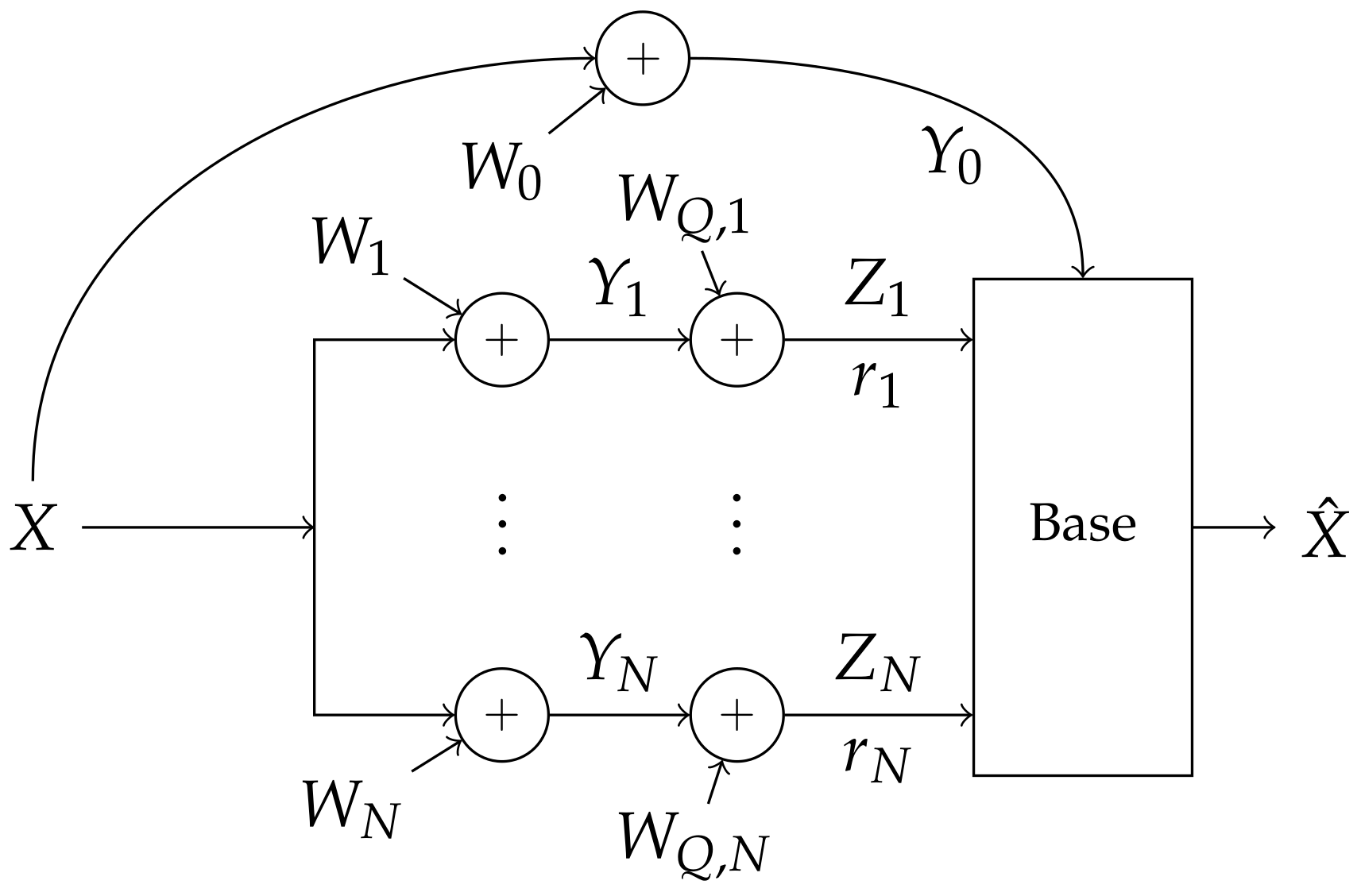
2. Problem Setup
- the channel is constant over time t, and
- the noise has covariance across receivers, and is independent over t.
- Every node in the system is informed of each quantizer’s behavior, and quantizers produce their compression using only local information. Formally, the probability distribution of factors:
- Quantizations are within the LAN constraint:
- channel fades ,
- noise covariance and
- maximum LAN throughput L.
- quantizers ,
- message modulation ,
- rates each helper should send to the base and
- fusion and decoding methods at the base to produce .
3. Bounds on Communications Rates
3.1. Achievable Rate by Decoding and Forwarding
- Helpers are informed of which helper is the best (best is derived from ).
- The transmitter and best helper coordinate a codebook of appropriate rate and distribution.
3.2. Achievable Rate through Gaussian Distortion
- The transmitter and base coordinate a codebook of appropriate rate and distribution.
- Each n-th helper is informed of an encoding rate (optimal choice derived from ).
- Each helper coordinates a random dither with the base.
- The base is informed of .
3.3. Achievable Rate through Distributed Compression
- The transmitter and base coordinate a codebook of appropriate rate and distribution.
- Each n-th helper is informed of a quantization rate and binning rate , (optimal choice derived from ).
- Each helper coordinates a random dither with the base.
- The base is informed of .
- The transmitter and base coordinate a codebook of appropriate rate and distribution.
- Each n-th helper is informed of a quantization rate , binning rate and hull parameter λ (optimal choice derived from ).
- Each helper coordinates a random dither with the base.
- The base is informed of .
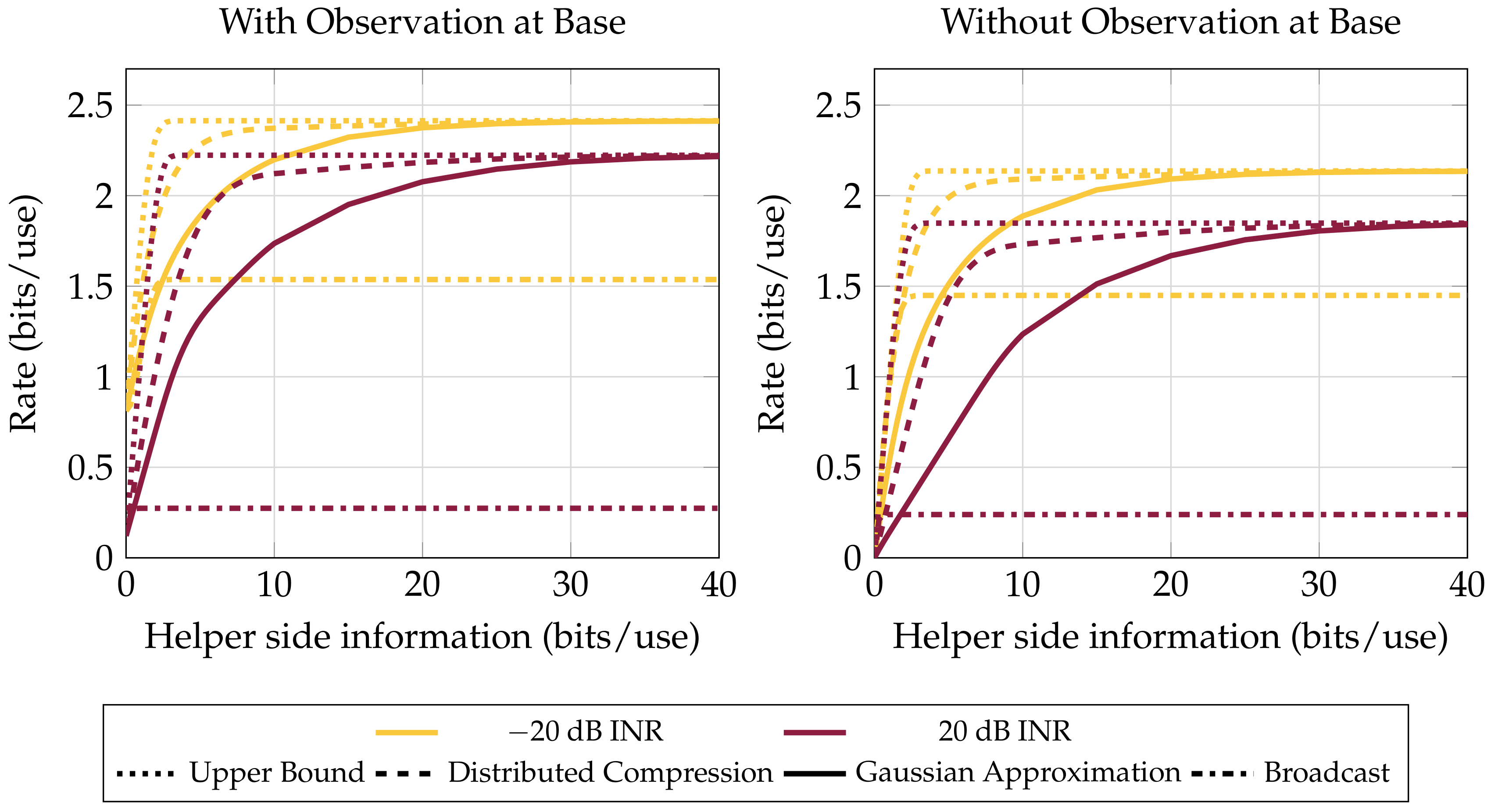
- Σ is diagonal (no interference).
- The base does not have its own full-precision observation of the broadcast ().
- The broadcaster must transmit a Gaussian signal.
- Construction of helper messages is independent of the transmitter’s codebook .
- Since the base has codebook knowledge, it is possible for the transmitter to send a direct message to the base, which is not accounted for in the compress-and-forward strategy used for .
- The Gaussian broadcast assumption is needed because of a counterexample given in Reference [1].
- Codebook independence is necessary because is strictly less than the upper bound in Equation (16), but, by Remark 3, this upper bound is achieved in some regimes.
4. Ergodic Bounds
- number of helpers N,
- LAN constraint L,
- noise covariance matrix , and
- channel (assumed to be static and precisely estimated a priori per each channel use).
4.1. Performance in the Presence of an Interferer
4.2. Path Diversity versus Performance
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Optimization Method
Appendix B. Achievability of Bounds
- Outline
- Transmitter setup
- Helper encoder setup
- Transmission
- Helper encoding and forwarding
- Decoding
- Error analysis
- Outline
- Transmitter setup
- Helper encoder setup
- Transmission
- Helper encoding
- Helper joint-compression and forwarding
- Decoding
- Error analysis
- : is not typical with anything in .
- : For there is some and where and , but any has . denotes the situation where the base identifies the wrong quantizations for all the receivers in S.
Appendix C. Proof of Conditional Capacity
- Σ is diagonal (no interference).
- The base does not have its own full-precision observation of the broadcast ().
- The broadcaster must transmit a Gaussian signal.
- Construction of helper messages is independent of the transmitter’s codebook .
References
- Sanderovich, A.; Shamai, S.; Steinberg, Y.; Kramer, G. Communication via Decentralized Processing. IEEE Trans. Inf. Theory 2008, 54, 3008–3023. [Google Scholar] [CrossRef]
- Sanderovich, A.; Shamai, S.; Steinberg, Y. On Upper bounds for Decentralized MIMO Receiver. In Proceedings of the 2007 IEEE International Symposium on Information Theory, Nice, France, 24–29 June 2007; pp. 1056–1060. [Google Scholar]
- Chapman, C.; Margetts, A.R.; Bliss, D.W. Bounds on the Information Capacity of a Broadcast Channel with Quantizing Receivers. In Proceedings of the IEEE 2015 49th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 8–11 November 2015; pp. 281–285. [Google Scholar]
- Kramer, G.; Gastpar, M.; Gupta, P. Cooperative Strategies and Capacity Theorems for Relay Networks. IEEE Trans. Inf. Theory 2005, 51, 3037–3063. [Google Scholar] [CrossRef]
- Bliss, D.W.; Kraut, S.; Agaskar, A. Transmit and Receive Space-Time-Frequency Adaptive Processing for Cooperative Distributed MIMO Communications. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 5221–5224. [Google Scholar]
- Quitin, F.; Irish, A.; Madhow, U. Distributed Receive Beamforming: A Scalable Architecture and Its Proof of Concept. In Proceedings of the IEEE 77th Vehicular Technology Conference (VTC Spring), Dresden, Germany, 2–5 June 2013; pp. 1–5. [Google Scholar]
- Vagenas, E.D.; Karadimas, P.; Kotsopoulos, S.A. Ergodic Capacity for the SIMO Nakagami-M Channel. EURASIP J. Wirel. Commun. Netw. 2009, 2009, 802067. [Google Scholar] [CrossRef]
- Love, D.J.; Choi, J.; Bidigare, P. Receive Spatial Coding for Distributed Diversity. In Proceedings of the 2013 Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 3–6 November 2013; pp. 602–606. [Google Scholar]
- Choi, J.; Love, D.J.; Bidigare, P. Coded Distributed Diversity: A Novel Distributed Reception Technique for Wireless Communication Systems. IEEE Trans. Signal Process. 2015, 63, 1310–1321. [Google Scholar] [CrossRef]
- Brown, D.R.; Ni, M.; Madhow, U.; Bidigare, P. Distributed Reception with Coarsely-Quantized Observation Exchanges. In Proceedings of the 2013 47th Annual Conference on Information Sciences and Systems (CISS), Altimore, MD, USA, 20–22 March 2013; pp. 1–6. [Google Scholar]
- Berger, T.; Zhang, Z.; Viswanathan, H. The CEO Problem [Multiterminal Source Coding]. IEEE Trans. Inf. Theory 1996, 42, 887–902. [Google Scholar] [CrossRef]
- Tavildar, S.; Viswanath, P.; Wagner, A.B. The Gaussian Many-Help-One Distributed Source Coding Problem. IEEE Trans. Inf. Theory 2010, 56, 564–581. [Google Scholar] [CrossRef]
- Yedla, A.; Pfister, H.D.; Narayanan, K.R. Code Design for the Noisy Slepian-Wolf Problem. IEEE Trans. Commun. 2013, 61, 2535–2545. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements Informations Theory; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. ACM SIGMOBILE Mob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- Telatar, I.E. Capacity of Multi-Antenna Gaussian Channels. Eur. Trans. Telecommun. 1999, 10, 585–595. [Google Scholar] [CrossRef]
- Gamal, A.E.; Kim, Y. Network Information Theory; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Weingarten, H.; Steinberg, S.; Shamai, S. The Capacity Region of the Gaussian Multiple-Input Multiple-Output Broadcast Channel. IEEE Trans. Inf. Theory 2006, 52, 3936–3964. [Google Scholar] [CrossRef]
- Wei, Y.; Cioffi, J.M. Sum Capacity of Gaussian Vector Broadcast Channels. IEEE Trans. Inf. Theory 2004, 50, 1875–1892. [Google Scholar]
- Zamir, R.; Feder, M. On lattice Quantization Noise. IEEE Trans. Inf. Theory 1996, 42, 1152–1159. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Slepian, D.; Wolf, J.K. Noiseless Coding of Correlated Information Sources. IEEE Trans. Inf. Theory 1973, 19, 471–480. [Google Scholar] [CrossRef]
- Costa, M. Writing on Dirty Paper (corresp.). IEEE Trans. Inf. Theory 1983, 29, 439–441. [Google Scholar] [CrossRef]
- Goldsmith, A. Wireless Communications; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Bliss, D.W.; Govindasamy, S. Adaptive Wireless Communications: MIMO Channels and Networks; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Jones, E.; Oliphant, T.; Peterson, P. SciPy: Open Source Scientific Tools for Python. 2001. Available online: http://www.scipy.org/ (accessed on 10 September 2017).
- Diggavi, S.N.; Cover, T.M. The Worst Additive Noise Under a Covariance Constraint. IEEE Trans. Inf. Theory 2001, 47, 3072–3081. [Google Scholar] [CrossRef]
- Ihara, S. On the Capacity of Channels with Additive Non-Gaussian Noise. Inf. Control 1978, 37, 34–39. [Google Scholar] [CrossRef]
- Zamir, R.; Feder, M. On Universal Quantization by Randomized Uniform/Lattice Quantizers. IEEE Trans. Inf. Theory 1992, 38, 428–436. [Google Scholar] [CrossRef]
| Complex circularly symmetric normal distribution with zero mean and Hermitian covariance matrix | |
| Mutual information, Shannon entropy and differential entropy | |
| Conjugate transpose of matrix , vector | |
| Vector with components indexed by S | |
| Determinant of a matrix | |
| Integers from a to b, inclusive | |
| Vector with non-negative elements | |
| Positive semidefinite matrix | |
| N-row vector of 1 s | |
| Element on row j, column k of a matrix | |
| Diagonal matrix where the diagonal element is the element of vector | |
| identity matrix | |
| Vector magnitude/2-norm | |
| Nonnegative real numbers |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chapman, C.D.; Mittelmann, H.; Margetts, A.R.; Bliss, D.W. A Decentralized Receiver in Gaussian Interference. Entropy 2018, 20, 269. https://doi.org/10.3390/e20040269
Chapman CD, Mittelmann H, Margetts AR, Bliss DW. A Decentralized Receiver in Gaussian Interference. Entropy. 2018; 20(4):269. https://doi.org/10.3390/e20040269
Chicago/Turabian StyleChapman, Christian D., Hans Mittelmann, Adam R. Margetts, and Daniel W. Bliss. 2018. "A Decentralized Receiver in Gaussian Interference" Entropy 20, no. 4: 269. https://doi.org/10.3390/e20040269
APA StyleChapman, C. D., Mittelmann, H., Margetts, A. R., & Bliss, D. W. (2018). A Decentralized Receiver in Gaussian Interference. Entropy, 20(4), 269. https://doi.org/10.3390/e20040269