Partition Function and Configurational Entropy in Non-Equilibrium States: A New Theoretical Model
Abstract
:1. Introduction
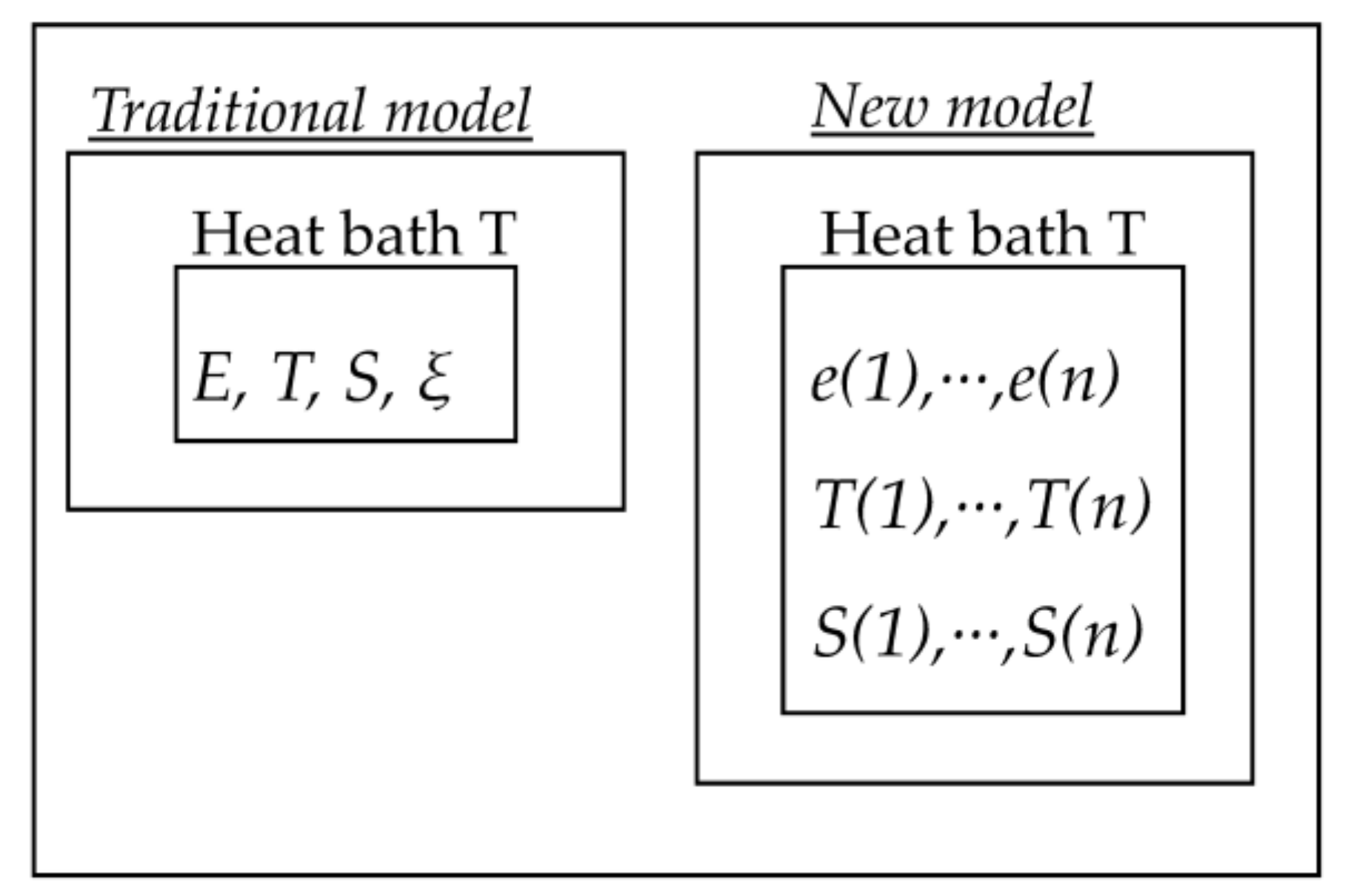
2. Theoretical Model Description
3. Computational Model
4. Results for Constant Temperatures
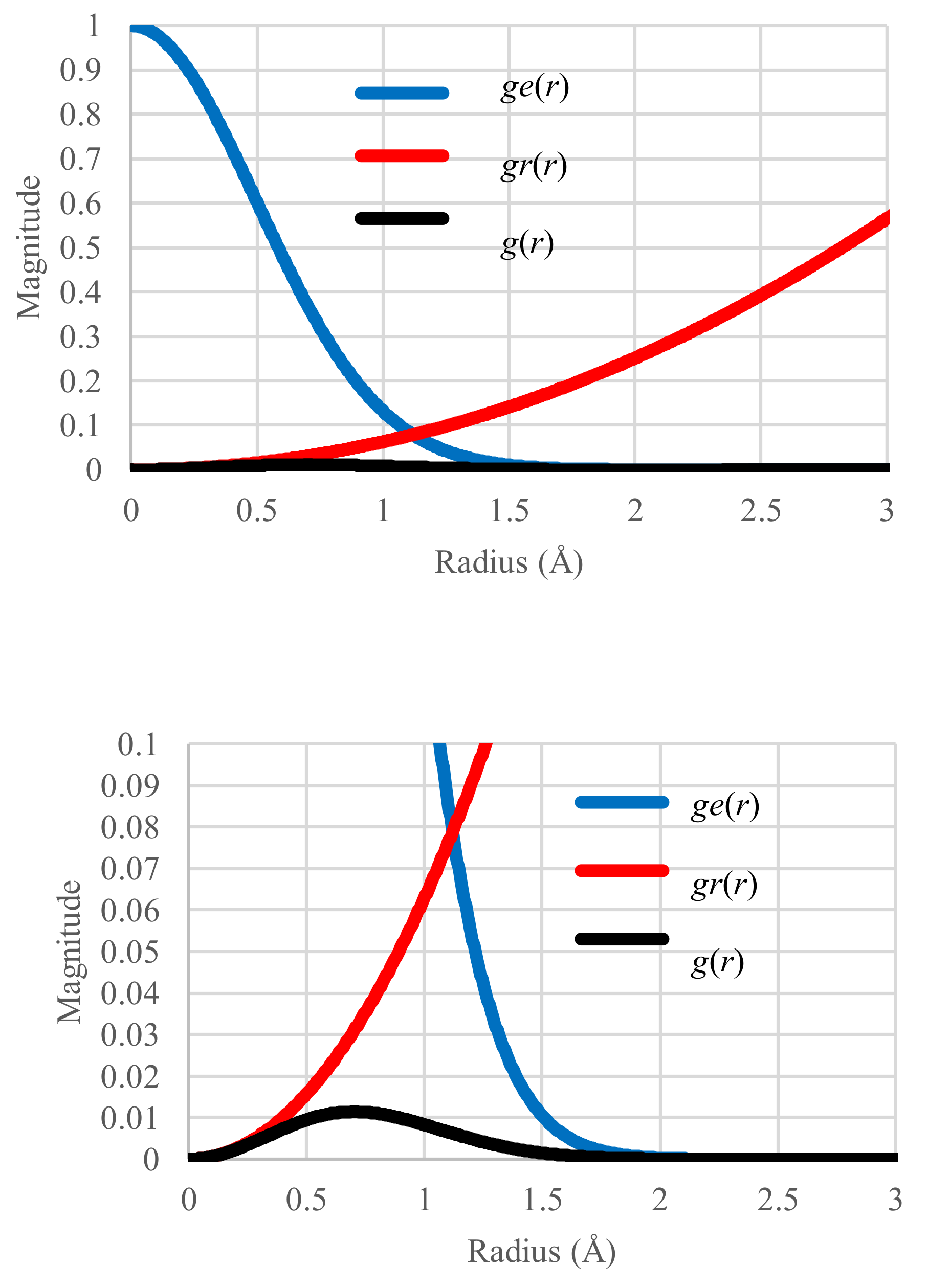
4.1. Standard Case in Equilibrium States
4.2. Temperature Sensitivity in Equilibrium States
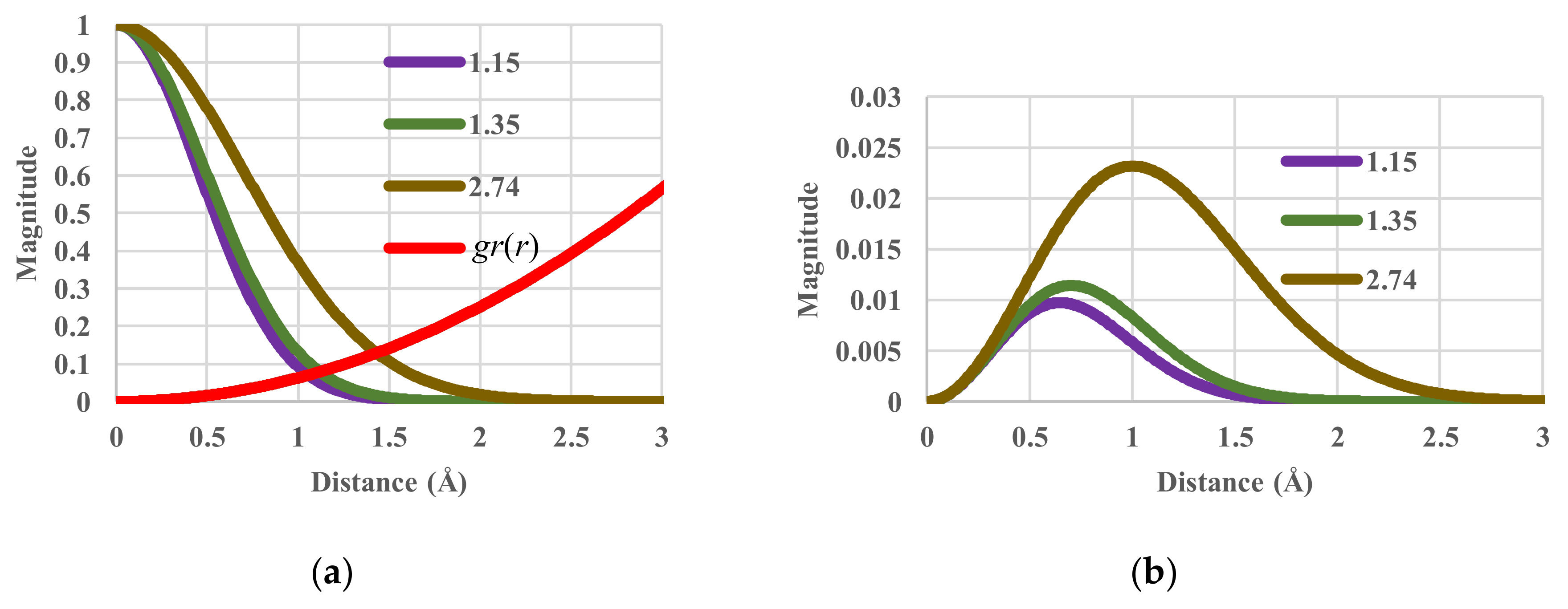
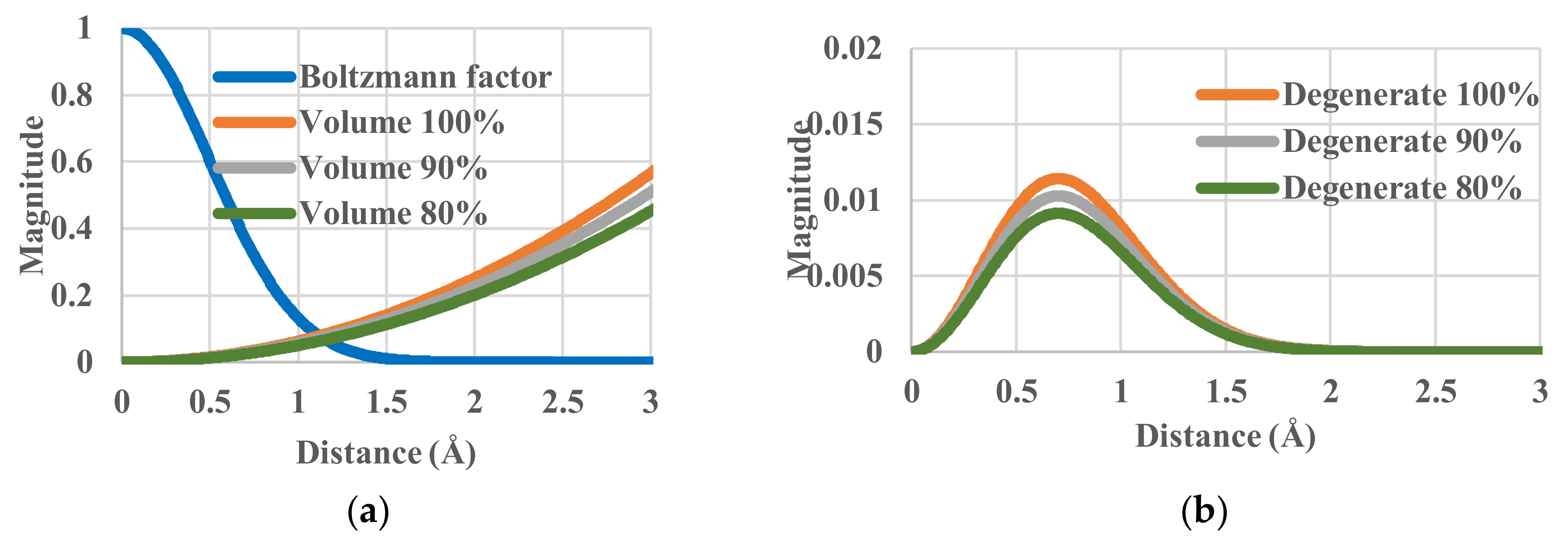
4.3. Effective-Volume Sensitivity in Equilibrium States
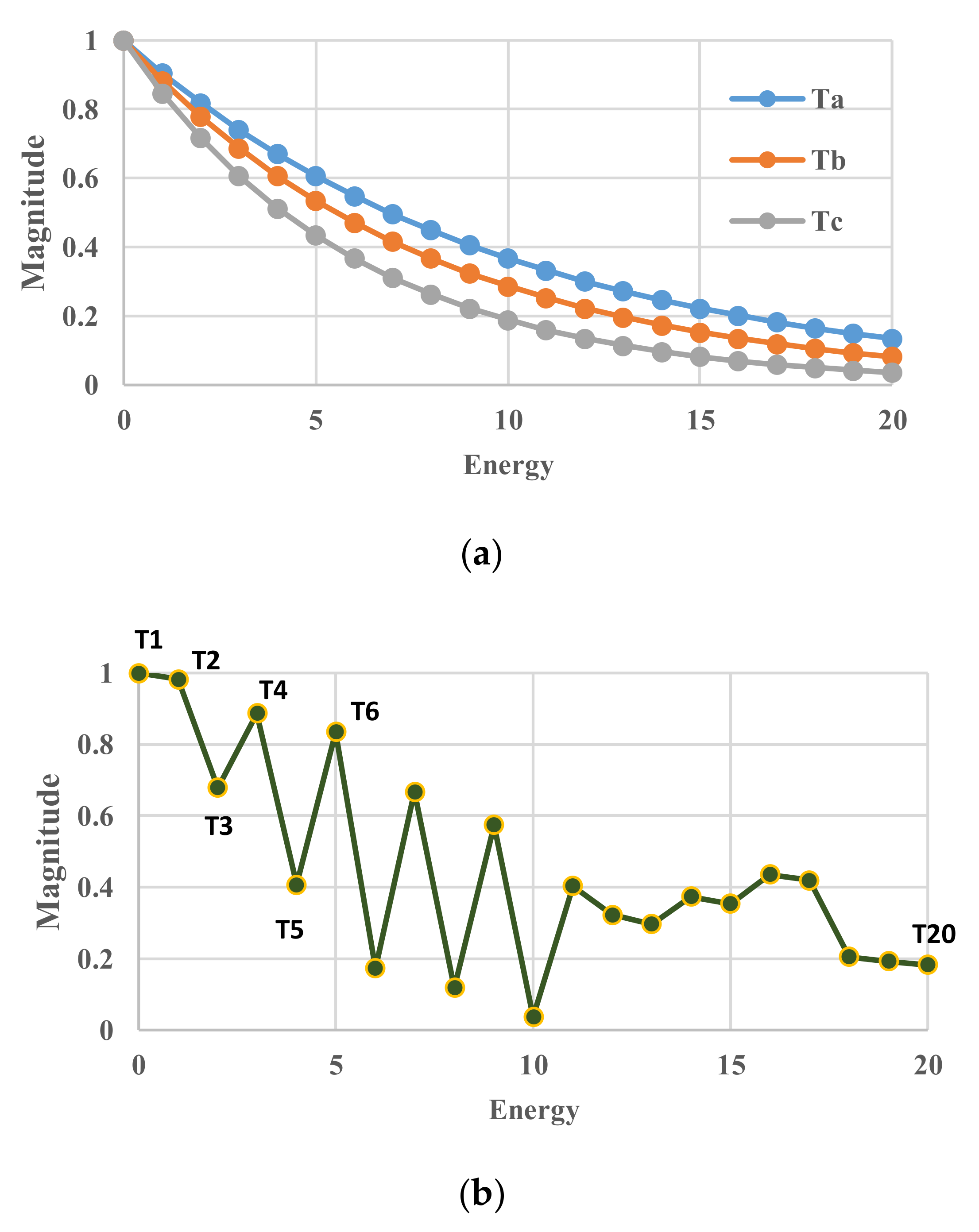
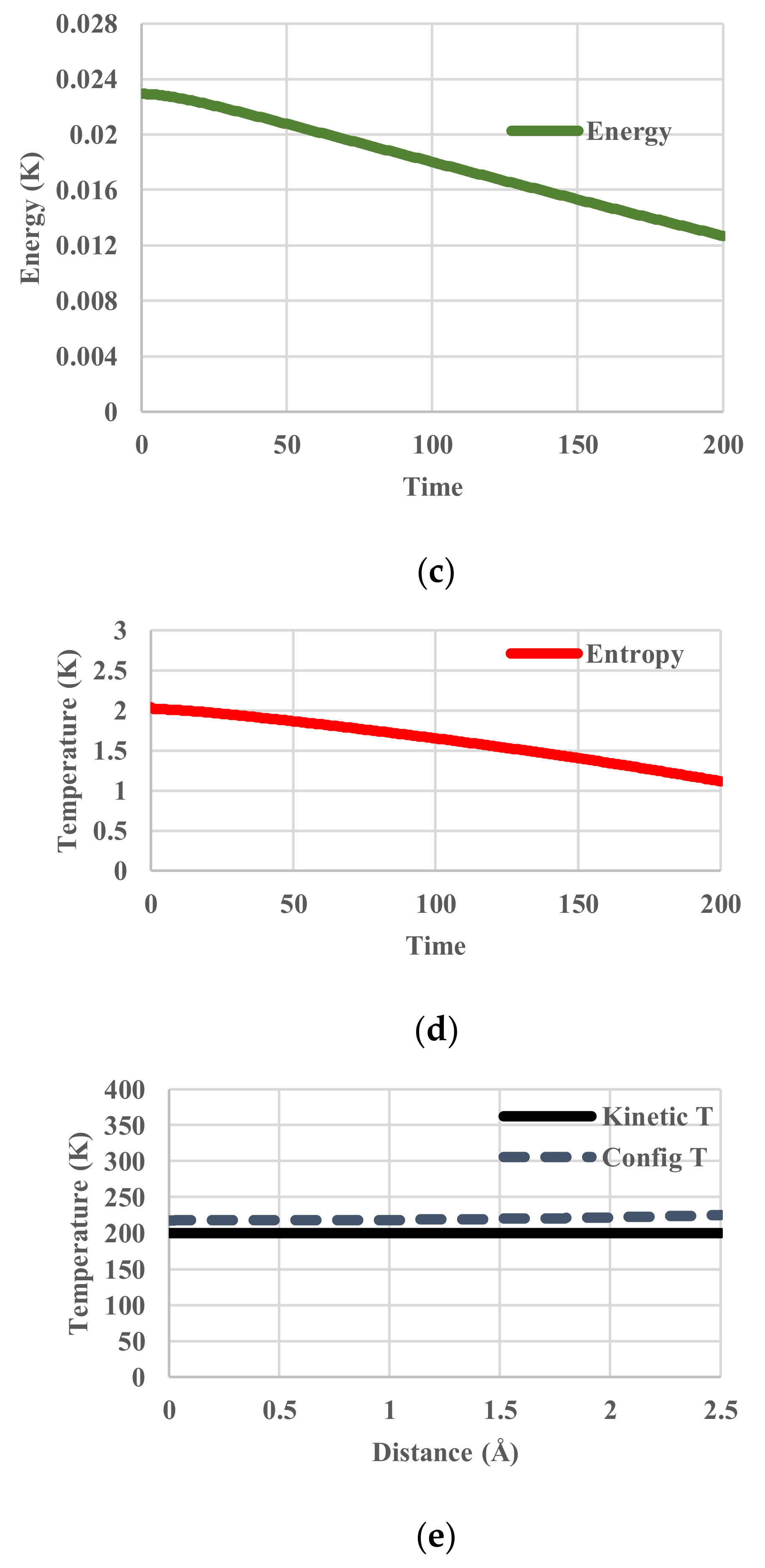
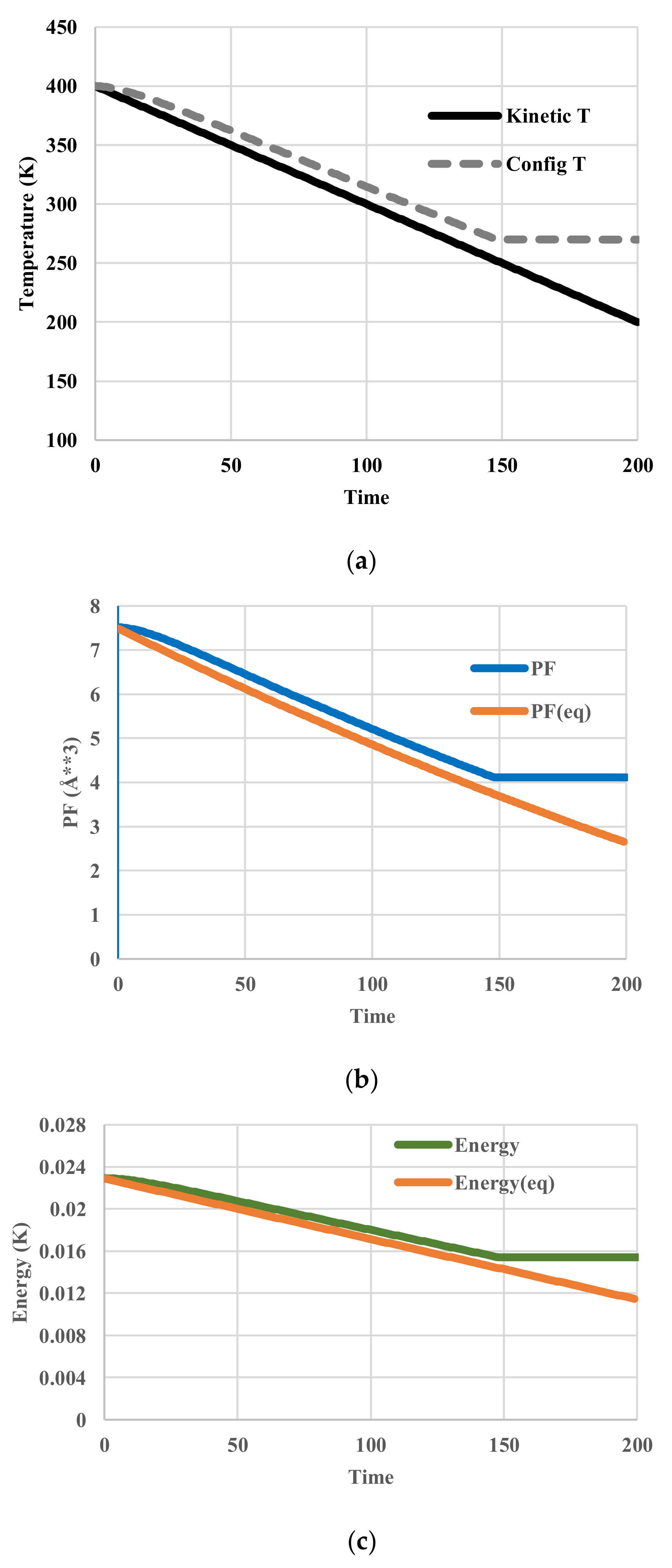
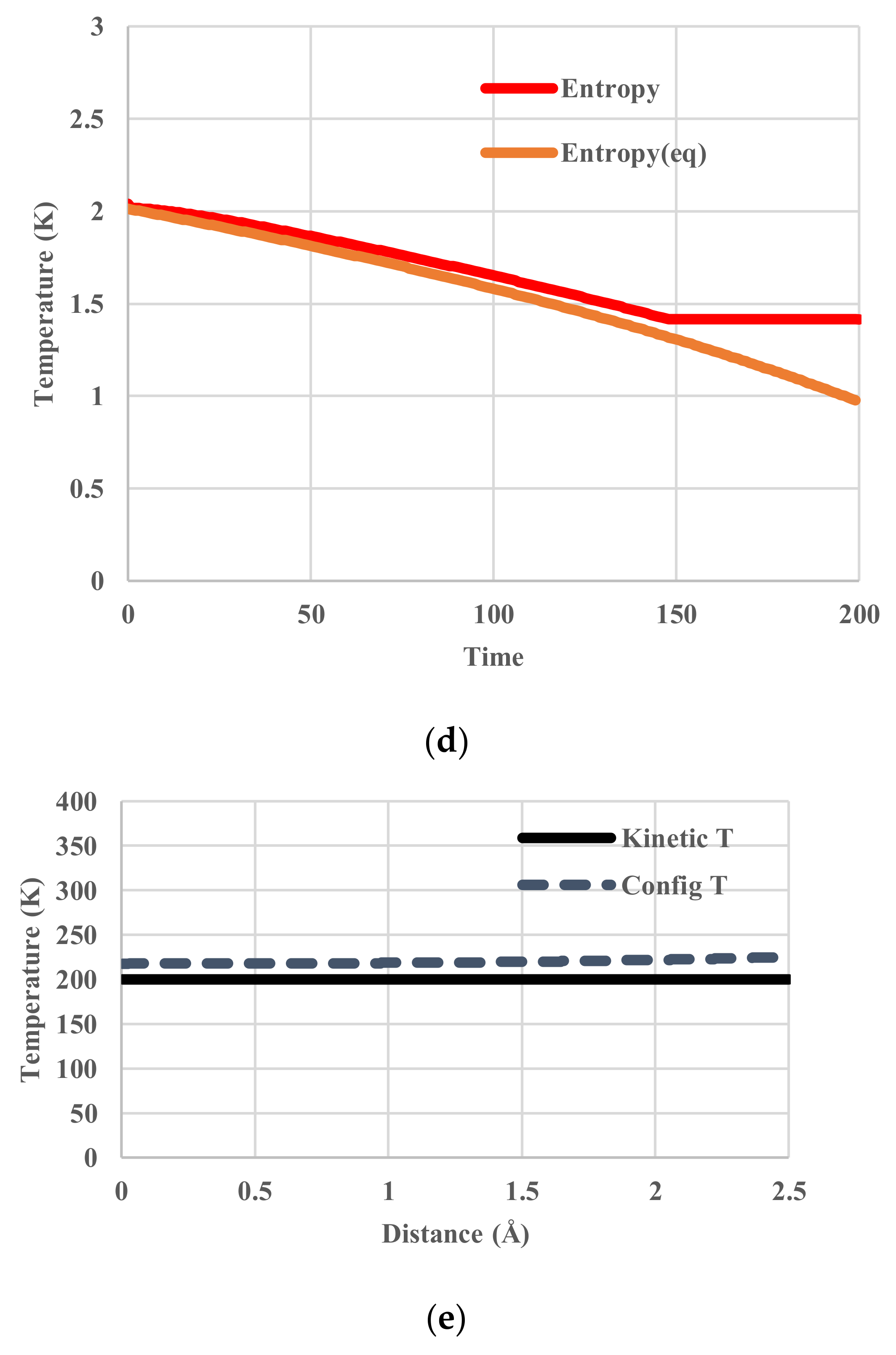
5. Results for Constant Cooling Rates
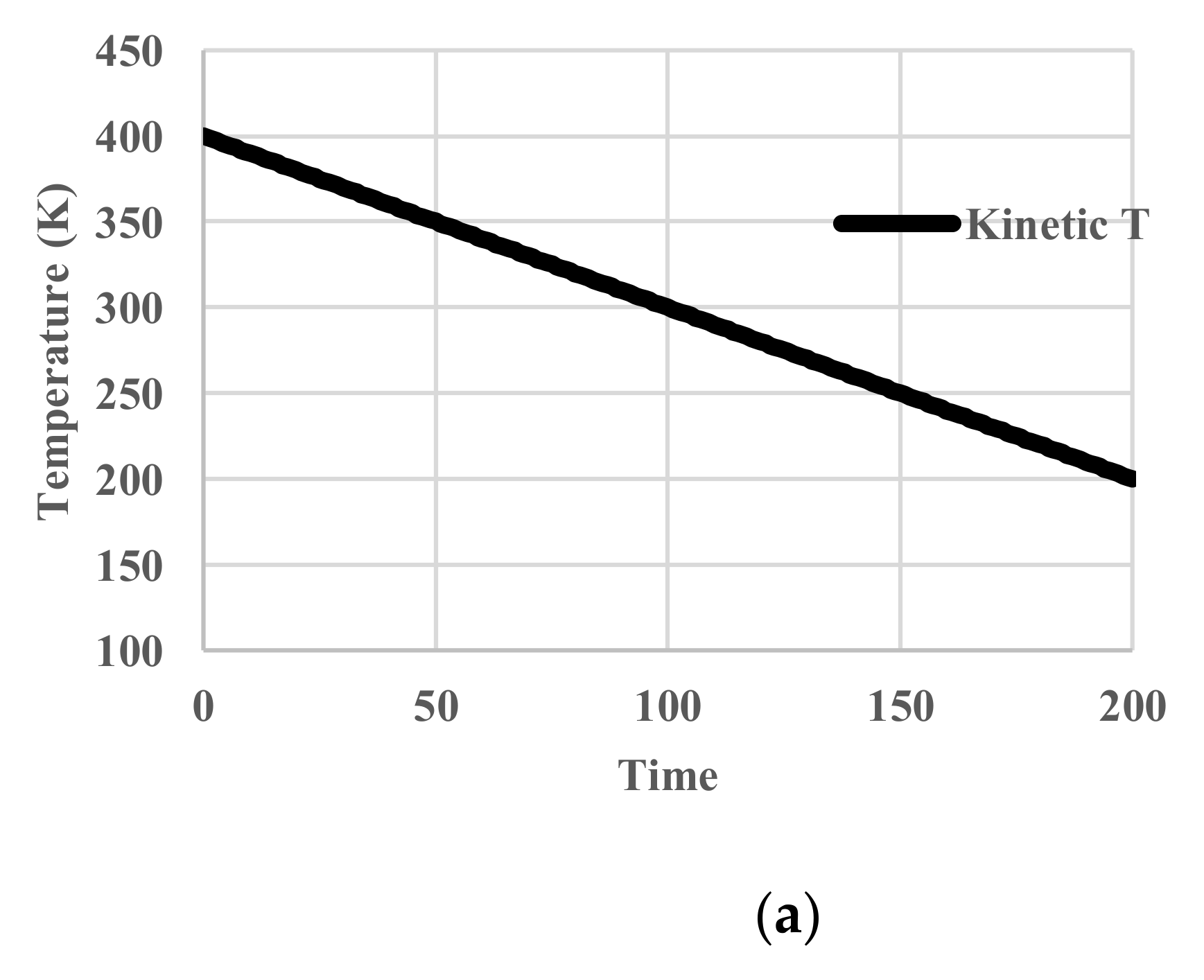
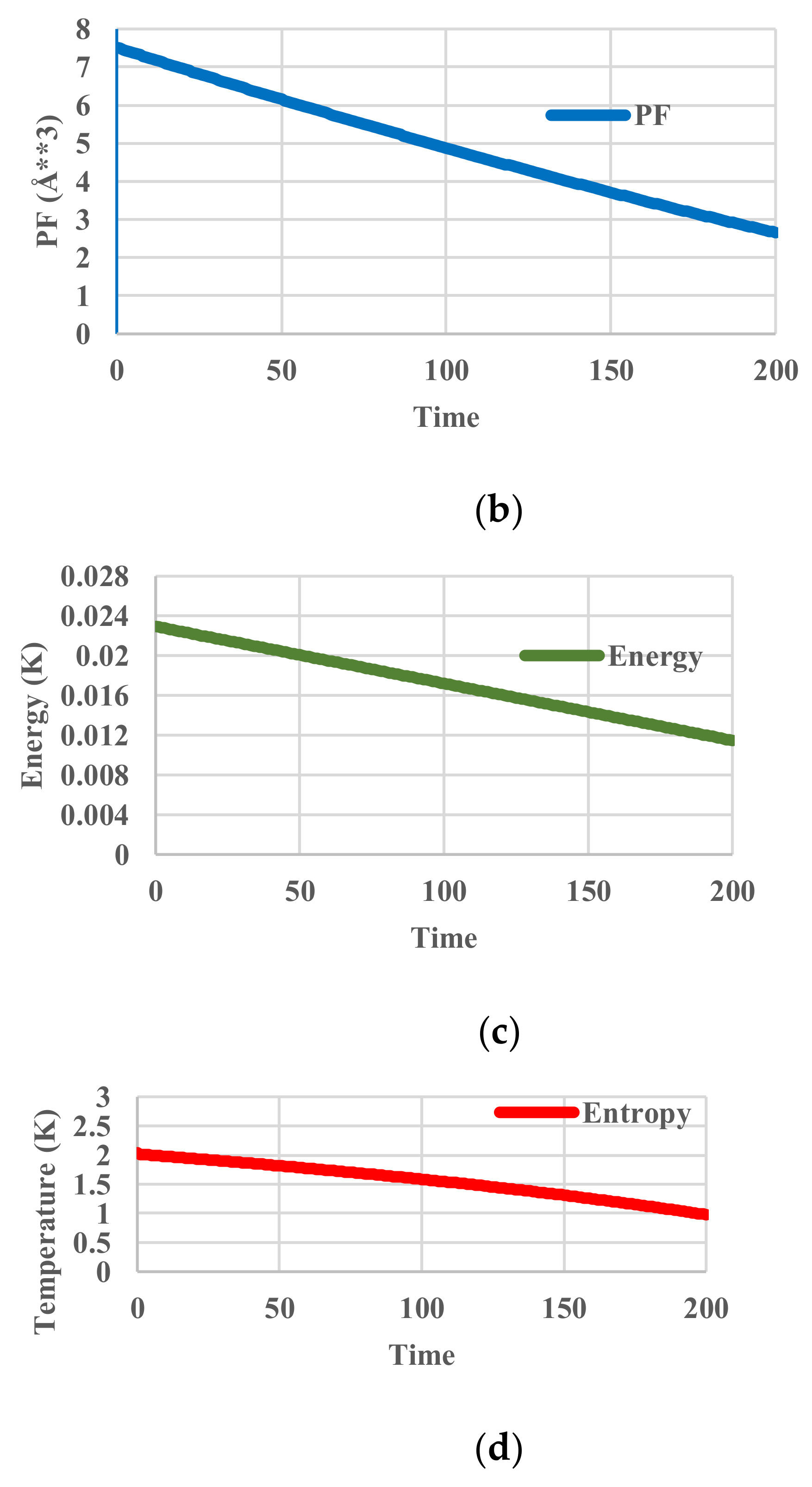
5.1. Without Relaxation Effects
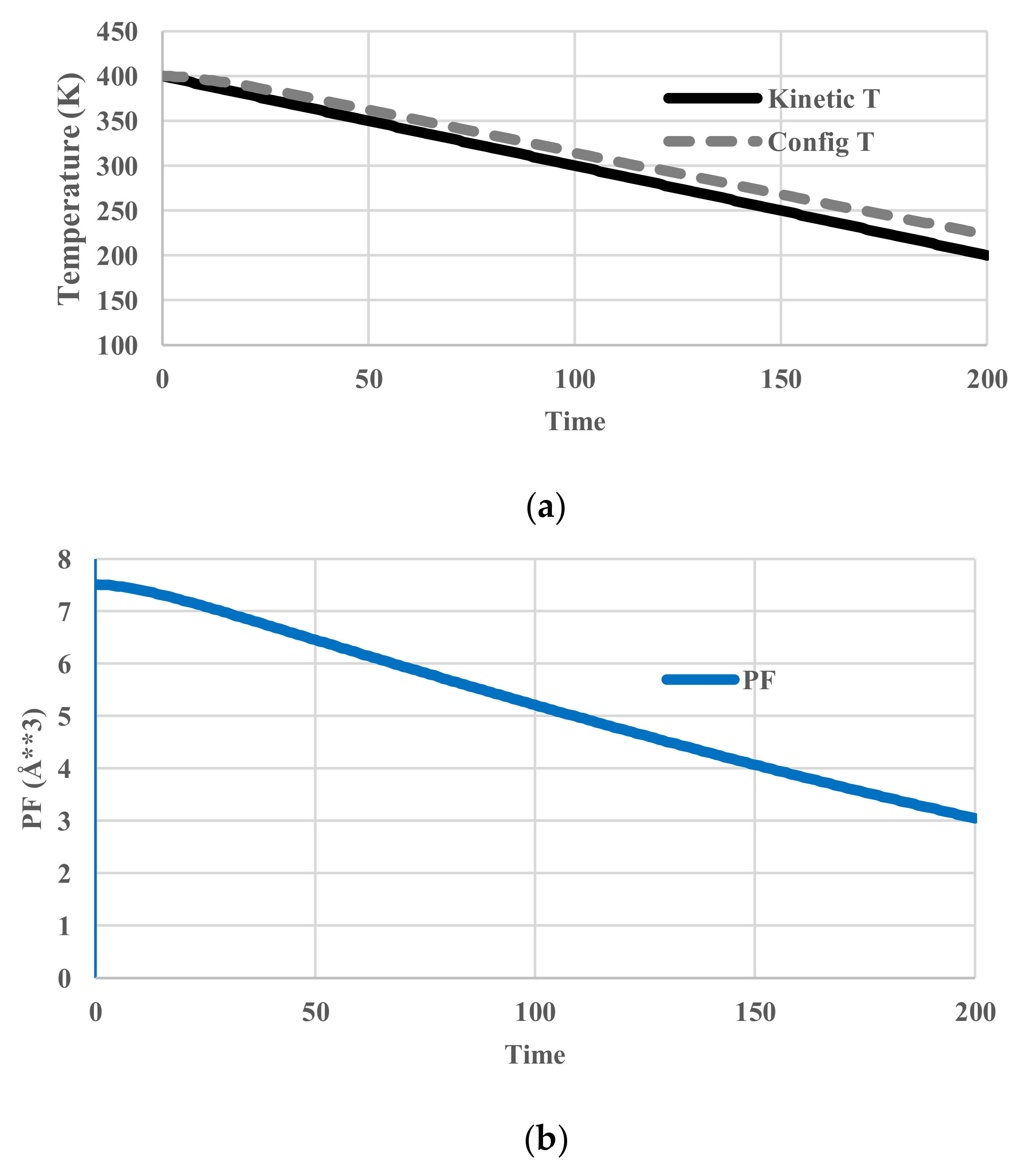
5.2. Arrhenius-Type Relaxation Effects
5.3. Vogel-Fulcher-Tammann-Type Relaxation Effects
6. Discussion
7. Conclusions
Author Contributions
Conflicts of Interest
Appendix A
Appendix B

References
- Gutzow, I.; Schmelzer, J.W.P. The Vitreous State: Thermodynamics, Structure Rheology, and Crystallization; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Nemilov, S.V. Thermodynamic and Kinetic Aspects of the Vitreous State; CRC Press: London, UK, 1994. [Google Scholar]
- De Donder, T.; van Rysselberghe, P. Thermodynamic Theory of Affinity: A Book of Principles; Stanford University Press: Stanford, CA, USA, 1936. [Google Scholar]
- Tropin, T.V.; Schmelzer, J.; Schick, C. On the dependence of the properties of glasses on cooling and heating rates: I. Entropy, entropy production, and glass transition temperature. J. Non-Cryst. Solids 2011, 357, 1291–1302. [Google Scholar] [CrossRef]
- Tool, A.Q. Relation between Inelastic Deformability and Thermal Expansion of Glass in its Annealing Range. J. Am. Ceram. Soc. 1946, 29, 240–253. [Google Scholar] [CrossRef]
- Koike, A.; Ryu, S.R.; Tomozawa, M. Adequacy Test of the Fictive Temperatures of Silica Glasses Determined by IR Spectroscopy. J. Non-Cryst. Solids 2005, 351, 3797–3803. [Google Scholar] [CrossRef]
- Ritland, H.N. Limitations of the Fictive Temperature Concept. J. Am. Ceram. Soc. 1956, 39, 403–406. [Google Scholar] [CrossRef]
- Takada, A.; Conradt, R.; Richet, P. Residual Entropy and Structural Disorder in Glass: A Two-level Model and a Review of Spatial and Ensemble vs. Temporal Sampling. J. Non-Cryst. Solids. 2013, 360, 13–20. [Google Scholar] [CrossRef]
- Takada, A.; Conradt, R.; Richet, P. Residual Entropy and Structural Disorder in Glass: Fluctuation Phenomena and Time-dependent Features as deduced from an Ising-type Structural Model. J. Non-Cryst. Solids 2013, 365, 53–58. [Google Scholar] [CrossRef]
- Takada, A.; Conradt, R.; Richet, P. Residual Entropy and Structural Disorder in Glass: A Review of History and an Attempt to resolve two Apparently Conflicting Views. J. Non-Cryst. Solids 2015, 429, 33–43. [Google Scholar] [CrossRef]
- Lennard-Jones, J.E.; Devonshire, A.F. Critical Phenomena in Gases. I. Proc. R. Soc. Lond. Ser. 1937, A163, 53–70. [Google Scholar] [CrossRef]
- Hirschfelder, J.; Stevenson, D.; Eyring, H. A Theory of Liquid Structure. J. Chem. Phys. 1937, 5, 896–912. [Google Scholar] [CrossRef]
- Henchman, R.H. Partition Function for a Simple Liquid Using Cell Theory Parametrized by Computer Simulation. J. Chem. Phys. 2003, 119, 400–406. [Google Scholar] [CrossRef]
- Leff, H.F.; Rex, A.F. (Eds.) Maxwell’s Demon 2; IOP Pub.: Bristol, UK, 2003. [Google Scholar]
- Takada, A.; Atake, T.; Richet, P. New description of structural disorder in silica glass. J. Non-Cryst. Solids 2009, 355, 694–699. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takada, A.; Conradt, R.; Richet, P. Partition Function and Configurational Entropy in Non-Equilibrium States: A New Theoretical Model. Entropy 2018, 20, 218. https://doi.org/10.3390/e20040218
Takada A, Conradt R, Richet P. Partition Function and Configurational Entropy in Non-Equilibrium States: A New Theoretical Model. Entropy. 2018; 20(4):218. https://doi.org/10.3390/e20040218
Chicago/Turabian StyleTakada, Akira, Reinhard Conradt, and Pascal Richet. 2018. "Partition Function and Configurational Entropy in Non-Equilibrium States: A New Theoretical Model" Entropy 20, no. 4: 218. https://doi.org/10.3390/e20040218
APA StyleTakada, A., Conradt, R., & Richet, P. (2018). Partition Function and Configurational Entropy in Non-Equilibrium States: A New Theoretical Model. Entropy, 20(4), 218. https://doi.org/10.3390/e20040218



