Global Optimization Employing Gaussian Process-Based Bayesian Surrogates †
Abstract
:1. Introduction
2. The Gaussian Process Method
3. Prediction of Function Values
4. Evaluation of the Hyperparameters
5. Utility Functions
6. Global Optimization Algorithm
7. Results in One and Two Dimensions
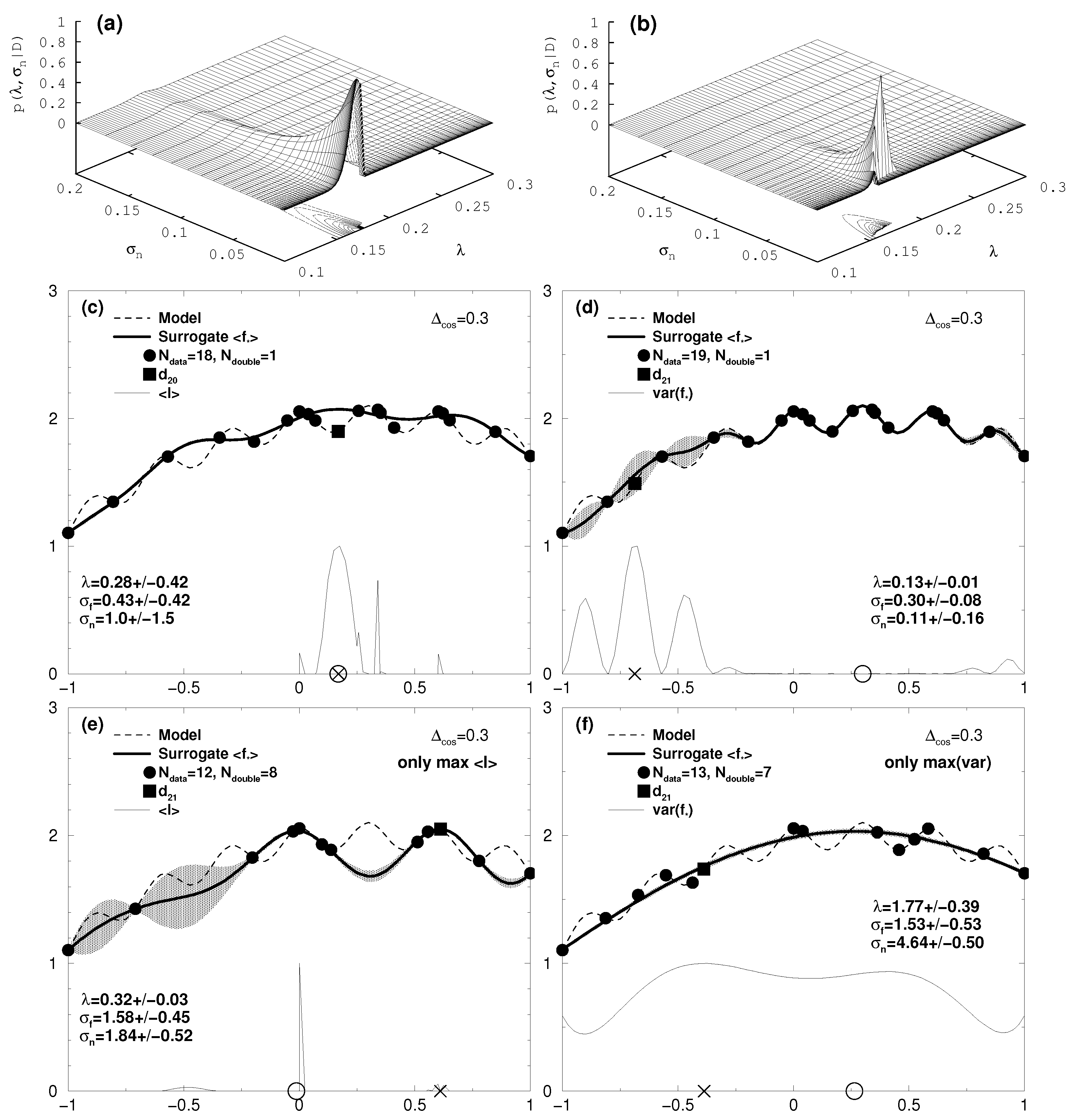
7.1. One-Dimensional Results
7.2. Two-Dimensional Results
8. Summary and Conclusions
Author Contributions
Conflicts of Interest
Appendix A. Notation Table
| N | number of input data vectors |
| number of elements in the input data vector | |
| number of points added to the data pool by optimization | |
| number of points for which standard error was reduced | |
| test input vector | |
| i-th input data vector | |
| matrix with input data vectors as columns | |
| matrix of the input data vectors expanded by the vector of grid points | |
| vector of grid points within region of interest | |
| grid point with largest utility | |
| target value at test input vector | |
| function of input data to describe target data | |
| maximum of the surrogate model function | |
| vector of the N target data | |
| uncertainty of the target data | |
| variance of the i-th target data | |
| -th element of the matrix of the variances of target data | |
| length scale to set up the notion of distance between input data vectors | |
| signal variance of the distribution over functions f | |
| overall noise in the data | |
| vector of the hyperparameters | |
| covariance of two input data vectors | |
| short notation for the i-th element of the vector of covariances between test | |
| input vector and input data vector | |
| -th element of the covariance matrix of the input data vectors | |
| covariance matrix of the expanded input | |
| RoI | region of interest to run Gaussian processes |
| I | improvement of the maximum of the surrogate model |
| utility of a target data obtained at input vector |
References
- Sacks, J.; Welch, W.; Mitchell, T.; Wynn, H. Design and Analysis of Computer Experiments. Stat. Sci. 1989, 4, 409–435. [Google Scholar] [CrossRef]
- Jones, D.R. A Taxonomy of Global Optimization Methods Based on Response Surfaces. J. Glob. Optim. 2001, 21, 345–383. [Google Scholar] [CrossRef]
- Barber, D. Bayesian Reasoning and Machine Learning; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Bishop, C. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Cohn, D. Neural Network Exploration Using Optimal Experiment Design. Neural Netw. 1996, 9, 1071–1083. [Google Scholar] [CrossRef]
- MacKay, D.J.C. Bayesian Approach to Global Optimization: Theory and Applications; Kluwer Academic: Norwell, MA, USA, 2013. [Google Scholar]
- Neal, R.M. Monte Carlo Implementation of Gaussian Process Models for Bayesian Regression and Classification. In Technical Report 9702; University of Toronto: Toronto, ON, Canada, 1997. [Google Scholar]
- Seo, S.; Wallat, M.; Graepel, T.; Obermayer, K. Gaussian process regression: active data selection and test point rejection. In Proceedings of the International Joint Conference on Neural Networks, Como, Italy, 24–27 July 2000; pp. 241–246. [Google Scholar]
- Gramacy, R.B.; Lee, H.K.H. Adaptive Design and Analysis of Supercomputer Experiments. Technometrics 2009, 51, 130–145. [Google Scholar] [CrossRef]
- Mockus, J. Bayesian Approach to Global Optimization; Springer: Berlin, Germany, 1989. [Google Scholar]
- Locatelli, M. Bayesian Algorithms for One-Dimensional Global Optimization. J. Glob. Optim. 1997, 10, 57–76. [Google Scholar] [CrossRef]
- Azimi, J.; Fern, A.; Fern, X. Batch Bayesian Optimization via Simulation Matching. In Advances in Neural Information Processing Systems 23; Lafferty, J.D., Williams, C.K.I., Shawe-Taylor, J., Zemel, R.S., Culotta, A., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2010; pp. 109–117. [Google Scholar]
- Azimi, J.; Jalali, A.; Fern, X. Hybrid Batch Bayesian Optimization. In Proceedings of the 29th International Conference on Machine Learning, Edinburgh, UK, 26 June–1 July 2012. [Google Scholar]
- Gonzalez, J.; Osborne, M.; Lawrence, N. GLASSES: Relieving The Myopia of Bayesian Optimisation. J. Mach. Learn. Res. 2016, 51, 790–799. [Google Scholar]
- Krige, D.G. A Statistical Approach to Some Basic Mine Valuation Problems on the Witwatersrand. J. Chem. Metal. Min. Soc. S. Afr. 1951, 52, 119–139. [Google Scholar]
- Matheron, G. Principles of geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Higdon, D. Space and space-time modeling using process convolutions. In Quantitative Methods for Current Environmental Issues; Springer: Berlin/Heidelberg, Germany, 2002; Volume 3754, pp. 37–56. [Google Scholar]
- Boyle, P.; Frean, M. Dependent Gaussian processes. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2005; Volume 17, pp. 217–224. [Google Scholar]
- Alvarez, M.; Luengo, D.; Lawrence, N. Latent force models. In Proceedings of the 12th International Conference on Artificial Intelligence and Statistics (AISTATS), Clearwater Beach, Florida, 16–18 April 2009; pp. 9–16. [Google Scholar]
- Alvarez, M.; Luengo, D.; Lawrence, N. Linear Latent Force Models Using Gaussian Processes. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2693. [Google Scholar] [CrossRef] [PubMed]
- Preuss, R.; von Toussaint, U. Prediction of Plasma Simulation Data with the Gaussian Process Method. In Bayesian Inference and Maximum Entropy Methods in Science and Engineering; Niven, R., Ed.; AIP Publishing: Melville, NY, USA, 2014; Volume 1636, p. 118. [Google Scholar]
- Rasmussen, C.; Williams, C. Gaussian Processes for Machine Learning; MIT Press: Cambridge, UK, 2006. [Google Scholar]
- Garnett, R.; Osborne, M.A.; Roberts, S.J. Bayesian Optimization for Sensor Set Selection. In Proceedings of the 9th ACM/IEEE International Conference on Information Processing in Sensor Networks, Stockholm, Sweden, 12–16 April 2010; ACM: New York, NY, USA, 2010; pp. 209–219. [Google Scholar]
- Osborne, M.A.; Garnett, R.; Roberts, S.J. Gaussian Processes for Global Optimization. 2009. Available online: http://www.robots.ox.ac.uk/~parg/pubs/OsborneGarnettRobertsGPGO.pdf (accessed on 15 March 2018).
- Gilks, W.R.; Richardson, S.; Spiegelhalter, D.J. Markov Chain Monte Carlo in Practice; Chapman & Hall: London, UK, 1996. [Google Scholar]
- Schonlau, M.; Welch, W.; Jones, D. Global Versus Local Search in Constrained Optimization of Computer Models. In New Developments and Applications in Experimental Design; Flournoy, N., Rosenberger, W.F., Wong, W.K., Eds.; Institute of Mathematical Statistics: Hayward, CA, USA, 1998; Volume 34, pp. 11–25. [Google Scholar]
- Törn, A.; Zilinskas, A. Lecture Notes in Computer Science; Global Optimization; Springer: Berlin, Germany, 1989; Volume 350. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Preuss, R.; von Toussaint, U. Optimization employing Gaussian process-based surrogates. In Proceedings of the 37th International Workshop on Bayesian Inference and Maximum Entropy Methods in Science and Engineering, Jarinu/SP, Brazil, 9–14 July 2017. [Google Scholar]
- Dixon, L.C.W.; Szego, G.P. The global optimisation problem: An introduction. In Towards Global Optimisation 2; Dixon, L.C.W., Szego, G.P., Eds.; North Holland: New York, NY, USA, 1978; pp. 1–15. [Google Scholar]
- Jylänki, P.; Vanhatalo, J.; Vehtari, A. Robust Gaussian Process Regression with a Student-t Likelihood. J. Mach. Learn. Res. 2011, 12, 3227–3257. [Google Scholar]
- Shah, A.; Wilson, A.G.; Ghahramani, Z. Studen-t Processes as Alternatives to Gaussian Processes. In Proceedings of the 17th International Conference on Artificial Intelligence and Statistics, Reykjavik, Iceland, 22–24 April 2014; JMLR W&CP: Reykjavik, Iceland, 2014; Volume 33, pp. 877–885. [Google Scholar]

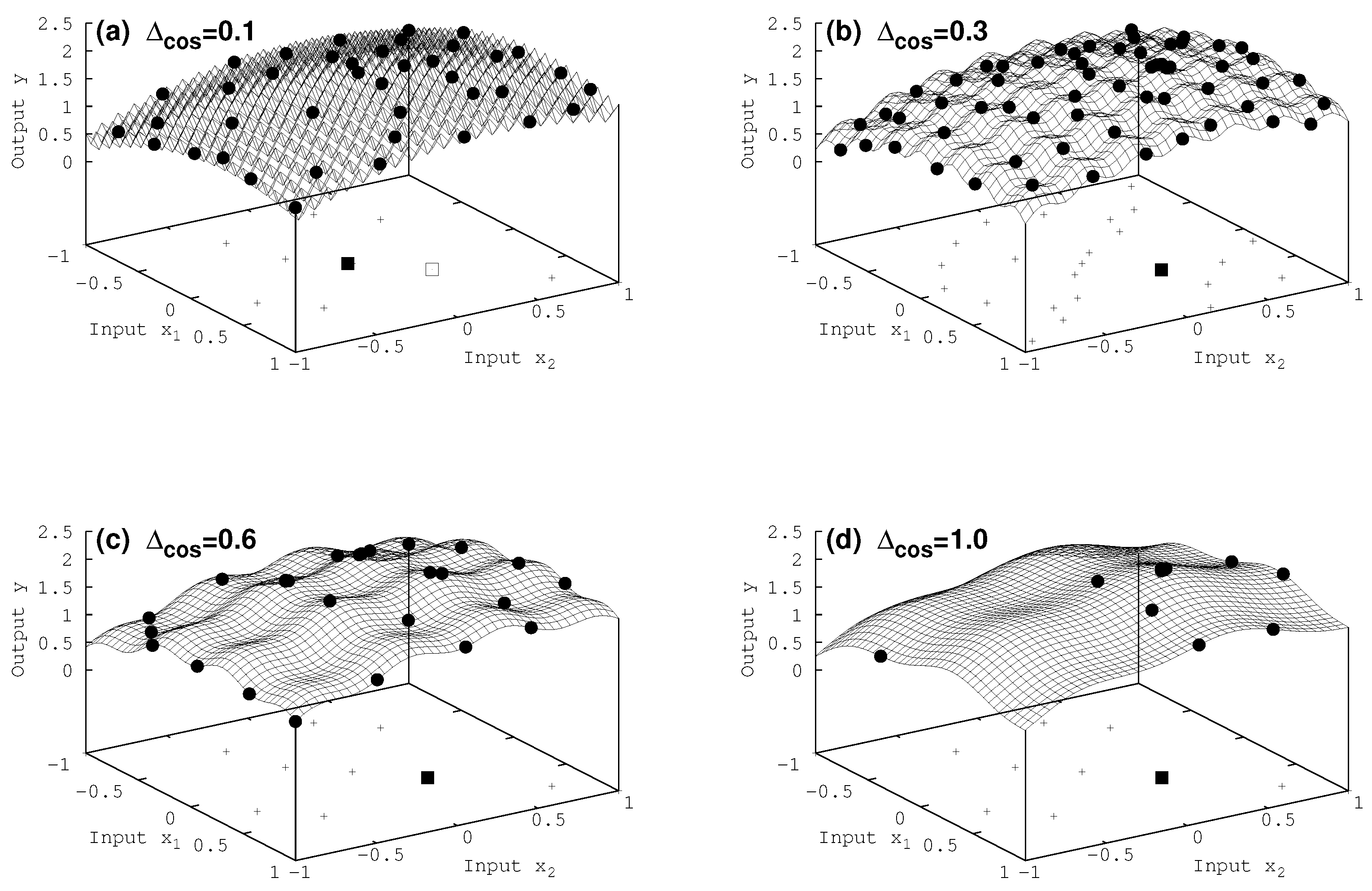
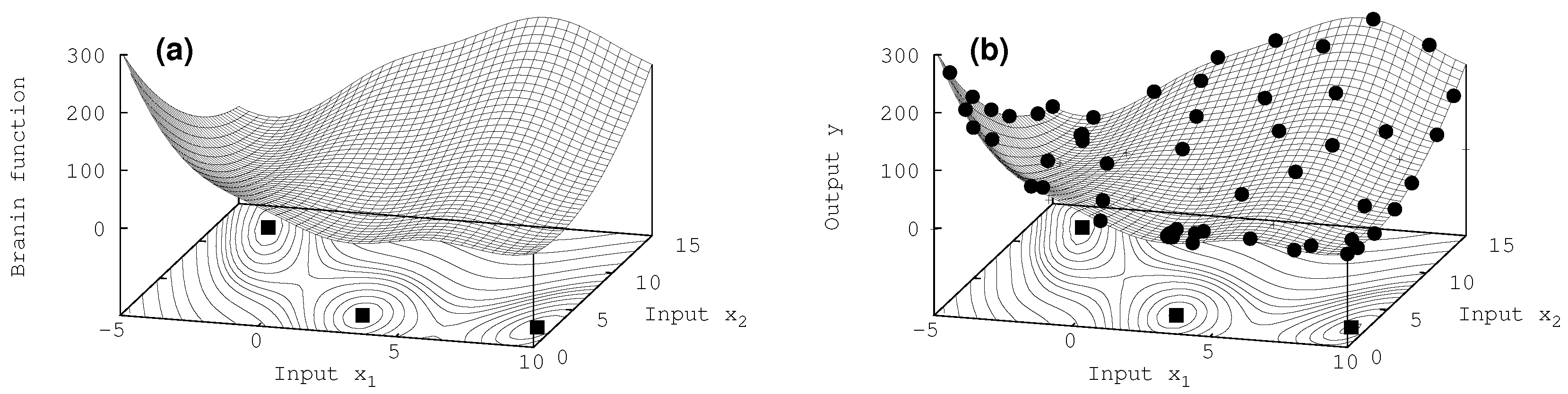
| Utility | = 0.1 | = 0.3 | = 0.6 | = 1.0 |
|---|---|---|---|---|
| 1D, = 0.01 | ||||
| EI | x = 0.54, y = 2.02 | x = 0.59, y = 2.06 | N = 17 | N = 15 |
| MV | x = 0.07, y = 2.01 | N = 58 | N = 21 | N = 13 |
| EI + MV | N = 112 | N = 20 | N = 10 | N = 15 |
| 1D, = 0.001 | ||||
| EI | x = −0.01, y = 2.06 | x = 0.68, y = 2.06 | x = 0.25, y = 2.09 | N = 6 |
| MV | x = 0.47, y = 1.99 | N = 22 | N = 11 | N = 8 |
| EI + MV | N = 9 | N = 34 | N = 10 | N = 8 |
| Annealing | N ≈ 700 | N ≈ 1100 | N ≈ 700 | N ≈ 600 |
| 2D, = 0.001 | ||||
| EI | = (0.1, 0.1), y = 2.1 | = (0.0, 0.0), y = 2.1 | = (−0.2, −0.2), y = 1.9 | = (0.3, 0.3), y = 2.2 |
| MV | = (−0.1, 0.1), y = 2.2 | = (0.4, 0.1), y = 2.2 | N = 84 | N = 70 |
| EI + MV | = (0.0, 0.0), y = 2.2 | N = 105 | N = 50 | N = 23 |
| Annealing | = (0.4, 0.5), y = 2.2 | N ≈ 1200 | N ≈ 1100 | N ≈ 800 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Preuss, R.; Von Toussaint, U. Global Optimization Employing Gaussian Process-Based Bayesian Surrogates. Entropy 2018, 20, 201. https://doi.org/10.3390/e20030201
Preuss R, Von Toussaint U. Global Optimization Employing Gaussian Process-Based Bayesian Surrogates. Entropy. 2018; 20(3):201. https://doi.org/10.3390/e20030201
Chicago/Turabian StylePreuss, Roland, and Udo Von Toussaint. 2018. "Global Optimization Employing Gaussian Process-Based Bayesian Surrogates" Entropy 20, no. 3: 201. https://doi.org/10.3390/e20030201
APA StylePreuss, R., & Von Toussaint, U. (2018). Global Optimization Employing Gaussian Process-Based Bayesian Surrogates. Entropy, 20(3), 201. https://doi.org/10.3390/e20030201





