Equilibrium States in Two-Temperature Systems
Abstract
1. Introduction
2. Generalized Forms of the H-Theorem
2.1. The H-Theorem from the Linear Fokker-Planck Equation
2.2. The H-Theorem from Nonlinear Fokker-Planck Equations
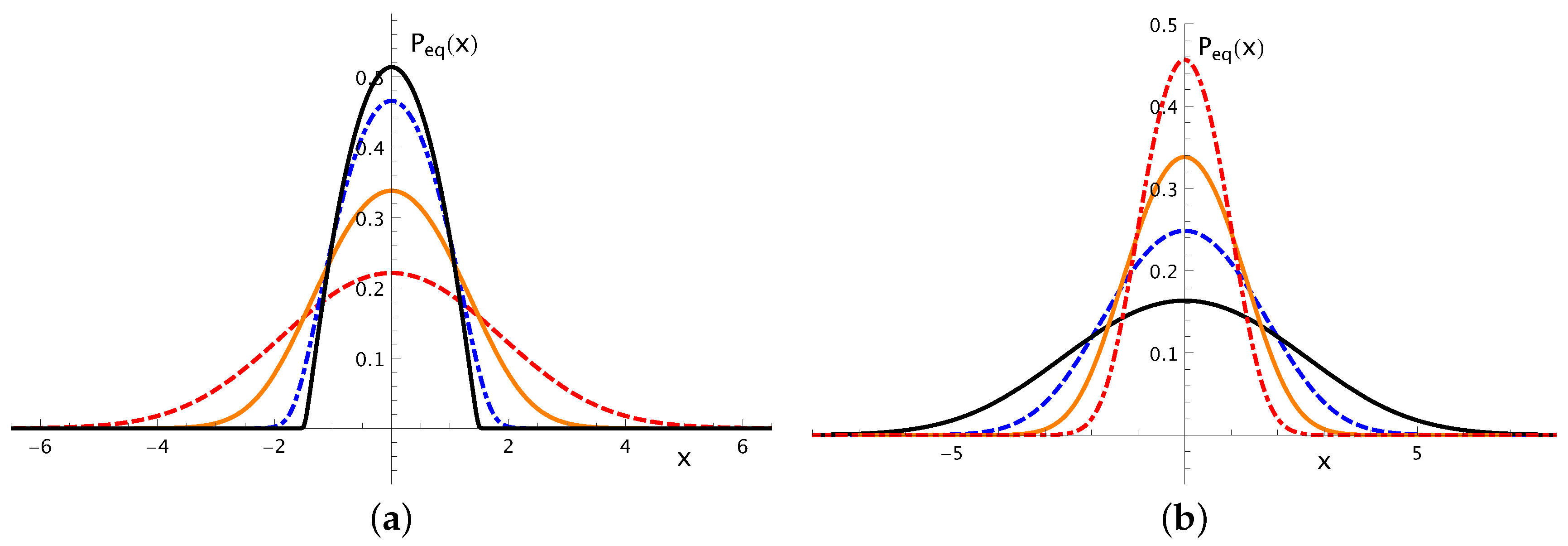
3. Equilibrium Distribution
4. Physical Application: Type-II Superconducting Vortices
5. Discussion and Conclusions
Acknowledgments
Conflicts of Interest
References
- Balian, R. From Microphysics to Macrophysics; Springer: Berlin, Germany, 1991; Volumes I and II. [Google Scholar]
- Reichl, L.E. A Modern Course in Statistical Physics, 2nd ed.; John Wiley and Sons: New York, NY, USA, 1998. [Google Scholar]
- Balakrishnan, V. Elements of Nonequilibrium Statistical Mechanics; CRC Press, Taylor and Francis Group: New York, NY, USA, 2008. [Google Scholar]
- Risken, H. The Fokker-Planck Equation, 2nd ed.; Springer: Berlin, Germany, 1989. [Google Scholar]
- Bouchaud, J.P.; Georges, A. Anomalous diffusion in disordered media: Statistical mechanisms, models and physical applications. Phys. Rep. 1990, 195, 127–293. [Google Scholar] [CrossRef]
- Vázquez, J.L. The Porous Medium Equation; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Frank, T.D. Nonlinear Fokker-Planck Equations: Fundamentals and Applications; Springer: Berlin, Germay, 2005. [Google Scholar]
- Plastino, A.R.; Plastino, A. Non-extensive statistical mechanics and generalized Fokker-Planck equation. Physica A 1995, 222, 347–354. [Google Scholar] [CrossRef]
- Tsallis, C.; Bukman, D.J. Anomalous diffusion in the presence of external forces: Exact time-dependent solutions and their thermostatistical basis. Phys. Rev. E 1996, 54, R2197–R2200. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics; Springer: New York, NY, USA, 2009. [Google Scholar]
- Tsallis, C. An introduction to nonadditive entropies and a thermostatistical approach to inanimate and living matter. Contemp. Phys. 2014, 55, 179–197. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Abe, S. A note on the q-deformation-theoretic aspect of the generalized entropies in nonextensive physics. Phys. Lett. A 1997, 224, 326–330. [Google Scholar] [CrossRef]
- Borges, E.P.; Roditi, I. A family of nonextensive entropies. Phys. Lett. A 1998, 246, 399–402. [Google Scholar] [CrossRef]
- Anteneodo, C.; Plastino, A.R. Maximum entropy approach to stretched exponential probability distributions. J. Phys. A 1999, 32, 1089–1097. [Google Scholar] [CrossRef]
- Curado, E.M.F. General Aspects of the Thermodynamical Formalism. Braz. J. Phys. 1999, 29, 36–45. [Google Scholar] [CrossRef]
- Curado, E.M.F.; Nobre, F.D. On the stability of analytic entropic forms. Physica A 2004, 335, 94–106. [Google Scholar] [CrossRef]
- Kaniadakis, G. Non-linear kinetics underlying generalized statistics. Physica A 2001, 296, 405–425. [Google Scholar] [CrossRef]
- Kaniadakis, G. Statistical mechanics in the context of special relativity. Phys. Rev. E 2002, 66, 056125. [Google Scholar] [CrossRef] [PubMed]
- Kaniadakis, G. Statistical mechanics in the context of special relativity II. Phys. Rev. E 2005, 72, 036108. [Google Scholar] [CrossRef] [PubMed]
- Hanel, R.; Thurner, S. A comprehensive classification of complex statistical systems and an axiomatic derivation of their entropy and distribution functions. Europhys. Lett. 2011, 93, 20006. [Google Scholar] [CrossRef]
- Hanel, R.; Thurner, S. When do generalized entropies apply? How phase space volume determines entropy. Europhys. Lett. 2011, 96, 50003. [Google Scholar] [CrossRef]
- Hanel, R.; Thurner, S. Generalized (c,d)-entropy and aging random walks. Entropy 2013, 15, 5324–5337. [Google Scholar] [CrossRef]
- Yamano, T. On a simple derivation of a family of nonextensive entropies from information content. Entropy 2004, 6, 364–374. [Google Scholar] [CrossRef]
- Kaniadakis, G. H-theorem and generalized entropies within the framework of nonlinear kinetics. Phys. Lett. A 2001, 288, 283–291. [Google Scholar] [CrossRef]
- Shiino, M. Free energies based on generalized entropies and H-theorems for nonlinear Fokker-Planck equations. J. Math. Phys. 2001, 42, 2540–2553. [Google Scholar] [CrossRef]
- Frank, T.D.; Daffertshofer, A. H-theorem for nonlinear Fokker-Planck equations related to generalized thermostatistics. Physica A 2001, 295, 455–474. [Google Scholar] [CrossRef]
- Frank, T.D. Generalized Fokker-Planck equations derived from generalized linear nonequilibrium thermodynamics. Physica A 2002, 310, 397–412. [Google Scholar] [CrossRef]
- Shiino, M. Stability analysis of mean-field-type nonlinear Fokker-Planck equations associated with a generalized entropy and its application to the self-gravitating system. Phys. Rev. E 2003, 67, 056118. [Google Scholar] [CrossRef] [PubMed]
- Chavanis, P.-H. Generalized thermodynamics and Fokker-Planck equations: Applications to stellar dynamics and two-dimensional turbulence. Phys. Rev. E 2003, 68, 036108. [Google Scholar] [CrossRef] [PubMed]
- Chavanis, P.-H. Generalized Fokker-Planck equations and effective thermodynamics. Physica A 2004, 340, 57–65. [Google Scholar] [CrossRef]
- Schwämmle, V.; Nobre, F.D.; Curado, E.M.F. Consequences of the H theorem from nonlinear Fokker-Planck equations. Phys. Rev. E 2007, 76, 041123. [Google Scholar] [CrossRef] [PubMed]
- Schwämmle, V.; Curado, E.M.F.; Nobre, F.D. A general nonlinear Fokker-Planck equation and its associated entropy. Eur. Phys. J. B 2007, 58, 159–165. [Google Scholar] [CrossRef]
- Chavanis, P.-H. Nonlinear mean field Fokker-Planck equations. Application to the chemotaxis of biological population. Eur. Phys. J. B 2008, 62, 179–208. [Google Scholar] [CrossRef]
- Schwämmle, V.; Curado, E.M.F.; Nobre, F.D. Dynamics of normal and anomalous diffusion in nonlinear Fokker-Planck equations. Eur. Phys. J. B 2009, 70, 107–116. [Google Scholar] [CrossRef]
- Shiino, M. Nonlinear Fokker-Planck equations associated with generalized entropies: Dynamical characterization and stability analyses. J. Phys. Conf. Ser. 2010, 201, 012004. [Google Scholar] [CrossRef]
- Ribeiro, M.S.; Nobre, F.D.; Curado, E.M.F. Classes of N-Dimensional Nonlinear Fokker-Planck Equations Associated to Tsallis Entropy. Entropy 2011, 13, 1928–1944. [Google Scholar] [CrossRef]
- Andrade, J.S., Jr.; da Silva, G.F.T.; Moreira, A.A.; Nobre, F.D.; Curado, E.M.F. Thermostatistics of overdamped motion of interacting particles. Phys. Rev. Lett. 2010, 105, 260601. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, M.S.; Nobre, F.D.; Curado, E.M.F. Time evolution of interacting vortices under overdamped motion. Phys. Rev. E 2012, 85, 021146. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, M.S.; Nobre, F.D.; Curado, E.M.F. Overdamped motion of interacting particles in general confining potentials: time-dependent and stationary-state analyses. Eur. Phys. J. B 2012, 85, 399. [Google Scholar] [CrossRef]
- Nobre, F.D.; Souza, A.M.C.; Curado, E.M.F. Effective-temperature concept: A physical application for nonextensive statistical mechanics. Phys. Rev. E 2012, 86, 061113. [Google Scholar] [CrossRef] [PubMed]
- Curado, E.M.F.; Souza, A.M.C.; Nobre, F.D.; Andrade, R.F.S. Carnot cycle for interacting particles in the absence of thermal noise. Phys. Rev. E 2014, 89, 022117. [Google Scholar] [CrossRef] [PubMed]
- Nobre, F.D.; Curado, E.M.F.; Souza, A.M.C.; Andrade, R.F.S. Consistent thermodynamic framework for interacting particles by neglecting thermal noise. Phys. Rev. E 2015, 91, 022135. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, M.S.; Casas, G.A.; Nobre, F.D. Second law and entropy production in a nonextensive system. Phys. Rev. E 2015, 91, 012140. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, M.S.; Nobre, F.D.; Curado, E.M.F. Comment on “Vortex distribution in a confining potential”. Phys. Rev. E 2014, 90, 026101. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, M.S.; Casas, G.A.; Nobre, F.D. Multi-diffusive nonlinear Fokker-Planck equation. J. Phys. A 2017, 50, 065001. [Google Scholar] [CrossRef]
- Souza, A.M.C.; Andrade, R.F.S.; Nobre, F.D.; Curado, E.M.F. Thermodynamic framework for compact q-Gaussian distributions. Physica A 2018, 491, 153–166. [Google Scholar] [CrossRef]
- Malacarne, L.C.; Mendes, R.S.; Pedron, I.T.; Lenzi, E.K. Nonlinear equation for anomalous diffusion: Unified power-law and stretched exponential exact solution. Phys. Rev. E 2001, 63, 030101. [Google Scholar] [CrossRef] [PubMed]
- Malacarne, L.C.; Mendes, R.S.; Pedron, I.T.; Lenzi, E.K. N-dimensional nonlinear Fokker-Planck equation with time-dependent coefficients. Phys. Rev. E 2002, 65, 052101. [Google Scholar] [CrossRef] [PubMed]
- Da Silva, L.R.; Lucena, L.S.; da Silva, P.C.; Lenzi, E.K.; Mendes, R.S. Multidimensional nonlinear diffusion equation: Spatial time dependent diffusion coefficient and external forces. Physica A 2005, 357, 103–108. [Google Scholar] [CrossRef]
- Nobre, F.D.; Curado, E.M.F.; Rowlands, G. A procedure for obtaining general nonlinear Fokker-Planck equations. Physica A 2004, 334, 109–118. [Google Scholar] [CrossRef]
- Curado, E.M.F.; Nobre, F.D. Derivation of nonlinear Fokker-Planck equations by means of approximations to the master equation. Phys. Rev. E 2003, 67, 021107. [Google Scholar] [CrossRef] [PubMed]
- Boon, J.P.; Lutsko, J.F. Nonlinear diffusion from Einstein’s master equation. Europhys. Lett. 2007, 80, 60006. [Google Scholar] [CrossRef][Green Version]
- Lutsko, J.F.; Boon, J.P. Generalized diffusion: A microscopic approach. Phys. Rev. E 2008, 77, 051103. [Google Scholar] [CrossRef] [PubMed]
- Zand, J.; Tirnakli, U.; Jensen, H.J. On the relevance of q-distribution functions: The return time distribution of restricted random walker. J. Phys. A 2015, 48, 425004. [Google Scholar] [CrossRef]
- Borland, L. Microscopic dynamics of the nonlinear Fokker-Planck equation: A phenomenological model. Phys. Rev. E 1998, 57, 6634–6642. [Google Scholar] [CrossRef]
- Borland, L. Ito-Langevin equations within generalized thermostatistics. Phys. Lett. A 1998, 245, 67–72. [Google Scholar] [CrossRef]
- Beck, C. Dynamical Foundations of Nonextensive Statistical Mechanics. Phys. Rev. Lett. 2001, 87, 180601. [Google Scholar] [CrossRef]
- Anteneodo, C.; Tsallis, C. Multiplicative noise: A mechanism leading to nonextensive statistical mechanics. J. Math. Phys. 2003, 44, 5194–5203. [Google Scholar] [CrossRef]
- Fuentes, M.A.; Cáceres, M.O. Computing the non-linear anomalous diffusion equation from first principles. Phys. Lett. A 2008, 372, 1236–1239. [Google Scholar] [CrossRef]
- Dos Santos, B.C.; Tsallis, C. Time evolution towards q-Gaussian stationary states through unified Itô-Stratonovich stochastic equation. Phys. Rev. E 2010, 82, 061119. [Google Scholar] [CrossRef] [PubMed]
- Casas, G.A.; Nobre, F.D.; Curado, E.M.F. Entropy production and nonlinear Fokker-Planck equations. Phys. Rev. E 2012, 86, 061136. [Google Scholar] [CrossRef] [PubMed]
- Arenas, Z.G.; Barci, D.G.; Tsallis, C. Nonlinear inhomogeneous Fokker-Planck equation within a generalized Stratonovich prescription. Phys. Rev. E 2014, 90, 032118. [Google Scholar] [CrossRef] [PubMed]
- Bianucci, M. Large Scale Emerging Properties from Non Hamiltonian Complex Systems. Entropy 2017, 19, 302. [Google Scholar] [CrossRef]
- Zapperi, S.; Moreira, A.A.; Andrade, J.S., Jr. Thermostatistics of overdamped motion of interacting particles. Phys. Rev. Lett. 2001, 87, 180601. [Google Scholar]
- Lenzi, E.K.; Mendes, R.S.; Tsallis, C. Crossover in diffusion equation: Anomalous and normal behaviors. Phys. Rev. E 2003, 67, 031104. [Google Scholar] [CrossRef] [PubMed]
- Andrade, R.F.S.; Souza, A.M.C.; Curado, E.M.F.; Nobre, F.D. A thermodynamical formalism describing mechanical interactions. Europhys. Lett. 2014, 108, 20001. [Google Scholar] [CrossRef]
- Ribeiro, M.S.; Nobre, F.D. Repulsive particles under a general external potential: Thermodynamics by neglecting thermal noise. Phys. Rev. E 2016, 94, 022120. [Google Scholar] [CrossRef] [PubMed]
- Khinchin, A.I. Mathematical Foundations of Information Theory; Dover Publications: New York, NY, USA, 1957. [Google Scholar]
- Valluri, S.R.; Gil, M.; Jeffrey, D.J.; Basu, S. The Lambert W function and quantum statistics. J. Math. Phys. 2009, 50, 102103. [Google Scholar] [CrossRef]
- Vieira, C.M.; Carmona, H.A.; Andrade, J.S., Jr.; Moreira, A.A. General continuum approach for dissipative systems of repulsive particles. Phys. Rev. E 2016, 93, 060103. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Curado, E.M.F.; Nobre, F.D. Equilibrium States in Two-Temperature Systems. Entropy 2018, 20, 183. https://doi.org/10.3390/e20030183
Curado EMF, Nobre FD. Equilibrium States in Two-Temperature Systems. Entropy. 2018; 20(3):183. https://doi.org/10.3390/e20030183
Chicago/Turabian StyleCurado, Evaldo M. F., and Fernando D. Nobre. 2018. "Equilibrium States in Two-Temperature Systems" Entropy 20, no. 3: 183. https://doi.org/10.3390/e20030183
APA StyleCurado, E. M. F., & Nobre, F. D. (2018). Equilibrium States in Two-Temperature Systems. Entropy, 20(3), 183. https://doi.org/10.3390/e20030183




