Quantifying Chaos by Various Computational Methods. Part 1: Simple Systems
Abstract
1. Introduction
2. Lyapunov Exponents
2.1. The Largest Lyapunov Exponent
2.2. Results
- (1)
- n = 1. In this case only a stable fixed point can be an attractor (node or focus). There exists one negative LE denoted by
- (2)
- n = 2. In 2D systems, there are two types of attractors: stable fixed points and limit cycles. The corresponding LEs follow:
- —stable fixed/fixed point;
- —stable limit cycle (one exponent is equal to zero).
- (3)
- n = 3. In 3D phase space, there exist four types of attractors: stable points, limit cycles, 2D tori and strange attractors. The following set of LEs characterizes possible dynamical situations to be met:
- —stable fixed point;
- —stable limit cycle;
- —stable 2D tori;
- —strange attractor.
3. Methods of Analysis of Lyapunov Exponents
3.1. Benettin Method
3.2. Wolf Method
3.3. Rosenstein Method
3.4. Kantz Method
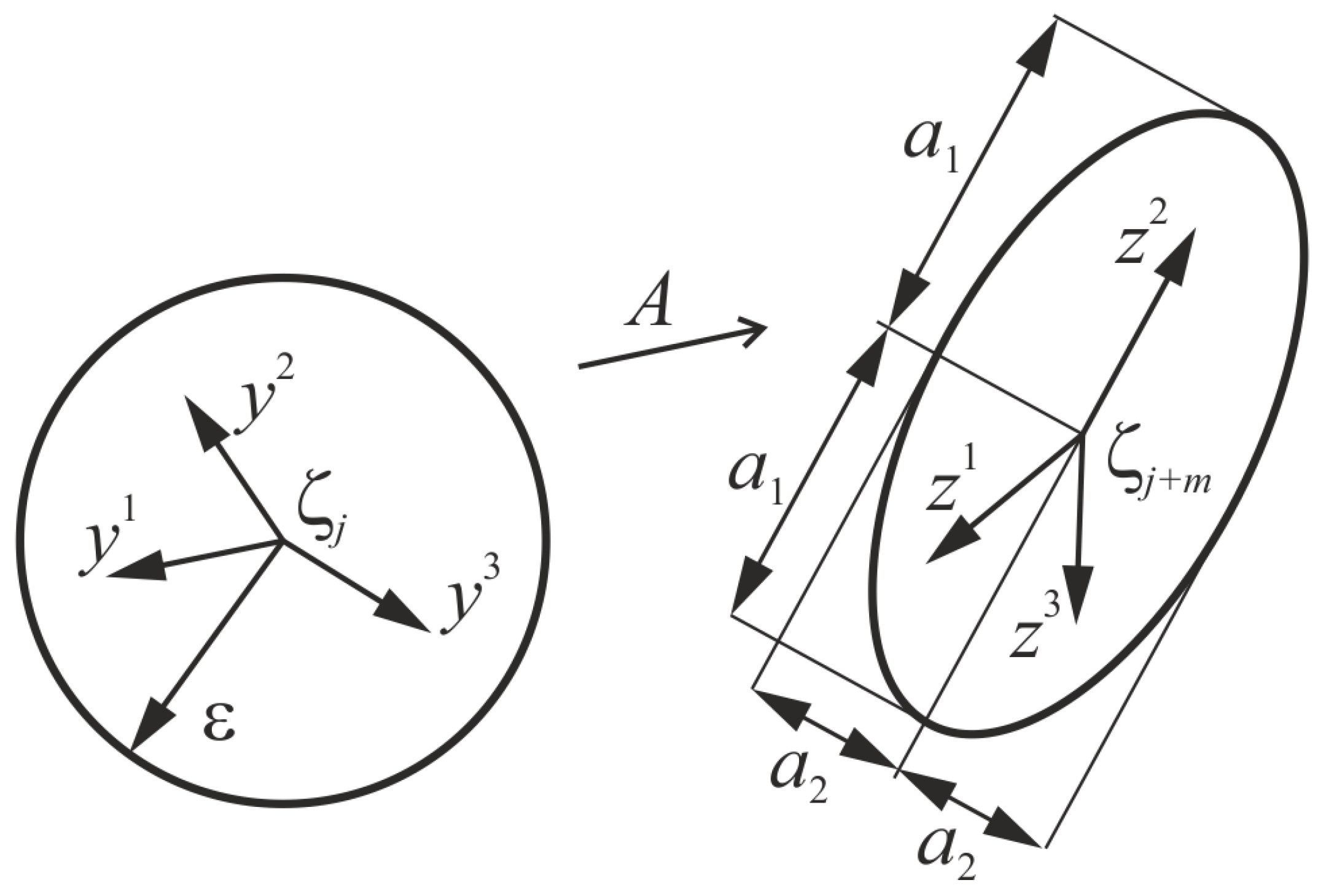
3.5. Computation of LLE Based on Synchronization of Nonnegative Feedback
3.6. Jacobi Method
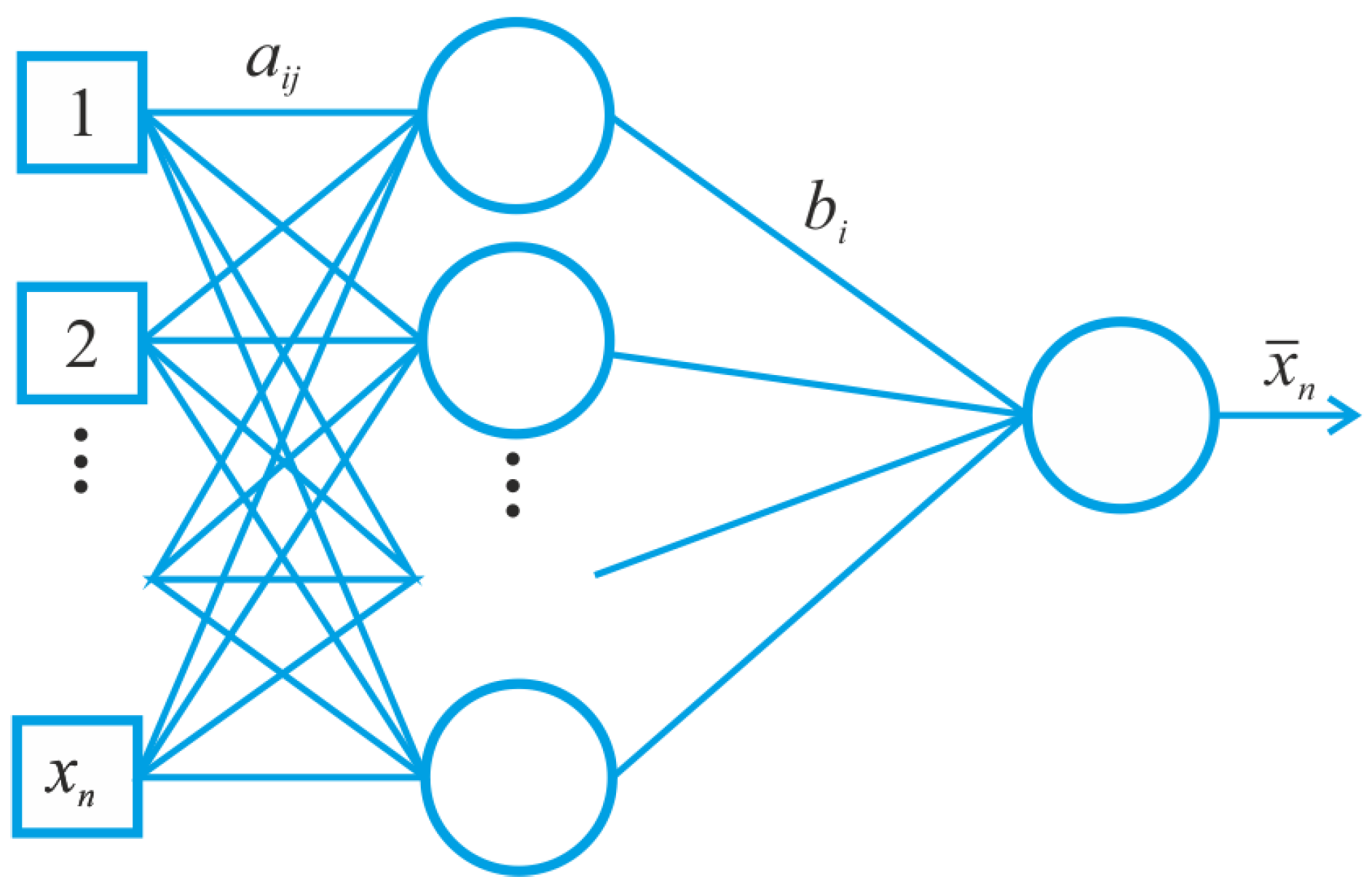
3.7. Modification of the Neural Network Method
- (i)
- the network is sensitive to the input information (information is given in the form of real numbers);
- (ii)
- the network is self-organizing, i.e., it yields the output space of solutions only based on the inputs;
- (iii)
- the neural network is a network of straight distribution (all connections are directed from input neurons to output neurons);
- (iv)
- owing to the synapses tuning, the network exhibits dynamic couplings (in the learning process, the tuning of the synaptic coupling takes place where W stands for the weighted coefficients of the network).
4. Wavelet Methods
Gauss Wavelets
5. Analysis of Classical Dynamical Systems by LEs and Gauss Wavelets
5.1. Logistic Map
 —only negative Lyapunov exponents,
—only negative Lyapunov exponents,  —one positive exponent,
—one positive exponent,  —two positive exponents,
—two positive exponents,  —three positive exponents).
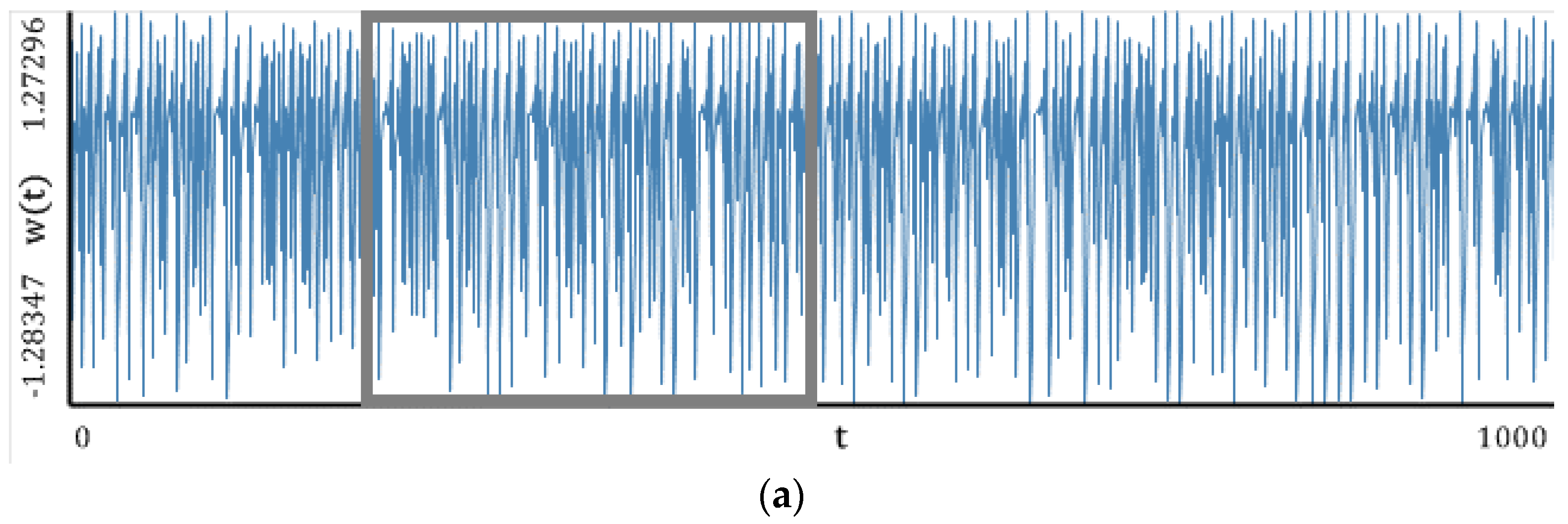
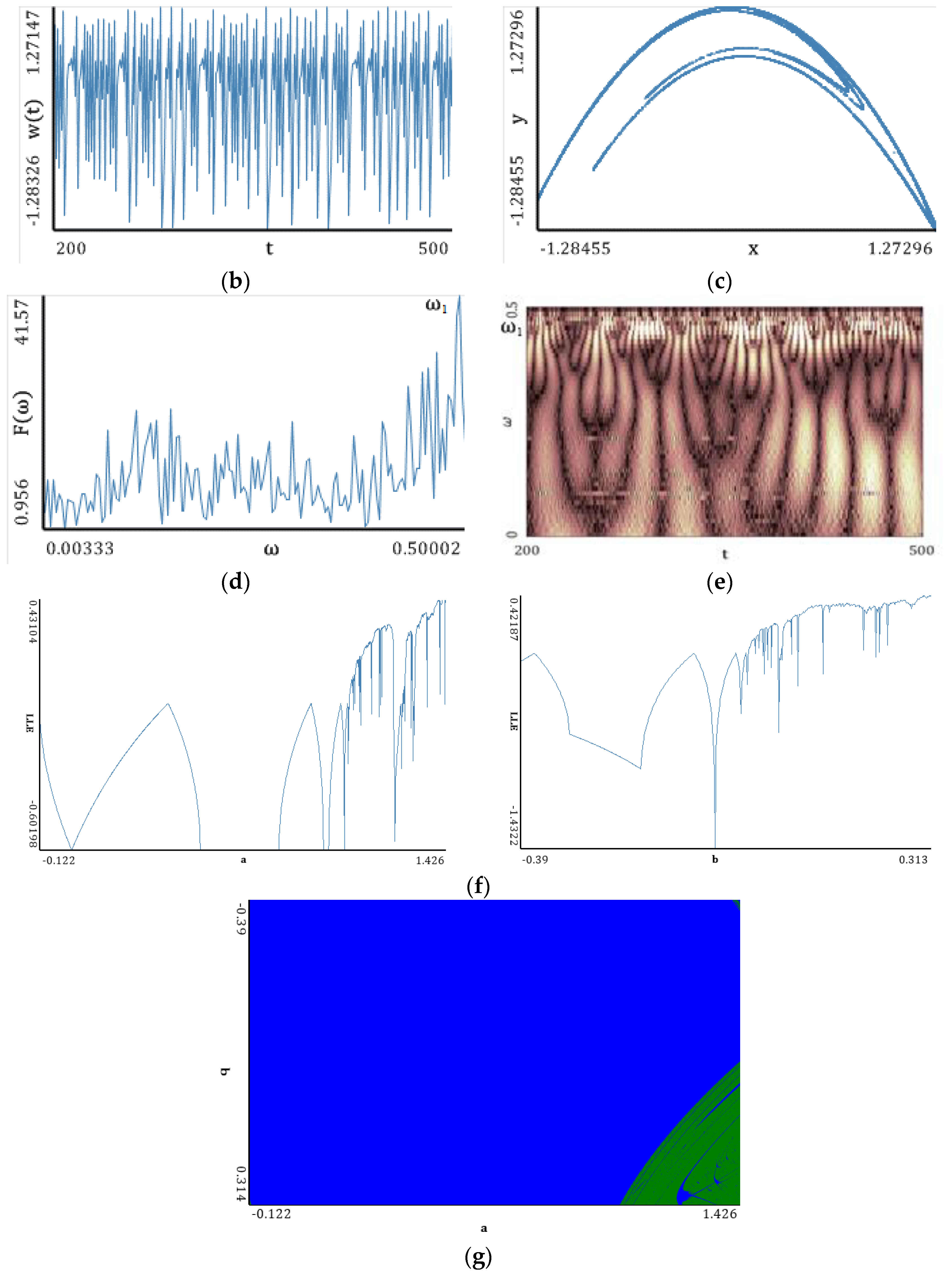
—three positive exponents).5.2. Hénon Map
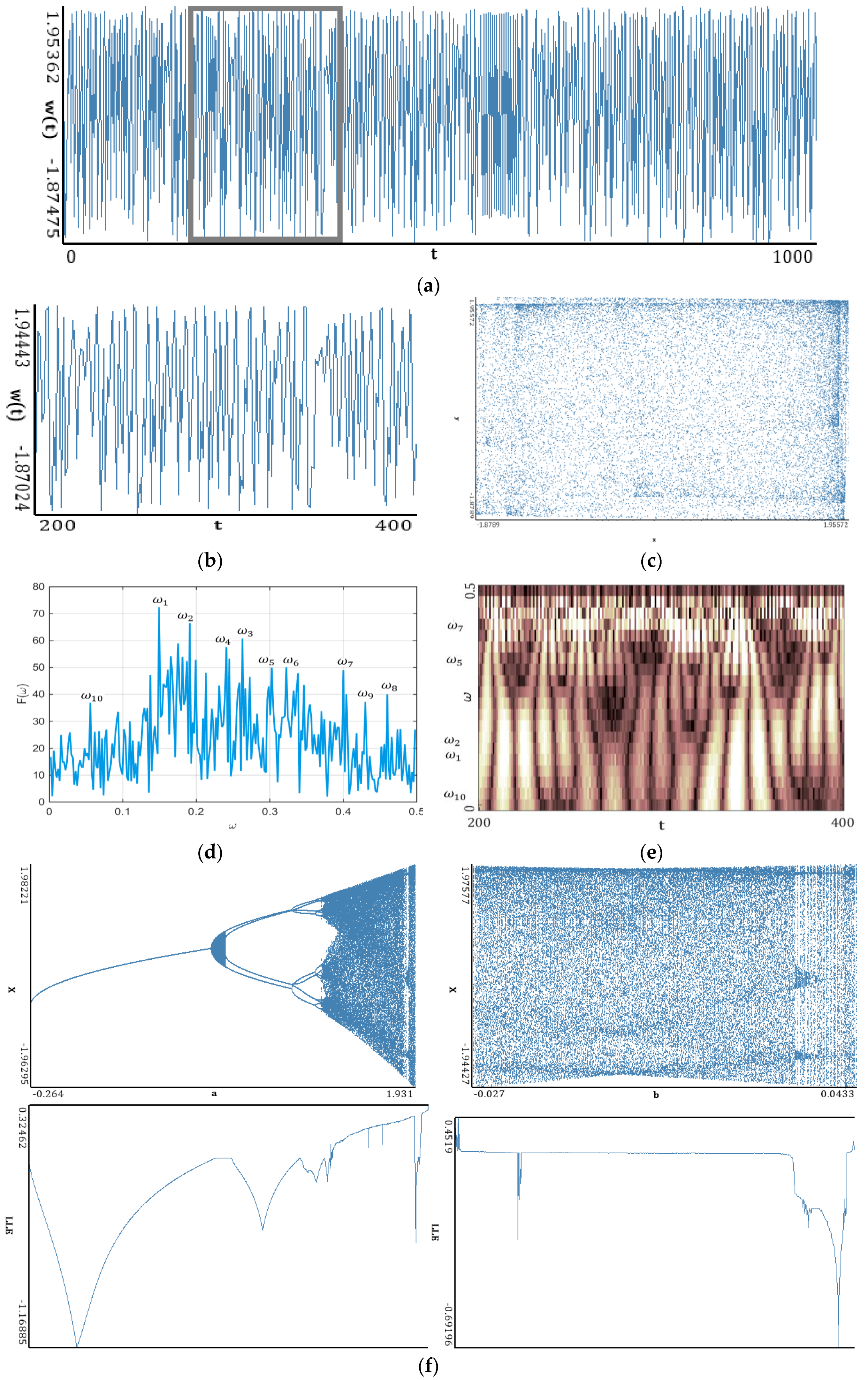
5.3. Hyperchaotic Generalised Hénon Map
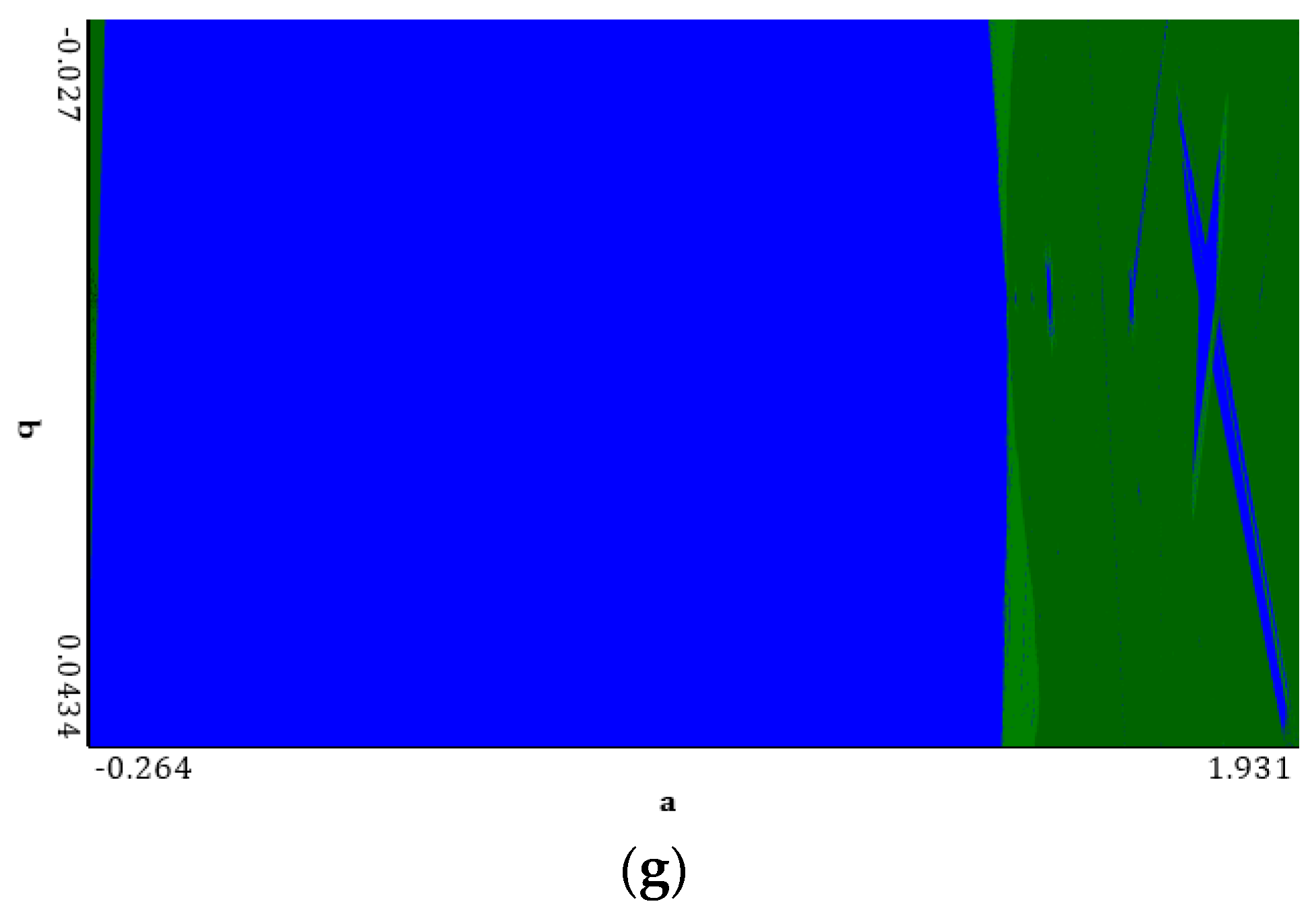
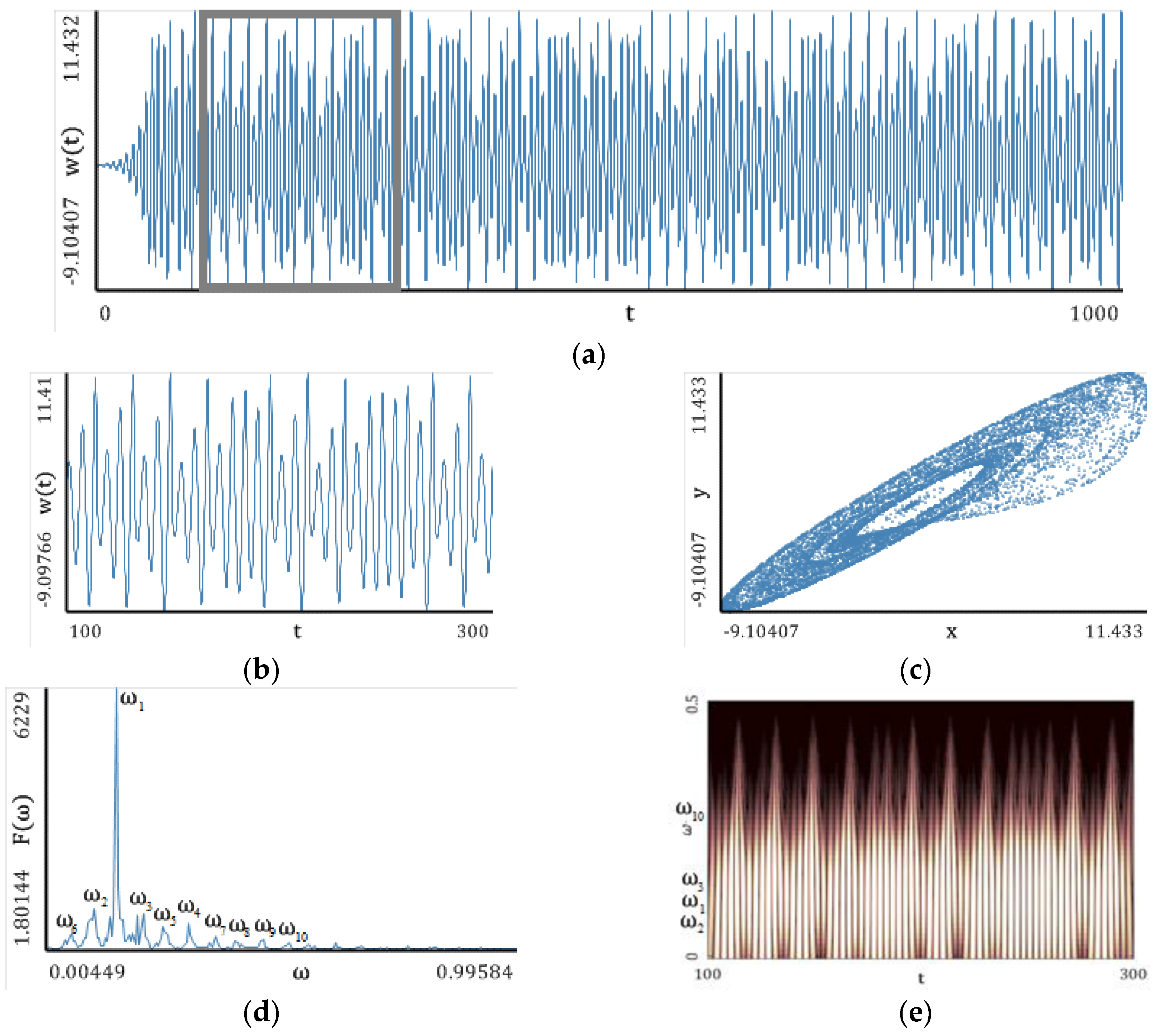
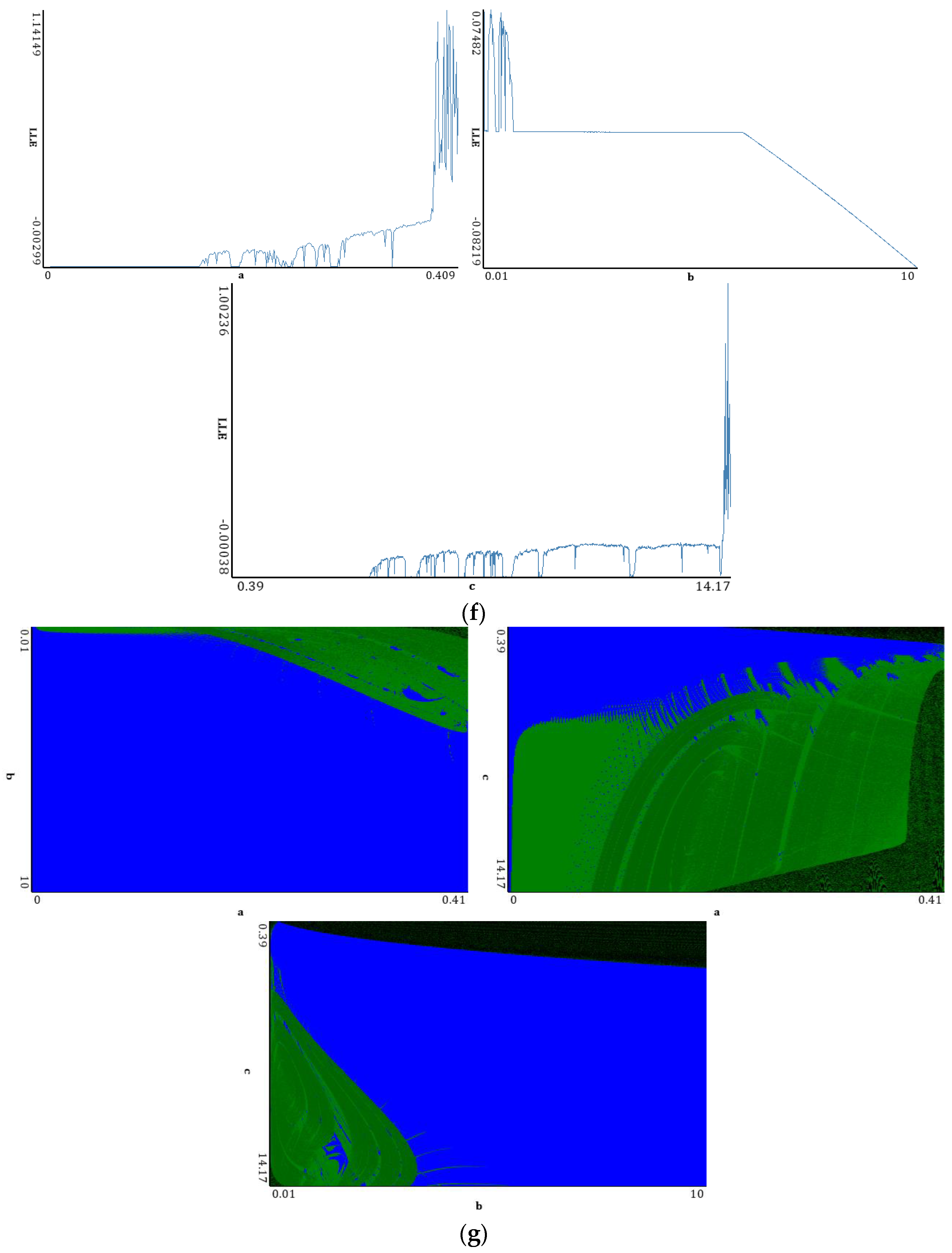
5.4. Rössler Attractor
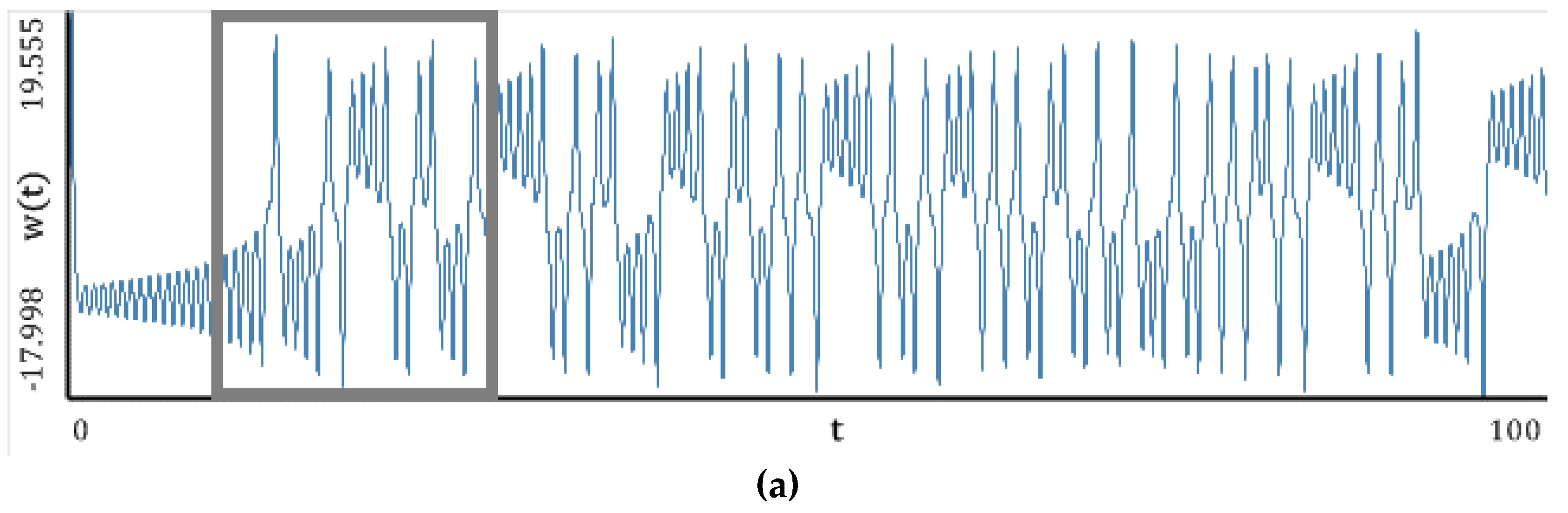
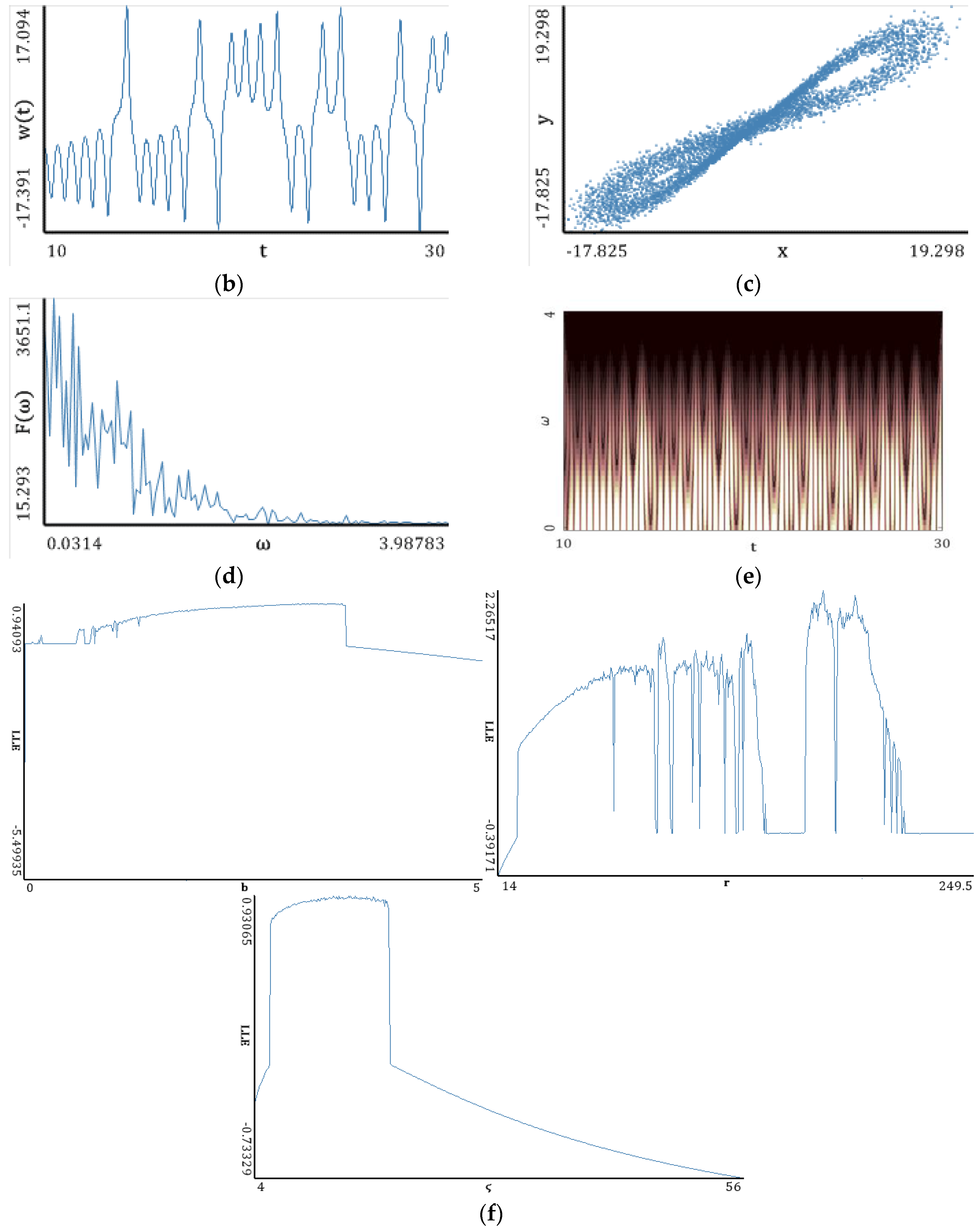
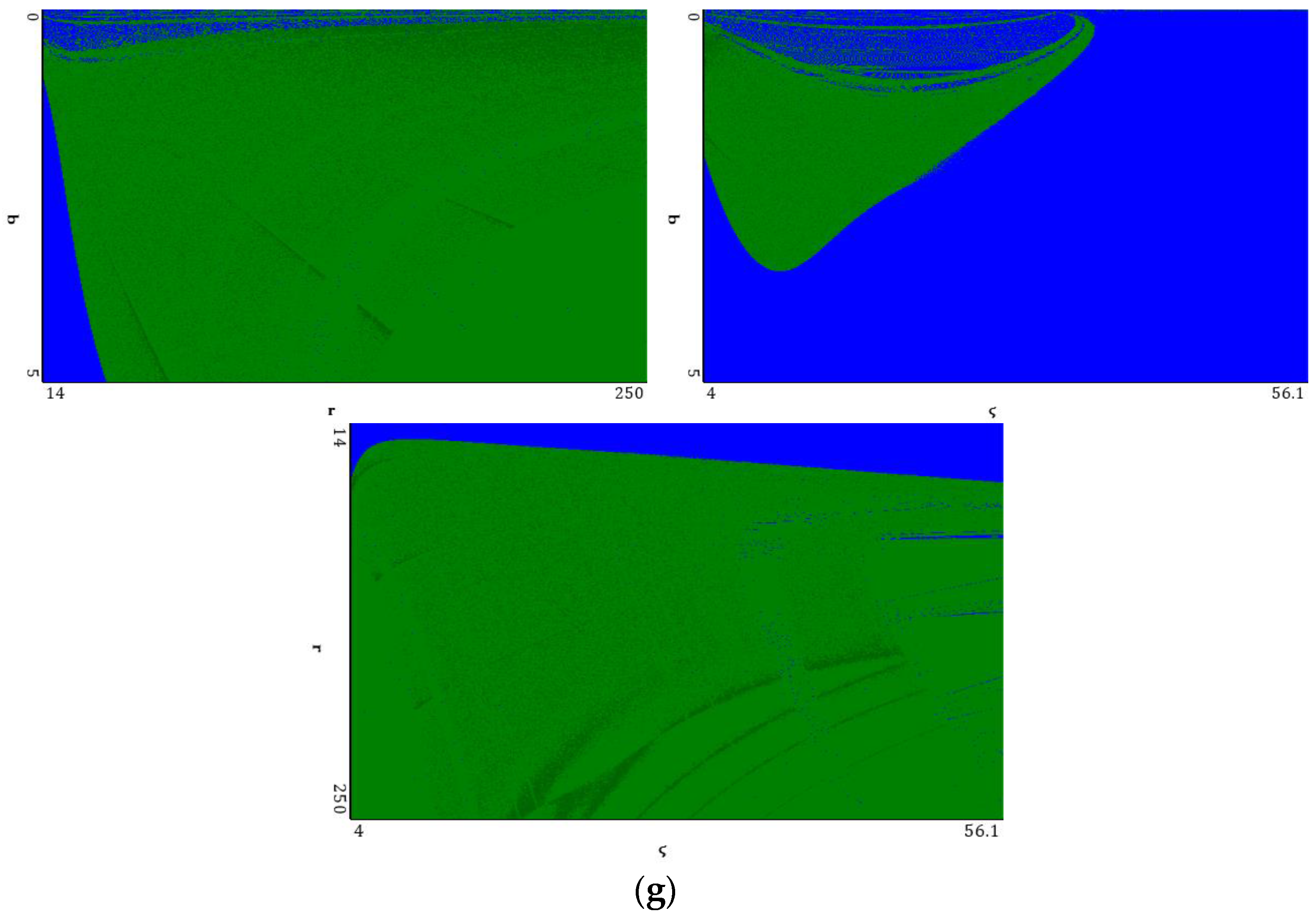
5.5. Lorenz Attractor
6. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Oseledec, V.I. A multiplicative ergodic theorem. Trans. Mosc. Math. Soc. 1968, 19, 197–231. [Google Scholar]
- Pesin, Y.B. Characteristic Lyapunov exponents and ergodic properties of smooth dynamical systems with invariant measure. Dokl. Akad. Nauk SSSR 1976, 226, 774–777. [Google Scholar]
- Rosenstein, M.T.; Collins, J.J.; de Luca, C.J. A practical method for calculating largest Lyapunov exponents from small data sets. Phys. D Nonlinear Phenom. 1993, 65, 117–134. [Google Scholar] [CrossRef]
- Kantz, H. A robust method to estimate the maximal Lyapunov exponent of a time series. Phys. Lett. A 1994, 185, 77–87. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Krysko, V.A.; Papkova, I.V.; Krysko, A.V. Deterministic Chaos in One-Dimentional Continuous Systems; World Scientific: Singapore, 2016. [Google Scholar]
- Stefański, A. Estimation of the largest Lyapunov exponent in systems with impacts. Chaos Solition Fractals 2000, 11, 2443–2451. [Google Scholar] [CrossRef]
- Stefański, A.; Kapitaniak, T. Estimation of the dominant Lyapunov exponent of non-smooth systems on the basis of maps synchronization. Chaos Solition Fractals 2003, 15, 233–244. [Google Scholar] [CrossRef]
- Dobriyan, V.; Awrejcewicz, J.; Krysko, V.A.; Papkova, I.V.; Krysko, V.A. On the Lyapunov exponents computation of coupled non-linear Euler-Bernoulli beams. In Proceedings of the Fourteenth International Conference on Civil, Structural and Environmental Engineering Computing, Cagliari, Italy, 3–6 September 2013; Civil-Comp Press: Stirlingshire, UK, 2013; p. 53. [Google Scholar]
- Krysko, A.V.; Awrejcewicz, J.; Kutepov, I.E.; Zagniboroda, N.A.; Dobriyan, V.; Krysko, V.A. Chaotic dynamics of flexible Euler-Bernoulli beams. Chaos 2014, 34, 043130. [Google Scholar]
- Vallejo, J.C.; Sanjuan, M.A.F. Predictability of orbits in coupled systems through finite-time Lyapunov exponents. New J. Phys. 2013, 15, 113064. [Google Scholar] [CrossRef]
- Vallejo, J.C.; Sanjuan, M.A.F. Predictability of Chaotic Dynamics. A Finite-Time Lyapunov Exponents Approach; Springer: Berlin, Germany, 2017. [Google Scholar]
- Hénon, M. A two-dimensional mapping with a strange attractor. Commun. Math. Phys. 1976, 50, 69–77. [Google Scholar] [CrossRef]
- Baier, G.; Klein, M. Maximum hyperchaos in generalized Henon maps. Phys. Lett. A 1990, 151, 281–284. [Google Scholar] [CrossRef]
- May, R. Simple mathematical model with very complicated dynamics. Nature 1976, 261, 45–67. [Google Scholar] [CrossRef]
- Peitgen, H.-O.; Jürgens, H.; Saupe, D. The Rössler Attractor. In Chaos and Fractals: New Frontiers of Science; Springer: Berlin, Germany, 2004; pp. 636–646. [Google Scholar]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Astafeva, N.M. Wavelet-analysis: Basic theory and examples of applications. Adv. Phys. Sci. 1996, 166, 1145–1170. [Google Scholar]
- Awrejcewicz, J.; Kudra, G.; Wasilewski, G. Experimental and numerical investigation of chaotic regions in the triple physical pendulum. Nonlinear Dyn. 2007, 50, 755–766. [Google Scholar] [CrossRef]
- Dmitriev, A.S.; Kislov, V. Stochastic Oscillations in Radiophysics and Electronics; Nauka: Moscow, Russia, 1989. [Google Scholar]
- Awrejcewicz, J.; Krysko, A.V.; Papkova, I.V. Routes to chaos in continuous mechanical systems. Part 3: The Lyapunov exponents, hyper, hyper-hyper and spatial–temporal chaos. Chaos Solition Fractals 2012, 45, 721–736. [Google Scholar] [CrossRef]
- Devaney, R.L. An Introduction to Chaotic Dynamical Systems; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Banks, J.; Brooks, J.; Davis, G.; Stacey, P. On Devaney’s definition of chaos. Am. Math. Mon. 1992, 99, 332–334. [Google Scholar] [CrossRef]
- Knudsen, C. Chaos without periodicity. Am. Math. Mon. 1994, 101, 563–565. [Google Scholar] [CrossRef]
- Gulick, D. Encounters with Chaos; McGraw-Hill: New York, NY, USA, 1992. [Google Scholar]
- Awrejcewicz, J.; Krylova, E.U.; Papkova, I.V.; Krysko, V.A. Wavelet-based analysis of the regular and chaotic dynamics of rectangular flexible plates subjected to shear-harmonic loading. Shock Vib. 2012, 19, 979–994. [Google Scholar] [CrossRef][Green Version]
- Benettin, G.; Galgani, L.; Strelcyn, J.M. Kolmogorov entropy and numerical experiments. Phys. Rev. A 1976, 14, 2338–2345. [Google Scholar] [CrossRef]
- Mackey, M.C.; Glass, L. Oscillation and chaos in physiological control systems. Science 1977, 197, 287–289. [Google Scholar] [CrossRef] [PubMed]
- Hudson, J.L.; Mankin, J.C. Chaos in the Belousov-Zhabotinskii reaction. J. Chem. Phys. 1981, 74, 6171. [Google Scholar] [CrossRef]
- Taylor, G.I. Stability of a viscous liquid contained between two rotating cylinders. Philos. Trans. R. Soc. Lond. A 1923, 223, 289–343. [Google Scholar] [CrossRef]
- Sato, S.; Sano, M.; Sawada, Y. Practical methods of measuring the generalized dimension and the largest Lyapunov exponent in high dimensional chaotic systems. Prog. Theor. Phys. 1987, 77, 1–7. [Google Scholar] [CrossRef]
- Eckmann, J.-P.; Ruelle, D. Ergodic theory of chaos and strange attractors. Rev. Mod. Phys. 1985, 57, 617–656. [Google Scholar] [CrossRef]
- Sprott, J.C. Chaos and Time Series Analysis; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Sprott, J.C. Elegant Chaos. Algebraically Simple Chaotic Flows; World Scientific: Singapore, 2010. [Google Scholar]
- Amabili, M.; Sarkar, A.; Païdoussis, M.P. Chaotic vibrations of circular cylindrical shells: Galerkin versus reduced-order models via the proper orthogonal decomposition method. J. Sound Vib. 2006, 290, 736–762. [Google Scholar] [CrossRef]
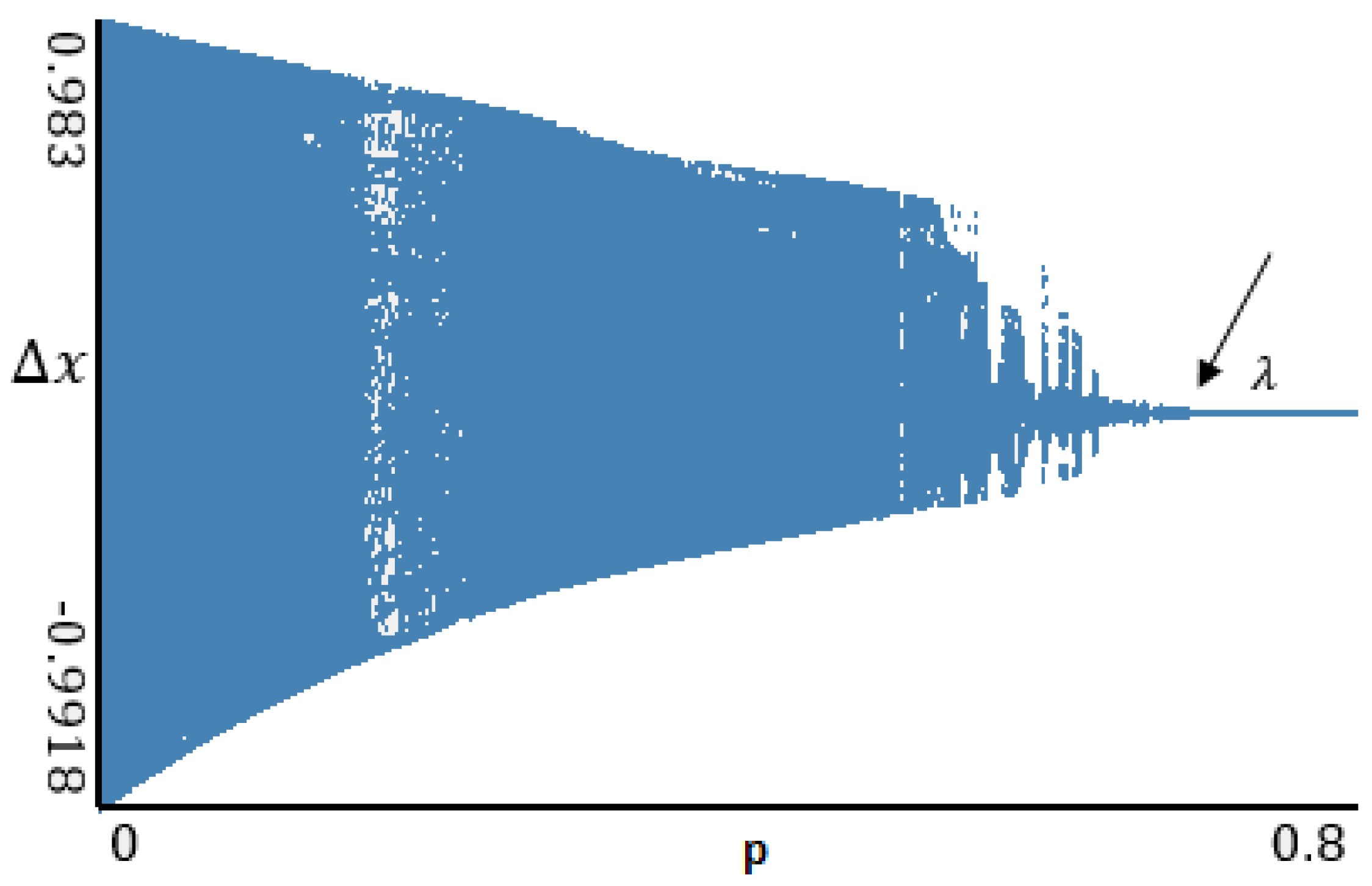
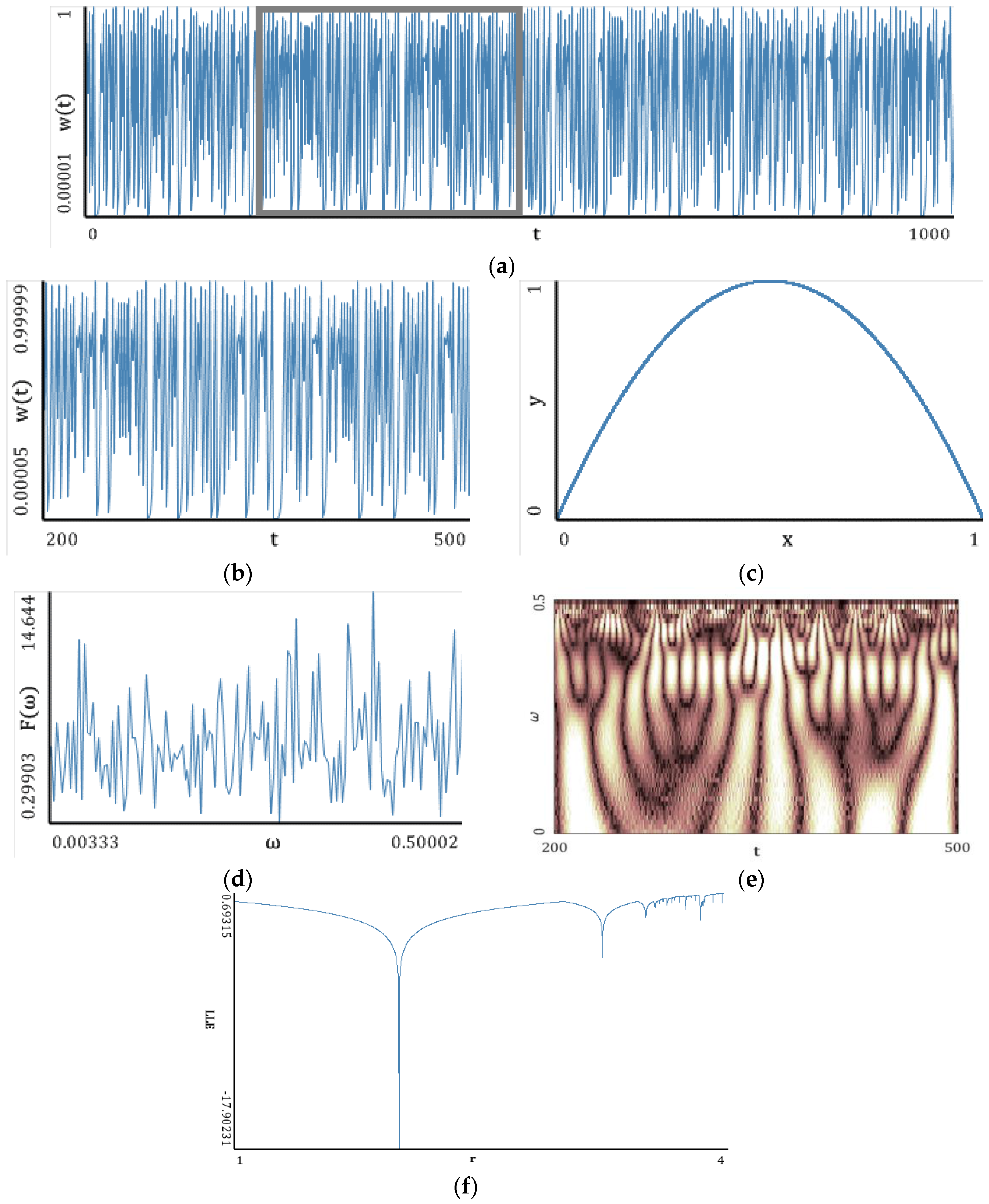
| LE Spectrum | |||
| Benettin Method | Neural Network | ||
| (LEs): 0.69315 Dimension Kaplan–Yorke (DKY): 1 Kolmogorov-Sinai entropy (KSE): 0.69315 Phase volume compression (PVC): 0.69315 | LEs: 0.69290 DKY: 1 EKS: 0.69290 PVC: 0.69290 | ||
| LLE | |||
| Wolf Method | Rosenstein Method | Kantz Method | Method of Synchronization |
| LLE: 0.99683 | LLE: 0.690553 | LLE: 0.69810 | LLE: 0.696 |
| Spectrum of LLEs | |||
| Benettin Method | Neural Network | ||
| LEs: 0.41919; −1.62316 DKY: 1.25826 EKS: 0.41919 PVC: −1.20397 | LEs: 0.41919; −1.62316 DKY: 1.25826 EKS: 0.41919 PVC: −1.20397 | ||
| LLEs | |||
| Wolf Method | Rosenstein Method | Kantz Method | Synchronization Method |
| LLE: 0.38788 | LLE: 0.414218 | LLE: 0.41912 | LLE: 0.40608 |
| Spectrum of LEs | |||
| Benettin Method | Neural Network | ||
| LEs: 0.27628; 0.25770; −4.04053 DKY: 2.13215 EKS: 0.53397 PVC: −3.50656 | LEs: 0.29251; 0.27104; −4.04583 DKY: 2.13929 EKS: 0.56355 PVC: −3.48227 | ||
| LLEs | |||
| Wolf Method | Rosenstein Method | Kantz Method | Synchronization Method |
| LLE: 0.45214 | LLE: 0.27930 | LLE: 0.26601 | 0.27250 |
| Spectrum of LEs | ||
| Benettin Method | Neural Network | |
| LE: 0.07135; 0.00000; −5.39420 DKY: 2.01323 KSE: 0.07135 PVC: −5.32285 | LE: 0.07593; −0.00060; −0.78178 DKY: 2.09635 EKS: 0.07593 PVC: −0.70646 | |
| LLEs | ||
| Wolf Method | Rosenstein Method | Kantz Method |
| LLE: 0.05855 | LLE: 0.0726 | LLE: 0.0774 |
| Spectrum of LEs | ||
| Benettin Method | Neural Network Method | |
| LE: 0.90557; 0.00000; −14.57214 DKY: 2.06214 EKS: 0.90557 PVC: −13.66656 | LE: 0.9490; 0.0610; −13.9101 DKY: 2.07261 EKS: 1.0101 PVC: −12.9000 | |
| LLEs | ||
| Wolf Method | Rosenstein Methhod | Kantz Method |
| LLE: 0.81704 | LLE: 0.836 | LLE: 0.807185 |
| Fourier Power Spectra (a) | |
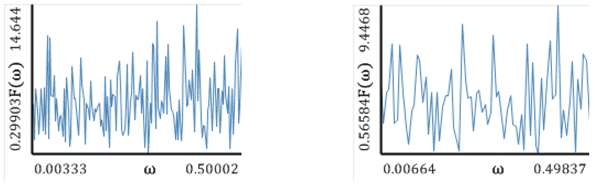 | |
| Gauss Wavelet Spectra (b) | |
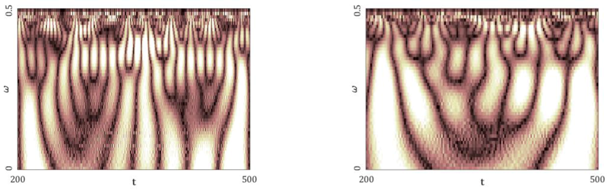 | |
| LLE (Wolf) | |
| 0.99961 | 1.00014 |
| LLE (Rosenstein) | |
| 0.69231 | 0.69065 |
| LLE (Kantz) | |
| 0.6981 | 0.69005 |
| LLE (Synchronization) | |
| 0.69400 | 0.69330 |
| LEs (Benettin) | |
| LES: 0.69318 DKY: 1.00000 KSE: 0.69318 PVC: 0.69318 | LES: 0.69400 DKY: 1.00000 KSE: 0.69400 PVC: 0.69400 |
| LEs (Neural Network) | |
| LES: 0.69290 DKY: 1 SE: 0.69290 PVC: 0.69290 | LES: 0.69107 DKY: 1.00000 KSE: 0.69107 PVC: 0.69107 |
| Fourier Power Spectra (a) | |
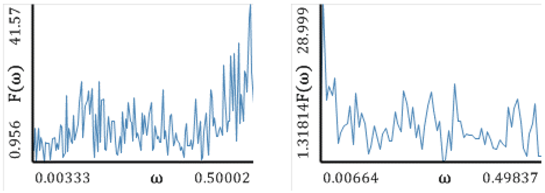 | |
| Gauss Wavelet Spectra (b) | |
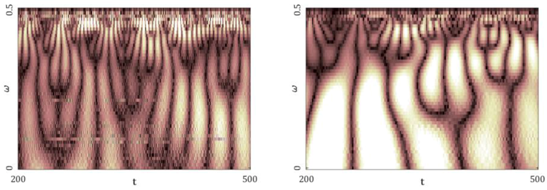 | |
| LLE (Wolf) | |
| 0.4158 | 0.39734 |
| LLE (Rosenstein) | |
| 0.41637 | 0.400635 |
| LLE (Kantz) | |
| 0.41912 | 0.41478 |
| LLE (Synchronization) | |
| 0.40608 | 0.40510 |
| All LEs (Benettin) | |
| LEs: 0.41919; −1.62316 DKY: 1.25826 EKs: 0.41919 PVC: −1.20397 | LEs: 0.41917; −1.62315 DKY: 1.25825 EKs: 0.41917 PVC: −1.20397 |
| All LEs (Neural Network) | |
| LEs: 0.41919; −1.62316 DKY: 1.25826 KSE: 0.41919 PVC: −1.20397 | LEs: 0.40924; −1.61321 DKY: 1.25368 KSE: 0.40924 PVC: −1.20397 |
| Fourier Power Spectra (a) | |
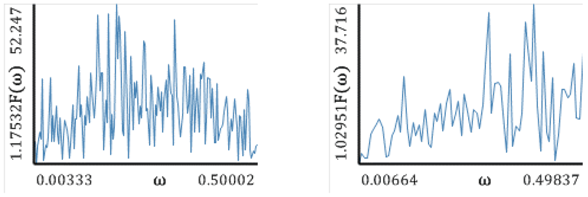 | |
| Gauss Wavelet Spectra (b) | |
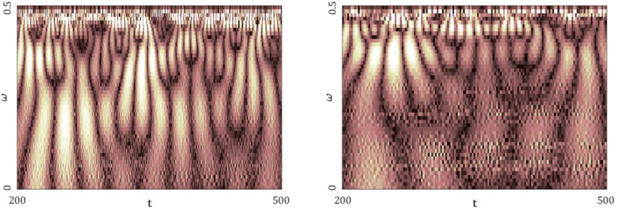 | |
| LLE (Wolf) | |
| 0.45214 | 0.46706 |
| LLE (Rosenstein) | |
| 0.27930 | 0.27459 (0.62515) |
| LLE (Kantz) | |
| 0.26601 | 0.3359 |
| LLE (Synchronization) | |
| 0.27250 | 0.27200 |
| All LEs (Benettin) | |
| LEs: 0.27628; 0.25770; −4.04053 DKY: 2.13215 KSE: 0.53397 PVC: −3.50656 | LEs: 0.27487; 0.25631; −4.03774 DKY: 2.13155 EKS: 0.53118 PVC: −3.50656 |
| All LEs (Neural Network) | |
| LEs: 0.29251; 0.27104; −4.04583 DKY: 2.13929 KSE: 0.56355 PVC: −3.48227 | LEs: 0.26304; 0.24387; −4.14321 DKY: 2.12235 KSE: 0.50691 PVC: −3.63630 |
| Fourier Power Spectrum | |||
 | |||
| Gauss Wavelets | |||
 | |||
| LLE (Wolf) | |||
| 0.07283 | 0.05855 | 0.01731 | 0.02544 |
| LLE (Rosenstein) | |||
| 0.083 | 0.0726 | 0.06553 | 0.606 |
| LLE (Kantz) | |||
| 0.0234 | 0.0208 | 0.02133 | 0.0215 |
| All LEs (Benettin) | |||
| LES: 0.07156; 0.00000; −5.38768 DKY: 2.01328 KSE: 0.07156 PVC: −5.31612 | LES: 0.06959; 0.00000; −5.21949 DKY: 2.01333 KSE: 0.06959 PVC: −5.14990 | LES: 0.06789; 0.00000; −4.34385 DKY: 2.01563 KSE: 0.06789 PVC: −4.27596 | LES: 0.06205; −0.00001; −2.84111 DKY: 2.02184 KSE: 0.06205 PVC: −2.77906 |
| All LEs (neural network) | |||
| LES: 0.06259; −0.07984; −0.32528 DKY: 1.78396 KSE: 0.06259 PVC: −0.34253 | LES: 0.07340; −0.02681; −0.23525 DKY: 2.19807 KSE: 0.07340 PVC: −0.18865 | LES: 0.07374; 0.00057; −0.36909 DKY: 2.20135 KSE: 0.07432 PVC: −0.29477 | LES: 0.07983; −0.02816; −0.91182 DKY: 2.05667 KSE: 0.07983 PVC: −0.86015 |
| Fourier Power Spectrum | |||
 | |||
| Gauss Wavelet | |||
 | |||
| LLE (Wolf) | |||
| 0.9721 | 0.81704 | 0.867 | 0.712 |
| LLE (Rosenstein) | |||
| 0.876 | 0.836 | 0.858 | 0.859 |
| LLE (Kantz) | |||
| 0.898 | 0.9 | 0.762667 | 0.84 |
| LES (Benettin) | |||
| LES: 0.90632; 0.00000; −14.57297 DKY: 2.06219 KSE: 0.90632 PVC: −13.66666 | LES: 0.90523; 0.00000; −14.57179 DKY: 2.06212 KSE: 0.90523 PVC: −13.66656 | LES: 0.90551; 0.00000; −14.57163 DKY: 2.06214 KSE: 0.90551 PVC: −13.66613 | LES: 0.90596; 0.00000; −14.57086 DKY: 2.06218 KSE: 0.90596 PVC: −13.66490 |
| LES (Neural Network) | |||
| LES: 0.91677; 0.04404; −6.464 DKY: 2.14864 EKS entropy: 0.96081 PVC: 0.89617 | LE: 0.9490; 0.0610; −13.9101 DKY: 2.07261 EKS: 1.0101 PVC: −12.9000 | LES: 0.8913; −0.3508; −14.3577 DKY: 2.03765 EKS: 0.8913 PVC: −13.8172 | LES: 0.7485; −0.05558; −23.3505 DKY: 2.0296 EKS: 0.7485 PVC: −22.65758 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Awrejcewicz, J.; Krysko, A.V.; Erofeev, N.P.; Dobriyan, V.; Barulina, M.A.; Krysko, V.A. Quantifying Chaos by Various Computational Methods. Part 1: Simple Systems. Entropy 2018, 20, 175. https://doi.org/10.3390/e20030175
Awrejcewicz J, Krysko AV, Erofeev NP, Dobriyan V, Barulina MA, Krysko VA. Quantifying Chaos by Various Computational Methods. Part 1: Simple Systems. Entropy. 2018; 20(3):175. https://doi.org/10.3390/e20030175
Chicago/Turabian StyleAwrejcewicz, Jan, Anton V. Krysko, Nikolay P. Erofeev, Vitalyj Dobriyan, Marina A. Barulina, and Vadim A. Krysko. 2018. "Quantifying Chaos by Various Computational Methods. Part 1: Simple Systems" Entropy 20, no. 3: 175. https://doi.org/10.3390/e20030175
APA StyleAwrejcewicz, J., Krysko, A. V., Erofeev, N. P., Dobriyan, V., Barulina, M. A., & Krysko, V. A. (2018). Quantifying Chaos by Various Computational Methods. Part 1: Simple Systems. Entropy, 20(3), 175. https://doi.org/10.3390/e20030175






