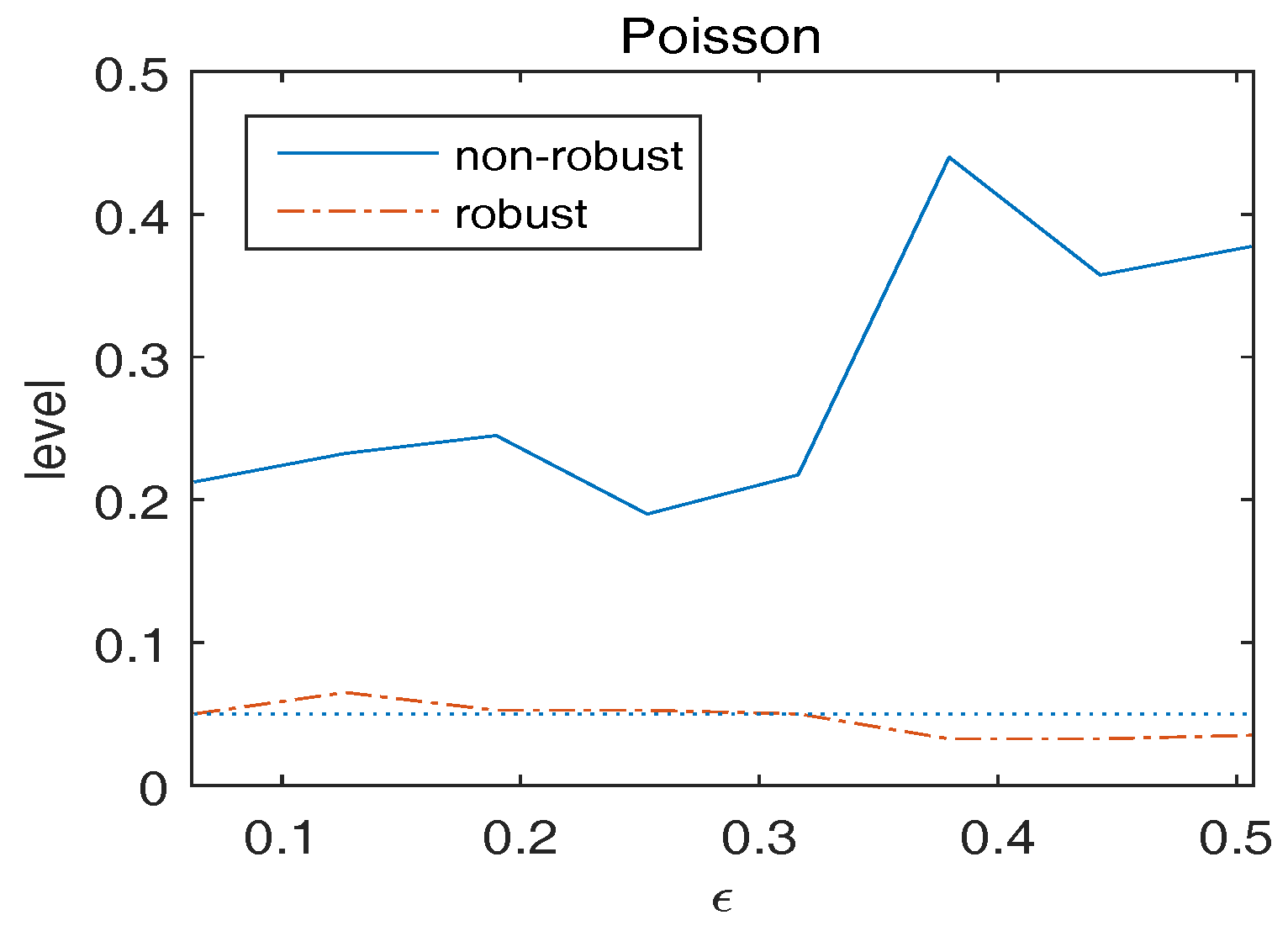
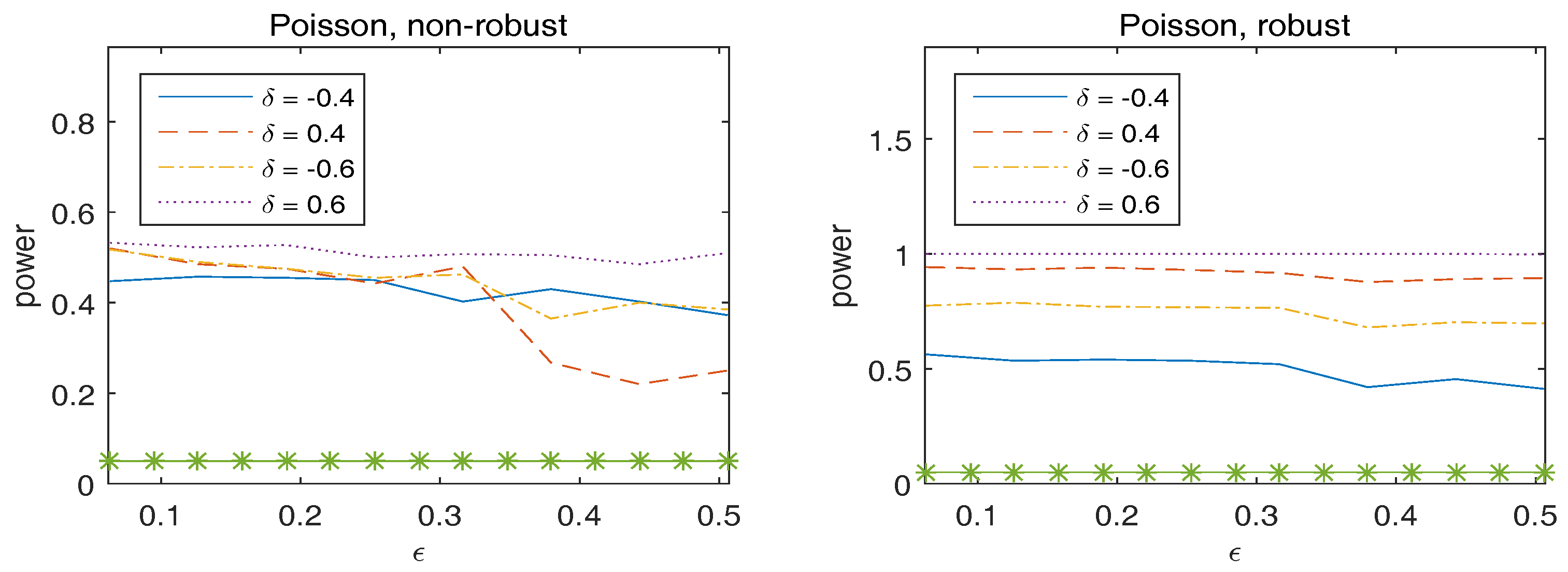
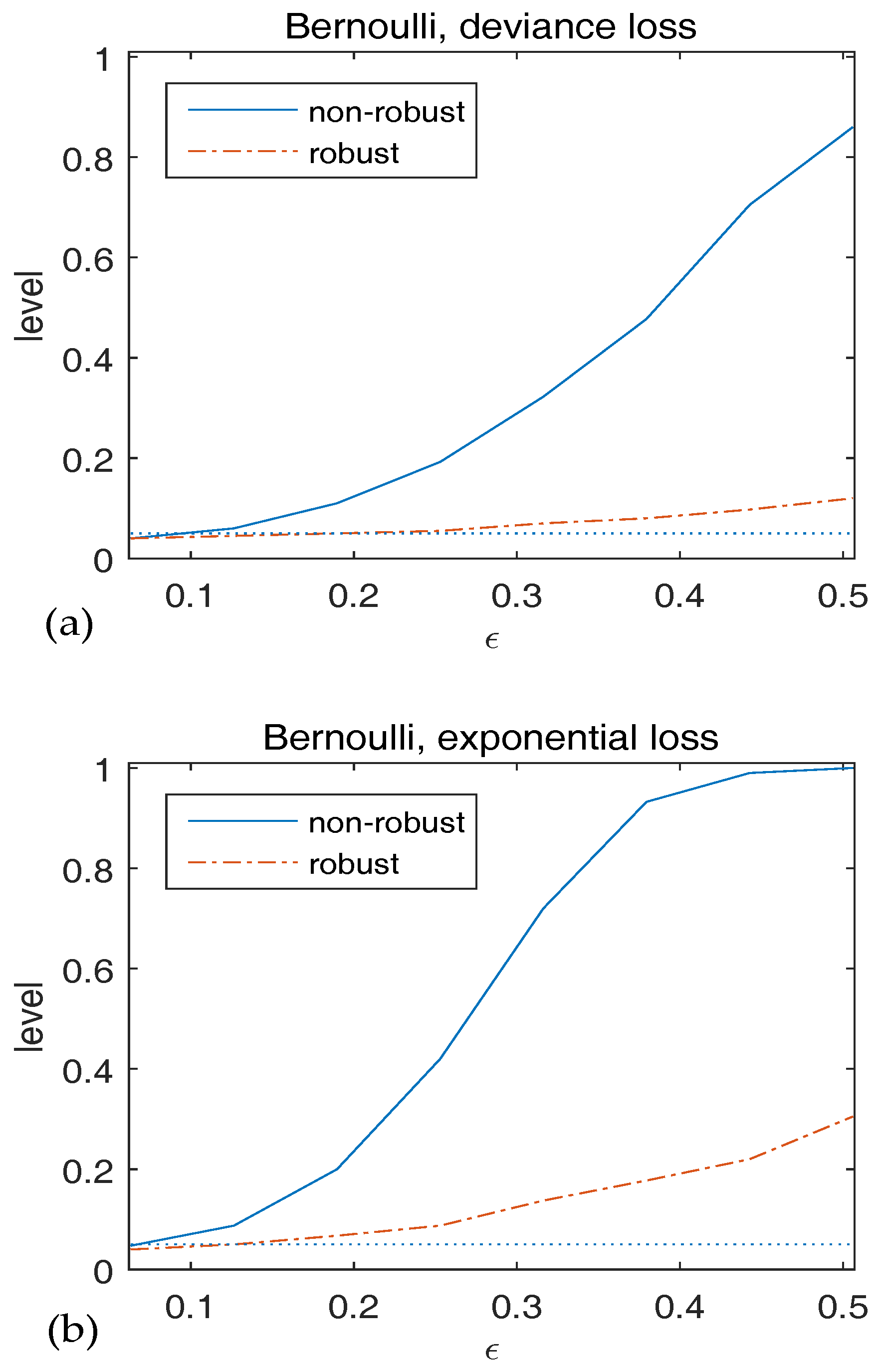
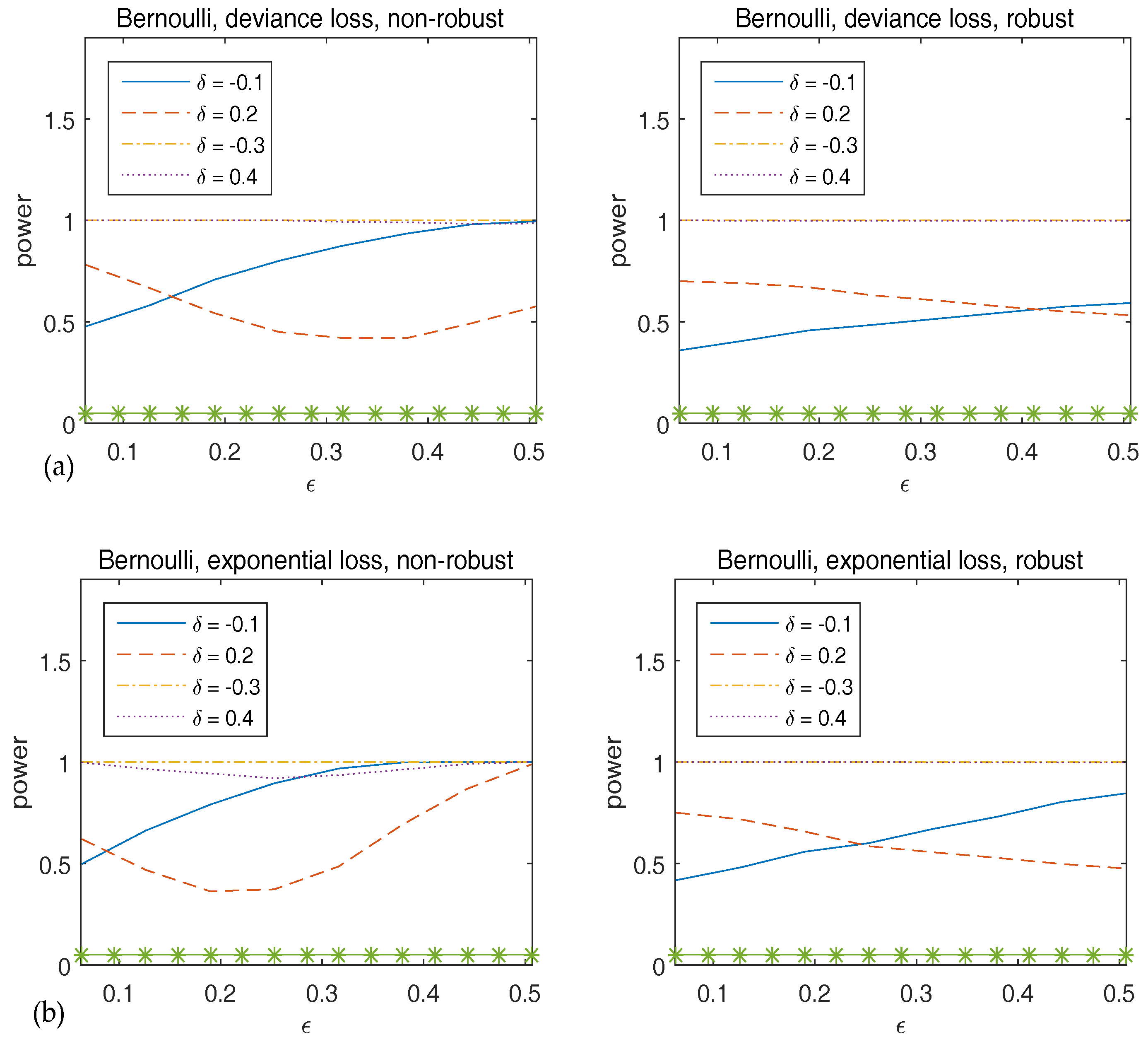
Appendix A. Conditions and Proofs of Main Results
We first introduce some necessary notations used in the proof.
Notations. For arbitrary distributions
K and
of
, define
Therefore, , , and . For notational simplicity, let and .
Define the following matrices,
The following conditions are needed in the proof, which are adopted from [
1].
Condition A.
- A0.
.
- A1.
is a bounded function. Assume that is a bounded, odd function, and twice differentiable, such that , , , and are bounded; , is continuous.
- A2.
is continuous, and . is continuous.
- A3.
is monotone and a bijection, is continuous, and .
- A4.
almost surely if the underlying distribution is .
- A5.
exists and is nonsingular.
- A6.
There is a large enough open subset of which contains , such that is bounded for all in the subset and all such that , where is a large enough constant.
- A7.
is positive definite, with eigenvalues uniformly bounded away from 0.
- A8.
is positive definite, with eigenvalues uniformly bounded away from 0.
- A9.
is bounded away from ∞.
Condition B.
- B4.
almost surely if the underlying distribution is J.
The following Lemmas A1–A9 are needed to prove the main theoretical results in this paper.
Lemma A1 (
)
. Assume Conditions A0–A7
and B4.
For in Equation (
10),
in Equation (
11)
and in Equation (
12),
if as , then is a local minimizer of such that . Furthermore, is unique. Proof. We follow the idea of the proof in [
25]. Let
and
. First, we show that there exists a sufficiently large constant
C such that, for large
n, we have
To show Equation (
A1), consider
where
.
By Taylor expansion,
where
for
located between
and
. Hence
since
and
. For
in Equation (
A2),
where
. Meanwhile, we have
where
and
. Thus,
For
in Equation (
A2), we observe that
We can choose some large
C such that
,
and
are all dominated by the first term of
in Equation (
A3), which is positive by the eigenvalue assumption. This implies Equation (
A1). Therefore, there exists a local minimizer of
in the
neighborhood of
, and denote this minimizer by
.
Next, we show that the local minimizer
of
is unique in the
neighborhood of
. For all
such that
,
and hence,
We know that the minimum eigenvalues of
are uniformly bounded away from 0,
Hence, for
n large enough,
is positive definite for all
such that
. Therefore, there exists a unique minimizer of
in the
neighborhood of
which covers
. From
we know
. From the definition of
, it’s easy to see that
is unique. ☐
Lemma A2 (
)
. Assume Conditions A0–A7
and B4.
For in Equation (
10),
in Equation (
11)
and in Equation (
12),
if as and the distribution of is , then there exists a unique local minimizer of such that . Furthermore, and . Proof. Let
and
. To show the existence of the estimator, it suffices to show that for any given
, there exists a sufficiently large constant
such that, for large
n we have
This implies that with probability at least
, there exists a local minimizer
of
in the ball
. To show Equation (
A4), consider
where
.
By Taylor expansion,
where
for
located between
and
.
Since
, the large open set considered in Condition
contains
when
n is large enough, say
where
N is a positive constant. Therefore, for any fixed
, there exists a bounded open subset of
containing
such that for all
in this set,
which is integrable with respect to
, where
C is a positive constant. Thus, for
,
For
in Equation (
A5),
where
. Meanwhile, we have
For
in Equation (
A5), we observe that
We will show that the minimum eigenvalue of
is uniformly bounded away from 0.
. Note
Since the eigenvalues of are uniformly bounded away from 0, so are those of and .
We can choose some large
such that
and
are both dominated by the first term of
in Equation (
A7), which is positive by the eigenvalue assumption. This implies Equation (
A4).
Next we show the uniqueness of
. For all
such that
,
We know that the minimum eigenvalues of are uniformly bounded away from 0. Following the proof of Lemma A1, we have and . It’s easy to see .
Hence, for n large enough, is positive definite with high probability for all such that . Therefore, there exists a unique minimizer of in the neighborhood of which covers . ☐
Lemma A3 (
)
. Assume Conditions A0–A7
and B4.
For in Equation (
10)
and in Equation (
12),
if as , the distribution of is and , thenwhere is any given matrix such that , with being a positive-definite matrix and is a fixed integer. Proof. Taylor’s expansion yields
where
lies between
and
. Below, we will show
First, . Following the proof of in Lemma A1, . Since , we have .
Therefore, which completes the proof. ☐
Lemma A4 (asymptotic normality of
)
. Assume Conditions A0–A8
and B4.
If as and the distribution of is , thenwhere , is any given matrix such that , with being a positive-definite matrix, is a fixed integer. Proof. From
, Taylor’s expansion yields
where
lies between
and
. Below, we will show
Similar arguments for the proof of of Lemma A2, we have .
Second, a similar proof used for
in Equation (
A5) gives
Third, by Equation (A9) and
, we see that
where
. From the proof of Lemma A2, the eigenvalues of
are uniformly bounded away from 0 and we complete the proof of Equation (
A8).
Following the proof for the bounded eigenvalues of
in Lemma A2, we can show that the eigenvalues of
are uniformly bounded away from 0. Hence, the eigenvalues of
are uniformly bounded away from 0, as are the eigenvalues of
. From Equation (
A8), we see that
It follows that
where
. Following (
A6) in Lemma A2, one can show that
for
n large enough.
To show
, we apply the Lindeberg-Feller central limit theorem in [
26]. Specifically, we check (I)
; (II)
for some
. Condition (I) is straightforward since
. To check condition (II), we can show that
. This yields
. Hence
Thus, we complete the proof. ☐
Lemma A5 (asymptotic covariance matrices
and
)
. Assume Conditions A0–A9
and B4.
If as , thenwhere , is any given matrix such that , with being a positive-definite matrix, and is a fixed integer. Proof. Since , it suffices to prove that .
First, we prove
. Note that
We know that and . Thus, .
Second, we show
. It is easy to see that
where
and
. We observe that
.
Third, we show . Note , where , and . Under Conditions and , it is straightforward to see that , and . Since , we conclude , and similarly and . Hence, .
Thus, we can conclude that and that the eigenvalues of and are uniformly bounded away from 0 and ∞. Consequently, and proof is finished. ☐
Lemma A6 (asymptotic covariance matrices
and
)
. Assume Conditions A0–A9
and B4.
If and the distribution of is , thenwhere is any given matrix such that , with being a positive-definite matrix, and is a fixed integer. Proof. Note that . Since , it suffices to prove that .
Following the proof of Proposition 1 in [
1], we can show that
and
.
To show , note , where , and . Following the proof in Lemma A2, it is straightforward to verify that , . In addition, .
Since , we conclude , and similarly and . Hence, .
Thus, we can conclude that and the eigenvalues of are uniformly bounded away from 0 and ∞ with probability tending to 1. Noting that . ☐
Lemma A7 (asymptotic distribution of test statistic)
. Assume Conditions A0–A9
and B4.
If and the distribution of is , thenwhere is any given matrix such that , with being a positive-definite matrix, and is a fixed integer. Proof. For term I, we obtain from Lemma A4 that
From Lemma A6, we get
Thus, by Slutsky theorem,
For term
, we see from Lemma A6 that
Similarly,
Combining (
A10) and (
A11) with Slutsky theorem completes the proof. ☐
Lemma A8 (Influence Function IF)
. Assume Conditions A1–A8
and B4.
For any fixed sample size n,where and is a positive constant such that with a sufficiently small constant. In addition, uniformly for all n and such that with a sufficiently small constant. Proof. We follow the proof of Theorem 5.1 in [
27]. Note
where
.
It suffices to prove that for any sequence
such that
, we have
Following similar proofs in Lemma A1, we can show that for
sufficiently small,
Next we will show that the eigenvalues of
are bounded away from 0.
Similarly, and . Since the eigenvalues of are bounded away from zero, , and could be sufficiently small, we conclude that for when c is sufficiently small, the eigenvalues of are uniformly bounded away from 0.
Define
. Following similar arguments for (
A6) in Lemma A2, for
j large enough,
. We will only consider
j large enough below. The two term Taylor expansion yields
where
lies between
and
.
Thus, from (
A13) and the fact
, we have
and we obtain that
Next, we will show that
as
for any fixed
n. Since
,
and also,
From Equations (A15) and (A16),
which, together with Equations (
A12) and (A14), implies that
This completes the proof. ☐
Lemma A9. Assume Conditions A1–A8 and B4 and . Let be the cumulative distribution function of distribution with δ the noncentrality parameter. Denote . Let . Then, for any fixed , under and under .
Proof. Since
, we have
To complete the proof, we only need to show that
and
(
) are bounded as
for all
. Note that
where
is the Gamma function, and
is the lower incomplete gamma function
which satisfies
Therefore,
From the results of Lemma A3, that
is bounded as
for all
under both
and
, so are
(
). Now, we consider the derivatives of
,
To complete the proof, we only need to show that () are bounded as for all , and is bounded under and as for all . The result for is straightforward from Lemma A3.
First, for the first order derivative of
,
Since
,
and
we conclude that
is uniformly bounded for all
as
.
Second, for the second order derivative of
,
with
Therefore,
. In addition,
Therefore, for all .
Finally, for the third order derivative of
,
Note:
where
Hence,
which implies that
for all
. In addition,
Hence, . Therefore, for all . Hence, we complete the proof. ☐
Proof of Theorem 1.
We follow the idea of the proof in [
10]. Lemma A7 implies that the Wald-type test statistic
is asymptotically noncentral
with noncentrality parameter
. Therefore,
where
as
for any fixed
. Let
. Then, for
close to 0, we have
where
. Note that under
Since from Lemma A8,
is uniformly bounded, we have
From Equation (A17)
since
from Lemma A9. We complete the proof. ☐
Proof of Corollary 1. For Part
, following the proof of Theorem 1, for any fixed
,
where
. From the assumption that
and
, we know
. Following the proof of Lemma A9,
. We finished the proof of part
.
Part is straightforward by applying Theorem 1 with . ☐
Proof of Theorem 2. Then,
is asymptotically
with
under
. Therefore,
, where
as
for any fixed
. Let
. Then, for
close to 0, we have
where
. Note that under
,
Then,
From Lemma A8,
and hence,
Since under by Lemma A9, we have as .
Since from Lemma A8,
is uniformly bounded,
From Equation (A18), we complete the proof. ☐
Proof of Corollary 2. The proof is similar to that for Corollary 1, using the results in Theorem 2. ☐