An Analysis of the Value of Information When Exploring Stochastic, Discrete Multi-Armed Bandits
Abstract
:1. Introduction
2. Literature Review
3. Methodology
3.1. Value of Information
3.2. Value-of-Information Policies
- τk:
- Temperature Term. This parameter can be interpreted as an inverse-temperature-like parameter. As approaches infinity, we arrive at a low-temperature thermodynamic system of particles. Such a collection particles will have low kinetic energy and hence their position will not vary greatly. In the context of learning, this situation corresponds to policies that will not change much due to a low-exploration search. Indeed, the allocation rule will increasingly begin to favor the arm with the highest current reward estimate, with ties broken randomly. All other randomly selectable arms will be progressively ignored. On the other hand, as goes to zero, we have a high-temperature system of particles, which has a high kinetic energy. The arm-selection policy can change drastically as a result. In the limit, all arms are pulled independently and uniformly at random. Values of the parameter between these two extremes implement searches for arms that are a blend of exploration and exploitation.
- γk:
- Mixing Coefficient Term. This parameter can be viewed as a mixing coefficient for the model: it switches the preference between the exponential distribution component and the uniform distribution component. For values of the mixing coefficient converging to one, the exponential component is increasingly ignored. The resulting arm-choice probability distributions become uniform. The chance of any arm being selected is the same, regardless of the expected pay-out. This corresponds to a pure exploration strategy. As the mixing coefficient becomes zero, the influence of the exponential term consequently rises. The values of will hence begin dictate how frequently a given arm will be chosen based upon its energy, as described by the reward pay-out, and the inverse temperature. Depending on the value of the inverse-temperature parameter, , the resulting search will either be exploration-intensive, exploitation-intensive, or somewhere in between.
| Algorithm 1: -changing Exploration: VoIMix |
 |
| Algorithm 2: -changing Exploration: AutoVoIMix |
 |
Automated Hyperparameter Selection
4. Simulations
4.1. Simulation Preliminaries
4.2. Value of Information Results and Analysis
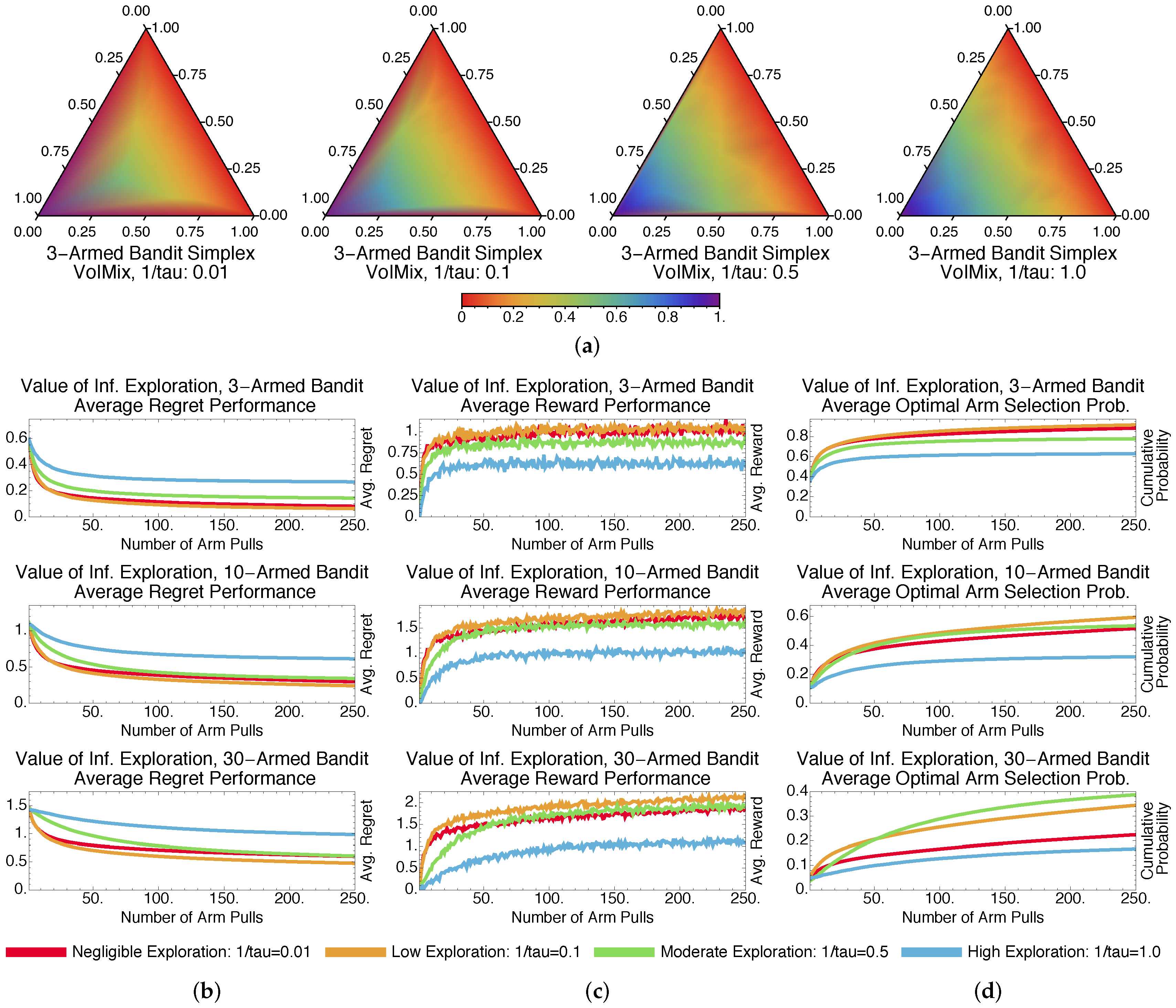
4.2.1. Fixed-Parameter Case
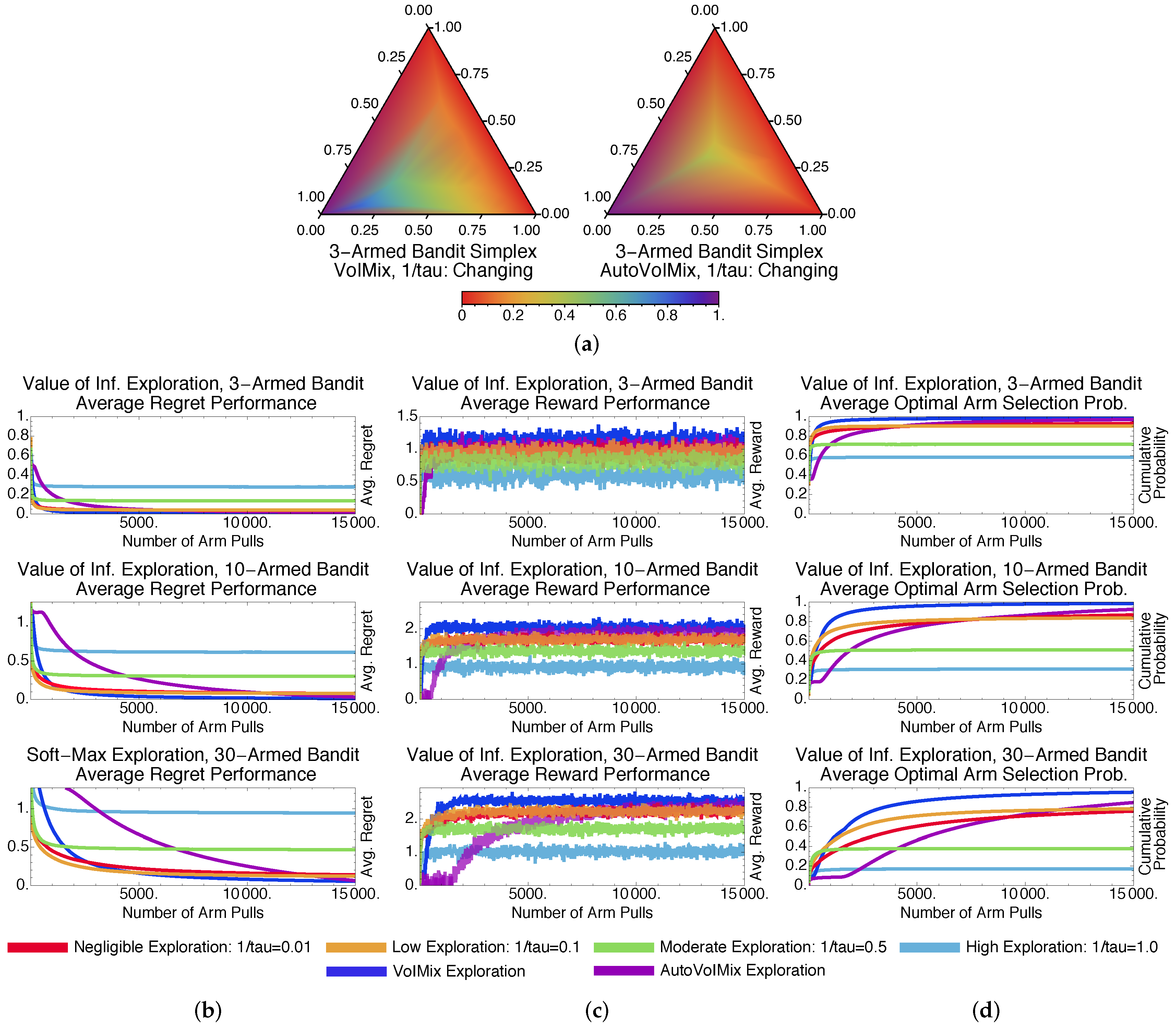
4.2.2. Adaptive-Parameter Case
4.2.3. Fixed- and Variable-Parameter Case Discussions
4.3. Methodological Comparisons
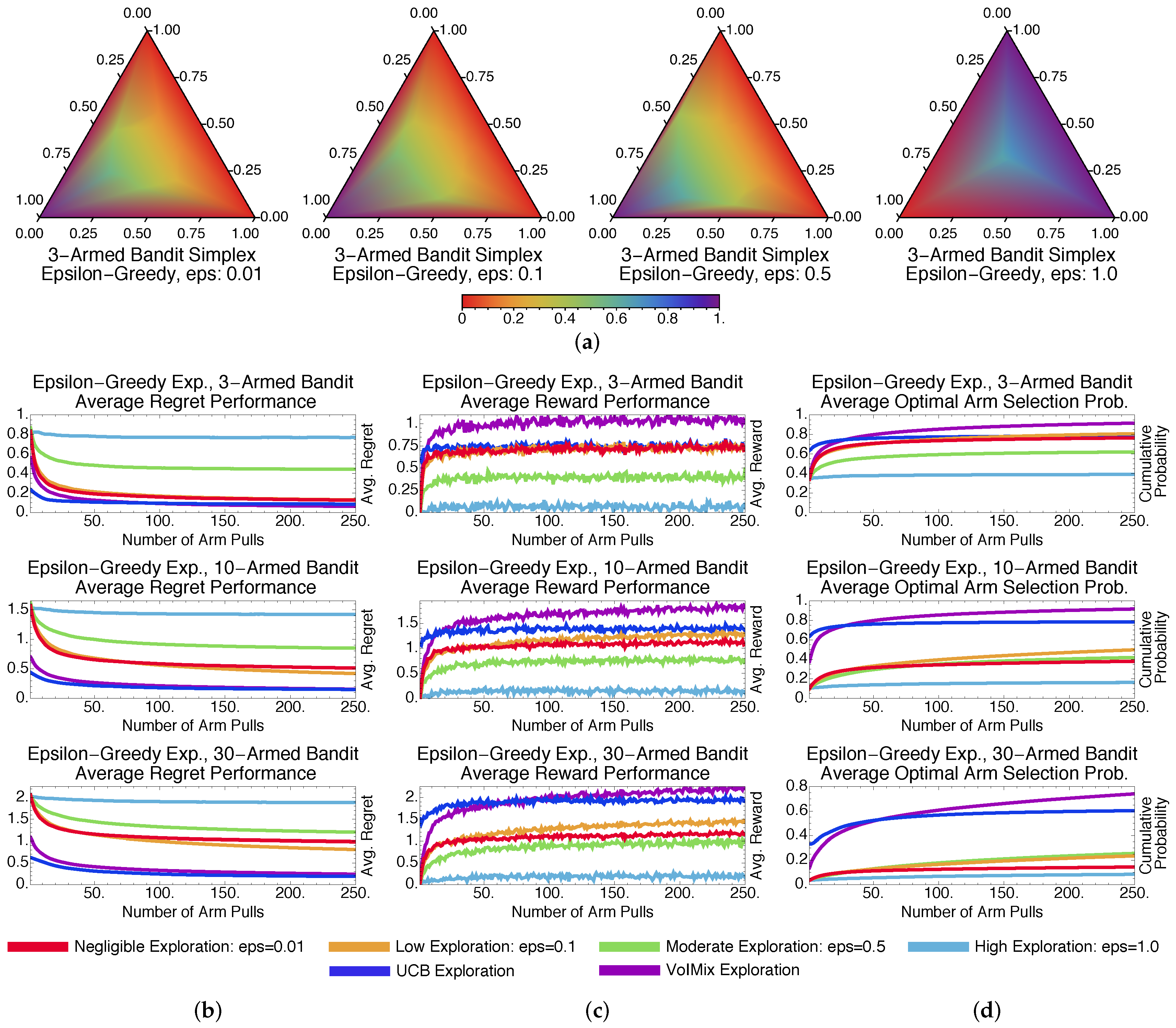
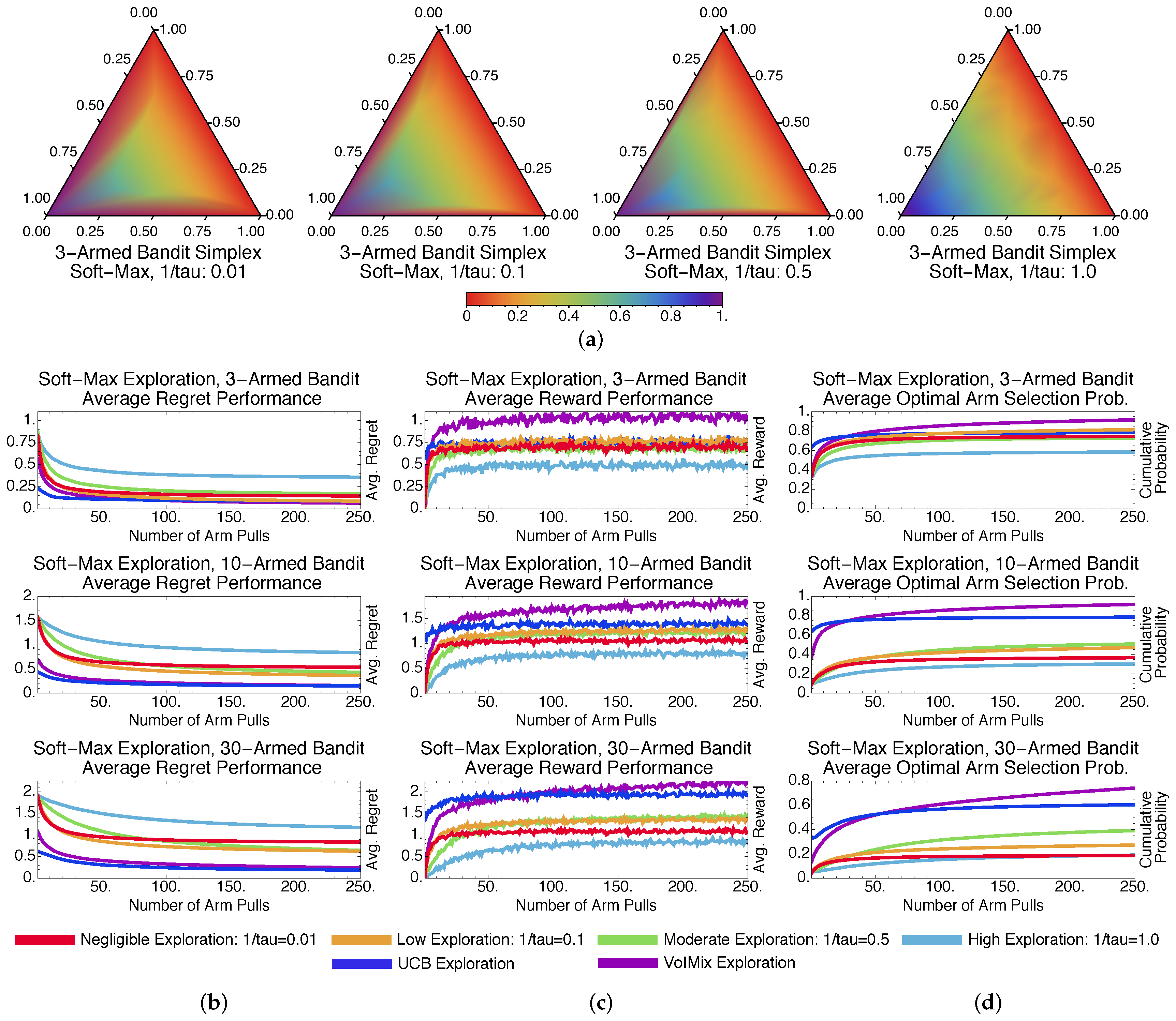
4.3.1. Stochastic Methods: -Greedy and Soft-Max
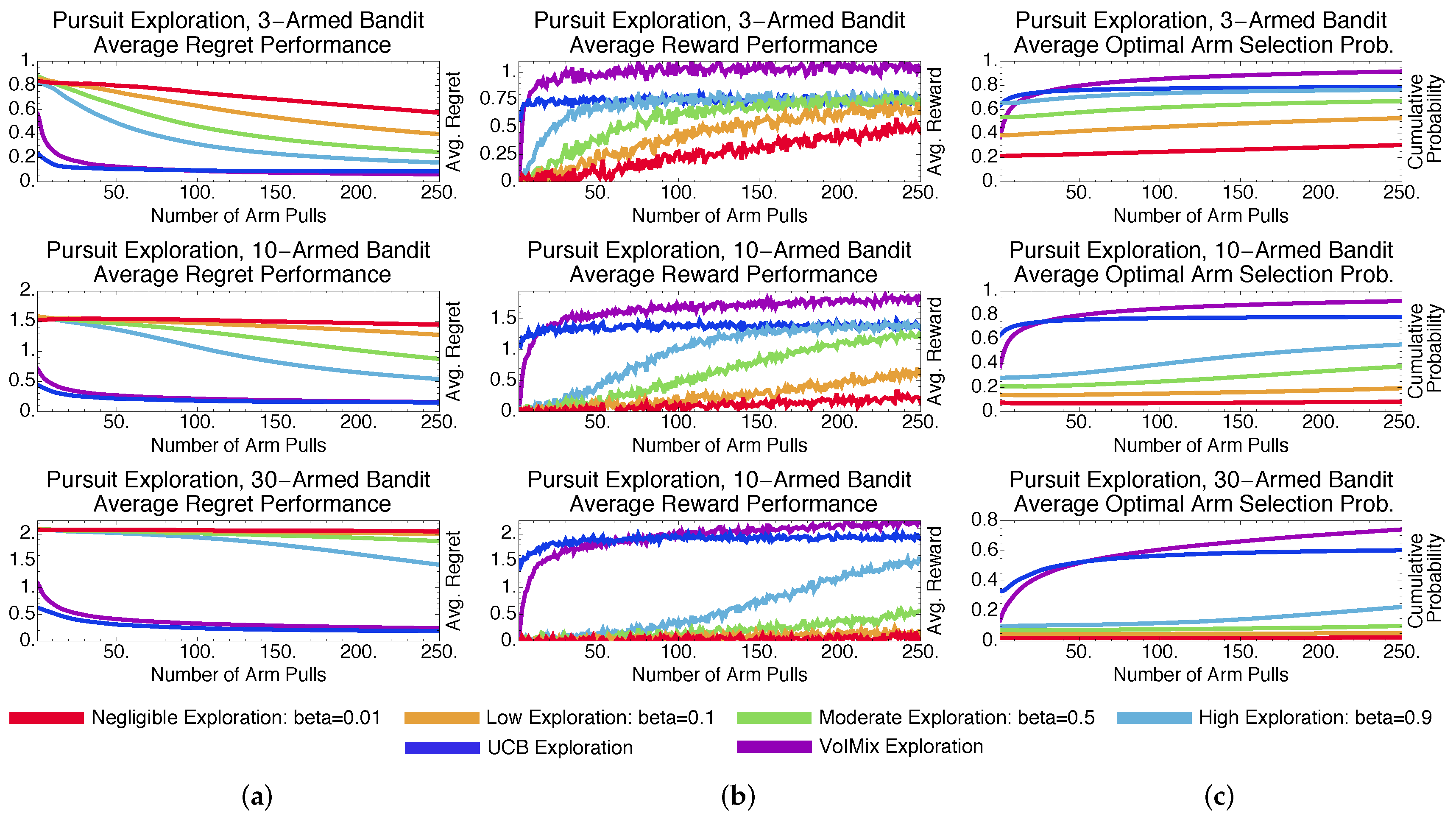
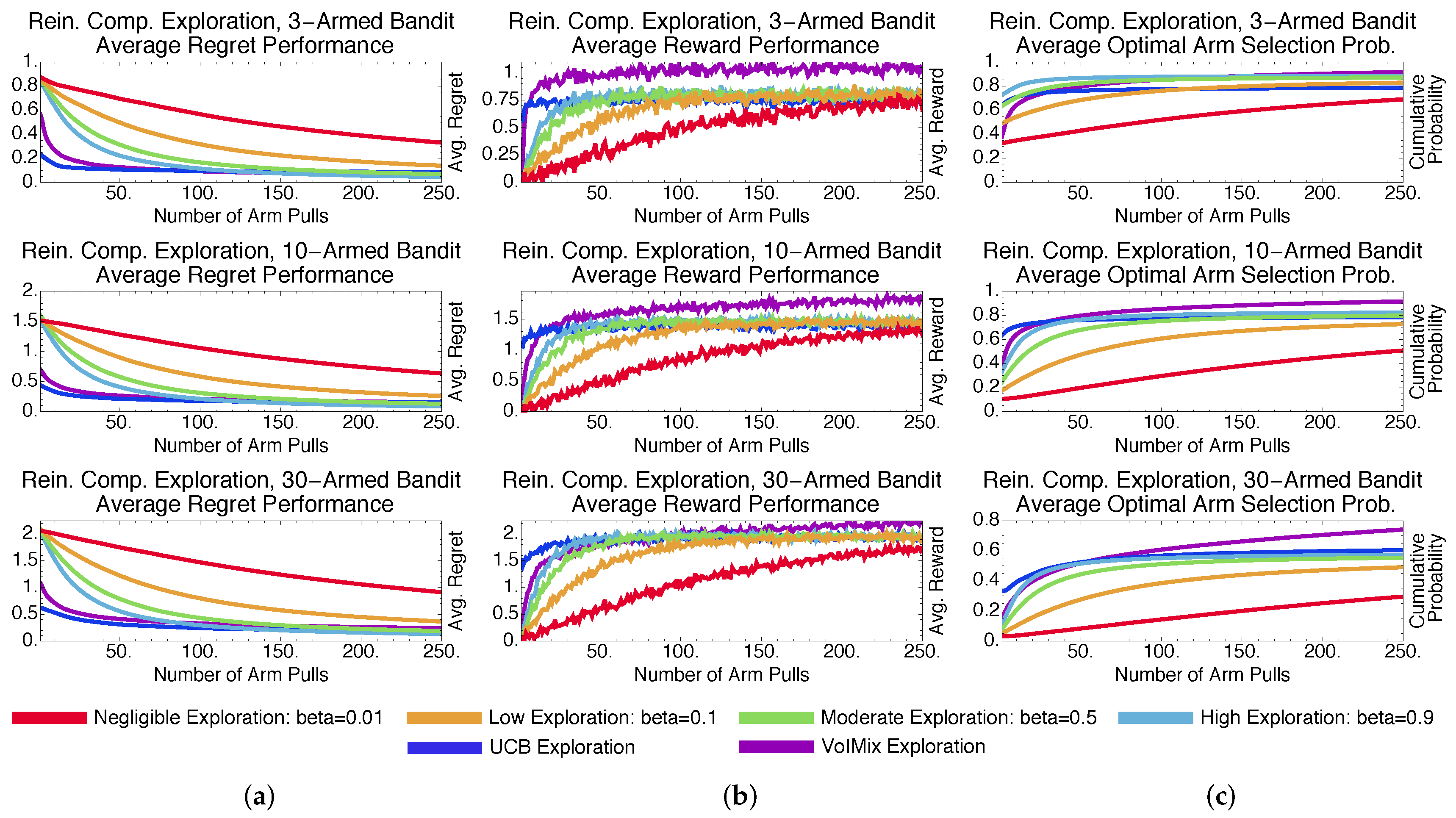
4.3.2. Stochastic Methods: Pursuit and Reinforcement Comparison
4.3.3. Deterministic Methods: Upper Confidence Bound
4.3.4. Methodological Comparisons Discussions
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Variable Notation
| Symbol | Description |
| Continuous space of real values | |
| Discrete space of slot-machine arms | |
| Total number of slot-machine arms | |
| T | Total number of arm pulls |
| s, k | A given arm pull index in the range ; index to a particular iteration or round |
| A given slot-machine arm, indexed by i; i takes values in the range | |
| The slot-machine arm that yields the best expected reward | |
| A particular slot machine arm i pulled at round k | |
| The real-valued reward obtained by pulling arm at round k; can also be interpreted as a random variable | |
| The expected reward for a non-optimal slot machine arm | |
| The expected reward for the optimal slot machine arm | |
| The variance of all slot machine arms | |
| A prior probability distribution that specifies the chance of choosing arm at round k | |
| A posterior-like probability distribution that specifies the chance of choosing arm at round k | |
| A probability distribution that specifies the chance of choosing arm independent of a given round k | |
| Equivalent to ; represents the arm-selection policy | |
| The expected value of random variable according to a probability distribution, e.g., represents | |
| The Kullback–Leibler divergence between two probability distributions, e.g., is the divergence between and | |
| A positive, real-valued information constraint bound | |
| A positive, real-valued reward constraint bound | |
| An estimate of the expected reward for slot machine arm at round | |
| A binary-valued indicator variable that specifies if slot machine arm was chosen at round k | |
| A non-negative, real-valued parameter that dictates the amount of exploration for the -greedy algorithm (GreedyMix) | |
| A non-negative, real-valued parameter that dictates the amount of exploration for soft-max-based selection (SoftMix) and value-of-information-based exploration (VoIMix) | |
| A non-negative, real-valued parameter that represents the mixing coefficient for value-of-information-based exploration (VoIMix and AutoVoIMix) | |
| A non-negative, real-valued hyperparameter that dictates the exploration duration for value-of-information-based exploration (AutoVoIMix) | |
| d | A positive, real-valued hyperparameter that dictates the exploration duration for value-of-information-based exploration (VoIMix) |
| , , | The values of , , , and d, respectively, |
| , | at a given round k |
| The mean loss incurred by choosing arm instead of arm : | |
| A random variable representing the ratio of the reward for a given slot machine arm to its chance of being selected: | |
| A random variable representing the expression | |
| A random variable representing the expression | |
| A -algebra: , | |
| A real-valued function parameterized by c: | |
| , | Real values inside the unit interval |
| A real-valued sequence for VoIMix or for AutoVoIMix | |
| A real-valued sequence for VoIMix or for AutoVoIMix |
Appendix A
References
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Thompson, W.R. On the likelihood that one unknown probability exceeds another in view of the evidence of two samples. Biometrika 1933, 25, 285–294. [Google Scholar] [CrossRef]
- Robbins, H. Some aspects of the sequential design of experiments. Bull. Am. Math. Soc. 1952, 58, 527–535. [Google Scholar] [CrossRef]
- Bubeck, S.; Cesa-Bianchi, N. Regret analysis of stochastic and non-stochastic multi-armed bandit problems. Found. Trends Mach. Learn. 2012, 5, 1–122. [Google Scholar] [CrossRef]
- Lai, T.L.; Robbins, H. Asymptotically efficient adaptive allocation rules. Adv. Appl. Math. 1985, 6, 4–22. [Google Scholar] [CrossRef]
- Auer, P. Using confidence bounds for exploration-exploitation trade-offs. J. Mach. Learn. Res. 2002, 3, 397–422. [Google Scholar]
- Auer, P.; Ortner, R. UCB revisited: Improved regret bounds for the stochastic multi-armed bandit problem. Period. Math. Hung. 2010, 61, 55–65. [Google Scholar] [CrossRef]
- Garivier, A.; Cappé, O. The KL-UCB algorithm for bounded stochastic bandits and beyond. In Proceedings of the Conference on Learning Theory (COLT), Budapest, Hungary, 24 July 2011; pp. 359–376. [Google Scholar]
- Cappé, R.; Garivier, A.; Maillard, O.A.; Munos, R.; Stoltz, G. Kullback–Leibler upper confidence bounds for optimal sequential allocation. Ann. Stat. 2013, 41, 1516–1541. [Google Scholar] [CrossRef]
- Agarwal, S.; Goyal, N. Analysis of Thompson sampling for the multi-armed bandit problem. J. Mach. Learn. Res. 2012, 23, 1–39. [Google Scholar]
- Honda, J.; Takemura, A. An asymptotically optimal policy for finite support models in the multiarmed bandit problem. Mach. Learn. 2011, 85, 361–391. [Google Scholar] [CrossRef]
- Honda, J.; Takemura, A. Non-asymptotic analysis if a new bandit algorithm for semi-bounded rewards. J. Mach. Learn. Res. 2015, 16, 3721–3756. [Google Scholar]
- Auer, P.; Cesa-Bianchi, N.; Fischer, P. Finite-time analysis of the multi-armed bandit problem. Mach. Learn. 2002, 47, 235–256. [Google Scholar] [CrossRef]
- McMahan, H.B.; Streeter, M. Tight bounds for multi-armed bandits with expert advice. In Proceedings of the Conference on Learning Theory (COLT), Montreal, QC, Canada, 18–21 June 2009; pp. 1–10. [Google Scholar]
- Stratonovich, R.L. On value of information. Izv. USSR Acad. Sci. Tech. Cybern. 1965, 5, 3–12. [Google Scholar]
- Stratonovich, R.L.; Grishanin, B.A. Value of information when an estimated random variable is hidden. Izv. USSR Acad. Sci. Tech. Cybern. 1966, 6, 3–15. [Google Scholar]
- Sledge, I.J.; Príncipe, J.C. Analysis of agent expertise in Ms. Pac-Man using value-of-information-based policies. IEEE Trans. Comput. Intell. Artif. Intell. Games 2017. [Google Scholar] [CrossRef]
- Sledge, I.J.; Príncipe, J.C. Partitioning relational matrices of similarities or dissimilarities using the value of information. arxiv, 2017; arXiv:1710.10381. [Google Scholar]
- Sledge, I.J.; Emigh, M.S.; Príncipe, J.C. Guided policy exploration for Markov decision processes using an uncertainty-based value-of-information criterion. arxiv, 2018; arXiv:1802.01518. [Google Scholar]
- Cesa-Bianchi, N.; Fischer, P. Finite-time regret bounds for the multi-armed bandit problem. In Proceedings of the International Conference on Machine Learning (ICML), San Francisco, CA, USA, 24–27 July 1998; pp. 100–108. [Google Scholar]
- Cesa-Bianchi, N.; Gentile, C.; Neu, G.; Lugosi, G. Boltzmann exploration done right. In Advances in Neural Information Processing Systems (NIPS); Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; MIT Press: Cambridge, MA, USA, 2017; pp. 6287–6296. [Google Scholar]
- Auer, P.; Cesa-Bianchi, N.; Freund, Y.; Schapire, R.E. The nonstochastic multi-armed bandit problem. SIAM J. Comput. 2002, 32, 48–77. [Google Scholar] [CrossRef]
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement learning: A survey. J. Artif. Intell. Res. 1996, 4, 237–285. [Google Scholar]
- Salganicoff, M.; Ungar, L.H. Active exploration and learning in real-valued spaces using multi-armed bandit allocation indices. In Proceedings of the International Conference on Machine Learning (ICML), Tahoe City, CA, USA, 9–12 July 1995; pp. 480–487. [Google Scholar]
- Strehl, A.L.; Mesterharm, C.; Littman, M.L.; Hirsh, H. Experience-efficient learning in associative bandit problems. In Proceedings of the International Conference on Machine Learning (ICML), Pittsburgh, PA, USA, 25–29 June 2006; pp. 889–896. [Google Scholar]
- Madani, O.; Lizotte, S.J.; Greiner, R. The budgeted multi-armed bandit problem. In Proceedings of the Conference on Learning Theory (COLT), Banff, AB, Canada, 1–4 July 2004; pp. 643–645. [Google Scholar]
- Kleinberg, R.D. Nearly tight bounds for the continuum-armed bandit problem. In Advances in Neural Information Processing Systems (NIPS); Saul, L.K., Weiss, Y., Bottou, L., Eds.; MIT Press: Cambridge, MA, USA, 2008; pp. 697–704. [Google Scholar]
- Wang, Y.; Audibert, J.; Munos, R. Algorithms for infinitely many-armed bandits. In Advances in Neural Information Processing Systems (NIPS); Koller, D., Schuurmans, D., Bengio, Y., Bottou, L., Eds.; MIT Press: Cambridge, MA, USA, 2008; pp. 1729–1736. [Google Scholar]
- Bubeck, S.; Munos, R.; Stoltz, G. Pure exploration in finitely-armed and continuous-armed bandits. Theor. Comput. Sci. 2011, 412, 1876–1902. [Google Scholar] [CrossRef]
- Vermorel, J.; Mohri, M. Multi-armed bandit algorithms and empirical evaluation. In Machine Learning: ECML; Gama, J., Camacho, R., Brazdil, P.B., Jorge, A.M., Torgo, L., Eds.; Springer: New York, NY, USA, 2005; pp. 437–448. [Google Scholar]
- Even-Dar, E.; Mannor, S.; Mansour, Y. PAC bounds for multi-armed bandit and Markov decision processes. In Proceedings of the Conference on Learning Theory (COLT), Sydney, Australia, 8–10 July 2002; pp. 255–270. [Google Scholar]
- Mannor, S.; Tsitsiklis, J.N. The sample complexity of exploration in the multi-armed bandit problem. J. Mach. Learn. Res. 2004, 5, 623–648. [Google Scholar]
- Langford, J.; Zhang, T. The epoch-greedy algorithm for multi-armed bandits. In Advances in Neural Information Processing Systems (NIPS); Platt, J.C., Koller, D., Singer, Y., Roweis, S.T., Eds.; MIT Press: Cambridge, MA, USA, 2008; pp. 817–824. [Google Scholar]
- Srinivas, S.; Krause, A.; Seeger, M.; Kakade, S.M. Gaussian process optimization in the bandit setting: No regret and experimental design. In Proceedings of the International Conference on Machine Learning (ICML), Haifa, Israel, 21–24 June 2010; pp. 1015–1022. [Google Scholar]
- Krause, A.; Ong, C.S. Contextual Gaussian process bandit optimization. In Advances in Neural Information Processing Systems (NIPS); Shawe-Taylor, J., Zemel, R.S., Bartlett, P.L., Pereira, F., Weinberger, K.Q., Eds.; MIT Press: Cambridge, MA, USA, 2011; pp. 2447–2455. [Google Scholar]
- Beygelzimer, A.; Langford, J.; Li, L.; Reyzin, L.; Schapire, R.E. Contextual bandit algorithms with supervised learning guarantees. In Proceedings of the International Conference on Artificial Intelligence and Statistics (AISTATS), Ft. Lauderdale, FL, USA, 11–13 April 2011; pp. 19–26. [Google Scholar]
- Sledge, I.J.; Príncipe, J.C. Balancing exploration and exploitation in reinforcement learning using a value of information criterion. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 1–5. [Google Scholar]
- Narendra, K.S.; Thathachar, M.A.L. Learning automata—A survey. IEEE Trans. Syst. Man Cybern. 1974, 4, 323–334. [Google Scholar] [CrossRef]
- Thathachar, M.A.L.; Sastry, P.S. A new approach to the design of reinforcement schemes for learning automata. IEEE Trans. Syst. Man Cybern. 1985, 15, 168–175. [Google Scholar] [CrossRef]
- Audibert, J.Y.; Munos, R.; Szepesvári, C. Exploration-exploitation tradeoff using variance estimates in multi-armed bandits. Theor. Comput. Sci. 2009, 410, 1876–1902. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sledge, I.J.; Príncipe, J.C. An Analysis of the Value of Information When Exploring Stochastic, Discrete Multi-Armed Bandits. Entropy 2018, 20, 155. https://doi.org/10.3390/e20030155
Sledge IJ, Príncipe JC. An Analysis of the Value of Information When Exploring Stochastic, Discrete Multi-Armed Bandits. Entropy. 2018; 20(3):155. https://doi.org/10.3390/e20030155
Chicago/Turabian StyleSledge, Isaac J., and José C. Príncipe. 2018. "An Analysis of the Value of Information When Exploring Stochastic, Discrete Multi-Armed Bandits" Entropy 20, no. 3: 155. https://doi.org/10.3390/e20030155
APA StyleSledge, I. J., & Príncipe, J. C. (2018). An Analysis of the Value of Information When Exploring Stochastic, Discrete Multi-Armed Bandits. Entropy, 20(3), 155. https://doi.org/10.3390/e20030155






