Sequential Change-Point Detection via Online Convex Optimization
Abstract
:1. Introduction
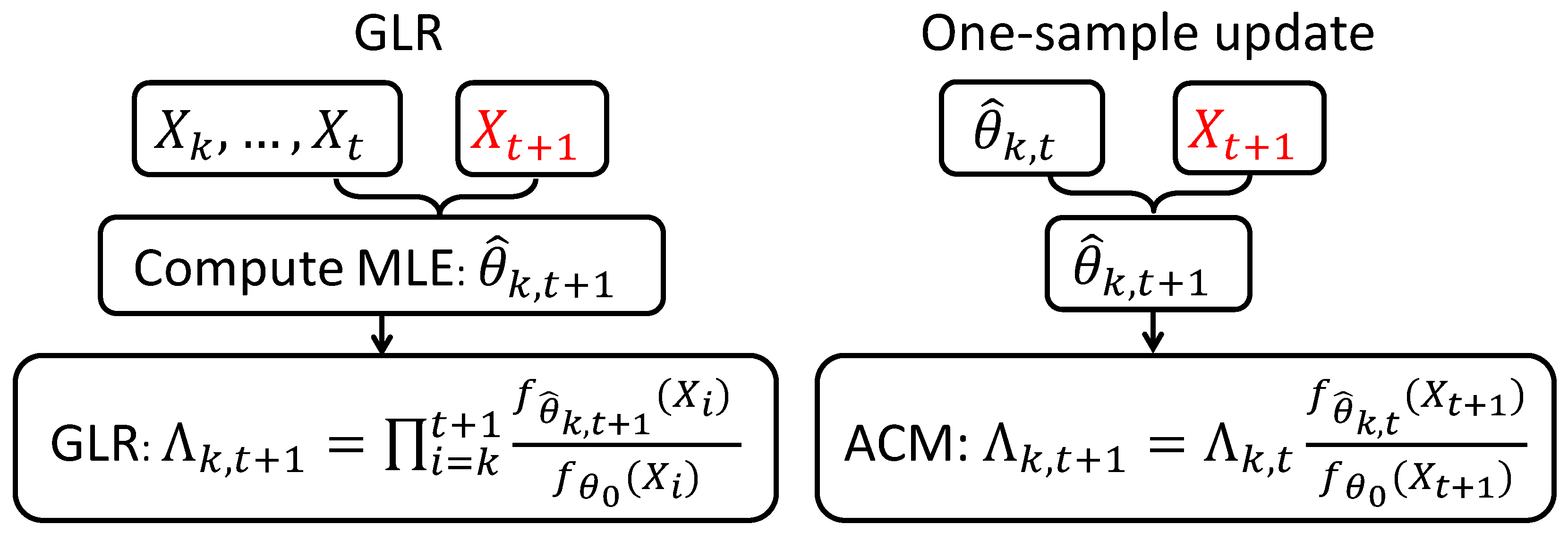
1.1. Motivation: Dilemma of CUSUM and Generalized Likelihood Ratio (GLR) Statistics
1.2. Application Scenario: Social Network Change-Point Detection
1.3. Contributions
1.4. Literature and Related Work
2. Preliminaries
2.1. One-Sided Sequential Hypothesis Test
2.2. Sequential Change-Point Detection
2.3. Exponential Family
2.4. Online Convex Optimization (OCO) Algorithms for Non-Anticipating Estimators
| Algorithm 1 Online mirror-descent for non-anticipating estimators. |
| Require: Exponential family specifications and ; initial parameter value ; sequence of data ; a closed, convex set for parameter ; a decreasing sequence of strictly positive step-sizes. |
| 1: . {Initialization} |
| 2: for all do |
| 3: Acquire a new observation |
| 4: Compute loss |
| 5: Compute likelihood ratio |
| 6: , {Dual update} |
| 7: |
| 8: {Projected primal update} |
| 9: end for |
| 10: return and . |
3. Nearly Second-Order Asymptotic Optimality of One-Sample Update Schemes
3.1. “One-Sided” Sequential Hypothesis Test
3.2. Sequential Change-Point Detection
3.3. Example: Regret Bound for Specific Cases
4. Numerical Examples
4.1. Detecting Sparse Mean-Shift of Multivariate Normal Distribution
4.2. Detecting the Scale Change in Gamma Distribution
4.3. Communication-Rate Change Detection with Erdos-Rényi Model
4.4. Point Process Change-Point Detection: Poisson to Hawkes Processes
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Proofs
References
- Siegmund, D. Sequential Analysis: Tests and Confidence Intervals; Springer: Berlin, Germany, 1985. [Google Scholar]
- Chen, J.; Gupta, A.K. Parametric Statistical Change Point Analysis; Birkhauser: Basel, Switzerland, 2000. [Google Scholar]
- Siegmund, D. Change-points: From sequential detection to biologu and back. Seq. Anal. 2013, 23, 2–14. [Google Scholar] [CrossRef]
- Tartakovsky, A.; Nikiforov, I.; Basseville, M. Sequential Analysis: Hypothesis Testing and Changepoint Detection; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Granjon, P. The CuSum Algorithm—A Small Review. 2013. Available online: https://hal.archives-ouvertes.fr/hal-00914697 (accessed on 6 February 2018).
- Basseville, M.; Nikiforov, I.V. Detection of Abrupt Changes: Theory and Application; Prentice Hall Englewood Cliffs: Upper Saddle River, NJ, USA, 1993; Volume 104. [Google Scholar]
- Lai, T.Z. Information bounds and quick detection of parameter changes in stochastic systems. IEEE Trans. Inf. Theory 1998, 44, 2917–2929. [Google Scholar]
- Lorden, G.; Pollak, M. Nonanticipating estimation applied to sequential analysis and changepoint detection. Ann. Stat. 2005, 33, 1422–1454. [Google Scholar] [CrossRef]
- Raginsky, M.; Marcia, R.F.; Silva, J.; Willett, R. Sequential probability assignment via online convex programming using exponential families. In Proceedings of the IEEE International Symposium on Information Theory, Seoul, Korea, 28 June–3 July 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1338–1342. [Google Scholar]
- Raginsky, M.; Willet, R.; Horn, C.; Silva, J.; Marcia, R. Sequential anomaly detection in the presence of noise and limited feedback. IEEE Trans. Inf. Theory 2012, 58, 5544–5562. [Google Scholar] [CrossRef]
- Peel, L.; Clauset, A. Detecting change points in the large-scale structure of evolving networks. In Proceedings of the 29th AAAI Conference on Artificial Intelligence (AAAI), Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Li, S.; Xie, Y.; Farajtabar, M.; Verma, A.; Song, L. Detecting weak changes in dynamic events over networks. IEEE Trans. Signal Inf. Process. Over Netw. 2017, 3, 346–359. [Google Scholar] [CrossRef]
- Cesa-Bianchi, N.; Lugosi, G. Prediction, Learning, and Games; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Hazan, E. Introduction to online convex optimization. Found. Trends Optim. 2016, 2, 157–325. [Google Scholar] [CrossRef]
- Siegmund, D.; Yakir, B. Minimax optimality of the Shiryayev-Roberts change-point detection rule. J. Stat. Plan. Inference 2008, 138, 2815–2825. [Google Scholar] [CrossRef]
- Azoury, K.; Warmuth, M. Relative loss bounds for on-line density estimation with the exponential family of distributions. Mach. Learn. 2001, 43, 211–246. [Google Scholar] [CrossRef]
- Page, E. Continuous inspection schemes. Biometrika 1954, 41, 100–115. [Google Scholar] [CrossRef]
- Lorden, G. Procedures for reacting to a change in distribution. Ann. Math. Stat. 1971, 42, 1897–1908. [Google Scholar] [CrossRef]
- Moustakides, G.V. Optimal stopping times for detecting changes in distributions. Ann. Stat. 1986, 14, 1379–1387. [Google Scholar] [CrossRef]
- Shiryaev, A.N. On optimum methods in quickest detection problems. Theory Probab. Appl. 1963, 8, 22–46. [Google Scholar] [CrossRef]
- Willsky, A.; Jones, H. A generalized likelihood ratio approach to the detection and estimation of jumps in linear systems. IEEE Trans. Autom. Control 1976, 21, 108–112. [Google Scholar] [CrossRef]
- Lai, T.L. Sequential changepoint detection in quality control and dynamical systems. J. R. Stat. Soc. Ser. B 1995, 57, 613–658. [Google Scholar]
- Lai, T.Z. Likelihood ratio identities and their applications to sequential analysis. Seq. Anal. 2004, 23, 467–497. [Google Scholar] [CrossRef]
- Lorden, G.; Pollak, M. Sequential change-point detection procedures that are nearly optimal and computationally simple. Seq. Anal. 2008, 27, 476–512. [Google Scholar] [CrossRef]
- Pollak, M. Average run lengths of an optimal method of detecting a change in distribution. Ann. Stat. 1987, 15, 749–779. [Google Scholar] [CrossRef]
- Mei, Y. Sequential change-point detection when unknown parameter are present in the pre-change distribution. Ann. Stat. 2006, 34, 92–122. [Google Scholar] [CrossRef]
- Yilmaz, Y.; Moustakides, G.V.; Wang, X. Sequential joint detection and estimation. Theory Probab. Appl. 2015, 59, 452–465. [Google Scholar] [CrossRef]
- Yılmaz, Y.; Li, S.; Wang, X. Sequential joint detection and estimation: Optimum tests and applications. IEEE Trans. Signal Process. 2016, 64, 5311–5326. [Google Scholar] [CrossRef]
- Yilmaz, Y.; Guo, Z.; Wang, X. Sequential joint spectrum sensing and channel estimation for dynamic spectrum access. IEEE J. Sel. Areas Commun. 2014, 32, 2000–2012. [Google Scholar] [CrossRef]
- Vo, B.N.; Vo, B.T.; Pham, N.T.; Suter, D. Joint detection and estimation of multiple objects from image observations. IEEE Trans. Signal Process. 2010, 58, 5129–5141. [Google Scholar] [CrossRef]
- Tajer, A.; Jajamovich, G.H.; Wang, X.; Moustakides, G.V. Optimal joint target detection and parameter estimation by MIMO radar. IEEE J. Sel. Top. Signal Process. 2010, 4, 127–145. [Google Scholar] [CrossRef]
- Baygun, B.; Hero, A.O. Optimal simultaneous detection and estimation under a false alarm constraint. IEEE Trans. Inf. Theory 1995, 41, 688–703. [Google Scholar] [CrossRef]
- Moustakides, G.V.; Jajamovich, G.H.; Tajer, A.; Wang, X. Joint detection and estimation: Optimum tests and applications. IEEE Trans. Inf. Theory 2012, 58, 4215–4229. [Google Scholar] [CrossRef]
- Kotlowski, W.; Grünwald, P. Maximum likelihood vs. sequential normalized maximum likelihood in on-line density estimation. In Proceedings of the Conference on Learning Theory (COLT), Budapest, Hungary, 9–11 July 2011; pp. 457–476. [Google Scholar]
- Anava, O.; Hazan, E.; Mannor, S.; Shamir, O. Online learning for time series prediction. In Proceedings of the Conference on Learning Theory (COLT), Princeton, NJ, USA, 12–14 June 2013; pp. 1–13. [Google Scholar]
- Wald, A.; Wolfowitz, J. Optimum character of the sequential probability ratio test. Ann. Math. Stat. 1948, 19, 326–339. [Google Scholar] [CrossRef]
- Barron, A.; Sheu, C.H. Approximation of density functions by sequences of exponential families. Ann. Stat. 1991, 19, 1347–1369. [Google Scholar] [CrossRef]
- Wainwright, M.J.; Jordan, M.I. Graphical models, exponential families, and variational inference. Found. Trends Mach. Learn. 2008, 1, 1–305. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. Mirror descent and nonlinear projected subgradient methods for convex optimization. Oper. Res. Lett. 2003, 31, 167–175. [Google Scholar] [CrossRef]
- Nemirovskii, A.; Yudin, D.; Dawson, E. Problem Complexity and Method Efficiency in Optimization; Wiley: Hoboken, NJ, USA, 1983. [Google Scholar]
- Shalev-Shwartz, S. Online learning and online convex optimization. Found. Trends® Mach. Learn. 2012, 4, 107–194. [Google Scholar] [CrossRef]
- The Implementation of the Code. Available online: http://www2.isye.gatech.edu/~yxie77/one-sampleupdate-code.zip (accessed on 6 February 2018).
- Agarwal, A.; Duchi, J.C. Stochastic Optimization with Non-i.i.d. Noise. 2011. Available online: http://opt.kyb.tuebingen.mpg.de/papers/opt2011_agarwal.pdf (accessed on 6 February 2018).
- Alqanoo, I.M. On the Truncated Distributions within the Exponential Family; Department of Applied Statistics, Al-Azhar University—Gaza: Gaza, Gaza Strip, 2014. [Google Scholar]
- Xie, Y.; Siegmund, D. Sequential multi-sensor change-point detection. Ann. Stat. 2013, 41, 670–692. [Google Scholar] [CrossRef]
- Siegmund, D.; Yakir, B.; Zhang, N.R. Detecting simultaneous variant intervals in aligned sequences. Ann. Appl. Stat. 2011, 5, 645–668. [Google Scholar] [CrossRef]
- Lipster, R.; Shiryayev, A. Theory of Martingales; Springer: Dordrecht, The Netherlands, 1989. [Google Scholar]
- Duchi, J.; Shalev-Shwartz, S.; Singer, Y.; Chandra, T. Efficient projections onto the ℓ1-ball for learning in high dimensions. In Proceedings of the International Conference on Machine learning (ICML), Helsinki, Finland, 5–9 June 2008; ACM: New York, NY, USA, 2008; pp. 272–279. [Google Scholar]
- Wang, Y.; Mei, Y. Large-scale multi-stream quickest change detection via shrinkage post-change estimation. IEEE Trans. Inf. Theory 2015, 61, 6926–6938. [Google Scholar] [CrossRef]
| CUSUM | 188.60 | 146.45 | 64.30 | 18.97 | 7.18 | 3.77 |
| Shrinkage | 17.19 | 9.25 | 6.38 | 4.96 | 4.07 | 3.55 |
| GLR | 19.10 | 10.09 | 7.00 | 5.49 | 4.50 | 3.86 |
| ASR | 45.22 | 19.55 | 12.62 | 8.90 | 7.02 | 5.90 |
| ACM | 45.60 | 19.93 | 12.50 | 9.00 | 7.03 | 5.87 |
| ASR-ℓ1 | 45.81 | 19.94 | 12.45 | 8.92 | 6.97 | 5.89 |
| ACM-ℓ1 | 19.24 | 10.17 | 7.51 | 6.11 | 5.41 | 4.92 |
| CUSUM | NaN | 481.2 | 33.75 | 14.37 | 12.04 |
| MOM | 3.41 | 32.87 | 40.86 | 11.42 | 7.21 |
| GLR | 2.40 | 23.79 | 33.29 | 9.07 | 5.67 |
| ASR | 3.95 | 32.34 | 45.18 | 13.45 | 8.55 |
| ACM | 3.70 | 31.80 | 47.20 | 12.42 | 7.87 |
| CUSUM | 473.11 | 2.06 | 2.00 | 2.00 | 2.00 | 2.00 |
| GLR | 2.00 | 1.96 | 1.27 | 1.00 | 1.00 | 1.00 |
| ASR | 8.64 | 6.39 | 5.08 | 3.92 | 3.36 | 2.94 |
| ACM | 8.67 | 6.37 | 5.07 | 3.88 | 3.32 | 2.94 |
| ACM | 33.03 | 27.75 | 20.39 | 16.16 |
| ASR | 38.59 | 24.96 | 20.17 | 13.91 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Y.; Xie, L.; Xie, Y.; Xu, H. Sequential Change-Point Detection via Online Convex Optimization. Entropy 2018, 20, 108. https://doi.org/10.3390/e20020108
Cao Y, Xie L, Xie Y, Xu H. Sequential Change-Point Detection via Online Convex Optimization. Entropy. 2018; 20(2):108. https://doi.org/10.3390/e20020108
Chicago/Turabian StyleCao, Yang, Liyan Xie, Yao Xie, and Huan Xu. 2018. "Sequential Change-Point Detection via Online Convex Optimization" Entropy 20, no. 2: 108. https://doi.org/10.3390/e20020108
APA StyleCao, Y., Xie, L., Xie, Y., & Xu, H. (2018). Sequential Change-Point Detection via Online Convex Optimization. Entropy, 20(2), 108. https://doi.org/10.3390/e20020108





