Spatial Measures of Urban Systems: from Entropy to Fractal Dimension
Abstract
1. Introduction
2. Theoretical Models
2.1. Generalized Entropy and Fractal Dimension
2.2. Scale Dependence and Entropy Conservation of Fractal Urban Systems
- Step 1: entropy H = 0; fractal dimension D = 0. For a point, the fractal dimension value can be obtained by L’Hospital’s rule.
- Step 2: entropy H = ln(5) =1.6094 nat; fractal dimension D = ln(5)/ln(3) = 1.465.
- Step 3: entropy H = ln(25) = 3.2189 nat; fractal dimension D = ln(25)/ln(9) = 1.465.
- Step 4: entropy H = ln(125) = 4.8283 nat; fractal dimension D = ln(125)/ln(27) = 1.465.
- ….
- Step 1: entropy H = 0; fractal dimension D = 2. For a surface, the fractal dimension can be obtained by L’Hospital’s rule.
- Step 2: entropy H = ln(5) = 1.6094 nat; fractal dimension D = −ln(5)/ln(1/3) = 1.465.
- Step 3: entropy H = ln(25) = 3.2189 nat; fractal dimension D = −ln(25)/ln(1/9) = 1.465.
- Step 4: entropy H = ln(125) = 4.8283 nat; fractal dimension D = −ln(125)/ln(1/27) = 1.465.
- ….
- Step 1: entropy H = 0; fractal dimension D = 0.
- Step 2: entropy H = −ln(1/17)/17 − 4 × 4 × ln(4/17)/17 = 1.5285 nat; box dimension D = ln(1/17)/ln(1/5) = 1.7604.
- Step 3: entropy H = −ln(1/289)/289 − 8 × 4 × ln(4/289)/289 − 16 × 16 × ln(16/289)/289 = 3.0569 nat; box dimension D = ln(1/289)/ln(1/25) = 1.7604.
2.3. Entropy-Based Fractal Dimension Analysis
3. Empirical Analysis
3.1. Study Area and Methods
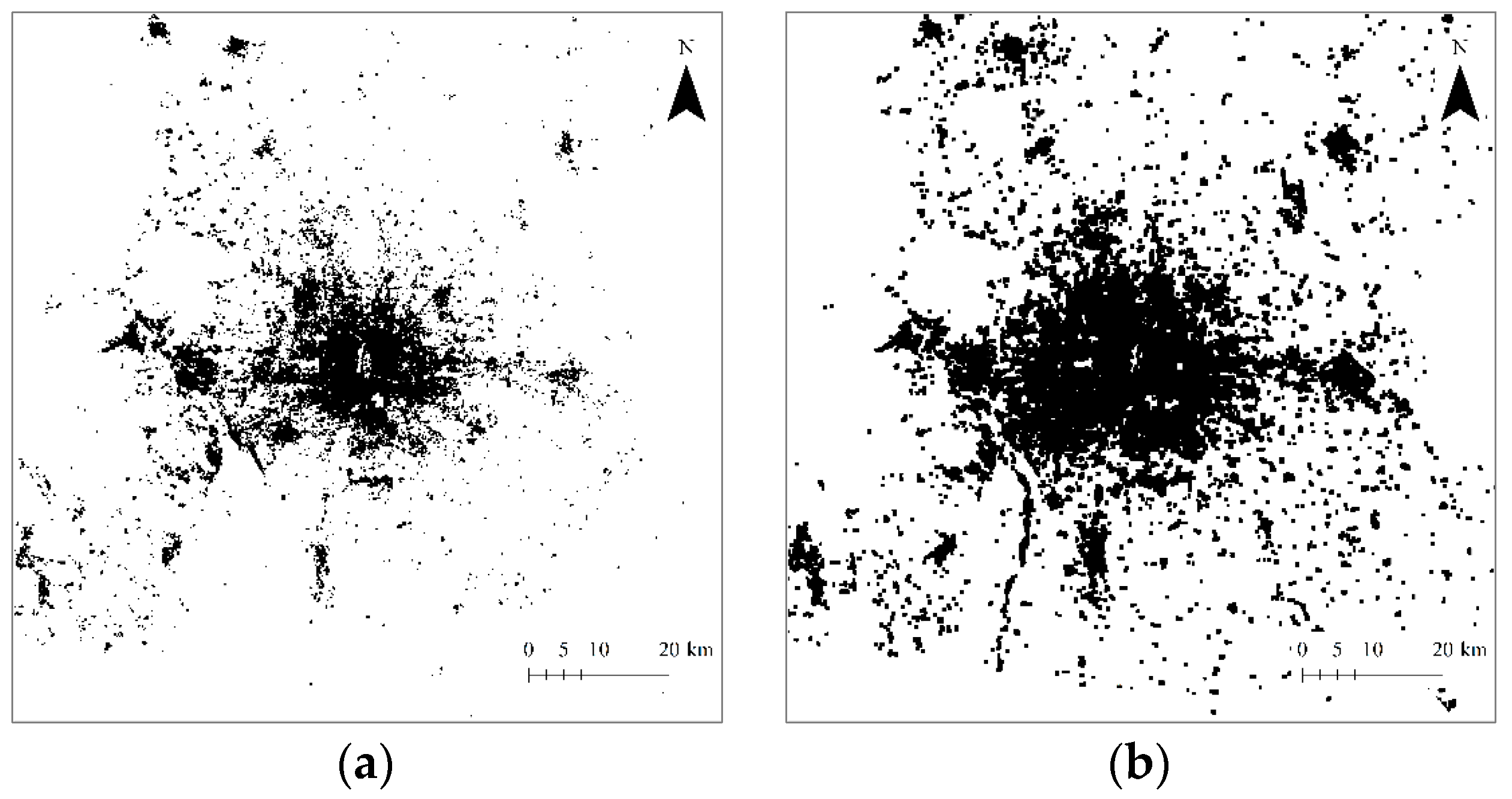
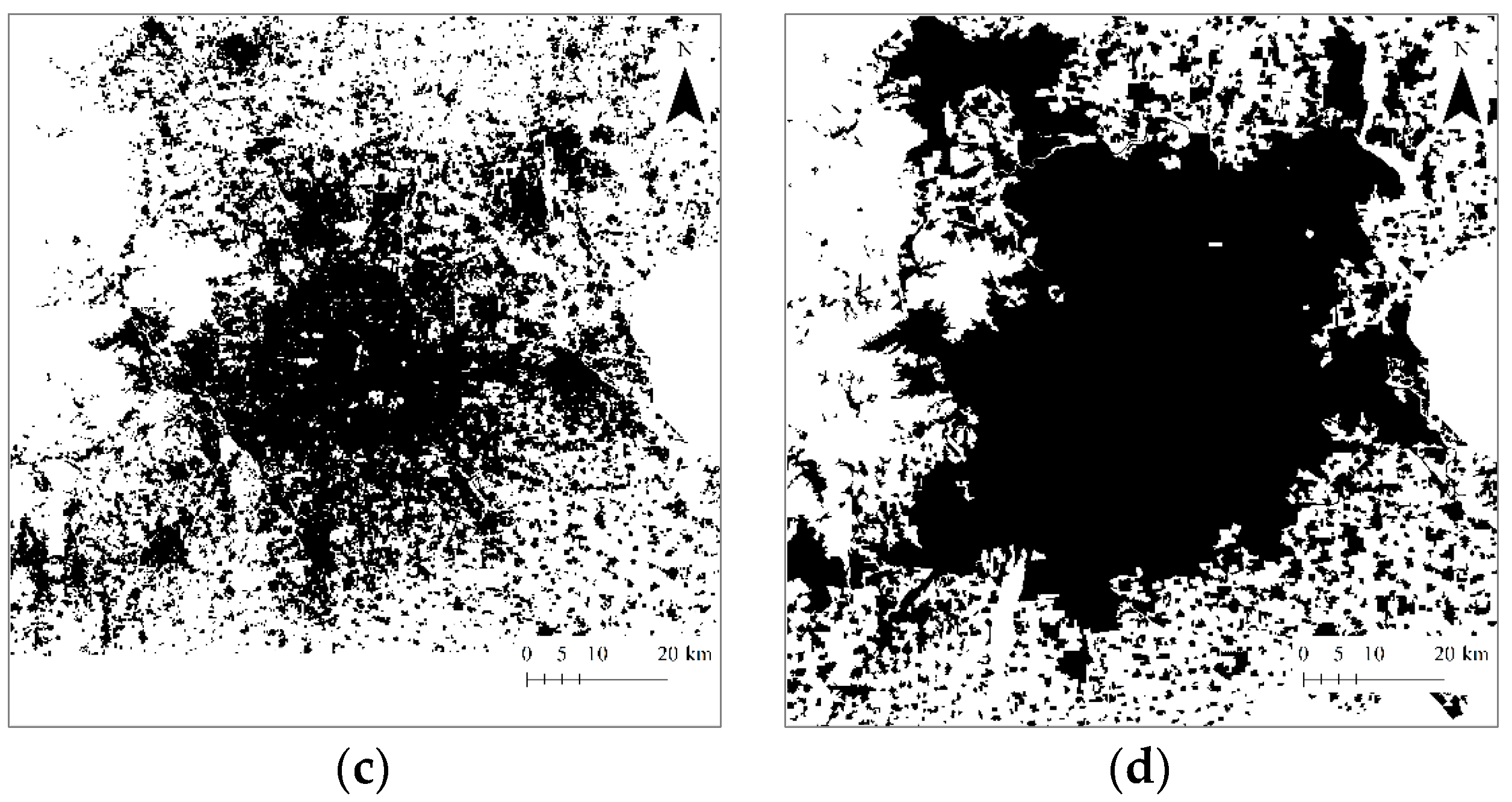
- Step 1: Defining an urban boundary based on the recent image. The most recent material we used was the remote sensing image of 2015. Based on this image, the boundary of Beijing city can be identified by using the “City Clustering Algorithm” (CCA) developed by Rozenfeld et al. [40,41]. The urban boundary can be called an urban envelope [15,32]. Then, a measure area can be determined in terms of the urban envelope [8].
- Step 2: Extracting the spatial datasets using the function box-counting method. First of all, we can extract the dataset from the image of the recent year (2015). A set of boxes is actually a grid of rectangular squares, each of which has an area of urban land use. The area may be represented by the pixel number. Therefore, in the dataset, each number represents a value of land-use area of the urban pattern falling into a box (square). Changing the linear size of the boxes, we will have different datasets. The box system forms a hierarchy of grids, which yield a hierarchy of spatial datasets. Applying the system of boxes to the images in different years, we have different datasets for calculating spatial entropy and fractal dimensions.
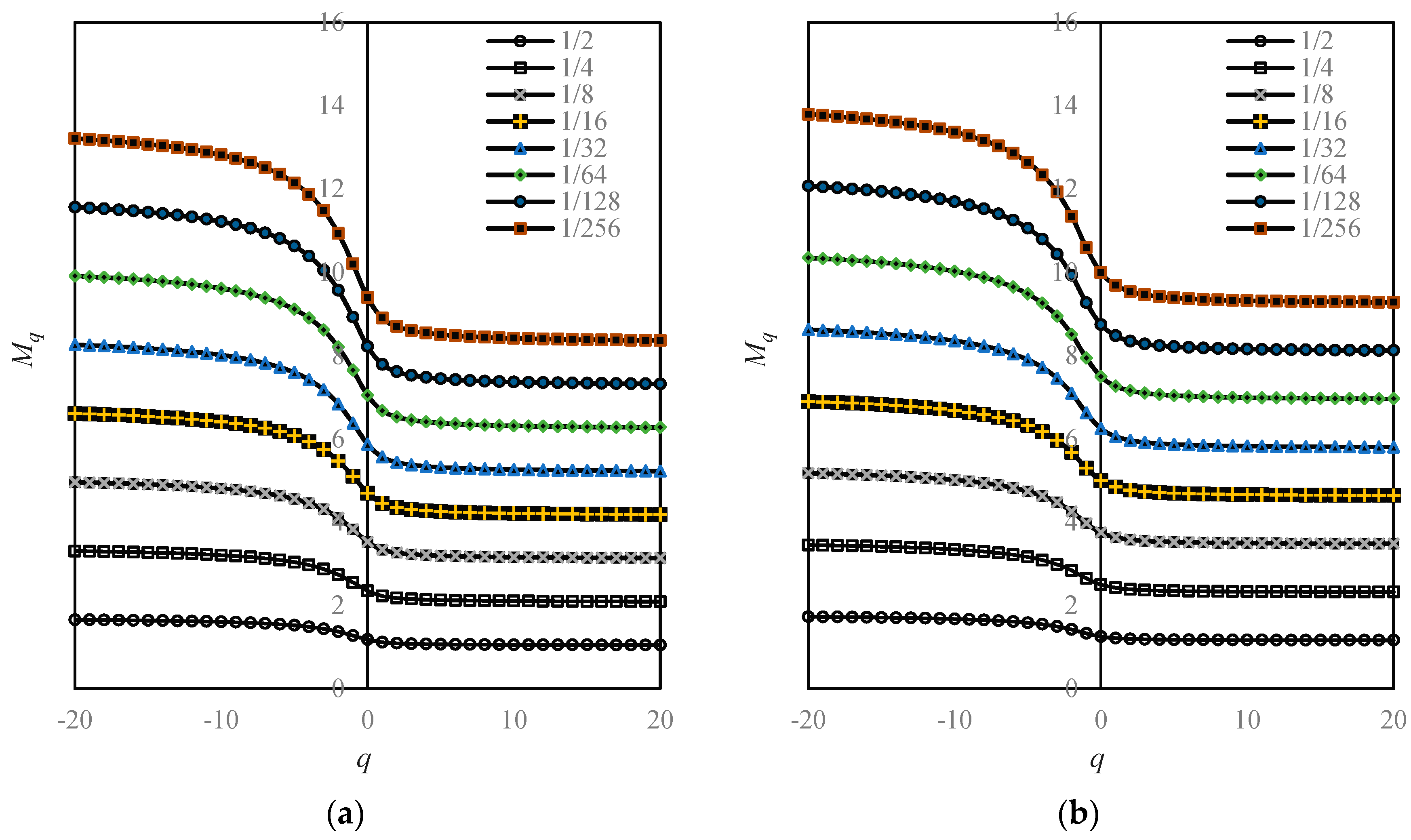
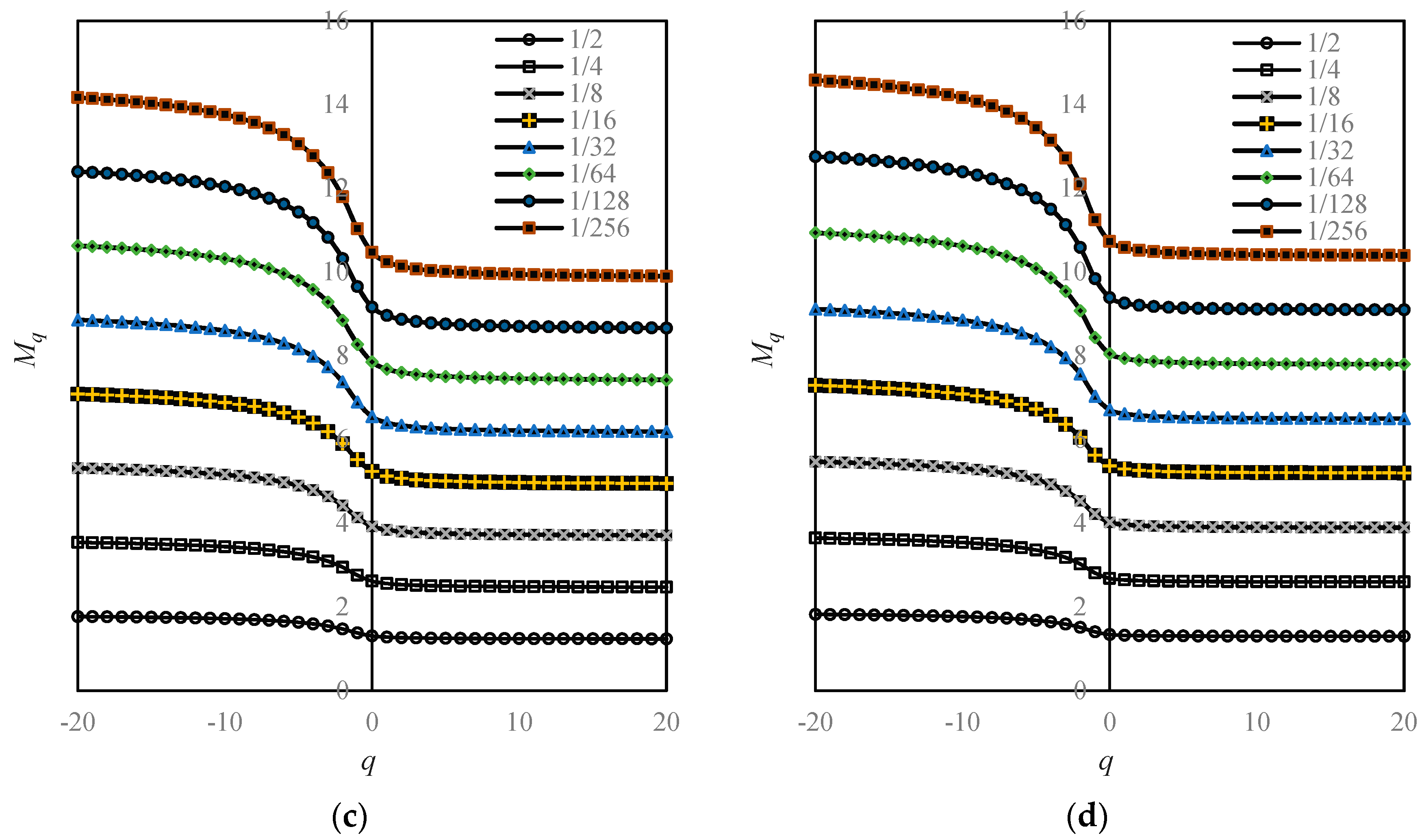
- Step 3: Calculate the spatial Renyi entropy and generalized Shannon entropy. Using Equations (5)–(8), we can compute the generalized entropies of urban land use based on a given linear size of functional boxes. For each linear size of boxes, we can obtain a Renyi entropy value or a generalized Shannon entropy value for Beijing’s urban form. For each year, we have a number of sets of entropy values based on different linear sizes of boxes. If the entropy values based on different box sizes have no significant differences, we can utilize the generalized entropy values to conduct a spatial analysis of urban form and growth.
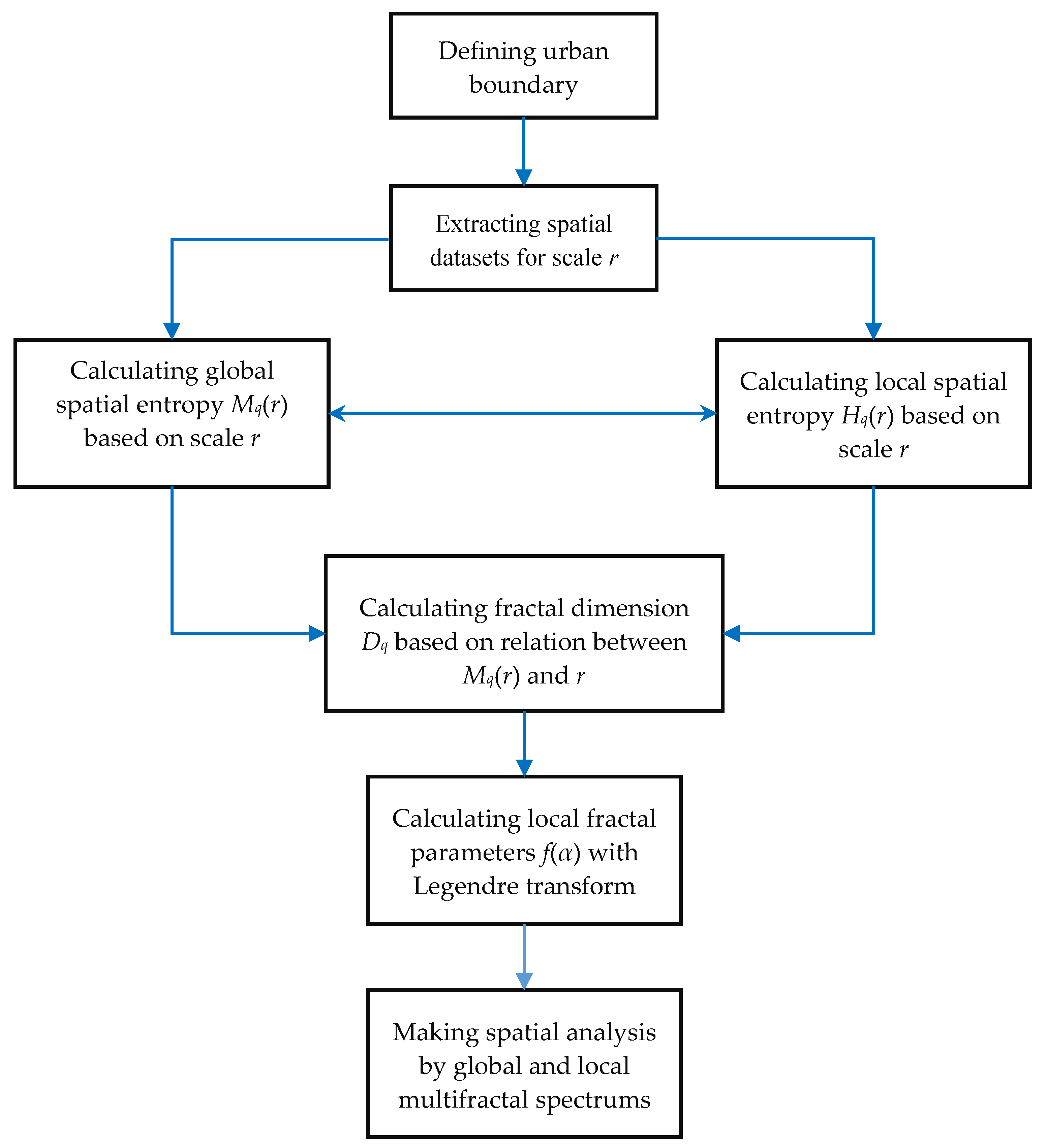
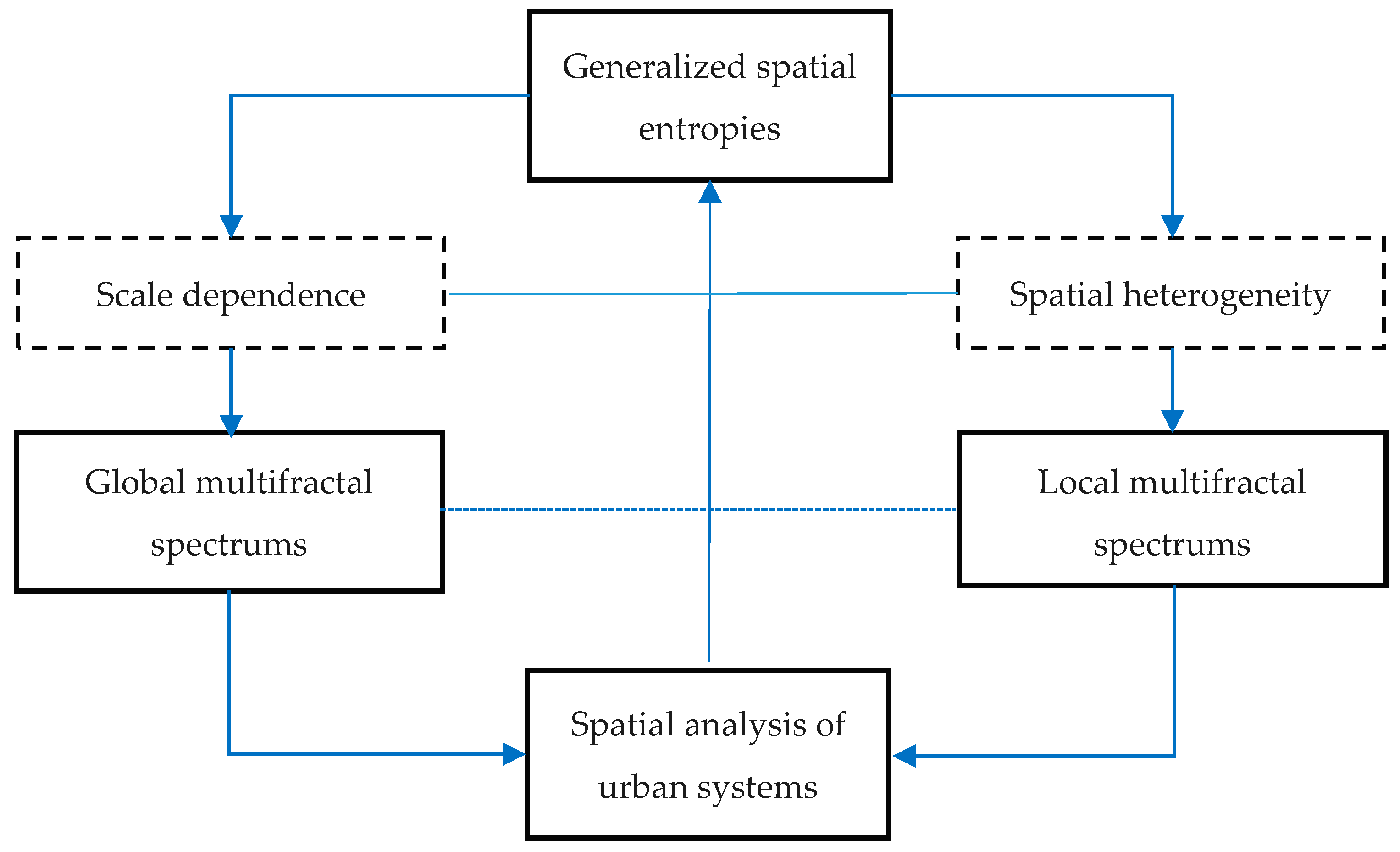
- Step 4: Computing the multifractal parameter spectrums. If the entropy values depend heavily on the linear sizes of boxes, we should transform the Renyi entropy into the generalized correlation dimension using Equation (4). For different linear sizes of boxes r, we have different Renyi entropy values, which are defined as Mq(r). As shown by Equation (5), there is a linear relation between ln(r) and Mq(r). Similarly, we can convert the generalized Shannon entropy values into local multifractal dimension using Equations (7) and (8). By using Legendre transform, as shown in Equations (11) and (12), a complete set of multifractal parameters can be obtained, and multifractal spectrums can be generated. The computational and analytical process can be illustrated as follows (Figure 4).
3.2. Results and Findings
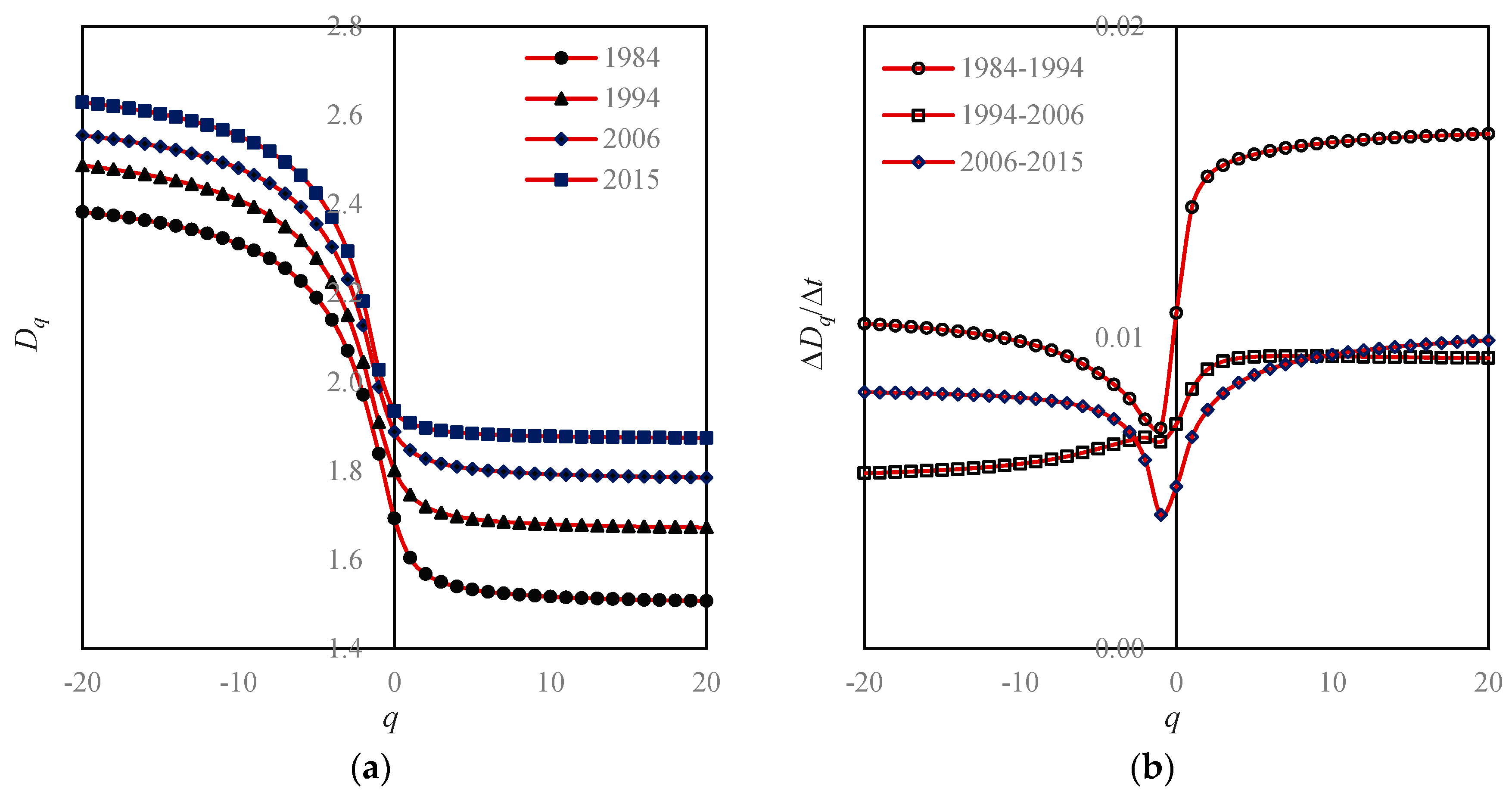
- First, Beijing’s space-filling speed was too fast, and space-filling extent was too high. From 1984 to 1994 to 2006 and then to 2015, the capacity dimension D0 values increased from 1.6932 to 1.8011 and 1.8877 to 1.9346. By means of the formula v = D0/2, we can calculate the space-filling rate of urban form [31,44], v; the results were 0.8466, 0.9005, 0.9439, and 0.9673. In recent years, the level of space filling is close to the upper limit of one.
- Second, spatial heterogeneity became weaker and weaker. From 1984 to 1994 and 2006 to 2015, the information dimension D1 values went up from 1.6048 to 1.7467 and 1.8468 to 1.9081. Using the formula u = 1 − D1/2, we can calculate the spatial redundancy rate of urban form, u; the results were 0.1976, 0.1267, 0.0766, and 0.0459. The spatial redundancy rate is in fact an index of spatial heterogeneity. A reduction of redundancy indicates a weakening process of spatial heterogeneity.
- Third, the urban growth of Beijing is characterized by stages. In the mass, the space-filling speed in the central area was obviously faster than that of the edge area (Figure 6 and Figure 7). Where the global feature is concerned, the characteristics are as below: From 1984 to 1994, the land-use speed in the central urban area was significantly higher than that in the fringe area; From 1994 to 2006, the gap of land-use speed between the central and peripheral areas decreased; from 2006 to 2015, the speed of land use in the central and peripheral areas was close to equilibrium (Figure 6b). Where the local level is concerned, the features are as below: From 1984 to 1994, the land-use speed in high-density areas was significantly higher than that in low-density areas. From 1994 to 2006, the situation reversed, and the land-use speed in low-density areas was significantly higher than that in high-density areas. From 2006 to 2015, the land-use speed in high-density areas was once again higher than that in low-density areas (Figure 7b).
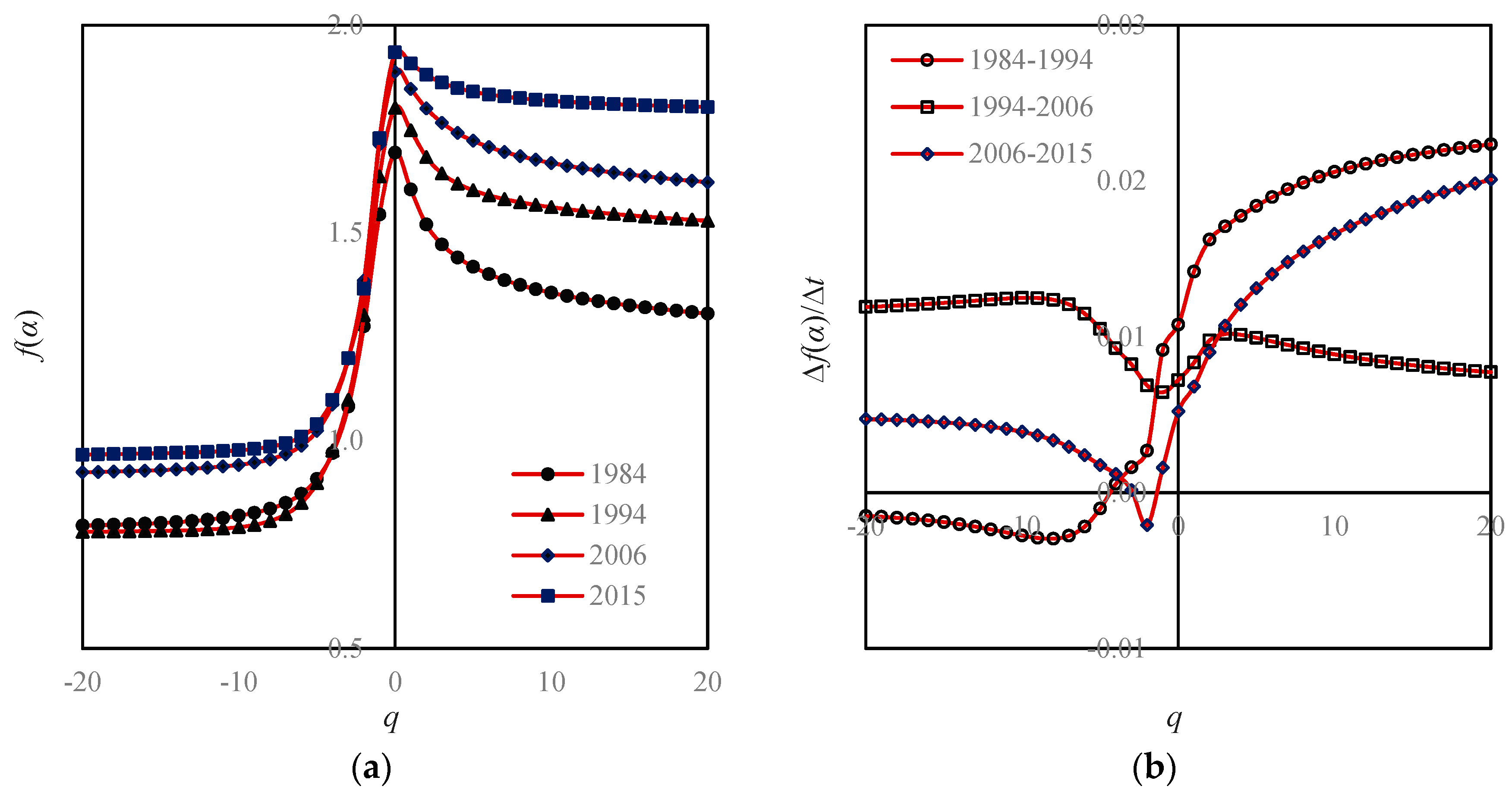
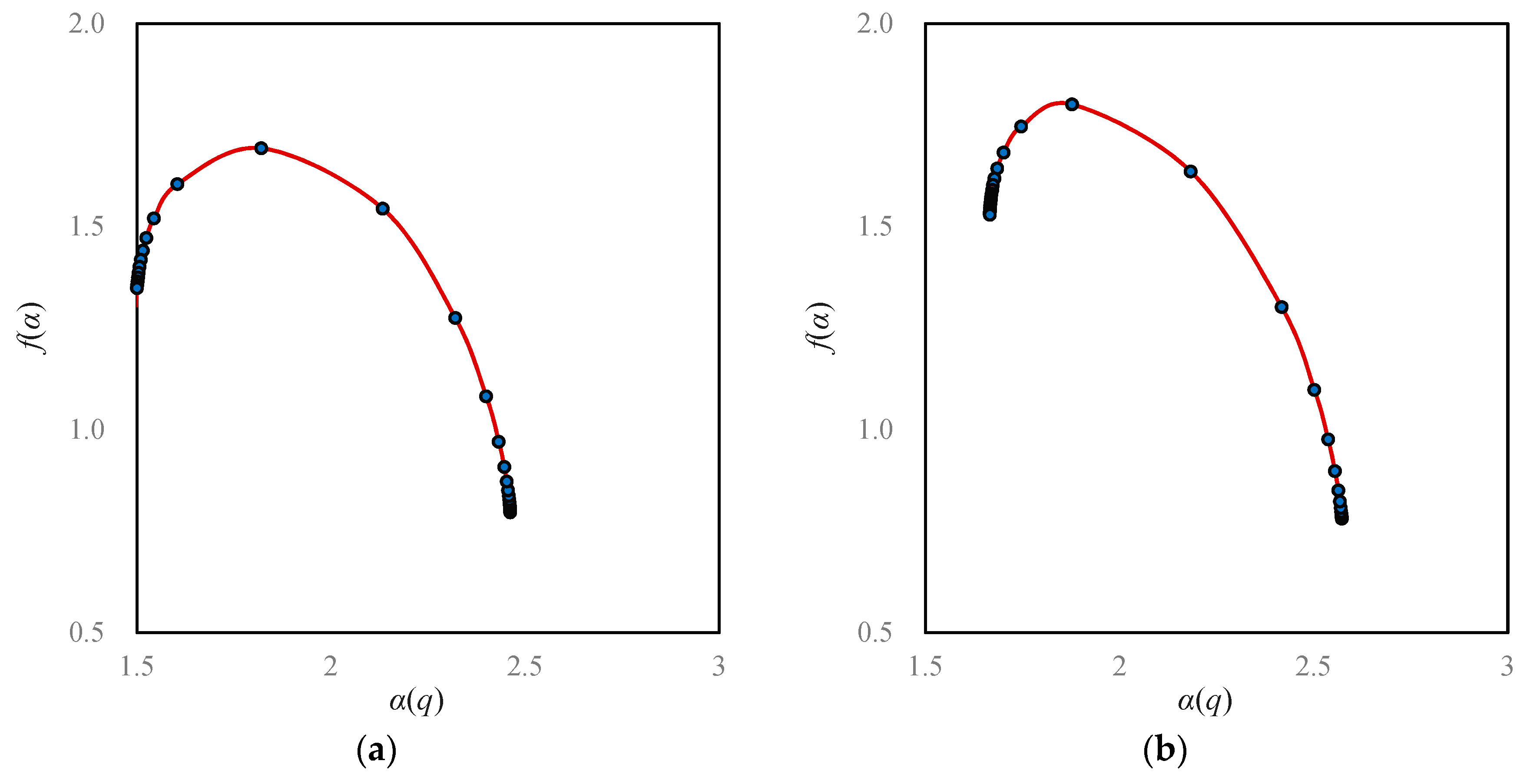
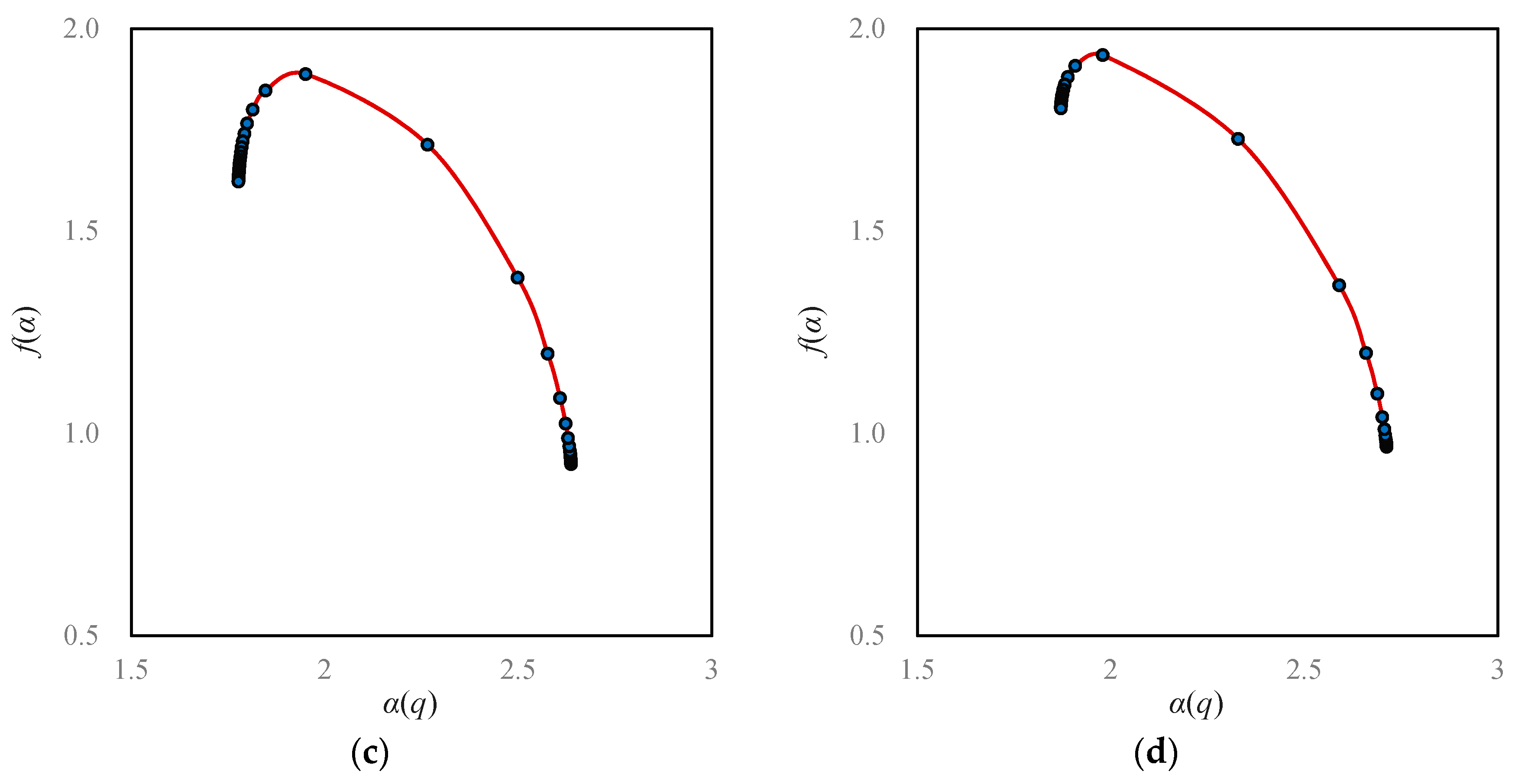
- Fourth, the growth of Beijing city is of outward expansion. On the whole, the closer to the center area, the faster the space-filling speed will be. In terms of local fractal spectrums, city development can be classified into two types: one is central aggregation, and the other is peripheral expansion [43]. The difference can be reflected by the local multifractal spectrums. The unbalance of urban spatial expansion leads to the asymmetry of f(α) curves. If the urban development is centralized, the peak of the spectral curve tilts to the right; on the contrary, if the urban development is characterized by periphery diffusion, the peak of the spectrum inclines to the left [43]. The peak values of Beijing’s f(α) curves are obviously left-sided, which imply that Beijing’s development is mainly a process of expanding to the periphery (Figure 8).
- Fifth, there was redundant correlation in Beijing’s urban fringe. Generally speaking, the generalized correlation dimension value lies between zero and two. However, when the order of moment q approaches negative infinity, the Dq values exceeded two, and became bigger and bigger (Figure 6). This suggests that there are too many messy patches of land use to fill the urban fringe.
- Sixth, the quality of spatial structure of Beijing city declined. A local multifractal spectrum is supposed to be a smooth single-peak curve. In 1984, the local fractal dimension spectral lines were regular. However, from 1995 to 2015, the f(α) curves deviated more and more from the normative spectral line (Figure 8).
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- De Blij, H.J.; Muller, P.O. Geography: Realms, Regions, and Concepts, 8th ed.; John Wiley & Sons: New York, NY, USA, 1997. [Google Scholar]
- Allen, P.M. Cities and Regions as Self-Organizing Systems: Models of Complexity; Routledge: London, UK; New York, NY, USA, 1997. [Google Scholar]
- Portugali, J. Complexity, Cognition and the City; Springer: Heidelberg, Germany, 2011. [Google Scholar]
- Wilson, A.G. Complex Spatial Systems: The Modelling Foundations of Urban and Regional Analysis; Pearson Education: Singapore, 2000. [Google Scholar]
- Bar-Yam, Y. Multiscale complexity/entropy. Adv. Complex Syst. 2004, 7, 47–63. [Google Scholar] [CrossRef]
- Batty, M.; Morphet, R.; Masucci, P.; Stanilov, K. Entropy, complexity, and spatial information. J. Geogr. Syst. 2014, 16, 363–385. [Google Scholar] [CrossRef] [PubMed]
- Cramer, F. Chaos and Order: The Complex Structure of Living Systems; Loewus, D.I., Translator; VCH Publishers: New York, NY, USA, 1993. [Google Scholar]
- Chen, Y.G.; Wang, J.J.; Feng, J. Understanding the fractal dimensions of urban forms through spatial entropy. Entropy 2017, 19, 600. [Google Scholar] [CrossRef]
- Ryabko, B.Y. Noise-free coding of combinatorial sources, Hausdorff dimension and Kolmogorov complexity. Probl. Peredachi Inf. 1986, 22, 16–26. [Google Scholar]
- Stanley, H.E.; Meakin, P. Multifractal phenomena in physics and chemistry. Nature 1988, 335, 405–409. [Google Scholar] [CrossRef]
- Chen, Y.-G. Defining urban and rural regions by multifractal spectrums of urbanization. Fractals 2016, 24, 1650004. [Google Scholar] [CrossRef]
- Chen, Y.-G. Normalizing and classifying shape indexes of cities by ideas from fractals. arXiv, 2017; arXiv:1608.08839. [Google Scholar]
- Vicsek, T. Fractal Growth Phenomena; World Scientific Publishing Co.: Singapore, 1989. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W. H. Freeman and Company: New York, NY, USA, 1982. [Google Scholar]
- Batty, M.; Longley, P.A. Fractal Cities: A Geometry of Form and Function; Academic Press: London, UK, 1994. [Google Scholar]
- Frankhauser, P. The fractal approach: A new tool for the spatial analysis of urban agglomerations. Popul. Engl. Sel. 1998, 10, 205–240. [Google Scholar]
- Liu, S.-D.; Liu, S.-K. An Introduction to Fractals and Fractal Dimension; Meteorological Press: Beijing, China, 1993. (In Chinese) [Google Scholar]
- Feder, J. Fractals; Plenum Press: New York, NY, USA, 1988. [Google Scholar]
- Meakin, P.; Coniglio, A.; Stanley, H.E.; Witten, T.A. Scaling properties for the surfaces of fractal and nonfractal objects: An infinite hierarchy of critical exponents. Phys. Rev. A 1986, 34, 3325–3340. [Google Scholar] [CrossRef]
- Jullien, R.; Botet, R. Aggregation and Fractal Aggregates; World Scientific Publishing Co.: Singapore, 1987. [Google Scholar]
- Halsey, T.C.; Jensen, M.H.; Kadanoff, L.P.; Procaccia, I.; Shraiman, B.I. Fractal measure and their singularities: The characterization of strange sets. Phys. Rev. A 1986, 33, 1141–1151. [Google Scholar] [CrossRef]
- Hentschel, H.E.; Procaccia, I. The infinite number of generalized dimensions of fractals and strange attractors. Phys. D Nonlinear Phenom. 1983, 8, 435–444. [Google Scholar] [CrossRef]
- Grassberger, P. Generalized dimension of strange attractors. Phys. Lett. A 1983, 97, 227–230. [Google Scholar] [CrossRef]
- Grassberger, P. Generalizations of the Hausdorff dimension of fractal measures. Phys. Lett. A 1985, 107, 101–105. [Google Scholar] [CrossRef]
- Chen, Y.-G.; Feng, J. Spatial analysis of cities using Renyi entropy and fractal parameters. Chaos Solitons Fractals 2017, 105, 279–287. [Google Scholar] [CrossRef]
- Chhabra, A.; Jensen, R.V. Direct determination of the f(α) singularity spectrum. Phys. Rev. Lett. 1989, 62, 1327–1330. [Google Scholar] [CrossRef] [PubMed]
- Chhabra, A.; Meneveau, C.; Jensen, R.V.; Sreenivasan, K.R. Direct determination of the f(α) singularity spectrum and its application to fully developed turbulence. Phys. Rev. A 1989, 40, 5284–5294. [Google Scholar] [CrossRef]
- Frisch, U.; Parisi, G. On the singularity structure of fully developed turbulence. In Turbulence and Predictability in Geophysical Fluid Dynamics and Climate Dynamics; Ghil, M., Benzi, R., Parisi, G., Eds.; North-Holland: New York, NY, USA, 1985; pp. 84–88. [Google Scholar]
- Chen, Y.-G.; Wang, J.-J. Multifractal characterization of urban form and growth: The case of Beijing. Environ. Plan. B Plan. Des. 2013, 40, 884–904. [Google Scholar] [CrossRef]
- Stigler, S. Stigler’s law of eponymy. In Science and Social Structure: A Festschrift for Robert K. Merton; Gieryn, T.F., Ed.; Academy of Sciences: New York, NY, USA, 1980; pp. 147–157. [Google Scholar]
- Chen, Y.-G. Fractal dimension evolution and spatial replacement dynamics of urban growth. Chaos Solitons Fractals 2012, 45, 115–124. [Google Scholar] [CrossRef]
- Longley, P.A.; Batty, M.; Shepherd, J. The size, shape and dimension of urban settlements. Trans. Inst. Br. Geogr. 1991, 16, 75–94. [Google Scholar] [CrossRef]
- White, R.; Engelen, G. Cellular automata and fractal urban form: A cellular modeling approach to the evolution of urban land-use patterns. Environ. Plan. A 1993, 25, 1175–1199. [Google Scholar] [CrossRef]
- Huang, L.-S.; Chen, Y.-G. A comparison between two OLS-based approaches to estimating urban multifractal parameters. Fractals 2018, 26, 1850019. [Google Scholar] [CrossRef]
- Lovejoy, S.; Schertzer, D.; Tsonis, A.A. Functional box-counting and multiple elliptical dimensions in rain. Science 1987, 235, 1036–1038. [Google Scholar] [CrossRef] [PubMed]
- Chen, T. Studies on Fractal Systems of Cities and Towns in the Central Plains of China. Master’s Thesis, Northeast Normal University, Changchun, China, 15 June 1995. (In Chinese). [Google Scholar]
- Feng, J.; Chen, Y.-G. Spatiotemporal evolution of urban form and land use structure in Hangzhou, China: Evidence from fractals. Environ. Plan. B Plan. Des. 2010, 37, 838–856. [Google Scholar] [CrossRef]
- Goodchild, M.F.; Mark, D.M. The fractal nature of geographical phenomena. Ann. Assoc. Am. Geogr. 1987, 77, 265–278. [Google Scholar] [CrossRef]
- Chen, Y.-G. The mathematical relationship between Zipf’s law and the hierarchical scaling law. Phys. A Stat. Mech. Its Appl. 2012, 391, 3285–3299. [Google Scholar] [CrossRef]
- Rozenfeld, H.D.; Rybski, D.; Andrade, D.S., Jr.; Batty, M.; Stanley, H.E.; Makse, H.A. Laws of population growth. Proc. Natl. Acad. Sci. USA 2008, 105, 18702–18707. [Google Scholar] [CrossRef]
- Rozenfeld, H.D.; Rybski, D.; Gabaix, X.; Makse, H.A. The area and population of cities: New insights from a different perspective on cities. Am. Econ. Rev. 2011, 101, 2205–2225. [Google Scholar] [CrossRef]
- Batty, M. Space, scale, and scaling in entropy maximizing. Geogr. Anal. 2010, 42, 395–421. [Google Scholar] [CrossRef]
- Chen, Y.-G. Multifractals of central place systems: Models, dimension spectrums, and empirical analysis. Phys. A Stat. Mech. Its Appl. 2014, 402, 266–282. [Google Scholar] [CrossRef]
- Chen, Y.-G. Logistic models of fractal dimension growth of urban morphology. Fractals 2018, 26, 1850033. [Google Scholar] [CrossRef]
- Anselin, L. The Moran scatterplot as an ESDA tool to assess local instability in spatial association. In Spatial Analytical Perspectives on GIS; Fischer, M., Scholten, H.J., Unwin, D., Eds.; Taylor & Francis: London, UK, 1996; pp. 111–125. [Google Scholar]
- Goodchild, M.F. GIScience, geography, form, and process. Ann. Assoc. Am. Geogr. 2004, 94, 709–714. [Google Scholar]
- Encarnação, S.; Gaudiano, M.; Santos, F.C.; Tenedório, J.A.; Pacheco, J.M. Urban dynamics, fractals and generalized entropy. Entropy 2013, 15, 2679–2697. [Google Scholar] [CrossRef]
- Fan, Y.; Yu, G.-M.; He, Z.-Y.; Yu, H.-L.; Bai, R.; Yang, L.-R.; Wu, D. Entropies of the Chinese land use/cover change from 1990 to 2010 at a county level. Entropy 2017, 19, 51. [Google Scholar] [CrossRef]
- Padmanaban, R.; Bhowmik, A.K.; Cabral, P.; Zamyatin, A.; Almegdadi, O.; Wang, S.G. Modelling urban sprawl using remotely sensed data: A case study of Chennai City, Tamilnadu. Entropy 2017, 19, 163. [Google Scholar] [CrossRef]
- Terzi, F.; Kaya, H.S. Dynamic spatial analysis of urban sprawl through fractal geometry: The case of Istanbul. Environ. Plan. B 2011, 38, 175–190. [Google Scholar] [CrossRef]
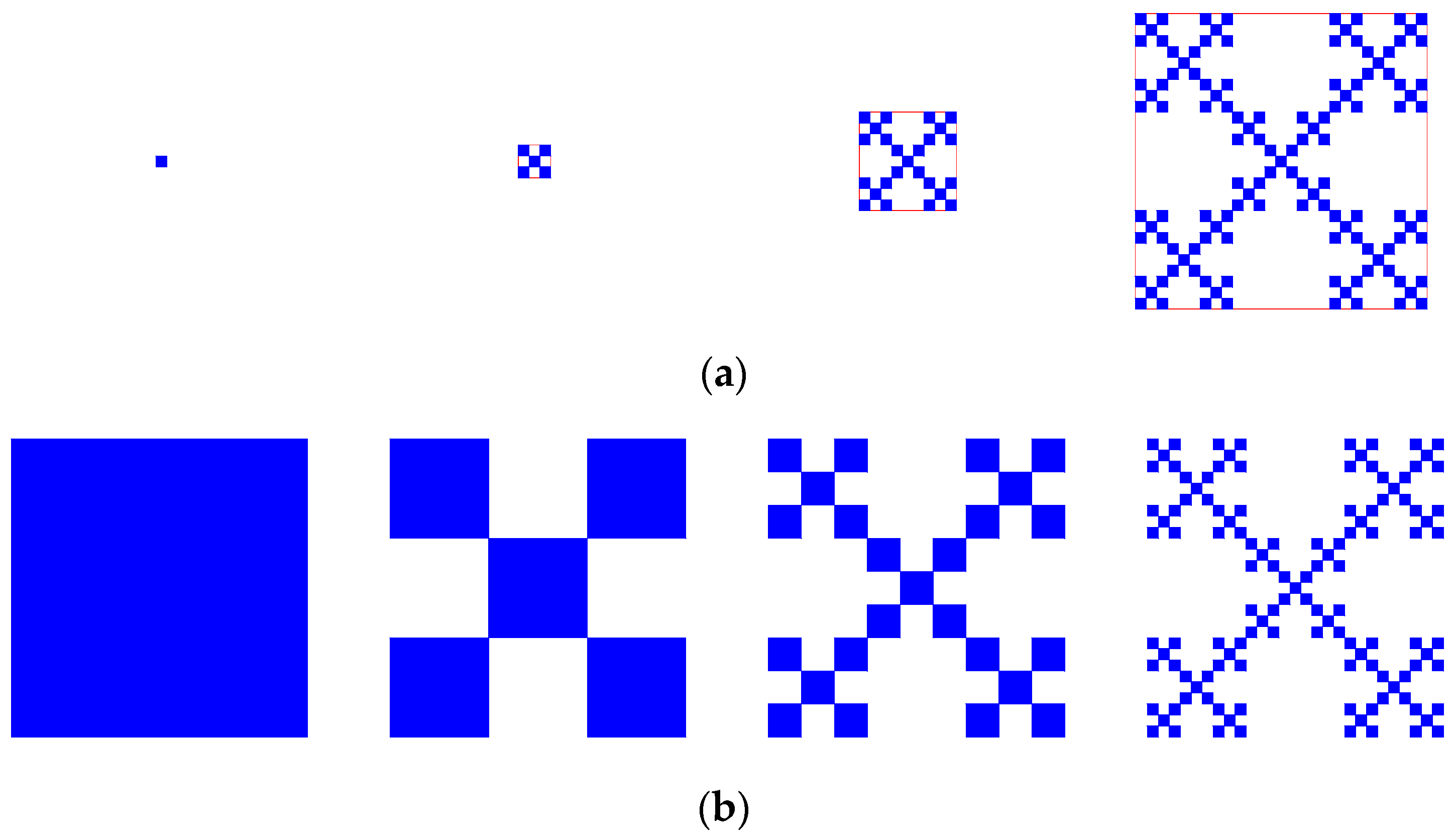

| Step for Fractal Generation | Figure 1a: Variable Size of Study Area and Measurement Scale | Figure 1b: Fixed Size of Study Area and Variable Measurement Scale | ||
|---|---|---|---|---|
| Entropy (nat) | Fractal Dimension | Entropy (nat) | Fractal Dimension | |
| 1 (outlier) | 0 | 0 | 0 | 2 |
| 2 | 1.6094 | 1.4650 | 1.6094 | 1.4650 |
| 3 | 3.2189 | 1.4650 | 3.2189 | 1.4650 |
| 4 | 4.8283 | 1.4650 | 4.8283 | 1.4650 |
| … | … | … | … | … |
| m | ln(5m−1) | ln(5m−1)/ln(3m−1) | ln(5m−1) | ln(5m−1)/ln(3m−1) |
| Step for Fractal Generation | Global Feature | Local Features | ||||
|---|---|---|---|---|---|---|
| Central Part | Peripheral Parts | |||||
| Entropy (nat) | Fractal Dimension | Entropy (nat) | Fractal Dimension | Entropy (nat) | Fractal Dimension | |
| 1 (outlier) | 0 | 0 | 0 | - | 0 | - |
| 2 | 1.5285 | 1.7604 | 0.1667 | 1.7604 | 1.3618 | 1.5791 |
| 3 | 3.0569 | 1.7604 | 1.5285 | 1.7604 | 1.5285 | 1.5791 |
| Moment Order q | Generalized Entropy Based on Different Scales r | |||||||
|---|---|---|---|---|---|---|---|---|
| r = 1/2 | r = 1/4 | r = 1/8 | r = 1/16 | r = 1/32 | r = 1/64 | r = 1/128 | r = 1/256 | |
| −20 | 1.8225 | 3.6449 | 5.4674 | 7.2898 | 9.1123 | 10.9347 | 12.7572 | 14.5797 |
| −15 | 1.8045 | 3.6089 | 5.4134 | 7.2179 | 9.0223 | 10.8268 | 12.6313 | 14.4357 |
| −10 | 1.7702 | 3.5405 | 5.3107 | 7.0809 | 8.8511 | 10.6214 | 12.3916 | 14.1618 |
| −5 | 1.6806 | 3.3612 | 5.0417 | 6.7223 | 8.4029 | 10.0835 | 11.7640 | 13.4446 |
| −4 | 1.6430 | 3.2859 | 4.9289 | 6.5718 | 8.2148 | 9.8578 | 11.5007 | 13.1437 |
| −3 | 1.5901 | 3.1801 | 4.7702 | 6.3602 | 7.9503 | 9.5403 | 11.1304 | 12.7204 |
| −2 | 1.5123 | 3.0246 | 4.5369 | 6.0493 | 7.5616 | 9.0739 | 10.5862 | 12.0985 |
| −1 | 1.4058 | 2.8116 | 4.2174 | 5.6232 | 7.0290 | 8.4348 | 9.8406 | 11.2464 |
| 0 | 1.3410 | 2.6820 | 4.0230 | 5.3640 | 6.7050 | 8.0460 | 9.3870 | 10.7280 |
| 1 | 1.3226 | 2.6452 | 3.9679 | 5.2905 | 6.6131 | 7.9357 | 9.2583 | 10.5809 |
| 2 | 1.3148 | 2.6296 | 3.9443 | 5.2591 | 6.5739 | 7.8887 | 9.2035 | 10.5183 |
| 3 | 1.3105 | 2.6209 | 3.9314 | 5.2419 | 6.5523 | 7.8628 | 9.1732 | 10.4837 |
| 4 | 1.3078 | 2.6155 | 3.9233 | 5.2311 | 6.5388 | 7.8466 | 9.1544 | 10.4621 |
| 5 | 1.3059 | 2.6119 | 3.9178 | 5.2237 | 6.5297 | 7.8356 | 9.1416 | 10.4475 |
| 10 | 1.3017 | 2.6035 | 3.9052 | 5.2069 | 6.5087 | 7.8104 | 9.1122 | 10.4139 |
| 15 | 1.3001 | 2.6003 | 3.9004 | 5.2006 | 6.5007 | 7.8008 | 9.1010 | 10.4011 |
| 20 | 1.2993 | 2.5986 | 3.8979 | 5.1972 | 6.4965 | 7.7957 | 9.0950 | 10.3943 |
| Moment Order q | Fractal Parameter and Goodness of Fit | ||||||
|---|---|---|---|---|---|---|---|
| Dq | R2 | τq | α(q) | R2 | f(α) | R2 | |
| −20 | 2.6293 | 0.8308 | −55.2143 | 2.7124 | 0.8113 | 0.9664 | 0.7092 |
| −15 | 2.6033 | 0.8369 | −41.6527 | 2.7122 | 0.8115 | 0.9698 | 0.7112 |
| −10 | 2.5539 | 0.8484 | −28.0929 | 2.7116 | 0.8120 | 0.9771 | 0.7159 |
| −5 | 2.4246 | 0.8790 | −14.5473 | 2.7015 | 0.8116 | 1.0397 | 0.7361 |
| −4 | 2.3703 | 0.8927 | −11.8515 | 2.6884 | 0.8082 | 1.0979 | 0.7423 |
| −3 | 2.2940 | 0.9137 | −9.1759 | 2.6592 | 0.8012 | 1.1983 | 0.7535 |
| −2 | 2.1818 | 0.9470 | −6.5454 | 2.5898 | 0.7984 | 1.3658 | 0.8074 |
| −1 | 2.0281 | 0.9874 | −4.0563 | 2.3288 | 0.8782 | 1.7275 | 0.9683 |
| 0 | 1.9346 | 0.9992 | −1.9346 | 1.9791 | 0.9951 | 1.9346 | 0.9992 |
| 1 | 1.9081 | 1.0000 | 0.0000 | 1.9081 | 1.0000 | 1.9081 | 1.0000 |
| 2 | 1.8968 | 0.9998 | 1.8968 | 1.8888 | 0.9994 | 1.8807 | 0.9987 |
| 3 | 1.8906 | 0.9995 | 3.7812 | 1.8810 | 0.9986 | 1.8618 | 0.9959 |
| 4 | 1.8867 | 0.9992 | 5.6601 | 1.8773 | 0.9982 | 1.8489 | 0.9927 |
| 5 | 1.8841 | 0.9989 | 7.5363 | 1.8752 | 0.9979 | 1.8399 | 0.9900 |
| 10 | 1.8780 | 0.9982 | 16.9021 | 1.8720 | 0.9974 | 1.8181 | 0.9824 |
| 15 | 1.8757 | 0.9979 | 26.2599 | 1.8712 | 0.9973 | 1.8086 | 0.9784 |
| 20 | 1.8745 | 0.9978 | 35.6151 | 1.8709 | 0.9972 | 1.8031 | 0.9757 |
| Parameter Level | Entropy | Fractal Dimension | |
| Global parameter | General | Renyi entropy spectrum | Global multifractal dimension spectrum |
| Special | Hartley entropy | Capacity dimension | |
| Shannon entropy | Information dimension | ||
| The second-order Renyi entropy | Correlation dimension | ||
| Connection | Legendre Transform | ||
| Local parameter | General | Generalized Shannon entropy spectrum | Local multifractal dimension spectrum |
| Mixed entropy | Singularity exponent spectrum | ||
| Special | Hartley entropy | Capacity dimension | |
| Shannon entropy | Information dimension | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Huang, L. Spatial Measures of Urban Systems: from Entropy to Fractal Dimension. Entropy 2018, 20, 991. https://doi.org/10.3390/e20120991
Chen Y, Huang L. Spatial Measures of Urban Systems: from Entropy to Fractal Dimension. Entropy. 2018; 20(12):991. https://doi.org/10.3390/e20120991
Chicago/Turabian StyleChen, Yanguang, and Linshan Huang. 2018. "Spatial Measures of Urban Systems: from Entropy to Fractal Dimension" Entropy 20, no. 12: 991. https://doi.org/10.3390/e20120991
APA StyleChen, Y., & Huang, L. (2018). Spatial Measures of Urban Systems: from Entropy to Fractal Dimension. Entropy, 20(12), 991. https://doi.org/10.3390/e20120991






