Multiscale Distribution Entropy Analysis of Short-Term Heart Rate Variability
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Entropy
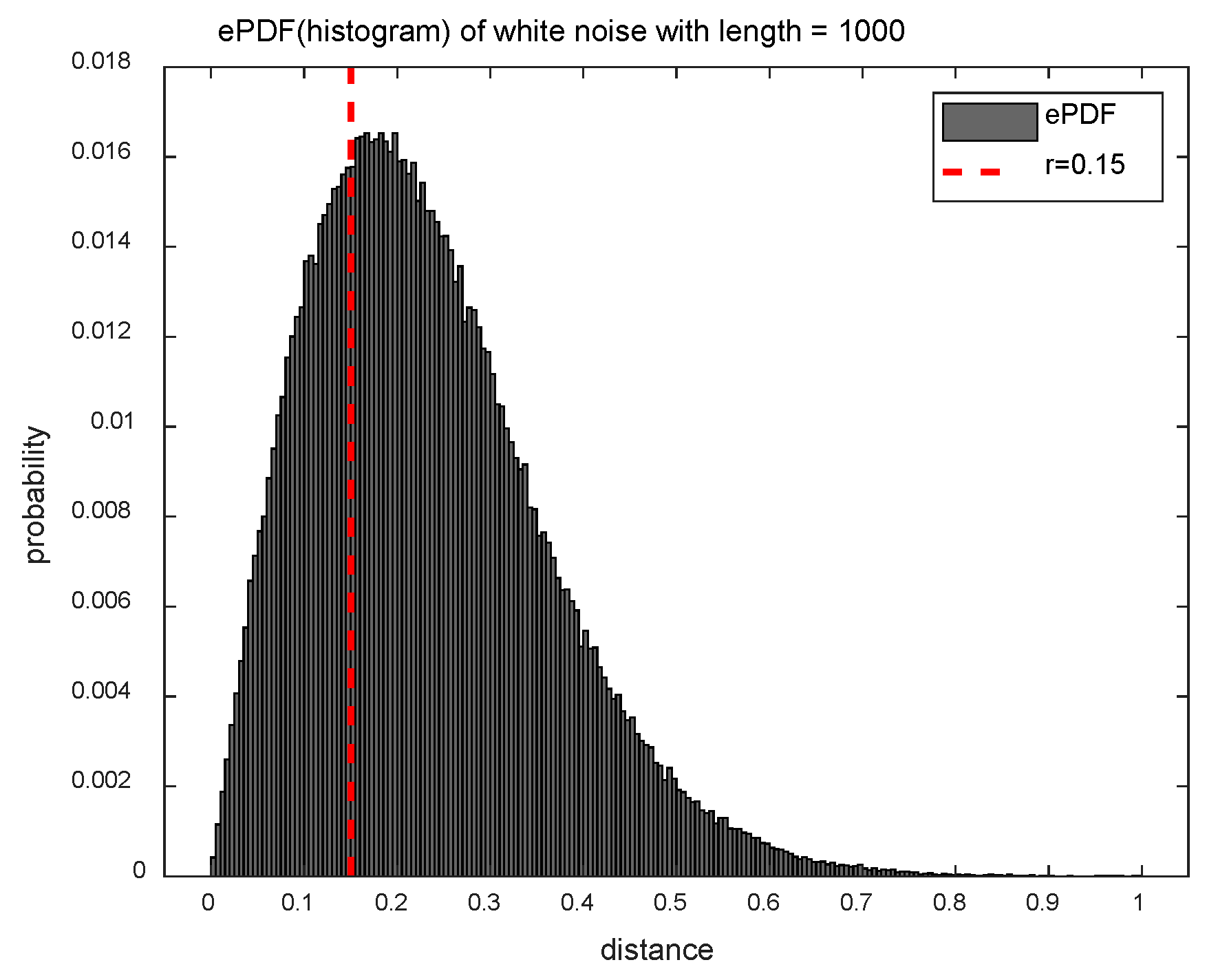
2.2. Distribution Entropy
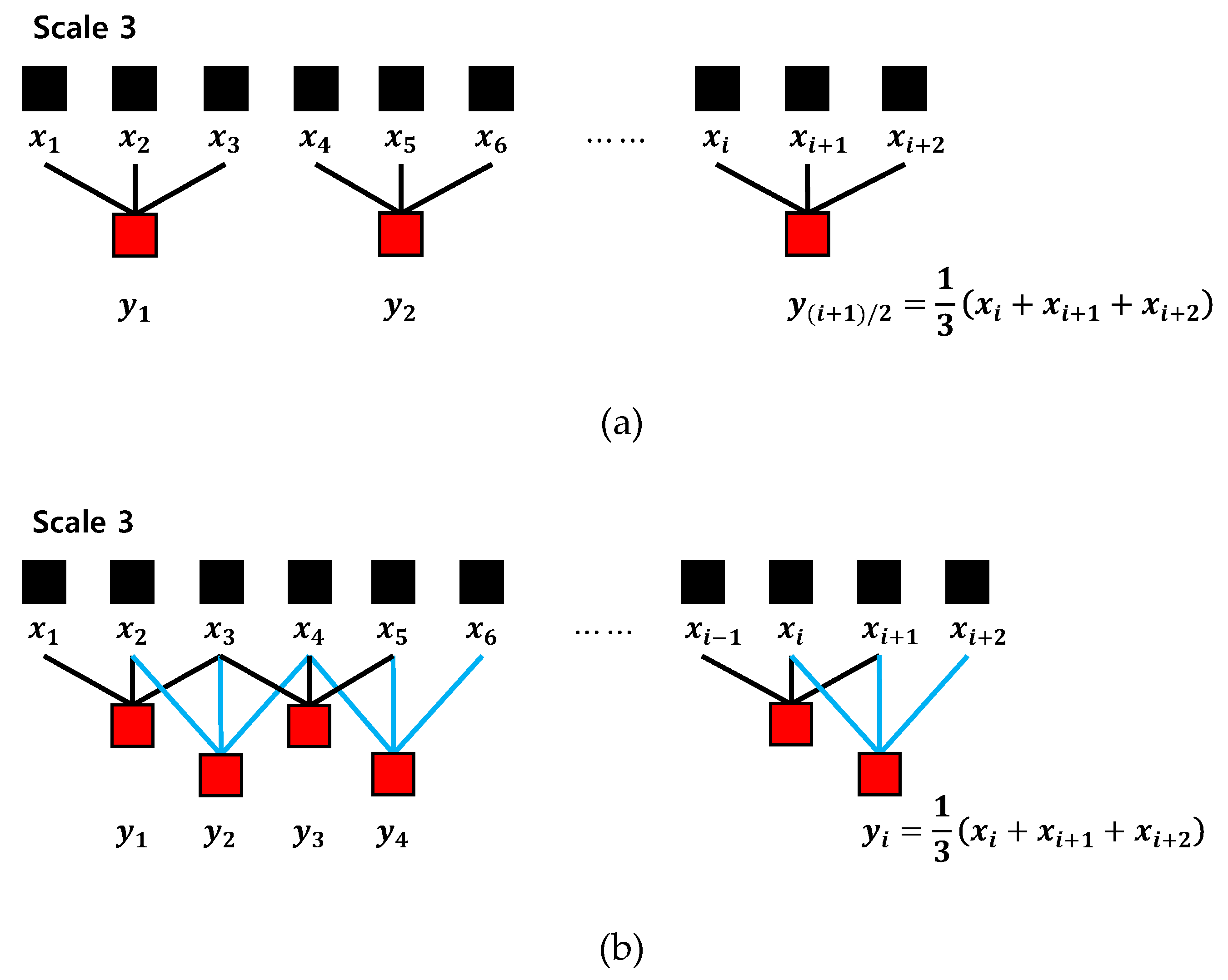
2.3. Multiscale Distribution Entropy
2.4. Evaluation Data
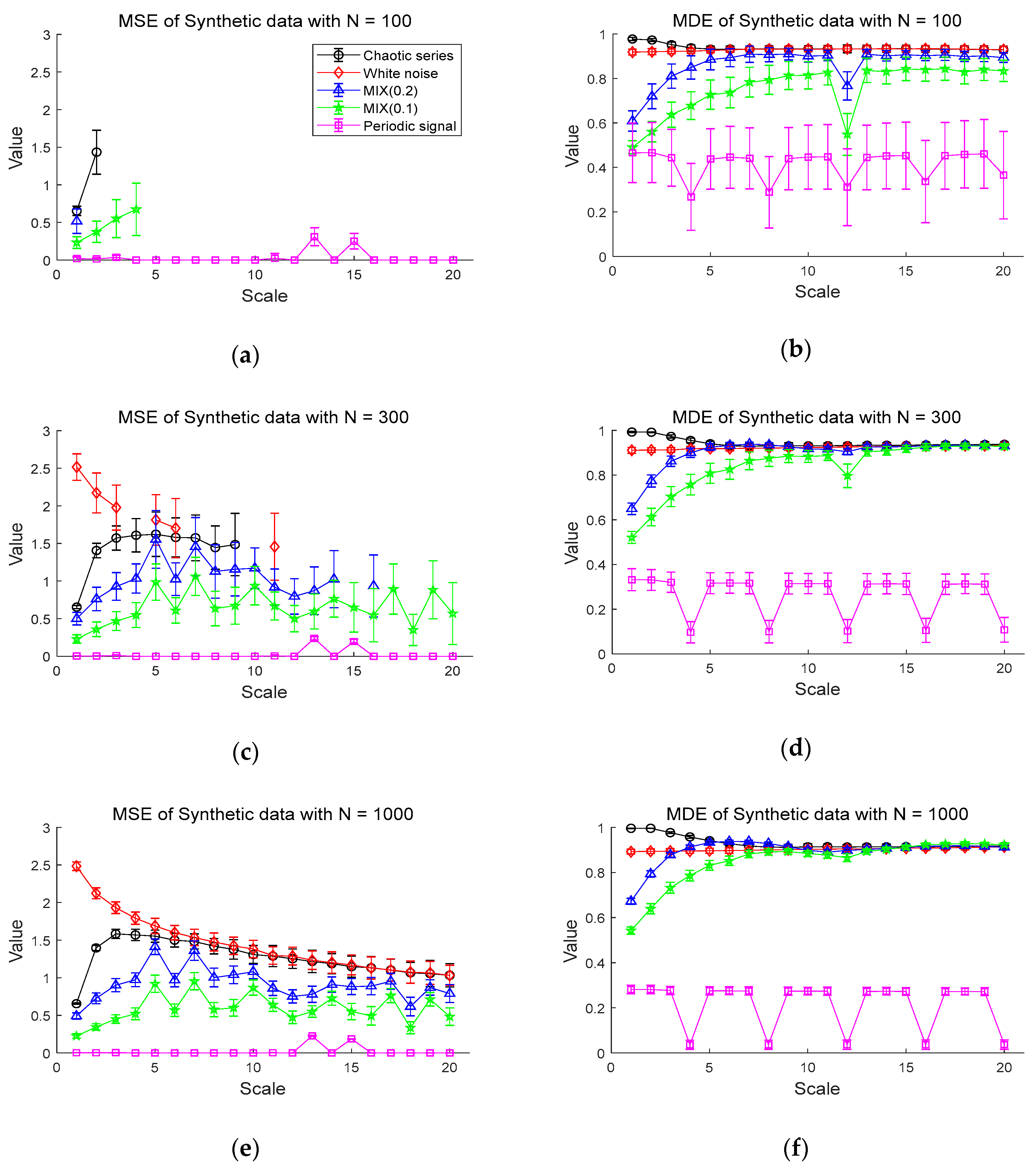
2.4.1. Synthetic Data
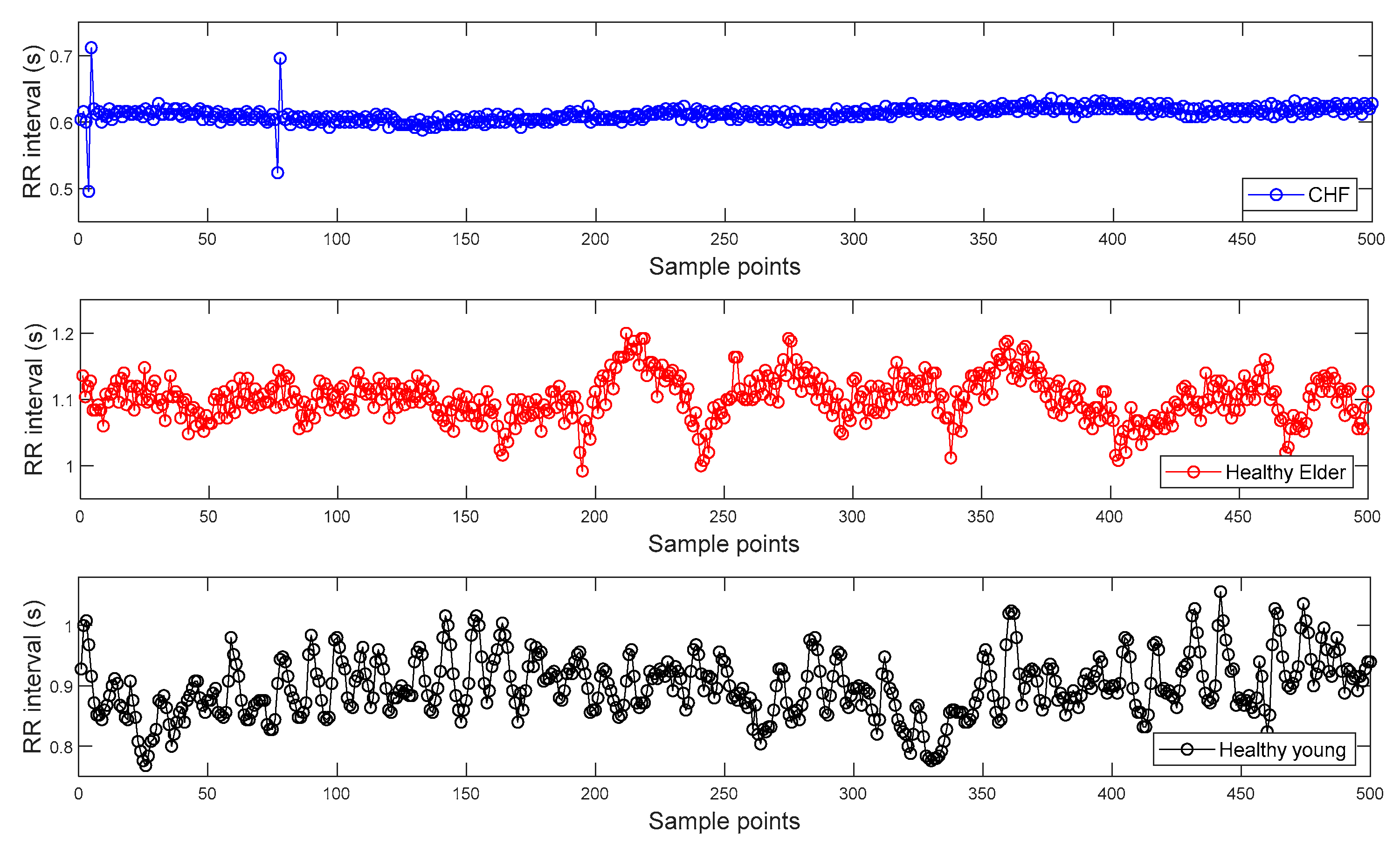
2.4.2. Real ECG Data
3. Results
3.1. Simulation Result Using Synthetic Data
3.2. Experiment Results Using Real Data
3.2.1. ECG Dataset I
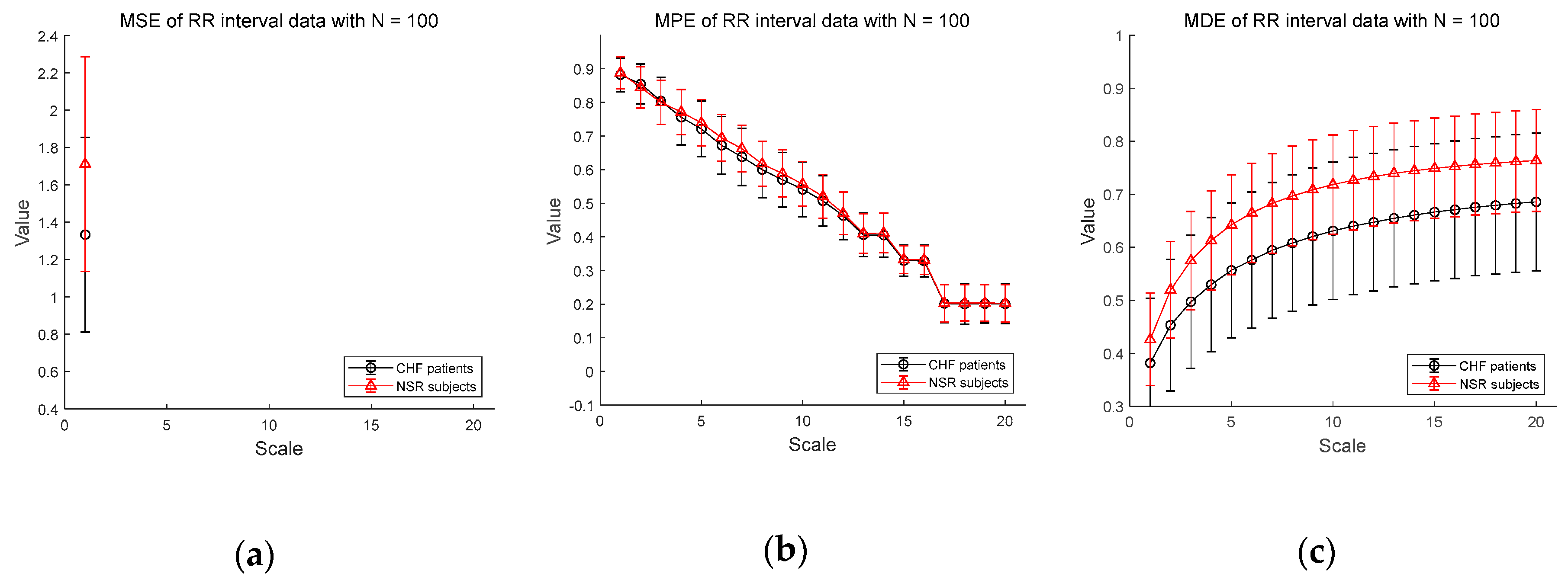
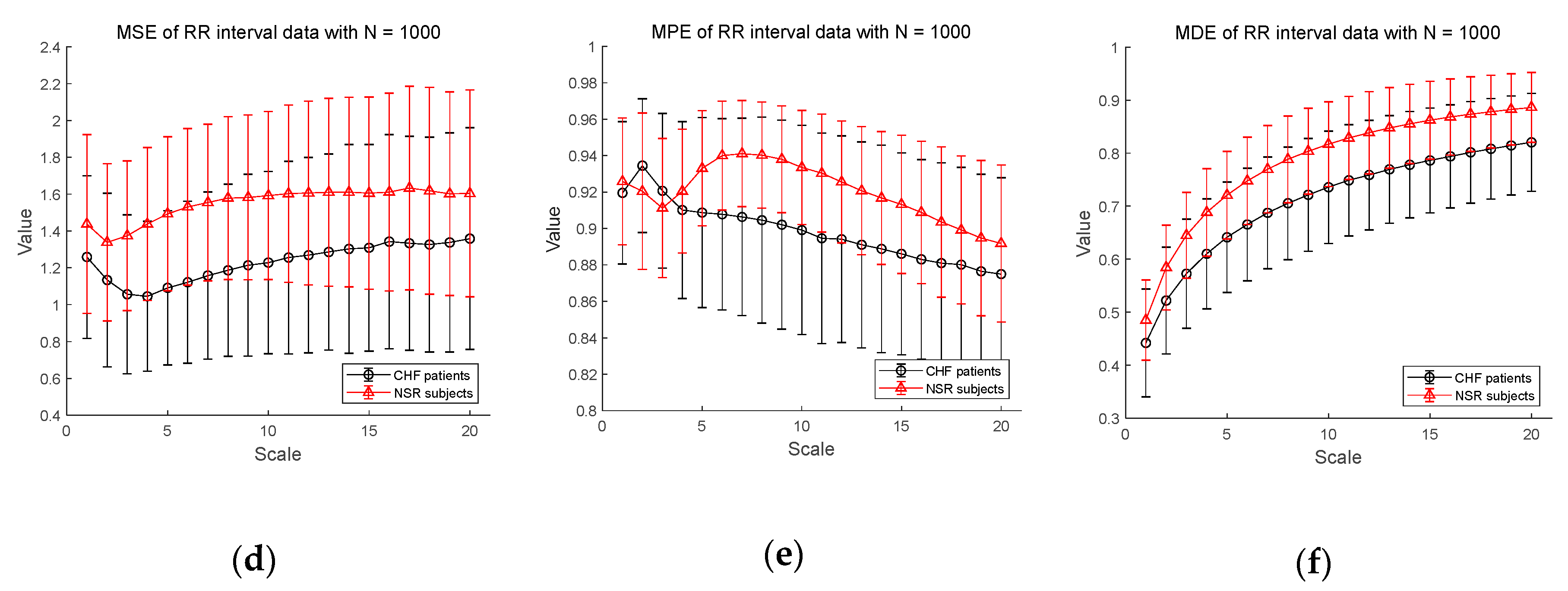
3.2.2. ECG Dataset II
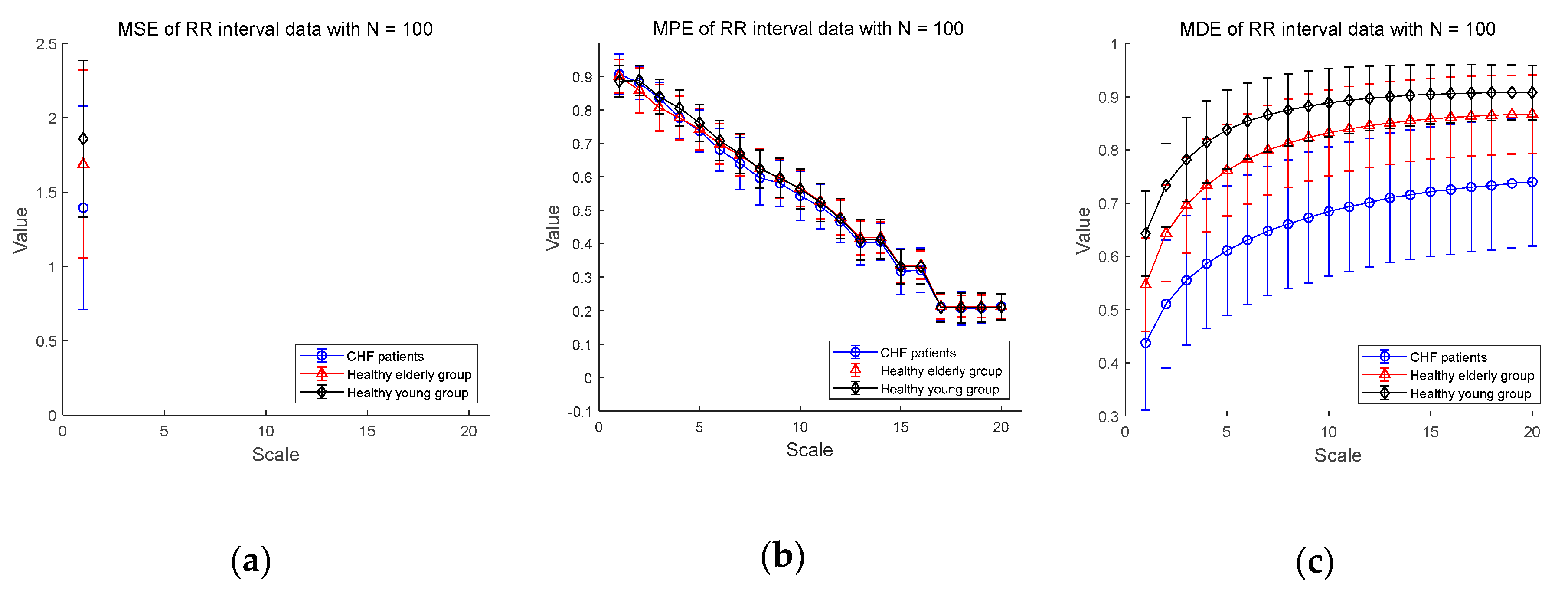
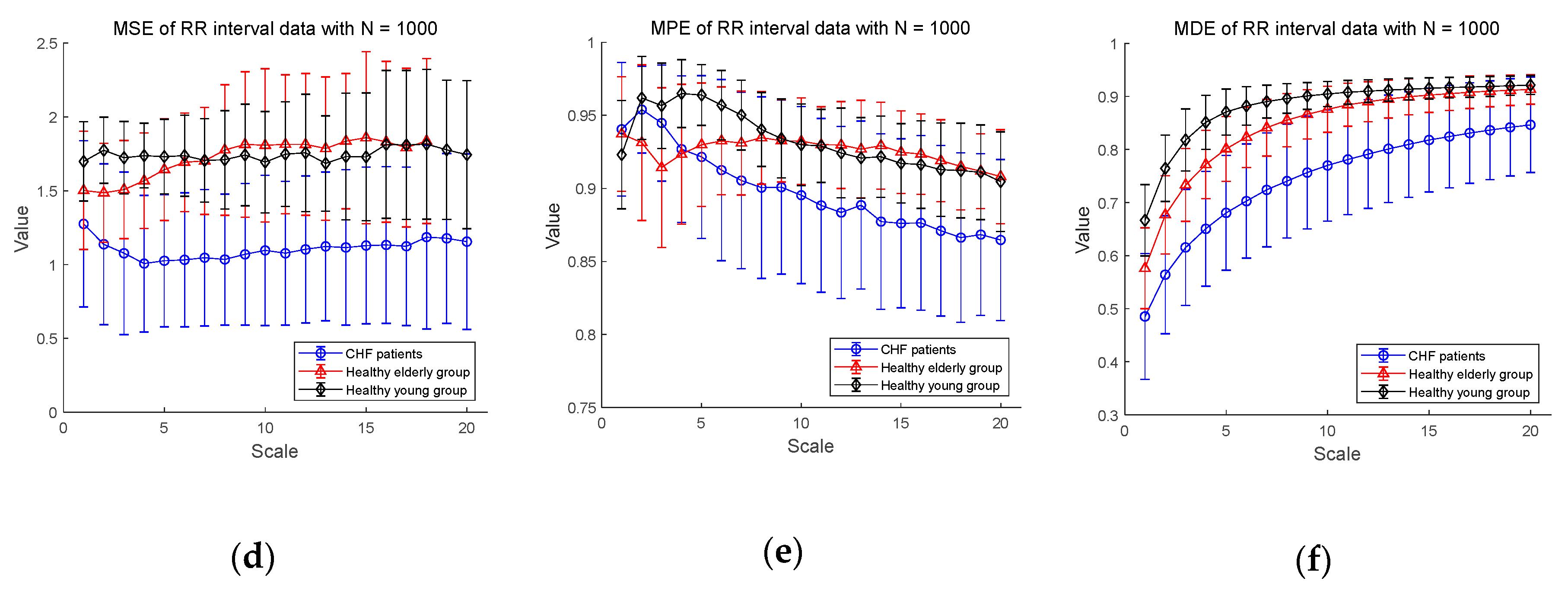
3.2.3. Statistical Analysis for CHF Patients, Healthy Elderly, and Healthy Young Groups
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kaplan Berkaya, S.; Uysal, A.K.; Sora Gunal, E.; Ergin, S.; Gunal, S.; Gulmezoglu, M.B. A survey on ECG analysis. Biomed. Signal Process. Control 2018, 43, 216–235. [Google Scholar] [CrossRef]
- İşler, Y.; Kuntalp, M. Combining classical HRV indices with wavelet entropy measures improves to performance in diagnosing congestive heart failure. Comput. Biol. Med. 2007, 37, 1502–1510. [Google Scholar] [CrossRef] [PubMed]
- Rajendra Acharya, U.; Paul Joseph, K.; Kannathal, N.; Lim, C.M.; Suri, J.S. Heart rate variability: A review. Med. Biol. Eng. Comput. 2006, 44, 1031–1051. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.-N.; Lee, M.-Y. Bispectral analysis and genetic algorithm for congestive heart failure recognition based on heart rate variability. Comput. Biol. Med. 2012, 42, 816–825. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale Entropy Analysis of Complex Physiologic Time Series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [PubMed]
- Goldberger, A.L.; Peng, C.-K.; Lipsitz, L.A. What is physiologic complexity and how does it change with aging and disease? Neurobiol. Aging 2002, 23, 23–26. [Google Scholar] [CrossRef]
- Villecco, F.; Pellegrino, A. Entropic Measure of Epistemic Uncertainties in Multibody System Models by Axiomatic Design. Entropy 2017, 19, 291. [Google Scholar] [CrossRef]
- Villecco, F.; Pellegrino, A. Evaluation of Uncertainties in the Design Process of Complex Mechanical Systems. Entropy 2017, 19, 475. [Google Scholar] [CrossRef]
- Sena, P.; Attianese, P.; Pappalardo, M.; Villecco, F. FIDELITY: Fuzzy Inferential Diagnostic Engine for on-LIne supporT to phYsicians. In Proceedings of the 4th International Conference on the Development of Biomedical Engineering, Ho Chi Minh City, Vietnam, 8–10 January 2012; IFMBE Proceedings. Springer: Berlin, Germany, 2013; pp. 396–400. [Google Scholar]
- Coifman, R.R.; Wickerhauser, M.V. Entropy-based algorithms for best basis selection. IEEE Trans. Inf. Theory 1992, 38, 713–718. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol.-Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Chen, W.; Wang, Z.; Xie, H.; Yu, W. Characterization of Surface EMG Signal Based on Fuzzy Entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef] [PubMed]
- Bandt, C.; Pompe, B. Permutation Entropy: A Natural Complexity Measure for Time Series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Al-Angari, H.M.; Sahakian, A.V. Use of Sample Entropy Approach to Study Heart Rate Variability in Obstructive Sleep Apnea Syndrome. IEEE Trans. Biomed. Eng. 2007, 54, 1900–1904. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Li, K.; Zhao, L.; Liu, F.; Zheng, D.; Liu, C.; Liu, S. Analysis of heart rate variability using fuzzy measure entropy. Comput. Biol. Med. 2013, 43, 100–108. [Google Scholar] [CrossRef] [PubMed]
- Shi, B.; Zhang, Y.; Yuan, C.; Wang, S.; Li, P. Entropy Analysis of Short-Term Heartbeat Interval Time Series during Regular Walking. Entropy 2017, 19, 568. [Google Scholar] [CrossRef]
- Pan, W.-Y.; Su, M.-C.; Wu, H.-T.; Lin, M.-C.; Tsai, I.-T.; Sun, C.-K. Multiscale Entropy Analysis of Heart Rate Variability for Assessing the Severity of Sleep Disordered Breathing. Entropy 2015, 17, 231–243. [Google Scholar] [CrossRef]
- Zhang, Y.-C. Complexity and 1/f noise. A phase space approach. J. Phys. I 1991, 1, 971–977. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef] [PubMed]
- Valenza, G.; Nardelli, M.; Bertschy, G.; Lanata, A.; Scilingo, E.P. Mood states modulate complexity in heartbeat dynamics: A multiscale entropy analysis. EPL 2014, 107, 18003. [Google Scholar] [CrossRef]
- Watanabe, E.; Kiyono, K.; Hayano, J.; Yamamoto, Y.; Inamasu, J.; Yamamoto, M.; Ichikawa, T.; Sobue, Y.; Harada, M.; Ozaki, Y. Multiscale Entropy of the Heart Rate Variability for the Prediction of an Ischemic Stroke in Patients with Permanent Atrial Fibrillation. PLoS ONE 2015, 10, e0137144. [Google Scholar] [CrossRef] [PubMed]
- Jinde, Z.; Chen, M.-J.; Junsheng, C.; Yang, Y. Multiscale fuzzy entropy and its application in rolling bearing fault diagnosis. Zhendong Gongcheng Xuebao/J. Vib. Eng. 2014, 27, 145–151. [Google Scholar]
- Ouyang, G.; Li, J.; Liu, X.; Li, X. Dynamic characteristics of absence EEG recordings with multiscale permutation entropy analysis. Epilepsy Res. 2013, 104, 246–252. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.-D.; Wu, C.-W.; Lee, K.-Y.; Lin, S.-G. Modified multiscale entropy for short-term time series analysis. Phys. A Stat. Mech. Appl. 2013, 392, 5865–5873. [Google Scholar] [CrossRef]
- Li, P.; Liu, C.; Li, K.; Zheng, D.; Liu, C.; Hou, Y. Assessing the complexity of short-term heartbeat interval series by distribution entropy. Med. Biol. Eng. Comput. 2015, 53, 77–87. [Google Scholar] [CrossRef] [PubMed]
- Pincus, S.M. Approximate entropy as a measure of system complexity. PNAS 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, E215–E220. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Tompkins, W.J. A Real-Time QRS Detection Algorithm. IEEE Trans. Biomed. Eng. 1985, BME-32, 230–236. [Google Scholar] [CrossRef]
| MSE Statistical Results for RR Interval Time Series | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| s | p-Value | ||||||||
| C - E | C - Y | E - Y | C - E | C - Y | E - Y | C - E | C - Y | E - Y | |
| 1 | 0.098 | 1.1 × 10−6 | 8.7 × 10−5 | 0.0014 | 2.5 × 10−8 | 3.6 × 10−4 | 1.3 × 10−5 | 4.8 × 10−14 | 8.5 × 10−7 |
| 2 | N/A | N/A | N/A | 4.7 × 10−7 | 5.5 × 10−13 | 1.0 × 10−5 | 6.7 × 10−10 | 1.5 × 10−21 | 8.0 × 10−15 |
| 3 | N/A | N/A | N/A | 2.4 × 10−10 | 1.8 × 10−17 | 1.9 × 10−4 | 8.4 × 10−14 | 3.2 × 10−25 | 5.3 × 10−10 |
| 4 | N/A | N/A | N/A | 3.9 × 10−14 | 3.1 × 10−19 | 0.019 | 2.3 × 10−17 | 2.2 × 10−26 | 2.7 × 10−07 |
| 5 | N/A | N/A | N/A | 1.3 × 10−11 | 2.8 × 10−15 | 0.311 | 1.3 × 10−20 | 1.9 × 10−28 | 0.005 |
| 6 | N/A | N/A | N/A | N/A | N/A | N/A | 1.9 × 10−21 | 8.8 × 10−27 | 0.089 |
| 7 | N/A | N/A | N/A | N/A | N/A | N/A | 3.7 × 10−19 | 1.2 × 10−22 | 0.512 |
| 8 | N/A | N/A | N/A | N/A | N/A | N/A | 1.6 × 10−20 | 1.1 × 10−22 | 0.847 |
| 9 | N/A | N/A | N/A | N/A | N/A | N/A | 3.5 × 10−21 | 2.2 × 10−23 | 0.353 |
| 10 | N/A | N/A | N/A | N/A | N/A | N/A | 1.4 × 10−19 | 5.1 × 10−20 | 0.175 |
| 11 | N/A | N/A | N/A | N/A | N/A | N/A | 5.2 × 10−18 | 6.8 × 10−20 | 0.673 |
| 12 | N/A | N/A | N/A | N/A | N/A | N/A | 1.6 × 10−19 | 2.3 × 10−21 | 0.359 |
| 13 | N/A | N/A | N/A | N/A | N/A | N/A | 1.3 × 10−17 | 1.0 × 10−17 | 0.086 |
| 14 | N/A | N/A | N/A | N/A | N/A | N/A | 3.7 × 10−18 | 5.0 × 10−20 | 0.853 |
| 15 | N/A | N/A | N/A | N/A | N/A | N/A | 1.9 × 10−13 | 2.2 × 10−14 | 0.448 |
| 16 | N/A | N/A | N/A | N/A | N/A | N/A | 1.6 × 10−13 | 4.7 × 10−16 | 0.945 |
| 17 | N/A | N/A | N/A | N/A | N/A | N/A | 1.0 × 10−11 | 1.6 × 10−14 | 0.695 |
| 18 | N/A | N/A | N/A | N/A | N/A | N/A | 1.6 × 10−15 | 2.2 × 10−19 | 0.936 |
| 19 | N/A | N/A | N/A | N/A | N/A | N/A | N/A | 3.2 ×10−16 | N/A |
| 20 | N/A | N/A | N/A | N/A | N/A | N/A | N/A | 4.1 × 10−13 | N/A |
| MPE Statistical Results for RR Interval Time Series | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| s | p-Value | ||||||||
| C - E | C - Y | E - Y | C - E | C - Y | E - Y | C - E | C - Y | E - Y | |
| 1 | 0.389 | 6.6 × 10−7 | 6.5 × 10−5 | 0.255 | 1.2 × 10−7 | 8.9 × 10−6 | 0.157 | 8.6 × 10−8 | 5.6 × 10−4 |
| 2 | 0.018 | 0.101 | 5.8 × 10−5 | 0.006 | 0.006 | 1.1 × 10−7 | 0.005 | 4.1 × 10−4 | 7.9 × 10−7 |
| 3 | 3.0 × 10−4 | 0.519 | 2.9 × 10−4 | 4.6 × 10−6 | 0.005 | 1.6 × 10−14 | 9.2 × 10−9 | 0.012 | 5.9 × 10−13 |
| 4 | 0.363 | 1.9 × 10−5 | 1.8 × 10−4 | 0.674 | 8.6 × 10−13 | 1.5 × 10−16 | 0.030 | 5.2 × 10−12 | 4.8 × 10−19 |
| 5 | 0.139 | 6.3 × 10−8 | 0.001 | 0.935 | 1.6 × 10−9 | 7.3 × 10−13 | 0.776 | 1.8 × 10−15 | 1.2 × 10−16 |
| 6 | 0.059 | 0.004 | 0.241 | 0.033 | 4.2 × 10−9 | 1.1 × 10−5 | 0.017 | 7.5 × 10−16 | 9.5 × 10−10 |
| 7 | 0.102 | 1.2 × 10−8 | 0.655 | 0.002 | 3.7 × 10−7 | 0.007 | 0.007 | 8.8 × 10−13 | 3.2 × 10−6 |
| 8 | 0.292 | 5.8 × 10−7 | 0.619 | 0.004 | 4.9 × 10−4 | 0.428 | 1.1 × 10−5 | 3.5 × 10−8 | 0.233 |
| 9 | 0.450 | 4.3 × 10−6 | 0.129 | 9.7 × 10−4 | 1.6 × 10−4 | 0.567 | 5.3 × 10−5 | 1.6 × 10−5 | 0.720 |
| 10 | 0.433 | 4.3 × 10−4 | 0.454 | 6.3 × 10−4 | 7.0 × 10−6 | 0.193 | 1.4 × 10−6 | 1.4 × 10−5 | 0.387 |
| 11 | 0.104 | 1.7 × 10−5 | 0.965 | 2.8 × 10−5 | 9.0 × 10−5 | 0.656 | 1.8 × 10−8 | 4.3 × 10−8 | 0.701 |
| 12 | 0.034 | 0.050 | 0.873 | 1.6 × 10−4 | 7.2 × 10−8 | 0.041 | 8.6 × 10−10 | 1.7 × 10−7 | 0.159 |
| 13 | 0.025 | 0.062 | 0.686 | 9.1 × 10−7 | 7.9 × 10−6 | 0.701 | 9.6 × 10−9 | 1.7 × 10−5 | 0.009 |
| 14 | 0.702 | 0.914 | 0.780 | 1.2 × 10−7 | 1.5 × 10−4 | 0.056 | 4.8 × 10−13 | 5.8 × 10−9 | 0.020 |
| 15 | 0.912 | 0.779 | 0.854 | 3.7 × 10−5 | 3.0 × 10−4 | 0.505 | 3.4 × 10−11 | 2.9 × 10−7 | 0.020 |
| 16 | 0.074 | 0.411 | 0.296 | 1.1 × 10−4 | 2.7 × 10−4 | 0.745 | 2.6 × 10−13 | 5.9 × 10−10 | 0.070 |
| 17 | 0.821 | 0.520 | 0.648 | 3.8 × 10−5 | 2.3 × 10−4 | 0.672 | 5.4 × 10−10 | 6.1 × 10−8 | 0.309 |
| 18 | 0.171 | 0.531 | 0.431 | 1.1 × 10−5 | 5.9 × 10−6 | 0.880 | 2.6 × 10−9 | 1.4 × 10−8 | 0.729 |
| 19 | 0.448 | 0.437 | 0.103 | 3.7 × 10−5 | 1.4 × 10−1 | 0.758 | 2.0 × 10−11 | 6.1 × 10−11 | 0.947 |
| 20 | 0.272 | 0.556 | 0.588 | 0.002 | 0.005 | 0.671 | 1.0 × 10−9 | 3.9 × 10−8 | 0.496 |
| MDE Statistical Results for RR Interval Time Series | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| s | p-Value | ||||||||
| C - E | C - Y | E - Y | C - E | C - Y | E - Y | C - E | C - Y | E - Y | |
| 1 | 2.8 × 10−15 | 3.6 × 10−26 | 6.9 × 10−15 | 2.1 × 10−11 | 9.2 × 10−26 | 5.5 × 10−16 | 1.8 × 10−10 | 3.1 × 10−26 | 1.1 × 10−16 |
| 2 | 1.7 × 10−18 | 7.2 × 10−31 | 1.3 × 10−13 | 2.7 × 10−15 | 7.1 × 10−32 | 1.1 × 10−14 | 1.7 × 10−14 | 1.6 × 10−31 | 1.0 × 10−16 |
| 3 | 4.9 × 10−21 | 5.5 × 10−33 | 2.0 × 10−12 | 6.5 × 10−18 | 2.3 × 10−34 | 2.7 × 10−14 | 2.8 × 10−17 | 5.6 × 10−34 | 3.5 × 10−17 |
| 4 | 1.1 × 10−21 | 1.5 × 10−33 | 4.3 × 10−12 | 1.3 × 10−18 | 1.6 × 10−34 | 1.3 × 10−14 | 3.9 × 10−35 | 3.9 × 10−35 | 4.7 × 10−18 |
| 5 | 2.5 × 10−23 | 3.3 × 10−34 | 1.5 × 10−11 | 1.2 × 10−13 | 9.7 × 10−35 | 1.2 × 10−14 | 1.8 × 10−35 | 1.8 × 10−35 | 6.1 × 10−17 |
| 6 | 2.1 × 10−23 | 1.7 × 10−34 | 4.8 × 10−11 | 2.6 × 10−20 | 5.7 × 10−35 | 2.4 × 10−14 | 5.4 × 10−35 | 5.4 × 10−35 | 2.0 × 10−15 |
| 7 | 3.1 × 10−23 | 5.8 × 10−34 | 3.0 × 10−10 | 4.9 × 10−20 | 2.2 × 10−34 | 2.4 × 10−13 | 1.1 × 10−33 | 1.1 × 10−33 | 8.1 × 10−13 |
| 8 | 2.1 × 10−23 | 8.0 × 10−34 | 2.0 × 10−9 | 4.6 × 10−20 | 3.4 × 10−34 | 3.0 × 10−12 | 1.6 × 10−32 | 1.6 × 10−32 | 1.4 × 10−10 |
| 9 | 6.7 × 10−23 | 2.1 × 10−33 | 4.5 × 10−9 | 1.9 × 10−20 | 4.4 × 10−34 | 9.1 × 10−11 | 6.9 × 10−32 | 6.9 × 10−32 | 1.9 × 10−9 |
| 10 | 6.9 × 10−23 | 2.1 × 10−33 | 9.6 × 10−9 | 3.3 × 10−20 | 1.4 × 10−33 | 2.9 × 10−9 | 9.6 × 10−31 | 9.6 × 10−31 | 8.9 × 10−8 |
| 11 | 1.7 × 10−22 | 3.3 × 10−33 | 2.0 × 10−8 | 3.8 × 10−20 | 2.3 × 10−33 | 2.5 × 10−8 | 3.3 × 10−30 | 3.3 × 10−30 | 4.8 × 10−6 |
| 12 | 2.4 × 10−22 | 2.9 × 10−33 | 2.5 × 10−8 | 4.6 × 10−20 | 1.5 × 10−32 | 1.6 × 10−7 | 5.9 × 10−29 | 5.9 × 10−29 | 1.8 × 10−5 |
| 13 | 2.6 × 10−22 | 1.1 × 10−32 | 5.7 × 10−8 | 1.9 × 10−20 | 4.6 × 10−32 | 7.4 × 10−7 | 2.4 × 10−27 | 2.4 × 10−27 | 1.4 × 10−4 |
| 14 | 8.0 × 10−22 | 7.9 × 10−33 | 1.0 × 10−7 | 8.8 × 10−20 | 4.4 × 10−31 | 2.1 × 10−6 | 2.8 × 10−25 | 2.8 × 10−25 | 6.0 × 10−4 |
| 15 | 3.2 × 10−21 | 4.5 × 10−32 | 2.3 × 10−7 | 3.5 × 10−19 | 3.8 × 10−30 | 4.8 × 10−6 | 4.0 × 10−23 | 4.0 × 10−23 | 0.001 |
| 16 | 1.0 × 10−20 | 1.1 × 10−31 | 3.8 × 10−7 | 4.7 × 10−18 | 1.1 × 10−28 | 4.8 × 10−6 | 7.6 × 10−21 | 7.6 × 10−21 | 8.8 × 10−4 |
| 17 | 3.5 × 10−20 | 2.4 × 10−31 | 4.4 × 10−7 | 1.6 × 10−17 | 2.7 × 10−27 | 1.7 × 10−5 | 2.2 × 10−18 | 2.2 × 10−18 | 0.004 |
| 18 | 7.9 × 10−20 | 3.4 × 10−31 | 9.6 × 10−7 | 1.6 × 10−17 | 4.0 × 10−27 | 3.7 × 10−5 | 1.1 × 10−16 | 1.1 × 10−16 | 0.005 |
| 19 | 2.1 × 10−19 | 1.4 × 10−30 | 1.4 × 10−6 | 7.6 × 10−17 | 1.8 × 10−26 | 1.2 × 10−9 | 5.8 × 10−16 | 5.8 × 10−16 | 0.006 |
| 20 | 5.3 × 10−19 | 1.9 × 10−30 | 4.0 × 10−6 | 1.7 × 10−16 | 7.0 × 10−26 | 1.1 × 10−5 | 2.4 × 10−14 | 2.4 × 10−14 | 0.015 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, D.-Y.; Choi, Y.-S. Multiscale Distribution Entropy Analysis of Short-Term Heart Rate Variability. Entropy 2018, 20, 952. https://doi.org/10.3390/e20120952
Lee D-Y, Choi Y-S. Multiscale Distribution Entropy Analysis of Short-Term Heart Rate Variability. Entropy. 2018; 20(12):952. https://doi.org/10.3390/e20120952
Chicago/Turabian StyleLee, Dae-Young, and Young-Seok Choi. 2018. "Multiscale Distribution Entropy Analysis of Short-Term Heart Rate Variability" Entropy 20, no. 12: 952. https://doi.org/10.3390/e20120952
APA StyleLee, D.-Y., & Choi, Y.-S. (2018). Multiscale Distribution Entropy Analysis of Short-Term Heart Rate Variability. Entropy, 20(12), 952. https://doi.org/10.3390/e20120952






