Computational Simulation of Entropy Generation in a Combustion Chamber Using a Single Burner
Abstract
1. Introduction
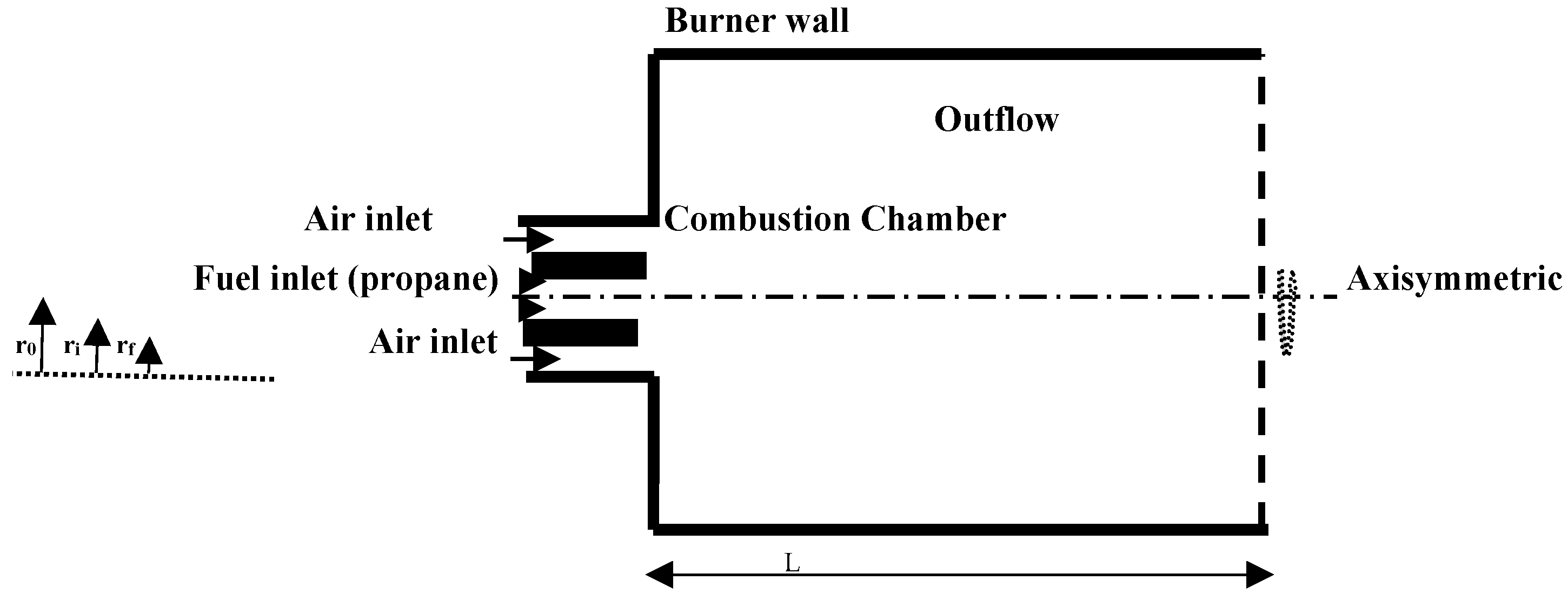
2. Computational Model
2.1. Mathematical Formulation
2.2. Combustion and Reaction Mechanism
2.3. Entropy Generation Rate
2.4. Numerical Tools
3. Simulation Results
3.1. Operating Values and Validation
3.2. Physical Fields
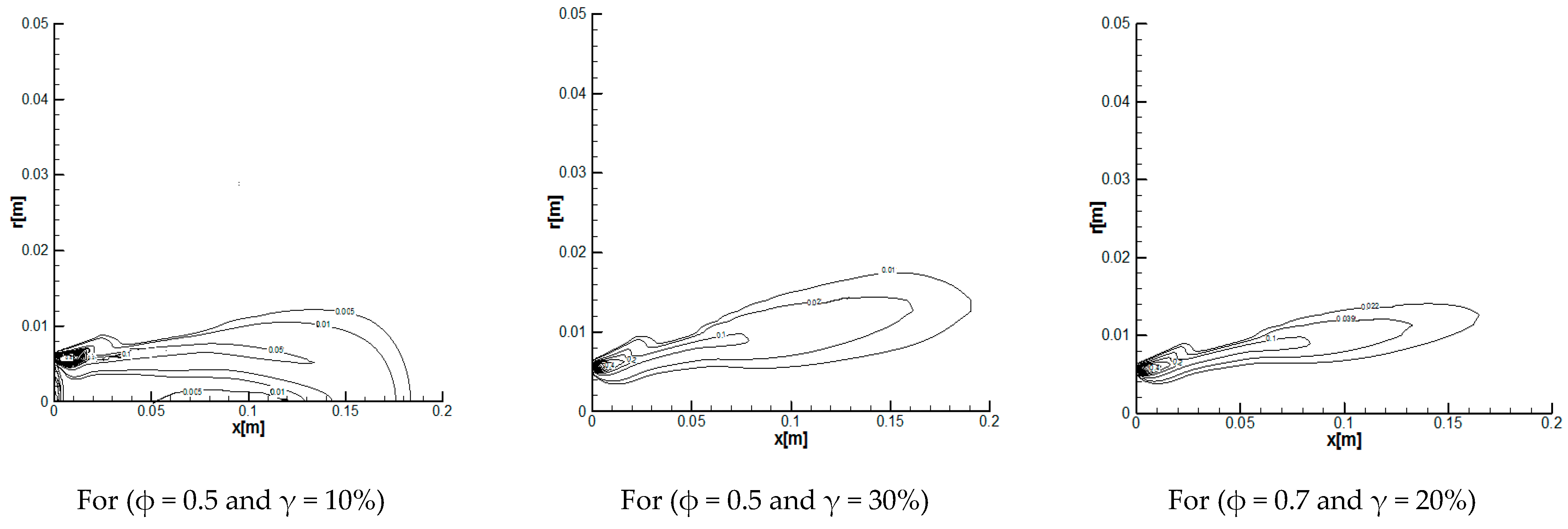
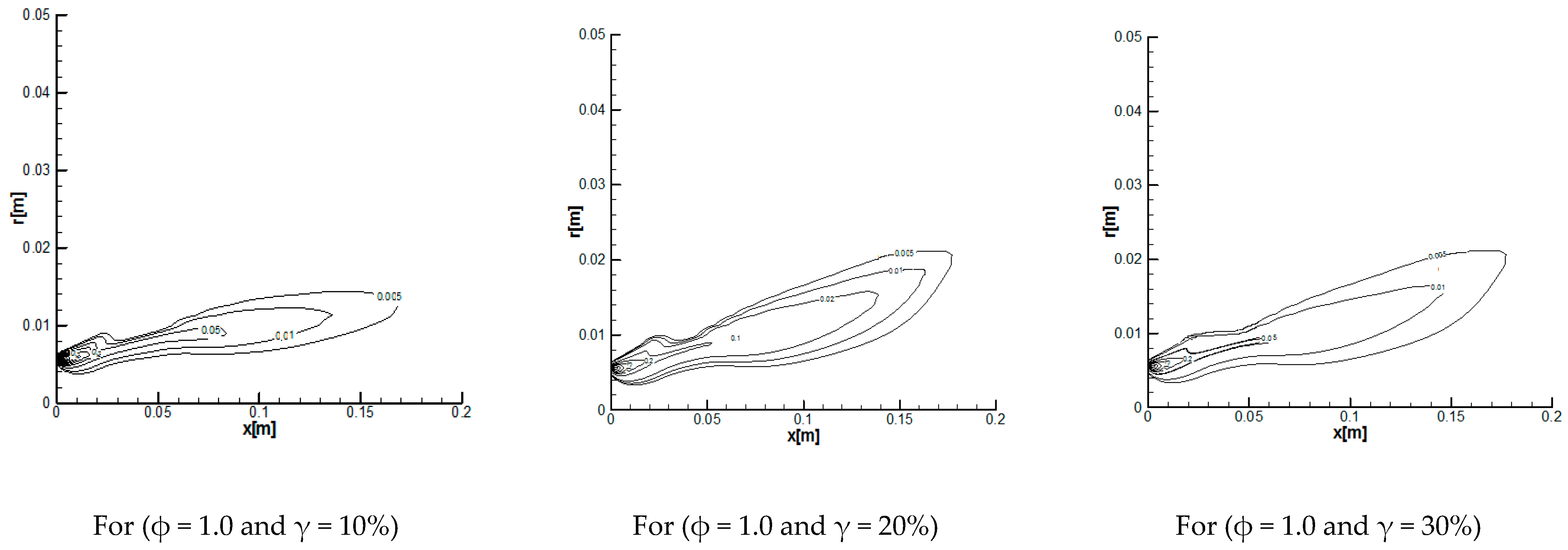
3.2.1. Reaction Rates
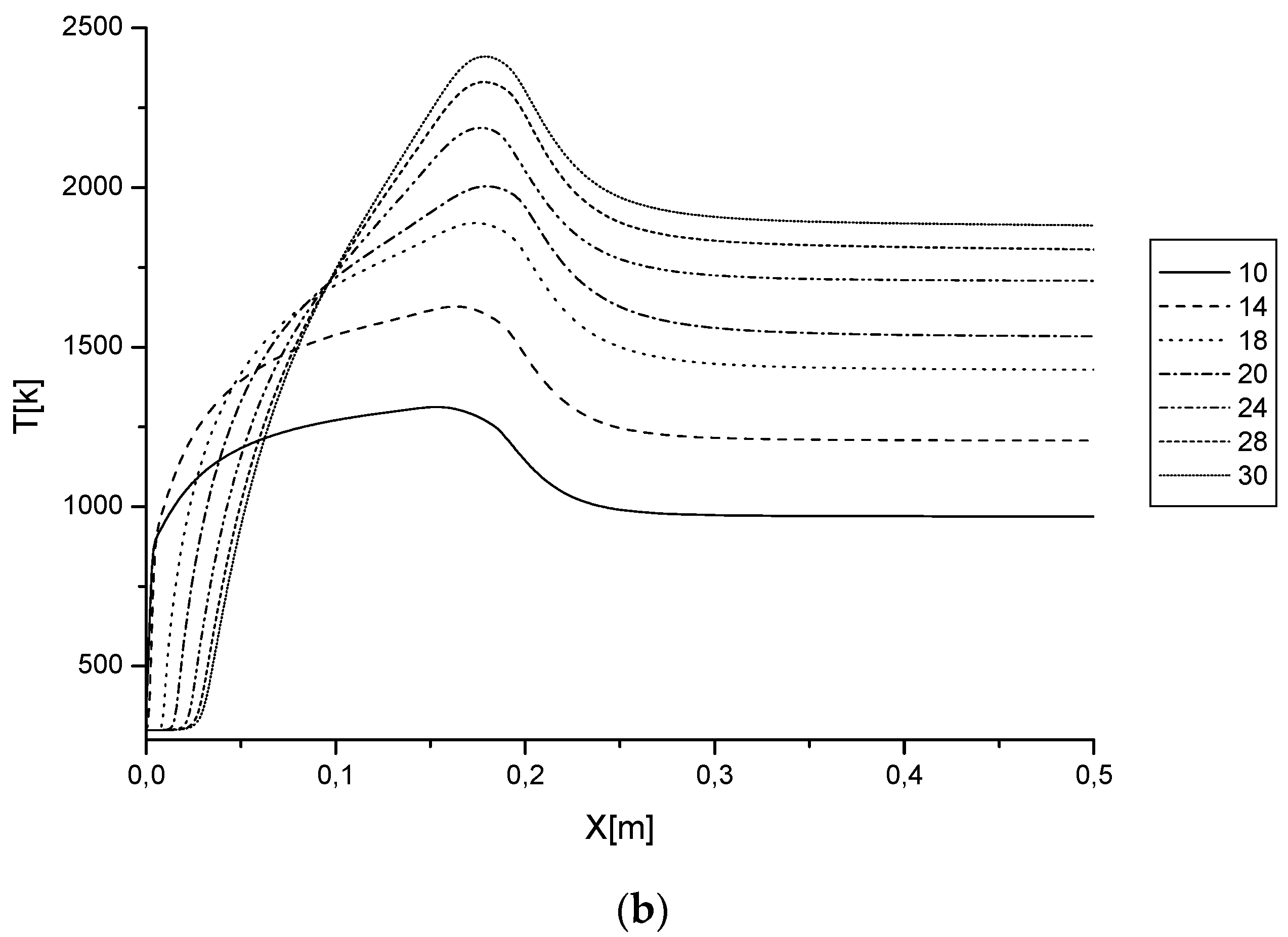
3.2.2. Temperature Distribution
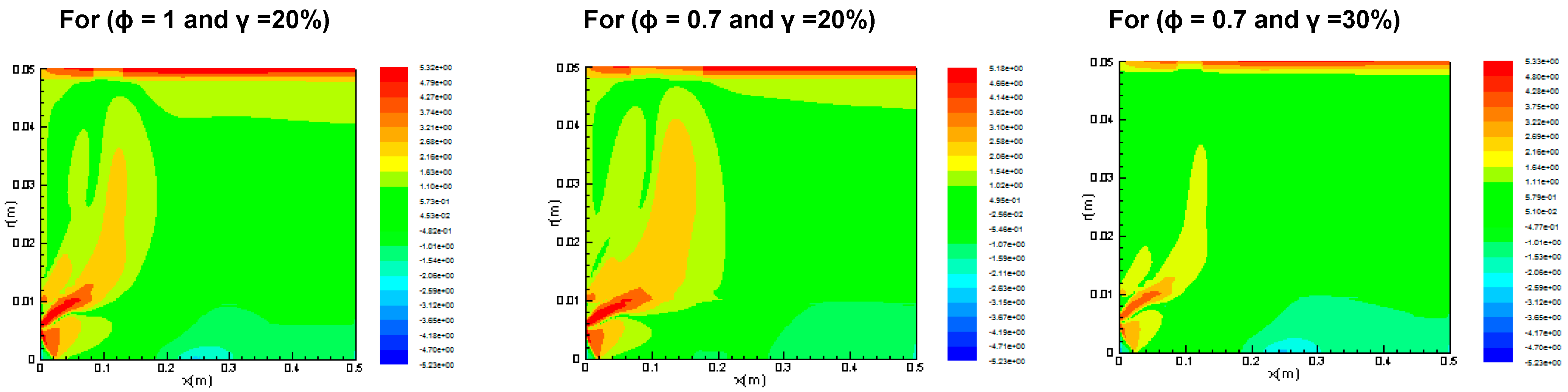
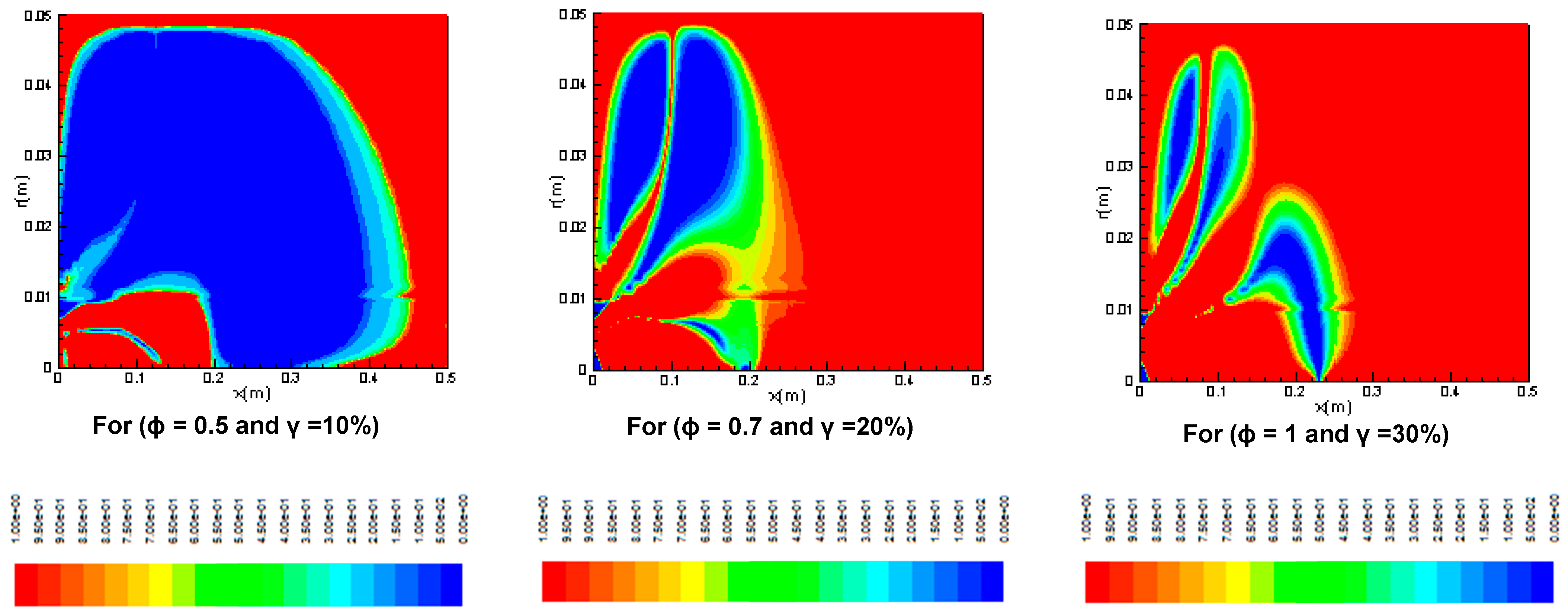
3.2.3. Entropy Generation and Bejan Number
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Latin Symbols | |
| Be | Bejan number |
| CFD | Computational fluid dynamics |
| Cμ, Cε1, Cε2 | Coefficients in k–ε turbulence model |
| fk,j | Specific force of volume acting on the species K in the direction i |
| H | Enthalpy |
| hk | Specific enthalpy of the species k |
| hs,k | Heat transfer coefficient, sensible enthalpy of species |
| K | Turbulent kinetic energy |
| L | Length of burner |
| LCV | Lower calorific value |
| P | Pressure |
| RNG | Renormalization group |
| R | Radial distance |
| Inner radius of air inlet | |
| Outer radius of air inlet | |
| Volumetric entropy generation rate | |
| T | Temperature |
| ui | Velocity in direction i |
| Vk,i | Velocity diffusion of the species k in direction i |
| Yk | Mass fraction of the species k |
| Greek Symbols | |
| Kronecker delta | |
| Turbulent energy dissipation rate | |
| Equivalence ratio | |
| Viscous dissipation | |
| Air excess ratio | |
| Dynamic viscosity | |
| Density | |
| Tangential direction | |
| Density of the species k | |
| Tensor of the constraint in plan i and the direction j | |
| Production rate of the k species. | |
| Heat transfer rate | |
| Tensor of the viscous constraints | |
| Subscripts | |
| F | Fuel |
| K | Species |
| N | Total number of species number |
| O | Oxidant |
| P | At constant pressure |
| S | Sensibility (enthalpy) |
| V | At constant volume |
| R | Radial |
| X | Axial |
| Amb | Ambient |
| Air | Air |
| Eff | Effective |
| Fric | Friction |
| Heat | Heat transfer |
| i,j | Indices of tensor notation |
| In | Inlet |
References
- BP 2011 Statistical Review of World Energy; The British Petroleum Company: London, UK, 2011.
- Bejan, A. Entropy Generation Through Heat and Fluid Flow; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Bejan, A. Entropy Generation Minimization; CRC Press: New York, NY, USA, 1995. [Google Scholar]
- Som, S.K.; Datta, A. Thermodynamic irreversibilities and exergy balance in combustion processes. Prog. Energy Combust. Sci. 2008, 34, 351–376. [Google Scholar] [CrossRef]
- Oztop, H.F.; Al-Salem, K. A review on entropy generation in natural and mixed convection heat transfer for energy systems. Renew. Sustain. Energy Rev. 2011, 16, 911–920. [Google Scholar] [CrossRef]
- Ko, T.H.; Wu, C.P. A numerical study on entropy generation induced by turbulent forced convection in curved rectangular ducts with various aspect ratios. Int. Commun. Heat Mass Transf. 2009, 36, 25–31. [Google Scholar] [CrossRef]
- Gazzah, M.H.; Belmabrouk, H. Local entropy generation in coflowing turbulent jets with variable density. Int. J. Numer. Methods Heat Fluid Flow 2014, 24, 1679–1695. [Google Scholar] [CrossRef]
- Gazzah, M.H.; Belmabrouk, H. Directed co-flow effects on local entropy generation in turbulent heated round jets. Comput. Fluids 2014, 105, 285–293. [Google Scholar] [CrossRef]
- Elkaroui, A.; Ben Haj Ayech, S.; Hichem Gazzah, M.; Mahjoub Saïd, N.; Le Palec, G. Numerical study of local entropy generation in a heated turbulent plane jet developing in a co-flowing stream. Appl. Math. Model. 2018, 62, 605–628. [Google Scholar] [CrossRef]
- Elkaroui, A.; Hichem Gazzah, M.; Mahjoub Saïd, N.; Bournot, P.; Le Palec, G. Entropy generation concept for a turbulent plane jet with variable density. Comput. Fluids 2018, 168, 328–341. [Google Scholar] [CrossRef]
- Mahmud, S.; Fraser, R.A. The second law analysis in fundamental convective heat transfer problem. Int. J. Thermal Sci. 2003, 42, 177–186. [Google Scholar] [CrossRef]
- Akih-Kumgeh, B. Toward improved understanding of the physical meaning of entropy in classical thermodynamics. Entropy 2016, 18, 270. [Google Scholar] [CrossRef]
- Kostic, M.M. The elusive nature of entropy and its physical meaning. Entropy 2014, 16, 953–967. [Google Scholar] [CrossRef]
- Yilbas, B.S.; Shuja, S.Z.; Rashid, M. Confined swirling jet impingement onto an adiabatic wall. Int. J. Heat Mass Transf. 2013, 46, 2947–2955. [Google Scholar]
- Shuja, S.Z.; Yilbas, B.S.; Budair, M.O. Local entropy generation in an impinging jet: Minimum entropy concept evaluating various turbulence models. Comput. Methods Appl. Mech. Eng. 2001, 190, 3623–3644. [Google Scholar] [CrossRef]
- Demirel, Y.; Kahraman, R. Entropy generation in a rectangular packed duct with wall heat flux. Int. J. Heat Mass Transf. 1999, 42, 2337–2344. [Google Scholar] [CrossRef]
- Bouras, F.; Soudani, A.; Si Ameur, A. Thermochemical study of internal combustion engine. Energy Procedia 2012, 18, 1086–1095. [Google Scholar] [CrossRef]
- Bouras, F.; Attia, M.E.H.; Khaldi, F. Entropy generation optimization in internal combustion. Engine Environ. Process. 2015, 2, 233–242. [Google Scholar] [CrossRef]
- Zimmermann, S.; Tiwari, M.K.; Meijer, I.; Paredes, S.; Michel, B.; Poulikakos, D. Hot water cooled electronics: Exergy analysis and waste heat reuse feasibility. Int. J. Heat Mass Transf. 2012, 55, 6391–6399. [Google Scholar] [CrossRef]
- Dunbar, W.R.; Lior, N. Sources of combustion irreversibility. Combust. Sci. Technol. 1994, 103, 41–61. [Google Scholar] [CrossRef]
- Goodarzi, M.; Safaei, M.; Hakan, R.; Oztop, F.; Karimipour, A.; Sadeghinezhad, E.; Dahari, M.; Kazi, S.N.; Jomhari, N. Numerical study of entropy generation due to coupled laminar and turbulent mixed convection and thermal radiation in an enclosure filled with a semitransparent medium. Sci. World J. 2014, 2014, 8. [Google Scholar] [CrossRef] [PubMed]
- Chen, S. Analysis of entropy generation in counter-flow premixed hydrogen air combustion. Int. J. Hydrog. Energy 2010, 35, 1401–1411. [Google Scholar] [CrossRef]
- Chen, S.; Li, J.; Han, H.; Liu, Z.; Zheng, C. Effects of hydrogen addition on entropy generation in ultra-lean counter-flow methane-air premixed combustion. Int. J. Hydrog. Energy 2010, 35, 3891–3902. [Google Scholar] [CrossRef]
- Chen, S.; Han, H.; Liu, Z.; Li, J.; Zheng, C. Analysis of entropy generation in non-premixed hydrogen versus heated air counter-flow combustion. Int. J. Hydrog. Energy 2010, 35, 4736–4746. [Google Scholar] [CrossRef]
- Chen, S.; Liu, Z.; Liu, J.; Li, J.; Wang, L.; Zheng, C. Analysis of entropy generation in hydrogen-enriched ultra-lean counter-flow methane-air non-premixed combustion. Int. J. Hydrog. Energy 2010, 35, 12491–12501. [Google Scholar] [CrossRef]
- Morsli, S.; El Ganaoui, M.; Sabeur, A. Numerical investigation of diffusion turbulent propane/air flame. Energy Environ. Biol. Biomed. 2014, 232, 18–23. [Google Scholar]
- Morsli, S.; Sabeur, A.; El Ganaoui, M. Simulation of a burner with different fuels and analysis based on entropy generation. Energy Procedia 2017, 139, 631–638. [Google Scholar] [CrossRef]
- Magnussen, B.F.; Hjertager, B.H. On mathematical models of turbulent combustion with special emphasis on soot formation and combustion. In Proceedings of the 16th Symposium (International) on Combustion, Cambridge, UK, 15–20 August 1976; The Combustion Institute: Pittsburgh, PA, USA, 1997. [Google Scholar]
- Ilbas, M.; Yılmaz, I.; Kaplan, Y. Investigations of hydrogen and hydrogen–hydrocarbon composite fuel combustion and NOx emission characteristics in a model combustor. Int. J. Hydrogen Energy 2005, 30, 1139–1147. [Google Scholar] [CrossRef]
- Fluent Inc. FLUENT 6.3.26 User’s Guide; Fluent Inc.: New York, NY, USA, 2006. [Google Scholar]
- Launder, B.E.; Spalding, D.B. Lectures in Mathematical Models of Turbulence; Academic Press: London, UK, 1972. [Google Scholar]
- Poinsot, T.; Veynante, D. Theoretical and Numerical Combustion; RT Edwards Inc.: Philadelphia, PA, USA, 2005. [Google Scholar]
- Pinho, C.E.L.; Delgado, J.M.P.Q.; Pilão, R.; Conde, J.; Pinho, C. Defect and diffusion. In Diffusion in Solids and Liquids III; Öchsner, A., Murch, G.E., Eds.; Trans Tech Publications: Zurich, Switzerland, 2008; Volume 273, pp. 144–149. [Google Scholar]
- Morsli, S.; Sabeur, A.; El Ganaoui, M. Numerical simulation of entropy generation in hydrogen-air burner. FDMP 2015, 4, 342–353. [Google Scholar]
- Yapici, H.; Kayataş, N.; Albayrak, B.; Baştürk, G. Numerical study of burner effect of oxygen fraction on local entropy generation in a methane-air. Sadhana 2004, 29, 641–667. [Google Scholar] [CrossRef]


| U Air (m/s) | |||
|---|---|---|---|
| ϕ = 0.5 | ϕ = 0.7 | ϕ = 1 | |
| 10 | 56.436 | 40.312 | 20.218 |
| 20 | 28.614 | 20.439 | 14.307 |
| 30 | 19.340 | 13.814 | 9.670 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morsli, S.; Sabeur, A.; El Ganaoui, M.; Ramenah, H. Computational Simulation of Entropy Generation in a Combustion Chamber Using a Single Burner. Entropy 2018, 20, 922. https://doi.org/10.3390/e20120922
Morsli S, Sabeur A, El Ganaoui M, Ramenah H. Computational Simulation of Entropy Generation in a Combustion Chamber Using a Single Burner. Entropy. 2018; 20(12):922. https://doi.org/10.3390/e20120922
Chicago/Turabian StyleMorsli, Souad, Amina Sabeur, Mohammed El Ganaoui, and Harry Ramenah. 2018. "Computational Simulation of Entropy Generation in a Combustion Chamber Using a Single Burner" Entropy 20, no. 12: 922. https://doi.org/10.3390/e20120922
APA StyleMorsli, S., Sabeur, A., El Ganaoui, M., & Ramenah, H. (2018). Computational Simulation of Entropy Generation in a Combustion Chamber Using a Single Burner. Entropy, 20(12), 922. https://doi.org/10.3390/e20120922





