Improving Entropy Estimates of Complex Network Topology for the Characterization of Coupling in Dynamical Systems
Abstract
1. Introduction
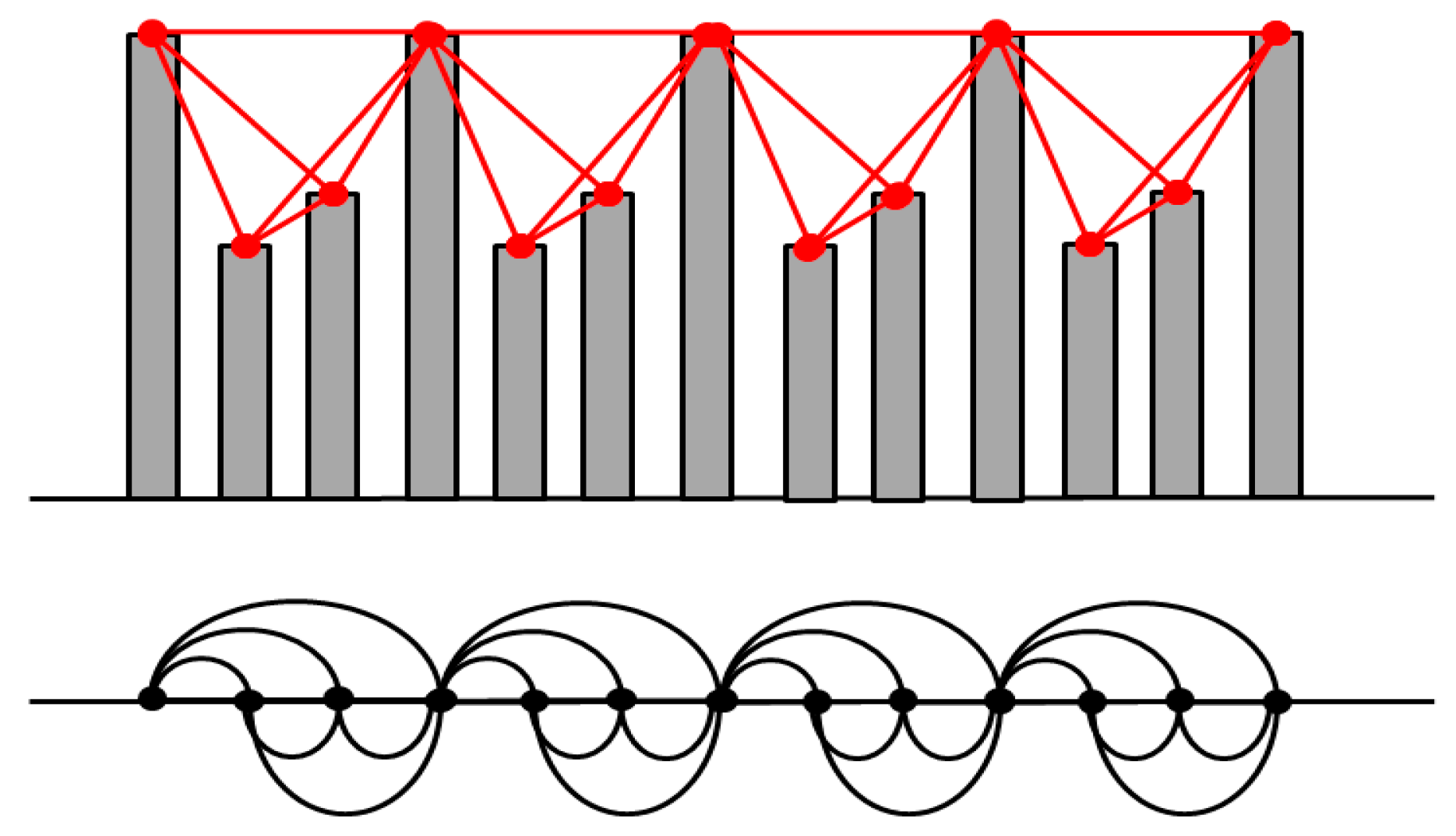
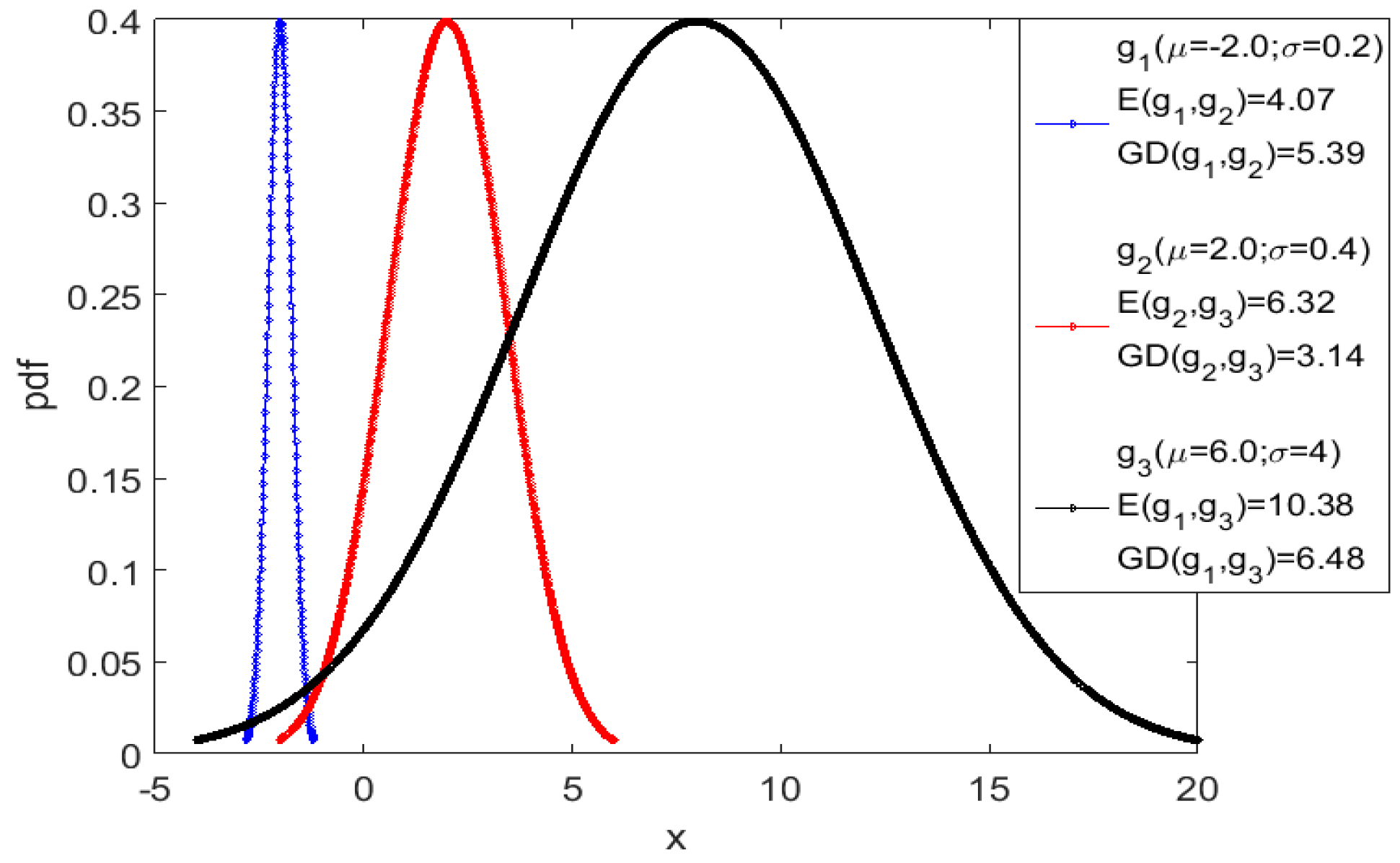
2. Geodesic Distance to Improve Visibility Graphs for the Analysis of Synchronization Experiments
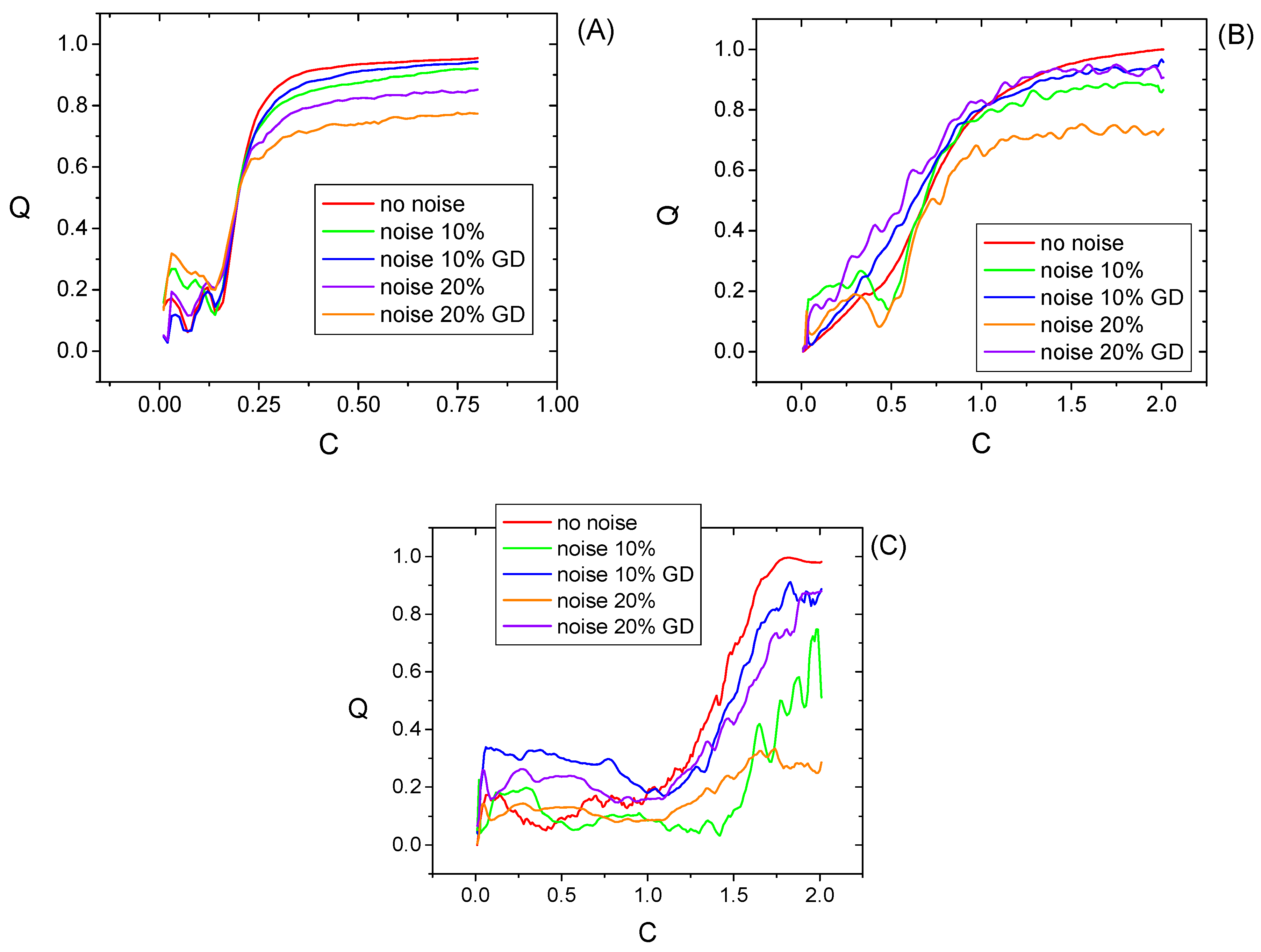
3. Tests with Synthetic Data
4. Real-World Applications
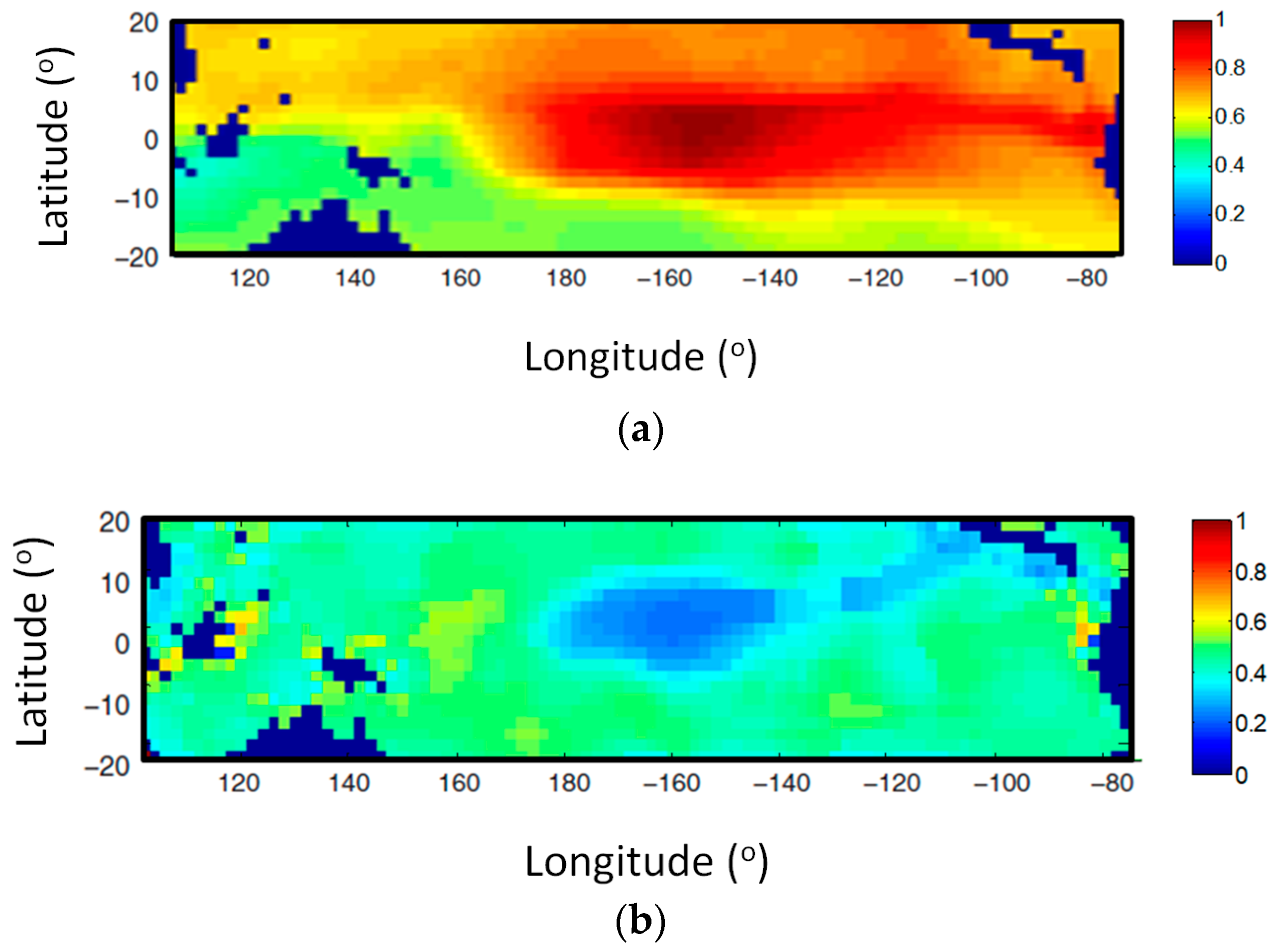
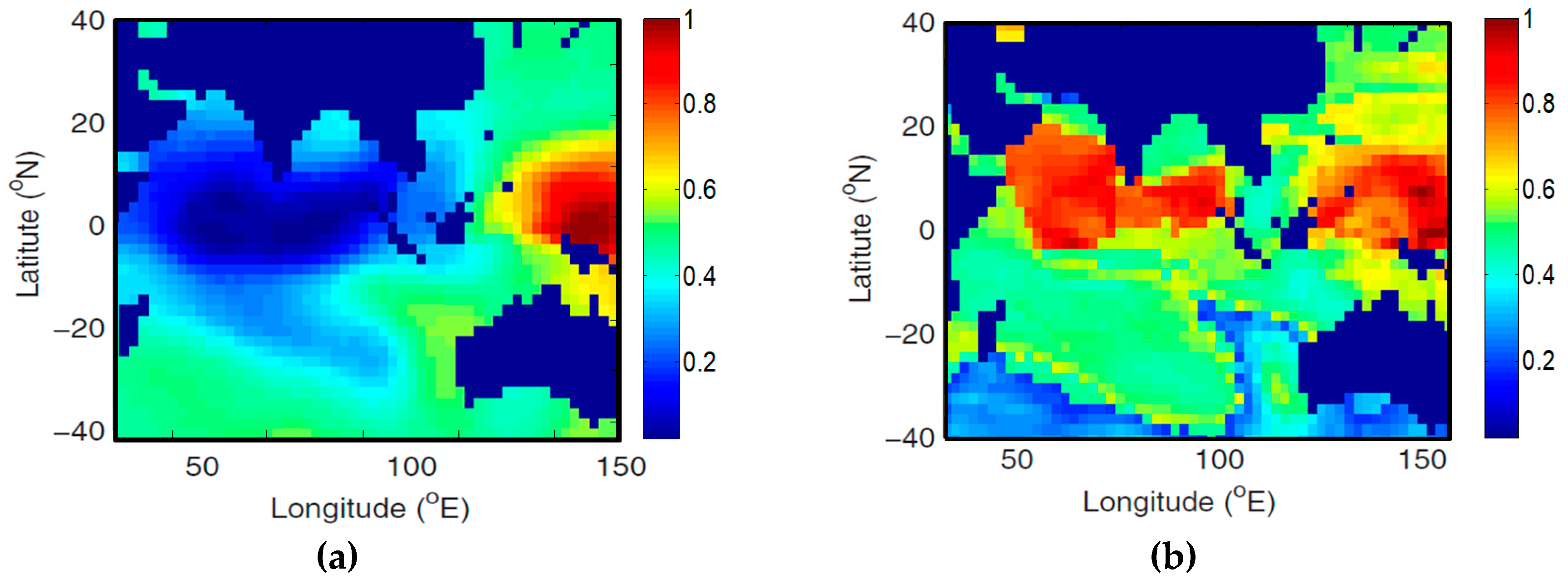
4.1. The Interaction between El Niño Southern Oscillation and the Indian Ocean Dipole
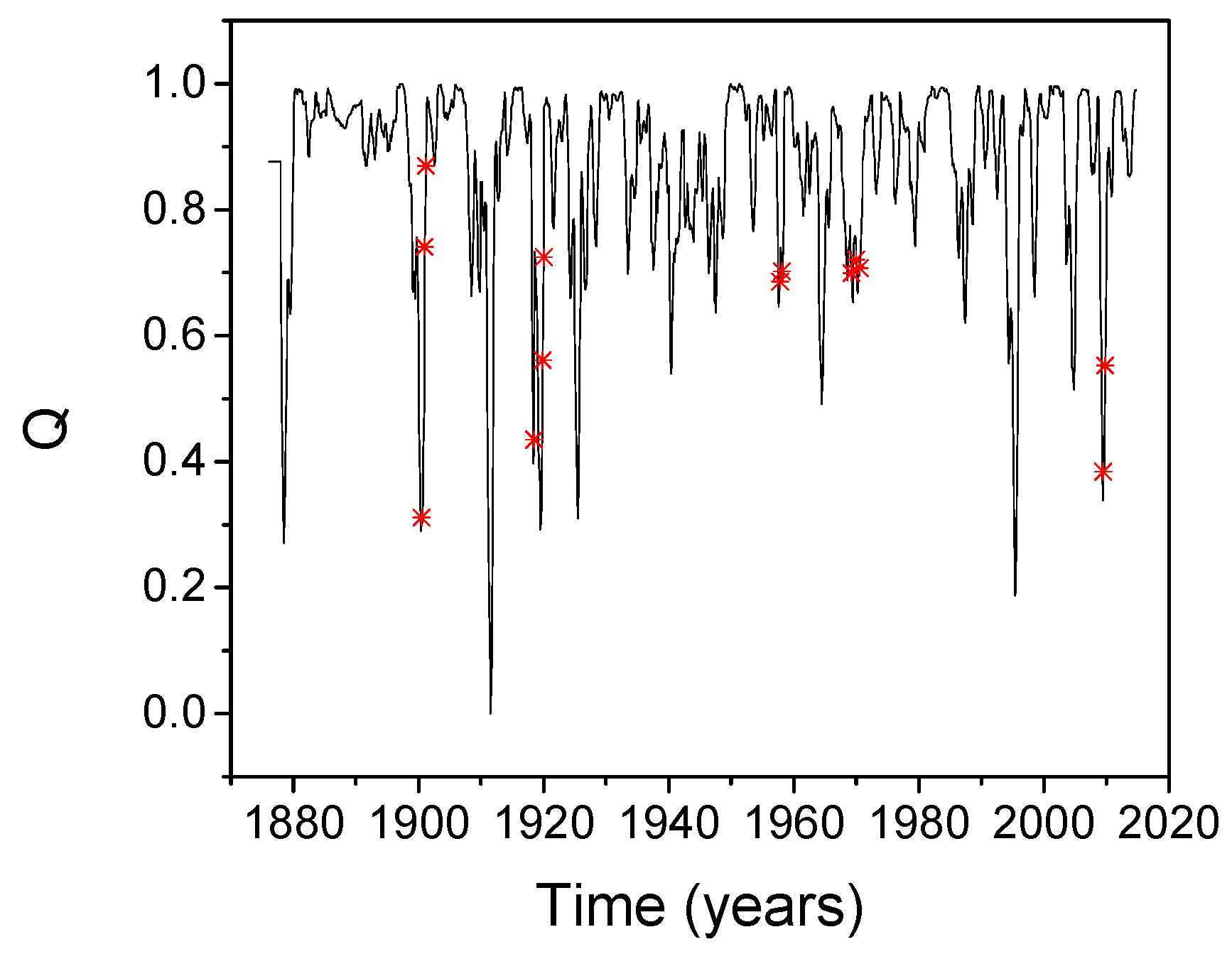
4.2. The Influence of the El Nino Southern Oscillation on Influenza Pandemic Occurrence
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pecora, L.M.; Carroll, T.L. Synchronization in Chaotic Systems. Phys. Rev. Lett. 1990, 64, 821–825. [Google Scholar] [CrossRef] [PubMed]
- Abarbanel, H.D.I.; Rulkov, N.F.; Sushchik, M.M.; Sushchik, M. Generalized synchronization of chaos: The auxiliary system approach. Phys. Rev. E 1996, 53, 4528–4535. [Google Scholar] [CrossRef]
- Rosenblum, M.G.; Pikovsky, A.S.; Kurths, J. From phase to lag synchronization in coupled chaotic oscillators. Phys. Rev. Lett. 1997, 78, 4193–4196. [Google Scholar] [CrossRef]
- Rosa, E.R.; Ott, E.; Hess, M.H. Transition to phase synchronization of chaos. Phys. Rev. Lett. 1998, 80, 1642–1645. [Google Scholar] [CrossRef]
- Femat, R.; Solis-Perales, G. On the Chaos Synchronization Phenomena. Phys. Lett. A 1999, 262, 50–60. [Google Scholar] [CrossRef]
- Brown, R.; Kocarev, L. A unifying definition of synchronization for dynamical systems. Chaos 2000, 10, 344–349. [Google Scholar] [CrossRef] [PubMed]
- Boccaletti, S.; Pecora, L.M.; Pelaez, A. Unifying framework for synchronization of coupled dynamical systems. Phys. Rev. E 2001, 63, 066219. [Google Scholar] [CrossRef] [PubMed]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Statist. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring Information Transfer. Phys Rev Lett 2000, 85, 461–464. [Google Scholar] [CrossRef] [PubMed]
- Hlavácková-Schindlera, K.; Palub, M.; Vejmelkab, M.; Bhattacharya, J. Causality detection based on information-theoretic approaches in time series analysis. Phys. Rep. 2007, 441, 1–46. [Google Scholar]
- Stama, C.J.; van Dijk, B.W. Synchronization likelihood: An unbiased measure of generalized synchronization in multivariate data sets. Physica D 2002, 163, 236–251. [Google Scholar] [CrossRef]
- Pawelzik, K. Nichtlineare Dynamik und Hirnaktivität: Charaktesierung Nichtlinearer Experimenteller Systeme durch Instabile Periodische Orbits, Vorhersagen und Informationsflüsse; Verlag Harri Deutsch: Frankfurt, Germany, 1991. (In German) [Google Scholar]
- Grassberger, P.; Procaccia, I. Measuring the Strangeness of Strange Attractors. Physica D 1983, 9, 189–208. [Google Scholar] [CrossRef]
- Janjarasjittab, S.; Loparo, K.A. An approach for characterizing coupling in dynamical systems. Physica D 2008, 237, 2482–2486. [Google Scholar] [CrossRef]
- Shabunin, A.; Demidov, V.; Astakhov, V.; Anishchenko, V. Information theoretic approach to quantify complete and phase synchronization of chaos. Phys. Rev. E 2002, 65, 056215. [Google Scholar] [CrossRef] [PubMed]
- Palus, M.; Stefanovska, A. Direction of coupling from phases of interacting oscillators: An information-theoretic approach. Phys. Rev. E 2003, 67, 055201(R). [Google Scholar] [CrossRef] [PubMed]
- Hempel, S.; Koseska, A.; Kurths, J.; Nikoloski, Z. Inner Composition Alignment for Inferring Directed Networks from Short Time Series. PRL 2011, 107, 054101. [Google Scholar] [CrossRef] [PubMed]
- Quiroga, R.Q.; Kreuz, T.; Grassberger, P. Event synchronization: A simple and fast method to measure synchronicity and time delay patterns. Phys. Rev. E 2002, 66, 041904. [Google Scholar] [CrossRef] [PubMed]
- Rulkov, N.F.; Sushchik, M.M.; Tsimring, L.S.; Abarbanel, H.D.I. Generalized synchronization of chaos in directionally coupled chaotic systems. Phys. Rev. E 1995, 51, 980–994. [Google Scholar] [CrossRef]
- Sugihara, G.; May, R.; Ye, H.; Hsieh, C.-H.; Deyle, E.; Fogarty, M.; Munch, S. Detecting Causality in Complex Ecosystems. Science 2012, 338, 496–500. [Google Scholar] [CrossRef] [PubMed]
- San Liang, X. Unraveling the cause-effect relation between time series. Phys. Rev. E 2014, 90, 052150. [Google Scholar] [CrossRef] [PubMed]
- Kreuz, T.; Mormann, F.; Andrzejak, R.G.; Kraskov, A.; Lehnertz, K.; Grassberger, P. Measuring synchronization in coupled model systems: A comparison of different approaches. Physica D 2007, 225, 29–42. [Google Scholar] [CrossRef]
- Mehraban, S.; Shirazi, A.H.; Zamani, M.; Jafari, G.R. Coupling between time series: A network view. EPL 2015, 103, 50011. [Google Scholar] [CrossRef]
- Zhang, J.; Small, M. Complex Network from Pseudoperiodic Time Series: Topology versus Dynamics. PRL 2006, 96, 238701. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Sun, J.; Luo, X.; Zhang, K.; Nakamura, T.; Small, M. Characterizing Pseudoperiodic Time Series through Complex Network Approach. Physica D 2008, 237, 2856–2865. [Google Scholar] [CrossRef]
- Lacasa, L.; Luque, B.; Ballesteros, F.; Luque, J.; Nuño, J.C. From time series to complex networks: The visibility graph. PNAS 2008, 105, 4972–4975. [Google Scholar] [CrossRef] [PubMed]
- Granger, C.W.J. Investigating Causal Relations by Econometric Models and Cross-spectral Methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Gonçalves, B.A.; Carpi, L.C.; Rosso, O.; Ravetti, M.G. Time series characterization via horizontal visibility graph and Information Theory. Physica A 2016, 464, 93–102. [Google Scholar] [CrossRef]
- Zhu, G.; Li, Y.; Wen, P. Epileptic seizure detection in EEGs signals using a fast weighted horizontal visibility algorithm. Comput. Methods Programs Biomed. 2014, 115, 64–75. [Google Scholar] [CrossRef] [PubMed]
- Supriya, S.; Siuly, S.; Wang, H.; Cao, J.; Zhang, Y. Weighted Visibility Graph with Complex Network Features in the Detection of Epilepsy. IEEE Access 2016, 4, 6554–6566. [Google Scholar] [CrossRef]
- Amari, S.-I.; Nagaoka, H. Methods of Information Geometry; Oxford University Press and the American Mathematical Society: Oxford, UK, 2000. [Google Scholar]
- Arwini, K.; Dodson, T.J. Information Geometry: Near Randomness and Near Independence; Springer: Berlin, Germany, 2008. [Google Scholar]
- Craciunescu, T.; Murari, A. Geodesic distance on Gaussian Manifolds for the robust identification of chaotic systems. Nonlinear Dyn. 2016, 86, 677–693. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Bianconi, G. The entropy of randomized network ensembles. EPL 2007, 81, 28005. [Google Scholar] [CrossRef]
- Korner, J.; Marton, K. Random access communication and graph entropy. IEEE Trans. Inf. Theory 1998, 34, 312–314. [Google Scholar] [CrossRef]
- Orsini, C.; Mitrović Dankulov, M.; Jamakovic, A.; Mahadevan, P.; Colomer-de-Simón, P.; Vahdat, A.; Bassler, K.E.; Torokzcai, Z.; Boguñá, M.; Caldarelli, G.; et al. Quantifying randomness in real networks. Nat. Commun. 2015, 6, 8627. [Google Scholar] [CrossRef] [PubMed]
- Estrada, E.; José, A.; Hatano, N. Walk entropies in graphs. Linear Algebra Appl. 2014, 443, 235–244. [Google Scholar] [CrossRef]
- Zenil, H.; Kiani, N.A.; Tegnér, J. Low-algorithmic-complexity entropy-deceiving graphs. Phys. Rev. E 2017, 96, 012308. [Google Scholar] [CrossRef]
- Morzy, M.; Kajdanowicz, T.; Kazienko, P. On Measuring the Complexity of Networks: Kolmogorov Complexity versus Entropy. Complexity 2017, 2017, 3250301. [Google Scholar] [CrossRef]
- Sengupta, D.C.; Sengupta, J.D. Application of graph entropy in CRISPR and repeats detection in DNA sequences. Comput. Mol. Biosci. 2016, 6, 41–51. [Google Scholar] [CrossRef]
- Mowshowitz, A.; Dehmer, M. Entropy and the complexity of graphs revisited. Entropy 2012, 14, 559–570. [Google Scholar] [CrossRef]
- Albregtsen, F. Statistical Texture Measures Computed from Gray Level Coocurrence Matrices. Available online: https://www.uio.no/studier/emner/matnat/ifi/INF4300/h08/undervisningsmateriale/glcm.pdf (accessed on 7 November 2018).
- Silva, L.E.V.; Senra Filho, A.C.S.; Fazan, V.P.S.; Felipe, J.C.; Murta Junior, L.O. Two-dimensional sample entropy: Assessing image texture through irregularity. Biomed. Phys. Eng. Express 2016, 2, 045002. [Google Scholar] [CrossRef]
- Rössler, O.E. An Equation for Continuous Chaos. Phys. Lett. A 1976, 57, 397–398. [Google Scholar] [CrossRef]
- Mormann, F.; Lehnertz, K.; David, P.; Elger, C.E. Mean phase coherence as a measure for phase synchronization and its application to the EEG of epilepsy patients. Physica D 2000, 144, 358–369. [Google Scholar] [CrossRef]
- Henon, M. A two-dimensional mapping with a strange attractor. Commun. Math. Phys. 1976, 50, 69–77. [Google Scholar] [CrossRef]
- Schiff, S.J.; So, P.; Chang, T.; Burke, R.E.; Sauer, T. Detecting dynamical interdependence and generalized synchrony through mutual prediction in a neural ensemble. Phys. Rev. E 1996, 54, 6708–6723. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic Nonperiodic Flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Ma, H.-C.; Chen, C.-C.; Chen, B.-W. Dynamics and transitions of the coupled Lorenz system. Phys. Rev. 1997, 56, 1550–1555. [Google Scholar] [CrossRef]
- Hahs, D.W.; Pethel, S.D. Distinguishing Anticipation from Causality: Anticipatory Bias in the Estimation of Information. Flow. Phys. Rev. Lett. 2011, 107, 128701. [Google Scholar] [CrossRef] [PubMed]
- Marwan, N.; Romano, M.C.; Thiel, M.; Kurths, J. Recurrence plots for the analysis of complex systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Marwan, N.; Trauth, M.H.; Vuille, M.; Kurths, J. Comparing modern and Pleistocene ENSO-like influences in NW Argentina using nonlinear time series analysis methods. Clim. Dynam. 2003, 21, 317–326. [Google Scholar] [CrossRef]
- Kodra, E.; Chatterjee, S.; Ganguly, A.R. Exploring Granger causality between global average observed time series of carbon dioxide and temperature. Theor. Appl. Climatol. 2011, 104, 325–335. [Google Scholar] [CrossRef]
- Leggett, L.M.W.; Ball, D.A. Granger causality from changes in level of atmospheric CO2 to global surface temperature and the El Niño–Southern Oscillation, and a candidate mechanism in global photosynthesis. Atmos. Chem. Phys. 2015, 15, 11571–11592. [Google Scholar] [CrossRef]
- Arjasakusuma, S.; Yamaguchi, Y.; Hirano, Y.; Zhou, X. ENSO- and Rainfall-Sensitive Vegetation Regions in Indonesia as Identified from Multi-Sensor Remote Sensing Data. ISPRS Int. J. Geo-Inf. 2018, 7, 103. [Google Scholar] [CrossRef]
- Attanasio, A.; Pasini, A.; Triacca, U. Has natural variability a lagged influence on global temperature? A multi-horizon Granger causality analysis. Dyn. Stat. Climate Syst. 2016, 1, dzw002. [Google Scholar] [CrossRef]
- Papagiannopoulou, C.; Miralles, D.G.; Decubber, S.; Demuzere, M.; Verhoest, N.E.C.; Dorigo, W.A.; Waegeman, W. A non-linear Granger-causality framework to investigate climate–vegetation dynamics. Geosci. Model Dev. 2017, 10, 1945–1960. [Google Scholar] [CrossRef]
- Mokhov, I.; Smirnov, D.A.; Nakonechny, P.I.; Kozlenko, S.S.; Seleznev, V.; Kurths, J. Alternating mutual influence of El-Niño/Southern Oscillation and Indian monsoon. Geophys. Res. Lett 2011, 38, L00F04. [Google Scholar] [CrossRef]
- Berkelhammer, M.; Sinha, A.; Mudelsee, M.; Cheng, H.; Yoshimura, K.; Biswas, J. On the low-frequency component of the ENSO–Indian monsoon relationship: A paired proxy perspective. Clim. Past. 2014, 10, 733–744. [Google Scholar] [CrossRef]
- Detto, M.; Wright, S.J.; Calderón, O.; Muller-Landau, H.C. Resource acquisition and reproductive strategies of tropical forest in response to the El Niño–Southern Oscillation. Nat. Commun. 2018, 9, 913. [Google Scholar] [CrossRef] [PubMed]
- Cane, M.A. Oceanograhic events during El Nino. Science 1983, 222, 1189–1195. [Google Scholar] [CrossRef] [PubMed]
- Klein, S.A.; Soden, B.J.; Lau, N.C. Remote Sea Surface Temperature Variations during ENSO: Evidence for a Tropical Atmospheric Bridge. J. Clim. 1999, 12, 917–932. [Google Scholar] [CrossRef]
- Webster, P.J.; Moore, A.M.; Loschnigg, J.P.; Leben, R.R. Coupled ocean-atmosphere dynamics in the Indian Ocean during 1997-98. Nature 1999, 401, 356–360. [Google Scholar] [CrossRef] [PubMed]
- Saji, N.H.; Goswami, B.N.; Vinayachandran, P.N.; Yamagata, T. A dipole mode in the tropical Indian Ocean. Nature 1999, 401, 360–363. [Google Scholar] [CrossRef] [PubMed]
- Fischer, A.S.; Terray, P.; Guilyardi, E.; Gualdi, S.; Delecluse, P. Two independent triggers for the Indian Ocean dipole zonal mode in a coupled GCM. J. Clim. 2005, 18, 3428–3449. [Google Scholar] [CrossRef]
- Annamalai, H.; Xie, S.-P.; McCreary, J.P.; Murtugudde, R. Impact of Indian Ocean sea surface temperature on developing El Niño. J. Clim. 2005, 18, 302–319. [Google Scholar] [CrossRef]
- Yuan, Y.; Li, C. Decadal variability of the IOD-ENSO relationship. Chin. Sci. Bull. 2008, 53, 1745–1752. [Google Scholar] [CrossRef]
- Fan, L.; LIU, Q.; Wang, C.; Guo, F. Indian Ocean Dipole Modes Associated with Different Types of ENSO. Development. J. Clim. 2017, 30, 2223–2249. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Dai, A.; Rasmussen, R.M.; Parsons, D.B. The Changing Character of Precipitation. Bull. Am. Meteor. Soc. 2003, 84, 1205–1218. [Google Scholar] [CrossRef]
- NOAA ESRL Physical Sciences Division Data. Available online: https://www.esrl.noaa.gov/psd/data/gridded/rsshelp.html (accessed on 23 October 2018).
- Japan Agency for Marine-Earth Science and Technology (JAMSTEC). Available online: http://www.jamstec.go.jp/e/ (accessed on 23 October 2018).
- Weinberger, D.; Baroux, N.; Grangeon, J.-P.; Ko, A.I.; Goarant, C. El Niño Southern Oscillation and leptospirosis outbreaks in New Caledonia. PLoS Negl. Trop. Dis. 2014, 8, e2798. [Google Scholar] [CrossRef] [PubMed]
- Vincenti-Gonzalez, M.F.; Tami, A.; Lizarazo, E.F.; Grillet, M.E. ENSO-driven climate variability promotes periodic major outbreaks of dengue in Venezuela. Sci. Rep. 2018, 8, 5727. [Google Scholar] [CrossRef] [PubMed]
- Hales, S.; Weinstein, P.; Souares, Y.; Woodward, A. El Nino and the Dynamics of Vector-Borne Disease Transmission. EHP 1999, 107, 99–102. [Google Scholar] [PubMed]
- Pascual, M.; Rodo, X.; Ellner, S.P.; Colwell, R.; Bouma, M.J. Cholera Dynamics and El Niño Southern Oscillation. Science 2000, 289, 1766–1769. [Google Scholar] [CrossRef] [PubMed]
- McGregor, G.R.; Ebi, K. El Niño Southern Oscillation (ENSO) and Health: An Overview for Climate and Health Researchers. Atmosphere 2018, 9, 282. [Google Scholar] [CrossRef]
- An, S.; Wang, B. Interdecadal change of the structure of the ENSO mode and its impact on the ENSO frequency. J. Clim. 2000, 13, 2044–2055. [Google Scholar] [CrossRef]
- Lowen, A.C.; Mubareka, S.; Steel, J.; Palese, P. Influenza virus transmission is dependent on relative humidity and temperature. PLoS Pathog. 2007, 3, e151. [Google Scholar] [CrossRef] [PubMed]
- Oluwole, O.S.A. Dynamic regimes of El Niño southern Oscillation and influenza Pandemic Timing. Front Public Health. 2017, 5, 301. [Google Scholar] [CrossRef] [PubMed]
- Ongena, J. Towards the realization on JET of an integrated H-mode scenario for ITER. Nucl. Fusion 2004, 44, 124–133. [Google Scholar] [CrossRef]
- Romanelli, F. Overview of JET results. Nucl. Fusion 2009, 49, 104006. [Google Scholar] [CrossRef]
- Kiptily, V.G.; Perez von Thun, C.P.; Pinches, S.D.; Sharapov, S.E.; Borba, D.; Cecil, F.E.; Darrow, D.; Goloborod’ko, V.; Craciunescu, T.; Johnson, T.; et al. Recent progress in fast ion studies on JET. Nucl. Fusion 2009, 49, 065030. [Google Scholar] [CrossRef]
- Puiatti, M.E.; Mattioli, M.; Telesca, G.; Valisa, M.; Coffey, I.; Dumortier, P.; Giroud, C.; Ingesson, L.C.; Lawson, K.D.; Maddison, G.; et al. Radiation pattern and impurity transport in argon seeded ELMy H-mode discharges in JET. Plasma Phys. Control. Fusion 2002, 44, 1863–1878. [Google Scholar] [CrossRef]
| Rössler | Hénon | Lorenz | |
|---|---|---|---|
| CD | 0.92 | 0.95 | 0.89 |
| 10% noise, ED | 0.84 | 0.83 | 0.75 |
| 10% noise, GD | 0.88 | 0.91 | 0.83 |
| 20% noise, ED | 0.79 | 0.74 | 0.71 |
| 20% noise, GD | 0.81 | 0.86 | 0.82 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Craciunescu, T.; Murari, A.; Gelfusa, M. Improving Entropy Estimates of Complex Network Topology for the Characterization of Coupling in Dynamical Systems. Entropy 2018, 20, 891. https://doi.org/10.3390/e20110891
Craciunescu T, Murari A, Gelfusa M. Improving Entropy Estimates of Complex Network Topology for the Characterization of Coupling in Dynamical Systems. Entropy. 2018; 20(11):891. https://doi.org/10.3390/e20110891
Chicago/Turabian StyleCraciunescu, Teddy, Andrea Murari, and Michela Gelfusa. 2018. "Improving Entropy Estimates of Complex Network Topology for the Characterization of Coupling in Dynamical Systems" Entropy 20, no. 11: 891. https://doi.org/10.3390/e20110891
APA StyleCraciunescu, T., Murari, A., & Gelfusa, M. (2018). Improving Entropy Estimates of Complex Network Topology for the Characterization of Coupling in Dynamical Systems. Entropy, 20(11), 891. https://doi.org/10.3390/e20110891








