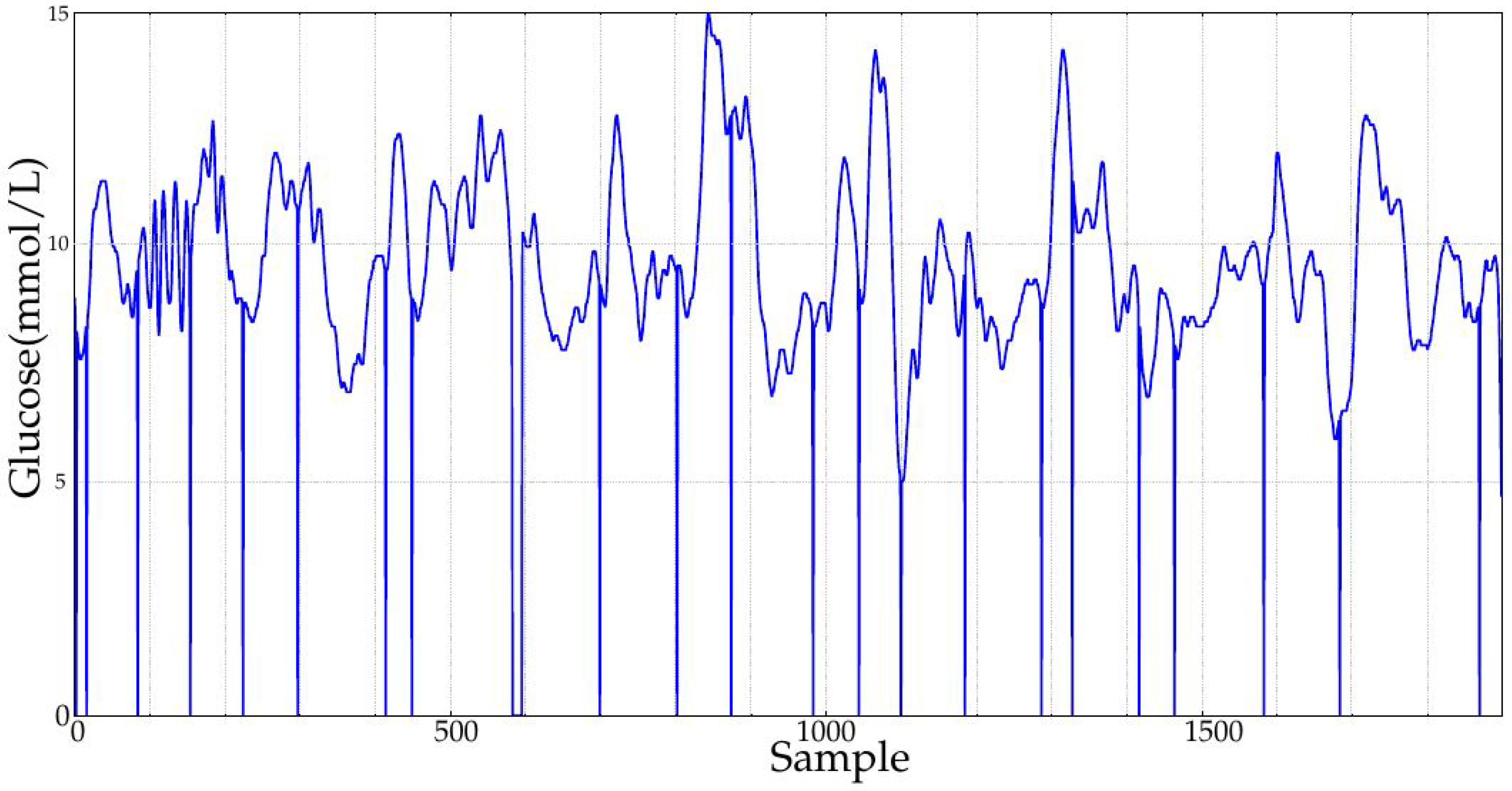
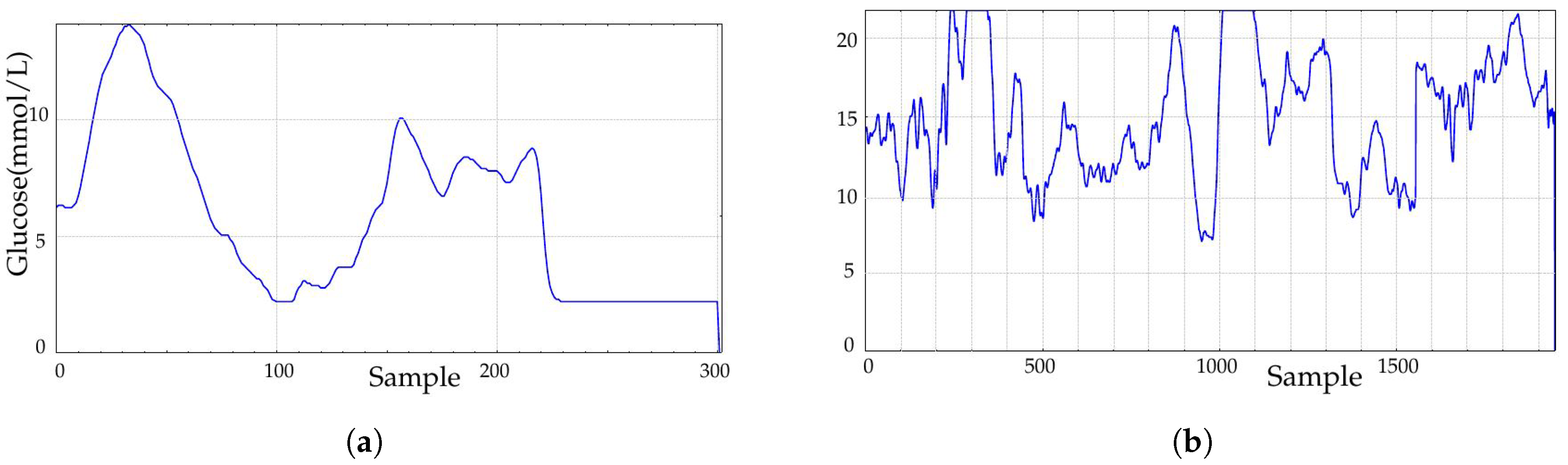
1. Introduction
The main idea of diabetes control is assessing a time series (blood glucose) [
1]. Traditionally, this was performed by means of punctual fasting blood measurements. This was obviously inappropriate. A slight improvement was self-monitoring through serial capillary blood controls performed by the patient [
2]. However, again, this was cumbersome and offered a poor overview of the time series. An important step was the use of glycosylated Hemoglobin (HbA1c), which provided an integrated assessment of the glucose blood levels of the last 8–12 weeks [
3]. This became a standard of care for many years. However, HbA1c has several drawbacks (it depends on hemoglobin levels, on the life span of red blood cells, etc.) [
4]. Furthermore, it is increasingly clear that raw blood glucose level is not the only relevant variable and that the glycemic profile (complexity, variability), which is not evaluated by HbA1c, is also clinically significant [
5]. Therefore, the development of a Continuous Glucose Monitoring System (CGMS) was universally perceived as an important improvement. Although its cost and some technical problems are refraining its generalization, many authors believe that CGMS will soon become a standard of care [
6].
The analysis of glucose time series using entropy estimators is a very difficult endeavor. Because of the technical constraints and patient inconvenience during portable CGM, records are usually very short (24 or 48 h, non-uniformly sampled at 5-, 10- or 20-min intervals, usually). As a result, the length of the time series available falls well below the recommended minimum length of
, where
m is the embedded dimension used in entropy estimators derived from Approximate Entropy (ApEn) [
7], such as Sample Entropy (SampEn) [
8] or Fuzzy Entropy (FuzzyEn) [
9], with usual values of
, or even higher.
In addition, devices of CGM need to be recalibrated, up to several times per day [
10], and mainly at the beginning of the ambulatory monitoring. Missing values are also frequently found in these records, due to device or sensor errors [
11]. Other problems encountered in blood glucose time series are sensor out-of-range or sensor disconnection values, causing a signal saturation or a flat reading during a time interval usually involving several contiguous samples.
Although the advent of new blood glucose monitoring technologies may reduce the incidence of the problems stated above, incorrect device or sensor manipulation, patient adherence, sensor detachment, time constraints, adoption barriers or affordability [
12,
13,
14,
15,
16] can still result in relatively short and artifacted records, as the ones analyzed in this paper.
CGM provides essential information related to the diagnosis and prognosis of the subjects. Moreover, CGM will become an indispensable tool for closed-loop control of future artificial pancreas, and the processing of any relevant information must be fast, robust and reliable. Traditionally, besides the usual all-or-nothing thresholds applied to detect hyper- or hypo-glycemia [
17,
18], this processing has been mainly based on a set of glucose variability metrics [
19,
20,
21]. More recently, this variability analysis has evolved into a more elaborated scheme using time series regularity, complexity or entropy estimators [
22]. Among all these proposed estimators, Detrended Fluctuation Analysis (DFA) [
23] is probably the most used method in the context of glucose data. This measure quantifies the long-term correlations of non-stationary time series, and it has been used to assess the fluctuations of glucose in normal daily life in diabetic and non-diabetic subjects [
24], as a predictor for the development of diabetes of patients at risk [
25], to study the initial phases of glucose metabolism dysfunction in hypertensive patients [
26], as a marker of risk for critical patients [
27] or to estimate insulin resistance also in diabetic and non-diabetic subjects [
28].
Other entropy estimators based on ApEn have been less extensively used in this context [
29], probably due to the problems stated above. Glycemic ApEn has been correlated with patient outcome after surgery, among other metrics [
30]. SampEn, its derivative multiscale entropy, mainly, has been used to study the complexity of glucose dynamics in diabetes [
31]. So far, FuzzyEn has not been included in any research work related to the analysis of blood glucose time series. However, these two methods have been extensively and successfully used in many other time series classification studies [
9,
32,
33,
34,
35,
36,
37,
38], not only physiological records [
39,
40], and have also demonstrated their robustness against signal artifacts [
41,
42,
43]. This is why these two entropy statistics were chosen for the present study.
Given the claimed better performance of FuzzyEn reported in the literature [
9], in comparison with its predecessors ApEn and SampEn, we wanted to study the applicability of this new metric to glycemia data, taking into account the possible ill effects caused by the record features stated above, and their characterization. Based on the dataset obtained from a study of the endocrine consequences of duodenal-jejunal exclusion [
44], this paper comparatively assesses the capability of SampEn and its derivative FuzzyEn to distinguish between classes, under different conditions in terms of record length, artifacts and border effects. The clinical implications of such a classifier can be varied and diverse. Changes in glucose dynamics could be correlated with other anthropometric, biochemical or hormonal characteristics [
44,
45] in order to try to anticipate the rate and intensity of metabolic improvements after the exclusion and better understand the possible mechanisms of its effects. It could also be used as a screening tool for patient/treatment selection.
The performance was assessed using the Area Under the ROC Curve (AUC) [
46] values obtained for the classification of two input classes (Months 1 and 10 for the database described in
Section 2.2). AUC is a widely-used measure in a diversity of classification schemes, including those based on entropy metrics in the context of biomedical applications [
32,
47,
48,
49,
50,
51].
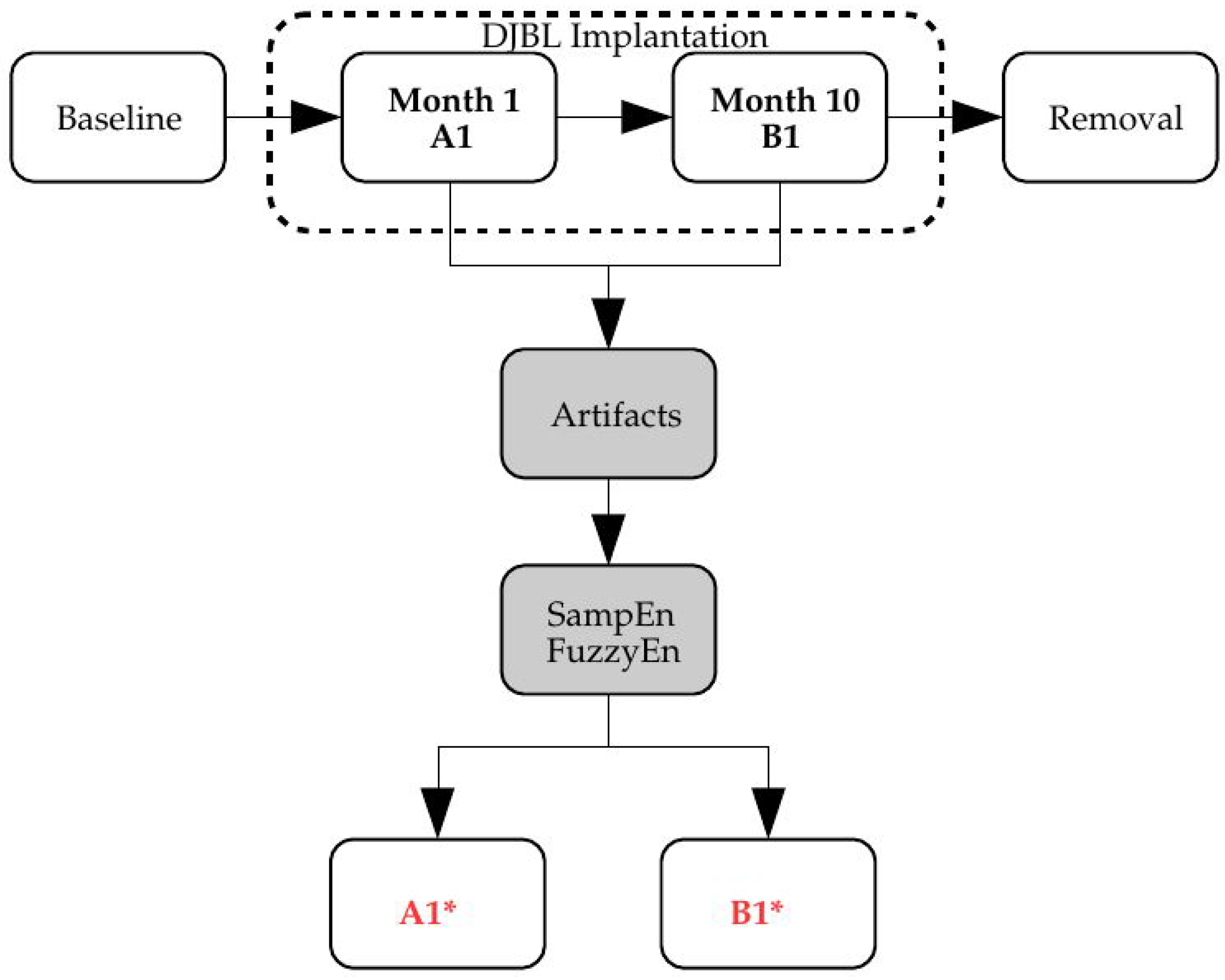
The metric for the classification was SampEn or FuzzyEn, and the input time series underwent different transformations to account for the effects targeted in this characterization study: record length (
Section 3.2), missing samples (
Section 3.3), sensor saturation (
Section 3.4) and time offset (
Section 3.5). The block diagram of the analysis proposed is shown in
Figure 1.
2. Materials and Methods
2.1. SampEn and FuzzyEn
SampEn was first introduced in [
8], as an improvement of ApEn, and FuzzyEn in [
9], also as an enhancement of SampEn. These methods were devised to characterize the level of irregularity, complexity, randomness or predictability found in time series, which is related to the dynamics of many physiological systems [
52], as is the case for the gluco-regulatory system. Both algorithms are quite similar, but FuzzyEn replaces the dissimilarity measure by a fuzzy function (membership function); and the subsequences are normalized in terms of zero mean, before computing such dissimilarity.
The input to both methods is a time series of length N: , from which a set of ordered subsequences of length is extracted: .
In SampEn, the maximum distance between 2 different subsequences
is computed. This distance is thresholded using a predefined parameter
r, the number of distances found,
, and for a specific
i, within such a threshold, stored in a counter
. This process is repeated
and the final value averaged:
An additional counter
is obtained using
. Finally, SampEn is obtained as:
In FuzzyEn, each local mean is first subtracted from every subsequence:
,
. The dissimilarity is now computed as
, where
is the fuzzy function selected, usually the exponential function
. The counters now become:
Finally, FuzzyEn is obtained as:
The performance of both metrics depends on the value of the parameters m and r, and specifically for FuzzyEn, n. These values are very application specific, and for optimal performance, an exploratory analysis of a range of values must be carried out in advance (grid search). During the experiments, and in all cases, r values tested ranged from 0.15–0.30, in 0.01 steps, and m values from 1 up to 3. This way, the influence of the parameters on the results was minimized, and only optimal configurations in the specified subset, in terms of maximum AUC, and in accordance with the recommended values for m and r, were considered.
2.2. Experimental Dataset
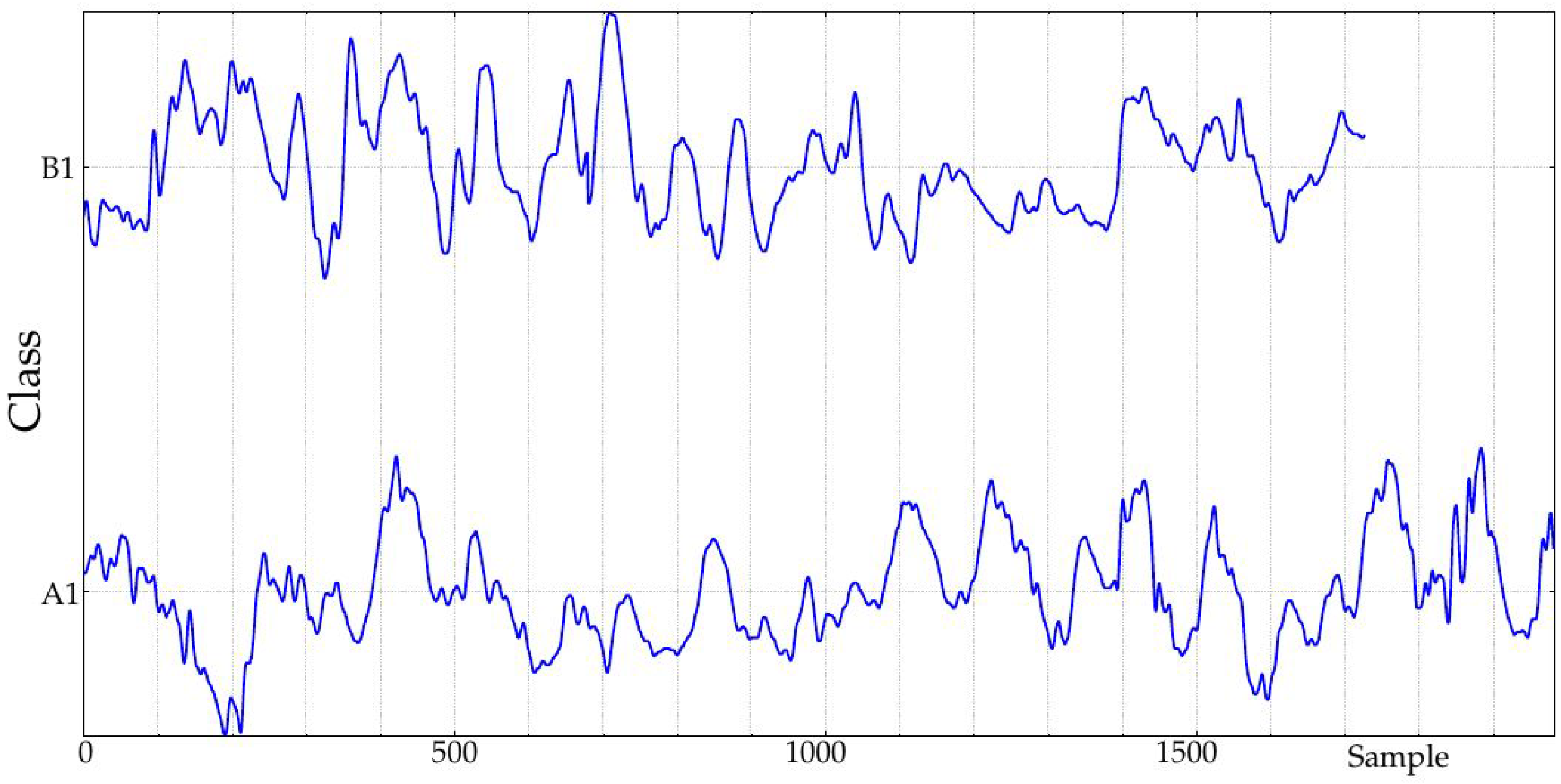
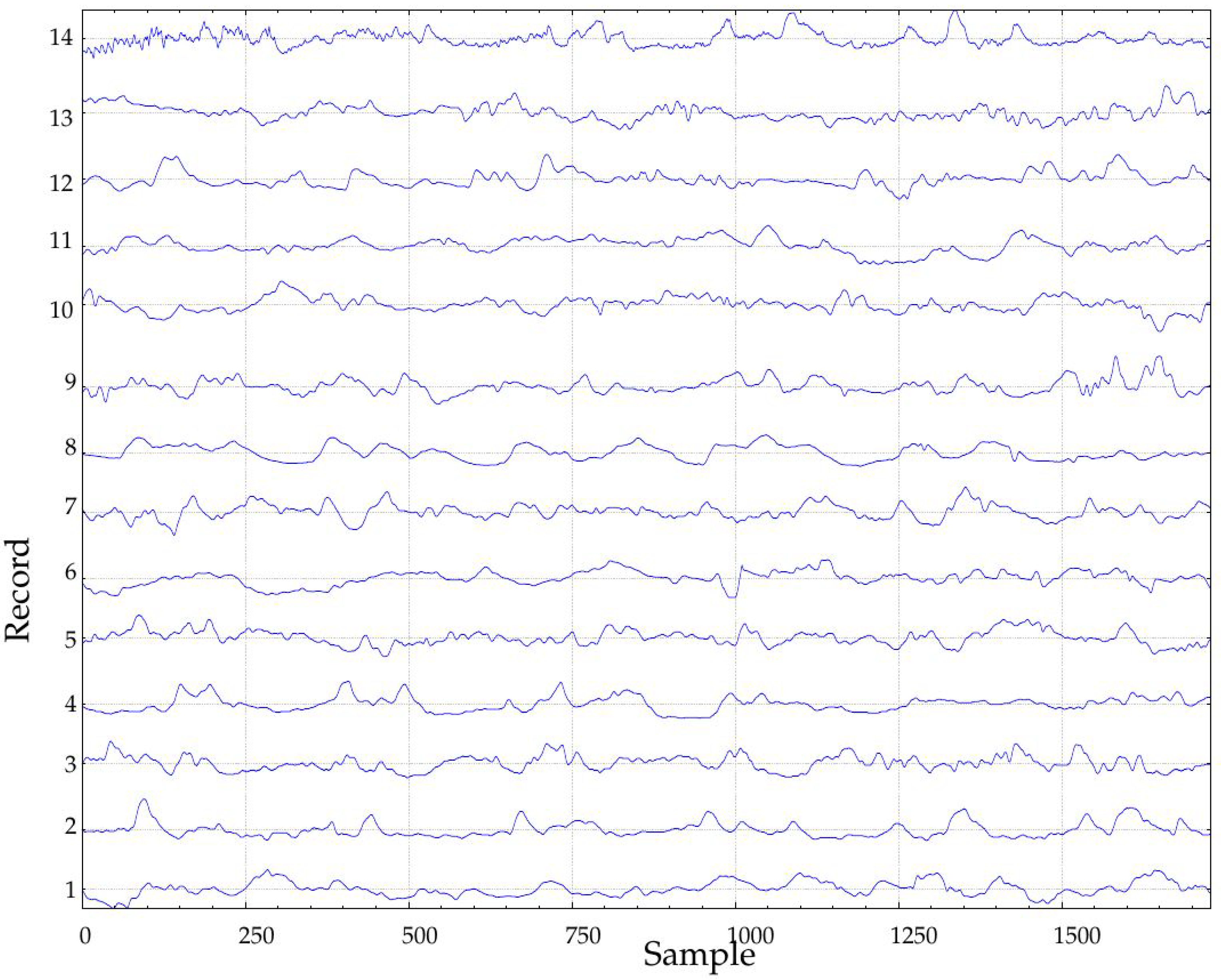
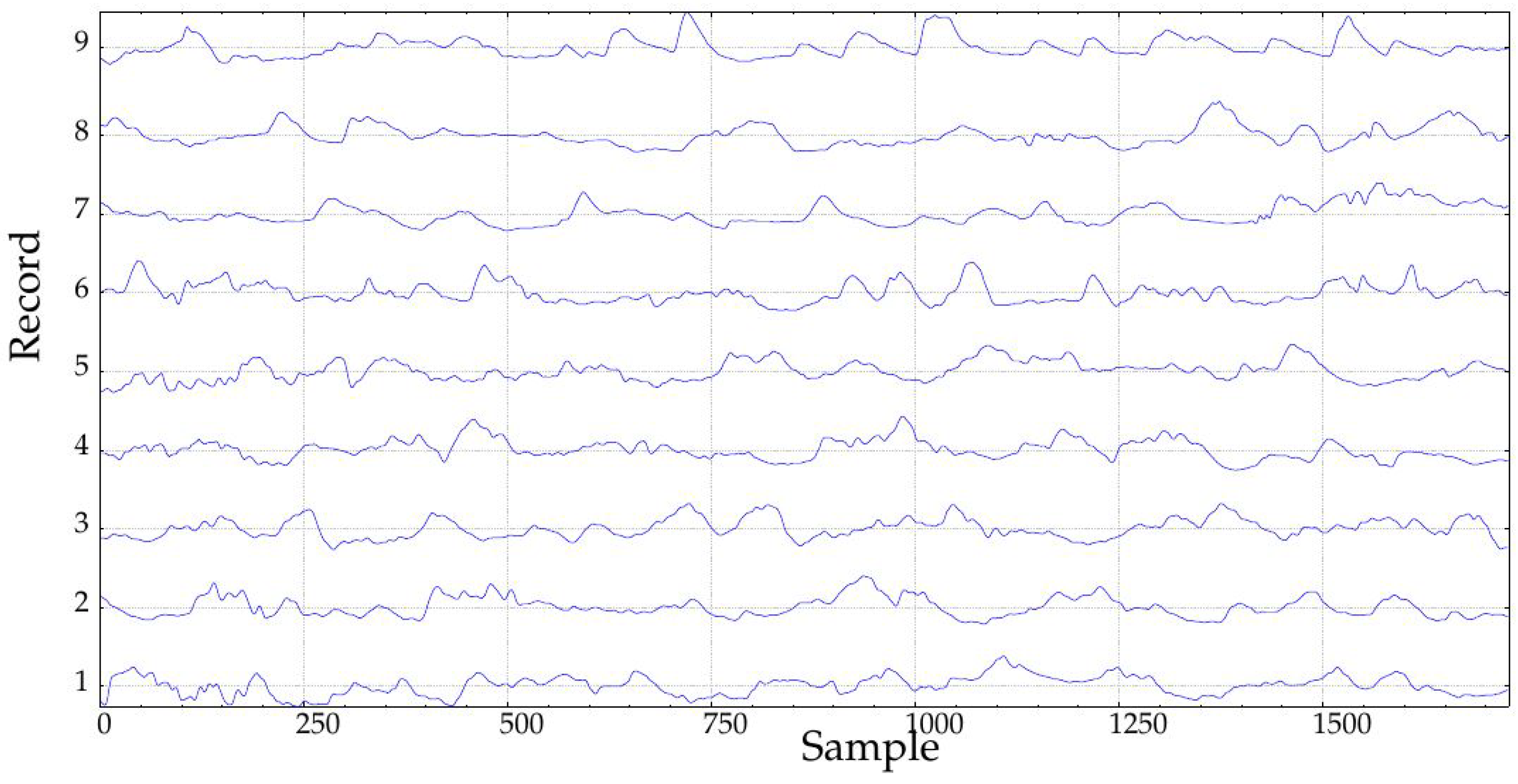
The experimental dataset was recorded at the Third Department of Medicine, Department of Endocrinology and Metabolism, Charles University in Prague, Czech Republic. This database contains 91 records of 30 diabetic patients that underwent a duodenal-jejunal bypass liner implantation. Records contain measurements at baseline (before implantation), 1 month and 10 months later and 3 months after removal. Durations span from a few hours (796 samples being the shortest) up to more than 6 days for a few records (2022 samples being the longest), with a sampling period of 5 min. Sensors had to be recalibrated twice per day, mainly at the beginning of the recordings, and that is why possible border effects were likely to be present during the first hours or even days of the recordings due to the learning curve.
In this study, only records obtained during the implantation (at Month 1, class A1, 24 records, and at Month 10, class B1, 23 records, 47 in total) were studied (
Figure 2). The rationale of this selection was to study the possible effects of such implantation. In the seminal endocrine study [
44], many physiological characteristics exhibited significant differences that could be arguably translated into measurable glucose control changes from A1 to B1. Specifically, that study assessed the influence of The Duodenal-Jejunal Bypass Liner (DJBL) on anthropometric parameters, glucose regulation and the metabolic and hormonal profile of diabetic obese patients. All the subjects experienced a significant body weight, waist circumference and body fat reduction, starting at one month after implantation, which further progressed until the 10 month. Glucose variability decreased during the period from the first month until the 10-month follow-up, which can be related to changes in glucose complexity or dynamics, as studied here [
52]. This effect was lost after DJBL removal, and that is why only classes A1 and B1 are analyzed in the present study. Fasting plasma insulin and C-peptide concentrations also decreased during that period. Other changes can be checked in [
44]. Of all 47 records, 36 corresponded to the same subjects (18 in each class). Incomplete pairs were therefore discarded. Additionally, paired tests always need less subjects [
53]. The percentage of missing samples in these records was close to 10% in the worst case, with a few records with no missing samples at all. Further details of this database can be found in [
44].
4. Discussion
This study analyses the impact of the typical artifacts found in blood glucose records on the class segmentation capabilities of SampEn and its derivative FuzzyEn. The influence of the parameters is practically removed by a grid search of the optimal configuration for the purpose of each experiment.
The main metric to quantify the performance of the methods was AUC, including a statistical significance assessment for some cases, an LOO cross-validation, and a global classification accuracy score for the optimal configuration. AUC is a very popular metric to assess the performance of a classifier due to its simplicity, robustness (insensitive to class asymmetry) and straightforward interpretability: if a classifier A has a greater AUC than a classifier B, A has a better average performance than B [
46]. AUC quantifies the classifier’s ability to avoid false classification [
60], with a performance threshold for random guessing of 0.5. In other words, the closer AUC is to 1.0, the better is the expected performance of the classifier.
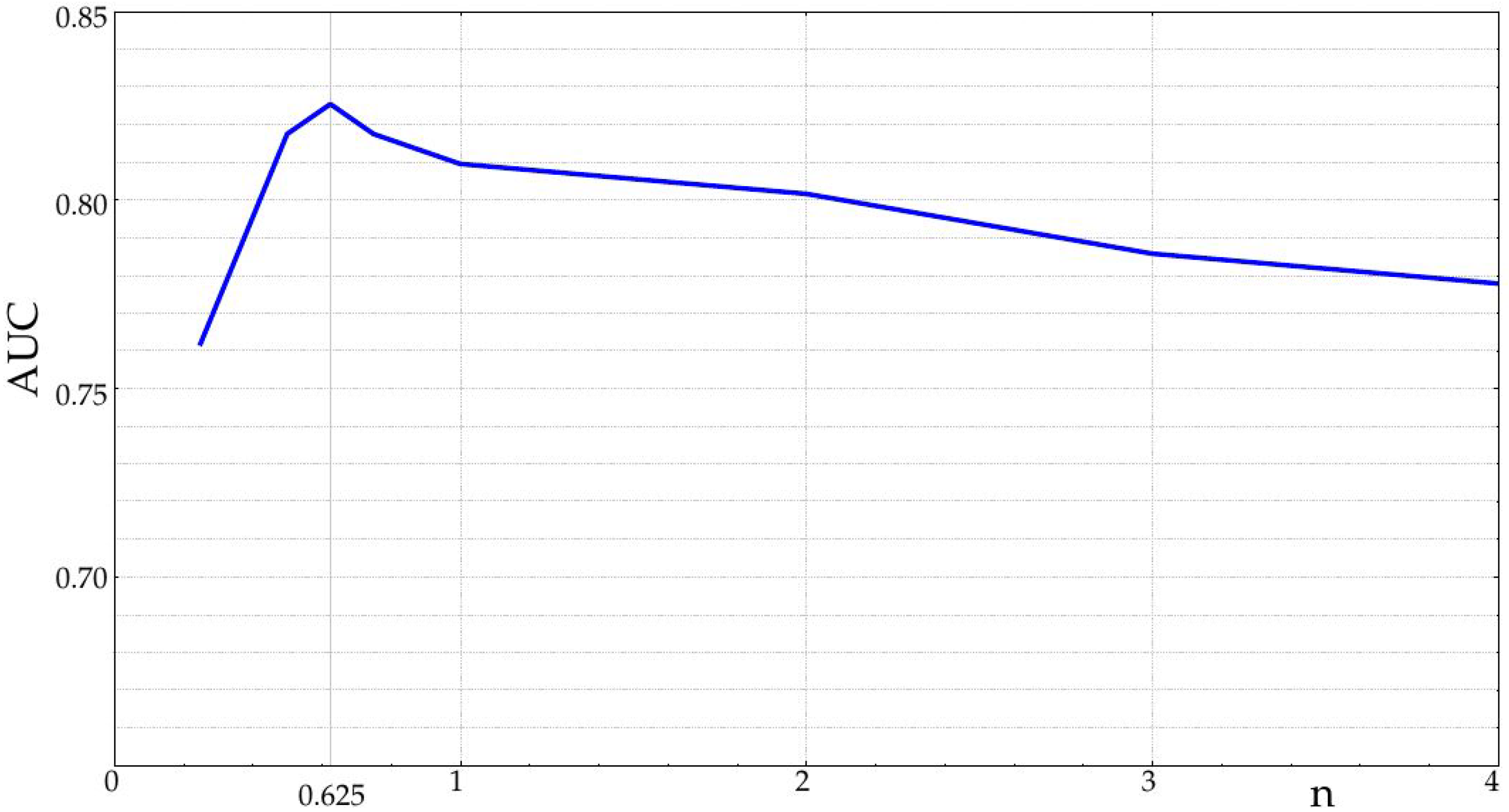
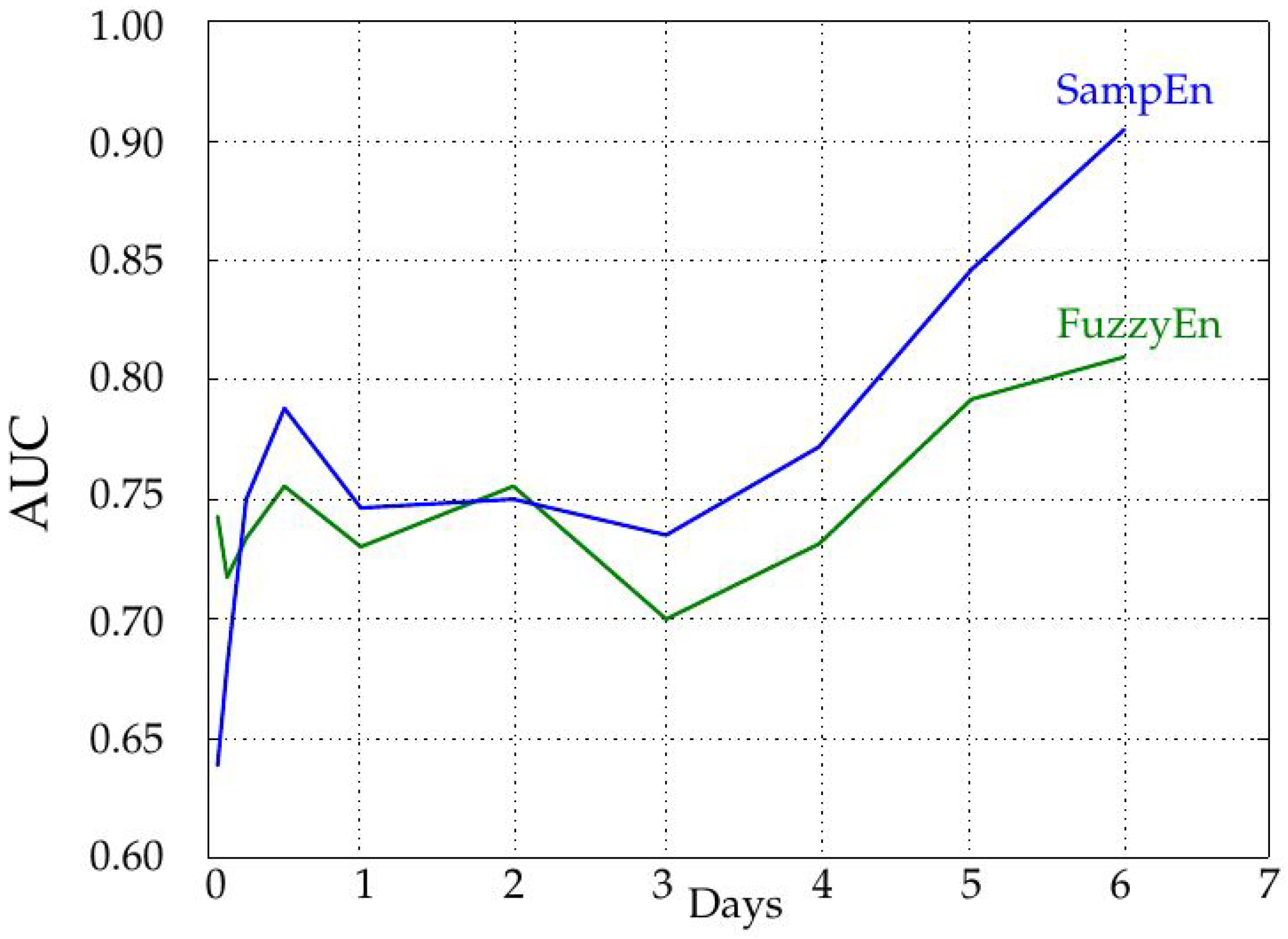
The influence of the record length was characterized by increasing the number of samples used in the entropy calculations in steps of 288 samples, that is one day. As depicted in
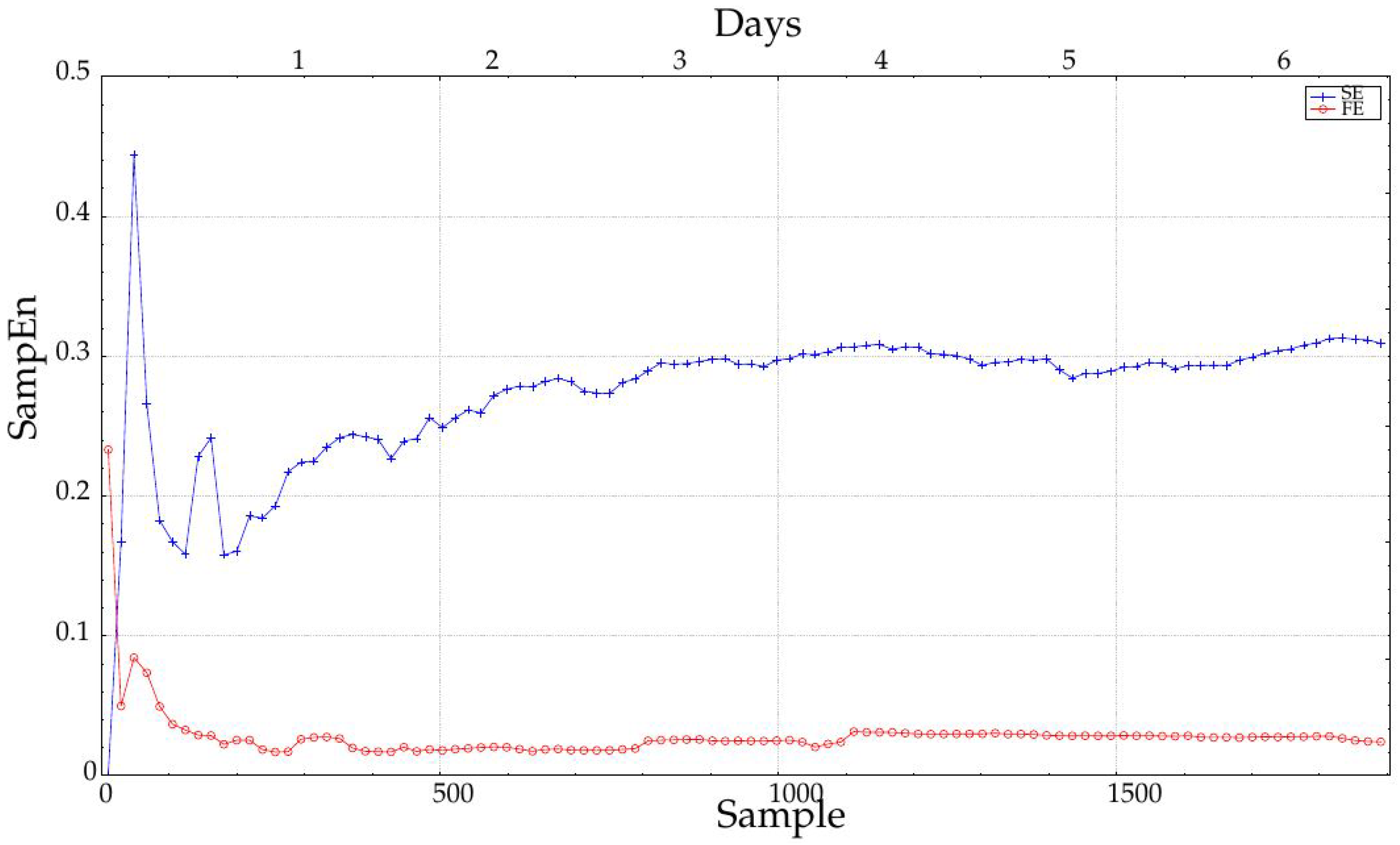
Figure 5, the longer the record, the higher the AUC, and therefore, the more separable the two classes are. The AUC remains more or less constant up to four days, and then, it increases significantly. This could be due to the achievement of a length that enables a more robust entropy estimation (greater than 1000 samples), as recommended in some works [
7] and visually justified in
Figure 8. However, it does not mean SampEn or FuzzyEn are not usable at short lengths, because the important feature is the dissimilarity between entropy values from each class, not their absolute values. In any case, SampEn yields better results than FuzzyEn for all the lengths except for extremely short records (only 18 or 36 samples). It is important also to note that records were cut from data at the center of the entire available records to avoid possible border effects and ensure more data stability.
The presence of one-sample gaps in the time series did have a significant impact on the separability of the two classes under analysis. Both metrics worsened their performance at each step, although FuzzyEn appeared to be a little bit more robust. Arguably, it can be hypothesized that these missing samples may hinder the classification of blood glucose records, and they should be avoided, if possible, or filtered out with some kind of interpolation. For real interference levels of 10%, the separability becomes very poor, even for a baseline AUC higher than 0.90. It is also important to note that this analysis was carried out in terms of classification performance, not in terms of changes in absolute entropy values, which surely took place [
43].
Sensor saturation is another record disturbance that also significantly damages classification performance. Even for very short saturated epochs (60 samples, five hours at one sample per five minutes, 3.5% of the six-day records), the two classes become almost undistinguishable. This is also another quite frequent issue in most blood glucose records, and it is almost impossible to remove using signal processing techniques, since the real signal cannot be reconstructed. Therefore, this disturbance should be detected and corrected as soon as possible at the acquisition stage.
The possible effect of the specific time window on the analysis is quantified in
Table 7. Time windows of three days were taken from the beginning of the records of at least six days long of the experimental database, and the calculations of SampEn and FuzzyEn were repeated for all the possible windows, shifted one day in each case, with two days overlapping. This experiment was devised to find out if the global differences found were due only to non-stationary changes, or if the differences were regularly distributed along the entire records. Although class differences are fairly significant in most of the epochs analyzed, there is a clear trend towards higher differences at later stages. This may be due to a more stable glucose monitoring, a better device calibration or just a correlation with the learning curve linked to the whole process of CGM. It is important to note, however, that the beginning of the records seems to be the most unreliable part in terms of class segmentation, namely there seems to be a border effect on CGM records that should be avoided during analysis.
In all cases analyzed, the class separability was higher using SampEn. Even skipping the subsequence mean normalization stage in FuzzyEn, the SampEn performance was higher, which means that this type of record requires a sharp dissimilarity function. The input parameters were quite consistent and stable. As for m and r, there was small intra-class variability, with optimal values close to for SampEn, for FuzzyEn and for both. The optimal n obtained for FuzzyEn was very low, .
5. Conclusions
There are no standardized metrics for CGMS evaluation and perhaps different goals on different patients may require different metrics. Specifically concerning complexity, it is crucial to choose the right complexity metric, optimize its parameters and analyze the influence of sample length, missing data, sensor saturation and time offset. This is precisely the goal of the present paper. We assessed the metric’s discriminating power comparing two time series of a sample of patients before and 10 months after undergoing a therapeutic maneuver (DJLB) known to modify glucose metabolism, and we evaluated if and how these metrics were able to detect those changes.
CGM data are an extremely useful source of metabolic information with a myriad of current and future applications. However, records are usually very short and noisy, mainly in terms of missing samples and sensor saturation, and these artifacts may arguably interfere with the correct interpretation of the results using the otherwise successful entropy features. This study was aimed at characterizing the changes induced by such artifacts, enabling the arrangement of countermeasures in advance.
As expected, record length is pivotal for a reliable entropy assessment of the records. Although classification potential was always higher than 0.75, even for 288 samples, measured in terms of AUC, more robust results were obtained for longer records. In any case, we would recommend not to use records shorter than 24 h, since it is important to cancel out the chronobiological effects on the glucose dynamics, for example sleep and the fasting periods and meals during the day. For shorter series, it would be necessary first to characterize these chronobiological effects.
Missing samples seem to interfere significantly with the estimation of the underlying dynamics in glucose time series. Even with a very low ratio of 2.5%, there was a significant reduction of the AUC obtained, and this reduction was consistent along all the ratios tested. As for relatively usual higher ratios of 10% missing samples, it could become impossible to distinguish between the two classes. Fortunately, this artifact can be easily removed by just interpolating the missing samples, and this should be a routine procedure in the preprocessing stages of this kind of biomedical record.
The saturation of readings is also a usual disturbance in CGM data. A single epoch of six saturated consecutive values in the entire 1728 sample record has a great impact on the AUC, greater than that of missing samples. Moreover, this artifact is very difficult to remove since it would entail the reconstruction of the missing values. As a consequence, it would be advisable to implement some kind of alarm to detect this situation and implement corrective measures as soon as possible, during the acquisition stage.
Time offset is another key element to ensure proper interpretation of the class separability. The beginning of the records is less powerful in this regard, whereas the maximum separability is achieved at later stages. It is well known that initial calibration and sensor stabilization may cause border effects in these recordings, but more recordings, including timestamps for events, would be necessary to find out exactly what are the factors influencing this trend. As a general recommendation, the longer the records, the better, and if possible, discard the initial samples for analysis.
As for the statistics employed, SampEn outperforms FuzzyEn in all cases. Despite being an evolution and improvement, FuzzyEn does not achieve the AUC obtained with SampEn, in contrast with previous works [
42], where FuzzyEn was clearly better. This means that derivatives are not necessarily always more effective than the original metrics, and more characterization studies would be necessary to define the optimal application domains in each case. However, despite the limitations of CGM data, classical regularity estimators can successfully be applied, as with other biomedical records.