1. Introduction
The relevance of heat devices optimization and the searching for global properties of energy converters is increasing due to a growing need of energetic requirements; not only for a better use of available energy, but also for maintenance cost, operation life-time, scale related control issues, etc. All these problems involve entropy production (
), heat waste, power output (
P) and efficiency
[
1,
2]. Along with maximum power and maximum efficiency or minimum entropy production, compromise based figures of merit have been found very valuable in the optimization analysis of heat devices [
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19]. In this framework, the so-called
function, defined as
, was proposed, offering useful insights since it represents a trade off between maximum power gain (
) and minimum power loss (
), with respect to the minimum and maximum available power output for a heat engine. Besides, it is easy to implement in any energy converter, isothermal or non-isothermal, because it does not require the explicit evaluation of the entropy generation, and it is independent on environmental parameters.
Recently, it has been pointed out that the problem of local stability of operation regimes can be related with the regime’s optimization itself [
20,
21]. Thus, the effects of external perturbations on the operation regime and on the energetic properties such as power output, efficiency and entropy production, can be addressed. A natural question arises: Could entropy give us information to distinguish particular behaviors inside the operation regimes’ basin of attraction? Recent papers have explored this question using a somewhat simple model, the so-called low-dissipation heat engine (LD-HE), which departs from a first order approximation in the entropy generation of irreversible heat devices [
5,
22,
23,
24]. Despite its simplicity, this model can be related with more complex heat engines’ models [
6,
25,
26,
27,
28,
29,
30,
31,
32,
33,
34]. These studies do not consider any specific information on the nature of the heat conduction mechanism but focus, instead, on dissipation and operation time symmetries, along with temporal constraints. Thus, due to its broad generality and independence of any heat transfer law, the low-dissipation approximation could be useful to provide general thermal properties for a variety of heat devices models in connection with its stability.
Among the mentioned connections of the low dissipation model, several scales are involved, from macroscopic models to microscopic ones. However, few systems have been analytically solved and limited precision in the control variables remains as an open question, being this the rationale for this stability study. In fact, in [
35], it has been pointed out the lack of a systematic and quantitative description of how limited control affects the performance of heat engines. This problem is closely connected with some recent works regarding power fluctuations and large efficiencies (see, for example, [
35,
36,
37]). In a related line of thought to this work, Pietzonka and Seifert proposed constancy as an additional ingredient in optimization [
36].
Since the specific mechanisms that cause heat flows in LD-HE’s models are unknown, for the study of local stability, we introduce ad hoc restitutive forces to perform such stability analysis. In fact, different restitutive forces are associated with different system’s dynamics and stable points characteristics, as discussed in References [
20,
21]. This work focuses on the simplest case of restitutive forces, linearly dependent on deviations from the stationary state in power output and output heat flux released to the cold heat reservoir. Such forces yield a rich dynamics of the basin of attraction in terms of the symmetries and the external bath temperatures. Consequently, a relevant behavior on the entropy trajectories is observed in connection with the two optimized operation performance regimes.
The work is organized as follows. For self contained purposes,
Section 2 summarizes some previous relevant results related with the LD-HE and the maximum power (MP) and maximum Omega (M
) operation regimes. In
Section 3, the stability dynamics and the main characteristics of the basin of attraction in relation with irreversible and endoreversible behaviors are analyzed. In
Section 4, a comparison of the evolution behavior of entropy production, power output and efficiency when the system evolves toward: (a) the stable point; or (b) the nullcline and eventually diverging to a nonphysical, no-heat engine state. Finally, some concluding remarks are presented in
Section 5.
2. Low Dissipation Model and Maximum Power and Omega Regimes
The low-dissipation approximation considers a first order irreversible depart from a Carnot cycle. The dissipation occurs in the contact with thermal reservoirs. As usual, the adiabatic processes are consider as instantaneous. Accordingly, the exchanged heat with the cold (at temperature
) and hot (at temperature
) thermal reservoirs are modeled as [
5]:
where
,
are, respectively, the contact times with the hot and cold reservoirs.
is the entropy change of the baseline Carnot cycle along the hot isothermal process; and
,
are the dissipation coefficients, containing all the information regarding intrinsic dissipation properties.
By defining the dimensionless variables
,
and
, being
, the main thermodynamic functions, total entropy production (
), efficiency and power output, can be written dimensionless as follows [
23]:
where ∼ refers to energy weighted by the heat output from the baseline Carnot cycle,
; and the currents are obtained by dividing by the dimensionless total time
. According to the above stated definition, the
function is given by
, whose dimensionless form is
The main results related to power output and Omega function maximization are presented.
In the LD-HE model and do not play a role in the optimization, since involves intrinsic properties of the device. For and given, both MP and M operation regimes accept global optimization through and .
The values that maximize
and
are [
24]
From now on, * indicates the steady-state value at MP or M
conditions. As expected,
is obtained. Depending on the dissipation coefficient asymmetries,
, both efficiencies take values on the following intervals:
where
is the Carnot efficiency. The upper bounds are achieved in the limit
and the lower bounds when
. In the symmetric case (
), both regimes efficiencies are:
where the paradigmatic Curzon–Ahlborn efficiency,
, is obtained for the MP case. On the other hand, efficiency and entropy production only accept optimization through
. For this reason, the M
figure of merit represents a suitable choice to compare the dynamics toward relaxation of the MP regime with another less entropy producing regime.
3. Local Stability
As proposed in [
20], the optimization variables
and
are dynamic variables governed via a dynamic system that considers departures from the stationary state (operation regime). The restitution forces are model as functions of
and
. The currents associated to
and
are [
20]:
To guarantee stability,
f and
g must be monotonically decreasing functions fulfilling that in the stationary state
. The simplest way to guarantee this [
38,
39,
40] is by assuming that the dynamics is described by the following linear ODE system with respect to
and
:
where
C and
D are positive constants and give the strength of the restitution forces, the larger they are, the fastest the system will evolve.
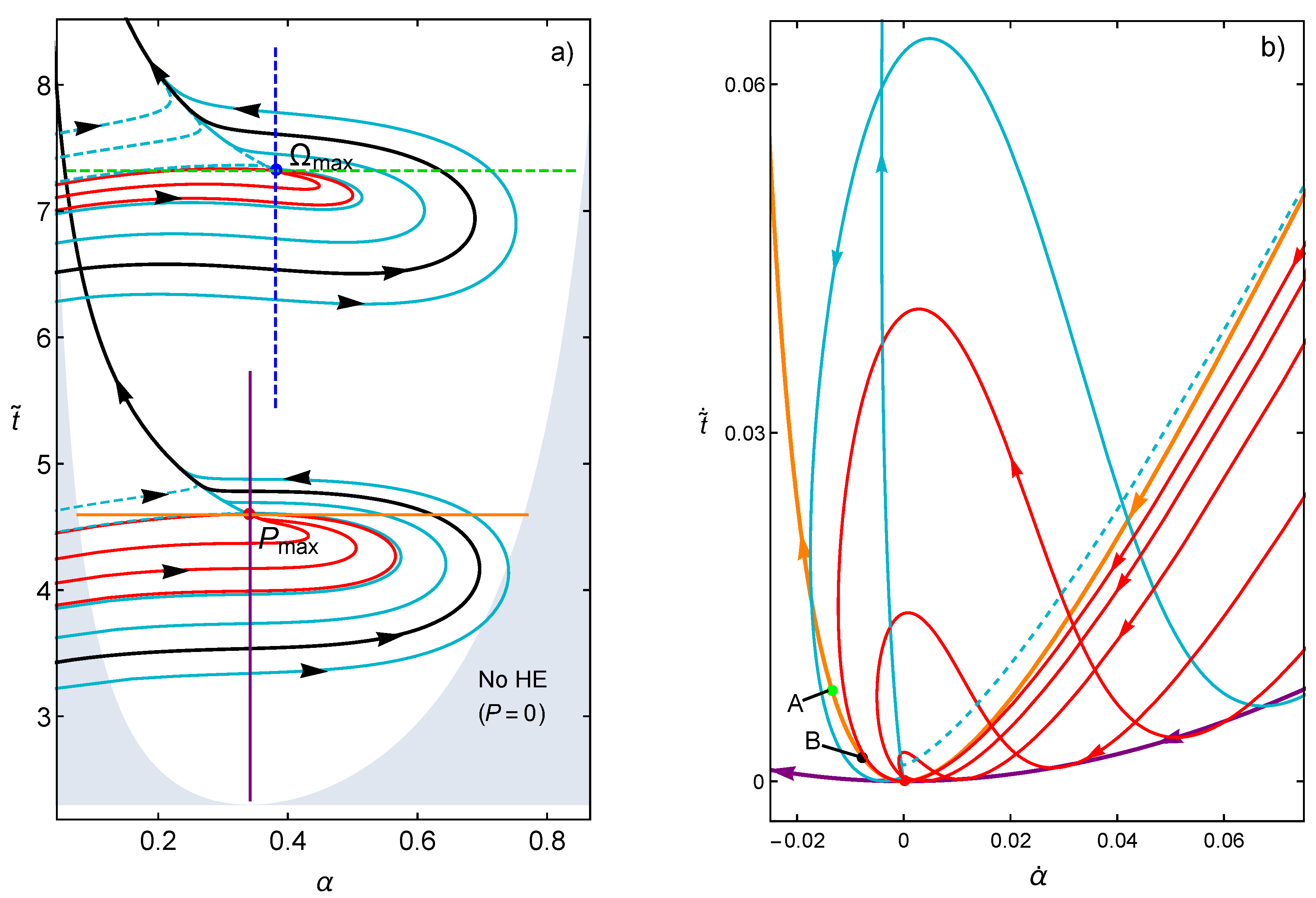
In
Figure 1, representative trajectories around the stationary state are plotted by solving Equations (
15) and (16). The main feature is the existence of a well defined basin of attraction with a rich dynamics around the stable point. In
Figure 1, three kind of curves are explicitly denoted. The red curves evolve to the stationary state while the rest of the curves evolve to the nullcline where
, either from the left (dashed blue curves) or from the right (solid blue curves). A black curve is shown as a representative case of a trajectory that surrounds the stability basin. The thermodynamics behavior in the three kind of trajectories are by no means obvious, and the influence of time constraints, as shown below, could indeed have relevant information on this regard.
In
Figure 1, vertical and horizontal lines for constant values of
or
, respectively, are also explicitly labeled in both cases. In Reference [
41], it is shown that these time constraints reproduce open and closed behaviors for the power vs. efficiency curves, typical from endoreversible (all irreversibilities coming from the coupling to external heat thermal baths) and irreversible (including irreversibilities coming from heat leaks and internal dissipation) heat engines. In
Figure 1b, the evolution of the same trajectories is shown in the
vs.
plane. The endoreversible limit comprise the points where for the same velocity in
, one obtains the smaller velocity in the operation time
(which is related to the irreversibility of the system). Notice how, as the system evolves, the trajectories tend to reach the endoreversible limit first, after that those evolving in the basin of attraction (red color) enter into a dynamics bounded by the irreversible limit while some trajectories arriving as the nullcline (blue color) can cross this limit.
The influence of the irreversible and endoreversible limits on the dynamic evolution of the system are further addressed in the next section, which contains a thermodynamic analysis of the relaxation trajectories to find the characteristic energetic behaviors associated with the basin of attraction.
4. Entropy, Efficiency and Power Evolution Toward Relaxation
The role of entropy and internal energy as stability criteria in thermodynamics is well known. In what appears a separate subject, the goal of optimization of energy converter is focused in obtaining the larger efficiencies and power-output with the less entropy generation, with the simultaneous optimization of the three quantities being an impossible task. In this section, we show that stability favors, to some extent, the simultaneous optimization of the three thermodynamics functions.
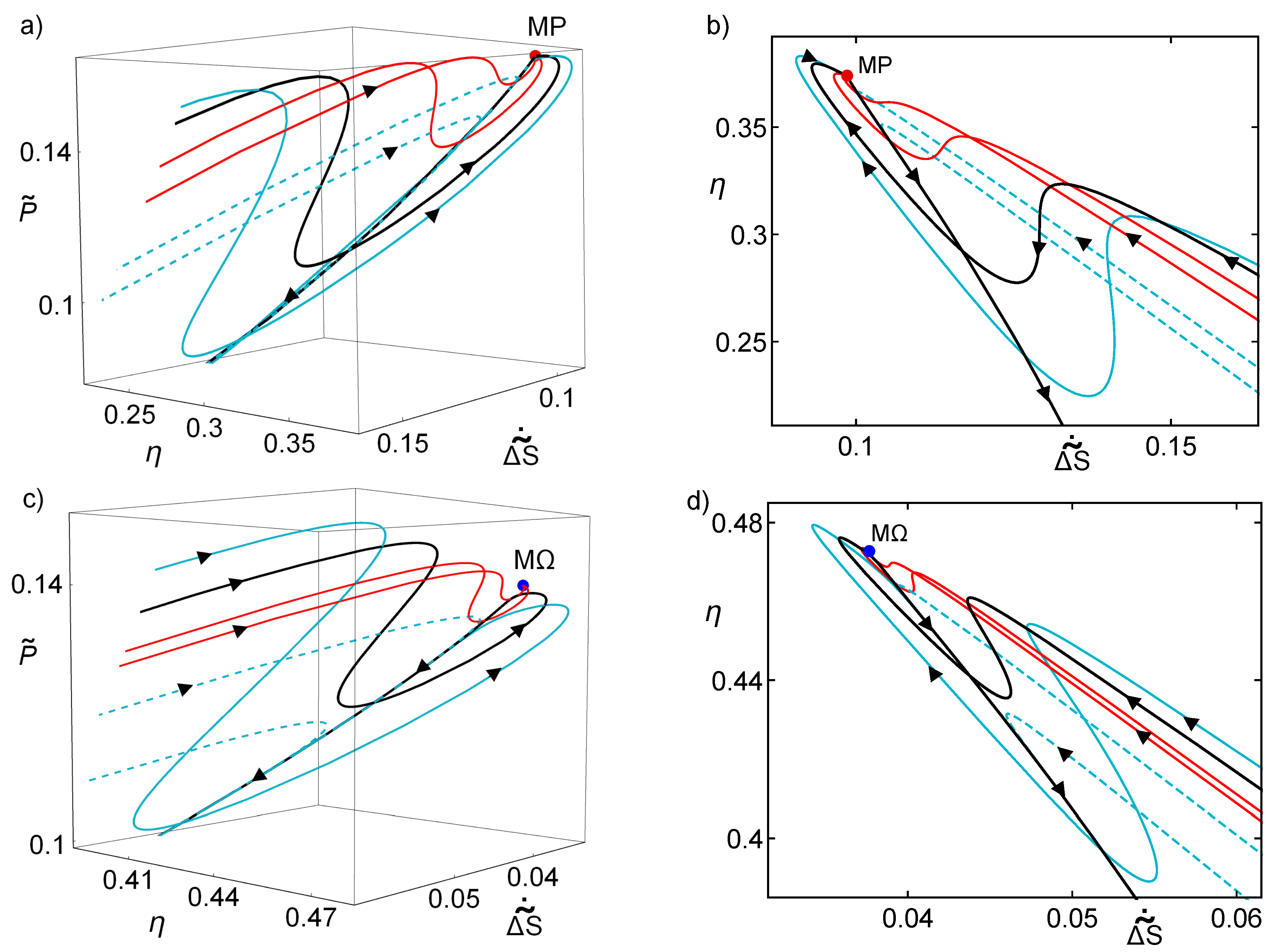
By solving numerically Equations (
15) and (16), the trajectories
can be computed and, by substituting them in Equations (
3)–(
5), the evolution of
,
and
in the relaxation after a perturbation on the system is obtained. These trajectories are depicted in
Figure 2 over the
–
–
surface.
Figure 2a,b shows some of these trajectories around the MP state and
Figure 2c,d shows some trajectories around the M
state. The difference between
Figure 2a,b is only the view point, the latter making emphasis in the relation between entropy and efficiency. The same is done for
Figure 2c,d for the M
regime. As in
Figure 1, blue continuous curves are those that go around the basin of attraction and arrive to the nullcline
, the black curve represents one of them, that orbits close to the stable point but do not converge to it. The dashed trajectories involves perturbation where
and arrive to the nullcline from the opposite side. Red trajectories are inside the basin of attraction for the MP state and they converge to the stationary state.
The dynamics around the MP stable point is such that, far from it, the solid blue curves evolve toward the upper values of
in trajectories of increasing efficiency and decreasing entropy (more noticeable in
Figure 2b). The curves start to orbit states of larger power while moving to the true MP state. In these oscillations, there are drops of power and efficiency and an increment of entropy. After one last oscillation that misses the stable point, the curves decay toward the nullcline in a trajectory where power output and efficiency decrease, and entropy production increases, finally ending in the no-HE region where the power output and efficiency are negative.
On the other hand, the dashed blue curves are such that they enter directly into the nullcline. The trajectories inside the basin of attraction follow the same dynamic as the blue curves but they present one small oscillation with a small power and efficiency drop and they rather enter into an orbit that quickly drives them to the stable point. These small drops of power and efficiency and very small increment of entropy, which only occurs close to the stable point, could be indeed the true difference between the states inside the basin of attraction and those states that evolve toward the nullcline.
The dynamics on the M
regime follows a very similar pattern, as depicted in
Figure 2c,d. The evolution of the curves still present oscillations over values of the power output, even when the fixed point is not the MP. A distinctive feature is that the trajectories are more lined and with a narrower basin of attraction. Notice that, when comparing with the MP results, the M
regime implies smaller entropy production trajectories and higher efficiency, in agreement with the bounds accounted for Equations (
9) and (10) for high asymmetries and Equations (
11) and (12) for the symmetric case. Notice in
Figure 2c,d the different scales in entropy and efficiency with respect to
Figure 2a,b
Therefore, all the above provides a firm basis to consider that stability could be linked to a compromise of performance among , , , in what we can call a thermodynamic “self-improvement” in the process of relaxation, with the smallest possible fluctuations on the performance of the engine.
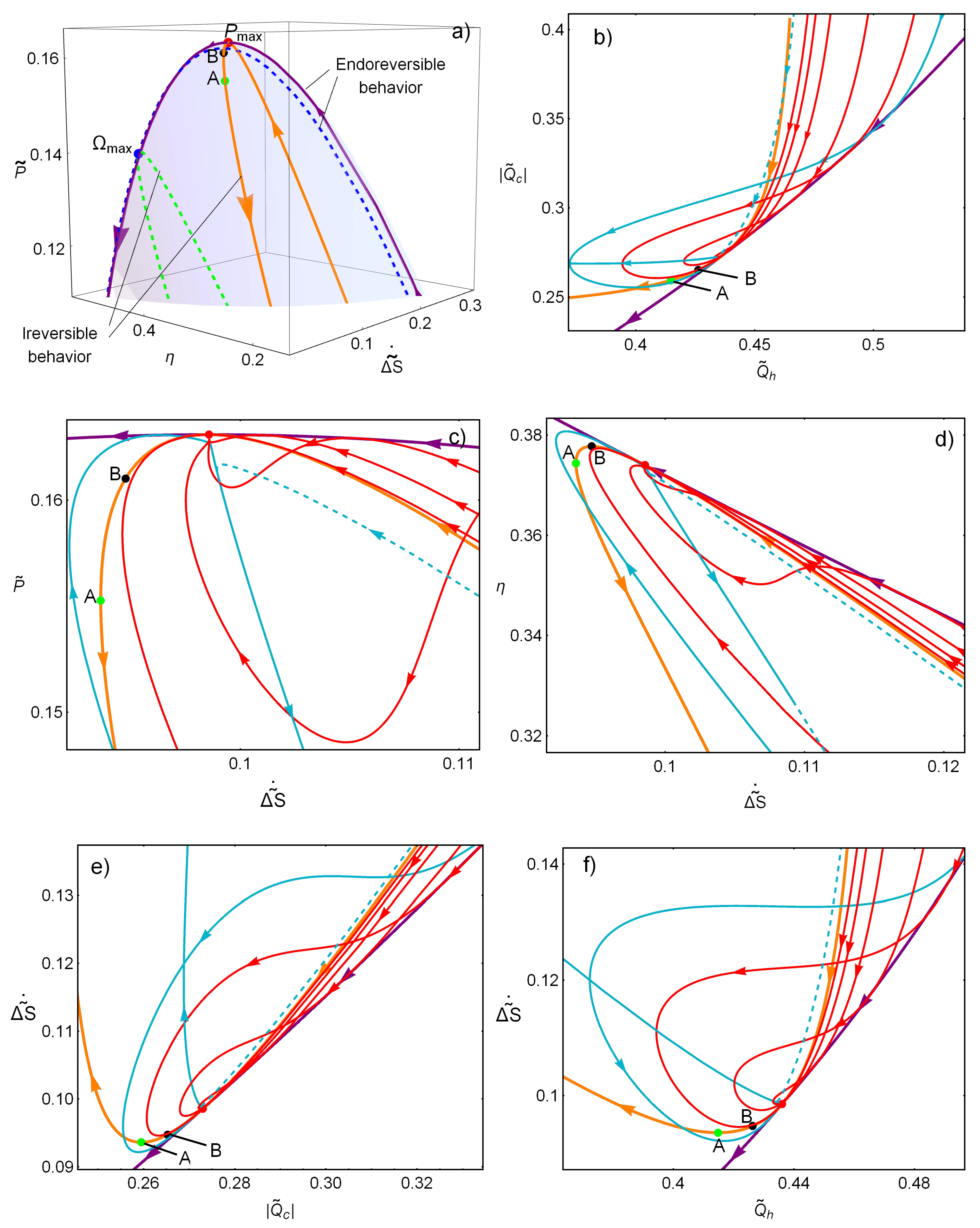
An interesting feature results from comparing the relaxation trajectories with the open (endoreverversible) and closed (irreversible) behaviors depicted in
Figure 3a, where the irreversible and endoreversible limits are displayed over the surface
-
-
, in continuous lines for the MP state and in dashed lines for the M
state. Both curves cross at the MP state, however, the irreversible limit displays, additionally, points of minimum entropy production (labeled as
A) and maximum efficiency (labeled as
B). The orientation of the arrows indicate the direction at which either
or
increase (from 0 to 1, and from 1 to
∞, respectively). It can be noticed that these times constraints are not arbitrarily located with respect to the trajectories on the basin of attraction.
As explained above, regarding
Figure 1b, far from the stable point, all trajectories tend to reach the endoreversible limit (given by the constraint
), while, near the stationary state, the trajectories are bounded by the irreversible limit given by
. The reason for this is a hierarchy/distinction in the relaxation behavior due to a thermodynamic self improvement attached to the stability dynamics. In the linear approximation (near the stationary state), it was obtained that the stability depends only on the relaxation of
[
24], corresponding to the time constraint depicted in
Figure 1a (horizontal line with
). Thus, trajectories in the basin of attraction are bounded by the irreversible limit; on the other hand, far from the stationary state, the trajectories display a preference for the endoreversible limit, which offers a number of advantageous features.
The preference to evolve toward the endoreversible limit can be understood by looking into
Figure 3b–f which apply for the MP regime (although the results are also valid for the M
state). In
Figure 3b, the endoreversible limit denote the lower value of heat waste for any given heat input. In
Figure 3c,d, the endoreversible limit gives the larger power and efficiency for a given entropy production.
Figure 3e,f shows that, additionally, it gives the lower entropy production for given heat output and input, respectively. Thus, the system evolution reveals a preference for a better compromise displayed by the endoreversible configuration, and the time constraints influence in a major way the dynamics toward relaxation.
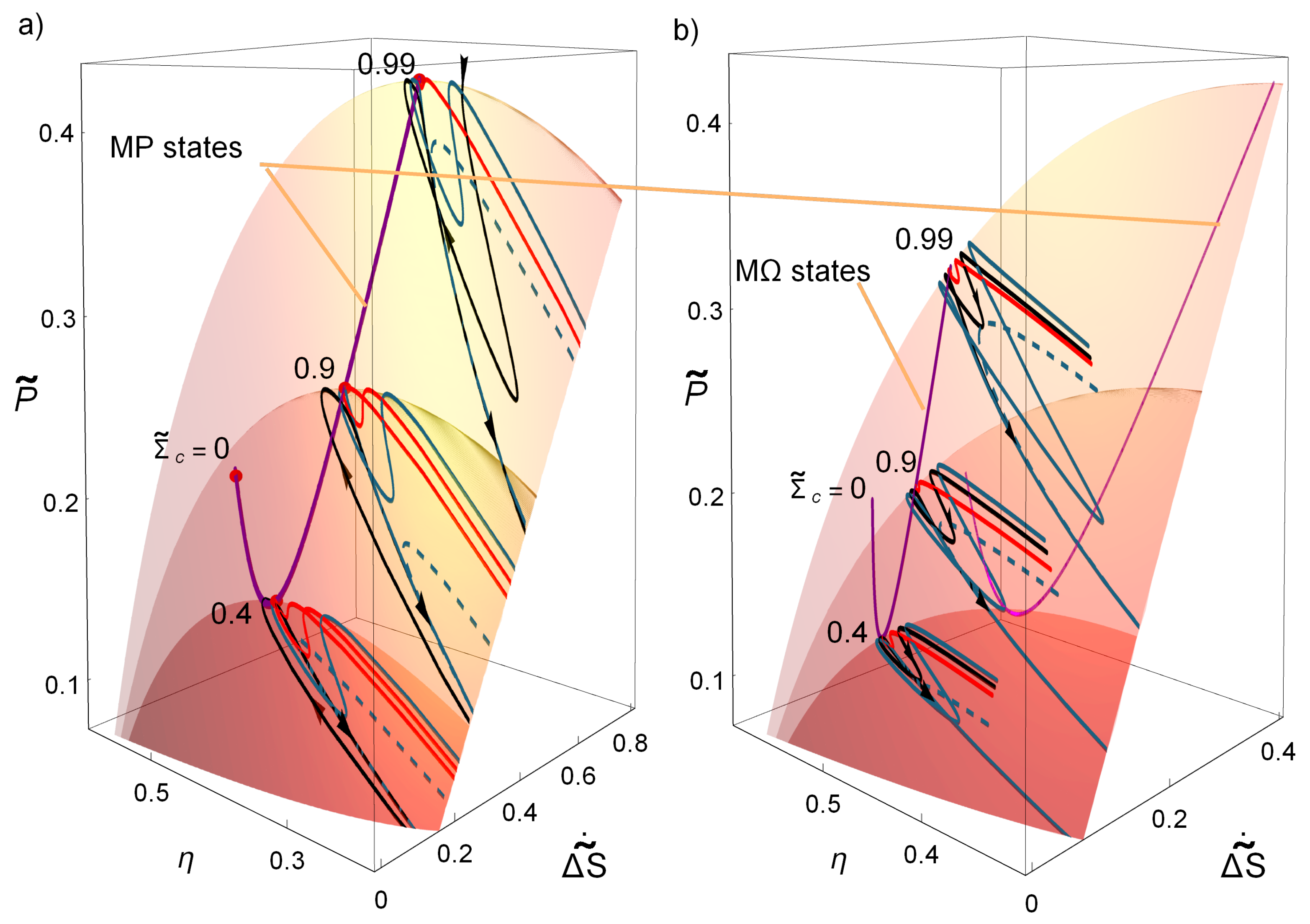
Next, the influence of the asymmetries keeping a fixed thermal gradient it is presented.
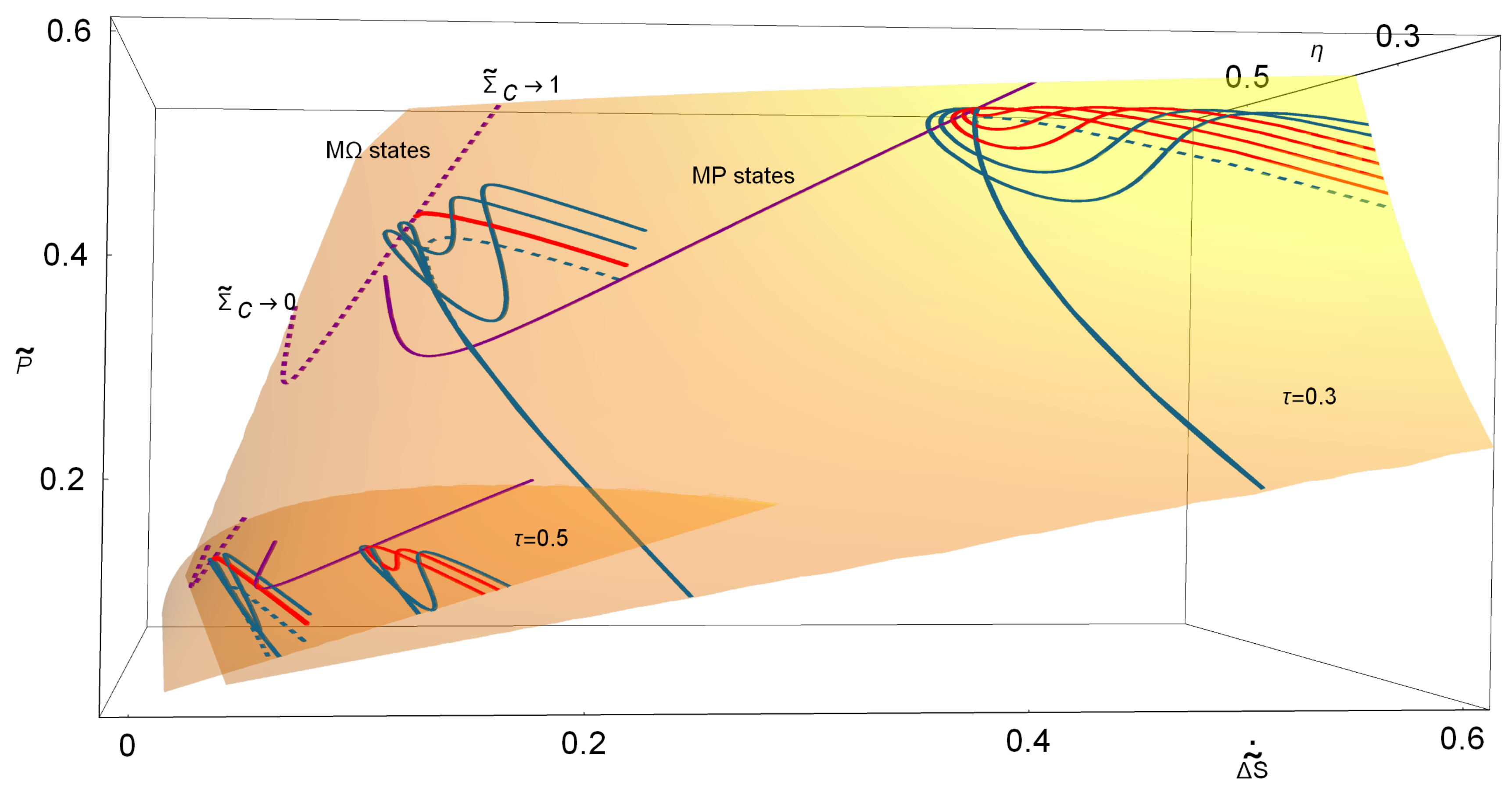
Figure 4 shows the
,
,
surfaces for three cases of
and for all possible values of
and
; in
Figure 4a for MP and in
Figure 4b for M
. Over the depicted surfaces lies the curve of MP states for all
(purple curve). The three MP states
represented in the figure have their own dynamics toward the stable point. Some representative trajectories are displayed over each surface. In this figure, it is noticeable that relaxation trajectories are more likely to evolve in the direction of increasing power and efficiency and decreasing entropy. Those arriving to the stable point, as stated above, have the smallest variations in entropy and efficiency, while all the trajectories arriving to the nullcline evolve to states of less power, less efficiency and larger entropy production. Thus, systematically in the search for the true MP, the orbits around the stable point always search for more “convenient” thermodynamic states. It can be also seen in
Figure 4 how larger values of
produce narrower basins of attraction, thus yielding trajectories with less variations of power output, efficiency and entropy production. The M
states, in comparison with MP states, have a better energetic evolution (less drops) but with the cost of having more constrained states.
Finally,
Figure 5 shows the difference on the dynamics when different thermal gradients are considered. As
decreases the surface where the evolution is held diminish its area and the trajectories are more leaned. As the thermal gradient is larger, the basin of attraction accepts larger perturbations but the nature of the trajectories is the same.
5. Conclusions
The analysis of the dynamics behind local stability of operation regimes, such as maximum power and maximum functions, reveals a feature that recently has started to gain certain attention: stability/constancy of heat devices should be considered as an additional ingredient in the optimization of heat devices; and there exists a kind of trade-off among stability, power output and efficiency. Here, the entropy production is added as another relevant aspect to consider.
It has been found that, for irreversible processes obeying the small dissipation assumption, the stability basin is associated with thermal behaviors of simultaneous improvement of the main thermodynamics quantities, power, efficiency and entropy, as well as small drops of their performance. A comparison of the relaxation trajectories with the open and closed P vs. behaviors of endoreversible and irreversible heat engines reveals that, far from the stable point, the trajectories tend to evolve to the endoreversible limit case, while, close to the stable point, the evolution occurs inside the region delimited by the irreversible limit behavior, and all trajectories crossing this boundary will diverge to a non-physical state. These qualitative behaviors apply for every value of the dissipation coefficient and for any thermal gradient, given by , although small numerical differences can be observed for concrete numerical values of these parameters.